Open Access Article
Open Access ArticleFirst-principles spectroscopy of aqueous interfaces using machine-learned electronic and quantum nuclear effects
Venkat
Kapil
 *a,
Dávid Péter
Kovács
*a,
Dávid Péter
Kovács
 b,
Gábor
Csányi
b,
Gábor
Csányi
 b and
Angelos
Michaelides
*a
b and
Angelos
Michaelides
*a
aYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: vk380@cam.ac.uk
bEngineering Laboratory, University of Cambridge, Cambridge, CB2 1PZ, UK
First published on 20th July 2023
Abstract
Vibrational spectroscopy is a powerful approach to visualising interfacial phenomena. However, extracting structural and dynamical information from vibrational spectra is a challenge that requires first-principles simulations, including non-Condon and quantum nuclear effects. We address this challenge by developing a machine-learning enhanced first-principles framework to speed up predictive modelling of infrared, Raman, and sum-frequency generation spectra. Our approach uses machine learning potentials that encode quantum nuclear effects to generate quantum trajectories using simple molecular dynamics efficiently. In addition, we reformulate bulk and interfacial selection rules to express them unambiguously in terms of the derivatives of polarisation and polarisabilities of the whole system and predict these derivatives efficiently using fully-differentiable machine learning models of dielectric response tensors. We demonstrate our framework's performance by predicting the IR, Raman, and sum-frequency generation spectra of liquid water, ice and the water–air interface by achieving near quantitative agreement with experiments at nearly the same computational efficiency as pure classical methods. Finally, to aid the experimental discovery of new phases of nanoconfined water, we predict the temperature-dependent vibrational spectra of monolayer water across the solid-hexatic-liquid phases transition.
1 Introduction
Vibrational spectroscopy is one of the most sought-after techniques for visualising the structure and dynamics of water. These approaches provide insights into complex interfacial phenomena such as the pH of the surface of water,1 the quasi-liquid layer on ice,2 and the melting temperature of water in ultra-confined cavities.3 Infrared (IR), Raman and sum-frequency generation (SFG) techniques – that provide complementary information on bonding and proximity to surfaces – possess high sensitivity to probe physiochemical properties of interfacial water relevant to numerous technologies like catalysis,4 clean energy,5 batteries,6 and tribology.7 In this respect, atomistic simulations play a central role in facilitating the interpretation of these techniques by providing direct links between structural motifs and their vibrational fingerprints. Traditionally, these simulations are performed at qualitative accuracy using empirical forcefields parameterised on quantum mechanical data and experimental bulk observables.8 Modelling aqueous interfaces with predictive accuracy requires first-principles methods which incorporate the quantum statistical mechanics of the electronic and nuclear degrees of freedom, without relying on experimental input into the models.The state-of-the-art first-principles framework for modelling aqueous interfaces9 combines classical molecular dynamics (MD) and density-functional theory (DFT). These approaches incorporate electronic quantum effects in the potential energy surface (PES)10,11 and dielectric responses12 but cannot describe quantum nuclear effects such as zero-point fluctuations, quantum tunnelling and equilibrium/kinetic isotope effects.13 State-of-the-art IR and Raman predictions include on-the-fly predictions of the total polarization and polarizabilities on classical trajectories. The SFG spectra, which require much longer trajectories to converge, are calculated with a further approximation using a surface-sensitive velocity auto-correlation formula.14 This simplification requires shorter trajectories but neglects the rigorous environment dependence of dielectric response tensors (referred to as non-Condon effects). Ambient-temperature quantum nuclear dynamics can be incorporated with first-principles path-integral (PI) quantum dynamics15,16 and machine learning potentials (MLPs).17,18 However, the PI approach introduces additional computational overhead and provides only semi-quantitative accuracy due to artefacts from approximations to exact quantum dynamics.19 Moreover, the computational overhead and accuracy artefacts become more pronounced as the temperature decreases, systematically worsening accuracy.19 These limitations create a void in the current state-of-the-art for predicting vibrational spectroscopy for aqueous systems such as crystalline and amorphous ice phases and general aqueous interfaces of solid, liquid, and solution phases.
This work presents a new ML-driven framework that dramatically enhances the accuracy and efficiency of full quantum modelling (see Fig. 1) of various vibrational spectroscopic techniques, at finite thermodynamic conditions. Our framework exploits advances in ML for predicting first-principles PES![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 and dielectric response tensors,21–23 at a lower cost than direct calculations. It further incorporates new quantum statistical mechanics methods to map quantum nuclear dynamics to classical MD
20 and dielectric response tensors,21–23 at a lower cost than direct calculations. It further incorporates new quantum statistical mechanics methods to map quantum nuclear dynamics to classical MD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 on an effective PES at greater accuracy and lower computational cost than previous methods. Our approach involves a straightforward training step to fit an effective quantum MLP that includes quantum nuclear effects24 and a physics-based ML model of the systems dielectric responses.17 In the prediction stage, we generate quantum trajectories via classical MD on the quantum MLPs, and predict dielectric response properties or their derivatives to model IR, Raman and SFG spectra rigorously. The ML models of the quantum PES and dielectric responses transfer to other phases and thermodynamic conditions with high accuracy, opening the door to modelling a wide range of bulk and interfacial aqueous systems that were hithertho not possible.
24 on an effective PES at greater accuracy and lower computational cost than previous methods. Our approach involves a straightforward training step to fit an effective quantum MLP that includes quantum nuclear effects24 and a physics-based ML model of the systems dielectric responses.17 In the prediction stage, we generate quantum trajectories via classical MD on the quantum MLPs, and predict dielectric response properties or their derivatives to model IR, Raman and SFG spectra rigorously. The ML models of the quantum PES and dielectric responses transfer to other phases and thermodynamic conditions with high accuracy, opening the door to modelling a wide range of bulk and interfacial aqueous systems that were hithertho not possible.
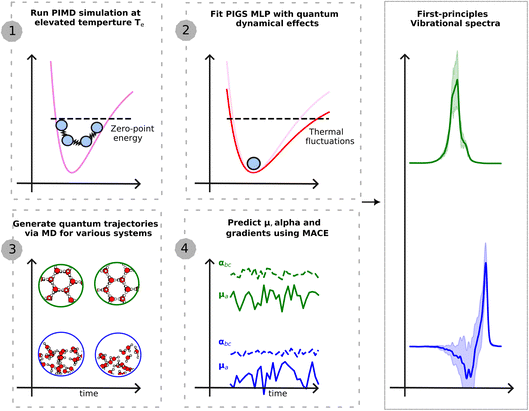 | ||
Fig. 1 Schematic illustration of the presented approach. The first step requires a single PIMD simulation at an elevated temperature to generate training data for a MLP that encodes quantum dynamical effects. We use BPNN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 to perform first-principles-level PIMD simulations. The second step fits the quantum MLP using PI centroid positions and PI centroid forces within the PIGS protocol.24 This potential is transferable to different phases and thermodynamic conditions. The third step generates quantum trajectories by performing classical MD on the quantum MLP. And the fourth step, applied differentiable and equivariant MACE 20 to perform first-principles-level PIMD simulations. The second step fits the quantum MLP using PI centroid positions and PI centroid forces within the PIGS protocol.24 This potential is transferable to different phases and thermodynamic conditions. The third step generates quantum trajectories by performing classical MD on the quantum MLP. And the fourth step, applied differentiable and equivariant MACE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 models of dielectric response functions to generate a time series of the polarization and polarizability and their derivatives. Time correlation functions of dielectric responses (derivatives) yield different vibrational spectroscopy intensities. 26 models of dielectric response functions to generate a time series of the polarization and polarizability and their derivatives. Time correlation functions of dielectric responses (derivatives) yield different vibrational spectroscopy intensities. | ||
We first demonstrate our framework’s capabilities by predicting the IR, Raman and SFG spectra of bulk water and ice with a near-quantitative agreement with experiments, at a much lower computational cost than earlier first-principles studies. Finally, to showcase the potential of our approach, we predict the temperature-dependent vibrational spectra of monolayer water across the Kosterlitz–Thouless-like two-step melting process.25
2 Theory and methods
Within linear response theory, the first-principles vibrational spectrum of a Hamiltonian of nuclei,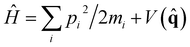 , at inverse temperature β = (kBT)−1 is estimated in terms of the standard quantum time-correlation function27 (TCF)
, at inverse temperature β = (kBT)−1 is estimated in terms of the standard quantum time-correlation function27 (TCF)CAB(t) = Z−1tr{e−βĤÂeiĤt/ℏ![[B with combining circumflex]](https://www.rsc.org/images/entities/b_char_0042_0302.gif) e−iĤt/ℏ}, e−iĤt/ℏ}, | (1) |
Eqn (1) can be understood simplistically as sampling nuclear positions from the system's Boltzmann distribution, performing quantum dynamics of the nuclear coordinates, and estimating the correlation of first-principles dielectric response time-derivatives: A ≡ A(q) on the initial and B ≡ B(q) on the time-evolved positions. The autocorrelation of the positions, i.e. C![[q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0071_0307.gif)
![[q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0071_0307.gif) (t) gives the vibrational density of states without any selection rules, C
(t) gives the vibrational density of states without any selection rules, C![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e153.gif)
![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e153.gif) (t) and C
(t) and C![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif)
![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) (t) relate to IR and Raman intensities respectively,29 and the cross-correlation C
(t) relate to IR and Raman intensities respectively,29 and the cross-correlation C![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e153.gif) a
a![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) bc(t) relates to the second order susceptibility
bc(t) relates to the second order susceptibility 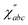 which determines the SFG intensity.30 A first-principles treatment of eqn (1) for aqueous systems typically requires three sequential steps: (1) selecting an electronic structure theory to model the PES and dielectric responses, (2) performing quantum nuclear dynamics on the PES to generate trajectories, and (3) calculating the intensities of vibrational spectra as TCFs of dielectric response functions. Unfortunately, each step presents unique challenges.
which determines the SFG intensity.30 A first-principles treatment of eqn (1) for aqueous systems typically requires three sequential steps: (1) selecting an electronic structure theory to model the PES and dielectric responses, (2) performing quantum nuclear dynamics on the PES to generate trajectories, and (3) calculating the intensities of vibrational spectra as TCFs of dielectric response functions. Unfortunately, each step presents unique challenges.
The high associated computational cost is the main challenge with accurately modelling a system's electronic structure. To this extent, DFT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10,11 is typically the method of choice, providing the best compromise between accuracy and computational cost. DFT avoids the high cost of calculating electronic wavefunctions by defining the ground state energy as a functional of the total electron density.10 While the exact functional remains unknown, approximate non-local functionals of the electron density can exhibit accuracy comparable to more sophisticated wavefunction-based methods.31 For instance, so-called meta-GGA32 or hybrid functionals33 with van der Waals (vdW) inclusions,34 are considered appropriate choices for correctly modelling the PES of bulk liquid water16,32 and its interface with a vacuum.35 Despite their relatively lower cost, DFT calculations are many orders of magnitude times costlier than empirical or first-principles forcefields,36–38 and therefore hinder study of large system sizes and long trajectories. Additionally, selecting an appropriate DFT functional for a new system can require stringent benchmarks,34 typically requiring comparisons with more-accurate correlated electronic structure methods39,40 and experiments.35
10,11 is typically the method of choice, providing the best compromise between accuracy and computational cost. DFT avoids the high cost of calculating electronic wavefunctions by defining the ground state energy as a functional of the total electron density.10 While the exact functional remains unknown, approximate non-local functionals of the electron density can exhibit accuracy comparable to more sophisticated wavefunction-based methods.31 For instance, so-called meta-GGA32 or hybrid functionals33 with van der Waals (vdW) inclusions,34 are considered appropriate choices for correctly modelling the PES of bulk liquid water16,32 and its interface with a vacuum.35 Despite their relatively lower cost, DFT calculations are many orders of magnitude times costlier than empirical or first-principles forcefields,36–38 and therefore hinder study of large system sizes and long trajectories. Additionally, selecting an appropriate DFT functional for a new system can require stringent benchmarks,34 typically requiring comparisons with more-accurate correlated electronic structure methods39,40 and experiments.35
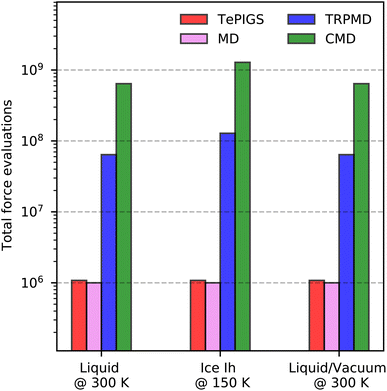
Once a DFT functional is selected, it can be straightforwardly combined with methods to time-evolve the nuclei on the PES. These techniques are typically MD for classical dynamics41 and PI approaches for quantum dynamics.42–45 Unfortunately, both approaches present accuracy limitations19 and have a high cost when combined with electronic structure calculations. For instance, due to the neglect of enhanced zero-point vibrational fluctuations46 and quantum tunnelling,47 classical MD does not fully sample the anharmonic regions of the O–H bond. PI methods, on the other hand, can correctly account for dynamical effects arising from thermodynamic quantum fluctuations.45 At ambient conditions, PI methods provide semi-quantitative accuracy in describing quantum nuclear motion at a modest overhead compared to classical approaches. Unfortunately, as the temperature is reduced, for instance, to study ice, PI methods become systematically expensive,48 and their artefacts lead to worsening accuracy.19 Both classical and PI trajectories can require around a million to a billion force evaluations for converged vibrational spectra (vide infra). Therefore, the total cost of generating trajectories with accurate electronic structure calculations can be very high even for ambient-temperature liquid water16 – arguably the simplest aqueous condensed phase system – and prohibitive for more complex systems.
Finally, evaluating vibrational spectra requires dielectric responses such as polarization and/or polarizabilities along the trajectories.29,30 These quantities can be generated from additional electronic structure calculations or on the fly during the simulation at an additional cost of a density functional perturbative calculation.49,50 Estimating the TCF in eqn (1) for IR and Raman spectra is straightforward, as their intensities are related to total dielectric responses. However, for SFG, which probes the water molecules at the interface, directly evaluating eqn (1) with the total first-principles polarization and polarizabilities of a water slab is problematic as it is a sum of two equal and opposite signals from its two interfaces.51 While this problem may be alleviated using molecular dielectric responses52 and by artificially mirroring the slab35 so that the SFG signals no longer cancel, the molecular identity of atoms is invalid for reactive systems or exhibits artefacts in general. These challenges highlight the need for a general and uniquely-defined expression of SFG intensity.
2.1 Modelling the Born–Oppenheimer PES with machine learning potentials
We first alleviate the high computational cost of modelling the Born–Oppenheimer PES of a system. To this end, we use state-of-the-art MLPs53–55 to predict total energies and forces at first-principles accuracy but at a fraction of their computational cost. MLPs represent the total energy of a system as a sum of atomic energies described as local non-linear functions of radial, angular, or high-order correlations between the neighbours of an atomic species. Due to their local and atom-centred nature, MLPs are transferable, size-extensive and their computational cost scales linearly with system size. These attributes enable training on first-principles total energies and forces of small systems and short trajectories and predictions for longer and larger simulations.56In this work, we use the Behler–Parrinello high-dimensional neural network (BPNN) framework57 for representing the PES of revPBE0-D3 bulk water and its interface with a vacuum. This scheme employs hand-crafted radial and angular symmetry functions for every atom type that encode up to three body correlations as inputs to a shallow feed-forward artificial neural network.58 The revPBE0-D3 DFT level describes the structure and dynamics of bulk water in excellent agreement with experiments16,59 and the revPBE0-D3+BPNN framework has been extensively used for thermodynamic and dynamical properties of bulk,17,59 interfacial,18,35 and nanoconfined water25 with classical and PI simulations.
2.2 Fast and accurate quantum dynamics using the Te PIGS approach
We next address the cost and complexity of performing quantum nuclear dynamics on the machine-learned Born–Oppenheimer PES. We use imaginary-time PI framework45 based techniques to approximate the quantum dynamics of the full system. These methods neglect quantum coherence effects but have the advantage of efficiently scaling to large systems. State of the art approaches include centroid molecular dynamics (CMD)42,60 and ring polymer molecular dynamics (RPMD)43 and their variants.61–64 These approaches are approximations to Matsubara dynamics65 – a rigorous classical theory for quantum dynamics due to equilibrium quantum fluctuations. Within CMD, the dynamics of the PI centroid approximates quantum TCFs.42 On the other hand, RPMD exploits the dynamics of the full PI and approximates quantum TCFs as correlations of observables over the PI.43 RPMD and CMD are exact in the harmonic and classical limits and are therefore suited for probing ambient-temperature quantum effects.66 However, their computational cost increases steeply with decreasing temperature, and so does their accuracy leading to spurious artefacts in their spectra, such as line shifts and broadening at low temperatures.19 Newer methods such as quasi-CMD67 – and its fast variant68 – attenuate the accuracy issue by working with physically-motivated curvilinear functions of the PI centroid. Unfortunately, quasi-CMD-based methods also display a rising computational cost at low temperatures and their accuracy is sensitive to the choice of quasi-centroid curvilinear functions.69We eliminate these shortcomings using the approach introduced in ref. 24 by some of us. This involves a temperature elevation (Te) ansatz for accurate TCF and PI coarse-grained simulations (PIGS) to map quantum nuclear dynamics to classical MD. The Teansatz alleviates the low-temperature artefacts by writing a TCF of a ground state system exactly in terms of its high-temperature (βe = (kBT)−1 with Te > T) limit,
| CAB(t;β) = β−1βeCAB(t;βe), | (2) |
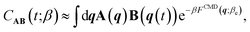 | (3) |
To evaluate eqn (3) at the cost of classical dynamics, we use the PIGS technique that applies a bottom-up coarse graining approach70 to calculate FCMD. We represent this function as the sum of the Born–Oppenheimer PES and a perturbation24 that we fit analogously to a standard MLP with a so-called “delta learning” scheme.71 We sample centroid positions and the difference between the centroid forces and the Born–Oppenheimer force on the centroid from a short equilibrium PIMD simulation at high temperatures, which converges with a few replicas. Using off-the-shelf MLP fitting protocols, we obtain an effective MLP that includes quantum dynamical effects by regressing the above differential force on centroid positions. Our training step24 requires a single 5–10 ps long efficiently sampled PIMD simulation with eight replicas at Te = 500 K, which is dramatically cheaper than typical PI simulations for converging IR and Raman vibrational spectra of liquid (few ns at 300 K with 32 replicas) and ice phases (few 100 ps at 150 K with 64 replicas).
2.3 Equivariant ML models of dielectric responses with non-condon effects
We address the final issue of speeding-up the predictions of first-principles dielectric response tensors. We exploit equivariant (invariant and covariant to the SO(3) group symmetry operations) atom-centred ML models72,73 that bypass finite-electric field electronic structure calculation and respect the physical symmetries of the rank-1 polarization and rank-2 polarizability tensors. We, amongst others, have combined equivariant ML of total polarization and polarizability tensors with classical or PI quantum dynamics methods to predict liquid water IR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17,74,75 and Raman spectra.17,18,22 A hurdle towards first-principles SFG modelling is that its computable expressions are written in terms of molecular polarization and polarizability tensors, which are ill-defined in first-principles modelling. Recent work in ref. 51 exploits that equivariant ML models predict polarization and polarizabilities as a sum of atomic contributions. This construct allows definitions of quasi molecular dielectric responses, which are sums of atomic components for the atoms in a molecule, as proxies for molecular polarizations and polarizabilities used to predict SFG intensities as has been done using forcefields.35 Unfortunately, these local molecular proxies are no longer straightforwardly or robustly defined for systems exhibiting reactivity or with localized charges.76
17,74,75 and Raman spectra.17,18,22 A hurdle towards first-principles SFG modelling is that its computable expressions are written in terms of molecular polarization and polarizability tensors, which are ill-defined in first-principles modelling. Recent work in ref. 51 exploits that equivariant ML models predict polarization and polarizabilities as a sum of atomic contributions. This construct allows definitions of quasi molecular dielectric responses, which are sums of atomic components for the atoms in a molecule, as proxies for molecular polarizations and polarizabilities used to predict SFG intensities as has been done using forcefields.35 Unfortunately, these local molecular proxies are no longer straightforwardly or robustly defined for systems exhibiting reactivity or with localized charges.76
Here, we provide a new expression for modelling SFG spectra that does not invoke a molecular identity for atoms and is also applicable to non-molecular and reactive systems. We take inspiration from ref. 74 that models first-principles IR spectroscopy in terms of the spatial derivative of the polarization. We rewrite the expression for the SFG susceptibility in terms of the spatial derivatives of the total polarization and polarizability tensors, which is naturally a sum of atomic contributions without invoking molecular identity of atoms. Our expression is particularly suited for first-principles modelling as the modern theory of polarization12 rigorously defines derivatives of dielectric responses. In contrast, first-principles modelling does not uniquely define molecular dielectric responses used in forcefield studies.14,52 We first reformulate the definition of the dielectric time-derivatives of a mirrored slab in terms of dielectric derivatives,
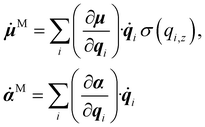 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77 model, which combines equivariance with a rigorous many-body expansion of atomic properties, leading to improved accuracy, extrapolation and data-efficiency as well as favourable scaling with the number of chemical species compared to earlier ML approaches. In contrast to ref. 74 that trains on spacial dielectric derivatives, we train our ML model on total polarization μ and polarizabilities α. Thanks to the PyTorch implementation of MACE with automatic differentiation, we can predict their analytical derivatives in a highly-efficient manner.
77 model, which combines equivariance with a rigorous many-body expansion of atomic properties, leading to improved accuracy, extrapolation and data-efficiency as well as favourable scaling with the number of chemical species compared to earlier ML approaches. In contrast to ref. 74 that trains on spacial dielectric derivatives, we train our ML model on total polarization μ and polarizabilities α. Thanks to the PyTorch implementation of MACE with automatic differentiation, we can predict their analytical derivatives in a highly-efficient manner.
3 Computational details
3.1 Workflow
As shown in Fig. 1, our overall workflow for predicting the vibrational spectrum of a system from first-principles requires these steps:1. Perform an efficiently sampled PIMD simulation using the MLP PES at Te = 500 K and fit FCMD(q;βe) to the centroid forces using the BPNN framework. At this temperature, 8 replicas are sufficient to converge quantum nuclear effects.
2. Perform a 100 ps NVT simulation on FCMD(q;βe), efficiently thermostatted with a generalized Langevin equation thermostat, to sample 10 initial positions and momenta.
3. Perform a 10 × 100 ps NVE simulation on FCMD(q;βe), sampling positions every 2.0 fs.
4. Predict ![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e153.gif) ,
, ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) on the NVE trajectories using the MACE models to calculate IR or Raman spectra, or
on the NVE trajectories using the MACE models to calculate IR or Raman spectra, or ![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e153.gif) M,
M, ![[small alpha, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e14c.gif) M for the SFG spectrum.
M for the SFG spectrum.
5. Calculate TCFs of position for the vibrational density of states and dielectric time derivatives for IR, Raman, or SFG spectra.
We note that, even with the most accurate trajectory-based method, Matsubara dynamics, the predicted O–H stretching band is blue-shifted by 22 cm−1 and slightly broadened w.r.t. to the exact quantum mechanical result – due to quantum coherence being neglected in classical dynamics.67 Therefore, at best, PI methods will be slightly blue-shifted and slightly broadened with respect to the experimental results. Any closer agreement will indicate error cancellation. For an apples-to-apples comparison with our predictions, we shift the experimental O–H stretching band to the blue by 22 cm−1.
3.2 Systems
We apply our framework to investigate the first-principles vibrational spectra of water in bulk, interfacial and nanoconfined environments. We focus on the O–H stretching region of the IR and Raman spectra of liquid water at 300 K, IR and Raman spectra of hexagonal ice (Ih) at 150 K, the SFG spectrum of the water–air interface at 300 K, and temperature-dependent vibrational spectrum of monolayer nanoconfined water. We compare the spectra of liquid water, ice, and the water–air interface with experiments.We model liquid water using a simulation cell from ref. 16–18 containing 64 molecules at experimental density in the NVT ensemble, Ih using a proton disordered simulation cell from ref. 17 containing 96 molecules at experimental density in the NVT ensemble, a slab of 160 molecules in vacuum from ref. 14 in the NVT ensemble, and monolayer water simulation cells containing 144 molecules from ref. 25 in the NPT ensemble at 1 GPa and temperatures 200 to 600 K.
3.3 Potential energy surfaces
We represent the PES of these systems using the BPNN model trained on revPBE0-D3 total energies and forces. To boost the performance of the short-ranged MLPs at the water–vacuum interface, as suggested in ref. 77 and 78, we explore hybrid models for liquid water, ice, and the water–air interface with baseline electrostatics of SPC point charges79 and a short-ranged MLP trained on the difference between the first-principles and baseline total energies and forces. Our BPNN framework uses symmetry functions and a training set from ref. 58 for liquid water, ice, and the water–air interface, and ref. 25 for monolayer nanoconfined water.To incorporate quantum nuclear effects for dynamics in MLPs, we use the BPNN framework with the same setup as in ref. 58 for modelling the PES of bulk water and the n2p2 code![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 for performing the training.
80 for performing the training.
3.4 Equivariant dielectric response models
We represent the first-principles polarization and polarizability surfaces using a single MACE model26 outputting both properties. This only requires implementing a new equivariant readout function compared to the standard MACE force field model. Our model uses 32 channels with equivariant messages up to L = 2 order. We use a cutoff of 6 Å and two message-passing layers resulting in a local model with a receptive field of 12 Å. The training data is obtained from PBE-functional DFT calculations on the dielectric responses of high-temperature liquid water72 calculated using the Quantum Espresso![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81 software. Following ref. 78, we use ML models trained on bulk water to predict the dielectric response tensors for the water–air interface. The success of this extrapolation can be understood in terms of the near-sightedness of aqueous dielectric response derivatives.82
81 software. Following ref. 78, we use ML models trained on bulk water to predict the dielectric response tensors for the water–air interface. The success of this extrapolation can be understood in terms of the near-sightedness of aqueous dielectric response derivatives.82
3.5 Simulations
All classical and path-integral MD simulations are performed with the i-PI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 83 software using the LAMMPS84 code as the force-provider. Classical and path-integral MD simulations are performed with a 0.50 fs timestep using the BAOAB
83 software using the LAMMPS84 code as the force-provider. Classical and path-integral MD simulations are performed with a 0.50 fs timestep using the BAOAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 integration scheme extended to path-integral MD.86 Classical NVT simulations use the optimal sampling generalized Langevin equation thermostat, while the PIMD simulations use the path-integral Langevin equation thermostats with a time-constant of 100
85 integration scheme extended to path-integral MD.86 Classical NVT simulations use the optimal sampling generalized Langevin equation thermostat, while the PIMD simulations use the path-integral Langevin equation thermostats with a time-constant of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fs.
fs.
4 Results
4.1 Validation on the IR and Raman spectrum of liquid water
We first validate our framework on the well-studied stretching IR and Raman bands of liquid water. As shown in Fig. 2, the experimental IR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 89 and anisotropic Raman spectra88 of liquid water display a broad band at around 3400 cm−1, while the experimental isotropic Raman spectrum90 contains a doublet around 3400 cm−1 with a shoulder at 3700 cm−1.
89 and anisotropic Raman spectra88 of liquid water display a broad band at around 3400 cm−1, while the experimental isotropic Raman spectrum90 contains a doublet around 3400 cm−1 with a shoulder at 3700 cm−1.
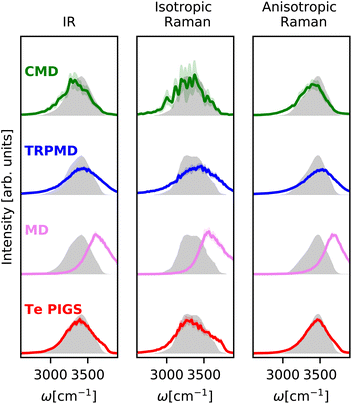 | ||
| Fig. 2 IR and Raman stretching band of liquid water at 300 K with the Te PIGS (red), MD (pink), TRPMD (blue), and CMD (green) and the experimental spectra87,88 (shifted by 22 cm−1 to account for the missing quantum coherence effects in simulation methods) in grey. All simulations are performed with a BPNN with SPC charges trained at the revPBE0-D3 level of theory. | ||
We predict these spectra using the workflow in Section 3. As shown in Fig. 2, the Te PIGS scheme gives an excellent description of the line position of the IR and the anisotropic Raman spectra in near quantitative agreement with experiments. The only disagreement, i.e. the slight broadening of peaks, is consistent with the limitations of all classical dynamics approaches as they neglect quantum coherence.67 Our approach also correctly describes the overall isotropic Raman band, including the high-frequency shoulder but does not recover the doublet.
We now compare our results with current simulation methods used to simulate the IR or Raman spectrum of water. Classical dynamics, which neglects quantum nuclear motion, is blue shifted as it suppresses sampling the anharmonic regions of the O–H bond softened due to hydrogen bonding. Typically, the frequency scale of classical results is rescaled by ∼0.96 to match the experiments or is performed with GGA DFT functionals that soften the O–H bond91 and fortuitously agree with experiments.16 State of the art for including quantum nuclear motion is partially-adiabatic61 CMD and thermostatted44 RPMD. Therefore, these methods require full PI simulations and are at least two orders of magnitude more expensive (see Fig. 6). We observe that these methods reproduce band positions and shapes with semi-quantitative accuracy in agreement with results of previous studies16–18 although their artefacts are visible at ambient conditions. The CMD spectrum is slightly red-shifted due to the onset of the curvature problem, and the TRPMD spectrum is slightly blue-shifted and significantly broadened. Comparing our classical MD predictions with previous first-principles16 and MLP classical simulations,88 at the revPBE0-D3 level of theory, which also does not recover a doublet in the isotropic Raman spectrum, we conclude that it is a shortcoming of the PES. To our knowledge, this is the first instance of first-principles modelling with a quantum description of both electrons and nuclei displaying this level of agreement for the O–H stretching band with the three experiments.
4.2 First-principles IR and Raman spectra of ice
We next investigate the challenging case of hexagonal ices IR and Raman spectra at 150 K. As shown in Fig. 3, the experimental IR spectrum92 exhibits a broad band with peaks at 3200 cm−1 and a shoulder at 3400 cm−1 and the Raman stretching band92 complements these features with peaks at 3100 and 3300 and a shoulder at 3400 cm−1. This system is a stress test for first-principles vibrational spectroscopy due to a fairly complex spectrum from different selection rules, the need for large simulation cells with proton disorder, and the severity of artefacts of classical and quantum dynamics methods at low temperatures. To our knowledge, these spectra have only been reproduced qualitatively with the MB-pol model93 at higher temperatures where the artefacts of CMD and MD are not as severe.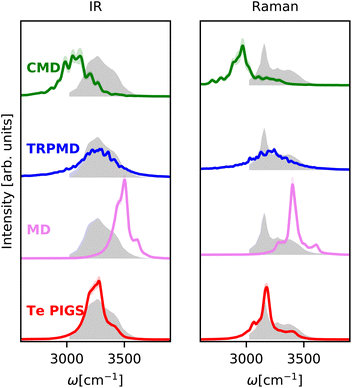 | ||
| Fig. 3 IR and Raman stretching band of polycrystalline ice at 150 K with the Te PIGS (red), MD (pink), TRPMD (blue), and CMD (green) and the experimental spectra92 (shifted by 22 cm−1 to account for the missing quantum coherence effects in simulation methods) in grey. All simulations are performed with a BPNN with SPC charges trained at the revPBE0-D3 level of theory. | ||
As shown in Fig. 3, incorporating quantum nuclear dynamics with the Te PIGS technique, our predicted IR and Raman spectra are in excellent agreement with the experiment and have a systematic improvement over the classical and the state-of-the-art quantum spectra. We predicted IR and Raman recover all known line positions in quantitative agreement with the experiments. However, residual errors exist in the relative intensities and width of the peaks, particularly in the IR spectrum. These are likely due to insufficient sampling of proton disorder in our simulation cell or the level of DFT for the PES and the dielectric responses. To put into perspective the difficulty in simulating quantum nuclear effects in vibrational spectra at low temperatures, we also compare predictions of state-of-the-art methods, which are severely shifted or featureless and over three orders of magnitude more expensive (see Fig. 6).
4.3 First-principles surface-sensitive spectroscopy
We next investigate the SFG spectrum of the water–air interface at 300K, particularly the imaginary component of the ssp susceptibility (χ(2)), which provides additional information on the orientation of the water molecules at the interface. We note that, unlike IR and Raman spectra of bulk water and ice, there is no consensus on the SFG spectrum of water.95 In particular, the relative intensities of the vibrational modes can differ massively depending on the Fresnel factor correction96 and the interfacial dielectric constant.97 In Fig. 4, we report the experimental susceptibility analyzed in ref. 94. The experimental data are taken from ref. 95 (after accounting for Fresnel effects using a slab model) from 3200 cm−1 to 3800 cm−1, noting that the positive features from 3000 cm−1 to 3200 cm−1 in the measurements of ref. 94 are spurious artifacts98 and do not correspond to any aqueous vibrational mode. This data contains a negative lobe at 3500 cm−1 corresponding to hydrogen-bonded molecules pointing towards the bulk region and a positive lobe at 3700 cm−1 with a shoulder at 3650 cm−1 (non-Condon effect) corresponding to the dangling O–H bonds. Given that the relative intensities of peaks are sensitively dependent on the choice of the Fresnel factor correction and the dielectric response of interfacial water, we only discuss band positions. Modelling SFG bands is extremely challenging as it requires long simulation statistics for molecules at the interface, atomic or molecular components of the polarization and the polarizability tensors with the environment dependence. It has, therefore, only been studied with forcefields like POLY2VS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 and MB-pol
35 and MB-pol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 and more recently with MLPs,18,51 with less accurate quantum dynamics methods.
52 and more recently with MLPs,18,51 with less accurate quantum dynamics methods.
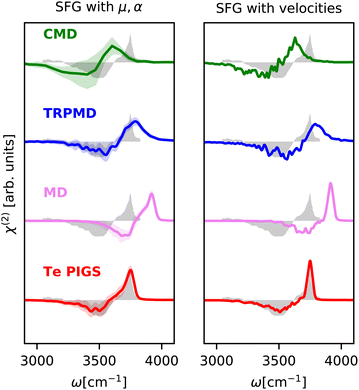 | ||
| Fig. 4 SFG stretching band of water–air interface at 300 K calculated with mirrored dielectric derivatives (eqn (4)) and the surface-sensitive velocity–velocity autocorrelation function (ssVVACF) using the Te PIGS (red), MD (pink), TRPMD (blue), and CMD (green) and the experimental spectra94 (shifted by 22 cm−1 to account for the missing quantum coherence effects in simulation methods) in grey. All simulations are performed with a BPNN with SPC charges trained at the revPBE0-D3 level of theory. | ||
As shown in Fig. 4, by incorporating quantum nuclear effects with the Te PIGS approach and calculating the SFG susceptibility with a surface-sensitive velocity autocorrelation function,14 we can recover the line positions of the positive and negative lobes of the SFG in quantitative agreement with the experiment. The only remaining disagreement, i.e. the missing shoulder, is an artefact of approximating the environment dependence of the dielectric responses via the velocity autocorrelation. Incorporating first-principles polarizations and polarizabilities with eqn (4), we can estimate the SFG of one of the interfaces of a water slab in a vacuum. By incorporating quantum nuclear effects, we describe very well the line positions of the main dangling bond peak and its shoulder arising from intermolecular coupling. We also reproduce the negative lobe, i.e. the bonded part of the O–H stretching mode, within the statistical errors. Our predictions also systematically improve over TRPMD and CMD, which are much more computationally demanding (see Fig. 6) but also display broad and shifted peaks.
4.4 Characterizing confined water phase transitions
Having showcased our capability to predict complicated vibrational spectra of bulk phases and interfaces, we apply our method to guide the experimental realization of new phases of nanoconfined25 water by predicting their first-principles vibrational spectra. We investigate the isobar at 1 GPa from 200 K to 600 K – a small region of the phase diagram of a monolayer of water in a graphene-like channel that exhibits a Kosterlitz–Thouless99,100 phase transition of a solid to a liquid via a hexatic phase. Our computational setup mimics a single layer of water encapsulated between two graphene sheets. The water molecules typically experience a lateral pressure of approximately 1 GPa due to the vdW forces between the graphene sheets and the termination of the edges. We model the water–carbon potential with a Morse potential101 (uniform in the lateral plane) and the vdW pressure by working in the NPlatT ensemble.As shown in Fig. 5, the temperature-dependent changes in the character of the O–H stretching band clearly show a first-order phase transition between the flat-rhombic and hexatic phase and provide support for a continuous phase transition between the hexatic and the liquid phase. At 200 K, we observe the flat-rhombic phase with two bands in the stretching region, corresponding to the in-plane zigzagging hydrogen bonding O–H bond and the dangling O–H bond. The doublet nature of these bands arises from coherent O–H vibrations. At 300 K, the doublet of the peaks vanishes due to the thermalized homogeneous broadening of the peaks, but the presence of two distinct bands confirms the absence of molecular rotation. At 300 K, we see evidence for a hexatic phase of water with a single band with a doublet feature, suggesting that water molecules are free to rotate between the 6-fold symmetric bonded and the dangling, configurations. From 400 K to 600 K, we observe a gradual emergence of a single broad spectrum indicating an isotropic liquid. We hope these spectroscopic features will help confirm the existence of the flat-rhombic, hexatic, and liquid phases of monolayer water.
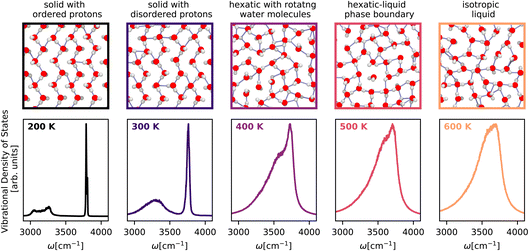 | ||
| Fig. 5 Temperature-dependent vibrational density of states of monolayer water25 across the solid–hexatic–liquid phase transition at a lateral pressure of 1 GPa calculated using the Te PIGS method. The spectra are colour-coded according to temperature. The top panels (border colours indicating temperatures) correspond to snapshots of monolayer water structures. All simulations are performed with a BPNN trained at the revPBE0-D3 level of theory. | ||
5 Discussion
To summarize, we present a new approach to model the first-principles vibrational spectra of bulk, interfacial and nanoconfined systems with predictive accuracy. We exploit MLPs for sampling and fully differentiable ML models of dielectric responses, to rigorously model bulk and surface-sensitive spectroscopy in terms of the derivatives of dielectric responses. In addition, we incorporate quantum nuclear effects implicitly in our MLPs using the recently developed PIGS method. With these ingredients, we can account for electronic and quantum nuclear effects in modelling bulk and interfacial vibrational spectra of diverse aqueous systems and obtain quantitative agreement with experiments. In all cases, we demonstrate the improved accuracy of our approach over state-of-the-art techniques. For IR and Raman spectra, the improved accuracy enables direct comparison of the fine features of the O–H stretching region with experiments to near quantitative accuracy. For SFG spectra, the high-fidelity MACE dielectric response gradients enable non-Condon effects without invoking any molecular identity for atoms, paving the way for modelling surface-sensitive spectroscopies of reactive systems.Although we focused on accurate modelling by incorporating electronic and quantum nuclear effects, our framework is computationally less demanding than other approaches. As shown in Fig. 6, which illustrates the total number of force evaluations and dielectric response calculations needed for the systems studied, our approach is many orders of magnitude cheaper than a full first-principles method, and with respect to previous approaches that combined MLPs and ML dielectric models with commonly used quantum nuclear dynamics methods like TRPMD and CMD. Barring the small overhead of training the Te-FES, our framework for full quantum vibrational spectroscopy has approximately the same cost as for classical spectra, even at low temperatures where standard methods have a divergingly high computational cost. Therefore, our framework provides predictive accuracy and an efficient and practical approach towards characterising complex aqueous interfaces. We believe the developments presented in this paper will simplify the modelling of full quantum spectra of generic systems and provide the methodology to accurately study open questions in interfaces such as proton disorder at the surface of ice, the quasi-liquid layer, pH of the surface of water, and reactivity at aqueous interfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The early stages of the work on sum frequency generation benefited greatly from discussions with Yair Litman, Jinggang Lan and David Wilkins. We thank Ilyes Batatia for assistance with MACE software implementation and acknowledge Stuart Althorpe, David Manolopolous, Xavier Rosas Advincula, Pin Yu Chew, Fabian Berger, Benjamin Shi, and Flaviano Della Pia for comments on the manuscript. We thank Xavier Rosas Advincula, Anna Bui and Pin Yu Chew for help with graphics and Mischa Bonn, Yuki Nagata and Felix Musil, for insightful discussions. V. K. acknowledges support from the Ernest Oppenheimer Early Career Fellowship and the Sydney Harvey Junior Research Fellowship, Churchill College, University of Cambridge. DPK acknowledges support from AstraZeneca and the EPSRC. AM acknowledges support from the European Union under the n-AQUA ERC project (101071937). We are grateful for computational support from the Swiss National Supercomputing Centre under project s1209, the UK National High Performance Computing service, ARCHER2, for which access was obtained via the UKCP consortium and the EPSRC grant EP/P022561/1, and the Cambridge Service for Data Driven Discovery (CSD3).Notes and references
- V. Buch, A. Milet, R. Vácha, P. Jungwirth and J. P. Devlin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7342 CrossRef CAS PubMed.
- M. A. Sánchez, T. Kling, T. Ishiyama, M.-J. van Zadel, P. J. Bisson, M. Mezger, M. N. Jochum, J. D. Cyran, W. J. Smit, H. J. Bakker, M. J. Shultz, A. Morita, D. Donadio, Y. Nagata, M. Bonn and E. H. G. Backus, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 227 CrossRef.
- K. V. Agrawal, S. Shimizu, L. W. Drahushuk, D. Kilcoyne and M. S. Strano, Nat. Nanotechnol., 2017, 12, 267 CrossRef CAS PubMed.
- D. Muñoz-Santiburcio and D. Marx, Chem. Rev., 2021, 121, 6293 CrossRef.
- Z. Zhang, L. Wen and L. Jiang, Nat. Rev. Mater., 2021, 6, 622 CrossRef CAS.
- Y. Liang and Y. Yao, Nat. Rev. Mater., 2022, 8, 109 CrossRef.
- N. Kavokine, M.-L. Bocquet and L. Bocquet, Nature, 2022, 602, 84 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- Y. Nagata, T. Ohto, E. H. G. Backus and M. Bonn, J. Phys. Chem. B, 2016, 120, 3785 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- R. Resta and D. Vanderbilt, Physics of Ferroelectrics: A Modern Perspective, in Topics in Applied Physics, Springer, Berlin, Heidelberg, 2007, pp. 31–68 Search PubMed.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529 CrossRef CAS.
- T. Ohto, K. Usui, T. Hasegawa, M. Bonn and Y. Nagata, J. Chem. Phys., 2015, 143, 124702 CrossRef.
- V. Kapil, J. VandeVondele and M. Ceriotti, J. Chem. Phys., 2016, 144, 054111 CrossRef CAS.
- O. Marsalek and T. E. Markland, J. Phys. Chem. Lett., 2017, 8, 1545 CrossRef CAS PubMed.
- V. Kapil, D. M. Wilkins, J. Lan and M. Ceriotti, J. Chem. Phys., 2020, 152, 124104 CrossRef PubMed.
- S. Shepherd, J. Lan, D. M. Wilkins and V. Kapil, J. Phys. Chem. Lett., 2021, 12, 9108 CrossRef CAS PubMed.
- A. Witt, S. D. Ivanov, M. Shiga, H. Forbert and D. Marx, J. Chem. Phys., 2009, 130, 194510 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032 CrossRef CAS.
- A. Grisafi and M. Ceriotti, J. Chem. Phys., 2019, 151, 204105 CrossRef.
- G. M. Sommers, M. F. C. Andrade, L. Zhang, H. Wang and R. Car, Phys. Chem. Chem. Phys., 2020, 22, 10592 RSC.
- M. Gastegger, K. T. Schütt and K.-R. Müller, Chem. Sci., 2021, 12, 11473 RSC.
- F. Musil, I. Zaporozhets, F. Noé, C. Clementi and V. Kapil, J. Chem. Phys., 2022, 157, 181102 CrossRef CAS.
- V. Kapil, C. Schran, A. Zen, J. Chen, C. J. Pickard and A. Michaelides, Nature, 2022, 609, 512 CrossRef CAS.
- I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, arXiv, 2022, preprint, arXiv:2206.07697 [cond-mat, physics:physics, stat] DOI:10.48550/arXiv.2206.07697.
- M. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, OUP Oxford, 2010 Search PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457 CrossRef.
- R. Zwanzig, Nonequilibrium Statistical Mechanics, Oxford University Press, 2001 Search PubMed.
- A. Morita and J. T. Hynes, J. Phys. Chem. B, 2002, 106, 673 CrossRef CAS.
- M. Del Ben, M. Schönherr, J. Hutter and J. VandeVondele, J. Phys. Chem. Lett., 2013, 4, 3753 CrossRef CAS.
- L. Ruiz Pestana, O. Marsalek, T. E. Markland and T. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 5009 CrossRef CAS.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1 CrossRef CAS.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- T. Ohto, M. Dodia, J. Xu, S. Imoto, F. Tang, F. Zysk, T. D. Kühne, Y. Shigeta, M. Bonn, X. Wu and Y. Nagata, J. Phys. Chem. Lett., 2019, 10, 4914 CrossRef CAS.
- V. Babin, G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2014, 10, 1599 CrossRef CAS.
- T. Hasegawa and Y. Tanimura, J. Phys. Chem. B, 2011, 115, 5545 CrossRef CAS.
- Q. Yu, C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Phys. Chem. Lett., 2022, 13, 5068 CrossRef CAS.
- A. Zen, J. G. Brandenburg, J. Klimeš, A. Tkatchenko, D. Alfè and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1724 CrossRef CAS.
- F. Della Pia, A. Zen, D. Alfè and A. Michaelides, J. Chem. Phys., 2022, 157, 134701 CrossRef CAS PubMed.
- A. Rahman, Phys. Rev., 1964, 136, A405 CrossRef.
- J. Cao and G. A. Voth, J. Chem. Phys., 1994, 100, 5106 CrossRef CAS.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, 3368 CrossRef CAS PubMed.
- M. Rossi, M. Ceriotti and D. E. Manolopoulos, J. Chem. Phys., 2014, 140, 234116 CrossRef.
- S. C. Althorpe, Eur. Phys. J. B, 2021, 94, 155 CrossRef CAS.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591 CrossRef CAS PubMed.
- M. Benoit, D. Marx and M. Parrinello, Nature, 1998, 392, 258 CrossRef CAS.
- F. Uhl, D. Marx and M. Ceriotti, J. Chem. Phys., 2016, 145, 054101 CrossRef PubMed.
- E. F. Hayes and R. G. Parr, J. Chem. Phys., 1965, 43, 1831 CrossRef CAS.
- R. P. Feynman, Phys. Rev., 1939, 56, 340 CrossRef CAS.
- Y. Litman, J. Lan, Y. Nagata and D. M. Wilkins, Fully First-Principles Surface Spectroscopy with Machine Learning, arXiv, 2023, preprint, arXiv:2305.09321 [physics] DOI:10.48550/arXiv.2305.09321.
- G. R. Medders and F. Paesani, J. Am. Chem. Soc., 2016, 138, 3912 CrossRef CAS PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073 CrossRef CAS.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759 CrossRef CAS PubMed.
- J. Behler, Chem. Rev., 2021, 121, 10037 CrossRef CAS PubMed.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- C. Schran, K. Brezina and O. Marsalek, J. Chem. Phys., 2020, 153, 104105 CrossRef CAS.
- B. Cheng, E. A. Engel, J. Behler, C. Dellago and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1110 CrossRef CAS.
- J. Cao and G. A. Voth, J. Chem. Phys., 1993, 99, 10070 CrossRef CAS.
- T. D. Hone, P. J. Rossky and G. A. Voth, J. Chem. Phys., 2006, 124, 154103 CrossRef.
- M. Rossi, P. Gasparotto and M. Ceriotti, Phys. Rev. Lett., 2016, 117, 115702 CrossRef.
- M. Rossi, V. Kapil and M. Ceriotti, J. Chem. Phys., 2018, 148, 102301 CrossRef.
- G. Trenins, M. J. Willatt and S. C. Althorpe, J. Chem. Phys., 2019, 151, 054109 CrossRef.
- T. J. H. Hele, M. J. Willatt, A. Muolo and S. C. Althorpe, J. Chem. Phys., 2015, 142, 134103 CrossRef.
- S. Habershon, D. E. Manolopoulos, T. E. Markland and T. F. Miller, Annu. Rev. Phys. Chem., 2013, 64, 387 CrossRef CAS PubMed.
- G. Trenins and S. C. Althorpe, J. Chem. Phys., 2018, 149, 014102 CrossRef.
- T. Fletcher, A. Zhu, J. E. Lawrence and D. E. Manolopoulos, J. Chem. Phys., 2021, 155, 231101 CrossRef CAS.
- C. Haggard, V. G. Sadhasivam, G. Trenins and S. C. Althorpe, J. Chem. Phys., 2021, 155, 174120 CrossRef CAS PubMed.
- J. Wang, S. Olsson, C. Wehmeyer, A. Pérez, N. E. Charron, G. de Fabritiis, F. Noé and C. Clementi, ACS Cent. Sci., 2019, 5, 755 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087 CrossRef CAS.
- A. Grisafi, D. M. Wilkins, G. Csányi and M. Ceriotti, Phys. Rev. Lett., 2018, 120, 036002 CrossRef CAS PubMed.
- D. M. Wilkins, A. Grisafi, Y. Yang, K. U. Lao, R. A. DiStasio and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3401 CrossRef CAS.
- P. Schienbein, J. Chem. Theory Comput., 2023, 19, 705 CrossRef CAS.
- R. Beckmann, F. Brieuc, C. Schran and D. Marx, J. Chem. Theory Comput., 2022, 18, 5492 CrossRef CAS.
- M. Veit, D. M. Wilkins, Y. Yang, R. A. DiStasio Jr and M. Ceriotti, J. Chem. Phys., 2020, 153, 024113 CrossRef CAS PubMed.
- S. P. Niblett, M. Galib and D. T. Limmer, J. Chem. Phys., 2021, 155, 164101 CrossRef CAS PubMed.
- Y. Litman, J. O. Richardson, T. Kumagai and M. Rossi, J. Am. Chem. Soc., 2019, 141, 2526 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269 CrossRef CAS.
- A. Singraber, J. Behler and C. Dellago, J. Chem. Theory Comput., 2019, 15, 1827 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. d. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- G. R. Medders and F. Paesani, J. Chem. Phys., 2015, 142, 212411 CrossRef PubMed.
- V. Kapil, M. Rossi, O. Marsalek, R. Petraglia, Y. Litman, T. Spura, B. Cheng, A. Cuzzocrea, R. H. Meißner, D. M. Wilkins, B. A. Helfrecht, P. Juda, S. P. Bienvenue, W. Fang, J. Kessler, I. Poltavsky, S. Vandenbrande, J. Wieme, C. Corminboeuf, T. D. Kühne, D. E. Manolopoulos, T. E. Markland, J. O. Richardson, A. Tkatchenko, G. A. Tribello, V. Van Speybroeck and M. Ceriotti, Comput. Phys. Commun., 2019, 236, 214 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- B. Leimkuhler and C. Matthews, J. Chem. Phys., 2013, 138, 174102 CrossRef.
- V. Kapil, J. Wieme, S. Vandenbrande, A. Lamaire, V. Van Speybroeck and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 3237 CrossRef CAS PubMed.
- Q. Sun, Chem. Phys. Lett., 2013, 568–569, 90 CrossRef CAS.
- T. Morawietz, O. Marsalek, S. R. Pattenaude, L. M. Streacker, D. Ben-Amotz and T. E. Markland, J. Phys. Chem. Lett., 2018, 9, 851 CrossRef CAS PubMed.
- J. E. Bertie and Z. Lan, Appl. Spectrosc., 1996, 50, 1047 CrossRef CAS.
- J. Sun, B. K. Clark, S. Torquato and R. Car, Nat. Commun., 2015, 6, 8156 CrossRef CAS PubMed.
- L. Wang, M. Ceriotti and T. E. Markland, J. Chem. Phys., 2014, 141, 104502 CrossRef PubMed.
- W. J. Smit, F. Tang, Y. Nagata, M. A. Sánchez, T. Hasegawa, E. H. G. Backus, M. Bonn and H. J. Bakker, J. Phys. Chem. Lett., 2017, 8, 3656 CrossRef CAS PubMed.
- D. R. Moberg, S. C. Straight, C. Knight and F. Paesani, J. Phys. Chem. Lett., 2017, 8, 2579 CrossRef CAS.
- S. Sun, R. Liang, X. Xu, H. Zhu, Y. R. Shen and C. Tian, J. Chem. Phys., 2016, 144, 244711 CrossRef PubMed.
- F. Tang, T. Ohto, S. Sun, J. R. Rouxel, S. Imoto, E. H. G. Backus, S. Mukamel, M. Bonn and Y. Nagata, Chem. Rev., 2020, 120, 3633 CrossRef CAS.
- X. Yu, K.-Y. Chiang, C.-C. Yu, M. Bonn and Y. Nagata, J. Chem. Phys., 2023, 158, 044701 CrossRef CAS PubMed.
- K.-Y. Chiang, T. Seki, C.-C. Yu, T. Ohto, J. Hunger, M. Bonn and Y. Nagata, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2204156119 CrossRef CAS.
- S. Sun, R. Liang, X. Xu, H. Zhu, Y. R. Shen and C. Tian, J. Chem. Phys., 2016, 145, 167102 CrossRef PubMed.
- J. M. Kosterlitz and D. J. Thouless, J. Phys. C: Solid State Phys., 1972, 5, L124 CrossRef CAS.
- J. M. Kosterlitz and D. J. Thouless, J. Phys. C: Solid State Phys., 1973, 6, 1181 CrossRef CAS.
- J. Chen, G. Schusteritsch, C. J. Pickard, C. G. Salzmann and A. Michaelides, Phys. Rev. Lett., 2016, 116, 025501 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |