Open Access Article
Open Access ArticleHydrophobic hydration of the hydrocarbon adamantane in amorphous ice†
Sukhpreet K.
Talewar
a,
Luis Carlos
Pardo
 b,
Thomas F.
Headen
b,
Thomas F.
Headen
 c,
Siriney O.
Halukeerthi
a,
Bharvi
Chikani
a,
Alexander
Rosu-Finsen
a and
Christoph G.
Salzmann
c,
Siriney O.
Halukeerthi
a,
Bharvi
Chikani
a,
Alexander
Rosu-Finsen
a and
Christoph G.
Salzmann
 *a
*a
aDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: c.salzmann@ucl.ac.uk
bGrup de Caracterització de Materials, Departament de Física, EEBE, Universitat Politècnica de Catalunya, and Barcelona Research Center in Multiscale Science and Engineering, C/Eduard Maristany 10, E-08019 Barcelona, Spain
cISIS Pulsed Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Harwell Campus, OX11 0QX, UK
First published on 19th June 2023
Abstract
Hydrophobic molecules are by definition difficult to hydrate. Previous studies in the area of hydrophobic hydration have therefore often relied on using amphiphilic molecules where the hydrophilic part of a molecule enabled the solubility in liquid water. Here, we show that the hydrophobic adamantane (C10H16) molecule can be fully hydrated through vapour codeposition with water onto a cryogenic substrate at 80 K resulting in the matrix isolation of adamantane in amorphous ice. Using neutron diffraction in combination with the isotopic substitution method and the empirical potential structure refinement technique, we find that the first hydration shell of adamantane is well structured consisting of a hydrogen-bonded cage of 28 water molecules that is also found in cubic structure II clathrate hydrates. The four hexagonal faces of the 51264 cage are situated above the four methine (CH) groups of adamantane whereas the methylene (CH2) groups are positioned below the edges of two adjoining pentagonal faces. The oxygen atoms of the 28 water molecules can be categorised on the basis of symmetry equivalences as twelve A, twelve B and four C oxygens. The water molecules of the first hydration shell display orientations consistent with those expected for a clathrate-hydrate-type cage, but also unfavourable ones with respect to the hydrogen bonding between the water molecules. Annealing the samples at 140 K, which is just below the crystallisation temperature of the matrix, removes the unfavourable orientations and leads to a slight increase in the structural order of the first hydration shell. The very closest water molecules display a tendency for their dipole moments to point towards the adamantane which is attributed to steric effects. Other than this, no significant polarisation effects are observed which is consistent with weak interactions between adamantane and the amorphous ice matrix. FT-IR spectroscopy shows that the incorporation of adamantane into amorphous ice leads to a weakening of the hydrogen bonds. In summary, the matrix-isolation of the highly symmetric adamantane in amorphous ice provides an interesting test case for hydrophobic hydration. Studying the structure and spectroscopic properties of water at the interface with hydrophobic hydrocarbons is also relevant for astrophysical environments, such as comets or the interstellar medium, where amorphous ice and hydrocarbons have been shown to coexist in large quantities.
Introduction
The structure and dynamics of water have been studied experimentally at a wide range of hydrophobic surfaces and interfaces1–4 as well as in the vicinity of small hydrophobic molecules.5–7 A cross-over in the hydration behaviour between these two regimes has been pointed out.8,9 Essentially, as the radii of the hydrophobic species increase, the water molecules are at some point expected to not be able to achieve full hydrogen bonding resulting in a reduction in the coordination number at the hydrophobic interface and hence dangling O–H bonds.Yet, the insolubility of larger hydrophobic molecules in water makes exploring this cross-over difficult and work in the area has mainly relied on larger amphiphilic molecules where the solubility is provided through a hydrophilic headgroup.10,11
In space, hydrophobic carbon species and amorphous ice have been found to coexist in large quantities. The dominant carbon species are polycyclic aromatic hydrocarbons (PAHs) and fullerenes, yet diamondoids with adamantane (C10H16) as the smallest molecular representative have been identified as well.12–15 Several studies have explored the spectroscopic and photochemical properties of PAH/amorphous ice mixtures.16–21 The aggregation of pyrene due to the crystallization of the amorphous ice matrix has been investigated22 and matrix-isolated 2-naphthol was used as a spectroscopic probe for investigating the mechanism of the glass transition of amorphous ice at around 136 K,23 which is governed by reorientation dynamics.24,25 Recently, we showed that the presence of C60 fullerene in amorphous ice influences its crystallisation temperature once the percolation threshold is reached.26 The thermal desorption properties of water are affected above 60 vol% C60.
Here, we achieve the matrix isolation of adamantane in amorphous ice and study the structure of water in its first hydration shell with neutron diffraction making use of the isotopic substitution method and the empirical structure refinement technique.27,28 The high symmetry of the adamantane molecule with its Td point group and almost spherical structure offers the advantage of simple structural analysis of water in its hydration shell. The possibility of hydrogen isotopic substitution for both the adamantane as well as water means that orientation correlations can be determined with high confidence. In addition to the neutron diffraction experiments, FT-IR spectroscopy is used to probe the effects of adamantane on the hydrogen bonding within the amorphous ice matrix.
Experimental
Materials
Protiated (C10H16) and deuterated (C10D16) adamantane were used as received from Sigma Aldrich with purities of ≥99% and 98 at% D, respectively. Ultrapure water (H2O, Milli-Q, Millipore) and heavy water (D2O, 99.9 at% D) were purchased from Sigma Aldrich.Sample preparation
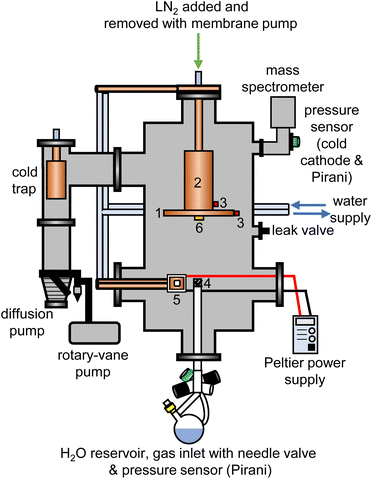
The experimental setup for the cryogenic matrix isolation of adamantane in amorphous ice was based on a high-vacuum box chamber purchased from Kurt Lesker as shown schematically in Fig. 1. A similar vacuum chamber was used in previous studies.26,29 The new vacuum chamber30 allowed adding liquid nitrogen at the top to cool an 8-inch diameter cryogenic deposition plate (1) directly. Furthermore, a more efficient cold trap was installed before the diffusion pump which could be removed easily for cleaning adamantane residues. The temperatures of the deposition plate (1) and liquid-nitrogen reservoir (2) were recorded with K-type thermocouples (3) using a purpose-made instrument containing an Adafruit Feather 32u4 microcontroller and two Adafruit MAX31856 Universal Thermocouple Amplifiers.The pressure of the vacuum chamber was monitored with a combination Pirani/cold cathode pressure gauge (PenningVac PTF 90, Oerlikon Leybold Vacuum) and routinely reached 2 × 10−6 mbar. Situated at the bottom of the chamber, a 32 cm long and 2.6 cm diameter stainless-steel tube allowed water vapour to be leaked into the chamber towards the deposition plate which was 15 cm away from the top of the inlet tube. The water-inlet system consists of a needle valve (EV 016 DOS AB, Oerlikon Leybold Vacuum) that allows for adjustment of the amount of water vapor dosed into the chamber and a Pirani pressure sensor (Thermovac TTR91, Oerlikon Leybold Vacuum) used to measure the water-vapour inlet pressure. A round-bottom flask fitted with a Young's tap held the liquid water and was attached to the inlet system. Prior to depositing H2O, D2O or a 50% mixture, several freeze–pump–thaw cycles were carried out to degas the water. The absence of dissolved gases and correct isotopic compositions were confirmed with mass spectrometry before each deposition experiment (Hiden HALO 100 with Faraday cup). To baffle the flow of water vapour into the chamber, an iron mesh (4) with 0.5 mm thick wires spaced 1 mm apart was placed directly on top of the water inlet tube.
For each deposition experiment, pellets of either 1 g C10H16 or C10D16 were prepared using a 13 mm-diameter piston-cylinder die and a hydraulic press (Hypress 30 tonne shop press with a powerteam P59B 700 bar hydraulic pump) with maximum pressures of 5 or 8 tonne for C10H16 and C10D16, respectively. For the deposition of adamantane, the vacuum chamber was fitted with a Peltier element (5) from RS Components (37.9 W, 3.9 A, 15.7 V, 30 × 30 mm) attached to an 80 W power supply. One side of the Peltier element was attached to a water-cooled copper finger whereas a 30 × 30 mm copper sample stage was placed on the other side with heat-conducting paste. The pellets were mounted onto the copper stage with heat conducting paste and the temperature of the sample stage was recorded with a K-type thermocouple connected to an IJ-software-based temperature controller.
At the beginning of a deposition experiment, a pellet of either C10H16 or C10D16 was cooled to 240 K to prevent sublimation of the material. The vacuum chamber was then evacuated to a base pressure of 2 × 10−6 mbar and the deposition plate was cooled to a base temperature of 82 K. Water vapour was then leaked into the chamber by adjusting the needle valve to achieve an inlet pressure of 1.00 × 10−1 mbar. At the same time, the voltage of the Peltier element was adjusted to obtain the appropriate temperature for a specific molar ratio of adamantane to water. The deposition time for a typical experiment was 4 hours during which ∼3.5 g of water entered the vacuum chamber.
Deposition rates were determined with a quartz-crystal microbalance (QCM), consisting of gold-plated AT-cut 6 MHz plano-convex quartz crystals (Inficon) which were placed inside an Allectra 710-SH sensor head firmly attached to the centre of the deposition plate (6). This sensor was connected to a reflection bridge and a 0.5–60 MHz N2PK vector network analyser through coaxial cables. During deposition, the changes in the fundamental frequency were recorded using the myVNA and QTZ softwares.31 The deposition rates were then calculated using a linear fit to the frequency versus time data.
In the case of H2O deposition, the inlet pressure of 1.00 × 10−1 mbar gave a deposition rate of 0.655 ± 0.002 μg cm−2 s−1. The corresponding molar deposition rate is 0.0363 ± 0.0001 μmol cm−2 s−1. The molar deposition rates of D2O and the 50% mixture were the same within error implying that ideal gas behaviour was valid at the inlet.
The deposition rates of C10H16 and C10D16 were controlled by adjusting the voltage and hence temperature of the Peltier element. To achieve 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 adamantane to water molar ratios, C10H16 and C10D16 were held at 255 K and 245 K, respectively, during the depositions. Overall, six 1
100 adamantane to water molar ratios, C10H16 and C10D16 were held at 255 K and 245 K, respectively, during the depositions. Overall, six 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 samples were prepared of the following isotopic compositions: C10H16@H2O, C10H16@HDO, C10H16@D2O, C10D16@H2O, C10D16@HDO and C10D16@D2O.
100 samples were prepared of the following isotopic compositions: C10H16@H2O, C10H16@HDO, C10H16@D2O, C10D16@H2O, C10D16@HDO and C10D16@D2O.
Following deposition, the samples were extracted from the chamber under liquid nitrogen and filled into flat-plate TiZr cans.
Neutron diffraction experiments
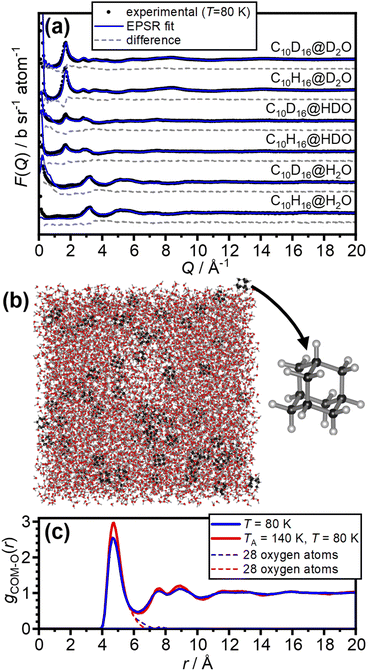
The internal dimensions of the null-scattering Ti0.68Zr0.32 alloy sample cells were 1 × 38 × 38 mm for the H2O and HDO samples, and 2 × 38 × 38 mm for the D2O samples. Neutron scattering measurements were carried out at 80 K for the as-made samples and after annealing at 140 K for 150 μA of proton current on the NIMROD diffractometer at the ISIS spallation neutron source at the Rutherford Appleton Laboratory, UK.32 NIMROD detects neutrons scattered by a sample at angles between 0.5 and 40° and a wavevector-transfer range of 0.02–50 Å−1 is covered.32The GudrunN software package33 was used to correct the raw scattering data for absorption and multiple scattering and to subtract any perturbation effects to the data caused by inelastic collisions. The “Iterate Gudrun” function in GudrunN was used to remove inelasticity features to obtain total structure factors, F(Q), of the samples.34 Datasets collected for the as-made sample at 80 K are shown in Fig. 2(a) and after annealing at 140 K in Fig. S1.†
The Empirical Potential Structure Refinement (EPSR) software27,28 was used to fit the experimental data and obtain structural models representing the sample. Briefly, EPSR starts with a standard classical Monte Carlo simulation using standard reference potentials for the inter- and intra-molecular force-fields. The predicted scattering for each isotopologue is then calculated from the simulation, and the difference between the simulated and experimental scattering used to iteratively develop an additional empirical potential. This is added to the reference potentials, driving the simulation towards matching the six datasets. For each simulation, a cubic box with an edge length of 64.673 Å was filled with 8000 H2O molecules and 80 C10H16 molecules corresponding to an atomic number density of 0.09641 Å−3. The average bond angles, lengths of C10H16, the 12-6 Lennard-Jones parameters and partial charges were taken from OPLS-AA (Optimized Potentials for Liquid Simulations of all atoms) force field.35 The SPC/E model was used for water.36 After convergence of the fits using empirical potentials, approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 model iterations were accumulated for both data sets.
000 model iterations were accumulated for both data sets.
The ANGULA software37–40 was used to extract the pair-distribution functions from the centre-of-mass of adamantane to the oxygen atoms of water, gCOM–O(r), spatial-density functions (SDFs) and orientation-correlation functions (OCFs).
FTIR spectroscopy
Circular CaF2 windows with 15 mm diameter and 2 mm thickness from UQG Optics were mounted onto the cryogenic deposition plate in the vacuum chamber. H2O with 5 wt% D2O and C10H16 were then codeposited at either 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 34
1 or 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio for 2.5 minutes. The optical windows were transferred into a modified Optistat DN-V cryostat from Oxford instruments that was precooled with liquid nitrogen. The cryostat was operated at a base pressure of 5 × 10−4 mbar.
1 molar ratio for 2.5 minutes. The optical windows were transferred into a modified Optistat DN-V cryostat from Oxford instruments that was precooled with liquid nitrogen. The cryostat was operated at a base pressure of 5 × 10−4 mbar.
FT-IR spectra were recorded in transmission geometry at 80 K using a Bruker Invenio-R spectrometer with a liquid-nitrogen cooled MCT detector and MIR source. A spectral resolution of 1 cm−1 was used and all spectra were recorded with 512 scans. Background spectra were recorded with blank CaF2 windows in the cryostat.
Results and discussion
The neutron diffraction data of the six as-made samples is shown in Fig. 2(a) together with the converged EPSR fits. The corresponding data and fits of the annealed samples are shown in Fig. S1.† The broad diffraction features illustrate the amorphous nature of the deposits and hence the successful matrix isolation of adamantane in amorphous ice. The diffraction data is well fitted with the EPSR approach which means that the corresponding structural models, such as the one shown in Fig. 2(b), can be used for the analysis of the structure of water in the hydration shell of adamantane.The pair-distribution function from the centre-of-mass (COM) of adamantane to the oxygen atoms of the water molecules, gCOM–O(r), is shown in Fig. 2(c). A well-defined first hydration shell is observed at ∼4.7 Å, and second and third hydration shells are visible below 10 Å. The annealing of the amorphous samples at 140 K leads to increases in the structural order of the hydration shells as indicated by sharper features in gCOM–O(r). Overall, it can be concluded that the adamantane is well hydrated within the amorphous ice matrix despite its hydrophobic nature.
The structure of the first hydration shell was investigated in more detail by determining angle-dependent pair-distribution functions. For this, the COM of adamantane was placed on the origin, the z axis aligned with the C–H bond of a methine (CH) group of adamantane and the x axis pointed towards a second CH group as shown in Fig. 3(a). Using the ANGULA software, the gCOM–O pair-distribution function was determined as a function of the polar angle θ, the azimuthal angle ϕ and the radial distance r. Typically, such pair-distributions would be analysed by averaging over the distance range of the first hydration shell. However, ANGULA offers the possibility to visualise the average local structure for increasing numbers of closest molecules. As shown in Fig. S2 and S3,† the oxygen atoms of the closest water molecules are found in what we call A and C type locations. Upon including the five closest water molecules, oxygen atoms are also found in B locations. Overall, the first hydration shell is highly structured with 28 distinct oxygen positions emerging for the five closest water molecules. Fig. 3(b) shows gCOM–O(θ, ϕ) of the 28 closest water molecules for the as-made samples. Overall, there are 12 A, 12 B and 4 C type oxygen positions. Consistent with the sharpening of the features in gCOM–O(r) shown in Fig. 2(c), the ‘dots’ become more defined after annealing as can be seen in Fig. 3(c).
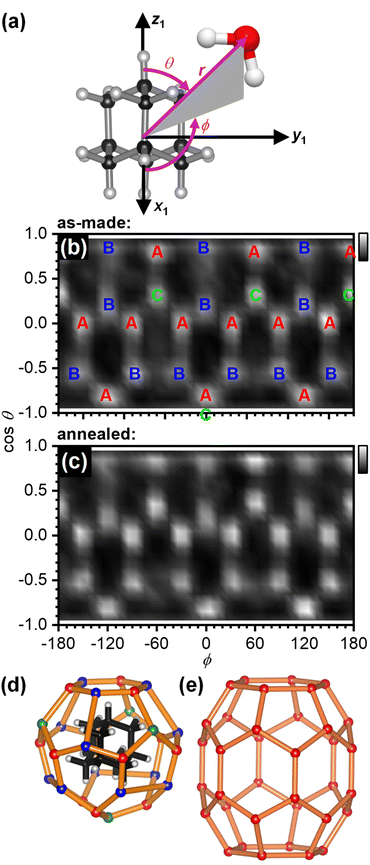 | ||
| Fig. 3 Structure of the first hydration shell of adamantane. (a) Definition of the spherical coordinates from the centre-of-mass of adamantane to the oxygen atom of water. (b and c) Angle-dependent pair-distribution function of the 28 closest oxygen atoms of the as-made samples and after annealing at 140 K. The three symmetry-distinct positions are labelled as A, B and C in (b). (d) 3D structures of the 51264 cage and (e) the ‘barrel-shaped’ 51268 cage.47–49 | ||
With respect to the hydrated adamantane, the oxygen atoms are located above the centres of triangles constituted by three of the hydrogen atoms of the adamantane. The A type oxygens are placed above triangles defined by the hydrogen atoms of two different CH2 and one CH group, the B type oxygens above the two hydrogen atoms of the same CH2 group and one CH group whereas the C type oxygens are located above the hydrogen atoms of three CH groups (see Fig. 3(d)).
The oxygen atoms in the first hydration shell form one type of six-membered and one type of five-membered ring. The four six-membered rings consist of alternating A and B type oxygens and have a CH bond pointing towards their centres. Each six-membered ring is surrounded by six five-membered rings. The twelve five-membered rings are built from B–B–A–C–A oxygen atoms where the midpoint of the B–B edge is located above a CH2 group of the adamantane. Each five-membered ring is surrounded by three other five-membered and two six-membered rings. Following the nomenclature of the cages of clathrate hydrates, this type of cage can be classified as 51264 and is well known to be found in cubic structure II clathrate hydrates where it coexists with pentagonal dodecahedral cages (512).41–43 Like the encapsulated adamantane molecule, the 51264 cage has Td point-group symmetry.
In principle, the adamantane molecule with its almost spherical shape could be expected to spin within a cage of water molecules. However, this is only observed above 208.6 K for bulk adamantane44–46 and is evidently not the case for our samples which were characterised at 80 K.
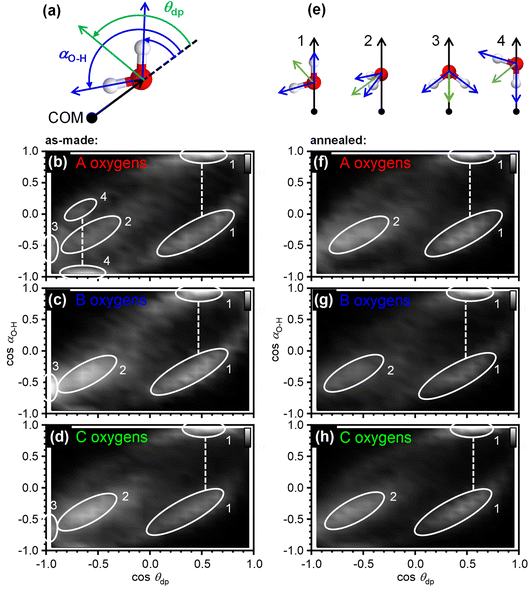
The orientation correlations of the water molecules in the first hydration shell of adamantane were analysed in a next step. For this, it was found to be useful to define two different angles with respect to the vector spanning from the COM of adamantane to the oxygen atom of a given water molecule as shown in Fig. 4(a). The deflection of the dipole moment away from the COM→O vector is defined as θdp whereas αO–H describes the angle between the COM→O vector and an O–H bond of the water molecule. One of the two O–H bonds of a given water molecule is randomly picked in ANGULA. Therefore, depending on the orientation of the water molecule, αO–H can in principle display two values.
The orientation-correlation functions of the as-made samples are shown in Fig. 4(b–d) for the water molecules with A, B and C-type oxygen atoms. As expected for hydrogen-bonded water molecules in approximately tetrahedral environments, strong orientation correlations are observed. The relevant orientations are shown schematically in Fig. 4(e) and indicated by circled locations in Fig. 4(b–d). Orientations 1 and 2 are those expected for hydrogen-bonded water molecules forming a clathrate-hydrate-type cage around a hydrophobic species. In the case of orientation 1, one of the O–H bonds points away from the centre of the hydrophobe whereas the second O–H bond takes part in the hydrogen-bonded network of the cage. This type of orientation is observed in two locations in Fig. 4(b–d) as two different values are possible for αO–H. Orientation 2 means that both O–H bonds are part of the hydrogen-bonded cage. Consequently, αO–H displays the same value for both O–H bonds and only one location is observed in Fig. 4(b–d).
Orientations 3 and 4 are incompatible with a hydrogen-bonded cage structure. Here, either the dipole moment of a water molecule or an O–H bond point directly towards the COM of adamantane. Orientation 3 is observed for all three types of water molecules and is particularly pronounced for the water molecules with B type oxygens. Orientation 4 on the other hand is mostly observed for the water molecules with A type oxygens. These two orientations should be regarded as a type of disorder that is expected to interfere or at least strain the hydrogen bonding within the 51264 cage.
Interestingly, after annealing at 140 K, orientations 3 and 4 are greatly reduced if not absent, and orientations 1 and 2 dominate as can be seen in Fig. 4(f–h). This means that during the deposition at 80 K, some of the water molecules end up in orientations that make hydrogen bonding difficult and this type of disorder can be removed by thermal annealing at temperatures above the orientational glass-transition temperature of the matrix.25 As observed earlier, the positional order of the atoms is increased through the thermal annealing (see Fig. 2(c) and 3(b, c)) which can now be understood from the elimination of the unfavourable type 3 and 4 orientations. The ability to detect the subtle structural changes upon thermal annealing suggests that the EPSR approach for structure reconstruction works very well for the adamantane/ice mixtures.
The arithmetic mean of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdp as a function of distance from the COM of adamantane is shown in Fig. 5. This shows that the very closest water molecules display a tendency for their dipole moments to point towards the adamantane. However, starting from distances around the first maximum in gCOM–O(r), the mean of cos
θdp as a function of distance from the COM of adamantane is shown in Fig. 5. This shows that the very closest water molecules display a tendency for their dipole moments to point towards the adamantane. However, starting from distances around the first maximum in gCOM–O(r), the mean of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdp oscillates closely around zero which means that no net polarisation effect of the water molecules with respect to the adamantane is observed. This is as expected for a nonpolar solute and it can be speculated that the slightly negative polarisation of the very closest water molecules can be attributed to steric effects.
θdp oscillates closely around zero which means that no net polarisation effect of the water molecules with respect to the adamantane is observed. This is as expected for a nonpolar solute and it can be speculated that the slightly negative polarisation of the very closest water molecules can be attributed to steric effects.
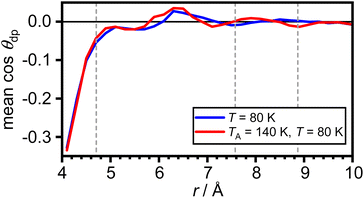 | ||
Fig. 5 Net polarisation effects of the hydrophobic hydration. Arithmetic mean of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdp as a function of distance from the COM of adamantane. The maxima in gCOM–O(r) from Fig. 2(c) are shown as grey dashed vertical lines. θdp as a function of distance from the COM of adamantane. The maxima in gCOM–O(r) from Fig. 2(c) are shown as grey dashed vertical lines. | ||
The effects of the incorporation of adamantane on the hydrogen bonding of the amorphous ice matrix was investigated with FT-IR spectroscopy. The O–H stretching mode of H2O is well known to be affected by complicated intra- and intermolecular coupling.50 This can be ‘switched off’ by adding small amounts of D2O to the initial sample solution which results in spatially well-separated O–D oscillators in the amorphous ice.24,51 The resulting so-called decoupled O–D modes, μO–D, are not affected by coupling phenomena and hence provide an accurate probe for the local hydrogen-bonding environments.52,53
Fig. 6 shows the FT-IR spectra of as-made pure amorphous ice, adamantane matrix-isolated in amorphous ice with molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 and 1
100 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 as well as pure vapour-deposited adamantane in the spectral ranges of μO–D and νC–H.24,54,55 The incorporation of adamantane into amorphous ice leads to an increase in the peak position of μO–D as indicated by the arrow in Fig. 6(a). This highlights a general weakening of the hydrogen bonds. Furthermore, the μO–D modes become increasingly asymmetric on the high-wavenumber side as more adamantane is matrix isolated. Consistent with the structure derived from neutron diffraction, this may indicate the presence of water molecules with strained or even disrupted hydrogen bonding.
34 as well as pure vapour-deposited adamantane in the spectral ranges of μO–D and νC–H.24,54,55 The incorporation of adamantane into amorphous ice leads to an increase in the peak position of μO–D as indicated by the arrow in Fig. 6(a). This highlights a general weakening of the hydrogen bonds. Furthermore, the μO–D modes become increasingly asymmetric on the high-wavenumber side as more adamantane is matrix isolated. Consistent with the structure derived from neutron diffraction, this may indicate the presence of water molecules with strained or even disrupted hydrogen bonding.
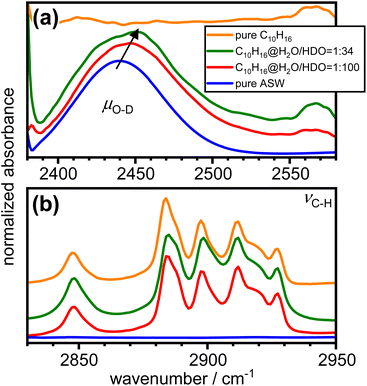 | ||
Fig. 6 FT-IR spectra of pure amorphous ice, adamantane matrix-isolated in amorphous ice at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 and 1 100 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 molar ratios and pure vapour-deposited adamantane in the spectral regions of (a) the decoupled O–D stretching modes24 and (b) the C–H stretching modes of adamantane.54 The spectra were shifted vertically for clarity. 34 molar ratios and pure vapour-deposited adamantane in the spectral regions of (a) the decoupled O–D stretching modes24 and (b) the C–H stretching modes of adamantane.54 The spectra were shifted vertically for clarity. | ||
The C–H stretching modes of adamantane54 shown in Fig. 6(b) are not significantly affected by the incorporation into amorphous ice. This is consistent with weak interactions between the adamantane and the surrounding amorphous ice.
Conclusions
Adamantane has been matrix-isolated in amorphous ice through cryogenic codeposition from the vapour phase. Using neutron diffraction in combination with the isotopic substitution method and the empirical potential structure refinement approach for structure reconstruction we found that the first hydration shell of adamantane is well structured and consists of a 51264 cage with 28 water molecules. Most of the orientations of the water molecules are as expected for a clathrate-hydrate-type cage. Yet, the as-made sample also displayed unfavourable orientations within the first hydration shell with water molecules where either the dipole moment or one of the O–H bonds of water pointed towards the adamantane. These structural features may indicate the onset of the expected structural cross-over from small hydrophobes towards hydrophobic surfaces.8,9 However, even larger hydrophobes than adamantane are probably needed to observe this more clearly. Also, annealing at 140 K led to a removal of the unfavourable orientations. Overall, only the closest water molecules display tendencies for the dipole moment of water to point towards the adamantane which we attribute to steric effects. For hydrated methane, such net polarisation effects were entirely absent.5 As observed with FT-IR spectroscopy, the incorporation of adamantane into amorphous ice leads to a weakening of the hydrogen bonds of the amorphous ice matrix. Similar effects were also found for water at the interface with liquid CCl4 and hexane.1The formation of a well-defined cage structure around adamantane suggests that a plethora of other cage types may exist upon hydrating larger hydrophobes. In principle, this could provide a first step for forming new types of clathrate hydrates upon crystallisation of the amorphous matrix. So far, this has only been achieved for small gaseous guest species.56
For adamantane, it has been suggested that it forms a structure H clathrate hydrate when methane is used as a help-gas.57 Yet, no crystallographic information has yet been obtained. Fig. 3(e) shows the structure of the ‘barrel-shaped’ 51268 cage found in hexagonal structure H clathrate hydrates which would be occupied by adamantane. The 51268 cage is the largest cage observed in clathrates so far.47–49 Our findings raise the question if adamantane actually forms a cubic structure II clathrate hydrate. Of course, it is also possible that the cage type changes from 51264 to 51268 upon the crystallisation of an adamantane clathrate hydrate. In any case, a variety of new types of clathrate hydrates with large cages have been predicted computationally58–62 and these may be accessible by crystallising amorphous mixtures of ice and large hydrophobic species. Future work will certainly develop towards hydrating larger hydrophobic molecules with potentially more complex shapes.
The potential formation of clathrate hydrates by heating amorphous mixtures of ice and hydrocarbons, such as adamantane, would have an impact on the physical properties of such mixtures in space including the desorption rates of water.63 As shown in this study, the incorporation of adamantane into amorphous ice leads to a weakening of the hydrogen bonds which in turn could affect the water desorption rates of the amorphous ice in space. The net polarisation effects of water in the hydration shell were found to be quite weak. Yet, it can be speculated that such polarisation effects64,65 could influence the surfaces charges of ice-coated hydrocarbons which in turn may influence the aggregation properties and hence formation of larger objects in space.
Author contributions
Conceptualization (CGS), formal analysis (SKT, TFH, LCP, CGS), investigation (SKT, LCP, TFH), methodology (SKT, CGS, TFH, LCP, SOH, BC, AR), supervision (CGS, LCP, TFH), visualization (SKT, LCP, TFH, CGS), writing – original draft (CGS, SKT) and writing – review & editing (all authors).Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding is acknowledged from the European Research Council under the European Union's Horizon 2020 research and innovation program (grant agreement No 725271). LCP acknowledges financial support from the projects PID2020-112975GB-I00 and 2021SGR-00343. We thank M. Zwijnenburg for comments on the first draft of the manuscript, S. Imberti for helpful discussions, and the ISIS facility for access to the NIMROD instrument. Experimental data is available at: https://doi.org/10.5286/ISIS.E.RB1910462.References
- L. F. Scatena, M. G. Brown and G. L. Richmond, Science, 2001, 292, 908–912 CrossRef CAS PubMed.
- D. K. Hore, D. S. Walker and G. L. Richmond, J. Am. Chem. Soc., 2008, 130, 1800–1801 CrossRef CAS PubMed.
- J. Monroe, M. Barry, A. DeStefano, P. Aydogan Gokturk, S. Jiao, D. Robinson-Brown, T. Webber, E. J. Crumlin, S. Han and M. S. Shell, Annu. Rev. Chem. Biomol. Eng., 2020, 11, 523–557 CrossRef CAS.
- S. Pullanchery, S. Kulik and S. Roke, J. Phys. Chem. B, 2022, 126, 3186–3192 CrossRef CAS.
- C. A. Koh, R. P. Wisbey, X. Wu, R. E. Westacott and A. K. Soper, J. Chem. Phys., 2000, 113, 6390–6397 CrossRef CAS.
- I. U. Goldschleger, G. Kerenskaya, V. Senekerimyan, K. C. Janda and V. A. Apkarian, Phys. Chem. Chem. Phys., 2008, 10, 7226–7232 RSC.
- M. Montagna, F. Sterpone and L. Guidoni, J. Phys. Chem. B, 2012, 116, 11695–11700 CrossRef CAS.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- D. Chandler, Nature, 2002, 417, 491 CrossRef CAS PubMed.
- D. T. Bowron and J. L. Finney, J. Phys. Chem. B, 2007, 111, 9838–9852 CrossRef CAS.
- D. T. Bowron, A. K. Soper and J. L. Finney, J. Chem. Phys., 2001, 114, 6203–6219 CrossRef CAS.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- B. H. Foing and P. Ehrenfreund, Nature, 1994, 369, 296–298 CrossRef CAS.
- J. Cami, J. Bernard-Salas, E. Peeters and S. E. Malek, Science, 2010, 329, 1180–1182 CrossRef CAS.
- O. Pirali, M. Vervloet, J. E. Dahl, R. M. K. Carlson, A. G. G. M. Tielens and J. Oomens, Astrophys. J., 2007, 661, 919 CrossRef CAS.
- Z. Guennoun, C. Aupetit and J. Mascetti, Phys. Chem. Chem. Phys., 2011, 13, 7340–7347 RSC.
- Z. Guennoun, C. Aupetit and J. Mascetti, J. Phys. Chem. A, 2011, 115, 1844–1852 CrossRef CAS PubMed.
- J. Bouwman, A. L. Mattioda, H. Linnartz and L. J. Allamandola, Astron. Astrophys., 2011, 525, A93 CrossRef.
- A. M. Cook, A. Ricca, A. L. Mattioda, J. Bouwman, J. Roser, H. Linnartz, J. Bregman and L. J. Allamandola, Astrophys. J., 2015, 799, 14 CrossRef.
- A. L. F. de Barros, A. L. Mattioda, A. Ricca, G. A. Cruz-Diaz and L. J. Allamandola, Astrophys. J., 2017, 848, 112 CrossRef.
- E. Michoulier, C. Toubin, A. Simon, J. Mascetti, C. Aupetit and J. A. Noble, J. Phys. Chem. C, 2020, 124, 2994–3001 CrossRef CAS.
- A. Lignell and M. S. Gudipati, J. Phys. Chem. A, 2015, 119, 2607–2613 CrossRef CAS.
- M. Fisher and J. P. Devlin, J. Phys. Chem., 1995, 99, 11584–11590 CrossRef CAS.
- J. J. Shephard, J. S. O. Evans and C. G. Salzmann, J. Phys. Chem. Lett., 2013, 4, 3672–3676 CrossRef CAS.
- J. J. Shephard and C. G. Salzmann, J. Phys. Chem. Lett., 2016, 7, 2281–2285 CrossRef CAS.
- S. O. Halukeerthi, J. J. Shephard, S. K. Talewar, J. S. O. Evans, A. Rosu-Finsen and C. G. Salzmann, J. Phys. Chem. A, 2020, 124, 5015–5022 CrossRef CAS PubMed.
- A. K. Soper, Chem. Phys., 1996, 202, 295–306 CrossRef CAS.
- A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204 CrossRef.
- S. K. Talewar, S. O. Halukeerthi, R. Riedlaicher, J. J. Shephard, A. E. Clout, A. Rosu-Finsen, G. R. Williams, A. Langhoff, D. Johannsmann and C. G. Salzmann, J. Chem. Phys., 2019, 151, 134505 CrossRef PubMed.
- S. K. Talewar, PhD thesis, University College London, 2021.
- D. Johannsmann, Phys. Chem. Chem. Phys., 2008, 10, 4516–4534 RSC.
- D. T. Bowron, A. K. Soper, K. Jones, S. Ansell, S. Birch, J. Norris, L. Perrott, D. Riedel, N. J. Rhodes, S. R. Wakefield, A. Botti, M. A. Ricci, F. Grazzi and M. Zoppi, Rev. Sci. Instrum., 2010, 81, 033905 CrossRef CAS PubMed.
- A. K. Soper, Mol. Phys., 2009, 107, 1667–1684 CrossRef CAS.
- A. K. Soper, ISRN Phys. Chem., 2013, 2013, 279463 Search PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- L. C. Pardo, ANGULA Software Download, https://gcm.upc.edu/en/members/luis-carlos/angula/ANGULA, accessed 5th January, 2021 Search PubMed.
- L. C. Pardo, A. Henao and A. Vispa, J. Non-Cryst. Solids, 2015, 407, 220–227 CrossRef CAS.
- L. C. Pardo, A. Henao, S. Busch, E. Guàrdia and J. L. Tamarit, Phys. Chem. Chem. Phys., 2014, 16, 24479–24483 RSC.
- A. J. Johnston, S. Busch, L. C. Pardo, S. K. Callear, P. C. Biggin and S. E. McLain, Phys. Chem. Chem. Phys., 2016, 18, 991–999 RSC.
- G. A. Jeffrey, in Inclusion Compounds, New York, 1984, vol. 1, pp. 135–190 Search PubMed.
- J. A. Ripmeester, C. I. Ratcliffe, D. D. Klug and J. S. Tse, Ann. N. Y. Acad. Sci., 1994, 715, 161–176 CrossRef CAS.
- J. S. Loveday and R. J. Nelmes, Phys. Chem. Chem. Phys., 2008, 10, 937–950 RSC.
- S.-S. Chang and E. F. Westrum Jr, J. Phys. Chem., 1960, 64, 1547–1551 CrossRef CAS.
- J. P. Amoureux, M. Bee and J. C. Damien, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2633–2636 CrossRef.
- A. B. Bazyleva, A. V. Blokhin, G. J. Kabo, M. B. Charapennikau, V. N. Emel'yanenko, S. P. Verevkin and V. Diky, J. Phys. Chem. B, 2011, 115, 10064–10072 CrossRef CAS.
- J. A. Ripmeester, J. S. Tse, C. I. Ratcliffe and B. M. Powell, Nature, 1987, 325, 135–136 CrossRef CAS.
- K. A. Udachin, C. I. Ratcliffe, G. D. Enright and J. A. Ripmeester, Supramol. Chem., 1997, 8, 173–176 CrossRef CAS.
- Y. Jin, M. Kida and J. Nagao, J. Phys. Chem. C, 2015, 119, 9069–9075 CrossRef CAS.
- E. Whalley, Can. J. Chem., 1977, 55, 3429–3441 CrossRef CAS.
- W. Hage, A. Hallbrucker, E. Mayer and G. P. Johari, J. Chem. Phys., 1994, 100, 2743–2747 CrossRef CAS.
- B. Minceva-Sukarova, W. F. Sherman and G. R. Wilkinson, Spectrochim. Acta, Part A, 1985, 41, 315–318 CrossRef.
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS.
- A. Patzer, M. Schütz, T. Möller and O. Dopfer, Angew. Chem., Int. Ed., 2012, 51, 4925–4929 CrossRef CAS PubMed.
- M. A. R. George, M. Förstel and O. Dopfer, Angew. Chem., Int. Ed., 2020, 59, 12098–12104 CrossRef CAS PubMed.
- E. Mayer and A. Hallbrucker, J. Chem. Soc., Chem. Commun., 1989,(12), 749–751 RSC.
- J. P. Lederhos, A. P. Mehta, G. B. Nyberg, K. J. Warn and E. D. Sloan, AIChE J., 1992, 38, 1045–1048 CrossRef CAS.
- J. Vatamanu and P. G. Kusalik, J. Am. Chem. Soc., 2006, 128, 15588–15589 CrossRef CAS.
- Y. Huang, C. Zhu, L. Wang, X. Cao, Y. Su, X. Jiang, S. Meng, J. Zhao and X. C. Zeng, Sci. Adv., 2016, 2, e1501010 CrossRef.
- Y. Huang, C. Zhu, L. Wang, J. Zhao and X. C. Zeng, Chem. Phys. Lett., 2017, 671, 186–191 CrossRef CAS.
- Y. Liu and L. Ojamäe, Phys. Chem. Chem. Phys., 2018, 20, 8333–8340 RSC.
- Y. Liu, W. Zhu, J. Jiang, C. Zhu, C. Liu, B. Slater, L. Ojamäe, J. S. Francisco and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104442118 CrossRef CAS PubMed.
- A. H. Delsemme and P. Swings, Ann. Astrophys., 1952, 15, 1–6 CAS.
- A. Rosu-Finsen, J. Lasne, A. Cassidy, M. R. S. McCoustra and D. Field, Phys. Chem. Chem. Phys., 2016, 18, 5159–5171 RSC.
- A. Rosu-Finsen, J. Lasne, A. Cassidy, M. R. S. McCoustra and D. Field, Astrophys. J., 2016, 832, 1 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00102d |
| This journal is © The Royal Society of Chemistry 2024 |