Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The influences of carbon donor ligands on biomimetic multi-iron complexes for N2 reduction†
Alexandra L.
Nagelski
 a,
Majed S.
Fataftah
a,
Majed S.
Fataftah
 a,
Melissa M.
Bollmeyer
a,
Melissa M.
Bollmeyer
 b,
Sean F.
McWilliams
a,
Samantha N.
MacMillan
b,
Sean F.
McWilliams
a,
Samantha N.
MacMillan
 b,
Brandon Q.
Mercado
a,
Kyle M.
Lancaster
b,
Brandon Q.
Mercado
a,
Kyle M.
Lancaster
 *b and
Patrick L.
Holland
*b and
Patrick L.
Holland
 *a
*a
aDepartment of Chemistry, Yale University, 225 Prospect Street, New Haven, Connecticut 06520, USA. E-mail: patrick.holland@yale.edu
bDepartment of Chemistry and Chemical Biology, Baker Laboratory, Cornell University, Ithaca, New York 14853, USA. E-mail: kml236@cornell.edu
First published on 6th August 2020
Abstract
The active site clusters of nitrogenase enzymes possess the only examples of carbides in biology. These are the only biological FeS clusters that are capable of reducing N2 to NH4+, implicating the central carbon and its interaction with Fe as important in the mechanism of N2 reduction. This biological question motivates study of the influence of carbon donors on the electronic structure and reactivity of unsaturated, high-spin iron centers. Here, we present functional and structural models that test the impacts of carbon donors and sulfide donors in simpler iron compounds. We report the first example of a diiron complex that is bridged by an alkylidene and a sulfide, which serves as a high-fidelity structural and spectroscopic model of a two-iron portion of the active-site cluster (FeMoco) in the resting state of Mo-nitrogenase. The model complexes have antiferromagnetically coupled pairs of high-spin iron centers, and sulfur K-edge X-ray absorption spectroscopy shows comparable covalency of the sulfide for C and S bridged species. The sulfur-bridged compound does not interact with N2 even upon reduction, but upon removal of the sulfide it becomes capable of reducing N2 to NH4+ with the addition of protons and electrons. This provides synthetic support for sulfide extrusion in the activation of nitrogenase cofactors.
Introduction
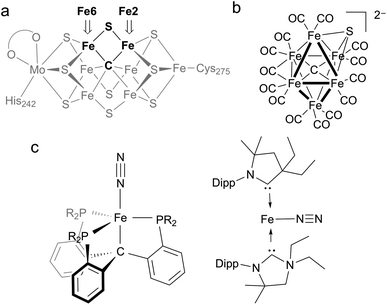
Nitrogenases are enzymes that accomplish the impressive feat of reducing N2 to NH4+ at ambient temperatures and pressures. The active site of the most thoroughly studied nitrogenase is the iron–molybdenum cofactor (FeMoco), a unique iron–sulfur cluster composed of one molybdenum and seven iron atoms held together with a number of bridging atoms (Fig. 1a).1 A range of kinetic, mutagenesis, and spectroscopic studies support N2 binding at the iron atoms of FeMoco,2–8 but the structures of intermediate species in the mechanism of N2 reduction remain unclear.1A distinguishing feature of the FeMoco is the central carbide (formally C4−), which is bound to six iron atoms in the resting state.9,10 Isotopic labeling studies show that the carbide is not exchanged during turnover.11 X-ray emission spectroscopy has shown that the iron-carbide bonds are highly covalent.12 The active-site clusters of nitrogenases are the only known examples of carbides in biological systems, and they are also the only catalysts for N2 reduction in nature, implying the carbide serves an essential role in this transformation. However, the specific role of the carbide during the catalytic cycle for N2 reduction remains obscure. One hypothesis for N2 binding to FeMoco proposes cleavage of hemilabile Fe–S bonds during catalysis, in which case the carbide may function to preserve structural integrity by anchoring the core structure of the cofactor.7,8,13,14 This idea is supported by several crystallographic studies showing that the belt sulfide S2B (which bridges Fe2 and Fe6) can be reversibly displaced from the cluster (Fig. 1a).7,8,14,15 These results suggest the Fe2/Fe6 locus as a primary substrate binding site in the cofactor. Another hypothesis proposes Fe–C bond cleavage during turnover to create an open coordination site on iron.3,16 This could be accompanied by C–H bond formation, an idea that is supported by recent work on a synthetic diiron complex containing a bridging carbyne.17 Other proposals involve direct interactions between the carbide and N2.18–20 The wide variety of these proposals underscores the limited understanding of the structural and electronic contributions of bridging carbon ligands to reactivity in iron–sulfur clusters.
Synthetic complexes offer useful insights as structural or functional models of nitrogenase, but accessing species with both carbon and sulfur donors has been challenging.21 In a recent study, Rauchfuss and coworkers reported the first synthetic example of an iron cluster with both carbide and sulfide (Fig. 1b), which have different bridging modes than FeMoco.22 In this compound, the CO ligands lead to low-spin iron centers that contrast with the high-spin iron centers found in FeMoco.
In functional synthetic models, mononuclear iron complexes have been used to gauge the N2-coordinating ability of compounds with Fe–C bonds.16,17,23–28 Of these complexes, only two systems produce NH4+ (3.3–4.6 equiv. NH4+/Fe) upon treatment with acid and reductant (Fig. 1c).16,27 A low-spin iron system, Fe(CPiPr3)N2, where CPiPr3 is tris(2-(diisopropylphosphino)phenyl)methyl, displays lengthening of Fe–C bonds during reduction. The other, (CAAC)2Fe (CAAC = cyclic (alkyl)(amino)carbene), is capable of mediating N2 reduction to NH4+.16,27,29 Studies of iron species with bridging carbon and sulfur ligands that are high-spin with greater electronic and structural fidelity to the Fe2/Fe6 site are needed to improve the understanding of how biological S- and C-based donors impact N2 reactivity.
Here, we present a new diiron complex that has both carbon and sulfur bridges between two high-spin iron centers, creating an Fe2CS diamond core that structurally overlays with a part of the core in FeMoco.30–32 Further, we systematically evaluate the electronic structure and N2 reducing ability of three related high-spin iron complexes with the carbon-based donors alkyl and alkylidene. Importantly, the high-spin iron alkyl and alkylidene complexes produce NH4+ from N2.
Results
Synthesis
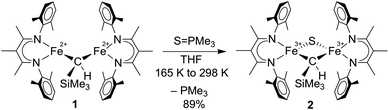
We previously reported the first high-spin iron complex with an unsupported alkylidene bridge, [LMeFe]2(μ-CHSiMe3) (1, where LMe = 3-methyl-2,4-bis(2,6-xylylimido)pentyl).33 Treatment of 1 with 1 equiv. of the sulfur atom transfer reagent Me3PS in a thawing THF solution forms one major species, [LMeFe]2(μ-S)(μ-CHSiMe3) (2), which was isolated in 89% yield (Scheme 1). This material is 95% pure as judged by Mössbauer spectroscopy, and was sufficient for extensive characterization. Extracting the crude reaction into Et2O and cooling to 233 K yielded green crystals. The molecular structure of 2 (Fig. 2a) has one sulfide bridge and one CHSiMe3 bridge between two identically-bonded iron(III) centers. The 1H NMR spectrum is consistent with each diketiminate environment having a single mirror plane perpendicular to the FeN2C3 plane, which agrees with the core symmetry but is surprising given the overall Cs symmetry expected for the molecule. While this may indicate dynamic cleavage of the Fe–C bonds, we have no other evidence for this behavior. It is also notable that the resonances in the 1H NMR spectrum are shifted and broadened, indicating population of paramagnetic states that is explored below through magnetic susceptibility measurements.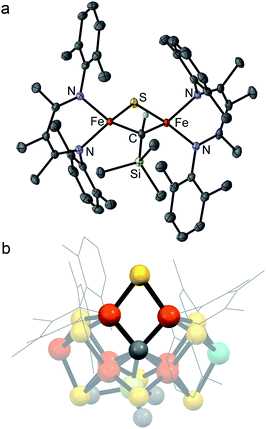 | ||
| Fig. 2 (a) Crystal structure of [LMeFe]2(μ-S)(μ-CHSiMe3) (2) with thermal ellipsoids shown at 50% probability. Color scheme: iron in orange, nitrogen in blue, carbon in gray, silicon in green, and sulfur in yellow. Hydrogen atoms have been omitted for clarity except on the alkylidene ligand. (b) Structural overlay of 2 with Fe2/Fe6/S2B/C rhomb in the FeMoco (nitrogenase crystal structure PDB 3U7Q). | ||
Several structural comparisons are striking. The average Fe–C bond length in the diiron(III) complex 2 is 1.994(2) Å, which is 0.030(8) Å longer than the average Fe–C bond in the diiron(II) complex 1 despite the higher oxidation state of iron. The sulfide bridge causes the Fe–C–Fe bond angle to decrease from 95.6(3)° in 1 to 81.74(6)° in 2. The diamond core in 2 is contracted relative to the one in a previously reported bis(sulfide) diiron(III) complex [LMeFeS]2, as in 2 the Fe–S bonds are 0.116(2) Å shorter and the Fe⋯Fe distance is 0.641(2) Å shorter.34,35 Importantly, the core of 2 overlays well with the rhomb containing Fe2 and Fe6 in FeMoco, as the Fe–C and Fe–S average bond lengths in both structures are similar (Fe–Cavg is 1.994(2) Å in 2vs. 2.00 Å in FeMoco; Fe–Savg is 2.217(8) Å in 2 and 2.25 Å in FeMoco for the Fe2/Fe6 rhomb).10 The Fe⋯Fe distance in 2 is 2.6027(6) Å, which matches the distances between belt iron atoms in the crystal structure of FeMoco (2.61 Å) quite well. The overall Fe/Fe/S/C core in 2 overlays with the Fe2/Fe6/S2B/C core of the resting state FeMoco with an root-mean-square deviation (RMSD) of 0.08 Å (Fig. 2b). These comparisons indicate that despite the difference in carbon coordination number, the alkylidene in 2 serves as an accurate structural model for the carbide bridge in FeMoco.
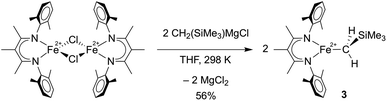
To compare the influence of the alkylidene in 1 to a mononuclear alkyl analogue, we also prepared a three-coordinate iron(II) alkyl complex with diketiminate supporting ligands using a known method.36,37 Adding 2.1 equiv. of MgBrCH2SiMe3 to a solution of [LMeFeCl]2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 in THF led to the trimethylsilylmethyl iron(II) complex 3, which could be isolated in 56% yield (Scheme 2). The X-ray crystallographic data of 3 reveal a planar three-coordinate iron center featuring an Fe–C bond length of 2.017(3) Å, which is comparable to the Fe–C bond lengths in other previously reported three-coordinate β-diketiminate iron(II) alkyl species.33,36,37,39,40 Similar to these related compounds, 3 has a high-spin electronic configuration (S = 2), as judged by the Evans method in solution (μeff in C6D6 at 298 K is 5.4(2) μB), and averaged C2v symmetry evident in its 1H NMR spectrum indicating rapid rotation around the Fe–C bond.
38 in THF led to the trimethylsilylmethyl iron(II) complex 3, which could be isolated in 56% yield (Scheme 2). The X-ray crystallographic data of 3 reveal a planar three-coordinate iron center featuring an Fe–C bond length of 2.017(3) Å, which is comparable to the Fe–C bond lengths in other previously reported three-coordinate β-diketiminate iron(II) alkyl species.33,36,37,39,40 Similar to these related compounds, 3 has a high-spin electronic configuration (S = 2), as judged by the Evans method in solution (μeff in C6D6 at 298 K is 5.4(2) μB), and averaged C2v symmetry evident in its 1H NMR spectrum indicating rapid rotation around the Fe–C bond.
Reduction of N2 to NH4+ by C-bound iron complexes
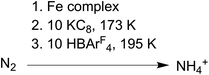
The conversion of N2 to NH4+ with the addition of reductant and acid was used to evaluate compounds 1–3 as functional models of nitrogenase. These studies used KC8 and [H(Et2O)2][BArF4] (HBArF4) under conditions similar to those in several catalytic systems (see ESI†).27,41 In our work, the reductant (10 equiv.) was added first to the complexes at 173 K and then the acid (10 equiv.) was added to the frozen mixture and stirred at 195 K (Scheme 3). This order of addition minimizes the potential for competitive protonation of the β-diketiminate ligand.42Using Et2O as solvent, complexes 1 and 3 generate 50–70% yield of NH4+ per complex while 2 produces only trace amounts (left side of Table 1). Analogous experiments using 1 and 3 performed under an atmosphere of 15N2 yield exclusively 15NH4+ and under an atmosphere of Ar yield < 5% of NH4+/complex (Fig. S6, 7 and Table S1†). These control experiments demonstrate the NH4+ formed by 1 and 3 is derived from N2, not from the diketiminate ligands or impurities. We also tested N2 reduction in THF (right side of Table 1), but the NH4+ yields were roughly five times lower than the analogous experiments in Et2O. We hypothesize that this difference is a result of less favorable N2 binding in THF (vide infra).
| Et2O | THF | |||||
|---|---|---|---|---|---|---|
| NH4+ per complex | % Yield per complex | % Yield per Fe | NH4+ per complex | % Yield per complex | % Yield per Fe | |
| a Ammonium determined using the indophenol method. Error represented as a range of multiple trials; lack of error bar indicates a single trial. | ||||||
| 1 | 1.12 ± 0.06 | 56 ± 3 | 28 ± 1 | 0.29 | 15 | 7.4 |
| 2 | 0.10 ± 0.05 | 5 ± 3 | 2 ± 2 | — | — | — |
| 3 | 1.37 ± 0.17 | 68 ± 7 | 68 ± 7 | 0.25 ± 0.03 | 13 ± 2 | 13 ± 2 |
| 4 | 1.10 ± 0.03 | 55 ± 1 | 55 ± 1 | 0.19 | 9 | 9 |
To explore the species responsible for NH4+ production from 1, we conducted low temperature 1H NMR studies with smaller amounts of reductant and acid. Reduction of 1 with 1.6 equiv. of KC8 in THF-d8 at 203 K showed trace amounts (<10%) of 1 and 3, but most of the mixture consisted of unidentified species that we were unable to isolate due to thermal decomposition above 203 K. Further attempts to isolate reduced forms of 1 were not successful (see ESI†). As a result, we cannot confidently attribute the N2 reduction by 1 to any one active species. However, we reason that since the conversion of 1 to 3 upon reduction is relatively low, the N2 reduction activity of 1 cannot be solely attributed to the formation of 3 under these conditions (see ESI† for further discussion). It is therefore evident that there is some reduced form of 1 (or a degradation product therefrom) that is capable of N2 binding and reduction to NH4+.
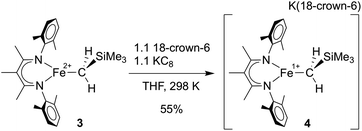
In separate reduction experiment, treatment of 3 with 1.2 equiv. of KC8 in the presence of 1.2 equiv. of 18-crown-6 in THF formed the iron(I) complex [LMeFeCH2SiMe3][K(18-crown-6)] (4) in 55% yield (Scheme 4). Treatment of 4 with additional reductant did not result in further chemical changes. It was possible to characterize 4 in detail, including an X-ray crystal structure that showed separated cations (in which two THF molecules are bound to K+ in addition to the 18-crown-6; see ESI†) and anions (in which the iron(I) ion is three-coordinate). The THF molecules are weakly bound to the K(18-crown-6) cation, as indicated by their absence in a low-quality crystal structure in which the K(18-crown-6)+ unit was coordinated to the supporting ligand. Microanalysis also indicated the absence of the THF molecules in the isolated solid.
We investigated the ability of 4 to produce NH4+ from N2 under conditions similar to those described above, and found that it generates NH4+ in comparable yields to 3 (Table 1). These experiments suggest that 4 is a feasible intermediate during the series of transformations leading to N2 reduction by 3.
N2 binding
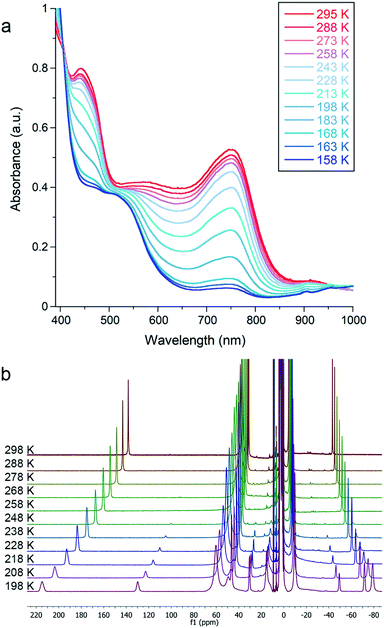
Cooling 1, 2, or 3 under N2 in THF-d8 yielded no spectroscopic changes (Fig. S8–S10 and S16†). In contrast, cooling an Et2O solution of 4 under 1 atm N2 resulted in a color change from green to red that was monitored using electronic absorption spectroscopy (Fig. 3a). Under 1 atm N2, a room-temperature solution of 4 in Et2O displayed prominent absorption bands at 450 and 750 nm whose intensity drastically decreased upon cooling. This marked change did not occur in upon cooling a sample under Ar (Fig. S18†), indicating that the changes come from N2 binding. Similar changes in the absorption spectrum were observed when cooling solutions of 4 in THF or 2-methyltetrahydrofuran (MeTHF) under N2 (Fig. S19–S21†). At 168 K, the decrease in the intensity of the bands corresponding to 4 was greatest in Et2O, followed by THF, then MeTHF (Fig. S17–21†). The higher conversion to 4–N2 in Et2O at a given temperature is attributable to the greater solubility of N2 in Et2O than in THF and MeTHF.43,44 Similar mononuclear complexes have demonstrated N2 bridging to a κ1-bound alkali cation.45 Thus, in addition to the differences in N2 solubility between these solvents, solvent coordination to the K(18-crown-6) cation could also contribute to the observed differences in N2 binding affinity of 4. Further, the N2 reduction experiments in Et2O generate approximately four-fold greater NH4+ yields than analogous experiments run in THF (vide supra).Due to decomposition at concentrations suitable for electronic absorption spectroscopy, we turned to 1H NMR spectroscopy for more reproducible quantification. Variable temperature experiments in Et2O-d10 allowed us to quantify the equilibrium between 4 and 4–N2, which are in slow exchange on the NMR time scale. Van't Hoff plots for N2 binding to 4 gave ΔH° = −20 ± 1 kJ mol−1 and ΔS° = −57 ± 3 J mol−1 K−1, where the large negative entropy is characteristic of binding a gas (Fig. S12†). A parallel experiment performed in THF-d8 yielded the thermodynamic parameters ΔH° = −26 ± 1 kJ mol−1 and ΔS° = −93 ± 5 J mol−1 K−1 (Fig. 3b and S14†). These parameters are similar to those for N2 binding to the related β-diketiminate iron(I) phenyl complex and other reported iron and cobalt complexes (Table S2†).27,46,47
Spin states and exchange coupling
The electronic structures of 1 and 2 provide valuable insights into the influences of S and C bridges in iron–sulfur clusters. The Mössbauer spectrum48 of 1 at 80 K displays signals with an isomer shift of 0.62 mm s−1, consistent with high-spin iron(II) centers.33 Inspection of the magnetic susceptibility of 1 reveals a sharp decrease in χMT with decreasing temperature, reaching a value of 0.12 cm3 K mol−1 at 2 K (Fig. 4), indicating that the two iron(II) centers are antiferromagnetically coupled. The value of χMT depends linearly on T up to a value of 2.17 cm3 K mol−1 at 225 K, which is consistent with two high-spin iron(II) centers that are antiferromagnetically coupled. To quantify the magnitude of the antiferromagnetic interaction, the data were fit to the Van Vleck equation according to the spin Hamiltonian: Ĥ = D(Ŝ1z2+ Ŝ2z2) + E[(Ŝ1x2 − Ŝ1y2) + (Ŝ2x2 − Ŝ2y2)] + (g1 + g2)μBSH − 2J(Ŝ1·Ŝ2). In this Hamiltonian, D and E are the axial and transverse zero-field splitting parameters, Ŝ1 and Ŝ2 are the spin operators, g1 and g2 are the isotropic g-values, and J is the magnitude of the exchange interaction. The best fit to the experimental data for 1 was accomplished with an exchange constant of J = −34(2) cm−1, and was relatively insensitive to the other parameters (see ESI†).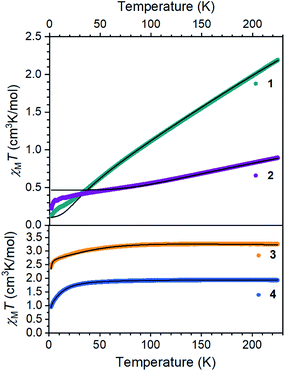 | ||
| Fig. 4 Dc magnetic susceptibility data for 1–4 collected under an applied magnetic field of 1000 Oe. Black lines represent fits to the data. | ||
Next, we examined the spin states in the diiron(III) complex 2, which has both C and S bridges. Its zero-field Mössbauer spectrum at 80 K displays a doublet with δ = 0.26 mm s−1 and |ΔEQ| = 1.95 mm s−1 (Fig. S22†). The isomer shift is much lower than that of 1, consistent with more oxidized iron centers. To support this assignment, we used density-functional (DFT) calculations at the B3LYP/def2-TZVP(Fe,Si,S,N,CHSiMe3)/def2-SVP(C,H) level to give geometry optimized structures in all six possible spin states, and these were used to predict Mössbauer spectra for each spin state using the spectroscopic validation we established for β-diketiminate complexes.49 A broken-symmetry model with two antiferromagnetically coupled high-spin iron(III) centers gave the lowest energy structure, reproduced the crystallographic structure with a RMSD of 0.24 Å, and predicted Mössbauer parameters (δ1 = 0.35 mm s−1, |ΔEQ|1 = 1.62 mm s−1, δ2 = 0.36 mm s−1, |ΔEQ|2 = 1.67 mm s−1) that are within error of the experimental values; the other spin state possibilities gave isomer shift values that deviated from experiment by at least 0.20 mm s−1 or gave two distinct doublets (see ESI† for details). Other four-coordinate diiron(III) sulfide complexes in the literature also have high-spin electronic configurations.50–53 The magnetic susceptibility of 2 displays a χMT value of 0.91 cm3 K mol−1 at 225 K that drops with decreasing temperature, supporting an antiferromagnetic exchange interaction between the iron(III) centers in 2 in agreement with the calculations. We modelled the dc susceptibility data with two high-spin iron(III) sites using the spin Hamiltonian described above with an exchange constant of J = −120(10) cm−1 and isotropic g = 2.0 (see ESI†).
The mononuclear compounds display χMT values of 3.26 (3) and 1.93 (4) cm3 K mol−1 at 225 K. These values are consistent with ground states of S = 2 for 3 (high-spin iron(II)) and S = 3/2 for 4 (high-spin iron(I)). The value of χMT decreases with decreasing temperature due to zero-field splitting. We fit the data with D values of −45.7(3) cm−1 for 3 and −14.9(2) cm−1 for 4. These large zero-field splitting parameters are consistent with those observed in other three-coordinate iron(II) complexes.54–58 The high-spin assignment is also consistent with the Mössbauer spectra of these mononuclear complexes, which display quadrupole doublets with δ = 0.43 mm s−1 and |ΔEQ| = 1.28 mm s−1 for 3, and δ = 0.41 mm s−1 and |ΔEQ| = 2.23 mm s−1 for 4 (Fig. S23 and S24†). These values are consistent with other high-spin iron(II) and iron(I) complexes in the literature, and DFT calculations similar to those described above validated these spin state assignments (see ESI†).55,59–61
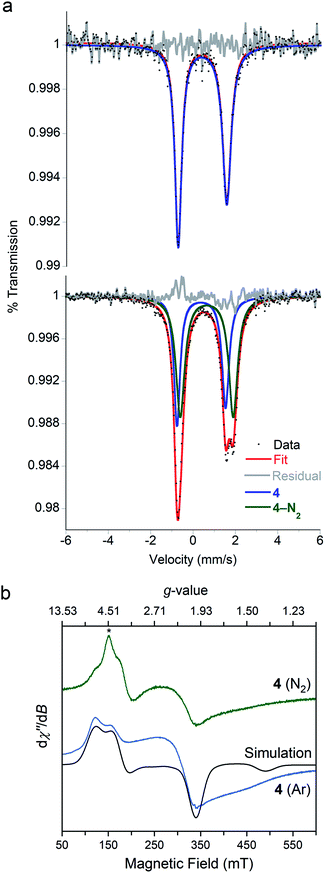
We were interested in the spin state of 4–N2, but our inability to isolate it prevented characterization by magnetometry. However, the Mössbauer spectrum of 4 flash frozen in N2-saturated MeTHF was collected at 80 K and displays an additional doublet that was not observed in a control experiment under Ar. We attribute this new signal to 4–N2 (Fig. 5a), for which the best fit has δ = 0.64 mm s−1 and |ΔEQ| = 2.55 mm s−1. The isomer shift is consistent with reported values of high-spin, four-coordinate iron(I) (S = 3/2) yet too high for reported values for iron(I) in low spin configurations (S = 1/2).55,59–61 Geometry optimizations were performed for both possible spin states of iron(I) in 4–N2, and DFT calculations49 were used to predict Mössbauer parameters for each model. The S = 3/2 model predicted parameters (δ = 0.64 mm s−1, |ΔEQ| = 2.14 mm s−1) that are close to the experimental values, while the S = 1/2 model (δ = 0.36 mm s−1, |ΔEQ| = 1.02 mm s−1) deviated substantially from the experimental data.
To corroborate our assignment of spin states for 4 and 4–N2 as high-spin iron(I), we measured the X-band EPR spectrum of 4 frozen in MeTHF under N2 and Ar at 77 K (Fig. 5b). The EPR spectrum under Ar displays three broad resonances with geff values of 2.1, 3.8 and 5.6 and are consistent with a S = 3/2 ground state. We simulated the EPR spectrum with the spin Hamiltonian employed to model the dc susceptibility data with |D| and |E| values of 12.9 cm−1 and 1.7 cm−1, and g values of 2.36, 2.33, and 2.05. The EPR spectrum for a sample of 4 flash-frozen under N2 displays an additional feature at geff = 5.4 that we attribute to 4–N2. The large effective g-value indicates that 4–N2 has a high-spin configuration (S = 3/2); however, due to the spectral convolution between 4 and 4–N2, we could not adequately model the EPR spectrum to extract the spin Hamiltonian parameters for 4–N2. The agreement with the DFT computations and the Mössbauer spectroscopy, however, supports this assignment of the iron(I) center as S = 3/2 in 4–N2.
Covalency of bonds
To assess the effect of replacing a bridging sulfide with an alkylidene on the Fe–S covalency, we compared sulfur K-edge X-ray absorption spectra (XAS) for 2 to the related bis-sulfide complex, [LMeFeS]2 (Fig. 6a), which also has two high-spin iron(III) centers, but these centers are instead bridged by two sulfide ligands.34 We examined the pre-edge areas at 2470 eV determined by peak fitting of the S K-edges, in order to quantify the S 3p character in the unoccupied metal d orbitals.62 The contribution from the two bridging sulfide ligands in [LMeFeS]2 is 14% S 3p and the contribution from the single bridging sulfide ligand in 2 is 6%. Because the 3p character in [LMeFeS]2 is twice the value for 2 and reflects the contributions from two sulfides instead of one, it follows that the Fe–S covalency per bond is not significantly perturbed by the substitution of an alkylidene for one of the sulfide ligands. This interpretation of the XAS agrees with the similar isomer shifts observed for 2 and [LMeFeS]2, which reflect the electron density at the iron centers (Fig. S17†).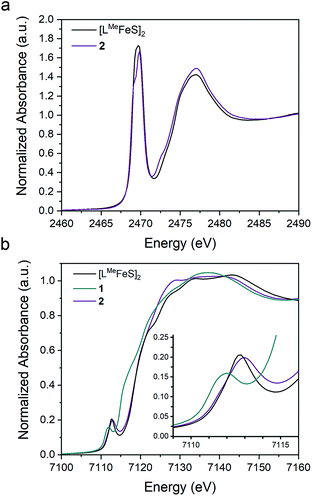 | ||
| Fig. 6 Overlay of the (a) S K-edge XAS spectra of 2 (purple) and [LMeFeS]2 (black) and (b) Fe K-edge XAS spectra of the 1 (teal), 2 (purple), and [LMeFeS]2 (black). | ||
Broken symmetry DFT calculations indicated strong antiferromagnetic coupling between iron centers in both [LMeFeS]2 and 2 (Fig. 7). The overlap (J) was −84 cm−1 for [LMeFeS]2 and −313 cm−1 for 2, but these values from a single reference DFT calculation relative to experiment are commonly overestimated.63–66 Calculated spectra (Fig. S41–43†) were thus obtained using the lowest energy solution with S = 0. It should be noted that the differences in intensities of the calculated S K-edges can be attributed to the difference in number of absorbers. Calculated S 3p character in the unoccupied d-orbitals was 11.94% for [LMeFeS]2 and 5.94% for 2. These calculations agree remarkably well with the experimental data described in the previous paragraph, and confirm that the Fe–S covalency is the same for both compounds. These results contrast with those presented in a study by Pollock et al., in which the replacement of a sulfide with an imido (NtBu2−) in [Fe2S2Cl4]2− decreased the iron–sulfur covalency.50
The Fe K-edge XAS obtained for 1, 2 and [LMeFeS]2 are presented in Fig. 6b. These data reveal a significant shift in the rising edges between 1 (7115 eV) and 2 (7118 eV), as expected for more oxidized iron sites. The overlaying pre-edge and edge features of 2 and [LMeFeS]2 in Fe K-edge XAS also reflect similar electronic structures at the iron centers, in agreement with the S K-edge XAS data described above, despite the substitution of the sulfide for an alkylidene.
Electronic structure
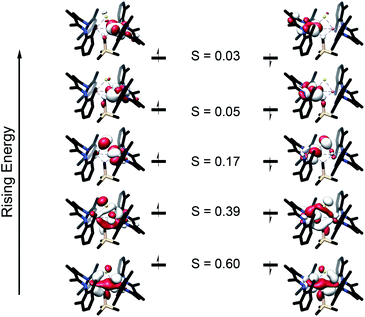
To further understand the nature of the bonding in these complexes, we analyzed the localized orbitals of the broken-symmetry DFT model using the intrinsic atomic orbital-intrinsic bond order (IAOIBO) method.67 From this analysis, the Mayer bond order68 (MBO) provides a convenient method to sum all of the contributions to the bond; it has been applied to FeMoco and related systems to understand the magnitude of bonding between two atoms.68,69 The MBOs for the Fe–C interactions are similar between 3 (0.87) and 1 (0.90). Upon the introduction of a sulfide ligand and oxidation of the iron centers, the Fe–C interactions of the bridging alkylidene in 2 display a similar MBO of 0.86. This MBO analysis demonstrates the similarity of Fe–C bonding across 1, 2, and 3, despite the differences in metal nuclearity, oxidation state, and carbon donor identity.Despite the comparable Fe–C MBO in 1 and 2, we sought to understand the electronic implications of the Fe–C–Fe angle contraction from 95.6(3)° in 1 to 81.74(6)° in 2. There is also a substantial distortion of the alkylidene carbon geometry away from tetrahedral moving from 1 (τ4 = 0.85) to 2 (τ4 = 0.65, see ESI†).70 Analysis of the localized Fe–C orbitals shows that in 1 the electron density in each orbital is more localized on one discrete Fe–C bond, while in 2 there is a delocalized bonding orbital with electron density between both iron centers and the alkylidene carbon (Fig. 8). The IAOIBO analysis of 2 shows the alkylidene exclusively forms σ bonds with the iron centers, while the sulfide forms one σ bond with each iron as well as π-bonding interactions. The covalency of the Fe–S bonds can be measured by summing the Fe–S bonding orbitals in 2, giving 23% Fe character and 77% S character. In the bis-sulfide complex [LMeFeS]2 these are similar (24% Fe, 76% S), consistent with the S K-edge XAS data described above that show similar Fe–S covalency for the compounds. The MBOs of the Fe–S bonds are also identical (1.1) between the two compounds, despite the 0.116(2) Å shorter Fe–S bonds and 0.641(2) Å shorter Fe⋯Fe distance in 2 compared to [LMeFeS]2. Significantly, the Fe–S MBOs in 2 (1.1) are similar to the Fe–S MBO values for the belt sulfides in FeMoco (0.9).69 It is also interesting that the Fe⋯Fe MBO in 2 (0.35) is similar to the Fe2⋯Fe6 MBO in FeMoco (0.32).69 These comparable MBO values between 2 and FeMoco underscore the electronic similarities between the model complex and the biological cluster site.
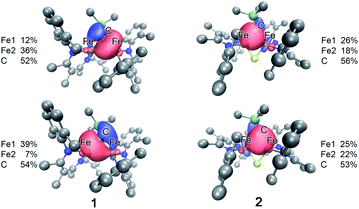 | ||
| Fig. 8 Isosurface plots of select Fe–C interactions in 1 (left) and 2 (right) with the total spin density for Fe and the alkylidene C listed for each plot. | ||
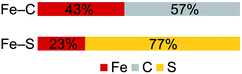
In contrast to the copious literature study of Fe–S bonding in FeS clusters,71–74 the Fe–C bonding interactions in high-spin complexes remain poorly understood. The incorporation of both a bridging alkylidene and sulfide into 2 allows us to assess the relative covalency of Fe–S and Fe–C bonds. The IAOIBO analysis reveals the average Fe–C electron distribution in the Fe–C bonds of 2 to be 43% Fe and 57% C in character, suggesting that the Fe–C bonds are more covalent than the Fe–S bonds (Fig. 9). Though the limited number of complexes in our studies prevented us from clearly distinguishing the oxidation-state dependence of covalency of Fe–C bonds, the diiron(II) alkylidene complex 1 reveals a similar total Fe/C electron distribution of 40% Fe and 60% C, which is consistent with the comparable Fe–C MBO values in 1 and 2. This orbital analysis provides insight into Fe–C bonding in high-spin iron complexes relevant to FeMoco.
Discussion
The diiron alkylidene sulfide complex 2 presented here incorporates structural elements relevant to nitrogenase, and the Fe/Fe/S2B/C diamond core overlays extremely well with the Fe2/Fe6/S/C rhomb in the resting state of FeMoco (Fig. 2b). Enzymatic studies implicate the Fe2 and Fe6 centers as a primary substrate binding site,7,8,14,15,75 and therefore it is particularly important that the core of our synthetic model structurally resembles these centers.In addition to the local structural similarity, the electronic structure of 2 has significant similarities to this site in FeMoco. First, the oxidation states are identical, based on the diiron(III) assignment for the Fe2/Fe6 sites in FeMoco based on SpReAD analysis.30 Se Kα-HERFD XAS studies on FeMoco with selective substitution of S2B with Se31 assign these iron centers as an antiferromagnetically-coupled diferric pair, which is consistent with QM/MM studies.32 In 2, the iron sites have high-spin electronic configurations and display antiferromagnetic coupling between the iron centers, which agrees with calculations indicating that the belt irons Fe2 and Fe6 in the resting state of FeMoco are antiferromagnetically coupled pairs.30–32
The comparison of XAS data between 2 and the analogous doubly sulfide-bridged complex [LMeFe(μ-S)]2 enables us to evaluate the influence of carbon donors within iron–sulfur clusters. This is significant because there are few other examples of high-spin iron–sulfur clusters with any carbon-based ligands.46,76,77 The sulfur pre-edge intensities from the S K-edge XAS data indicate that the marker sulfide does not change its covalency from the addition of the carbon-based bridge. The similarity in Mössbauer isomer shifts of the iron(III) sites in 2 and its bis-sulfide analogue further emphasizes the similarity of C and S bridges in terms of their influences on the iron centers. Within 2, though, the Fe–C bonds are more covalent than the Fe–S bonds and form exclusively σ-interactions in contrast to the π interactions contributed by sulfides (see ESI, Fig. S33–S35†). The contracted Fe–C–Fe angle in 2 gives a delocalized orbital that stretches over both iron atoms and the carbon atom (Fig. 8 above), contributing to the greater antiferromagnetic exchange coupling observed in 2. An analogous superexchange interaction between the iron centers facilitated by the carbon bridge could help to rationalize the different coupling present in FeMoco compared to other FeS clusters.12,78,79
Naturally, there are differences between the carbon bridges in these synthetic complexes compared to FeMoco as well. For example, the average Fe–C MBO in complexes 1 and 2 (0.9) are higher than the average Fe–C MBO in FeMoco (0.32).69 The variation in the Fe–C MBO between complexes 1 and 2 and the FeMoco may be attributed to the coordination of the carbide to six iron centers (μ6) rather than the two iron centers in 1 and 2 (μ2).
The ability of the complexes to reduce N2 was assessed by adding KC8 and HBArF4, a mixture that provides a substantial driving force for NH4+ formation (effective bond dissociation free energy [BDFE] of 0; chemical overpotential of 1220 kJ mol−1).16,27,41,80,81 The iron complexes 1, 3, and 4 reduce N2 to NH4+ to give 1.1–1.4 ± 0.1 equiv. NH4+ per complex, while complex 2 gives little NH4+. We ascribe the difference to the open coordination sites in 1 and 3, while the iron centers in 2 are four-coordinate. The differences in oxidation state are less likely to be important because our N2 reduction experiments used a 10-fold excess of reductant relative to the complex. The necessity for a coordinatively unsaturated iron center in these N2 reduction studies parallels N2 reduction in nitrogenase, as enzymatic studies imply S2B dissociation upon binding substrates.7,8,14 It has been hypothesized that dissociation of S2B in the initial stages of FeMoco reduction could be the “trigger” that brings about N2 binding and reduction, and in this context we see that the formal loss of an S atom moving from 2 to 1 causes a change from very little N2 reduction activity (2) to significant N2 conversion to NH4+ (1). Thus, these synthetic complexes support the importance of sulfur dissociation for bringing about N2 reducing ability in iron–carbon–sulfur clusters.
It is informative to compare the reactivity of 1 and 3 with other diketiminate–iron complexes that lack C and S ligands. We previously reported that addition of four or more equivalents of reductant to [LMeFe(μ-Cl)]2 under N2 forms complexes M2[LMeFe(μ-N2)]3 (M = K, Rb, Cs).82 These clusters, which lack C and S ligands, possess iron centers in lower oxidation states (Fe02Fe1+) yet they do not form measurable amounts of NH4+ upon the addition of acid. Similarly, previously reported diketiminate-supported iron complexes containing bridging FeNNFe cores do not react with acid to give NH4+.83–85 In contrast, we see here that the incorporation of C-based ligands and an open coordination site leads to the ability to reduce N2 to NH4+. Though we were unable to deconvolute the influence of the nuclearity and the carbon ligand identity on N2 reduction ability in these studies, it appears that the presence of an Fe–C bond is beneficial for N2 reduction. We note that two previous carbon-ligated iron systems from Peters and coworkers yield NH4+ (3.3–4.6 equiv. NH4+/Fe) as well.16,27
Though we isolated the carbon-ligated low-valent species relevant to the N2 reduction studies from 3, the mechanism of N2 reduction by the diiron alkylidene complex 1 remains unclear. However, a recent article by Agapie and co-workers described a diiron μ-alkylidyne μ-hydride complex with a Fe/Fe/H/C core, which undergoes Fe–C bond cleavage and C–H bond formation to give various products including iron(II) alkyl and alkylidene species with N2 bound.17 These may bear resemblance to the intermediates during N2 reduction by 1. This gains significance because the Fe/Fe/H/C diamond core in the alkylidyne complex is in a more reduced state (closer to the level of N2-binding FeMoco intermediates) than the diiron alkylidene sulfide 2. However, the mechanisms may be different since the strong-field phosphine ligand sphere in the alkylidyne complex is less electronically similar to the FeMoco than the weak-field ligand sphere present in 1, 2, and 3 that gives rise to high-spin iron centers.
Conclusions
This paper has presented a series of complexes that helps to understand the influence of Fe–C bonding on the electronic structure and N2 reactivity of high-spin iron sites like those in the FeMoco of nitrogenase. The mononuclear iron(II) alkyl 3 and the diiron(II) alkylidene 1 can reduce N2 to NH4+ upon addition of acid and reductant, suggesting that Fe–C bonds are beneficial for N2 reduction. Importantly, the lack of a sulfur bridge is essential for N2 reduction activity, supporting the idea that sulfur dissociation is a reasonable step toward N2 binding in FeMoco.The structural relevance of 1 to the resting state of FeMoco was extended by incorporating a sulfide ligand to give 2, which has both a carbon donor and a sulfide as bridges. Complex 2 has nearly identical metrical parameters as the Fe2/Fe6/S2B/C rhomb within the FeMoco resting state structure, and the antiferromagnetic coupling of the iron(III) centers in 2 aligns well with the analogous coupling of Fe2 and Fe6 in FeMoco. In both dinuclear complexes 1 and 2, the bridging ligands facilitate electronic communication between the iron centers, giving rise to antiferromagnetic coupling. The addition of a bridging sulfide ligand in 2 enhances the antiferromagnetic coupling interaction. The IAOIBO picture of the Fe–C interactions in 1 and 2 depicts highly covalent Fe–C bonds which can mediate superexchange, suggesting that the presence of a carbon ligand may contribute to the different exchange interactions observed in FeMoco compared to other FeS clusters.
The study of the bonding interactions in these simplified structural models also shows a surprisingly strong similarity between Fe–C bonds and Fe–S bonds. First, S K-edge XAS experiments show that the substitution of an alkylidene for a bridging sulfide minimally influences the Fe–S covalency in the other bridge. Further, the similar Fe–C Mayer bond orders in 1–3 are similar despite differences in the identity of the carbon ligand, the iron oxidation state, and the complex nuclearity. This property of the Fe–C bonds is reminiscent of the well-known similarity of Fe–S interactions in different oxidation states of iron–sulfur clusters.86 The insights provided by these model complexes improve our understanding of the Fe–C interactions at high spin iron sites, which helps refine our hypotheses about the structural and electronic implications of the carbide in FeMoco, and the key determinants of N2 reduction by the enzyme.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the National Institutes of Health (GM-065313 to P. L. H.) and R35GM124908 (to K. M. L.). A. L. N. was supported in part by a Berson Graduate Research Fellowship. M. M. B. is an NSF Graduate Research Fellow. We thank Dr Nicholas Bingham and Prof. Peter Schiffer for magnetometry measurements. We thank Dr Daniel DeRosha for thoughtful discussion that contributed to the synthetic improvement of 1. We thank Reagan Hooper for assistance with calculations. We thank Ragnar Björnsson for helpful discussions on calculations, and for sharing pre-publication data on nitrogenase calculations. We thank Dr Kazimer Skubi for thoughtful feedback on the manuscript. We thank the Yale Center for Research Computing for guidance and use of the research computing infrastructure. XAS data were obtained at SSRL, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract no. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the Department of Energy's Office of Biological and Environmental Research and by NIGMS (including P41GM103393). The work at SSRL was also supported by the U.S. Department of Energy Office of Basic Energy Sciences proposal no. 100487.Notes and references
- B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114, 4041–4062 CrossRef CAS PubMed.
- P. C. Dos Santos, R. Y. Igarashi, H.-I. Lee, B. M. Hoffman, L. C. Seefeldt and D. R. Dean, Acc. Chem. Res., 2005, 38, 208–214 CrossRef CAS PubMed.
- S. J. George, B. M. Barney, D. Mitra, R. Y. Igarashi, Y. Guo, D. R. Dean, S. P. Cramer and L. C. Seefeldt, J. Inorg. Biochem., 2012, 112, 85–92 CrossRef CAS PubMed.
- P. M. C. Benton, M. Laryukhin, S. M. Mayer, B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Biochemistry, 2003, 42, 9102–9109 CrossRef CAS PubMed.
- H.-I. Lee, R. Y. Igarashi, M. Laryukhin, P. E. Doan, P. C. Dos Santos, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2004, 126, 9563–9569 CrossRef CAS PubMed.
- B. M. Barney, R. Y. Igarashi, P. C. Dos Santos, D. R. Dean and L. C. Seefeldt, J. Biol. Chem., 2004, 279, 53621–53624 CrossRef CAS PubMed.
- T. Spatzal, K. A. Perez, O. Einsle, J. B. Howard and D. C. Rees, Science, 2014, 345, 1620 CrossRef CAS PubMed.
- T. Spatzal, K. A. Perez, J. B. Howard and D. C. Rees, eLife, 2015, 4, e11620 CrossRef PubMed.
- K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977 CrossRef CAS PubMed.
- T. Spatzal, M. Aksoyoglu, L. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Science, 2011, 334, 940 CrossRef CAS PubMed.
- J. A. Wiig, C. C. Lee, Y. Hu and M. W. Ribbe, J. Am. Chem. Soc., 2013, 135, 4982–4983 CrossRef CAS PubMed.
- J. A. Rees, R. Bjornsson, J. K. Kowalska, F. A. Lima, J. Schlesier, D. Sippel, T. Weyhermüller, O. Einsle, J. A. Kovacs and S. DeBeer, Dalton Trans., 2017, 46, 2445–2455 RSC.
- I. Čorić, B. Q. Mercado, E. Bill, D. J. Vinyard and P. L. Holland, Nature, 2015, 526, 96 CrossRef PubMed.
- D. Sippel, M. Rohde, J. Netzer, C. Trncik, J. Gies, K. Grunau, I. Djurdjevic, L. Decamps, S. L. A. Andrade and O. Einsle, Science, 2018, 359, 1484 CrossRef CAS PubMed.
- W. Kang, C. C. Lee, A. J. Jasniewski, M. W. Ribbe and Y. Hu, Science, 2020, 368, 1381 CrossRef CAS PubMed.
- S. E. Creutz and J. C. Peters, J. Am. Chem. Soc., 2014, 136, 1105–1115 CrossRef CAS PubMed.
- C. H. Arnett and T. Agapie, J. Am. Chem. Soc., 2020, 142, 10059–10068 CrossRef CAS PubMed.
- M. L. McKee, J. Phys. Chem. A, 2016, 120, 754–764 CrossRef CAS PubMed.
- P. E. M. Siegbahn, J. Am. Chem. Soc., 2016, 138, 10485–10495 CrossRef CAS PubMed.
- P. E. M. Siegbahn, J. Comput. Chem., 2018, 39, 743–747 CrossRef CAS PubMed.
- I. Čorić and P. L. Holland, J. Am. Chem. Soc., 2016, 138, 7200–7211 CrossRef PubMed.
- L. Liu, T. B. Rauchfuss and T. J. Woods, Inorg. Chem., 2019, 58, 8271–8274 CrossRef CAS PubMed.
- A. K. Hickey, S. A. Lutz, C.-H. Chen and J. M. Smith, Chem. Commun., 2017, 53, 1245–1248 RSC.
- B. M. Lindley, B. P. Jacobs, S. N. MacMillan and P. T. Wolczanski, Chem. Commun., 2016, 52, 3891–3894 RSC.
- F. Lissel, F. Schwarz, O. Blacque, H. Riel, E. Lörtscher, K. Venkatesan and H. Berke, J. Am. Chem. Soc., 2014, 136, 14560–14569 CrossRef CAS PubMed.
- Z. Ouyang, J. Cheng, L. Li, X. Bao and L. Deng, Chem.–Eur. J., 2016, 22, 14162–14165 CrossRef CAS PubMed.
- G. Ung and J. C. Peters, Angew. Chem., Int. Ed., 2015, 54, 532–535 CAS.
- S. C. Bart, E. Lobkovsky and P. J. Chirik, J. Am. Chem. Soc., 2004, 126, 13794–13807 CrossRef CAS PubMed.
- G. Ung, J. Rittle, M. Soleilhavoup, G. Bertrand and J. C. Peters, Angew. Chem., Int. Ed., 2014, 53, 8427–8431 CrossRef CAS PubMed.
- T. Spatzal, J. Schlesier, E.-M. Burger, D. Sippel, L. Zhang, S. L. A. Andrade, D. C. Rees and O. Einsle, Nat. Commun., 2016, 7, 10902 CrossRef CAS PubMed.
- J. T. Henthorn, R. J. Arias, S. Koroidov, T. Kroll, D. Sokaras, U. Bergmann, D. C. Rees and S. DeBeer, J. Am. Chem. Soc., 2019, 141, 13676–13688 CrossRef CAS PubMed.
- B. Benediktsson and R. Bjornsson, Inorg. Chem., 2017, 56, 13417–13429 CrossRef CAS PubMed.
- M. E. Reesbeck, K. Grubel, D. Kim, W. W. Brennessel, B. Q. Mercado and P. L. Holland, Inorg. Chem., 2017, 56, 1019–1022 CrossRef CAS PubMed.
- M. E. Reesbeck, M. M. Rodriguez, W. W. Brennessel, B. Q. Mercado, D. Vinyard and P. L. Holland, J. Biol. Inorg Chem., 2015, 20, 875–883 CrossRef CAS PubMed.
- D. E. DeRosha, N. A. Arnet, B. Q. Mercado and P. L. Holland, Inorg. Chem., 2019, 58, 8829–8834 CrossRef CAS PubMed.
- J. Vela, J. M. Smith, R. J. Lachicotte and P. L. Holland, Chem. Commun., 2002, 2886–2887 RSC.
- J. Vela, S. Vaddadi, T. R. Cundari, J. M. Smith, E. A. Gregory, R. J. Lachicotte, C. J. Flaschenriem and P. L. Holland, Organometallics, 2004, 23, 5226–5239 CrossRef CAS.
- M. M. Rodriguez, E. Bill, W. W. Brennessel and P. L. Holland, Science, 2011, 334, 780 CrossRef CAS PubMed.
- J. M. Smith, R. J. Lachicotte and P. L. Holland, Organometallics, 2002, 21, 4808–4814 CrossRef CAS.
- T. J. J. Sciarone, A. Meetsma and B. Hessen, Inorg. Chim. Acta, 2006, 359, 1815–1825 CrossRef CAS.
- J. Fajardo and J. C. Peters, J. Am. Chem. Soc., 2017, 139, 16105–16108 CrossRef CAS PubMed.
- K. C. MacLeod, S. F. McWilliams, B. Q. Mercado and P. L. Holland, Chem. Sci., 2016, 7, 5736–5746 RSC.
- R. Battino, T. R. Rettich and T. Tominaga, J. Phys. Chem. Ref. Data, 1984, 13, 563–600 CrossRef CAS.
- F. L. Gibanel, M. C. López, F. M. Royo, J. Pardo and J. S. Urieta, Fluid Phase Equilib., 1993, 87, 285–294 CrossRef CAS.
- S. F. McWilliams, E. Bill, G. Lukat-Rodgers, K. R. Rodgers, B. Q. Mercado and P. L. Holland, J. Am. Chem. Soc., 2018, 140, 8586–8598 CrossRef CAS PubMed.
- D. L. M. Suess, C. Tsay and J. C. Peters, J. Am. Chem. Soc., 2012, 134, 14158–14164 CrossRef CAS PubMed.
- S. F. McWilliams, D. L. J. Broere, C. J. V. Halliday, S. M. Bhutto, B. Q. Mercado and P. L. Holland, Nature Search PubMed , in press.
- E. Münck, Aspects of 57Fe Mössbauer Spectroscopy, in Physical Methods in Bioinorganic Chemistry, ed. L. Que Jr, University Science Books, New York, 2000, pp. 287–319 Search PubMed.
- S. F. McWilliams, E. Brennan-Wydra, K. C. MacLeod and P. L. Holland, ACS Omega, 2017, 2, 2594–2606 CrossRef CAS PubMed.
- C. J. Pollock, L. L. Tan, W. Zhang, K. M. Lancaster, S. C. Lee and S. DeBeer, Inorg. Chem., 2014, 53, 2591–2597 CrossRef CAS PubMed.
- D. S. Marlin, M. M. Olmstead and P. K. Mascharak, Inorg. Chim. Acta, 2000, 297, 106–114 CrossRef CAS.
- C. G. Werncke, J. Pfeiffer, I. Müller, L. Vendier, S. Sabo-Etienne and S. Bontemps, Dalton Trans., 2019, 48, 1757–1765 RSC.
- S. Yao, F. Meier, N. Lindenmaier, R. Rudolph, B. Blom, M. Adelhardt, J. Sutter, S. Mebs, M. Haumann, K. Meyer, M. Kaupp and M. Driess, Angew. Chem., Int. Ed., 2015, 54, 12506–12510 CrossRef CAS PubMed.
- S. F. McWilliams, P. C. Bunting, V. Kathiresan, B. Q. Mercado, B. M. Hoffman, J. R. Long and P. L. Holland, Chem. Commun., 2018, 54, 13339–13342 RSC.
- S. A. Stoian, J. Vela, J. M. Smith, A. R. Sadique, P. L. Holland, E. Münck and E. L. Bominaar, J. Am. Chem. Soc., 2006, 128, 10181–10192 CrossRef CAS PubMed.
- H. Andres, E. L. Bominaar, J. M. Smith, N. A. Eckert, P. L. Holland and E. Münck, J. Am. Chem. Soc., 2002, 124, 3012–3025 CrossRef CAS PubMed.
- K. P. Chiang, P. M. Barrett, F. Ding, J. M. Smith, S. Kingsley, W. W. Brennessel, M. M. Clark, R. J. Lachicotte and P. L. Holland, Inorg. Chem., 2009, 48, 5106–5116 CrossRef CAS PubMed.
- G. Christou, D. Gatteschi, D. N. Hendrickson and R. Sessoli, MRS Bull., 2011, 25, 66–71 CrossRef.
- S. A. Stoian, Y. Yu, J. M. Smith, P. L. Holland, E. L. Bominaar and E. Münck, Inorg. Chem., 2005, 44, 4915–4922 CrossRef CAS PubMed.
- M. P. Hendrich, W. Gunderson, R. K. Behan, M. T. Green, M. P. Mehn, T. A. Betley, C. C. Lu and J. C. Peters, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17107 CrossRef CAS PubMed.
- P. Gütlich, E. Bill and A. X. Trautwein, Mössbauer spectroscopy and transition metal chemistry: fundamentals and applications, Springer-Verlag, Berlin, 2010 Search PubMed.
- F. Neese, B. Hedman, K. O. Hodgson and E. I. Solomon, Inorg. Chem., 1999, 38, 4854–4860 CrossRef CAS PubMed.
- G. David, F. Wennmohs, F. Neese and N. Ferré, Inorg. Chem., 2018, 57, 12769–12776 CrossRef CAS PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- F. Neese, T. Petrenko, D. Ganyushin and G. Olbrich, Coord. Chem. Rev., 2007, 251, 288–327 CrossRef CAS.
- S. Yogendra, T. Weyhermüller, A. W. Hahn and S. DeBeer, Inorg. Chem., 2019, 58, 9358–9367 CrossRef CAS PubMed.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, J. Chem. Soc., Dalton Trans., 2001, 2095–2108 RSC.
- B. Benediktsson and R. Bjornsson, Inorg. Chem., 2020, 59 DOI:10.1021/acs.inorgchem.0c01320.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC.
- T. V. Harris and R. K. Szilagyi, J. Comput. Chem., 2014, 35, 540–552 CrossRef CAS PubMed.
- J. K. Kowalska, A. W. Hahn, A. Albers, C. E. Schiewer, R. Bjornsson, F. A. Lima, F. Meyer and S. DeBeer, Inorg. Chem., 2016, 55, 4485–4497 CrossRef CAS PubMed.
- A. Dey, C. L. Roche, M. A. Walters, K. O. Hodgson, B. Hedman and E. I. Solomon, Inorg. Chem., 2005, 44, 8349–8354 CrossRef CAS PubMed.
- P. K. Mascharak, W. H. Armstrong, Y. Mizobe and R. H. Holm, J. Am. Chem. Soc., 1983, 105, 475–483 CrossRef CAS.
- L. C. Seefeldt, I. G. Dance and D. R. Dean, Biochemistry, 2004, 43, 1401–1409 CrossRef CAS PubMed.
- M. Ye, N. B. Thompson, A. C. Brown and D. L. M. Suess, J. Am. Chem. Soc., 2019, 141, 13330–13335 CrossRef CAS PubMed.
- T. A. Scott, C. P. Berlinguette, R. H. Holm and H.-C. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9741 CrossRef CAS PubMed.
- A. T. Thorhallsson, B. Benediktsson and R. Bjornsson, Chem. Sci., 2019, 10, 11110–11124 RSC.
- R. Bjornsson, F. Neese, R. R. Schrock, O. Einsle and S. DeBeer, J. Biol. Inorg Chem., 2015, 20, 447–460 CrossRef CAS PubMed.
- I. Pappas and P. J. Chirik, J. Am. Chem. Soc., 2016, 138, 13379–13389 CrossRef CAS PubMed.
- C. J. M. van der Ham, M. T. M. Koper and D. G. H. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191 RSC.
- K. Grubel, W. W. Brennessel, B. Q. Mercado and P. L. Holland, J. Am. Chem. Soc., 2014, 136, 16807–16816 CrossRef CAS PubMed.
- J. M. Smith, A. R. Sadique, T. R. Cundari, K. R. Rodgers, G. Lukat-Rodgers, R. J. Lachicotte, C. J. Flaschenriem, J. Vela and P. L. Holland, J. Am. Chem. Soc., 2006, 128, 756–769 CrossRef CAS PubMed.
- T. R. Dugan, K. C. MacLeod, W. W. Brennessel and P. L. Holland, Eur. J. Inorg. Chem., 2013, 3891–3897 CrossRef CAS PubMed.
- J. M. Smith, R. J. Lachicotte, K. A. Pittard, T. R. Cundari, G. Lukat-Rodgers, K. R. Rodgers and P. L. Holland, J. Am. Chem. Soc., 2001, 123, 9222–9223 CrossRef CAS PubMed.
- H. Beinert, R. H. Holm and E. Münck, Science, 1997, 277, 653 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Syntheses, spectroscopy, and crystallography (PDF). CCDC 2009739–2009741. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03447a |
| This journal is © The Royal Society of Chemistry 2020 |