Synthesis, crystallographic study and solid-state properties of metal-free perovskites with P-atom containing A-site cations

Abstract

A P-atom was introduced at the A-site in the metal-free perovskite A(NH₄)X₃ using diprotonated 1,3,5-triaza-7-phosphaadamantane (pta), where X are Br⁻, I⁻, and BF₄⁻ anions, labeled as p-Br, p-I, and p-BF₄, respectively. The pta is analogous to hexamethylenetetramine (hmta) with one N-atom replaced by a P-atom. The p-Br and p-BF₄ perovskites were not isostructural with the corresponding perovskite structure with hmta as the A-site cation. p-Br undergoes a phase transition from an ordered phase to a thermally disordered plastic crystalline phase, whereas the hmta-analog h-Br does not. p-I exhibited greenish photoluminescence, in contrast to the orangish photoluminescence observed in the dabco-based metal-free perovskites. Introduction of the P-atom at the A-site molecule led to differences in phase transition and photoluminescence, providing a new molecular design for metal-free perovskites.

---

Introduction

Extensive research and development of perovskite compounds have been conducted because of their diverse applications in electric, magnetic, and optical materials. Perovskites like BaTiO₃ (BTO) and Pb(Zr, Ti)O₃, which are traditional inorganic examples, have been utilized in various applications, including capacitors, sonar systems, speakers, and actuators, due to their ferroelectric and/or piezoelectric properties.^1,2 In response to growing requirements for energy-efficient, cost-effective, and environmentally sustainable materials, molecular ferroelectrics have garnered substantial interest.^3–7 Among molecular-based ferroelectric materials, the development of the metal-free perovskite structures has emerged as a notable trend in recent years.^7–25

Metal-free perovskites are an emerging material group. The ferroelectric properties were reported in 2018 (ref. 7) after a report on their crystal structure in 2002.⁸ The spontaneous polarisation of MDABCO(NH₄)I₃ (MDABCO = methylated and protonated diazabicyclo[2.2.2]octane) reaches 19 μC cm⁻², which is comparable to 26 μC cm⁻² for BTO. Solid-state properties, for example, piezoelectricity, X-ray detection, mechanical property, elastic property, electrocaloric effects, electro-optic property and photoluminescence (PL), have been investigated via tailoring and tuning their properties through the design of A-site molecules.^13–25 Solid solutions are also achieved for the A-site with spherical molecules towards tuning these solid-state properties like metal-containing perovskites.²⁶ In addition to the three-dimensional quasi-cubic perovskites, the two-dimensional layered perovskite A₂B₂X₄ was also developed.²⁷

The perovskite is a typical structure for a ternary ionic compound. The structure is based on the lock-salt-type arrangement of BX, but one {BX₆} octahedron is substituted by the A ion. Molecules can also adopt a perovskite structure if they meet the requirements of charge balance and the geometric restriction known as the Goldschmidt tolerance factor. A conventional metal-free perovskite has an ABX₃ stoichiometric composition and consists of the divalent cation A²⁺, which derived by protonation and/or methylation of the N-atom in a cyclic or spherical organic amine. The B-site is composed of either H₃O⁺ or NH₄⁺, and the X site consists of ions including halide ions, ClO₄⁻ and BF₄⁻.^9–11 Along with NH₄⁺, alkali ions like Rb⁺ utilize perovskite structures.¹² The inorganic metal containing perovskite often exhibits ferroelectric properties, which is indicated by spontaneous distortion of {BX₆} and transition to a highly symmetrical cubic phase. They are attributed to the separation of the d-orbitals of the metal at the B-site, for example, Ti⁴⁺ in BTO. Thus, the reduction in symmetry in metal-free perovskites originates from another mechanism, for example, the symmetry and ability to form hydrogen bonds of the A-site molecule with the X anion. Not only ferroelectricity, but also a linear correlation was found between the band gap and the lowest unoccupied molecular orbital energies of the A²⁺ cations, indicating that the semiconducting properties are tailored through the molecular design of the A-site cation.²⁴

The understanding and development of the metal-free perovskite family has been achieved through an investigation of the A-site cation. This study investigated 1,3,5-triaza-7-phosphaadamantane (pta) as a candidate for the A-site cation (Fig. 1). This compound is a derivative of hmta where one P-atom has replaced the N-atom (Fig. 1). The hmta is non-centrosymmetric and has been crystallised with perovskite structures; (H₂hmta)(NH₄)Br₃ (h-Br)²⁸ and (H₂hmta)(NH₄)(BF₄)₃ (h-BF₄).²⁹ Thus, pta, which is isostructural with hmta, is expected to change properties such as phase transition and photoluminescence from other metal-free perovskites with N atoms. Herein, three newly isolated metal-free perovskite crystals, represented by the formula (H₂pta)(NH₄)X₃ with X being Br⁻, I⁻, and BF₄⁻, have been characterised in terms of their crystal structure, phase transition properties and photoluminescence.

Fig. 1 Molecular structures of hmta, pta and H₂pta²⁺.

Results and discussion

Synthetic procedures

Block crystals, which were colourless and of high quality, were isolated from an aqueous solution of pta with HX after evaporation in air. Compositions determined by CHN elemental analysis agreed with (H₂pta)(NH₄)X₃. Single crystal X-ray structure analysis (SC-XRD) at room temperature confirmed a quasi-cubic three-dimensional perovskite structure. Structural purities were validated from powder XRD analysis. Further details on crystallization and analyses are summarised in the ESI.†

Crystallographic studies

In the compound H₂pta²⁺, two of the N-atoms were protonated as shown in Fig. 1. For hmta, the non-protonated nitrogen atom is distinguished by variations in the length of its C–N bond relative to the protonated nitrogen atom.²⁸ The C–N bond length in the protonated N of hmta is approximately 1.5 Å, which is longer than the bond length in the non-protonated form, which is less than 1.5 Å. Protonated and non-protonated nitrogen atoms were distinguished in the crystal p-X based on their C–N bond lengths.

For p-Br, the space group was the polar Pna2₁ at ambient temperature. In the p-I and p-BF₄ crystals, the A-site molecule was statically disordered with the P- and N-atoms positioned with ∼50% crystallographic occupancy. However, two NH⁺ were orientated toward anti-parallel directions, crystallising into the centrosymmetric space groups of Cmce and P4₂/n (Fig. 2). Crystals of p-Br and p-BF₄ are not isostructural with the hmta-based perovskites h-Br and h-BF₄. The larger P-atom in the pta molecule influences the orientation of molecules and symmetry of {NH₄X₆} octahedra.

Fig. 2 Crystal structures of (a) p-Br, (b) p-I and (c) p-BF₄. H atoms on C atoms were omitted except for the N⁺–H bond shown by the red line. The octahedron represents the {NH₄X₆} structural unit where the black lines in (c) represent B–F bonds.

Structure and intermolecular interactions. The structure around H₂pta²⁺ is shown in Fig. S2-1 to S2-4† highlighting the interactions, which worked on H₂pta²⁺. The NH⁺ groups on pta molecules interacted with X anions, resulting in a strong structural relationship between the orientation of H₂pta²⁺ and the distortion of {NH₄X₆} octahedra. The shortest distances between NH⁺ of pta to Br⁻ or I⁻ were 3.308 Å (253 K) and 3.674 Å (253 K), respectively. They are longer than the mean values of the (CCC)N⁺–H⋯X (Br⁻ or I⁻) distance of 3.247(7) Å and 3.50(3) Å, indicating weak interaction.³⁰ Also, the distances between the protonated N of H₂pta²⁺ and F atom in p-BF₄ was 2.879 Å (233 K), which is comparable to the weak interaction observed in NH₄BF₄ (2.914 Å).³¹

Table 1 summarises certain crystallographic data of p-X and h-X. The volume of the lattice per formula unit (V/Z) and the volume of the octahedron (V_oct) both rose as the size of the X anion was large and as N (hmta) was substituted for P (pta). Distortion indices (D) were calculated from the interatomic distances between the N-atom of the ammonium ion and the centre of the X anion (Br, I, and B atoms). The bond angle variance, denoted by (A, deg²), was calculated for the octahedra. For regular octahedra, these values converge to zero. As the size of the anion grew, D and A for p-X and h-X concurrently decreased, implying a correlation between the sizes of anion and the distortion of octahedral structures for metal-free perovskites.

Table 1 Summary of structural data characterised by SC-XRD

	p-Br	p-I	p-BF 4	h-Br	h-BF 4
Calculations of D and A are shown in the ESI.†
T, K	253	253	233	253	252
V/Z, Å^3	328.3	363.6	394.2	309.8	376.1
V oct, Å^3	54.3	60.1	65.5	51.6	62.4
D	0.0134	0.0050	0.0016	0.0160	0.0062
A, deg^2	147	134	19	165	50
t	0.949	0.933	0.928	0.912	0.892
μ	0.75	0.66	0.63	0.75	0.63
r A, Å	2.63			2.45
r B, Å	1.46
r X, Å	1.96	2.20	2.32	1.96	2.32

---

Traditional tolerance factor. The perovskite structure is often predicted by the tolerance factor t and octahedral factor μ. These values are given bywhere r_A, r_B, and r_X are the radii of molecules and/or ions occupying A, B, and X sites, respectively. The parameter μ is a geometric requirement for octahedral {BX₆} structures. The quasi-cubic perovskite structures are expected for the cases of 0.813 < t < 1.107 and 0.414 < μ < 0.90.^24,32r_A, r_B and r_X values are summarised in Table 1 with t and μ. However, it is difficult to determine the intrinsic radius of the A-site molecular cations. Thus, we estimate the radius as the distance between the centre of mass of the organic cation and the atom with the largest distance to it.²⁴ Radii were estimated from SC-XRD data to 2.63 Å and 2.45 Å for H₂pta²⁺ and H₂hmta²⁺, respectively. The difference in radii is slightly smaller than that expected from the vdW radii of N (1.55 Å) and P (1.80 Å), 0.25 Å.

The t values of p-Br, p-I, and p-BF₄ were estimated to be 0.949, 0.933, and 0.928, respectively. Fig. 3a shows a map of t and μ for p-X and h-X. The t values were within the range for the perovskite structure. The metal-free perovskite with Br⁻ salts were also reported for not only pta and hmta but also dabco and other compounds. However, quasi-cubic perovskite structures with Cl⁻ and F⁻ have not yet been isolated, except for the case in which water molecules are crystallised to occupy a space within the lattice.⁸ The border of μ to maintain the perovskite structure in h-X and p-X is between 0.75 (X = Br) and 0.81 (X = Cl).

Fig. 3 (a) Map of t and μ for p-X and h-X in which τ is represented with colour graduation ranged from blue to red (colour scale shown in figure). (b) Plots of t and τ with r_A for different X (Cl⁻, Br⁻, I⁻ and BF₄⁻).

The structure at t = 1 corresponds to an ideal cubic perovskite structure with regular {BX₆} octahedra. In the structural model with r_A of 2.63 Å and 2.45 Å for H₂pta²⁺ and H₂hmta²⁺, an ideal cubic structure is expected towards smaller anions X in the relationship between t and r_X in eqn (1). However, the experimental facts based on the values of D and A above show the opposite trend. Distortion of the octahedron increases with increasing anion size, indicating the limitation of a simple geometry model and/or contribution of the hydrogen bond in the lattice.

Consideration with new tolerance factor. Recently, Bartel et al. developed a new tolerance factor τ using an analytics approach, which has the formwhere n_A is the oxidation state of the A-site metal. The perovskite structure satisfied τ < 4.18. The accuracy of the traditional tolerance factor by eqn (1) is low for halide perovskites (chlorides 51%, bromides 56% and iodides 33%), but the consideration with the new tolerance factor resulted in high accuracy; chlorides 90%, bromides 93% and iodides 91% including organic–inorganic hybrids.³³ As τ decreases, the probability P(τ) for being a perovskite increases from 0 to 1, where P(τ) = 0.5 at τ = 0.418. Perovskites with an inorganic–organic hybrid structure also meet this revised tolerance factor with a charge of organic cation as n_A.

The τ values for p-X and h-X were determined using a value of +2 for n_A, and a graph illustrating their relationships with μ and t is presented in Fig. 3. Values below 4.18 indicate perovskite shown in blue, while values above 4.18 indicate non-perovskite shown in red (see also Table S7-1†). Data for metal-free perovskites do not align with the τ-based assessment. As the anion size decreases, τ-based probability increases, despite a lack of reported metal-free perovskites with F⁻ (this is also inconsistent with the t–μ plot analysis). Fig. 3b shows the plots of t and τ against r_A for X = Cl⁻, Br⁻, I⁻ and BF₄⁻. The τ has minimum value at r_A/r_B = e, at which r_A is calculated to 3.97 Å, however this is too large to form a perovskite structure, as expected from the traditional tolerance factor t.

These mismatches with t and τ originated from the fewer examples of metal-free perovskites reported compared to inorganic perovskites. The composition A²⁺B⁺(X⁻¹)₃, characteristic for metal-free perovskites, does not adopt the perovskite structure in inorganic metal-containing oxides or halides. For example, BaNaBr₃ is not a perovskite and these compounds are treated as ‘non-perovskites’ in machine learning. The exploration of metal-free perovskites as a material group is still in its early stages, and further research is needed to develop successful analytic approaches that consider a wider range of materials with different A-site cations.

Temperature dependence of the crystal structure

A peak was observed at 400 K in the DSC diagram of p-Br, suggesting a phase transition. The temperature-dependent SC-XRD analysis between 250 and 415 K determined the structure. The space group at the high temperature phase was determined to be Pm3̄m, where H₂pta²⁺ lost orientational order and {NH₄Br₆} adopted the regular octahedron structure (Fig. S2-2, Table S2-1†). Changes in entropy and enthalpy for the initial heating process were 4.46 kJ mol⁻¹ and 10.6 J mol⁻¹ K⁻¹, respectively. These results suggest that the phase change is an order–disorder type. However, upon repeating a heating–cooling cycle, peaks shifted to low temperature and broadened. We consider this is due to the defect. By thermogravimetry (TG) measurement of p-Br, p-I and p-BF₄ (Fig. S3-1†), weight loss was observed above ∼450 K, indicating the defect is originated from the structural defect caused by a structural change and/or a small quantity of thermal decomposition of pta.

The plots in Fig. 4 show the unit cell volume per ABX₃ composition (V/Z) and normalised lattice parameters (see also Table S2-1†). The crystal structure was determined to be orthorhombic at temperatures below 391 K. At temperatures above this point, the crystal structure well defined with the cubic system. At 391 K, the R_int value is 0.1375 for the orthorhombic system, which is higher than 0.0439 for the cubic system (Fig. S2-8†).

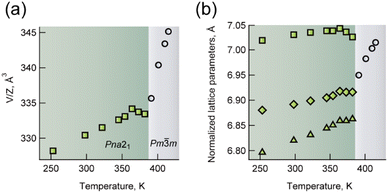Fig. 4 A plot of (a) V/Z and (b) normalised lattice parameters of p-Br (square = b, diamond = a and triangle = c) with temperature.

The unit cell along the crystallographic b-direction decreases above 364 K, which corresponds to the contraction of its lattice volume. At 391 K, the lattice volume started to increase again. Similar negative thermal expansion was observed in perovskite compounds when the reduction of structural distortion from the lower symmetry structure exceeded the degree of thermal expansion, for example, PbTiO₃.³⁴ The transition between polar and plastic crystalline phases is typical behaviour for ferroelectric crystals. The complex permittivity of p-Br was characterised between 120 and 370 K. Continuous increases in both real and imaginary parts were observed, indicating enhanced thermal motion in the crystal (Fig. S5-1†). However, no obvious electric field switching of spontaneous polarisation was observed using single crystals at 20.0 kV cm⁻¹ and 1–100 Hz, where spherical hysteresis indicates the leakage current (Fig. S5-2†). In contrast to p-Br, no thermal anomalies, which indicates phase transition to the plastic crystal, were observed for p-I and p-BF₄. This is because entropy change enough to phase transition was not gained from the random disorder structure of H₂pta²⁺ in p-I and p-BF₄.

Comparing h-Br with p-Br, only the latter undergoes a phase transition to a plastic crystalline phase. Lattice entropies of both are considered to be comparable because the P-atom does not form strong interactions, such as hydrogen bond, in p-Br. Thus, there are two possible reasons; the larger size and lower symmetry of pta. Phase transition to the plastic crystalline phase is expected from a larger lattice with weak interaction for p-Br. This is expected from the larger t value of p-Br. The latter reason by symmetry resulted to the high phase transition entropy of p-Br. In general for organic molecular solids, high symmetry molecules have higher melting points. This is because the number of possible states in the disordered liquid phase is reduced in a high symmetry molecule. Thus, the entropy changes in T = ΔH/ΔS for the melt goes small.³⁵ One approach to a quantitative estimation of the melting point is reported with entropy estimated by R ln(σ), where σ depends on the point group of the molecule under consideration.

With the structure–property relationship, H₂pta²⁺ (C_s: σ = 1), which is a low symmetric analog of H₂hmta²⁺ (C_2v: σ = 2), is expected to lose orientational order at lower temperatures. The R ln(σ) values estimated for H₂hmta²⁺ and H₂pta²⁺ are 5.76 and 0, respectively. With ΔH = TΔS, the virtual phase transition temperature of h-Br can be estimated to ∼920 K given if ΔH is identical to that of p-Br; ΔH/ΔS = 4.46 × 10³/(10.6 − R ln(2)). This rough estimation agrees with the tendency of h-Br to decompose before the phase transition to the plastic crystalline phase. Further understanding of the relationship between the molecular symmetry at the A-site and transition temperature to the plastic crystalline phase will lead to insight into the design of ferroelectric materials and plastic crystals.

Photoluminescence

Iodides of metal-free perovskites A(NH₄)I₃ showed PL, for example, A = MDABCO (Med-I) and methylated and protonated piperazine (C₅N₂H₁₄²⁺) (Mepi-I).^19–21 In addition to these iodides, the single crystal of p-I also showed PL. Fig. 5 shows the PL and photoluminescent excitation (PLE) spectra with a picture of the crystals under UV light. The intensities were represented by relative values, which were determined by the maximum peak intensity as a unit. The PL colour of p-I was greenish, which differed from the orangish PL of Med-I and MePi-I. In the PLE spectrum, the strongest peak was observed at 327 nm with a sub-peak at 360 nm and a shoulder around 380 nm. This corresponds to the spectrum of Med-I, which shows two strong peaks at 314 and 334 nm, a sub-peak at 360 nm and a shoulder at 375 nm. Also, the PLE spectrum of p-I quantitatively agrees with MePi-I, which showed a main peak at 307 nm. In the PL spectrum, a broad peak appeared at 550 nm, which was shifted from 610 nm (Med-I)²⁰ and 572 nm (MePi-I),²¹ agreeing with the visual colour differences between greenish and orangish. The mechanism of the PL and redshift of PL in p-I has not been fully clarified yet. The self-trapped excitons and/or the photo-induced reaction-ref are both considered.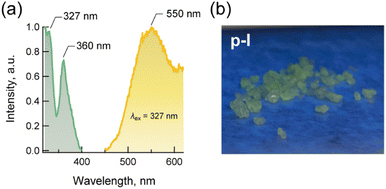

Fig. 5 (a) PL and PLE (exited at 327 nm) spectra of p-H and (b) photograph of the single crystals p-I under UV light.

Conclusions

The development of a metal-free perovskite structure has been achieved through the investigation of organic cations, which occupy the A-site in A(NH₄)X₃. Herein, metal-free perovskite structures containing phosphorus atoms, 1,3,5-triaza-7-phosphaadamantane (pta), were isolated with X = Br⁻, I⁻, and BF₄⁻, and their structure and properties were studied. The bromide salt (p-Br) undergoes a phase transition involving the orientational order–disorder of H₂pta²⁺. In the p-I and p-BF₄ crystals, the H₂pta²⁺ molecules exhibited random orientation with their neutral nitrogen and phosphorus atoms in a state of disorder. The phase transition to the plastic crystalline phase observed for p-Br was attributed to the size and molecular symmetry of pta compared to hmta. A new tolerance factor obtained from machine learning of the inorganic metal-containing perovskite was employed to p-X and h-X; however, successful assignment was not obtained, indicating further discovery of the metal-free perovskite with the variable A-site anion. In addition to other A(NH₄)I₃, p-I also exhibited PL but with a greenish colour, at room temperature. Introduction of the P-atom at the A-site molecule led to differences in the structure and phase transition compared with the N-atom analog in the adamantane-type A-site cation, indicating a new material design for metal-free perovskites.

Data availability

Crystallographic data for the structures reported in this article have been deposited at the Cambridge Crystallographic Data Centre, under deposition numbers CCDC 2424321–2424324, 2424326 and 2424518–2424529. All other relevant data generated and analysed during this study, which include analytical, spectroscopic, crystallographic, thermal and dielectric data, are included in this article and its ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from JSPS KAKENHI and, the cooperative research program of the Network Joint Research Centre for Materials and Devices of Japan and “Extensive contribution of structural sciences from leading edge materials to cultural & archaeological works” from Yamaguchi University.

Notes and references

1. A. S. Bain and P. Chand, Ferroelectrics: Principles and Applications, Wiley, 2017.
2. R. Waser, Nanoelectronics and Information Technology: Advanced Electronic Materials and Novel Devices, Wiley, 3rd edn, 2012.
3. Q. Pan, Z. X. Gu, R. J. Zhou, Z. J. Feng, Y. A. Xiong, T. T. Sha, Y. M. You and R. G. Xiong, Chem. Soc. Rev., 2024, 53, 5781–5861.
4. X. Song, G. Hodes, K. Zhao and S. Liu, Adv. Energy Mater., 2021, 11, 2003331.
5. Q. Cui, S. F. Liu and K. Zhao, J. Phys. Chem. Lett., 2022, 13, 5168–5178.
6. R. Taheri-Ledari, F. Ganjali, S. Zarei-Shokat, M. Saeidirad, F. Ansari, M. Forouzandeh-Malati, F. Hassanzadeh-Afruzi, S. M. Hashemi and A. Maleki, Energy Fuels, 2022, 36, 10702–10720.
7. H. Y. Ye, Y. Y. Tang, P. F. Li, W. Q. Liao, J. X. Gao, X. N. Hua, H. Cai, P. P. Shi, Y. M. You and R. G. Xiong, Science, 2018, 361, 151–155.
8. C. A. Bremner, M. Simpson and W. T. A. Harrison, J. Am. Chem. Soc., 2002, 124, 10960–10961.
9. M. Szafrański, Cryst. Growth Des., 2018, 18, 7106–7113.
10. S. L. Chen, Y. Shang, C. T. He, L. Y. Sun, Z. M. Ye, W. X. Zhang and X. M. Chen, CrystEngComm, 2018, 20, 7458–7463.
11. L. Ye, Z. X. Gong, C. Shi, J. J. Ma, H. Liang, F. W. Qi, D. Y. E. Dian-Yu, C. F. Wang, Y. Zhang and H. Y. Ye, CrystEngComm, 2019, 21, 7043–7047.
12. S. N. Cheng, K. Ding, T. Zhang, Z. X. Zhang, C. Y. Su, J. Z. Ge, Y. Zhang and D. W. Fu, Chem. – Eur. J., 2021, 27, 17655–17659.
13. H. Wang, H. Liu, Z. Zhang, Z. Liu, Z. Lv, T. Li, W. Ju, H. Li, X. Cai and H. Han, npj Comput. Mater., 2019, 5, 1–9; H. S. Wu, B. T. Murti, J. Singh, P. K. Yang and M. L. Tsai, Adv. Sci., 2022, 9, 1–13.
14. X. Song, Q. Cui, Y. Liu, Z. Xu, H. Cohen, C. Ma, Y. Fan, Y. Zhang, H. Ye, Z. Peng, R. Li, Y. Chen, J. Wang, H. Sun, Z. Yang, Z. Liu, Z. Yang, W. Huang, G. Hodes, S. Liu and K. Zhao, Adv. Mater., 2020, 32, 2004183; Z. Li, G. Peng, H. Chen, C. Shi, Z. H. Li and Z. Jin, Angew. Chem., Int. Ed., 2022, 61, e202207198.
15. M. G. Ehrenreich, Z. Zeng, S. Burger, M. R. Warren, M. W. Gaultois, J. C. Tan and G. Kieslich, Chem. Commun., 2019, 55, 3911–3914.
16. L. C. An, K. Li, Z. G. Li, S. Zhu, Q. Li, Z. Z. Zhang, L. J. Ji, W. Li and X. H. Bu, Small, 2021, 17, 1–10.
17. R. Gao, X. Shi, J. Wang, G. Zhang and H. Huang, Adv. Funct. Mater., 2021, 31, 1–11.
18. Y. Gao, S. Meshkat, A. Johnston, C. Zheng, G. Walters, Q. Feng, X. Wang, M. J. Sun, A. M. Najarian, D. Xue, Y. K. Wang, M. I. Saidaminov, O. Voznyy, S. Hoogland and E. H. Sargent, ACS Appl. Mater. Interfaces, 2021, 13, 19042–19047.
19. T. Handa, R. Hashimoto, G. Yumoto, T. Nakamura, A. Wakamiya and Y. Kanemitsu, Sci. Adv., 2022, 8, eabo1621.
20. X. Song, Q. Li, J. Han, C. Ma, Z. Xu, H. Li, P. Wang, Z. Yang, Q. Cui, L. Gao, Z. Quan, S. Liu and K. Zhao, Adv. Mater., 2021, 33, 2102190.
21. Z. Li, G. Peng, Z. H. Li, Y. Xu, T. Wang, H. Wang, Z. Liu, G. Wang, L. Ding and Z. Jin, Angew. Chem., Int. Ed., 2023, 62, e202218349.
22. H. S. Choi, S. Li, I. H. Park, W. H. Liew, Z. Zhu, K. C. Kwon, L. Wang, I. H. Oh, S. Zheng, C. Su, Q. H. Xu, K. Yao, F. Pan and K. P. Loh, Nat. Commun., 2022, 13, 6–12.
23. S. D. Gale, H. J. Lloyd, L. Male, M. R. Warren, L. K. Saunders, P. A. Anderson and H. H. M. Yeung, CrystEngComm, 2022, 24, 7272–7276.
24. J. Bie, D. B. Yang, M. G. Ju, Q. Pan, Y. M. You, W. Fa, X. C. Zeng and S. Chen, JACS Au, 2021, 1, 475–483.
25. Z. X. Zhang, H. F. Ni, J. S. Tang, P. Z. Huang, J. Q. Luo, F. W. Zhang, J. H. Lin, Q. Q. Jia, G. Teri, C. F. Wang, D. W. Fu and Y. Zhang, J. Am. Chem. Soc., 2024, 146, 27443–27450.
26. H. Morita, R. Tsunashima, S. Nishihara and T. Akutagawa, CrystEngComm, 2020, 22, 2279–2282.
27. H. S. Choi, J. Lin, G. Wang, W. P. D. Wong, I. H. Park, F. Lin, J. Yin, K. Leng, J. Lin and K. P. Loh, Science, 2024, 384, 60–66.
28. H. Morita, R. Tsunashima, S. Nishihara, K. Inoue, Y. Omura, Y. Suzuki, J. Kawamata, N. Hoshino and T. Akutagawa, Angew. Chem., Int. Ed., 2019, 58, 9184–9187.
29. J. Moriguchi, T. Koga, N. Tsunoji, S. Nishihara, T. Akutagawa, A. Masuya-Suzuki and R. Tsunashima, Chem. Commun., 2024, 60, 12181–12184.
30. T. Steiner, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 456–463.
31. M. J. R. Clark and H. Lynton, Can. J. Chem., 1969, 47, 2579–2586.
32. C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702–707.
33. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693.
34. R. J. D. Tilley, Perovskites: Structure-Property Relationships, Wiley, 2016, p. 281.
35. J. Wei, Ind. Eng. Chem. Res., 1999, 38, 5019–5027.

---

Footnote

† Electronic supplementary information (ESI) available: Details of experiment, XRD, TG-DTA, DSC, dielectric properties, and crystallographic consideration. CCDC 2424321–2424324, 2424326, 2424518–2424529. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5ce00177c

---