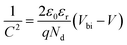Computational analysis of LiMgI₃: a promising material for solar energy conversion

Abstract

This work employs density functional theory (DFT) using CASTEP to investigate the structural, electronic, and optical properties of cubic LiMgI₃ as an absorber material. The lattice parameters we examined match quite well with earlier theoretical results, and the phonon dispersion confirmed its dynamic stability. The electronic band structure and density of states (DOS) revealed that LiMgI₃ is a semiconductor, with band gaps of 1.162 eV using the GGA method and 1.922 eV using the HSE06 hybrid functional. Optical properties were evaluated within the photon energy range of 0–14 eV, key optical characteristics-such as absorption coefficient, reflectivity, refractive index, dielectric response, optical conductivity, and energy loss, all indicating excellent light-harvesting potential. To assess its device applicability, SCAPS-1D simulation software was used to model various solar cell architectures with LiMgI₃ as the absorber. A total of 60 configurations combining different electron transport layers (ETLs) such as WS₂, IGZO, TiO₂, ZnO, ZnS, and PCBM, and hole transport layers (HTLs) like Cu₂O, CuO, CBTS, CuI, P3HT, PEDOT:PSS, CuSCN, Spiro-OMeTAD, PTAA, and CdTe were evaluated. The ITO/WS₂/LiMgI₃/Cu₂O/Ni structure yielded the best performance, with a power conversion efficiency (PCE) of 20.73%, open circuit voltage (V_OC) of 1.495 V, a short circuit current (J_SC) of 15.78 mA cm⁻², and fill factor (FF) of 87.81%. This study analyzes how absorber and electron transport layer (ETL) thickness affect key photovoltaic parameters. It also examines the valence band offset (VBO) and conduction band offset (CBO) characteristics of different ETLs. The study further investigates the impact of series and shunt resistances, temperature, quantum efficiency (QE), capacitance–voltage (C–V) Characteristics, generation–recombination response, current density–voltage (J–V) characteristics, and impedance spectra on improving device performance. The exceptional photon capture efficiency of LiMgI₃ perovskite solar cells (PVSKs) holds significant potential for advancing photovoltaic and optoelectronic device technologies.

---

1 Introduction

The growing global demand for energy, driven by population and economic expansion, has been predominantly supported by fossil fuel sources such as coal, petroleum, and natural gas.^1,2 However, these non-renewable resources contribute significantly to CO₂ emissions, posing serious environmental and sustainability concerns.^3,4 In response, the progress in sustainable and clean energy technologies, particularly solar photovoltaics (PV), has gained critical importance in addressing climate change.^5–9

Among the emerging PV technologies, perovskite solar cells (PSCs) have attracted considerable attention due to their remarkable rise in power conversion efficiency (PCE) from 3.8% in 2009 to over 25% in recent years.^10,11 The halide perovskite absorber material is expressed by the formula ABX₃, where A is a monovalent cation, B denotes a divalent metal, and X indicates a halide anion.¹² These materials exhibit tunable bandgaps, high absorption rates, minimal exciton binding energies, and long carrier diffusion lengths, making them ideal candidates for high-efficiency solar cells.^13–17 Hybrid organic–inorganic perovskites, especially those incorporating formamidinium (FA) or methylammonium (MA) cations, have demonstrated efficiencies above 20%.¹⁸ Their low-cost fabrication and solution-processable nature mark them as promising third-generation PV technologies.¹⁹ Despite their advantages, the sustained performance over time of organic–inorganic hybrid perovskite photovoltaic devices remains a significant challenge due to their susceptibility to degradation under chemical and thermal pressure.²⁰ Furthermore, the toxicity of lead-based perovskites raises environmental and health concerns, hindering commercialization.^21–25 Although lead-free photovoltaic cells generally have lower efficiency than their lead (Pb)-based counterparts, finding non-toxic alternatives is critical. As a result, elements like tin (Sn²⁺), germanium (Ge²⁺), antimony (Sb²⁺), and bismuth (Bi²⁺) are being used to substitute Pb in the B-site.^18,26 However, magnesium (Mg) was selected over Sn²⁺, Ge²⁺, Sb²⁺, and Bi²⁺ due to its greater chemical stability, environmental safety, and promising optoelectronic properties.²⁷ Sn²⁺ and Ge²⁺ are prone to oxidation, while Sb²⁺ and Bi²⁺ typically lead to indirect bandgaps and limited charge transport.²⁸ In contrast, Mg offers a direct bandgap of 1.92 eV (Heyd–Scuseria–Ernzerhof) and a high absorption coefficient (>10⁵ cm⁻¹), positioning LiMgI₃ as a promising lead-free perovskite absorber for stable and efficient solar cells.

The stability of perovskite materials has been enhanced through the addition of K and Rb atoms,^29–32 especially in compounds like KGeX₃ and RbGX₃ (where X = Cl or Br). CsPbCl₃, CsPbBr₃, and CsPbI₃ have gained significant interest for their excellent optoelectronic properties. CsPbCl₃ has a large bandgap (>3.0 eV), making it unsuitable for photovoltaic applications.^18,33–35 In contrast, CsPbBr₃ offers a balanced 2.3 eV bandgap and superior phase stability, leading to improved device longevity and light absorption.^36–38

The selection of electron transport layers (ETLs) and hole transport layers (HTLs) plays a crucial role in determining the efficiency and durability of perovskite solar cells (PSCs). The material properties of transport layers significantly influence the stability and performance of PSCs. When selecting an HTL for PSCs, it is crucial to consider material features such as cost, hole mobility, and valence band offset.³⁹ Since the development of dye-sensitized solar cells (DSSCs), TiO₂ has been valued as an important ETL material because of its extensive bandgap and chemical stability.^40–44 In contrast, polymer-based hole transport layers like Spiro-MeOTAD and P3HT⁴⁵ provide thermal and moisture resistance, enhancing device longevity.⁴⁶ Recently, copper barium thiocyanate (CBTS) has emerged as a promising inorganic HTL due to its stability, non-toxic nature, and tunable bandgap.^47,48 A maximum PCE of 28.4% is recorded in PSCs using TiO₂ as the ETL and MASnI₃ as the absorbing layer.⁴⁹ According to recent research, CsPbI₃-based devices with CBTS as HTL achieved PCE values of 16.71%, 17.90%, 17.86%, 14.47%, 17.76%, and 17.82% when using PCBM, TiO₂, ZnO, C₆₀, IGZO, and WS₂ as ETLs, respectively.^50,51 In their experimental study, Song et al.⁵² found that CsSnI₃ had a PCE of 2.02%. Conversely, Adnan et al.,⁵³ through theoretical analysis, improved the PCE to 15.83%. Based on our analysis, LiMgI₃, the absorber material, is non-toxic and therefore a better option for our society. On the other hand, density functional theory (DFT) is widely used to study the optical and electrical properties of halide perovskites for photovoltaic applications.^54–56 Experimental and theoretical investigations conducted in recent times have provided fresh perspectives on the structure of CsSnCl₃.^57–59 To evaluate LiMgI₃'s potential as an absorber material for solar cells, an extensive examination of its structural, optical, and electrical features will be performed.

The objective of this research is to assess the structural, electronic, and optical properties of the LiMgI₃ absorber, employing first-principles methods within the DFT framework, and using CASTEP software. We calculated the lattice parameters and unit cell volumes of the LiMgI₃ compound using both the hybrid HSE06 (Heyd–Scuseria–Ernzerhof) and generalized gradient approximation (GGA) methods. The bandgap (E_g) values from GGA and HSE06 confirm the semiconducting nature without bands crossing the Fermi level. Additionally, we analyzed crucial optical properties such as absorption, reflectivity, refractive index, dielectric function, conductivity, and loss function. We aimed to identify the optimal combinations of WS₂, IGZO, TiO₂, ZnO, ZnS, PCBM as ETLs, along with Cu₂O, CuO, CBTS, CuI, P3HT, PEDOT:PSS, CuSCN, Spiro-OMeTAD, PTAA and CdTe as HTLs, paired with the LiMgI₃ absorber, for optimizing device performance via SCAPS-1D simulation techniques. In our current study, we investigated various thicknesses and defect densities for the absorber, ETL, and HTL layers. Furthermore, we evaluated the series and shunt resistance, current–voltage (J–V) characteristics, capacitance–voltage (C–V) responses, quantum efficiency (QE), impedance study, generation and recombination rates, and valence and conduction band offsets across different ETLs to gain further insights into the solar cell architectures studied.

2 Materials used and methodology

2.1 DFT-based first-principles study of LiMgI₃ absorber

This research utilizes density functional theory (DFT) with the Cambridge Serial Total Energy Package (CASTEP) framework to analyze the structural, optical, and electronic features of the alkali halide perovskite LiMgI₃.^60–62 This approach utilizes the generalized gradient approximation (GGA) for the exchange-correlation potential, specifically using the Perdew–Burke–Ernzerhof (PBE) parameter.^60,63 For precise determination of the electronic band gaps of the subject compound, the HSE06 hybrid functional (Heyd–Scuseria–Ernzerhof) is utilized.⁶² Additionally, to simulate the interactions between valence electrons and ionic cores, the Vanderbilt-type ultrasoft pseudopotential method was employed.⁶⁴ Elastic constants were derived using the linear finite strain–stress approach, implemented within the CASTEP code.⁶⁵ The atomic calculations utilized the electronic configurations of Li – 1s, 2s, 3p Mg – 2s, 2p, 3s and I – 4d, 5s, 5p. To find the lowest energy state of the stable structure, the Broyden–Fletcher–Goldfarb–Shanno (BFGS)⁶⁶ algorithm was applied. To sample k-points in the first Brillouin zone (BZ), the Monkhorst–Pack grid method⁶⁷ was applied to expand the plane-wave basis set, using a cutoff energy of 400 eV for GGA and 800 eV for HSE06. Accurate reciprocal space sampling was achieved by integrating the Brillouin zone using a 6 × 6 × 6 k-point mesh for GGA and a 2 × 2 × 2 mesh for HSE06, based on the Monkhorst–Pack method. The convergence criteria are defined as 5 × 10⁻⁶ eV per atom for total energy, 5 × 10⁻⁴ Å for maximum displacement, 0.03 eV Å⁻¹ for maximum force, 0.001 Å for the maximum displacement, and 0.05 GPa for maximum stress. The cutoff energy (eV) vs. final energy (eV) for LiMgI₃, and number of K-points vs. final energy (eV) for LiMgI₃ was illustrated in Fig. S2 and S3.†

2.2 Numerical modeling using SCAPS-1D

This computational approach helps clarify the core principles of solar cells while focusing on the main parameters that impact their performance. Fig. 1 displays the SCAPS-1D simulation process. SCAPS-1D software employs numerical techniques to solve critical one-dimensional semiconductor equations.^68–71 Poisson's equation (eqn (1))⁷² relates the distribution of charges to the electrostatic potential, as illustrated in eqn (1).in the above equation, the relative permittivity is denoted by ε_r, ε₀ indicates the permittivity of free space, N_D and N_A represent the ionized donor and acceptor densities, ρ_p and ρ_n stand for the electron and hole distributions, n and p represent electron and hole densities, q represents the electronic charge, and ψ signifies the electronic potential. The continuity equation, which simultaneously analyses recombination, generation, drift, and diffusion processes, is regarded as the fundamental governing equation. Eqn (2) and (3) provide the respective formulations for changes in electron and hole concentrationsHere, the current densities of electrons and holes are represented by J_n and J_p; G_n and G_p for electron and hole generation; and R_n and R_p refer to electron and hole recombination rates. The charge carrier drift-diffusion equations, provided in eqn (4) and (5) below, are employed to determine the electron and hole current densities in solar cells.

J_n = qμ_nnε + qD_n∂n (4)

J_p = qμ_ppε + qD_p∂p (5)

in the above equation, μ_n and μ_p indicate the mobilities of carriers, while D_n and D_p are the diffusion coefficients for electrons and holes, respectively. According to the Einstein relationship, the carrier's mobility and lifetime both affect the diffusion coefficient.⁷³ Moreover, the newly adapted E_g-sqrt model, which is a variant of the conventional sqrt (hv − E_g) model, was utilized to obtain the absorption constant for films. This relationship is expressed through the “Tauc laws” and can be seen in eqn (6).Here, α denotes the absorption coefficient, E_g represents the bandgap, and hv indicates the photon energy. The model constants α₀ and β₀ are related to the traditional constants A and B through eqn (7) and (8) as shown below

Fig. 1 The simulation procedure applied in SCAPS-1D.

2.3 LiMgI₃-based PSC structure

Fig. 2a shows the optimized solar cell's schematic construction. The single halide perovskite solar cell is structured by associating the LiMgI₃ absorber layer with the ETL, HTL, front and back contact. Throughout the investigation, we used a branch of ETL (WS₂, IGZO, TiO₂, ZnO, ZnS, and PCBM) and HTL (Cu₂O, CuO, CBTS, CuI, P3HT, PEDOT:PSS, CuSCN, Spiro-OMeTAD, PTAA, and CdTe) to identify the best-performing device. The ITO/WS₂/LiMgI₃/Cu₂O/Ni configuration was identified as the most computationally efficient solar cell among these numerous configurations. LiMgI₃ halide perovskite provides the ability to absorb light. It is confirmed by the investigation that the doped ETL and HTL form ohmic contacts, which efficiently confine photons and charge on both surfaces. The simulation's input parameters for the ITO, absorber layer, and ETLs are shown in Table 1, with the parameters for all HTLs found in Table 2. The input parameters for the interfacial defect layers are also provided in Table 3. All simulations have employed the AM 1.5 G sun spectrum, which has a power density of 1000 W m⁻² at 300 K and a frequency of 1 MHz.

Fig. 2 (a) The design configuration of the LiMgI₃-based PSC. (b) Energy band alignment between the different ETL and HTL materials of LiMgI₃ absorber.

Table 1 Input parameters of ITO,⁷⁴ ETLs,^50,74,76 absorber layers (LiMgI₃)

Parameters	ITO	WS2	TiO2	IGZO	ZnO	ZnS	PCBM	LiMgI3
Thickness (nm)	500	100	30	30	50	75	50	1000
Bandgap, Eg (eV)	3.5	1.8	3.2	3.05	3.3	2.80	2	1.92
EA (eV)	4	3.95	4	4.16	4	3.80	3.9	3.92
εr	9	13.6	9	10	9	9.00	3.9	6.96
NC (cm^−3)	2.2 × 10^18	1 × 10^18	2 × 10^18	5 × 10^18	3.7 × 10^18	2.2 × 10^18	2.5 × 10^21	6.26 × 10^17
NV (cm^−3)	1.8 × 10^19	2.4 × 10^19	1.8 × 10^19	5 × 10^18	1.8 × 10^19	1.8 × 10^19	2.5 × 10^21	1.46 × 10^18
μn (cm^2 V^−1 s^−1)	20	100	20	15	100	100	0.2	446
μh (cm^2 V^−1 s^−1)	10	100	10	0.1	25	25	0.2	54.7
ND (cm^−3)	1 × 10^21	1 × 10^18	9 × 10^16	1 × 10^17	1 × 10^18	1 × 10^19	2.9 × 10^17	1 × 10^9
NA (cm^−3)	0	0	0	0	0	1 × 10^6	0	0
Nt (cm^−3)	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15

---

Table 2 Input parameters of different HTLs^50,74,77

Parameters	Cu2O	CuO	CBTS	CuI	P3HT	PEDOT:PSS	CuSCN	Spiro-OMeTAD	PTAA	CdTe
Thickness (nm)	50	50	100	100	50	50	50	200	150	200
Bandgap, Eg (eV)	2.2	1.51	1.9	3.1	1.7	1.6	3.6	3	2.96	1.5
EA (eV)	3.4	4.07	3.6	2.1	3.5	3.4	1.7	2.2	2.3	3.9
εr	7.5	18.1	5.4	6.5	3	3	10	3	9	9.4
NC (cm^−3)	2 × 10^19	2.2 × 10^19	2.2 × 10^18	2.2 × 10^19	2 × 10^21	2.2 × 10^18	2.2 × 10^19	2.2 × 10^18	2 × 10^21	8 × 10^17
NV (cm^−3)	1 × 10^19	5.5 × 10^20	1.8 × 10^19	1 × 10^19	2 × 10^21	1.8 × 10^19	1.8 × 10^18	1.8 × 10^19	2 × 10^21	1.8 × 10^19
μn (cm^2 V^−1 s^−1)	200	100	30	100	1.8 × 10^−3	4.5 × 10^−2	100	2.1 × 10^−3	1	3.2 × 10^2
μh (cm^2 V^−1 s^−1)	8600	0.1	10	43.9	1.86 × 10^−2	4.5 × 10^−2	25	2.16 × 10^−3	40	4 × 10^1
ND (cm^−3)	0	0	0	0	0	0	0	0	0	0
NA (cm^−3)	1 × 10^18	1 × 10^15	1 × 10^18	1 × 10^18	1 × 10^18	1 × 10^18	1 × 10^18	1 × 10^18	1 × 10^18	2 × 10^14
Nt (cm^−3)	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15	1 × 10^15

---

Table 3 Interface parameters used in this perovskite solar cell⁵⁰

Interface	Defect type	Capture cross section: electrons/holes (cm^2)	Energetic distribution	Reference for defect energy levels, Et	Interface defect density (cm^−2)
ETL/LiMgI3	Neutral	1 × 10^−17	Single	Above the VB maximum	1 × 10^10
		1 × 10^−18
LiMgI3/Cu2O	Neutral	1 × 10^−18	Single	Above the VB maximum	1 × 10^10
		1 × 10^−19

---

2.4 The energy band structure of the LiMgI₃ absorber with various ETLs and HTLs

Fig. 2b illustrates various solar cell configurations, each utilizing distinct types of ETL, HTL, absorbers, and front and back contacts. We conducted an in-depth analysis of six ETLs and ten HTLs, exploring 60 possible combinations in the ITO/ETL/LiMgI₃/HTL/Ni configuration to determine the best theoretical pairing for the LiMgI₃ absorber layer, as shown in Fig. 2b. According to Fig. 2b, our study found that WS₂, featuring an energy gap of 1.8 eV, delivered the best results as an ETL in combination with Cu₂O HTLs for single halide LiMgI₃ devices. The front electrode, positioned at the incident plane of light, demands both high transmittance and excellent electrical conductivity. One of the most common materials for front electrodes is indium-tin-oxide (ITO), a type of transparent conductive oxide (TCO). Previous studies have indicated that the surface work function (WF) of ITO is approximately 3.5 eV.⁷⁴ The selection of TCO materials in LiMgI₃ PSCs is usually made by considering the device structure, band-gap compatibility, and the temperature needed for device fabrication. The back electrode is typically composed of metal materials like Ni. A high-quality back electrode can improve carrier collection and boost both the stability and efficiency of the device.⁷⁵ Due to the mesoporous or planar structure adopted by most LiMgI₃ PSCs, the Au electrode (WF ∼ 5.1 eV) is the most suitable, as depicted in Fig. 2b.

3 Result and discussion

3.1 DFT result analysis

3.1.1 Structural properties and dynamical stability. The LiMgI₃ alkali-based single halide perovskite compounds take on a cubic ABM₃ structure that corresponds to the Pm3̄m crystallographic space group (no. 221). The standard structural arrangement of this LiMgI₃ material is demonstrated in Fig. 3a. This material's unit cells are made up of a formula unit with five atoms. The lattice parameters and unit cell volumes for the LiMgI₃ compound are calculated using both the hybrid HSE06 (Heyd–Scuseria–Ernzerhof) and the generalized gradient approximation (GGA) methods. The GGA (HSE06) technique yields a lattice parameter of 5.805 (5.483) Å for LiMgI₃ and a unit cell volume of 195.617 (164.850) ų. LiMgI₃ demonstrates the highest stability and ideal structure when the Li atom is located at the 1a Wyckoff position (0, 0, 0), the Mg atom is positioned at the 1b Wyckoff position (1/2, 1/2, 1/2), and the I atom is located at the 3c Wyckoff position (1/2, 0, 1/2). For this compound, all lattice parameters were relaxed throughout the geometry optimization procedure. This calculation indicates that the lattice parameters and unit cell volume of LiMgI₃ are consistent with earlier theoretical findings,⁷⁸ confirming the accuracy of our current results.

Fig. 3 (a) Crystal structure of LiMgI₃ material (b) phonon dispersion plot of LiMgI₃.

A material's dynamic stability is an important consideration when considering its feasibility for practical applications involving time-dependent external influences. Fig. 3b depicts the phonon dispersion curve (PDC), which is important in determining a material's dynamic stability. We computed the phonon dispersion curves at the high-symmetry locations (W–L–Γ–X–W–K) inside the Brillouin zone (BZ) to assess the dynamic stability of LiMgI₃. Dynamically stable crystalline materials are characterized by the absence of imaginary frequencies inside the Brillouin zone.⁷⁹ In contrast, the existence of an imaginary component suggests the occurrence of dynamic instability.⁸⁰ The phonon dispersion curve (PDC) of LiMgI₃ do not display any negative frequencies, indicating that this compound is dynamically stable. Nine optical modes and three acoustic modes are created by this stability, with the acoustic modes being zero at the Γ-point, as shown in Fig. 3b.

3.1.2 Electronic properties and of LiMgI₃.
3.1.2.1 Electronic band structure. The electronic band structure plays an integral part in comprehending material properties such as conductivity⁸¹ and band gap, which are essential for the development of electronic and optoelectronic devices. The band structures of the investigated compound are presented in Fig. 4a and b using the GGA and HSE06 techniques, respectively. Both local functionals (GGA) and nonlocal functionals (HSE06) have been used to produce an accurate band gap and electronic band structure (EBS) prediction. However, the hybrid function (HSE06) is a more dependable method than GGA.⁷⁷ The band spectrum is computed along directions of high symmetry (X–R–M–Γ–R) inside the Brillouin zone and it covers an energy spectrum from −6 to +8 eV. In both diagrams, a red dotted line placed at 0 eV represents the Fermi level (E_F). Energy levels above the Fermi level (E_F) indicate conduction bands, whereas energy levels below the Fermi level (E_F) indicate valence bands. A direct band gap is the result of the conduction band minimum (CBM) and valence band maximum (VBM) being located at the same high symmetry point, while an indirect band gap is the result of their being located at separate high symmetry points.⁸² In both methods, the material obviously has an indirect band gap as the valence band maximum and conduction band minimum are detected at separate high-symmetry sites in the HSE06 and GGA functionals. The band gap values calculated using GGA (HSE06) are 1.162 (1.922) eV. For both the HSE06 and GGA functionals, the bands do not interact with each other or cross the Fermi level, suggesting a semiconducting nature.

Fig. 4 Electronic band structure (a) GGA, (b) HSE06 of LiMgI₃, and total and partial density of states (c) GGA, (d) HSE06 of LiMgI₃.

3.1.2.2 DOS of LiMgI₃. Investigating a compound's partial and total densities of states (PDOS and TDOS) offers crucial information on atomic bonding as well as the unique contributions made by atoms and orbitals to different forms of conductivity (such as electrical, thermal, and optical) and electronic transport characteristics.⁸³ Fig. 4c and d display the TDOS and PDOS of LiMgI₃, respectively. The TDOS and PDOS of the studied compound were investigated using both GGA (Fig. 4c) and HSE06 (Fig. 4d) functionals. A black dotted line at 0 eV represents the Fermi level, which is positioned between the valence and conduction bands. The valence band top in LiMgI₃ is found between −3 eV and 0 eV when using GGA functionals and between −4 eV and 0 eV with HSE06 functionals. The valence band maximum for both functionals is mainly dominated by the I-p state. In both GGA (Fig. 4c) and HSE06 functionals (Fig. 4d) Mg-p and Mg-s states are the minor contributor to the valence band. For the GGA functional, the conduction band is primarily influenced by Li-p and Mg-p states, whereas for the HSE06 functional, Li-p and I-s states are the top contributors. The conduction band in the GGA method shows minor effects from Mg-s and Li-s states, while the HSE06 method reveals minimal contributions from Mg-p and Mg-s states.
3.1.2.3 Transport properties of LiMgI₃. Understanding the effective mass is essential to comprehending how charge carriers respond to outside factors like electric fields.⁸⁴ The effective mass and hole are calculated using a formula based on the E–K dispersion relation of the materials, as illustrated below:Here, the value of ℏ is 1.05 × 10⁻³⁴. The values of d²E/dk² are derived from the E–K dispersion curve by fitting parabolic curves at symmetry points. Using eqn (1), we computed the effective hole mass and electron mass as 0.321m₀ and 0.0393m₀, respectively. This material is most likely p-type since it has a higher effective hole mass than electron mass Reduced effective mass facilitates carrier transport, making it ideal for solar materials.⁸⁴ The following formula uses the effective masses to determine the mobility (μ_e for electrons and μ_h for holes).⁸⁵Here, μ symbolizes mobility, and τ represents the carrier's relaxation duration. For iodide PVSK materials, a constant relaxation time of 10⁻¹⁴ seconds is advised according to the literature.⁸⁶ The mobility of electrons and holes in LiMgI₃ was measured at 446 and 54.7 cm² V⁻¹ s⁻¹, respectively. We computed other electronic characteristics by applying the effective mass, such as the effective N_C and N_V at 300 K using the following formulas.⁸⁷

3.1.3 Optical properties. The effectiveness of a material in capturing and converting solar energy is largely determined by its optical properties, which describe its ability to absorb and manage light. The optical property of a material generally describes its behavior when exposed to electromagnetic radiation, especially in the visible light spectrum.⁸⁸ The optical properties of LiMgI₃, including absorption coefficient, reflectivity, refractive index, dielectric function, conductivity, and loss function, are analyzed using photon energy in the 0–14 eV range through both GGA and HSE06 methods. In Fig. 5, the optical properties of LiMgI₃ are depicted for both the GGA and HSE06 methods.

Fig. 5 Optical properties: (a) absorption, (b) reflectivity, (c) refractive index, (d) dielectric function, (e) conductivity and (f) loss function for LiMgI₃.

The absorption coefficient of a material, which indicates how much light at a particular wavelength would reach the material before absorption and is used to determine the solar energy conversion efficiency, yields the quantity of absorption per optical medium unit length illustrated in Fig. 5a. The absorption spectra for LiMgI₃, as calculated by both GGA and HSE06 methods, start from a non-zero energy level, signifying the existence of a band gap due to its semiconducting properties. The HSE06 approach displays a beginning point close to 5 eV, whereas the GGA method's absorption spectra for LiMgI₃ start at around 2 eV. For the HSE06 method, the absorption peak value is approximately 2.25 at an energy of 8 eV. Conversely, for the GGA method, the peak absorption value is approximately 2 at 6.8 eV. The HSE06 method shows slightly higher absorption compared to the GGA method. The high absorption capacity of this material makes it a prime choice for solar cell applications.

Reflectivity is assessed by measuring how much light a compound reflects when it is subjected to light. Reflectivity is determined by the ratio of the incident wave's energy to the energy of the wave reflected from the surface.⁸⁹ The reflectivity spectra of LiMgI₃, plotted against photon energy, are presented in Fig. 5b using the HSE06 and GGA methods. The starting points of the reflectivity spectra differ between the GGA and HSE06 methods. The peak reflectivity value is 0.35 at 13.3 eV for the GGA method and 0.335 at 8 eV for the HSE06 method. It is noteworthy that the reflectivity spectra show a downward trend in the UV region.

The refractive index is a dimensionless value that numerically describes how light or radiation moves through a medium.⁹⁰ The real and imaginary components of the refractive index for LiMgI₃ are shown in Fig. 5c. The real part of the refractive index begins at 2.1 for the GGA method and 1.8 for the HSE06 method. Each method shows almost identical peak values, with 2.75 for HSE06 and 2.7 for GGA. The refractive index decreases significantly in the ultraviolet part of the spectrum for both methods.

The dielectric function is a key parameter related to the rate of charge carrier recombination in a material.⁹¹ The real and imaginary components of the dielectric function are illustrated in Fig. 5d. The complex dielectric function, represented by ε₁ + ε₂, combines the real (ε₁) and imaginary (ε₂) parts. The real part begins at 4.5 for the GGA functional and at 3.3 for the HSE06 functional when measured at 0 eV. The peak values for GGA and HSE06 are 7 at 6.2 eV and 6.8 at 4.3 eV, respectively, which are nearly identical.

Optical conductivity measures how well a material conducts electric current in response to an electromagnetic field. It quantifies the interaction between light and the material, indicating how the material absorbs or reflects light. The optical conductivity of LiMgI₃ is depicted in Fig. 5e. The peak real part conductivity for LiMgI₃ is 6.66 with HSE06 and 4.9 with GGA, showing greater conductivity for the HSE06 method. In contrast, the imaginary part decreases steadily in both infrared and visible regions.

The loss function (L) is crucial for understanding how energy is lost through heating, scattering, or dispersion as light moves through a material.^92,93 Fig. 5f provides an illustration of the loss function spectra for LiMgI₃. The drop in the loss function at lower energies is associated with the increased absorption in that specific area. The energy equivalent of the largest peak in the loss function is plasma frequency.⁹⁴ The plasma frequency of LiMgI₃ differs between the GGA and HSE06 methods, with the peak of the loss function appearing at distinct energy points. The peak value of the loss function is 3.25 for the HSE06 method at 17 eV and 3 for the GGA method at 15.45 eV.

3.1.4 Thermo-mechanical properties of LiMgI₃. The mechanical and thermal parameters presented in Table S1† were derived using the established formulas reported for A₂BIrCl₆ (A = Cs, Rb; B = Na, K)⁹⁵ and ANiX (A = Sc, Ti, Y, Zr, Hf; X = Bi, Sn)⁸¹ in previously published literature. The mechanical and thermal characteristics of LiMgI₃ reveal a material with relatively soft and ductile behavior, suggesting its potential suitability for flexible and low-temperature device applications.⁹⁶ To evaluate the stability of the composites, it is essential to consider the Born–Huang stability criterion,^97,98 which is expressed as follows:

C₁₁ + 2C₁₂ > 0 (spinodal criteria), (13)

C₁₁ − C₁₂ > 0 (Born criteria), (14)

C₄₄ > 0 (shear criteria) (15)

Table S3† demonstrates that the elastic constants C₁₁, C₁₂, and C₄₄ for LiMgI₃ fulfill the mechanical stability requirements. The elastic constant tends as follows: C₁₁ < C₁₂ < C₄₄. The computed bulk modulus B (15.50 GPa) and shear modulus G (6.84 GPa) are relatively low, implying that the material is compressible and less resistant to shape deformation. The Young's modulus Y of 17.89 GPa supports this observation, confirming the soft nature of the crystal. Poisson's ratio (ν) serves as an indicator of whether a material behaves in a brittle or ductile manner. Values under 0.26 typically point to brittleness and covalent bonding, whereas those over 0.26 imply ductility and ionic bonding. Based on the data presented in Table S3,† it can be inferred that the materials LiMgI₃ (≈0.30) demonstrate ductile behavior and are characterized by ionic bonding, as their Poisson's ratio values are above 0.26. On the other hand, Pugh's ratio (B/G = 2.27) exceeding the critical threshold of 1.75, LiMgI₃ demonstrates ductile characteristics and possess ionic bond. Thermal analysis shows that the compound has a relatively low density of 4.14 g cm⁻³, and modest sound velocities (longitudinal (V_l),: 2.43 km s⁻¹, transverse V_t: 1.28 km s⁻¹) leading to an average sound velocity (ν_m) of 1.43 km s⁻¹. The Debye temperature (θ_D) is a key parameter that reflects several material properties, particularly thermal conductivity and elastic nature. A high Debye temperature typically signifies that a material is stiff, strongly bonded, and supports fast sound wave propagation.⁹⁹ The Debye temperature (θ_D), calculated as 77.66 K, indicates low vibrational energy and weak atomic bonding, which aligns with the observed softness. A minimum thermal conductivity (K_min) of 0.191 W m⁻¹ K⁻¹ further suggests poor heat conduction, a favorable trait for thermoelectric applications where thermal insulation is desirable. As indicated in Table S3,† LiMgI₃ is employed in thermal barrier coatings (TBC),¹⁰⁰ primarily due to its low thermal conductivity and Debye temperature. Table S3† exhibit that LiMgI₃ has a higher melting temperature (T_m), suggesting that the bonding atom is stronger. The thermo-mechanical properties of LiMgI₃ are presented in Table S3.†

3.2 Investigation of SCAPS-1D outcomes

3.2.1 Influence of HTL layer. The HTL in PSCs collects holes from the LiMgI₃ material and facilitates their transfer to the nickel (Ni) back metal contact. To improve device efficiency, SCAPS-1D simulations incorporated ten different types of HTLs, as presented in Table 2. Fig. 6 provides a visual overview of the HTL optimization process. Fig. 6a demonstrates that when WS₂ is used as the ETL with Cu₂O as the HTL, the perovskite device configuration achieves a PCE of 20.73%, which is superior to other HTL configurations. A maximum PCE of 25.50% was achieved with IGZO ETL and Cu₂O HTL in Fig. 6c. With a PCE of 25.24%, Fig. 6b shows that TiO₂ as ETL with Cu₂O as HTL showed greater optimization than other HTL. Similarly, when compared to other HTLs, ZnO, ZnS, and PCBM as HTL showed the best optimization. The PCEs for the device designs depicted in Fig. 6d–f are 25.25%, 25.25%, and 19.47%, respectively. Among the tested HTLs, Cu₂O showed the best performance. Therefore, it is considered the most suitable HTL for optimizing the simulated device designs.

Fig. 6 The change in performance parameters such as V_OC (V), J_SC (mA cm⁻²), FF (%), PCE (%) is studied for LiMgI₃ absorber-based PSCs with various HTLs and Ni as the back metal contact, using ETLs of (a) WS₂, (b) TiO₂, (c) IGZO, (d) ZnO, (e) ZnS, and (f) PCBM.

3.2.2 Optimization strategies for ETL. The electron transport layer (ETL) in the setup of perovskite solar cells (PSCs) extracts electrons from the perovskite material (LiMgI₃) and directs them to the ITO layer. It also plays a crucial role in preventing the recombination of electrons in the ITO with the holes in the absorber layer.¹⁰¹ To optimize the performance of the device design, simulations were conducted with each electron transport layer (ETL) paired with distinct hole transport layers (HTLs) in the LiMgI₃ perovskite absorber, as shown in Table 1. The investigation included a range of ETLs such as WS₂, IGZO, TiO₂, ZnO, ZnS, and PCBM. All ETL displayed maximum optimization with Cu₂O as HTL after simulating every possible combination between the ETL layer and HTL layer using LiMgI₃ absorber and Ni metal contact. Consequently, out of 60 combinations, six sets of device configurations showed the highest level of optimized performance and efficiency. The performance parameters V_OC, J_SC, FF, and PCE are shown in Table 4 and showed good agreement results in these six device configurations.

Table 4 The photovoltaic performance results for our LiMgI₃ simulation configurations

Optimized devices	VOC (V)	JSC (mA cm^−2)	FF (%)	PCE (%)
ITO/WS2/LiMgI3/Cu2O/Ni	1.495	15.785	87.81	20.73
ITO/IGZO/LiMgI3/Cu2O/Ni	1.509	15.348	88.48	20.50
ITO/TiO2/LiMgI3/Cu2O/Ni	1.501	15.349	87.89	20.25
ITO/ZnO/LiMgI3/Cu2O/Ni	1.502	15.349	87.86	20.26
ITO/ZnS/LiMgI3/Cu2O/Ni	1.503	15.348	87.81	20.26
ITO/PCBM/LiMgI3/Cu2O/Ni	1.416	15.361	89.49	19.47

---

3.2.3 Energy band diagram. The energy band diagram of the six optimized alkali-based single halide perovskite LiMgI₃ material is illustrated, in Fig. 7. The energy level alignment has a considerable impact on the efficiency and performance of PSCs. Holes created in the conduction band of the ETL of the perovskite solar cells (PSCs) are transferred to the HTL, while the electrons produced by light are collected at the indium-tin-oxide (ITO) and the back contact metal (Ni). To transfer the electron to the absorber–ETL interface, the electron affinity of the ETL must be greater than that of the LiMgI₃. Similarly, the HTLs ionization energy must be lower than the LiMgI₃. The efficiency and performance of PSC are significantly influenced by the alignment of the energy levels, which is achieved by reducing the gaps in the contact between these two materials. WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM ETLs have bandgaps of 1.8, 3.2, 3.05, 3.3, 2.80, and 2 eV, respectively, hence, their outcomes exhibit similarity when using the same heterostructure. Each device's quasi-Fermi levels, F_n and F_p, coexisted with the corresponding valence band energy (E_V) and conduction band energy (E_C) in Fig. 7a–f. In each ETL, F_p was positioned over the E_V while F_n and E_C kept up their harmonically similar operations.

Fig. 7 Energy band diagram of solar cells structure with different ETLs of (a) WS₂, (b) TiO₂, (c) IGZO, (d) ZnO, (e) ZnS, and (f) PCBM.

3.2.4 Impact of valance band offset (VBO), and conduction band offset (CBO). To ensure effective charge transport, PSCs require a completely depleted absorber layer. Consequently, both CBO (between the ETL and PVK) and VBO (between the absorber and HTL) must be considered as crucial factors.¹⁰² When sunlight hits the perovskite absorber, it generates electron–hole pairs. These charge carriers are then separated and directed to their designated contacts for collection. The efficiency of this separation process is largely influenced by the valence band offsets (VBO) and conduction band offsets (CBO) at the interfaces between the absorber and the HTL, as well as the absorber and the ETL. The device's efficiency is significantly impacted by these band offsets.

CBO = X_Absorber − X_ETL (16)

Three major barrier types are observed at the ETL/absorber interface: virtually flat, cliff-like, and spike-like.¹⁰³ A negative conduction band offset (CBO) results in a cliff-like barrier when the ETL's electron affinity (X_ETL) is greater than the absorber's (X_Absorber), signifying a lower conduction band minimum in the ETL. When no CBO is present, a flat barrier occurs, leading to no energy difference between the layers, which allows for easy charge transfer across the interface. Conversely, the formation of a spike-like barrier happens when the ETL's CBM is greater than the absorber's (X_ETL < X_Absorber), resulting in a positive CBO.

The VBO at the junction of the absorber and the HTL is characterized as.¹⁰⁴

VBO = X_HTL − X_Absorber + E_g,HTL − E_g,Absorber (17)

in this equation, VBO represents the valance band offsets. X_HTL HTL indicates the electron affinity of the HTL, and E_g,HTL, and E_g,Absorber indicates the bandgaps of the HTL and absorber. A cliff-like barrier arises, marked by a negative valence band offset when the VBM of the absorber is positioned lower than the HTL. The absence of a band offset is represented by a flat barrier with a VBO value of zero. Conversely, if the HTL's VBM is lower than the absorber's, a spike-like barrier with a positive VBO is seen. For our VBO calculations, Cu₂O HTL is selected due to its suitability for our device setup, as shown in Fig. 6. The analysis indicates that WS₂, TiO₂, IGZO, and ZnO ETLs CBO present a cliff-like barrier, which does not adversely impact charge carrier movement (Table 5). In contrast, ZnS and PCBM ETLs CBO demonstrate a spike-like barrier. However, all six configurations ultimately VBO show a cliff-like barrier as summarized in Table 5.

Table 5 Corresponding VBO, CBO value for different ETLs

Absorber	ETLs	CBO		VBO
LiMgI3	Six ETLs	Values	Comment (barrier)	Values	Comment (barrier)
	WS2	−0.03	Cliff-like	−0.24	Cliff-like
	TiO2	−0.08	Cliff-like	−0.24	Cliff-like
	IGZO	−0.24	Cliff-like	−0.24	Cliff-like
	ZnO	−0.08	Cliff-like	−0.24	Cliff-like
	ZnS	0.12	Spike-like barrier	−0.24	Cliff-like
	PCBM	0.05	Spike-like barrier	−0.24	Cliff-like

---

Eqn (16) and (17) were used to estimate the CBO and VBO.¹⁰² For WS₂ the CBO and VBO is

The CBO at the ETL/absorber interface is defined as = X_Absorber − X_ETL = 3.92 − 3.95 = −0.03 eV

So, in this case, it is a Cliff-like barrier, where the CBO is negative.

The VBO occurring at the contact between the ETL and absorber is defined as = 3.4 − 3.92 + 2.2 − 1.92 = −0.24 eV

So, for both cases, it is a cliff-like barrier, where the CBO and VBO are negative. Similarly, we can calculate the CBO and VBO of other ETLs.

3.2.5 Influence of absorber and ETL thickness on cell performance. The ETL stands between the ITO and absorber layer, and it has an extensive effect on the photon coupling in the absorber layer.¹⁰⁵ The thickness of the absorber layer and ETL layer plays a crucial role in enhancing the photovoltaic output characteristics of the SCs. To achieve the highest efficiency in solar cells, it is necessary to optimize the output of photovoltaic (PV) systems.¹⁰⁶ This section uses a contour plot to analyze the effect of the LiMgI₃ absorber layer and the thicknesses of the six optimized ETL layers on the PV performance of the PSC structures. Selecting the appropriate absorber and ETL combination is the first and most important step in building high-performance SCs.

For this research, we employed WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM as the ETLs, with LiMgI₃ as the absorber and Cu₂O as the HTL. For investigating the impact of the six optimized PSCs on the PV performance parameters such as V_OC, J_SC, FF, and PCE contour maps, the absorber layer thickness and ETL thickness were varied from 0.4 to 1.2 μm and 0.03 to 0.11 μm, respectively, during the simulation which displayed in Fig. 8–11.

Fig. 8 The V_OC (V) contour graphs for ETLs like (a) WS₂, (b) TiO₂, (c) IGZO, (d) ZnO, (e) ZnS, and (f) PCBM.

The contour graphs in Fig. 8a–f illustrate the impact of simultaneously changing the LiMgI₃ absorber layer and ETL thickness on the open-circuit voltage (V_OC) of the studied SCs. Fig. 8c demonstrates that the V_OC levels reached the maximum level when the absorber layer thickness varied between 0.4 and 0.5 μm, while the ETL thickness varies from 0.03 to 0.11 μm. Out of all the structures investigated, the ITO/IGZO/LiMgI₃/Cu₂O/Ni PSC structure found the highest V_OC value, which was about 1.546 V. The WS₂ based ETL device exhibited the lowest V_OC of 1.533 V among all the PSCs under study, with absorber thickness around 0.4–0.5 μm and ETL thickness ranging from 0.03 to nearly 0.05 μm, as displayed in Fig. 8a.

Fig. 8 demonstrates that reducing the thickness of the ETL layer and absorber layer leads to a raise in the value of V_OC. The reason for this is increasing the thickness of the absorber layer leads to a higher rate of carrier recombination, resulting in an increase in the saturation current and impacting the photocurrent.¹⁰⁶

Fig. 9 depicts the impact of changes in the thicknesses of the LiMgI₃ and ETL layers on the short-circuit current density (J_SC) in the investigated SC structures. The greatest J_SC 15.94 mA cm⁻² value for WS₂ as an ETL-associated SC is shown in Fig. 9a when the absorber thickness is 1 to 1.2 μm and the ETL thickness is around 0.05 to 0.11 μm. The PCBM as an ETL-associated solar cell configurations exhibits a lowest J_SC value, demonstrating approximately 15.55 mA cm⁻² when absorber layer thicknesses are between 1 and 1.2 μm and ETL thickness is between 0.03 and close to 0.74 μm (Fig. 9f).Conversely, The other four ETL (TiO₂, IGZO, ZnO and ZnS) associated SC structures shows the similar J_SC value of 15.56 mA cm⁻². The J_SC values for all SCs rise as the thickness of the absorber layer increases, due to the fact that the spectral response becomes greater at longer wavelengths.¹⁰⁷

Fig. 9 The J_SC (mA cm⁻²) contour graphs for ETLs like (a) WS₂, (b) TiO₂, (c) IGZO, (d) ZnO, (e) ZnS, and (f) PCBM.

The instance of the fill factor (FF) variation after simultaneously changing the absorber and ETL thickness is illustrated in Fig. 10. As an ETL-associated solar design, WS₂ demonstrates the opposite characteristics, as the FF values grow as the absorber and the thickness of the ETL layer drop (Fig. 10a). The FF reached 88.37% when WS₂ was used as the ETL, with absorber and ETL thicknesses varying from 0.3 to 0.325 μm and 0.03 to 0.9 μm, as demonstrated in Fig. 10a. Conversely, when using PCBM as an ETL, Fig. 10f demonstrates that the FF values enhance as the thickness of the ETL layer and absorber increases. In this scenario, the FF values reach a maximum of 89.76%, which is the highest of the six structures. As the absorber thickness is 0.6 to 1.2 μm and 0.03 to nearly 0.06 μm as the ETL thickness varies. A similar trend can be observed for solar structures connected to TiO₂, IGZO, and ZnO (Fig. 10b–d), as an increase in absorber thickness leads to a rise in FF values. As seen in Fig. 10d and e, For ZnO and ZnS as ETL and Cu₂O as HTL, the lowest value of FF is 88.1%. The absorber thickness for ZnO is 1–1.2 μm, and the absorber thickness for ZnS is 0.4 to about 0.425 μm. In both cases, the ETL thickness ranges from 0.03 to 0.11 μm.

Fig. 10 The FF (%) contour graphs for ETLs like (a) WS₂, (b) TiO₂, (c) IGZO, (d) ZnO, (e) ZnS, and (f) PCBM.

The effect of changing absorber and ETL thickness on the PCE is shown in Fig. 11. Out of the six solar structures that were optimized, the ETL WS₂/HTL solar structure had the best PCE of around 20.92%. This was noted when the absorber thickness was between 1 and 1.2 μm and the ETL thickness was greater than 0.04 μm, depicted in Fig. 11a. The ETL TiO₂/HTL Cu₂O-, ETL IGZO/HTL Cu₂O-, ETL ZnO/HTL Cu₂O-, and ETL ZnS/HTL Cu₂O-based solar cells demonstrated a comparable PCE of around 20.52%, 20.75%, 20.52%, and 20.53% respectively, by varying the thickness of the absorber and ETL layers (Fig. 11b–e). As indicated in Fig. 11f, the solar cell with PCBM ETL and Cu₂O HTL displays the lowest PCE of approximately 19.78%, occurring when the absorber thickness is between 0.9 and 1.2 μm and the ETL thickness is under 0.05 μm.

Fig. 11 The PCE (%) contour graphs for ETLs like (a) WS₂, (b) TiO₂, (c) IGZO, (d) ZnO, (e) ZnS, and (f) PCBM.

3.2.6 Impact of series resistance. Fig. 12 illustrates the effect of modifying the series resistance (R_s) in the LiMgI₃ layer on the photovoltaic performance of the solar cell. Both the series resistance (R_s) and shunt resistance (R_sh) play crucial roles in determining the efficiency of SCs. These resistances primarily originate from the junctions between the different layers of the SC, the metal contacts on the left and right sides, and imperfections that may occur during the manufacturing process. These factors collectively have a major impact on the SCs performance.⁵⁰ Fig. 12 illustrates that in the ITO/ETL/LiMgI₃/Cu₂O/Ni structures, the series resistance (R_s) varied from 1 to 6 Ω cm², while the shunt resistance was held constant at 10⁵ Ω cm². Across all six configurations of LiMgI₃ perovskite devices, a decrease in efficiency (PCE) was observed as R_s increased, as shown in Fig. 12d. In Fig. 12d, the initial PCEs of WS₂ and IGZO as ETL-associated structures were about 20.49% and 20.27%. However, as series resistance (R_s) increased, the overall efficiency dropped because the higher series resistance (R_s) led to increased power loss.¹⁰⁸ From Fig. 12d we can see that a similar pattern was observed in the case of TiO₂, ZnO, and ZnS, ETL-associated structures, but these structures show lower PCE than the WS₂ and IGZO ETL structures. Specifically, the PCE for TiO₂, ZnO, and ZnS in ETL-based LiMgI₃ perovskite devices decreased from approximately 20.03% to 18.9%. Additionally, solar cells with PCBM ETL showed a drop in PCE from nearly 19.02% to 17.91%. Our study revealed that PCBM ETL structures showed lower PCE values than the other five ETL-associated structures as R_s was increased (Fig. 12d). According to Fig. 12c also shows that the FF decreased with rising R_s, with IGZO and PCBM ETL structures presenting FF values of about 88% and 87%, respectively. The SCs connected with WS₂, TiO₂, ZnO, and ZnS as ETL structures demonstrated lower fill factors (FF) than those with IGZO and PCBM, which had starting FF values of approximately 86%. In previous research, it was observed that changes in R_s did not markedly influence the J_SC or V_OC. However, an increase in R_s caused a significant drop in both FF and power conversion efficiency (PCE), a pattern that is consistent with findings in both inorganic and organic solar cells.^109,110 Fig. 12b indicates that the (J_SC) remained nearly constant across all six solar cell structures as the series resistance (R_s) increased. Among these, WS₂ ETL-based structures exhibited a higher J_SC of approximately 15.78 mA cm⁻², whereas PCBM ETL-based structures had a lower J_SC of about 15.31 mA cm⁻². The J_SC values for solar cells with TiO₂, IGZO, ZnO, and ZnS as ETL structures were similar, approximately 15.34 mA cm⁻². These values were lower than the J_SC values for WS₂ ETL-based structures but exceeded those for PCBM ETL-based structures. Fig. 12a indicate that the V_OC remained nearly constant across all six solar cell structures as series resistance (R_s) increased. However, the PCBM ETL-based structure exhibited an exceptionally low V_OC of approximately 1.40 V. In contrast, the other five structures all showed similar V_OC values of around 1.50 V. It can be observed that choosing the minimum R_s is beneficial to reduce its effect on PCE and FF, leading to improved solar cell efficiency.

Fig. 12 Series resistance R_s affects the following performance metrics: (a) V_OC, (b) J_SC, (c) FF, (d) PCE of (ITO/ETL/LiMgI₃/Cu₂O/Ni) ETL = WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM.

3.2.7 Impact of shunt resistance. In this research, the shunt resistance (R_sh) was varied within the range of 10¹ to 10⁶ Ω cm², with the series resistance (R_s) held constant across all six optimized solar cell designs. This variation was conducted to assess its impact on key performance metrics such as V_OC, J_SC, FF, and PCE, as depicted in Fig. 13. In PSCs, the shunt resistance (R_sh) is primarily affected by leakage pathways, such as pinholes in the photoactive layer and recombination losses. Conversely, the series resistance (R_s) is influenced by factors including internal resistances, interface barriers, charge-collection layers, and metal-based electrodes.¹¹¹ Under ideal one-sun illumination conditions, the Shockley equation, provided in eqn (18) and (19), describes the current–voltage (J–V) behavior of a solar cell.¹¹²in the above equations, J_PH is the photocurrent density, J₀ is the reverse bias saturation current density, q_e stands for the elementary charge, n is the diode ideality factor, k is the Boltzmann constant (1.38 × 10²³ J K⁻¹), and T_e is the ambient temperature (298 K), R_s represents the series resistance, R_sh represents the shunt resistance. Eqn (18) and (19) reveal an inverse relationship between the shunt resistance (R_sh) and both the J_SC and V_OC, meaning that as R_sh increases, J_SC and V_OC also increase. It can be seen that as R_sh rises, the values of V_OC, FF, and PCE also increase, while J_SC remains constant across all six structures, as illustrated in Fig. 13a–d. According to Fig. 13a, c and d shows a significant increase in V_OC, FF, and PCE within the R_sh range of 10¹ to 10² Ω cm². After this rapid rise, these values level out and remain unchanged as R_sh continues to increase. The J_SC values were identical across all six configurations. The PSC with the PCBM ETL displayed the lowest J_SC at around 15.31 mA cm⁻², whereas the PSC with the WS₂ ETL demonstrated the highest J_SC, approximately 15.78 mA cm⁻², as shown in Fig. 13b. Among all the configurations, the PSC with the PCBM ETL achieved the highest FF of approximately 88.82%. In contrast, the FF values for the structures with WS₂, TiO₂, IGZO, ZnO, and ZnS ETLs were relatively similar, each around 87%, as depicted in Fig. 13c. For the SC structures using different ETLs, including WS₂, TiO₂, IGZO, ZnO, and ZnS, the V_OC remained consistently around 1.4 V when the R_sh was set to 10² Ω cm². It was noted that the PSC with the PCBM (ETL) exhibited the lowest V_OC, measured at 1.3 V. The impact of R_sh on V_OC and FF, influenced by charge transfer and recombination processes, appears to be significant.¹¹³ Among the six ETL configurations tested, the WS₂ ETL structure exhibited the highest PCE of 20.73%, whereas the PCBM ETL structure had the lowest PCE of 19.24%, as depicted in Fig. 13d. To enhance solar cell efficiency (PCE) and fill factor (FF), it is beneficial to select the highest possible R_sh. Achieving optimal device performance requires minimizing the series resistance while maximizing the shunt resistance.¹¹⁴

Fig. 13 Shunt resistance R_sh affects the following performance metrics: (a) V_OC, (b) J_SC, (c) FF, (d) PCE of (ITO/ETL/LiMgI₃/Cu₂O/Ni) ETL = WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM.

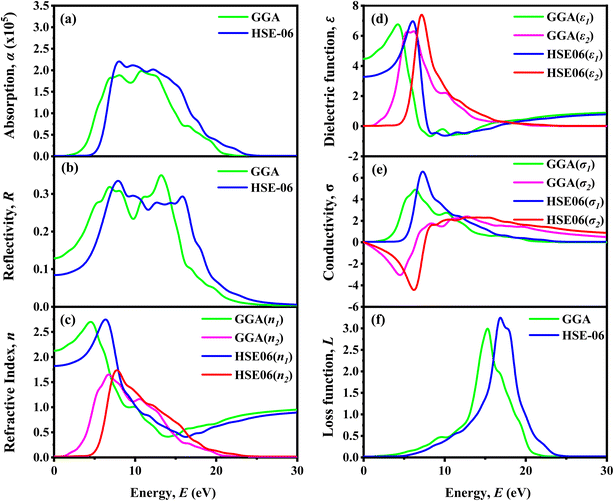
3.2.8 Impact of temperature. The device's performance was assessed within a temperature range of 300 K to 450 K. Analyzing the stability of solar cells requires understanding their performance under elevated thermal conditions. Fig. 14 demonstrates how temperature affects six distinct PSC configurations. It reveals that changes in temperature result in variations in V_OC, J_SC, FF, and PCE for each of the six configurations. Fig. 14a, c and d shows that the V_OC, FF, and PCE decline as the temperature increases. However, the device with WS₂ ETL exhibits a slightly higher J_SC with rising temperatures, as shown in Fig. 14b. In our investigation, the J_SC values of TiO₂, IGZO, ZnO, and ZnS ETL-based structures were almost similar J_SC, which was almost 15.34 mA cm⁻². It can be observed that the WS₂ ETL-based solar structure shows the highest J_SC (≈15.78 mA cm⁻²), while the lowest value is observed in the PCBM (≈15.31 mA cm⁻²) ETL structure as shown in Fig. 14b. Solar cells using PCBM as the ETL exhibit the highest FF among the six ETL configurations, beginning at around 89.5%. Although the lowest FF values are observed in the IGZO ETL structure. Moreover, higher temperatures can lead to decreased V_OC and PCE because of increased carrier recombination. As temperatures increase, both the diffusion length and R_s are affected, leading to an almost immediate impact on the FF and PCE of the device.^113,115 As illustrated in Fig. 14a, the V_OC for all six structures followed a consistent downward trend with increasing temperature. The PCBM ETL PSC exhibited the lowest V_OC of about 1.40 V, while the remaining five ETL PSCs showed a higher V_OC, approximately 1.5 V. In our analysis, it can be seen that the WS₂, TiO₂, IGZO, ZnO and ZnS ETLs structure showed almost above 20.25% PCE while the PCBM ETL showed about 19.24% PCE, which was almost reduced efficiency (Fig. 14d). The decrease in V_OC for all optimal device configurations with higher temperatures is attributed to the inverse correlation between V_OC and the reverse saturation current density (J₀). As the temperature rises, J₀ increases, as detailed in eqn (20)whereas represents the thermal voltage. As the temperature of the PSC increases, the number of defects rises and the V_OC decreases, consistent with previous research.¹¹⁶ A noticeable decline in short-circuit performance with increasing temperature is evident in Fig. 14a–d.

Fig. 14 Temperature's impact on performance metrics (a) V_OC, (b) J_SC, (c) FF, (d) PCE of (ITO/ETL/LiMgI₃/Cu₂O/Ni) ETL = WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM.

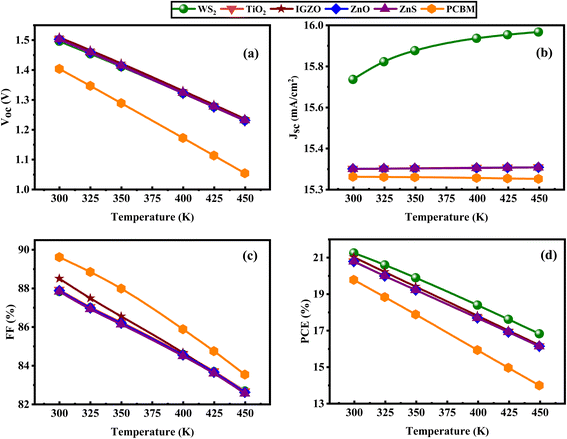
3.2.9 Analysis of capacitance and Mott–Schottky (MS). The influence of voltage, ranging from −0.8 to 0.8 V, on capacitance and Mott–Schottky (M–S) properties is demonstrated in Fig. 15a and b. Through capacitance–voltage (C–V) measurements, the M–S analytical approach facilitates the calculation of built-in voltage (V_bi) and charge carrier density (N_d). The junction capacitance per unit area (C) is deduced from eqn 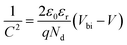(21).Here, ε₀ refers to the vacuum permittivity, ε_r represents the dielectric constant of the donor material, q denotes the electronic charge, and V is the applied voltage (Fig. 15b).^117,118 The gradient of the linear part reveals N_d, and the built-in voltage V_bi is found by extending the line to the voltage axis. Fig. 15a and b illustrate that the frequency remains constant at 1 MHz while the voltage varies from −0.8 V to 0.8 V. The device coupled with IGZO and PCBM ETL exhibits voltage-independent capacitance between −0.8 V and 0.8 V. In Fig. 15a, it is observed that the capacitance of structures with WS₂, TiO₂, ZnO, and ZnS ETLs remains unaffected by changes in voltage, indicating that the depletion layer capacitance dominates as the applied voltage increases.¹¹⁹ Therefore, the dependence of capacitance on the applied voltage indicates the potential for using the device as a voltage-regulated SC. The Mott–Schottky method, known for its reliability and widespread use, enables the calculation of the built-in potential (V_bi) by investigating the difference between electrode performance and doping concentration.¹²⁰ The well-reliable and recognized Mott–Schottky analysis is used to analyze the V_bi.¹²¹

Fig. 15 Investigation of (a) capacitance (C), (b) Mott–Schottky (1/C²) trends, (c) charge generation rate, and (d) recombination rate for all six configurations.

The Mott–Schottky (M–S) method, emphasizing capacitance–voltage characteristics, is a well-established approach for analyzing space charge distributions in semiconductors, such as those due to junction capacitance.¹²² Our analysis indicates that Fig. 15b follows a unique trend, differing from the earlier figure. In this case, the voltage decreases linearly from −0.8 to 0.8 V for all six PSCs, which is in agreement with other studies.^123,124 For PCBM and IGZO-based ETLs, M–S values started to decrease after reaching certain voltages, specifically beyond 0.4 V for PCBM and 0.5 V for IGZO. Conversely, the structures utilizing WS₂, TiO₂, ZnO, and ZnS ETLs showed a decrease in capacitance only after exceeding 0.6 V, as shown in Fig. 15b.

3.2.10 Influence of generation and recombination rate. The generation rate of a SC depends on both the location within the device and the wavelength of the incident light. It reflects the number of electron–hole pairs generated at each point due to photon absorption at specific wavelengths. This generation rate is essential for optimizing the efficiency of solar cells.¹²⁵ The graphical depiction of the generation and recombination rates for the six layouts is presented in Fig. 15c and d. In the carrier generation process, electron–hole pairs are formed when electrons move from the valence band to the conduction band. For all six designs, Fig. 15c displays that the generation rates peak at 1.2 μm for WS₂ configuration. The electron–hole pair generation, G(x), is calculated using the incoming photon flux, N_phot(λ,x), and SCAPS-1D as described in eqn (22):

G(λ,x) = α(λ,x)N_phot(λ,x) (22)

Recombination occurs when electrons in the conduction band and holes recombine and are effectively annihilated, which is the reverse process of generation.⁷⁴ During recombination, the defect characteristics of each layer play a crucial role, resulting in the formation of energy states that have a substantial impact on the recombination process. It can be seen in Fig. 15d that the WS₂, TiO₂, IGZO, ZnO and ZnS ETL-based structures experience a delayed start in their recombination process. In Fig. 15d, the structure shows its optimal recombination rates between (1.1 and 1.2) for ITO/PCBM/LiMgI₃/Cu₂O/Ni configurations. Fig. 15d distinctly indicate that the PCBM as an ETL-based solar structure showed the highest recombination rate at the position of around 1.2 μm. In the range from 1.1 to 1.2 μm, an increased recombination rate is observed because more electrons from the conduction band transition across the energy barrier to occupy valence band positions. This shift affects the recombination rate of electron–hole pairs in the solar device.

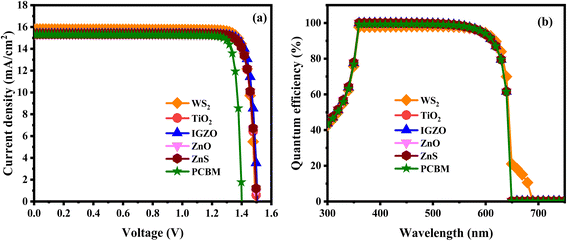
3.2.11 JV and QE characteristics. Current density measures the electric current passing through a specific area and is essential for evaluating device performance. Fig. 16a illustrates the current–voltage density for an ITO/ETL/LiMgI₃/Cu₂O/Ni device configuration across six different ETLs. The voltage is supplied between 0 and 1.8 V. Firstly, the photocurrent values in all six combinations are nearly identical. All structures follow the same pattern between 0.0 and 1.5 V. Subsequently, WS₂, TiO₂, IGZO, ZnO, and ZnS PSCs experience a decrease in photocurrent around 1.4–1.6 V. Conversely, PCBM PSC experience a decrease in photocurrent around 1.3–1.4 V. It can be seen that in the initial optimization WS₂, TiO₂, IGZO, ZnO, and ZnS ETLs showed better J–V characteristics (in terms of J_SC and V_OC) for the solar structure than the PCBM ETLs. Initially, the photocurrent of the five (WS₂, TiO₂, IGZO, ZnO, and ZnS) PSCs is high J_SC approximately >15.32 mA cm⁻² when the V_OC was about (0–1.5 V). However, the PCBM ETLs associated structure lowest J_SC value of 15.31 mA cm⁻², when the V_OC was about (0–1.4 V). To accurately assess the photovoltaic parameters of a PSC, it is crucial to understand electron–hole recombination behaviors. The J–V curve of a perovskite layer reflects this understanding. Fig. 16b illustrates the correlation between the wavelength and quantum efficiency (QE) of the optimized device WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM ETLs. Here, the wavelength is adjusted between 300 and 900 nm. The QE charts for each device under investigation are represented in Fig. 16b. When the wavelength was 360 nm, the six PSCs had the best QE of (97–99%). When the wavelength was about 610 nm, all the PSCs displayed the optimal QE is 92%. Recombination diminishes the QE in solar cells when charge carriers are unable to reach the external circuit. Factors affecting the collection probability also have a significant impact on QE. For instance, carriers produced near the surface may be influenced by modifications to the front surface. At longer wavelengths, free carrier absorption in heavily doped surface layers can lead to a reduction in quantum efficiency.¹²² The study reveals that with rising voltage, the QE improves due to reduced recombination. Subsequently, QE starts to fall as the wavelength changes across all configurations. An increase in absorber thickness usually results in better QE, as a larger absorber can absorb a greater number of photons.¹²⁶

Fig. 16 (a) J–V characteristics and (b) QE response of the single halide PSCs.

3.2.12 Optimization of absorber/ETL interface layer defect density. The effect of defect density (N_t) at the interface between ETLs and the LiMgI₃ absorber on photovoltaic characteristics such as V_OC, J_SC, FF, and PCE is shown in Fig. 17, with defect densities ranging from 10¹⁰ to 10¹⁸ cm⁻². Fig. 17 shows that when N_t grows, the performance parameters of PSCs decrease due to higher recombination rates, resulting in a decrease in PCE. Specifically, V_OC, J_SC, FF, and PCE remain almost constant when N_t is ≤10¹³ cm⁻², but they slightly decline (WS₂, TiO₂, IGZO, ZnO and PCBM) when N_t reaches ≥10¹⁴ cm⁻². For a WS₂-based ETL structure, V_OC drops from approximately ∼1.49 to 1.43 V, J_SC drop from ∼15.78 to 8.43 mA cm⁻², FF increases from ∼87.80 to 87.90%, and subsequently, the PCE decreases from ∼20.73 to ∼10.69%. Solar cell heterostructures with TiO₂, IGZO, ZnO, and PCBM ETLs demonstrate enhanced performance when the ETLs/LiMgI₃ interface has a defect density (N_t) of ≤1 × 10¹³ cm⁻². Among the five ETLs (WS₂, TiO₂, IGZO, ZnO, and PCBM), V_OC, J_SC, FF, and PCE show similar trends, whereas the ZnS ETL-based structure consistently maintains stable values. Therefore, it is concluded that a defect density of 10¹⁰ cm⁻² is optimal for subsequent analyses and should be maintained to achieve the best results. The range of N_t was chosen for V_OC analysis due to its higher sensitivity to defect density compared to J_SC. The interface recombination limit for V_OC can be defined using eqn (23).¹²⁷where S_t signifies the recombination velocity at the interface. A denotes the ideality factor, and ∅_c represents the effective barrier height.

Fig. 17 Investigating the influence of ETL/LiMgI₃ interface defect levels on V_OC (V), J_SC (mA cm⁻²), FF (%), and PCE (%) of LiMgI₃.

3.2.13 Nyquist plot. The real and imaginary impedance components (Z_re and Z_im) for several ETLs are depicted in the Nyquist plot in Fig. 18. The behavior of different halide-based perovskite materials can be effectively studied using impedance analysis techniques.¹⁰² The Y-axis of this plot represents the geometrical capacitance, indicating where carriers accumulate at the interface layers, while the X-axis shows the resistance associated with recombination. Each plot exhibits a single semi-circle, process within the frequency range of 1 Hz to 1 MHz. The real (Z_re) and imaginary (Z_im) parts of impedance are plotted against each other. Nyquist plot provides an in-depth qualitative analysis of resistive losses, capacitance, and recombination defects affecting the device.¹²⁸ The expanded semi-circle in the IGZO ETL-based structure indicates higher resistance indicates increased impedance or resistance. The WS₂ ETL-based structure demonstrates a smaller semi-circle, which reflects lower impedance, smoother charge transport, and better interface characteristics compared to other ETLs. The TiO₂, ZnO, ZnS, and PCBM ETLs had a similar trend. However, the Nyquist plot is observed in the case of TiO₂, IGZO, ZnO, and ZnS ETL-based structures, which were much lower than WS₂ structures but also higher than PCBM structures (Fig. 18). The resistance observed at high frequencies is related to the material's recombination resistance. Additionally, the capacitance measured at these frequencies reflects the geometric capacitance resulting from charge accumulation at the interfaces.¹²⁹ In high-frequency measurements, the resistance observed is indicative of the material's recombination resistance. At the same time, the capacitance at these frequencies represents the geometric capacitance, which is associated with the accumulation of charge at the interfaces.¹³⁰

Fig. 18 Nyquist plot of the various ETL materials (WS₂, TiO₂, IGZO, ZnO, ZnS, and PCBM) based structure with LiMgI₃ absorber.

3.2.14 Comparison of SCAPS-1D results with previous work. The performance parameters of the six device configurations examined in this study are compared with the most recently published optimal configurations in Table 6. According to Table 6, the LiMgI₃ single halide perovskite-based solar cell presented here has a higher PCE value than the same-series device structures reported in earlier publications. The presented device structures utilizing WS₂, IGZO, TiO₂, ZnO, ZnS, and PCBM as ETLs achieved PCE values of 20.73%, 20.50%, 20.25%, 20.26%, 20.26%, and 19.47%, respectively. This is significantly higher than the previously published and FTO/SnS₂/KGeCl₃/Cu₂O structure, which reported a PCE of approximately 15.83%.⁵³ FTO/TiO₂/CsSnI₃/m-MTDATA/Au structure shows around 2.02% PCE.¹³¹ The V_OC values of the presented solar structures are almost similar except the FTO/TiO₂/KSnI₃/Spiro-OMeTAD/Au structure is less than the previous published device configurations. In our same series of previously published device structures the ITO/TiO₂/MASnI₃/Spiro-OMeTAD/Au, ITO/PCBM/CsSnI₃/NiO₂/Al, and ITO/PCBM/CsSnI₃/CuI/Au show lowest J_SC than – LiMgI₃ base device structure. All presented solar structures show a J_SC of greater than 15 mA cm⁻² except FTO/SnS₂/KGeCl₃/Cu₂O, FTO/C₆₀/KGeCl₃/PEDOT:PSS, and C₆₀/CsGeCl₃/PEDOT:PSS structure.^53,132 The FF values of the LiMgI₃-based solar structure are much higher than those of the previously published device structure. Table 6 shows that the presented six solar structures show more effective performance than the previously reported solar cells. Table 6 reveals that the six solar cell configurations presented here are more efficient than previously reported CsSnI₃-based solar cells, which had efficiency levels below 16%, while our LiMgI₃ absorber achieves much higher performance. The first six LiMgI₃-based solar cell device structures of Table 6 used a different ETL which shows higher efficiency than our previously published device structure. We examined absorber characteristics such as thickness, which differ from those in previous theoretical studies of device structures. Additionally, the ETL and HTL combinations we studied do not align with the properties of those previously explored in theoretical research. In addition, the optical properties change from one absorber to another, resulting in differences in solar energy absorption. The LiMgI₃ absorber we examined demonstrated superior optical properties, as evidenced by the 20.73% PCE performance in the ITO/WS₂/LiMgI₃/Cu₂O/Ni structure.¹³³ Based on these factors, we can infer that our LiMgI₃ solar cell exhibits a higher PCE compared to similar structured absorbers solar cells.

Table 6 PV performance parameters of our simulated configurations of LiMgI₃^a

Optimized devices	Types	VOC (V)	JSC (mA cm^−2)	FF (%)	PCE (%)	Ref.
a Theo. = theoretical, Exp. = experimental.
ITO/WS2/LiMgI3/Cu2O/Ni	Theo.	1.49	15.78	87.81	20.73	This work
ITO/IGZO/LiMgI3/Cu2O/Ni	Theo.	1.50	15.34	88.48	20.50	This work
ITO/TiO2/LiMgI3/Cu2O/Ni	Theo.	1.50	15.34	87.89	20.25	This work
ITO/ZnO/LiMgI3/Cu2O/Ni	Theo.	1.50	15.34	87.86	20.26	This work
ITO/ZnS/LiMgI3/Cu2O/Ni	Theo.	1.50	15.34	87.81	20.26	This work
ITO/PCBM/LiMgI3/Cu2O/Ni	Theo.	1.41	15.36	89.49	19.47	This work
FTO/SnS2/KGeCl3/Cu2O	Theo.	0.545	41.91	69.24	15.83	53
FTO/C60/KGeCl3/PEDOT:PSS	Theo.	0.702	31.29	65.36	14.37	132
FTO/TiO2/RbGeBr3/P3HT/Au	Theo.	0.96	14.47	85.70	11.89	134
C60/CsGeCl3/PEDOT:PSS	Theo.	0.703	21.39	64.60	9.8	132
FTO/TiO2/KSnI3/Spiro-OMeTAD/Au	Theo.	1.70	15.85	36.13	9.77	135
FTO/TiO2/CsSnI3/Au	Exp.	0.34	20.63	54.18	3.83	136
FTO/TiO2/CsSnI3/m-MTDATA/Au	Exp.	0.24	22.70	0.37	2.02	131
ITO/TiO2/MASnI3/Spiro-OMeTAD/Au	Theo.	0.88	16.80	0.42	6.40	137
ITO/PCBM/CsSnI3/NiO2/Al	Theo.	0.52	10.21	62.50	3.31	138
ITO/PCBM/CsSnI3/CuI/Au	Theo.	0.91	14.24	78.11	10.10	139

---

4 Conclusion

This work presents a comprehensive analysis of the optoelectronic and photovoltaic characteristics of LiMgI₃ perovskite by integrating DFT and SCAPS-1D modeling. By employing first-principles calculations through density functional theory (DFT) for the first time, we comprehensively examined the structural, electrical, transport, and optical properties of LiMgI₃, a single halide perovskite. The structural investigation indicates that LiMgI₃ compounds possess a cubic structure. The lattice parameters and unit cell volume of LiMgI₃ align with previous theoretical findings. The stability of this compound is demonstrated by its phonon dispersion curve. Through the analysis of the electrical band structure, it is evident that this material has an indirect band gap, confirming its semiconducting character. Moreover, the analysis of optical properties indicates the possible use of this particular perovskite in solar cells due to its extensive absorption capability and low energy band gap. The photovoltaic characteristics of this compound were investigated by using LiMgI₃ as the absorber material in a single perovskite solar cell construction, with various ETL and HTL layers. Among the studied configurations, the ITO/WS₂/LiMgI₃/Cu₂O/Ni structure demonstrated superior photovoltaic performance due to optimal band alignment, efficient charge extraction, and reduced recombination at interfaces. WS₂ serves as an effective electron transport layer with good conductivity and stability, while Cu₂O provides favorable valence band alignment with LiMgI₃ for hole transport. This synergistic combination facilitates efficient carrier separation and transport, leading to enhanced device performance. The PCE of 20.73%, V_OC of 1.49 V, J_SC of 15.78 mA cm⁻², and FF of 87.81% are observed in the ITO/Cu₂O/LiMgI₃/WS₂/Ni combination. The thickness of the absorber and ETL has been varied to optimize the device's performance. The impact of series resistance, shunt resistance, and temperature on device performance are explored in this investigation. A decreasing nature of efficiency has been seen with increasing series resistance and temperature which is inverse in the case of shunt resistance. In addition, we incorporate Mott–Schottky and capacitance analyses, as well as the generation and recombination rates, into our investigation. The properties of QE and JV are also addressed. The efficiency of the device has been seen to be significantly impacted by the interface defect density. These findings are crucial for researchers studying single halide perovskite-based PSC because they allow for the creation of suitable SC configurations before the production and testing of these devices.

4.1 Limitation

While LiMgI₃-based perovskites show promising theoretical optoelectronic properties, several practical challenges must be addressed before realizing efficient and scalable solar cells. One key concern is the chemical stability of LiMgI₃ under ambient conditions, as the presence of lithium and iodine may lead to high sensitivity to moisture, oxygen, and temperature.¹⁴⁰ This could necessitate encapsulation techniques or processing in an inert atmosphere. However, such issues are common with emerging perovskite materials and can be effectively managed through further experimental optimization and material engineering.

4.2 Future work

This analysis highlights a number of prospective paths for continuing the research:

(1) The absorber layer LiMgI₃ demonstrates diverse qualities and promising behavior in photovoltaic applications, suggesting its suitability for use in multi-junction solar cell configurations.

(2) To explore whether incorporating a window layer, buffer layer, or other design elements can enhance solar cell efficiency without exceeding the theoretical limit of 33%-a new lead halide hetero-structure solar cell utilizing LiMgI₃ could be engineered.

(3) The economic feasibility of producing LiMgI₃-based solar cells largely depends on the scalability of the synthesis and fabrication processes.

Data availability

Data will be made available upon request.

Author contributions

Md. Raihan Kabir: investigation, methodology, data curation, conceptualization, and writing the original manuscript; Nazmul Shahadath: formal analysis, methodology, data curation, conceptualization, and review-editing; Md. Tarekuzzaman: formal analysis, methodology, data curation, software, conceptualization, and review-editing; Md. Abu Bakkar Siddique: formal analysis, validation and review-editing; O. Alsalmi: data curation, validation, and formal analysis; Md. Rasheduzzaman: formal analysis, validation, and review-editing; Md Abdul Qader: formal analysis and review-editing; M. Moazzam Hossen: formal analysis and review-editing; Md. Zahid Hasan: formal analysis, data curation, validation, supervision, and review-editing.

Conflicts of interest

There is no conflict to declare.

Abbreviations

DFT	Density functional theory
PVSK	Perovskite
PSC	Perovskite solar cell
PCE	Power conversion efficiency
JSC	Short-circuit current density
VOC	Open-circuit voltage
FF	Fill factor
ETL/HTL	Electron/hole-transport layer
ITO	Indium tin oxide
PV	Photovoltaic
J–V	Current density–voltage
WS2	Tungsten disulfide
TiO2	Titanium dioxide
IGZO	Indium gallium zinc oxide
ZnO	Zinc oxide
ZnS	Zinc sulphide
PCBM	Phenyl-C61-butyric acid methyl ester
CuI	Copper iodide
Cu2O	Copper(I) oxide
CuO	Copper(II) oxide
CBTS	Copper barium tin sulfide
hν	Energy of photon
G(x)	Generation rate
n/p	Concentrations of electrons and holes
WF	Work function
	Effective mass of the electron/hole
Fn/p	Fermi level of the electron/hole
Ni	Nickel
EC/EV	Energy level of the conduction/valence band
PTAA	Poly(triarylamine)
PEDOT:PSS	Poly(3,4-ethylene-dioxythiophene):polystyrene sulfonate
CuSCN	Copper(I) thiocyanate
CdTe	Cadmium telluride
P3HT	Poly(3-hexylthiophene-2,5-diyl)
Spiro-OMeTAD	2,2′,7,7′-Tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene
SCAPS	Solar cell capacitance simulator

Acknowledgements

The authors extend their appreciation to Umm Al-Qura University, Saudi Arabia for funding this research work through grant number: 25UQU4300099GSSR06. Funding statement: This research work was funded by Umm Al-Qura University, Saudi Arabia under grant number: 25UQU4300099GSSR06.

References

1. O. Ellabban, H. Abu-Rub and F. Blaabjerg, Renewable Sustainable Energy Rev., 2014, 39, 748–764.
2. K. Dedecker and G. Grancini, Adv. Energy Mater., 2020, 10, 2001471.
3. I. Hamideddine, H. Jebari, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, Int. J. Energy Res., 2022, 46, 20755–20765.
4. B. Padha, S. Verma, P. Mahajan and S. Arya, ECS Trans., 2022, 107, 12073–12081.
5. L. Calió, S. Kazim, M. Grätzel and S. Ahmad, Angew. Chem., Int. Ed., 2016, 55, 14522–14545.
6. L. Chen, C. Li, Y. Zhao, J. Wu, X. Li, Z. Qiao, P. He, X. Qi, Z. Liu and G. Wei, Chem. Eng. J., 2021, 425, 131599.
7. S. Arya, P. Mahajan, R. Gupta, R. Srivastava, N. K. Tailor, S. Satapathi, R. R. Sumathi, R. Datt and V. Gupta, Prog. Solid State Chem., 2020, 60, 100286.
8. P. Mahajan, B. Padha, S. Verma, V. Gupta, R. Datt, W. C. Tsoi, S. Satapathi and S. Arya, J. Energy Chem., 2022, 68, 330–386.
9. P. Mahajan, R. Datt, W. Chung Tsoi, V. Gupta, A. Tomar and S. Arya, Coord. Chem. Rev., 2021, 429, 213633.
10. Y. Chen, L. Zhang, Y. Zhang, H. Gao and H. Yan, RSC Adv., 2018, 8, 10489–10508.
11. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
12. M. Kulbak, D. Cahen and G. Hodes, J. Phys. Chem. Lett., 2015, 6, 2452–2456.
13. S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391–402.
14. Y. Zhou and K. Zhu, ACS Energy Lett., 2016, 1, 64–67.
15. Y. Zhou, M. Yang, S. Pang, K. Zhu and N. P. Padture, J. Am. Chem. Soc., 2016, 138, 5535–5538.
16. N. Saleh, S. Al-Trawneh, H. Al-Dmour, S. Al-Taweel and J. P. Graham, J. Fluoresc., 2015, 25, 59–68.
17. H. Al-Dmour, R. H. Alzard, H. Alblooshi, K. Alhosani, S. AlMadhoob and N. Saleh, Front. Chem., 2019, 7, 561.
18. T. Miyasaka, A. Kulkarni, G. M. Kim, S. Öz and A. K. Jena, Adv. Energy Mater., 2020, 10, 1902500.
19. P. Gao, M. Grätzel and M. K. Nazeeruddin, Energy Environ. Sci., 2014, 7, 2448–2463.
20. P. Zhao, J. Su, Z. Lin, J. Wang, J. Zhang, Y. Hao, X. Ouyang and J. Chang, Adv. Theory Simul., 2020, 3, 2000055.
21. H. Al-Dmour, D. M. Taylor and J. A. Cambridge, J. Phys. D: Appl. Phys., 2007, 40, 5034–5038.
22. H. Al-Dmour and D. M. Taylor, Appl. Phys. Lett., 2009, 94, 223309.
23. T. He, Y. Jiang, X. Xing and M. Yuan, Adv. Mater., 2020, 32, 1903937.
24. A. N. Singh, S. Kajal, J. Kim, A. Jana, J. Y. Kim and K. S. Kim, Adv. Energy Mater., 2020, 10, 2070129.
25. J. Xu, R. Saklatvala, S. Mittal, S. Deshmukh and A. Procopio, Advanced Science, 2020, 7, 1903394.
26. R. Sharma, A. Sharma, S. Agarwal and M. S. Dhaka, Sol. Energy, 2022, 244, 516–535.
27. G. Souadi, Inorg. Chem. Commun., 2024, 167, 112768.
28. A. S. Belousov, E. V. Suleimanov, I. Shafiq and H. Li, J. Environ. Chem. Eng., 2025, 13, 116750.
29. S. K. Mitro, M. Saiduzzaman, A. Biswas, A. Sultana and K. M. Hossain, Mater. Today Commun., 2022, 31, 103532.
30. S. K. Mitro, M. Saiduzzaman, T. I. Asif and K. M. Hossain, J. Mater. Sci.: Mater. Electron., 2022, 33, 13860–13875.
31. D. Behera, B. Akila, S. K. Mukherjee, T. A. Geleta, A. Shaker and M. M. Salah, Crystals, 2023, 13, 1437.
32. M. M. Namisi, R. J. Musembi, W. M. Mulwa and B. O. Aduda, Comput. Condens. Matter., 2023, 34, e00772.
33. K. Wang, Z. Jin, L. Liang, H. Bian, D. Bai, H. Wang, J. Zhang, Q. Wang and S. Liu, Nat. Commun., 2018, 9, 4544.
34. E. Smecca, Y. Numata, I. Deretzis, G. Pellegrino, S. Boninelli, T. Miyasaka, A. La Magna and A. Alberti, Phys. Chem. Chem. Phys., 2016, 18, 13413–13422.
35. H. Al-Dmour and Department of Physics, Faculty of Science, Mutah University, AIMS Mater. Sci., 2021, 8, 261–270.
36. G. Tong, L. K. Ono and Y. Qi, Energy Technol., 2020, 8, 1900961.
37. S. Arya, A. Singh, A. Ahmed, B. Padha, A. Banotra, U. Parihar, A. K. Sundramoorthy, S. Dixit and N. I. Vatin, J. Energy Chem., 2025, 105, 193–223.
38. R. Kour, S. Arya, S. Verma, J. Gupta, P. Bandhoria, V. Bharti, R. Datt and V. Gupta, Glob. Chall., 2019, 3, 1900050.
39. S. Arya, A. Sharma, A. Singh, A. Ahmed, A. Dubey, B. Padha, S. Khan, R. Mahadeva, A. Khosla and V. Gupta, ECS Sens. Plus, 2024, 3, 022601.
40. M. K. Hossain, M. T. Rahman, M. K. Basher, M. J. Afzal and M. S. Bashar, Results Phys., 2018, 11, 1172–1181.
41. M. K. Hossain, M. T. Rahman, M. K. Basher, M. S. Manir and M. S. Bashar, Optik, 2019, 178, 449–460.
42. H. Al Dmour, East Eur. J. Phys., 2023, 555–561.
43. A. M. D. A. Jaber, A. Alsoud, S. R. Al-Bashaish, H. Al Dmour, M. S. Mousa, T. Trčka, V. Holcman and D. Sobola, Technologies, 2024, 12, 87.
44. Department of Physics, Faculty of Science, Mutah University, H. Al-Dmour, D. M. Taylor and School of Electronic Engineering, Bangor University, J. Ovonic Res., 2023, 587–596.
45. B. Gil, A. J. Yun, Y. Lee, J. Kim, B. Lee and B. Park, Electron. Mater. Lett., 2019, 15, 505–524.
46. K. Sobayel, Md. Akhtaruzzaman, K. S. Rahman, M. T. Ferdaous, Z. A. Al-Mutairi, H. F. Alharbi, N. H. Alharthi, M. R. Karim, S. Hasmady and N. Amin, Results Phys., 2019, 12, 1097–1103.
47. D. Shin, B. Saparov, T. Zhu, W. P. Huhn, V. Blum and D. B. Mitzi, Chem. Mater., 2016, 28, 4771–4780.
48. R. Chakraborty, K. M. Sim, M. Shrivastava, K. V. Adarsh, D. S. Chung and A. Nag, ACS Appl. Energy Mater., 2019, 2, 3049–3055.
49. C. Devi and R. Mehra, J. Mater. Sci., 2019, 54, 5615–5624.
50. M. K. Hossain, M. H. K. Rubel, G. F. I. Toki, I. Alam, Md. F. Rahman and H. Bencherif, ACS Omega, 2022, 7, 43210–43230.
51. D. Sabba, H. K. Mulmudi, R. R. Prabhakar, T. Krishnamoorthy, T. Baikie, P. P. Boix, S. Mhaisalkar and N. Mathews, J. Phys. Chem. C, 2015, 119, 1763–1767.
52. T.-B. Song, T. Yokoyama, J. Logsdon, M. R. Wasielewski, S. Aramaki and M. G. Kanatzidis, ACS Appl. Energy Mater., 2018, 1, 4221–4226.
53. Md. A. F. Siddique and A. S. Md. Sayem Rahman, Mater. Sci. Eng., B, 2024, 303, 117268.
54. F.-T. -Zahra, Md. M. Islam, Md. M. Hasan, Md. R. Islam and S. Ahmad, J. Phys. Chem. Solids, 2024, 191, 112037.
55. Md. T. Hossain, M. M. Hasan, F.-T. Zahra, S. Swargo, R. Al-Arefeen Dhroobo, Md. R. Al Amin, F. M. A. Sieam, S. T. Disha and Md. R. Islam, Phys. B, 2024, 690, 416131.
56. A. H. Mahedi, Md. S. Rahman, Md. Tarekuzzaman, H. Al-Dmour, Md. Rasheduzzaman, M. M. Hossen, Y. Arafat and Md. Z. Hasan, Sol. Energy, 2025, 289, 113338.
57. T. Das, G. Di Liberto and G. Pacchioni, J. Phys. Chem. C, 2022, 126, 2184–2198.
58. M. Ben Bechir and M. H. Dhaou, RSC Adv., 2021, 11, 21767–21780.
59. N. L. Dey, Md. S. Reza, A. Ghosh, H. Al-Dmour, M. Moumita, Md. S. Reza, S. Sultana, A. K. M. Yahia, M. Shahjalal, N. S. Awwad and H. A. Ibrahium, J. Phys. Chem. Solids, 2025, 196, 112386.
60. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr.–Cryst. Mater., 2005, 220, 567–570.
61. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
62. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
63. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
64. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
65. F. D. Murnaghan, Am. J. Math., 1937, 59, 235–260.
66. T. H. Fischer and J. Almlof, J. Phys. Chem., 1992, 96, 9768–9774.
67. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192.
68. Md. Hasan Ali, A. T. M. Saiful Islam, M. D. Haque, Md. Ferdous Rahman, M. Khalid Hossain, N. Sultana and A. Z. M. Touhidul Islam, Mater. Today Commun., 2023, 34, 105387.
69. R. Pandey, S. Bhattarai, K. Sharma, J. Madan, A. K. Al-Mousoi, M. K. A. Mohammed and M. K. Hossain, ACS Appl. Electron. Mater., 2023, 5, 5303–5315.
70. A. K Al-Mousoi, M. K. A. Mohammed, S. Q. Salih, R. Pandey, J. Madan, D. Dastan, E. Akman, A. A. Alsewari and Z. M. Yaseen, Energy Fuels, 2022, 36, 14403–14410.
71. A. K. Al-Mousoi, M. K. A. Mohammed, R. Pandey, J. Madan, D. Dastan, G. Ravi, P. Sakthivel and G. A. Babu, RSC Adv., 2022, 12, 32365–32373.
72. R. A. Jabr, M. Hamad and Y. Mohanna, Int. J. Electr. Eng. Educ., 2007, 44, 23–33.
73. Y. H. Khattak, Modeling of high power conversion efficiency thin film solar cells, PhD thesis, Universitat Politècnica de València, 2019.
74. M. K. Hossain, A. A. Arnab, R. C. Das, K. M. Hossain, M. H. K. Rubel, Md. F. Rahman, H. Bencherif, M. E. Emetere, M. K. A. Mohammed and R. Pandey, RSC Adv., 2022, 12, 34850–34873.
75. C. Chen, X. Lu, X. Hu, G. Liang and G. Fang, J. Mater. Chem. C, 2024, 12, 16–28.
76. Md. S. Reza, Md. F. Rahman, A. Kuddus, M. K. A. Mohammed, A. K. Al-Mousoi, Md. R. Islam, A. Ghosh, S. Bhattarai, R. Pandey, J. Madan and M. K. Hossain, RSC Adv., 2023, 13, 31330–31345.
77. M. S. Uddin, M. K. Hossain, M. B. Uddin, G. F. I. Toki, M. Ouladsmane, M. H. K. Rubel, D. I. Tishkevich, P. Sasikumar, R. Haldhar and R. Pandey, Adv. Electron. Mater., 2024, 10, 2300751.
78. K. W. Guji, T. A. Geleta, N. Bouri and V. J. Ramirez Rivera, Nanoscale Adv., 2024, 6, 4479–4491.
79. J. Li, Y. Liu, J. Bai, C. Xie, H. Yuan, Z. Cheng, W. Wang, X. Wang and G. Zhang, Applied Physics Reviews, 2023, 10, 031416.
80. J. W. Wafula, J. W. Makokha and G. S. Manyali, Results Phys., 2022, 43, 106132.
81. M. Tarekuzzaman, M. H. Ishraq, M. A. Rahman, A. Irfan, M. Z. Rahman, M. S. Akter, S. Abedin, M. A. Rayhan, M. Rasheduzzaman, M. M. Hossen and M. Z. Hasan, J. Comput. Chem., 2024, 45(29), 2476–2500.
82. R. Geiger, T. Zabel and H. Sigg, Front. Mater., 2015, 2, 52.
83. S. Kerdsongpanya, B. Alling and P. Eklund, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195140.
84. S. Mahmud, M. A. Ali, M. M. Hossain and M. M. Uddin, Vacuum, 2024, 221, 112926.
85. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
86. Q. Mahmood, U. Hani, T. I. Al-Muhimeed, A. A. AlObaid, B. Ul Haq, G. Murtaza, T. H. Flemban and H. Althib, J. Phys. Chem. Solids, 2021, 155, 110117.
87. A. J. Kale, R. Chaurasiya and A. Dixit, Adv. Theory Simul., 2021, 4, 2000224.
88. Md. M. Hossain, Md. A. Ali, Md. M. Uddin, S. H. Naqib and A. K. M. A. Islam, ACS Omega, 2021, 6, 33899–33913.
89. M. Roknuzzaman, M. A. Hadi, M. J. Abden, M. T. Nasir, A. K. M. A. Islam, M. S. Ali, K. Ostrikov and S. H. Naqib, Comput. Mater. Sci., 2016, 113, 148–153.
90. E. Keaney, J. Shearer, A. Panwar and J. Mead, J. Compos. Mater., 2018, 52, 3299–3307.
91. M. A. Rashid, M. Saiduzzaman, A. Biswas and K. M. Hossain, Eur. Phys. J. Plus, 2022, 137, 649.
92. S. Hayat, R. M. A. Khalil, M. I. Hussain, A. M. Rana and F. Hussain, Solid State Commun., 2022, 344, 114674.
93. D. Pottmaier, E. R. Pinatel, J. G. Vitillo, S. Garroni, M. Orlova, M. D. Baró, G. B. M. Vaughan, M. Fichtner, W. Lohstroh and M. Baricco, Chem. Mater., 2011, 23, 2317–2326.
94. M. A. Hadi, M. Roknuzzaman, F. Parvin, S. H. Naqib, A. K. M. A. Islam and M. Aftabuzzaman, J. Sci. Res, 2013, 6, 11–27.
95. Md. Tarekuzzaman, N. Shahadath, M. Montasir, O. Alsalmi, M. H. Mia, H. Al-Dmour, Md. Rasheduzzaman and Md. Z. Hasan, RSC Adv., 2025, 15, 13643–13661.
96. M. Manzoor, A. Tewari, S. Ansar, Y. A. Kumar and R. Sharma, J. Inorg. Organomet. Polym., 2025, 35, 795–812.
97. M. Born, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160–172.
98. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, Oxford, 1954.
99. Md. T. Hossain, J. Islam, M. Hasan and K. Hossain, Phys. B, 2024, 691, 416355.
100. R. Darolia, Int. Mater. Rev., 2013, 58, 315–348.
101. T. Kim, J. Lim and S. Song, Energies, 2020, 13, 5572.
102. K. Sekar, L. Marasamy, S. Mayarambakam, H. Hawashin, M. Nour and J. Bouclé, RSC Adv., 2023, 13, 25483–25496.
103. M. R. Kabir, M. H. Ishraq, M. Tarekuzzaman, N. I. Nahid, J. K. Modak, S. Ahmad, A. M. Arfi, M. Rasheduzzaman and M. Z. Hasan, Eng. Res. Express, 2025, 7, 015319.
104. K. Sekar, L. Marasamy, S. Mayarambakam, H. Hawashin, M. Nour and J. Bouclé, RSC Adv., 2023, 13, 25483–25496.
105. M. K. Hossain, M. K. A. Mohammed, R. Pandey, A. A. Arnab, M. H. K. Rubel, K. M. Hossain, M. H. Ali, Md. F. Rahman, H. Bencherif, J. Madan, Md. R. Islam, D. P. Samajdar and S. Bhattarai, Energy Fuels, 2023, 37, 6078–6098.
106. M. K. Hossain, A. A. Arnab, D. P. Samajdar, M. H. K. Rubel, M. M. Hossain, Md. R. Islam, R. C. Das, H. Bencherif, Md. F. Rahman, J. Madan, R. Pandey, S. Bhattarai, M. Amami and D. K. Dwivedi, Energy Fuels, 2023, 37, 13377–13396.
107. M. Khalid Hossain, G. F. Ishraque Toki, I. Alam, R. Pandey, D. P. Samajdar, M. Ferdous Rahman, M. Rasidul Islam, M. H. K. Rubel, H. Bencherif, J. Madan and M. K. A. Mohammed, New J. Chem., 2023, 47, 4801–4817.
108. D. Jayan K, V. Sebastian and J. Kurian, Sol. Energy, 2021, 221, 99–108.
109. J. D. Servaites, S. Yeganeh, T. J. Marks and M. A. Ratner, Adv. Funct. Mater., 2010, 20, 97–104.
110. E. E. Van Dyk and E. L. Meyer, Renewable Energy, 2004, 29, 333–344.
111. K. Tvingstedt, L. Gil-Escrig, C. Momblona, P. Rieder, D. Kiermasch, M. Sessolo, A. Baumann, H. J. Bolink and V. Dyakonov, ACS Energy Lett., 2017, 2, 424–430.
112. Y. Li, B. Ding, Q.-Q. Chu, G.-J. Yang, M. Wang, C.-X. Li and C.-J. Li, Sci. Rep., 2017, 7, 46141.
113. S. R. Raga, E. M. Barea and F. Fabregat-Santiago, J. Phys. Chem. Lett., 2012, 3, 1629–1634.
114. A. Sunny, S. Rahman, M. M. Khatun and S. R. A. Ahmed, AIP Adv., 2021, 11, 065102.
115. F. Behrouznejad, S. Shahbazi, N. Taghavinia, H.-P. Wu and E. Wei-Guang Diau, J. Mater. Chem. A, 2016, 4, 13488–13498.
116. M. K. Hossain, M. H. K. Rubel, G. F. I. Toki, I. Alam, Md. F. Rahman and H. Bencherif, ACS Omega, 2022, 7, 43210–43230.
117. S. Lin, Bell Syst. Tech. J., 1965, 44, 2245–2269.
118. X. Zhang, X. Chen, Y. Chen, N. A. Nadege Ouedraogo, J. Li, X. Bao, C. B. Han, Y. Shirai, Y. Zhang and H. Yan, Nanoscale Adv., 2021, 3, 6128–6137.
119. Md. Samiul Islam, K. Sobayel, A. Al-Kahtani, M. A. Islam, G. Muhammad, N. Amin, Md. Shahiduzzaman and Md. Akhtaruzzaman, Nanomaterials, 2021, 11, 1218.
120. E. H. Jung, N. J. Jeon, E. Y. Park, C. S. Moon, T. J. Shin, T.-Y. Yang, J. H. Noh and J. Seo, Nature, 2019, 567, 511–515.
121. M. Y. Rahman and S. M. Mominuzzaman, Exploring Lead Free Mixed Halide Double Perovskites Solar Cell, arXiv, 2024, preprint, arXiv:2401.09584,  DOI:10.48550/arXiv.2401.09584.
122. M. K. Hossain, M. K. A. Mohammed, R. Pandey, A. A. Arnab, M. H. K. Rubel, K. M. Hossain, M. H. Ali, Md. F. Rahman, H. Bencherif, J. Madan, Md. R. Islam, D. P. Samajdar and S. Bhattarai, Energy Fuels, 2023, 37, 6078–6098.
123. G. G. Malliaras, J. R. Salem, P. J. Brock and C. Scott, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R13411–R13414.
124. A. A. Goje, N. A. Ludin, M. A. Mat Teridi, U. Syafiq, M. A. Ibrahim, F. Nawab and A. A. Syakirin, IOP Conf. Ser.: Mater. Sci. Eng., 2023, 1278, 012004.
125. M. K. Hossain, D. P. Samajdar, R. C. Das, A. A. Arnab, Md. F. Rahman, M. H. K. Rubel, Md. R. Islam, H. Bencherif, R. Pandey, J. Madan and M. K. A. Mohammed, Energy Fuels, 2023, 37, 3957–3979.
126. Mamta, K. K. Maurya and V. N. Singh, J. Sci.: Adv. Mater. Devices, 2022, 7(2), 100445.
127. N. Jensen, R. M. Hausner, R. B. Bergmann, J. H. Werner and U. Rau, Prog. Photovoltaics, 2002, 10, 1–13.
128. S. Bhattarai, R. Pandey, J. Madan, S. Tayeng, P. K. Kalita, M. Z. Ansari, L. Ben Farhat, M. Amami and M. K. Hossain, RSC Adv., 2023, 13, 26851–26860.
129. E. Von Hauff and D. Klotz, J. Mater. Chem. C, 2022, 10, 742–761.
130. A. Guerrero, J. Bisquert and G. Garcia-Belmonte, Chem. Rev., 2021, 121, 14430–14484.
131. M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127.
132. C. Li and I. Tlili, Eng. Anal. Bound. Elem., 2023, 155, 425–431.
133. K. Deepthi Jayan and V. Sebastian, in 2021 7th International Conference on Electrical Energy Systems (ICEES), 2021, pp. 623–628.
134. S. Valizadeh, A. Shokri, A. Sabouri-Dodaran, N. Fough and F. Muhammad-Sukki, Results Phys., 2024, 57, 107351.
135. G. Pindolia, S. M. Shinde and P. K. Jha, Mater. Chem. Phys., 2023, 297, 127426.
136. T.-B. Song, T. Yokoyama, J. Logsdon, M. R. Wasielewski, S. Aramaki and M. G. Kanatzidis, ACS Appl. Energy Mater., 2018, 1, 4221–4226.
137. N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068.
138. N. Wang, Y. Zhou, M. Ju, H. F. Garces, T. Ding, S. Pang, X. C. Zeng, N. P. Padture and X. W. Sun, Adv. Energy Mater., 2016, 6, 1601130.
139. M. K. Hossain, G. F. I. Toki, D. P. Samajdar, M. Mushtaq, M. H. K. Rubel, R. Pandey, J. Madan, M. K. A. Mohammed, Md. R. Islam, Md. F. Rahman and H. Bencherif, ACS Omega, 2023, 8, 22466–22485.
140. J. Zhuang, J. Wang and F. Yan, Nano-Micro Lett., 2023, 15, 84.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra02550h

---