Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
LearnCK: mass conserving neural network reduction of chemistry and species of microkinetic models†
Sashank
Kasiraju
 a and
Dionisios G.
Vlachos
a and
Dionisios G.
Vlachos
 *ab
*ab
aRAPID Manufacturing Institute and Delaware Energy Institute, University of Delaware, 221 Academy St., Newark, Delaware 19716, USA. E-mail: vlachos@udel.edu
bDepartment of Chemical and Biomolecular Engineering, University of Delaware, 150 Academy St., Newark, Delaware 19716, USA
First published on 11th September 2023
Abstract
Reduction of chemical reaction mechanisms has been long studied to minimize the computational cost of reacting flows or the number of parameters of catalytic reaction models for estimation from experimental data. Conventional reduction techniques encompass either a tabulation of the reaction rates of elementary reactions or a reduction of elementary reactions. We introduce a Python-TensorFlow tool to learn chemical kinetics (LearnCK) systematically and automatically from microkinetic models using artificial neural networks (NNs). The approach constructs overall reactions among stable species only and interconversion rates and dramatically reduces the number of species and, thus, of the differential equations (the most expensive aspect in reacting flows). Doing this also removes the stiffness and nearly eliminates the complexity and cost of estimating the entire thermochemistry and kinetic rate expressions for computing reaction rates. Python programming automates training data generation, extracts metadata for fitting the NNs, and deploys the NN model. Since NNs are black boxes, we propose an approach to conserve mass. We demonstrate the method for the ammonia synthesis on Ru and the methane non-oxidative coupling over a single-atom Fe/SiO2 catalyst. The latter model includes over 500 gas and surface species and a combined 9300 gas and surface reactions. We demonstrate a nearly 1000-fold computational speedup and exceptional predictive accuracy using up to 8 overall reactions. The NN model is embedded in macroscopic reactor flow models to estimate uncertainty.
1. Introduction
Microkinetic models (MKMs) of complex homogeneous and heterogeneous reaction mechanisms have become commonplace.1–8 The conservation species equations of chemical kinetics are highly nonlinear and stiff, require specialized solvers and expertise, and are costly for large reaction mechanisms. As a result, their penetration to reacting flow simulators, such as computational fluid dynamics (CFD), and systems tasks, such as optimization and control, has been slow.9–13 An overview of the current strategies and challenges in the application of CFD to reactive flows has been discussed.14,15The computational singular perturbation method was introduced thirty years ago to remove stiffness of chemical kinetics and potentially reduce the network.16 Optimization has also been employed as a mathematical programming-based rigorous approach to eliminate inconsequential reactions based on preset performance metrics.17–19
In chemical reaction engineering, mechanism reduction has often been employed to mitigate numerical complexity, improve computational tractability, and better understand the overall reaction. A key approach has employed the separation of time scales by identifying key species and rate-limiting step(s). Common approaches involve local sensitivity analysis (LSA), principal component analysis (PCA), reaction path analysis (RPA), quasi-steady-state (QSS), partial equilibrium (PE) analysis, and most abundant surface intermediates (MASI).20,21 For catalytic MKMs, our group has applied a posteriori mechanism reduction where MASIs, RDS, etc. are determined after the solution has been obtained. Simple order 1 asymptotics have then been used to derive closed-form rate expressions that are consistent with the MKM physics. These expressions expose all the fundamental reaction rate and equilibrium constants and are interpretable (in the AI nomenclature). These often entail pencil and paper calculations.22–25 Aside from reducing detailed mechanisms, a priori assumptions, such as the RDS, PE, QSS, and MASI, have been commonplace in catalysis to create overall rate expressions for comparison to experiments, mechanism discrimination, and parameter estimation. The famous Langmuir–Hinshelwood–Hougen–Watson (LHHW) models are a manifestation of this approach.
In a complementary pioneering approach of Pope, the in situ adaptive tabulation (ISAT)26,27 method that tabulates the rates of elementary reactions on the fly of a simulation has generated intensive research. The combustion community has extensively used it to accelerate CFD simulations of chemically reacting flows.27–29 For every simulation at runtime, the reaction rate table is built by running the full MKM. The table can become large and inefficient; for unseen conditions, the MKM must be used to update the table.30 ISAT does not reduce the size and stiffness of the system. It eliminates the computation of reaction rates by interpolating within the reaction rates table and, by doing this, it saves considerable computational time. The technique has been applied to other problems, e.g., kinetic Monte Carlo simulations31,32 and real-time control.33
Neural networks (NNs) are universal function approximators34,35 of high-dimensional nonlinear functions that can be ideal surrogates of chemical kinetics. The combustion research community has embraced NNs to tackle several challenges in the temporal evolution of standalone complex kinetic models or in conjunction with CFD simulations. Some examples include modeling the temporal evolution of a reduced combustion chemical system,36 large-scale eddy simulations of turbulent flames,37–39 machine learning in reaction flow CFD,40 and on-the-fly NN-based numerical integration for combustion.41 Recently several articles described specialized applications embedding NNs inside numerical integrators to describe the time evolution of ordinary differential equations (ODEs) describing the chemical kinetics of reacting species. Firstly, kinetics-informed NN42 and chemical reaction NN (CRNN)43 describe NN frameworks that satisfy physical constraints and design equations set by the ODEs describing chemical reaction systems and can be used to elucidate reaction mechanisms and pathways from experimental data. ChemNODE,44 a new type of NN named neural ordinary differential equations (NODEs),45 is computationally efficient but has not been demonstrated for stiff systems. Physics-informed NN-based models (PINN) do not perform well for stiff ODEs;46,47 alternatives such as stiff-PINN48 and MPINN46 were developed to alleviate stiffness. Stiff-PINN48 reduces the system complexity by ignoring short-lived species with the quasi-steady-state approximation. The resulting DAEs must be hand-calculated on a case-by-case basis; MPINN46 employs multiple PINNs to handle species with different time scales, but it is not clear how the method handles very large systems. A residual NN (ResNet)-based deep NN model called KiNet49 employs several deeply stacked ResNets (in the stack each time step requires an independent ResNet) for efficient backward propagation through time networks. However, due to the very deep stacking of multiple ResNets, the computational complexity and memory required depend on the number of time steps, and it is unclear how the method scales with system size (number of individual species tracked). More recently, NNs and multivariate spline interpolation were used to approximate reduced-order MKMs constructed using traditional methods such as the partial equilibrium index and the degree of rate control.50 In this approach forward, backward, and net rates of elementary reactions (of the reduced model) were captured using a latent asinh51 and logarithmic50 transformation. Finally, a method augmenting a modification of CRNNs with an Euler integrator to model stiff atmospheric chemistry52 was developed, where the adaptive time step of integration is estimated from the NNs eliminating the need to calculate computationally expensive Jacobians. All these methods solve the complete high-dimensional problem or the reduction of the problem to a lower dimensional manifold (Stiff-PINN) requires hand-calculations and is not scalable to very large reaction networks.
Here, we propose a new detailed kinetic model reduction using deep NNs (DNNs) without analysis, tabulation, or human intervention. We only consider key reactants and products seen in experiments, and track ‘user-defined’ rates of a handful of overall reactions connecting these species. The approach is both computationally efficient, as it reduces both reactions and species and removes stiffness, and is also a tabulator, as it parametrizes rates vs. the local reactor conditions. We first describe the procedure used to generate training data, fit the NNs, and then deploy them within numerical integrators as surrogates in reactor models. We discuss the implications of mass conservation as NNs do not follow physical laws a priori and quantify the uncertainty resulting due to the errors. The entire methodology is tested on a proof-of-concept MKM system (NH3 decomposition to N2 and H2, with a total of 18 gas and surface species and 14 surface reactions) and a very complex MKM model (methane coupling to C2–C10 products, with over 500 species and ca. 9300 gas- and surface-phase reactions).
2. Methods
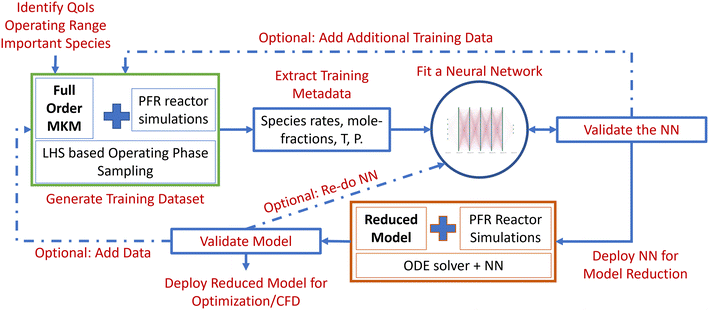
2.1 The model reduction workflow
The algorithm entails the following steps: a) identification of the phase space and quantities of interest (QoIs), b) generation of training data (within the operating window) using Latin hypercube sampling (LHS)-based full-order MKM simulations, c) processing and transformation of the training dataset, d) construction and training of the DNNs, e) construction of an NN surrogate-based numerical integrator (reduced model), and f) evaluation, validation and uncertainty quantification (UQ) of the reduced model and the underlying NN. The outline of the workflow is shown in Fig. 1. We describe each of the steps and the overall algorithm next.2.2 Phase-space and QoI identification
First the phase-space of operating conditions, such as temperature, pressure, feed flowrate, feed composition, residence time, etc., is defined, so that the NN can reliably predict within it. For a large full-order MKM system with hundreds of species (short-lived intermediates and long-lived reactants and products), we need to identify long-lived species which contribute the most to the reactor concentration (see the example of methane chemistry). The key QoIs which need to be predicted by the NN-integrated reduced model are defined (e.g., species concentrations or conversion or selectivity).2.3 Creating the dataset
We perform plug flow reactor (PFR) simulations by approximating a PFR as a series of 100 CSTRs; each CSTR in a single simulation serves as an independent datapoint of a different local composition (and potentially a different temperature and pressure) within this phase-space using sampling methods, such as LHS. Each PFR simulation provides the low-dimensional manifold of chemical kinetics staring from the initial conditions and moving toward equilibrium downstream. The dataset comprises data from several hundred PFR simulations, each providing 100 datapoints. PFR simulations of large reaction networks are feasible, not as time consuming, and robust.2.4 Data transformation
The input features required by the NNs in this work are local concentration of (selected) species, temperature, and pressure; the output responses are turnover frequencies (sometimes normalized using the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 scale). These input features are scaled using a MinMaxScaler,53 such that each feature has a maximum value of 1.0 and a minimum value of 0.0:
10 scale). These input features are scaled using a MinMaxScaler,53 such that each feature has a maximum value of 1.0 and a minimum value of 0.0: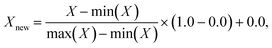 | (1) |
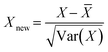 | (2) |
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) is the mean, Var(X) is the variance, and Xnew is the normalized dataset.
is the mean, Var(X) is the variance, and Xnew is the normalized dataset.
The predicted targets using a NN could include turnover frequencies (TOFs), steady-state rates, conversion, selectivity, etc. In this work on heterogeneous catalytic models, TOFs are chosen which only depend on the temperature, pressure, and local composition of reactants and products for a given catalyst and are agnostic to feed flowrate and residence time. Depending on the order of magnitude of TOFs in the training dataset, they are sometimes represented in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 scale to ensure very low rates are accounted for accurately. The dataset is split randomly 70
10 scale to ensure very low rates are accounted for accurately. The dataset is split randomly 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 into training and testing sets, respectively.
30 into training and testing sets, respectively.
2.5 Construction and training of the NN
The input features required by the NNs in this work are local concentration of (selected) species, temperature and pressure and the output responses are TOFs (sometimes normalized using the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 scale). TensorFlow55 was used to construct a simple feed-forward DNN. Overfitting is suppressed with early stopping, which stops network training when the loss-function does not improve, after a pre-defined number of epochs. While the entire architecture of the DNN, i.e., layer depth, number of neurons in each layer, combinations of activation functions, regularization, and dropout penalty, can be custom designed and improved using hyper-parameter optimization, the networks described here are simple and homogeneous (only one type of activation function and the same number of neurons in each layer) to demonstrate feasibility of the concept. DNNs in this work are typically 5 layers deep, with 50 neurons in each layer, and use an identical activation function, either rectified linear units (ReLU)55,56 or Gaussian error linear unit (GELU).55,57
10 scale). TensorFlow55 was used to construct a simple feed-forward DNN. Overfitting is suppressed with early stopping, which stops network training when the loss-function does not improve, after a pre-defined number of epochs. While the entire architecture of the DNN, i.e., layer depth, number of neurons in each layer, combinations of activation functions, regularization, and dropout penalty, can be custom designed and improved using hyper-parameter optimization, the networks described here are simple and homogeneous (only one type of activation function and the same number of neurons in each layer) to demonstrate feasibility of the concept. DNNs in this work are typically 5 layers deep, with 50 neurons in each layer, and use an identical activation function, either rectified linear units (ReLU)55,56 or Gaussian error linear unit (GELU).55,57
The choice of hyper-parameters could have an effect on the NN performance as shown for a couple of parameters in Fig. S3† (activation function) and Fig. S4† (hidden layer depth), but the difference is negligible. However, we note that the NN architecture considered in this work might not be ideal for all chemically reacting systems and therefore appropriate hyper-parameter optimization must be carefully performed for optimal results. The tunable parameters within the DNN are fitted via the well-regarded stochastic gradient descent method, Adam optimizer offered by the TensorFlow library, with a learning rate of 0.001, using the mean absolute error (MAE) loss metric for the objective function evaluated for the entire training dataset (between the TOFs predicted by the DNNs and MKM simulations).
2.6 DNN-surrogate-based PFR numerical simulations
The Python-SciPy stiff ODE solver solve_ivp,58 specifically the LSODA59,60 algorithms, is employed to numerically solve the steady-state PFR simulation using the DNN reaction rates. The Jacobian matrix is approximated with finite differences using the default implementation within the SciPy solve_ivp58 solver. The governing equations for a detailed or a coarse-grained kinetic model are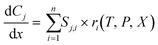 | (3) |
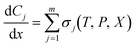 | (4) |
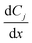 is the rate of change of concentration of species j along a differential length (dx), Sj,i is the stoichiometric coefficient of species j in elementary reaction i, and ri(T, P, C) is the rate of elementary reaction i at the current pressure (P), temperature (T), and composition (X). The summation extends over the entire networks of n elementary reactions. Similarly, σj(T, P, X) is the rate of species j from all overall reactions j and the summation extends over all overall reactions m. In a MKM simulator, the elementary rate is expressed by the modified Arrhenius rate expression, and the species rate is calculated using the elementary rates and the stoichiometry matrix. The DNNs can approximate the species production rate, i.e., the entire rhs (see ammonia case-study) or the overall reaction rates (see methane case-study), by accepting identical inputs (T, P, X). Note that DNNs are black boxes which could predict species consumption even when the species concentration is zero, resulting in negative concentrations. Therefore, in the coarse-grained kinetic model we ensure that the species mass and mole balances are always positive by constraining the species conservation equations and clipping rates which result in negative concentrations.
is the rate of change of concentration of species j along a differential length (dx), Sj,i is the stoichiometric coefficient of species j in elementary reaction i, and ri(T, P, C) is the rate of elementary reaction i at the current pressure (P), temperature (T), and composition (X). The summation extends over the entire networks of n elementary reactions. Similarly, σj(T, P, X) is the rate of species j from all overall reactions j and the summation extends over all overall reactions m. In a MKM simulator, the elementary rate is expressed by the modified Arrhenius rate expression, and the species rate is calculated using the elementary rates and the stoichiometry matrix. The DNNs can approximate the species production rate, i.e., the entire rhs (see ammonia case-study) or the overall reaction rates (see methane case-study), by accepting identical inputs (T, P, X). Note that DNNs are black boxes which could predict species consumption even when the species concentration is zero, resulting in negative concentrations. Therefore, in the coarse-grained kinetic model we ensure that the species mass and mole balances are always positive by constraining the species conservation equations and clipping rates which result in negative concentrations.
The DNN-surrogate-based PFR model does not involve surface species and their coverages, and, therefore, one does not need initial conditions for surfaces. One only needs inlet concentrations of gas reactants.
2.7 Validation and UQ for the NN-surrogate and the reduced model
The difference between the output responses, i.e., the point predictions of TOFs by the NN-based model and the full-order MKM (training dataset), gives the necessary validation and UQ for the NN. This can be used to improve the NN architecture by performing hyper-parameter optimization or updating the training dataset. Similarly, the difference between the MKM and NN-based solutions (QoI) along a PFR provides the actual error of the reduced model vs. the full-order model.To summarize, we generate a training dataset within the operating conditions window by running multiple PFR simulations with the full MKM. The training dataset consists of local operating conditions, species concentrations, and either species rates or rates of overall reactions. The training dataset is fitted with a DNN which accepts local operating conditions and species concentrations to predict overall reaction on species rates. PFR simulations accept the trained DNN as a surrogate model for the full MKM. Since the DNN-based PFR model only tracks the long-lived gas-phase species via overall reactions connecting them, neither surface coverages nor elementary reactions are invoked, an important difference from previously published work.50 This approach results in significant calculation speedup while eliminating stiffness. This workflow is demonstrated using two examples: a) a simple ammonia chemistry model where rates of production/consumption of each of the species are related via stoichiometry and b) the complex methane coupling chemistry with 9000+ elementary reactions.
2.8 Ammonia (NH3) chemistry
The MKM for NH3 decomposition on Ru has a total of 18 gas and surface species and 14 surface reactions (it entails step and terrace sites) and is taken from our previous work.1,61,62 The species and reactions are given in Section ESI-1.† The training data were generated using OpenMKM63 for a PFR (length of 1 cm, volume of 1 cm3) using LHC sampling for pressures from 1 to 10 atm, temperatures between 600 and 1000 K, and volumetric flow rates between 0.01 and 0.20 cm3 s−1. The predicted output metrics are the TOFs of NH3, N2 and H2. In the training dataset, the TOFs spanned several orders of magnitude: ∼10−10–102 (1 s−1). Since there is only one overall reaction, the TOFs of the stable species are related by stoichiometry. However, TOFs of all three species were trained to assess how well mass-conservation is obeyed without imposing it. A total of 1200 conditions were simulated, and 100 training points were extracted from each reactor. DNN used 5 input parameters (T, P, XNH3, XN2, XH2), where Xi is the mole fraction of species i. Fig. S1 and S2a† depict the nodes and connections in this NN. The training and validation error as a function of training epochs is plotted in Fig. S2b,† with training and validation errors decreasing steadily.2.9 Methane (CH4) coupling chemistry
Methane coupling to ethylene and other products is a complex network with 47 surface species, over 500 gas-phase species and a total of ∼9300 gas- and surface-phase reactions.64 The training data used 200 operating conditions picked via LHS, within the phase boundaries of (P = 1 atm, temperature 1250 to 1300 K, and volumetric flow rate of 0.025 to 1 cm3 s−1) using the CHEMKIN65–67 chemical kinetics package. Mole fractions and TOFs of key species were obtained from these simulations. Only species which contributed cumulatively to 99.9% of the mole fraction (with decreasing contribution) are considered; these are CH4, H2, C2H2, C2H4, C2H6, C3H4, C3H6, C6H6, C7H8, and C10H8. To preserve mass and enforce stoichiometry on top of the black-box DNNs, overall reaction TOFs instead of species TOFs are fitted. These overall reactions are constructed to connect the species using expert knowledge as explained below in the section “overall reactions”. While the DNN model predictions of overall reaction rates have errors, stemming from the reduction, mass is conserved as we parametrize reaction rates and use stoichiometry to compute all species rates. The NN architecture, sampling, and the PFR simulation numerics remain the same for both example cases. The simplicity and automation of various steps, via modular Python programming, enabled trivial scale-up of the methodology from the simple 14-reaction system to the ∼9300 reactions.3. Results and discussion
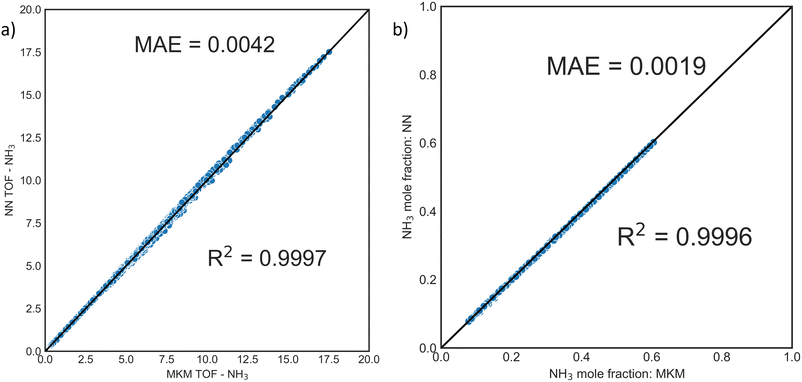
3.1 Assessing accuracy and training procedures using ammonia chemistry as a testbed
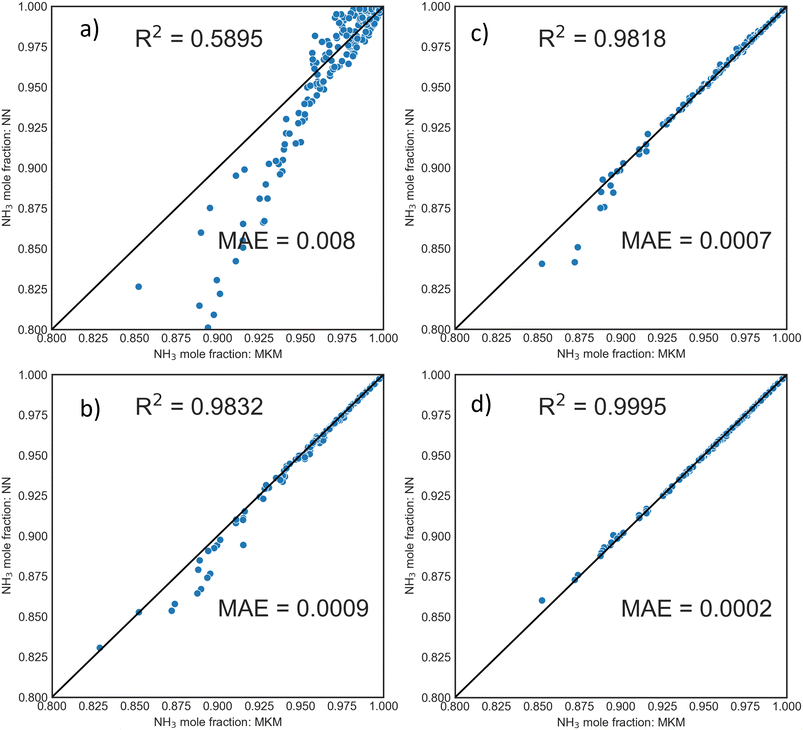
The training dataset was generated using OpenMKM63 with the procedure and operating condition window described in the Methods section. DNNs were trained on the TOF of NH3, and the TOFs of H2 and N2 were estimated from the stoichiometry of the overall reaction (2NH3 ⇌ N2 + 3H2). Fig. 2a depicts the parity plot from the MKM and the DNN. DNNs display excellent performance with R2 of 0.9997; the prediction error and mean were ∼0.001 and ∼0.002 in TOF units. This surrogate model performed well for reactor calculations. Fig. S5† depicts the parity in the exit mole fractions of 1200 independent PFR simulations (ground-truth) and the DNN surrogate, with a mean absolute error of ∼0.0048 (dimensionless units).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 individual samples. Smaller datasets generated using LHS and full factorial (FF) design for 100 and 400 conditions were tested. The trained DNN then predicted 400 new PFR conditions at completely random P, T, and flowrates. Parity plots of exit mole fraction using DNNs trained from samples generated by FF design and LHS are shown in Fig. 3. For a fixed number of samples, the LHS-based dataset is superior to the FF design, even with as few as 100 PFR samples (10
000 individual samples. Smaller datasets generated using LHS and full factorial (FF) design for 100 and 400 conditions were tested. The trained DNN then predicted 400 new PFR conditions at completely random P, T, and flowrates. Parity plots of exit mole fraction using DNNs trained from samples generated by FF design and LHS are shown in Fig. 3. For a fixed number of samples, the LHS-based dataset is superior to the FF design, even with as few as 100 PFR samples (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 individual points).
000 individual points).
3.2 CH4 coupling chemistry
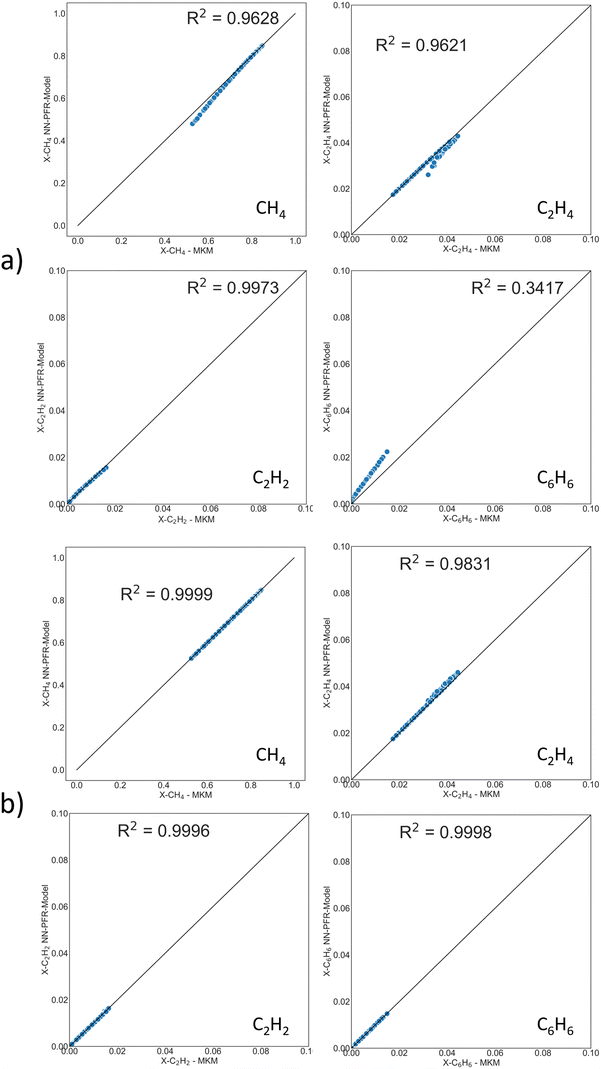
The operating window is given in the Methods section. This MKM contains 500+ species and 9300+ elementary reactions. It is impractical to fit these many TOFs. RPA (Fig. S9†) cannot even help in visualizing the network. Therefore, stable species with the largest mole fraction contribution to a cumulative ∼99.5% were selected. In Fig. S10,† the cumulative histogram depicts the number of species comprising 99.5% of the PFR exit mole fraction for 200 PFR simulations, i.e., at the PFR exit, 3 species make up the 99.5% cutoff for ∼75 simulations, 5 species appear in ∼110, and so on and so forth, up to a total of 9 unique species cumulatively for the entire dataset. Table S1† depicts the percentage of these occurrences for each key species at the PFR exit. C2H4 contributes to the 99.5% exit mole fraction cutoff at 60% of the training dataset (i.e., 120 out of 200 PFR runs). Ultimately, the DNN surrogate model only considers 9 key species, as shown in Table S1.† The mass/mole fraction cutoff could be adjusted for every system to incorporate species of interest, including trace products or impurities.In MKMs based on elementary reactions, short-lived species of low concentrations (for example a CH3 radical) can play a crucial role in dictating rate-limiting steps, major flux pathways, and surface coverages. In the reduced DNN-based PFR model, we only track long-lived gas species connected by “non-elementary” overall reaction steps, such as (2CH4 → C2H4 + 2H2), which do not contain these intermediates. The overall reactions encompass the information of elementary steps and intermediate species implicitly in the DNN.
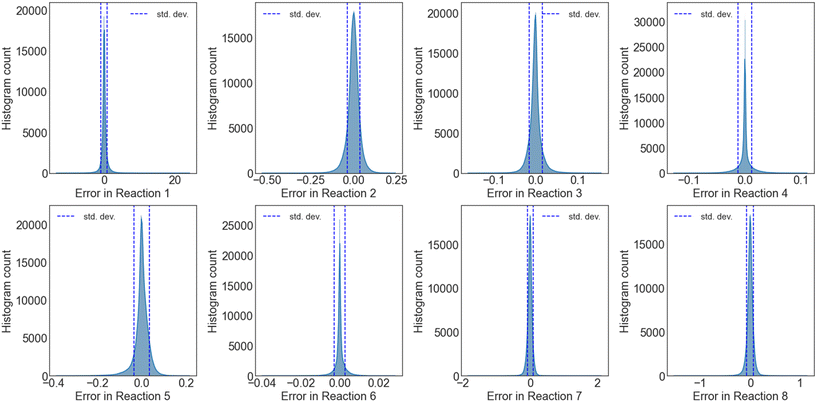
Two reaction sets, shown in Table 1, were chosen for this case. Set A was designed such that the reaction rates can be obtained from the respective product species, such as C2H4 or C6H6, using the stoichiometric matrix inversion. Set B was constructed using stoichiometry by which the rate of a reaction is equal to the rate of the hydrocarbon product (species rate). The last two overall reactions track the rates of CH4 and H2 to trace products (mole fraction <0.05) for the C and H balance. The rate of methane is easy to compute from the rates of reactions and the stoichiometric coefficients. Note that these overall reactions simply obey stoichiometry rather than physical pathways. They allow an easy estimation of rates needed in the material balances.
| No. | Reaction set A | Mathematically convenient set B |
|---|---|---|
| 1 | 2CH4 ⇌ C2H4 + 2H2 | 2CH4 ⇌ C2H4 + 2H2 |
| 2 | 3C2H4 ⇌ C2H2 + H2 | 2CH4 ⇌ C2H2 + 3H2 |
| 3 | 2C2H4 + H2 ⇌ C3H6 + CH4 | 3CH4 ⇌ C3H6 + 3H2 |
| 4 | 6CH4 ⇌ C6H6 + 9H2 | 6CH4 ⇌ C6H6 + 9H2 |
| 5 | C3H4 + H2 ⇌ C2H2 + CH4 | 3CH4 ⇌ C3H4 + 4H2 |
| 6 | C7H8 + H2 ⇌ C6H6 + CH4 | 7CH4 ⇌ C7H8 + 10H2 |
| Balance trace reactions: | Balance trace reactions: | |
| 7 | xCH4 ⇌ CxHy(g) + (4x − 1.0y)H(g) | xCH4 ⇌ CxHy(g) + (4x − 1.0y)H(g) |
| 8 | (4x − 1y)H(g) ⇌ (2x − 0.5y)H2(g) | (4x − 1y)H(g) ⇌ (2x − 0.5y)H2(g) |
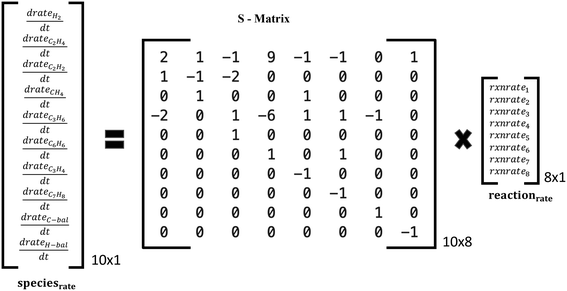 | ||
| Fig. 4 Schematic of species production rates and overall reaction rates via the stoichiometric matrix for the reaction set A in Table 1. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points per network times 100 networks) for reaction sets A (no trace reactions) and B, respectively. The mean, minimum, and the maximum for each overall reaction rate, the mean average error, and the standard deviation for the global dataset (2 million data points) are tabulated in Tables S2 (reaction set A) and S3† (reaction set B). From the UQ distribution and the tabulated statistics, the uncertainty of the NN for 100 networks is equivalent to the UQ from a single network.
000 points per network times 100 networks) for reaction sets A (no trace reactions) and B, respectively. The mean, minimum, and the maximum for each overall reaction rate, the mean average error, and the standard deviation for the global dataset (2 million data points) are tabulated in Tables S2 (reaction set A) and S3† (reaction set B). From the UQ distribution and the tabulated statistics, the uncertainty of the NN for 100 networks is equivalent to the UQ from a single network.
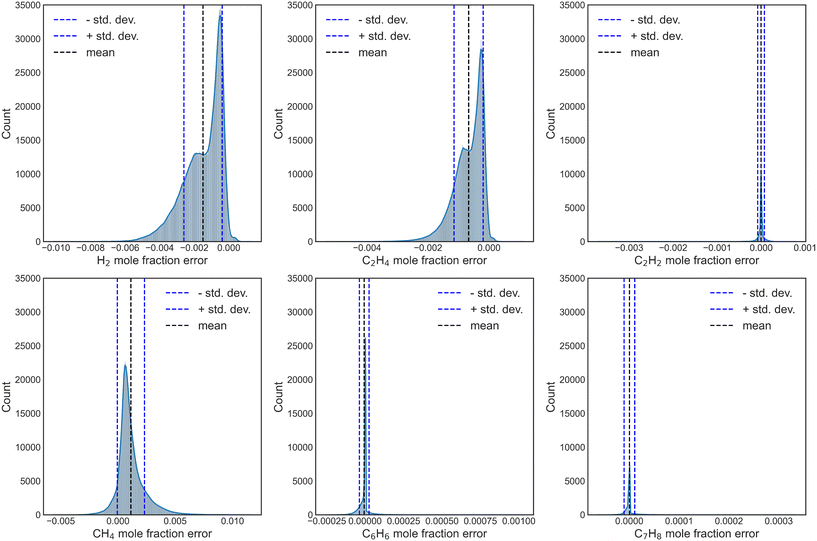
Further, the propagation error and uncertainty during numerical integration of the surrogate NN models were also explored, by simulating 200 conditions with each of the independently trained NNs, for a total aggregate of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 surrogate-DNN PFR simulations. Fig. S15† and 7 depict the UQ for reaction sets A and B, respectively. While the UQ histograms for H2 and C2H4 are not perfectly Gaussian, the standard deviations are incredibly low, highlighting the efficacy and accuracy of this method.
000 surrogate-DNN PFR simulations. Fig. S15† and 7 depict the UQ for reaction sets A and B, respectively. While the UQ histograms for H2 and C2H4 are not perfectly Gaussian, the standard deviations are incredibly low, highlighting the efficacy and accuracy of this method.
4. Conclusions
We have developed a procedure to systematically reduce complex, stiff, high-dimensional chemical reaction networks using DNN models. These surrogate models approximate the rates of reactants and products only as a function of local reactor conditions and deduce rates of overall reactions connecting these species. By discarding unnecessary species (reaction intermediates and products of low fraction), the DNN-surrogate models are very small and computationally efficient with minimal (if any) stiffness. The approach was tested on a simple 14-elementary-reaction MKM for ammonia decomposition on Ru and highly complex 9300+ elementary reactions for non-oxidative methane coupling. The results demonstrate exceptional computational speed-up and accuracy. Care should be taken to use the DNN surrogate within the range of training operating conditions, and consider mass conservation, distance from chemical equilibrium, and appropriate overall reactions, as discussed herein.Author contributions
Sashank Kasiraju developed the algorithm, performed the simulations, and wrote the manuscript. Dionisios G. Vlachos proposed the algorithm, supervised the project, wrote the manuscript, and acquired funding for this project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The method development was supported from the Department of Energy's Office of Energy Efficient and Renewable Energy's Advanced Manufacturing Office under Award Number DE-EE0007888-9.5. The Delaware Energy Institute gratefully acknowledges the support and partnership of the State of Delaware toward the RAPID projects. The methane non-oxidative coupling work was supported by the Department of Energy's Office of Fossil Energy under Award Number DE-FE0031877. The authors would like to acknowledge Dr. Himaghna Bhattacharjee for several valuable discussions and guidelines for implementing DNNs in this project. The authors would like to specially thank Dr. Maximilian Cohen for extremely valuable discussions surrounding mass conserving neural network schemes, generation/choice of overall reaction sets, and UQ. The authors would also like to acknowledge Kelly Walker for designing the LearnCK logo.References
- G. R. Wittreich, K. Alexopoulos and D. G. Vlachos, Microkinetic Modeling of Surface Catalysis, 2020, pp. 1377–1404 Search PubMed.
- V. Prasad, A. M. Karim, A. Arya and D. G. Vlachos, Assessment of Overall Rate Expressions and Multiscale, Microkinetic Model Uniqueness via Experimental Data Injection: Ammonia Decomposition on Ru/γ-Al2O3 for Hydrogen Production, Ind. Eng. Chem. Res., 2009, 48(11), 5255–5265 CrossRef CAS.
- J. E. Sutton and D. G. Vlachos, Building large microkinetic models with first-principles' accuracy at reduced computational cost, Chem. Eng. Sci., 2015, 121, 190–199 CrossRef CAS.
- M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, A C1microkinetic model for methane conversion to syngas on Rh/Al2O3, AIChE J., 2009, 55(4), 993–1008 CrossRef CAS.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, A review of multiscale modeling of metal-catalyzed reactions: Mechanism development for complexity and emergent behavior, Chem. Eng. Sci., 2011, 66(19), 4319–4355 CrossRef CAS.
- G. R. Wittreich, G. H. Gu, D. J. Robinson, M. A. Katsoulakis and D. G. Vlachos, Uncertainty Quantification and Error Propagation in the Enthalpy and Entropy of Surface Reactions Arising from a Single DFT Functional, J. Phys. Chem. C, 2021, 125(33), 18187–18196 CrossRef CAS.
- V. Prasad and D. G. Vlachos, Multiscale Model and Informatics-Based Optimal Design of Experiments: Application to the Catalytic Decomposition of Ammonia on Ruthenium, Ind. Eng. Chem. Res., 2008, 47(17), 6555–6567 CrossRef CAS.
- V. Prasad, A. M. Karim, Z. Ulissi, M. Zagrobelny and D. G. Vlachos, High throughput multiscale modeling for design of experiments, catalysts, and reactors: Application to hydrogen production from ammonia, Chem. Eng. Sci., 2010, 65(1), 240–246 CrossRef CAS.
- M. Maestri and A. Cuoci, Coupling CFD with detailed microkinetic modeling in heterogeneous catalysis, Chem. Eng. Sci., 2013, 96, 106–117 CrossRef CAS.
- T. Maffei, G. Gentile, S. Rebughini, M. Bracconi, F. Manelli, S. Lipp, A. Cuoci and M. Maestri, A multiregion operator-splitting CFD approach for coupling microkinetic modeling with internal porous transport in heterogeneous catalytic reactors, Chem. Eng. J., 2016, 283, 1392–1404 CrossRef CAS.
- R. Uglietti, M. Bracconi and M. Maestri, Coupling CFD-DEM and microkinetic modeling of surface chemistry for the simulation of catalytic fluidized systems, React. Chem. Eng., 2018, 3(4), 527–539 RSC.
- L. A. Vandewalle, G. B. Marin and K. M. Van Geem, catchyFOAM: Euler–Euler CFD Simulations of Fluidized Bed Reactors with Microkinetic Modeling of Gas-Phase and Catalytic Surface Chemistry, Energy Fuels, 2021, 35(3), 2545–2561 CrossRef CAS.
- B. Partopour and A. G. Dixon, Reduced Microkinetics Model for Computational Fluid Dynamics (CFD) Simulation of the Fixed-Bed Partial Oxidation of Ethylene, Ind. Eng. Chem. Res., 2016, 55(27), 7296–7306 CrossRef CAS.
- G. D. Wehinger, M. Ambrosetti, R. Cheula, Z.-B. Ding, M. Isoz, B. Kreitz, K. Kuhlmann, M. Kutscherauer, K. Niyogi, J. Poissonnier, R. Réocreux, D. Rudolf, J. Wagner, R. Zimmermann, M. Bracconi, H. Freund, U. Krewer and M. Maestri, Quo vadis multiscale modeling in reaction engineering? – A perspective, Chem. Eng. Res. Des., 2022, 184, 39–58 CrossRef CAS.
- D. Micale, C. Ferroni, R. Uglietti, M. Bracconi and M. Maestri, Computational Fluid Dynamics of Reacting Flows at Surfaces: Methodologies and Applications, Chem. Ing. Tech., 2022, 94(5), 634–651 CrossRef CAS.
- S. H. Lam and D. A. Goussis, The CSP method for simplifying kinetics, Int. J. Chem. Kinet., 1994, 26(4), 461–486 CrossRef CAS.
- I. P. Androulakis, Kinetic mechanism reduction based on an integer programming approach, AIChE J., 2000, 46(2), 361–371 CrossRef CAS.
- I. Banerjee and M. G. Ierapetritou, Development of an adaptive chemistry model considering micromixing effects, Chem. Eng. Sci., 2003, 58(20), 4537–4555 CrossRef CAS.
- B. Bhattacharjee, D. A. Schwer, P. I. Barton and W. H. Green, Optimally-reduced kinetic models: reaction elimination in large-scale kinetic mechanisms, Combust. Flame, 2003, 135(3), 191–208 CrossRef CAS.
- H. Huang, M. Fairweather, A. S. Tomlin, J. F. Griffiths and R. B. Brad, A dynamic approach to the dimension reduction of chemical kinetic schemes, in Computer Aided Chemical Engineering, ed. L. Puigjaner and A. Espuña, Elsevier, 2005, vol. 20, pp. 229–234 Search PubMed.
- A. S. Tomlin, M. J. Pilling, T. Turányi, J. H. Merkin and J. Brindley, Mechanism reduction for the oscillatory oxidation of hydrogen: Sensitivity and quasi-steady-state analyses, Combust. Flame, 1992, 91(2), 107–130 CrossRef CAS.
- Y. K. Park and D. G. Vlachos, Chemistry reduction and thermokinetic criteria for ignition of hydrogen–air mixtures at high pressures, J. Chem. Soc., Faraday Trans., 1998, 94(6), 735–743 RSC.
- S. Raimondeau, M. Gummalla, Y. K. Park and D. G. Vlachos, Reaction network reduction for distributed systems by model training in lumped reactors: Application to bifurcations in combustion, Chaos, 1999, 9(1), 95–107 CrossRef CAS PubMed.
- A. B. Mhadeshwar and D. G. Vlachos, Is the water–gas shift reaction on Pt simple?, Catal. Today, 2005, 105(1), 162–172 CrossRef CAS.
- S. Deshmukh and D. Vlachos, A reduced mechanism for methane and one-step rate expressions for fuel-lean catalytic combustion of small alkanes on noble metals, Combust. Flame, 2007, 149(4), 366–383 CrossRef CAS.
- S. B. Pope, Computationally efficient implementation of combustion chemistry using in situ adaptive tabulation, Combust. Theory Modell., 1997, 1(1), 41–63 CrossRef CAS.
- L. Lu and S. B. Pope, An improved algorithm for in situ adaptive tabulation, J. Comput. Phys., 2009, 228(2), 361–386 CrossRef.
- J. M. Blasi and R. J. Kee, In situ adaptive tabulation (ISAT) to accelerate transient computational fluid dynamics with complex heterogeneous chemical kinetics, Comput. Chem. Eng., 2016, 84, 36–42 CrossRef CAS.
- M. A. Singer, S. B. Pope and H. N. Najm, Operator-splitting with ISAT to model reacting flow with detailed chemistry, Combust. Theory Modell., 2006, 10(2), 199–217 CrossRef CAS.
- M. Bracconi, M. Maestri and A. Cuoci, In situadaptive tabulation for the CFD simulation of heterogeneous reactors based on operator-splitting algorithm, AIChE J., 2017, 63(1), 95–104 CrossRef CAS.
- A. Varshney and A. Armaou, in Dynamic optimization of stochastic systems using in situ adaptive tabulation, 2006 American Control Conference, 14-16 June 2006, 2006, p. 7 Search PubMed.
- A. Varshney and A. Armaou, Reduced order modeling and dynamic optimization of multiscale PDE/kMC process systems, Comput. Chem. Eng., 2008, 32(9), 2136–2143 CrossRef CAS.
- J. D. Hedengren and T. F. Edgar, In Situ Adaptive Tabulation for Real-Time Control, Ind. Eng. Chem. Res., 2005, 44(8), 2716–2724 CrossRef CAS.
- K. Hornik, M. Stinchcombe and H. White, Multilayer feedforward networks are universal approximators, Neural Netw., 1989, 2(5), 359–366 CrossRef.
- A. R. Barron, Universal approximation bounds for superpositions of a sigmoidal function, IEEE Trans. Inf. Theory, 1993, 39(3), 930–945 Search PubMed.
- J. A. Blasco, N. Fueyo, C. Dopazo and J. Ballester, Modelling the Temporal Evolution of a Reduced Combustion Chemical System With an Artificial Neural Network, Combust. Flame, 1998, 113(1–2), 38–52 CrossRef CAS.
- B. A. Sen and S. Menon, Turbulent premixed flame modeling using artificial neural networks based chemical kinetics, Proc. Combust. Inst., 2009, 32(1), 1605–1611 CrossRef CAS.
- B. A. Sen and S. Menon, Linear eddy mixing based tabulation and artificial neural networks for large eddy simulations of turbulent flames, Combust. Flame, 2010, 157(1), 62–74 CrossRef CAS.
- B. A. Sen, E. R. Hawkes and S. Menon, Large eddy simulation of extinction and reignition with artificial neural networks based chemical kinetics, Combust. Flame, 2010, 157(3), 566–578 CrossRef CAS.
- A. J. Sharma, R. F. Johnson, D. A. Kessler and A. Moses, Deep Learning for Scalable Chemical Kinetics, AIAA scitech 2020 forum, 2020, p. 0181 Search PubMed.
- C. Chi, G. Janiga and D. Thévenin, On-the-fly artificial neural network for chemical kinetics in direct numerical simulations of premixed combustion, Combust. Flame, 2021, 226, 467–477 CrossRef CAS.
- G. S. Gusmão, A. P. Retnanto, S. C. da Cunha and A. J. Medford, Kinetics-informed neural networks, Catal. Today, 2023, 417, 113701 CrossRef.
- W. Ji and S. Deng, Autonomous Discovery of Unknown Reaction Pathways from Data by Chemical Reaction Neural Network, J. Phys. Chem. A, 2021, 125(4), 1082–1092 CrossRef CAS PubMed.
- O. Owoyele and P. Pal, ChemNODE: A neural ordinary differential equations framework for efficient chemical kinetic solvers, Energy and AI, 2022, 7, 100118 CrossRef.
- R. T. Chen, Y. Rubanova, J. Bettencourt and D. K. Duvenaud, Neural ordinary differential equations, Advances in neural information processing systems, 2018, vol. 31 Search PubMed.
- Y. Weng and D. Zhou, Multiscale Physics-Informed Neural Networks for Stiff Chemical Kinetics, J. Phys. Chem. A, 2022, 126(45), 8534–8543 CrossRef CAS.
- S. Wang, Y. Teng and P. Perdikaris, Understanding and Mitigating Gradient Flow Pathologies in Physics-Informed Neural Networks, SIAM J. Sci. Comput., 2021, 43(5), A3055–A3081 CrossRef.
- W. Ji, W. Qiu, Z. Shi, S. Pan and S. Deng, Stiff-PINN: Physics-Informed Neural Network for Stiff Chemical Kinetics, J. Phys. Chem. A, 2021, 125(36), 8098–8106 CrossRef CAS PubMed.
- W. Ji and S. Deng, KiNet: A deep neural network representation of chemical kinetics, arXiv, 2021, preprint, arXiv:2108.00455, DOI:10.48550/arXiv.2108.00455.
- F. A. Döppel and M. Votsmeier, Efficient machine learning based surrogate models for surface kinetics by approximating the rates of the rate-determining steps, Chem. Eng. Sci., 2022, 262, 117964 CrossRef.
- F. A. Döppel and M. Votsmeier, Efficient neural network models of chemical kinetics using a latent asinh rate transformation, React. Chem. Eng., 2023 10.1039/D3RE00212H.
- Y. Huang and J. H. Seinfeld, A Neural Network-Assisted Euler Integrator for Stiff Kinetics in Atmospheric Chemistry, Environ. Sci. Technol., 2022, 56(7), 4676–4685 CrossRef.
- Scikit Learn, Data preprocessing and Normalization using the MinMaxScaler, https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html, (accessed March 1, 2023).
- S. Caratzoulas and D. G. Vlachos, Converting fructose to 5-hydroxymethylfurfural: a quantum mechanics/molecular mechanics study of the mechanism and energetics, Carbohydr. Res., 2011, 346(5), 664–672 CrossRef CAS PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, R. Jozefowicz, Y. Jia, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, M. Schuster, R. Monga, S. Moore, D. Murray, C. Olah, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/ Search PubMed.
- K. Fukushima, Cognitron: A self-organizing multilayered neural network, Biol. Cybern., 1975, 20(3–4), 121–136 CrossRef CAS PubMed.
- D. Hendrycks and K. Gimpel, Gaussian error linear units (gelus), arXiv, 2016, preprint, arXiv:1606.08415, DOI:10.48550/arXiv.1606.08415.
- S. Caratzoulas and D. G. Vlachos, Molecular dynamics study of the stabilization of the silica hexamer Si6O15(6-) in aqueous and methanolic solutions, J. Phys. Chem. B, 2008, 112(1), 7–10 CrossRef CAS PubMed.
- L. Petzold, Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations, SIAM J. Sci. Statist. Comput., 1983, 4(1), 136–148 CrossRef.
- A. C. Hindmarsh, Toward a systematized collection of ODE solvers, Lawrence Livermore National Lab., CA (USA), 1982 Search PubMed.
- J. Lym, G. R. Wittreich and D. G. Vlachos, A Python Multiscale Thermochemistry Toolbox (pMuTT) for thermochemical and kinetic parameter estimation, Comput. Phys. Commun., 2020, 247, 106864 CrossRef CAS.
- G. R. Wittreich, S. Liu, P. J. Dauenhauer and D. G. Vlachos, Catalytic resonance of ammonia synthesis by simulated dynamic ruthenium crystal strain, Sci. Adv., 2022, 8(4), eabl6576 CrossRef CAS.
- B. Medasani, S. Kasiraju and D. G. Vlachos, OpenMKM: An Open-Source C++ Multiscale Modeling Simulator for Homogeneous and Heterogeneous Catalytic Reactions, J. Chem. Inf. Model., 2023, 63(11), 3377–3391 CrossRef CAS PubMed.
- H. E. Toraman, K. Alexopoulos, S. C. Oh, S. Cheng, D. Liu and D. G. Vlachos, Ethylene production by direct conversion of methane over isolated single active centers, Chem. Eng. J., 2021, 420, 130493 CrossRef CAS.
- R. J. Kee, F. M. Rupley and J. A. Miller, Chemkin-II: A Fortran chemical kinetics package for the analysis of gas-phase chemical kinetics, DOI:10.2172/5681118, Sandia National Laboratories Report, SAND89–8009, 1989.
- M. E. Coltrin, R. J. Kee and F. M. Rupley, Surface CHEMKIN (Version 4. 0): A Fortran package for analyzing heterogeneous chemical kinetics at a solid-surface---gas-phase interface, DOI:10.2172/6128661, Sandia National Laboratories Report, SAND-90-8003B, 1991.
- M. E. Coltrin, R. J. Kee and F. M. Rupley, Surface chemkin: A general formalism and software for analyzing heterogeneous chemical kinetics at a gas-surface interface, Int. J. Chem. Kinet., 1991, 23(12), 1111–1128 CrossRef CAS.
- M. Cohen, T. Goculdas and D. G. Vlachos, Active learning of chemical reaction networks via probabilistic graphical models and Boolean reaction circuits, React. Chem. Eng., 2023, 8(4), 824–837 RSC.
- R. Penrose, A generalized inverse for matrices, Math. Proc. Cambridge Philos. Soc., 2008, 51(3), 406–413 CrossRef.
- A. Bjerhammar, Rectangular reciprocal matrices, with special reference to geodetic calculations, Bull Geod., 1951, 20(1), 188–220 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: This document lists several figures and tables with data mentioned in this paper. See DOI: https://doi.org/10.1039/d3re00279a |
| This journal is © The Royal Society of Chemistry 2024 |