Open Access Article
Open Access ArticleLight-driven nanomotors with reciprocating motion and high controllability based on interference techniques†
Mohammadbagher
Mohammadnezhad
a,
Salah Raza
Saeed
bd,
Sarkew Salah
Abdulkareem
c and
Abdollah
Hassanzadeh
 *a
*a
aDepartment of Physics, University of Kurdistan, Sanandaj, Iran. E-mail: a.hassanzadeh@uok.ac.ir
bAdvanced Polymeric Materials Research Lab., Department of Physics, College of Science, University of Sulaimani, Sulaimani, Iraq
cDepartment of Physics, College of Science, University of Halabja, Iraq
dDepartment of Computer Science, Cihan University, Sulaimaniya 46001, Kurdistan Region, Iraq
First published on 29th December 2023
Abstract
In this paper, we investigate the controlled movement of optically trapped nano-particles in an interference optical lattice. The suggested interferometric optical tweezers setup utilizes the superposition of three orthogonal Gaussian standing waves to create 3D optical lattices. Dynamic control over the constructed lattices can be achieved simply by changing the incident beam parameters using a polarizer or a phase shifter. The trapping properties of the generated optical lattices for a dielectric Rayleigh particle are numerically evaluated using a MATLAB program. The simulation results showed that the generated lattices can be translated by altering the relative phase between the interfering beams. More complex transformations and geometries can be achieved by changing other properties of the interfering beams such as the polarization state. This simple setup enables the construction of a rich variety of dynamic optical lattices and offers promising applications in colloidal and biological science such as controlling the diffusion of colloidal particles and stretching or compressing tethered polymeric molecules. This interferometric method can also be used in light-driven nanomotors with high controllability.
Introduction
A nanomotor is a nanoscale energy transducer that converts diverse forms of energy into useful mechanical work.1 Nanomotors have shown great promise for many biomedical and environmental applications.1,2 Different propulsion mechanisms have been proposed and used to power nanomotors. For example, nanomotors can be propelled by electric fields,3 magnetic fields,4 ultrasound5 or light.1 Light-driven nanomotors have demonstrated several distinct advantages over other nanomotors, for example high spatial resolution, high controllability and programmability of light-driven nanomotors.2,6The external degrees of freedom of microscopic particles can be controlled by using the mechanical action of light which is known as optical manipulation or optical trapping. This technique has received great attention due to advantages such as the contactless nature of the optical forces.7 Most tweezers systems exploit the optical force produced by a highly focused laser beam to confine a small particle near the beam focus.8 However, a single beam is capable of manipulating only one object, and to have enhanced levels of control over the microscopic world, the use of multiple-traps is necessary.9
One of the special types of multiple-traps with crucial importance is a periodic trapping potential which is best suitable for some specific applications, such as particle sorting,10 particle arrangement,11 and creation and evolution of large arrays of colloids.12
There are several methods to create periodic multiple-traps, each with its own advantages and disadvantages.13 One of the most popular and powerful methods to create a periodic potential, an optical lattice, is the use of the interference effects of multiple coherent beams.14 One important advantage of using interference methods to produce an optical lattice is that the geometry of the lattice is under complete control.15
However, although a rich variety of different interferometric configurations were proposed and studied,16–18 more work is needed to take advantage of powerful features of interference approaches.
In our earlier studies, we suggested a number of different interferometric trapping setups, and their potential applications in optical manipulation were discussed.19–22
A dynamic control over periodic interference traps can enhance the capabilities of such periodic patterns and pave the way to some great new applications. One way to do this is to use holographic techniques,23 but the manipulability of holographic methods is considerably limited by the speed of the beam control.9
In this paper a novel interferometric configuration to create 3D dynamic optical lattices is proposed, and its potential applications in different areas are discussed. Dynamic control over the trap positions and distances can be achieved by adjusting the polarization state or relative phase of the interfering beams.
Theory
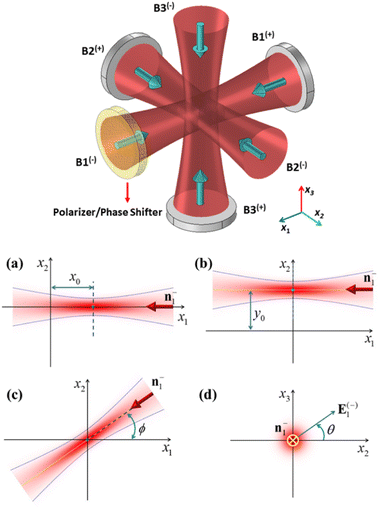
The proposed setup exploits the interference of three pairs of mutually perpendicular counter-propagating Gaussian beams of wavelength λ0 = 632.8 nm to create optical lattices, as schematically illustrated in Fig. 1. Dynamic control of the generated lattices can be achieved through a phase shifter or a linear polarizer element incorporated in the optical path of the laser beams before entering the sample chamber. Static and dynamic behavior of dielectric nanoparticles with a refractive index of np = 1.59 in the interference region of the incident beams is investigated.In this research, it is assumed that the radius of the particle, a, is much smaller than the incident wavelength, and therefore the dipole (Rayleigh) approximation can be sufficiently accurate to calculate the optical force on the particle and potential energy.24
The scattering forces cancel each other out resulting in a pure conservative gradient force which can be derived from potential energy U as follows25
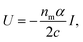 | (1) |
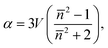 | (2) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = np/nm, respectively. As can be seen from eqn (1), the potential energy of a very small particle in an optical field is proportional to the light intensity. The optical intensity of a monochromatic wave is proportional to the absolute square of the spatial part of the electric field; I = (Y/2)|E|2, where Y is the admittance of the propagation medium (in our case where the particle is suspended in water Y = 3.53 × 10−3 S). It is convenient to use the notations x1, x2 and x3 to represent the Cartesian coordinate variables x, y and z, and el to denote the unit vector along the positive xl axis (throughout this paper, x, y and z are equivalent to x1, x2 and x3). The electric field of the Gaussian beam propagating along the positive xl axis can be expressed as:
= np/nm, respectively. As can be seen from eqn (1), the potential energy of a very small particle in an optical field is proportional to the light intensity. The optical intensity of a monochromatic wave is proportional to the absolute square of the spatial part of the electric field; I = (Y/2)|E|2, where Y is the admittance of the propagation medium (in our case where the particle is suspended in water Y = 3.53 × 10−3 S). It is convenient to use the notations x1, x2 and x3 to represent the Cartesian coordinate variables x, y and z, and el to denote the unit vector along the positive xl axis (throughout this paper, x, y and z are equivalent to x1, x2 and x3). The electric field of the Gaussian beam propagating along the positive xl axis can be expressed as:| E(+)l = E0(w0/wl)exp[−(rmn/wl)2]exp(−iφlmn)êm, l, m, n = 1, 2, 3 and cyclic permutations | (3) |
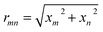 , ϕlmn = kxl + krmn2/2Rl − ψl,
, ϕlmn = kxl + krmn2/2Rl − ψl, 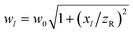 , Rl = xl[1 + (zR/xl)2], and ψl = tan−1(xl/zR), in which k = 2π/λ is the wavenumber of the trapping laser in the surrounding medium and zR = kw02/2 is the Rayleigh range. E0 and w0 are the electric field amplitude at the beam center and the beam waist radius, respectively.
, Rl = xl[1 + (zR/xl)2], and ψl = tan−1(xl/zR), in which k = 2π/λ is the wavenumber of the trapping laser in the surrounding medium and zR = kw02/2 is the Rayleigh range. E0 and w0 are the electric field amplitude at the beam center and the beam waist radius, respectively.
For the beams propagating along the negative xl axis, the only change in eqn (3) is ϕlmn → −ϕlmn. The total optical field can be expressed as the superposition of the individual fields:
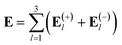 | (4) |
Once the total electric field is determined, the intensity distribution and in turn the potential energy can be computed from eqn (1). For small particles, the trapping stability is strongly affected by the Brownian diffusion of the particle,8 and to compare the potential depth with the Brownian thermal energy we normalize the potential energy to the thermal energy of the particle ET (at room temperature, ET = 4.04 × 10−21 J).
Results and discussion
Based on the above mathematical formulations, a MATLAB program was written to numerically evaluate the trapping properties of the optical lattices created by superimposing three orthogonal Gaussian standing waves. To examine the validity of the MATLAB codes, the simulation codes were run for the specific case of plane waves corresponding to very large values of w0. It was observed that as w0 increases to very large values, the simulation results (not shown) approach the result expected from interfering plane waves, verifying the validity of the MATLAB programs. In the case of interfering plane waves, the generated optical lattices are expected to consist of identical traps (with equal depth) which are exactly centered at the sites of a three-dimensional cubic lattice with a lattice constant of d = λ/2. For Gaussian beams, there is a small deviation of trap centers from cubic lattice points, and also the central traps have better confinement than peripheral traps. The difference between the Gaussian beam lattices and those of plane waves becomes smaller as the spot size of the interfering Gaussian beams, w0, increases. The simulation result for the case of Gaussian beams of spot sizes w0 = 4λ is presented in Fig. 2. This figure shows the normalized potential energy (U/ET) of the particle in the interference region of the Gaussian beams (see Visualization 1† which shows the iso-surface of the normalized potential energy from different viewpoints). To provide a better understanding of the trapping properties of optical lattices, a two-dimensional view of the normalized potential energy and corresponding optical force is presented in Fig. 3.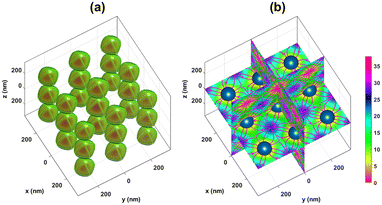 | ||
| Fig. 2 Normalized potential energy (in ET = KBT) of a dielectric nanoparticle (np = 1.59 and a = 50 nm) placed in the constructed optical lattices. (a) Iso-surface of the normalized potential energy at an iso-value of 10 as well as the inside structure of the iso-surfaces (slice plots of normalized potential contours). (b) Slice plots of normalized potential energy at three orthogonal slice planes, namely xy, yz and xz planes, as well as the corresponding optical forces (streamlines). The colorbar indicates the normalized potential energy of the particle. The dark blue spheres represent the trapped nanoparticles. The simulation parameters are chosen as: λ0 = 632.8 nm, nm = 1.33 (water), and w0 = 4λ ≈ 1.9 μm and the total incident power is normalized to 1 W (E0 ≈ 4.1 × 106 V m−1). The simulation region is a cube with a side of 700 nm. See also Visualization 1† which shows the iso-surface of normalized potential energy from different viewpoints. | ||
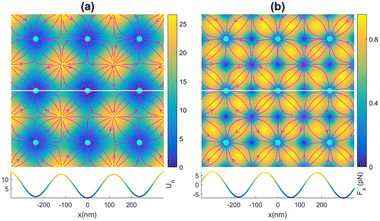 | ||
Fig. 3 (a) Top plot: x–y profile of the normalized potential energy of the particle and the corresponding optical force (streamlines). Stable equilibrium points are marked by cyan circles. The colorbar indicates the normalized potential energy of the particle. Bottom plot: normalized potential profile along the white line. (b) Top plot: the magnitude of the optical force in the x–y plane. The colorbar denotes the magnitude of the optical force, 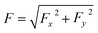 , in piconewton. Bottom plot: x component of the optical force, Fx(x), along the white line. The simulation parameters are the same as those in Fig. 1. , in piconewton. Bottom plot: x component of the optical force, Fx(x), along the white line. The simulation parameters are the same as those in Fig. 1. | ||
A dynamic control over the constructed lattices can be achieved by changing the parameters of the incident beams such as the beam phase. Here we focus on the effects of changing the properties of only one of the interfering beams, namely beam 1(−) (the beam propagating in the negative x1 direction), on the constructed lattices. This means that we do not change two parameters at the same time. Fig. 4 shows how the normalized potential energy of the particle is influenced by changing various parameters of beam 1(−). Fig. 4a shows a reference result obtained by interfering 3 orthogonal Gaussian standing waves expressed by using eqn (3), corresponding to the case in Fig. 2. It is included only for comparison purposes. Fig. 4b shows the result for the case where the focal plane of beam 1(−) is shifted in the x1 direction (axial offset, see panel (a) of Fig. 1) by x0 = zR ≈ 2.4 × 10−5 m. As can be seen from Fig. 4b this axial offset leads to a shift in the interfering lattice along the x1 direction. Moreover, the depth of traps decreases on increasing the axial offset, especially in the x1 direction. Therefore, a better confinement can be achieved for the case of zero offset. An ESI video (see visualization 2†) is also provided to demonstrate the evolution of the potential energy with the axial offset. The effects of the lateral offset (a displacement along the direction transverse to the beam axis, see panel (b) of Fig. 1) are shown in Fig. 4c, which correspond to the case where the axis of beam 1(−) is displaced along the x2 direction by using y0 = w0 ≅ 1.9 μm. An ESI video (see visualization 3†) is also provided to show how the potential energy evolves with the lateral offset. As can be seen from the numerical results, this lateral offset leads to a decrease in trap depth particularly in the x1 direction but the change in trap positions is very small. Furthermore, traps situated in the region x2 < 0 exhibit weaker confinement relative to the traps in the region x2 > 0. Fig. 4d shows the trapping potential for the case where the phase of beam 1(−) is shifted by δ = π rad, i.e. ϕ123 → ϕ123 + π. It can be seen that changing the relative phase between beam 1(+) and beam 1(−) results in a displacement of the constructed lattices along the x1 axis. An arbitrary 3D displacement can be achieved by controlling the relative phase between the counterpropagating beams in all three dimensions x1, x2 and x3. The displacement of the optical lattices can be exploited for controlled deposition of optically trapped colloidal particles on a surface. Moreover, the trapped particles in these moving lattices can act as nanomotors where their movement is controlled by optical force. Reciprocating motion of the trapped particles can also be accomplished by periodically changing the phase of beam 1(−). The evolution of the trapping potential with the phase of beam 1(−) can be seen in the ESI video (see visualization 4†).
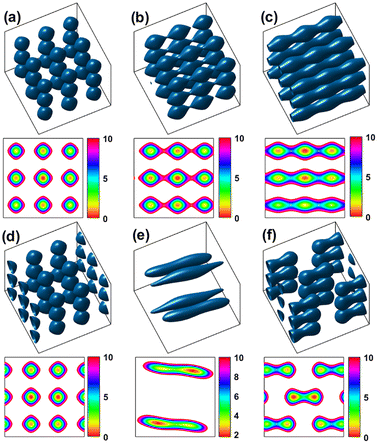 | ||
| Fig. 4 Influence of changing the beam parameters on the normalized potential energy. The first and third rows show isosurfaces of the normalized potential energy in a 3D view, and the second and fourth rows show the corresponding x–y profiles. (a) Representative reference result obtained by taking the interfering beams exactly the same as those expressed by using eqn (3), corresponding to the case in Fig. 2. (b) Axial offset effects of beam 1(−) on the potential landscape: beam 1(−) is axially offset by x0 = zR ≈ 4 μm. (c) Lateral offset effects of beam 1(−): the beam is laterally offset by y0 = w0 ≈ 1.9 μm along the x2 axis. (d) Effects of introducing a phase shift of δ = π rad to beam 1(−). (e) Effects of changing the propagation direction of beam 1(−) by an angle ϕ = 2π/5 rad along the x3 axis. (f) Effects of the polarization state of beam 1(−) on the potential energy: the polarization vector of beam 1(−) is rotated by an angle θ = 4π/5 rad along the x1 axis. The other simulation parameters are the same as in Fig. 2 (see visualizations 2 to 6†). | ||
The effect of changing the propagation direction of beam 1(−), n−1, on the trapping potential is shown in Fig. 4e. Here, n−1 is rotated by an angle ϕ = π/4 around the x3 axis (ϕ is the counterclockwise angle from the x1 axis to n−1, see panel (c) of Fig. 1). To provide a better understanding of the behavior of the generated lattices on changing propagation direction ϕ an ESI video (see visualization 5†) is also available. This result is of crucial importance for both micromechanical and microfluidic applications. These produced dynamic optical lattices make it possible to attach two or more colloidal particles together through attractive forces between the particles such as van der Waals forces. This particle attachment can increase the sedimentation rate of a colloidal suspension. These dynamic lattices also provide a means to control the orientation of non-spherical trapped particles such as nanorods and nanowires. The effects of changing the polarization state of beam 1(−) on the trapping potential can be seen in Fig. 4f. Here, the polarization vector of the beam 1(−), e−1, is rotated by an angle θ = π/4 around the x1 axis (θ is the counterclockwise angle from the x2 axis to e−1, see panel (d) of Fig. 1). An ESI video (see visualization 6†) is also provided to visualize the evolution of trapping potential with polarization direction θ. The result obtained in Fig. 4f is highly significant for micro-manipulation applications, and thus needs to be considered again to work on its details.
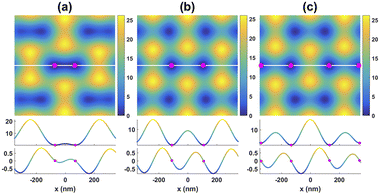
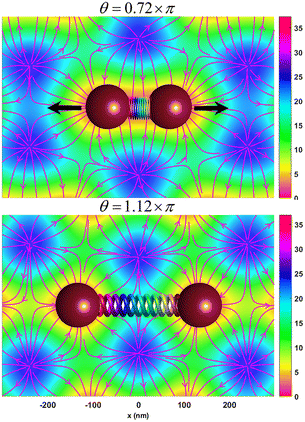
Fig. 5 shows the effects of changing the polarization direction of beam 1(−) on the potential energy of the particle. As can be seen in Fig. 5, as the angle θ increases from 18π/25 to 28π/25, the distance between the two adjacent trapping sites in the interfering region increases from 140 nm to 265 nm, and vice versa on decreasing the angle θ from 28π/25 to 18π/25.
These simulation results suggest the possibility of stretching or compressing tethered polymeric molecules such as DNA or actin by adjusting the polarization state of the interfering beams (see Fig. 6 and visualization 7†).
 | ||
| Fig. 6 DNA stretching or compressing with dynamic lattices generated by adjusting the polarization state of beam 1(−). The streamlines show the optical force field lines on the xy plane, and the colorbar values indicate normalized potential energy profile in the xy plane. An animation of DNA stretching and compressing is also given in visualization 7.† | ||
Here, it is assumed that the restoring force exerted by the stretched DNA on the nanobeads has a negligible effect on the position of the trapped beads. Moreover, these generated dynamic lattices can be used to bring colloidal particles into contact and attach them together. The reverse process, particle detachment, can also be achieved using these dynamic lattices (see visualization 6†). It is also possible to control the diffusion of colloidal particles in a suspension using such dynamic lattices. Another important application of these dynamic lattices is found in constructing nanomotors with high controllability. The propulsion mechanism of these light-driven nanomotors is the optical force on nano-objects, and the motion of these nanomotors can be steered along arbitrary trajectories in a simple way. A more flexible dynamic control over the generated lattices can be achieved by adjusting the parameters of all three negative propagating beams (beam 1(−), 2(−) and 3(−)) simultaneously.
It should be mentioned that low index particles can also be stably trapped in these optical lattices, but low index particles are confined around the points of the lowest intensity (see visualization 8†).
The ability to have effective dynamic control over the generated lattices by adjusting the interfering beam parameters opens up many potential applications in various areas of science, particularly in colloidal physics, microfluidics and materials science. We believe that the interference technique has great potential and versatility in the field of optical trapping.
Conclusions
In this work, a simple and effective way to dynamically control 3D optical lattices created by three orthogonal Gaussian standing waves was introduced. The trapping properties of these dynamic lattices for a Rayleigh particle were investigated numerically by writing a MATLAB code based on the dipole approximation. The effects of changing the parameters of only one of the interfering beams on the generated lattices were considered, and the simulation results were presented in both figures and videos. The results showed that the generated lattices can be effectively controlled in a simple way by changing the beam parameters of one of the incident beams. We believe that the presented results can find profound implications in various areas of the optical trapping field such as colloidal science and biomedical areas.Conflicts of interest
There are no conflicts to declare.Notes and references
- H. Wang and M. Pumera, Chem. Rev., 2015, 115, 8704–8735 CrossRef CAS PubMed.
- J. Wang, Z. Xiong, J. Zheng, X. Zhan and J. Tang, Acc. Chem. Res., 2018, 51, 1957–1965 CrossRef CAS PubMed.
- R. Zhuang, D. Zhou, X. Chang, Y. Mo, G. Zhang and L. Li, Appl. Mater. Today, 2022, 26, 101314 CrossRef.
- J. Liu, Z. Huang, H. Yue, R. Zhuang, L. Li, X. Chang and D. Zhou, Nanoscale, 2023, 15, 15831–15839 RSC.
- F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li, L. Ren, J. Liu, J. Yang and M. Dao, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1522–1527 CrossRef CAS PubMed.
- A. Ozcelik, J. Rufo, F. Guo, Y. Gu, P. Li, J. Lata and T. J. Huang, Nat. Methods, 2018, 15, 1021–1028 CrossRef CAS PubMed.
- A. Ohlinger, S. Nedev, A. A. Lutich and J. Feldmann, Nano Lett., 2011, 11, 1770–1774 CrossRef CAS PubMed.
- Z. Liu and D. Zhao, Opt. Express, 2012, 20, 2895–2904 CrossRef PubMed.
- K. Onda and F. Arai, Opt. Express, 2012, 20, 3633–3641 CrossRef PubMed.
- K. Ladavac, K. Kasza and D. G. Grier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 010901 CrossRef CAS PubMed.
- M. Šiler and P. Zemánek, Opt. Commun., 2007, 275, 409–420 CrossRef.
- D. G. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- I. Verdeny, A. Farré, J. Mas Soler, C. López Quesada, E. Martín Badosa and M. Montes Usategui, Óptica Pura y Aplicada, 2011, 44, 527–551 Search PubMed.
- K. Dholakia and P. Reece, Nano Today, 2006, 1, 18–27 CrossRef.
- I. Bloch, Nat. Phys., 2005, 1, 23–30 Search PubMed.
- A. Casaburi, G. Pesce, P. Zemánek and A. Sasso, Opt. Commun., 2005, 251, 393–404 CrossRef CAS.
- F. Nan and Z. Yan, Adv. Funct. Mater., 2019, 29, 1808258 CrossRef.
- E. Schonbrun, R. Piestun, P. Jordan, J. Cooper, K. D. Wulff, J. Courtial and M. Padgett, Opt. Express, 2005, 13, 3777–3786 CrossRef PubMed.
- M. Mohammadnezhad and A. Hassanzadeh, J. Opt. Soc. Am. B, 2017, 34, 983–990 CrossRef.
- M. Mohammadnezhad and A. Hassanzadeh, J. Nanophotonics, 2017, 11, 036007 CrossRef.
- M. Mohammadnezhad, S. R. Saeed and A. Hassanzadeh, J. Opt., 2019, 21, 105404 CrossRef CAS.
- M. Mohammadnezhad, S. S. Abdulkareem and A. Hassanzadeh, Opt. Lett., 2022, 47, 4024–4027 CrossRef CAS.
- M. Yevnin, D. Kasimov, Y. Gluckman, Y. Ebenstein and Y. Roichman, Biomed. Opt. Express, 2013, 4, 2087–2094 CrossRef PubMed.
- M. Dienerowitz, M. Mazilu and K. Dholakia, J. Nanophotonics, 2008, 2, 021875 CrossRef.
- A. Usman, W.-Y. Chiang and H. Masuhara, Sci. Prog., 2013, 96, 1–18 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00678f |
| This journal is © The Royal Society of Chemistry 2024 |