Open Access Article
Open Access ArticleThe chimera of 2D- and 1D-graphene magnetization by hydrogenation or fluorination: critically revisiting old schemes and proposing new ones by ab initio methods†
Andrea
Albino
 a,
Francesco
Buonocore
a,
Francesco
Buonocore
 b,
Massimo
Celino
b and
Federico
Totti
b,
Massimo
Celino
b and
Federico
Totti
 *a
*a
aDipartimento di Chimica “Ugo Schiff” & INSTM RU, Università degli Studi di Firenze, Via della Lastruccia 3, Sesto Fiorentino (FI) 50019, Italy. E-mail: federico.totti@unifi.it
bAgenzia nazionale per le nuove tecnologie, l'energia e lo sviluppo economico sostenibile (ENEA), Casaccia Research Centre, Roma 00123, Italy
First published on 22nd January 2024
Abstract
Graphene is an ideal candidate material for spintronics due to its layered structure and peculiar electronic structure. However, in its pristine state, the production of magnetic moments is not trivial. A very appealing approach is the chemical modification of pristine graphene. The main obstacle is the control of the geometrical features and the selectivity of functional groups. The lack of a periodic functionalization pattern of the graphene sheet prevents, therefore, the achievement of long-range magnetic order, thus limiting its use in spintronic devices. In such regards, the stability and the magnitude of the instilled magnetic moment depending on the size and shape of in silico designed graphane islands and ribbons embedded in graphene matrix will be computed and analysed. Our findings thus suggest that a novel and magneto-active graphene derivative nanostructure could become achievable more easily than extended graphone or nanoribbons, with a strong potential for future spintronics applications with a variable spin-current density.
1 Introduction
Spintronics is the study of basic physical principles underlying the generation of spin-polarized currents in semiconductors and metals.1–4 The goal of spintronics is to understand the interaction between the particle's spin and its solid-state environments and to combine different materials to make composite devices. The prototypical kind of device is the spin valve, the term coined in 1991 by Dieny.5Graphene, hereafter called G-ene for brevity, is an ideal candidate material for spintronics6,7 due to its layered structure and peculiar weak spin–orbit coupling that facilitates spin transport and modulation of electrical properties.8–13 G-ene is a two-dimensional (2D) allotrope of carbon isolated for the first time in 2004 by mechanical exfoliation of pyrolytic graphite.14 Chemical vapor deposition (CVD) technique is today the most widely used because it allows to achieve large scale production.15
Using G-ene in possible applications, such as photodetectors, sensors, organic light-emitting diodes, organic thin film transistors, supercapacitor, and catalytic applications, photovoltaics, or spintronics, it is essential to finely modulate its electronic and magnetic properties.
It presents unusual mesoscopic effects.16 These effects originate from the boundary conditions required for the wave functions, and depend also on the type of edges exhibited at the termination of a mesoscopic sample. The most studied edges, zigzag (ZZ) and armchair (AC),17 have drastically different electronic and magnetic properties.18 ZZ edges can sustain edge (surface) states and resonances that are not present in the AC case.
G-ene application in electronics suffers from a major drawback: graphene is, in its pristine state, a zero-band-gap semiconductor.19,20 Furthermore, in the absence of d or f electrons, the production of magnetic moments is not trivial. Several ways have been explored to tune electronic structure of G-ene. It was found experimentally that a band gap can be opened by confinement effects of electrons in graphene nanoribbons,21 or by applying a potential difference over a graphene bilayer.22 A different approach, opening a challenging playground for chemists,23–25 is chemical modification of pristine G-ene. The main obstacle is the control of the geometrical features and of the selectivity of functional groups.26 The lack of periodic functionalization patterns prevents the achievement of long range ferromagnetic order, thus limiting the potentialities in applications.27
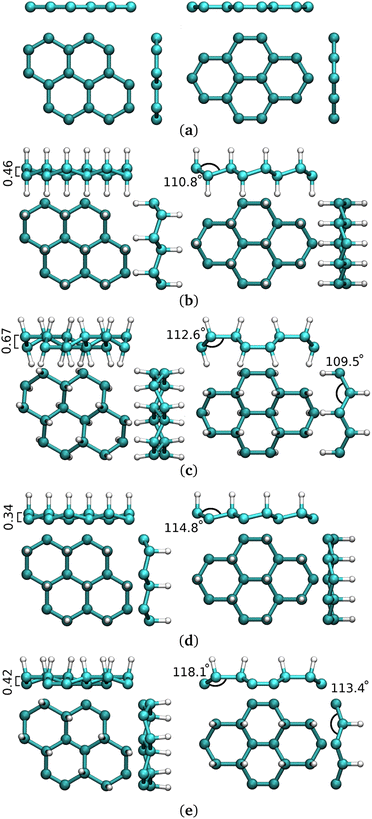
Hydrogenation of G-ene is an attractive solution and it is foreseen to both open a band gap and to produce a magnetic behavior.28–32 Magnetic properties are highly dependent on the hydrogenation degree, while hydrogenation is a reversible process. In this light, hydrogenated G-ene could undoubtedly become a prominent two-dimensional nanomaterial with finely controlled properties33 The 100% hydrogenated derivative (C1H1)n, called graphane (G-ane), was experimentally ascertained29,34–39 and theoretically predicted to open a band gap.40–42 Various isomers have been reported for graphane structures, such as boat and chair,32,43,44 with the latter as the most energetically favorable one. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry can be difficult to achieve at the experimental level while partially hydrogenated scenarios can be much easier to obtain. Partial hydrogenation occurred as a misstep of full-hydrogenation process,44 or obtained by electron-beam lithography techniques.37 50% hydrogenated G-ene (empirical formula, C2H), discussed hereafter, is called graphone (G-one) (Fig. 1d and e). It shows several theoretical45 and experimental evidences that, along with the opening of a band gap as in G-ane, a magnetic moment can be induced for partial hydrogenation. Implantation of magnetic moment by hydrogenation was achieved is several ways, by adsorption of G-ene on a substrate,29,38,46,47 patterned hydrogenation by e-beam lithography,48 CVD,49 creation of H-vacancies in G-ane flakes,50 stoichiometric fluorination,51 substitution of fluorine atoms with different functional groups,52 adatoms implantation.53 Following the intensely debated topic of ferromagnetism in G-ene derivatives, magnetic ordering was detected in some of the aforementioned studies,46,48 others showing only paramagnetic behavior.51 The amount of introduced magnetic moment and the ordering of magnetic moments had scarce and controversial experimental evidences.29,38,50,51 The defect-induced magnetism experimentally prompted and measured on hydrogenated G-ene derivatives29,38 has reached only fractions of μB per carbon atom. It is worth mentioning that in literature it is not always clearly stated whether such values refer to the unit cell or to a single carbon atom, for instance.
1 stoichiometry can be difficult to achieve at the experimental level while partially hydrogenated scenarios can be much easier to obtain. Partial hydrogenation occurred as a misstep of full-hydrogenation process,44 or obtained by electron-beam lithography techniques.37 50% hydrogenated G-ene (empirical formula, C2H), discussed hereafter, is called graphone (G-one) (Fig. 1d and e). It shows several theoretical45 and experimental evidences that, along with the opening of a band gap as in G-ane, a magnetic moment can be induced for partial hydrogenation. Implantation of magnetic moment by hydrogenation was achieved is several ways, by adsorption of G-ene on a substrate,29,38,46,47 patterned hydrogenation by e-beam lithography,48 CVD,49 creation of H-vacancies in G-ane flakes,50 stoichiometric fluorination,51 substitution of fluorine atoms with different functional groups,52 adatoms implantation.53 Following the intensely debated topic of ferromagnetism in G-ene derivatives, magnetic ordering was detected in some of the aforementioned studies,46,48 others showing only paramagnetic behavior.51 The amount of introduced magnetic moment and the ordering of magnetic moments had scarce and controversial experimental evidences.29,38,50,51 The defect-induced magnetism experimentally prompted and measured on hydrogenated G-ene derivatives29,38 has reached only fractions of μB per carbon atom. It is worth mentioning that in literature it is not always clearly stated whether such values refer to the unit cell or to a single carbon atom, for instance.
 | ||
| Fig. 1 Side and top views of G-ene, G-ane and G-one structures in the isolated phase. (a) Pristine G-ene. (b) Chair G-ane. (c) Boat G-ane. (d) Chair G-one. (e) Boat G-one. | ||
Among G-one isomers, only the chair one (Fig. 1d) is found to be ferromagnetic54 with ca. 1 μB per sp2 C atom. The hypothetically possible magnetism of one moment unit per carbon atom, as calculated for the chair-type G-one isomer, has never been close to be achieved experimentally. The stabilization of the chair-type G-one isomer is hard to achieve due to the simultaneous need of: (i) selectivity for the 1,3,5 G-ene ring positions for hydrogenation; (ii) inhibition of migration to vicinal substitutions: (iii) inhomogeneity in the hydrogenation process and the limited coverage percentage.47,55,56 The boat isomer (Fig. 1e), showing diamagnetic behaviour, lies several atomic units lower in energy. The stabilization of the chair vs. boat configuration was studied at the experimental57 and theoretical level58 also in the case of fluorination.
The theoretical results were replicated in this work (see ESI† for more details) and were used to benchmark the proposed computational protocol. G-ene derivatives computational studies available in literature are usually restricted to one single structure of the G-one conformational space, or G-ane's,59,60 separately. The lack of a transversal analysis between G-one and G-ane structures, both as infinite periodic systems or as a local environment at interfaces, motivates us to enlarge the studies of the energy stability and magnetic analysis to a wider range of G-ene derivatives. Non-periodic structures were evaluated to tune the material towards maximization of spin density per unit area, leading to the new design of islands of G-ane diluted in a G-ene matrix.
2 Methods
Modeling large systems in a more realistic environment in an ab initio computational framework has become possible only in the past few years thanks to overall progress of both computational resources and theoretical approaches, enabling extensive work on more and more complex systems comprising hundreds of atoms in one unit cell.61 The modeling of surfaces through slabs within PBC showed to be mandatory to have a reliable picture of the substrate@adsorbate scenarios.62 The packages of software CP2K were used for the periodic DFT calculations.63 Calculation of energy and forces were performed by direct diagonalization using the Quickstep module.64,65 Core electrons of Au, C and H elements are represented by GTH pseudopotentials.66–68 Valence electrons for the same elements are described with pseudo-wavefunctions expanded in Gaussian-type orbitals and the density is represented in a plane wave auxiliary basis set (GPW) as implemented for the DZVP-MOLOPT-SR-GTH bases set in CP2K, SR stands here for short range and these sets were chosen to achieve a more efficient calculations of very large systems. A comparison of this basis set and the heavier version DZVP-MOLOPT-GTH is shown in Table S5 in ESI† and it highlights how the choice does not affect the results on structural, electronic and magnetic properties. The revised Perdew–Burke–Ernzerhof (revPBE) functional69,70 was chosen for the calculation. The rVV10 non-local dispersion corrections71 were also included. The conjugate gradient72 (CG) minimizing procedure was employed to carry out the structure optimization. The convergence of the plane waves basis cut-off was reached for 500 Ry with a convergence threshold of 1 × 10−7 a.u. for the SCF energy and 4.5 × 10−4 a.u. per Å for the forces. The plane-waves cut-off was chosen for these systems to gain a level of precision mandatory for the study of magnetic properties and it is in the upper bound of the range used for other complex molecular magnetic systems.73–762.1 Supercell choice
Only Γ-point calculations were carried out.77,78 The correct accounting of the symmetry and inclusion of enough k-points were assured choosing 256 G-ene unit cells to build up the supercell. A comparison of the computed electronic structure with the ones reported in literature79 is also showed. The supercell was selected arranging three n × n arrays of G-ene non-primitive hexagonal unit cells, each containing two carbon atoms, with n = 12, 14, 16. The correct electronic density of states was achieved for n = 16 (see Fig. S1 in ESI†).The 16 × 16 array of unit cells was also found to have the best matching between the Au(111) and G-ene supercells dimensions (vide infra). The Au(111) slab contains four layers of 192 atoms each, for a total of 768 gold atoms. A close match between substrate and adsorbate is mandatory to avoid biased interaction and consequently significant artificial stretching or compression of the two lattices. The periodicity of the substrate@adsorbate system is equal to the Au(111) surface and almost perfectly double the size of the pristine G-ene. For this reason, when designing the atom slab, an even number of G-ene rings in a row is necessary to fulfill the periodic boundary conditions (Fig. 2). The structural and cell parameters are reported in Table S1 in ESI.† A further important issue is the interactions between replica along the z axis: the finite vacuum layer thickness was here set to 70 Å to minimize this spurious contribution to the total energy.
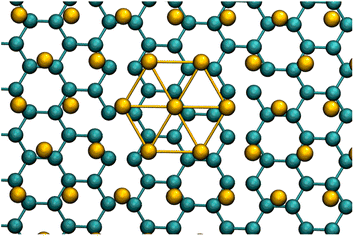 | ||
| Fig. 2 G-ene@Au(111) superlattice, the lattice parameter of Au is twice the size of the G-ene structure. See DOS and structure in Fig. S8 in ESI.† | ||
The number of atoms in the partially hydrogenated systems is the same for several structures presented in this work, allowing a stability analysis through a direct comparison of G-one and G-ane/G-ene energies. The ribbons and islands structures have an even number of H atoms; an odd number would imply the existence of an unpaired electron in the carbon backbone, that is a metastable state where the reaction with further hydrogen is very likely.80
All the G-ene, G-ane, and G-one supercells were also relaxed to check the error introduced by constraining their cells to the optimized Au(111) cell parameters for the subsequent simulations.
Computed lattice parameters a and b are 2.470/2.470 Å for G-ene vs. an experimental value of 2.46 Å;20 2.537/2.537 Å for chair G-one; 2.542/2.542 Å for chair G-ane; 2.568/2.589 Å for boat G-one, 2.585/2.496 Å for boat G-ane. Therefore, the above-mentioned constraining introduced an error of ∼1% for chair structures and ∼4% for boat structures. Being the former the only structures of interest of this study, 1% of error can be considered negligible.
2.2 Broken-symmetry state calculations for exchange coupling estimation
In the broken-symmetry, BS, formalism,81 which is commonly utilized for quantitative estimates of exchange-coupling constants in polynuclear transition metal complexes, a one-to-one correspondence is established between the energy of a Slater determinant built up with orbitals localized on different centers and bearing electrons with opposite spin computed and the energy of a microstate with mS = 0 computed using the effective Heisenberg–Dirac–Vleck spin Hamiltonian.![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) HDvV = JS1·S2 HDvV = JS1·S2 | (1) |
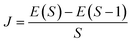 | (2) |
In eqn (2), E(S) represents the energy of a state with total spin S. J is the magnetic exchange-coupling constant, and eqn (1) is often used to reproduce experimental data. In the case of positive J, the antiferromagnetic (AF) state is the ground state; in the case of negative J, the ferromagnetic (FM) state is the fundamental one. The energy of the BS state for a binuclear system with spin S1 = S2 is a weighted average of the energies of pure-spin multiplets, and J may be calculated using the equation:
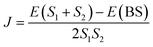 | (3) |
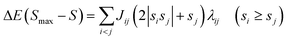 | (4) |
2.3 Benchmark systems
The reliability and generalizability of a proposed computational protocol is based on the accurate reproduction of the available observables. In consideration of the fact that most of the systems considered in this work do not have or have a limited number of experimental data to be compared to, it is of basic importance to test our computational protocol on similar systems where there is an abundance of them. For such a reason, our reference calculations were performed on one layer of pristine G-ene supercell through a Γ-point approach and extended to hydrogenated and fluorinated systems already known from literature, such as G-one, G-ane, FG-one, and FG-ane. An extensive description of this benchmarking is reported in ESI† and a comparison with the existing calculations is reported in Table S1.†3 Results and discussions
Two main approaches aimed to achieve a stabilization of the magnetic moments for homogenous and non-homogenous hydrogenation will be presented. In the first scenario, the adsorption of both types of G-one isomers on a substrate Au(111) will be tested to investigate the effects of the new substrate@surface interactions to stabilize the FM vs. the NM phase. In the case of non-homogenous hydrogenation, this work shows a selective patterning of hydrogenation positions to form localized islands characterized by a local G-ane structure. In this regard, a wide variety of different new hydrogenation patterns will be studied and compared to some already presented in the literature. All these systems will be studied within the same computational framework, allowing a detailed and reliable comparison of structural, energetic, and magnetic properties.3.1 Adsorption on Au(111)
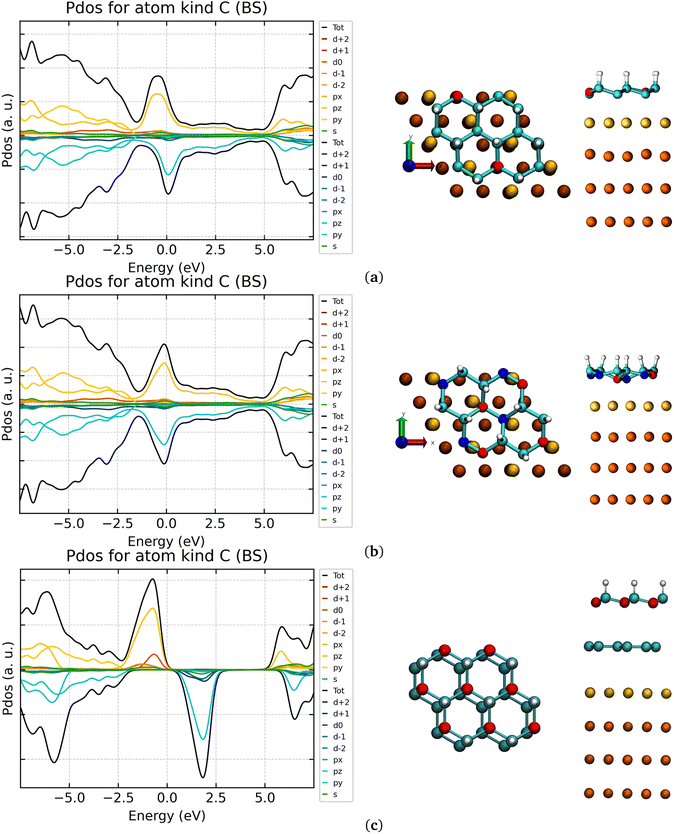
Several studies were focused on the adsorption of hydrogenated G-ene derivatives on metallic surfaces.46,85,86 All of them make use of materials with lattice parameters not matching the G-ene one. This is not the case when using the Au(111) (or Cu(111)) surface, where an almost perfect matching with the G-ene and its derivatives can be observed.46In the chair-type G-one, the hydrogenated carbon atoms positions 1,3,5 in Fig. S4 in ESI† belong to one carbon honeycomb structure sublattice while the unsaturated carbon atoms positions 2,4,6 in Fig. S4 in ESI† belong to the other one. This fact results in all the hydrogen atoms being on the same side of the G-one layer, as already stated above. The Au(111) surface could, in principle, stabilize the ferromagnetic chair-type G-one via the formation of extended σ/π interactions with the gold atoms positioned at a reciprocal distance commensurate to the carbon atoms one.
Both the chair- and boat-type G-one isomers deposition was simulated to quantify the energy stabilization granted by substrate–adsorbate interactions. The symmetry of the isolated G-one is lowered during adsorption on the gold surface for both isomers. In the case of the chair G-one, the unit cell is now composed by 8 atoms and the lattice parameters (2.497 Å in G-ene) become a distribution of values in the range 2.462–2.545 Å. Shorter bond lengths correspond to Csp2 atoms. The single C–C bond distances stretch (1.486–1.517 Å) resulting in increased distribution of carbon atoms positions along the z axis, Δz, in the range 0.163–0.466 Å. It is worth noting that such a variation was not observed for pristine G-ene passing from the isolated to the adsorbed scenario, where the C–C bonds maintain the same lengths of 1.442 Å and Δz of 0.000 Å. The C–H bond is shrunk down to 1.120 Å (see Table S1 in ESI† for a comparison with isolated phases). The C–Au distance is in the range 2.211–2.671 Å, compared to 3.487 Å obtained for pristine G-ene adsorbed on Au(111). Shorter C–Au distances correspond to Csp2 atoms. The chair-type isomer, adsorbed with the hydrogen atoms pointing away from the surface, strongly interacts with the surface retaining only 1/4 of the original magnetic moments present in the isolated phase. The 3/4 of total sp2 carbon atoms (192 out of 256) are in a quasi-atop position to the first layer of gold atoms (yellow Au atoms in Fig. 3a and b). They establish a covalent bonding interaction with Au atoms, witnessed by a significant quenching of the magnetic moment. A different situation is expected for those sp2 carbon atoms being atop to gold atoms in the second layer (orange Au atoms in Fig. 3a–c). Here the C–Au bonding interactions are reduced and, therefore the quenching of the unpaired electron (carbon atoms drawn in red) is not complete. The 192 quasi-atop C atoms retain indeed a ∼0.15–20 μB magnetic moment per atom, while the remaining 64 C atoms retain 0.54 μB per atom, that is roughly one half of the isolated system value. Even if a partial quenching of the magnetic moment was observed upon adsorption, a considerable fraction of magnetic moment is still retained.
The magnetic exchange constant via the broken symmetry approach was calculated, obtaining a reduction from 50 cm−1 to 3 cm−1. Such a reduction can be explained by: (i) the distance intercurring between sp2 carbon atoms retaining magnetic moment doubled with respect to the isolated scenario, being the spin-polarized C atoms now four bonds apart from each other; (ii) the interaction between sp2 carbon atoms with the valence density of states of the gold surface that leads to the formation of covalent bonds. However, the retained FM behavior witnesses a certain degree of wavefunction localization, specifically in those positions where C atoms are not on a quasi-atop configuration to Au atoms. The Au–Csp2 interaction becomes evident from the analysis of the DOS of the carbon atoms (see Fig. 3). A clear spin polarization is still evident but the band gap between the two Csp2 spin components computed for the isolated scenario is filled by the new Au–Csp2 covalent interactions.
For the boat-type G-one isomer, a stronger decrease of symmetry was found in comparison to chair one. The unit cell is composed of 16 atoms and the 1,3 vicinal C–C length, i.e. the cell parameter of G-ene, is in the range of 2.462–2.545 Å. The C–C bonds and the Δz values span wider lengths distributions compared to the chair-type G-one, 1.380–1.564 Å and 0.331–0.676 Å, respectively. The C–H bond shrunk down to 1.120 Å. The C–Au distance is in the range 2.214–2.890 Å, compared to 3.487 Å obtained for the pristine G-ene adsorbed on Au(111), the shorter distances are the Csp2–Au while the longer ones correspond to Csp3–Au distances.
The outcomes of these calculations indicate that the magnetic moment (even if partially quenched) can be maintained also in the adsorbed scenario but, unfortunately, the energy stabilization of ∼3 a.u. for chair-type G-one is still not enough to make it more stable than the boat-type isomer being still ∼5 a.u. more stable (see Table S1 in ESI†). The adsorbed scenario with the hydrogen atoms pointing toward the surface was not considered in virtue of the fact that the hydrogenation process can happen only on the exposed G-ene face being the other inhibited by the strong interaction with the gold surface. Only in the presence of defects, intercalation of the hydrogen atoms could take place but this will be a subject of future work.
Considering that the substitution of the hydrogen with fluorine reduced the ΔEchair–boat by ∼2 a.u. (Table 1), the next step of the investigation led us to the adsorption of the FG-one on the same substrate to verify if concurrent stabilization energy effects could take place. The polarization of the C–F bond has a detrimental effect on the carbon magnetic moment leading to a stronger interaction with the substrate (Au–C = 2.172–2.621 Å). A non-magnetic phase was found for both FG-one isomers, although it was expected only for the boat phase from the calculations already made on the isolated systems.
| System | Magnetism | Energy (a.u.) |
|---|---|---|
| G-one chair@Au | FM | −28577.889420 |
| G-one chair@Au | AF | −28577.887105 |
| G-one boat@Au | NM | −28582.711844 |
As a further step attempting stabilization of the magnetic moment in hydrogenated and fluorinated G-ene derivatives by surface interactions, a new pristine G-ene layer was intercalated as buffer layer between Au(111) and G-one. Usually, the stacking of two G-ene layers show two kinds of symmetries called AA or AB.87 Neither of them is obtained for the G-ene@G-one system; a configuration in between the two was nonetheless found (Fig. 3c). The structure of Au(111)@G-ene@G-one preserves the C–C bond lengths (1.483 Å) and lattice parameters (2.498 Å) of the isolated phase. The G-ene/G-one distances are in the range 3.261–3.609 Å, being the shorter distance between the G-enesp2/G-onesp2 carbon atoms and the longer the G-enesp2/G-onesp3 one. The G-ene/Au distance in Au(111)@G-ene@G-one is the same of the Au(111)@G-ene, say, 3.500 Å. Indeed, as for the structural parameters, the electronic DOS of G-one C atoms recovers the original shape observed in the isolated system (Fig. 3). An intercalated buffer layer is hence decoupling the two systems, and can be exploited to restore their original properties, thanks to the strong π-network that insulates from covalent interactions with the surface.
However, the stabilization mechanisms leaning on introduction of the Au substrate showed not to be enough to make stable FM or AF phases of G-one and FG-one.
3.2 Islands
An alternative route to instill significant spin moment in G-ene is to introduce interfaces already observed in 1D structures (i.e., nanoribbons) lowering the dimensionality to 0D. In other words, systems where the G-ene is embedded in G-ane matrix. Such a scenario can be obtained saturating with hydrogen atoms specific carbon atoms rows in G-ene, or, alternatively, creating vacancies in a stoichiometric G-ane structure.88 Moreover, contrarily to the extended systems, as G-one, where the activation barrier for H migration is very low89 the direct and inverse H migration are limited once G-ane islands are formed.90At the G-ene/G-ane interfaces, a spin polarization mechanism can be induced on the ZZ edge states,91 and contrarily to G-ene nanoribbons, a stable injection of the magnetic moment is possible. The stability of such interfaces has been recently ascertained.92 Furthermore, during the hydrogenation process there is a significant probability for the formation of different domains of sp3 carbon atoms showing H frustration.93 In other words, the ideal sequence of alternating H atoms above and below the G-ene plane is broken (frustrated) across multiple sp3 domains, leading to the impossibility to achieve complete hydrogenation, and consequently, to the presence of some sp2 carbon atoms domain interposed to different sp3 domains. This aspect makes the strategy of building small domains of fully hydrogenated G-ene appealing because of the presence of fewer constrains in the design of multiple adjacent domains and its potentiality as feasible way to implant magnetic moments in G-ene with the perspective of a controlled patterning and scaling-up on the G-ene backbone.48,94 The electronic properties of such systems are similar to a free standing G-ene nanoribbon95 being the spin-polarized states localized in the sp2 G-ene domain. The spin-polarization is extended up to the 1,3 vicinal spin-polarized sp2 carbon atoms.95,96
The rows of Csp2 atoms in the G-ene domain in the vicinity of the interface are composed of ferromagnetically coupled spins; when the geometric pattern of the hydrogenation allows for the formation of non-communicating rows (like two opposite sides of a ribbon or the borders of an island whose continuity is disrupted by the lack of vicinal 1,3 sp2 C atoms), each row tends to be antiferromagnetically coupled to the others. Therefore, the ground state of such systems is overall antiferromagnetic. The study of these systems shows that the spin population on each edge reaches a plateau value of 0.25 μB per unit cell when they are at least 12 Csp2 rows far apart. Such a result indicates that a significant magnetic moment can be instilled but, at the same time, that a high density of hydrogenated portions, i.e., one or two Csp2 rows apart, cannot be achieved due to the competing quenching of the momentum.
To overcome this limitation and to test an alternative way to maximize the magnitude of magnetic moment per unit cell, we investigated the possibility of spin moment implantation when the 1D dimensionality of the ribbon structure is further lowered to 0D islands, allowing a richer design of the interfaces. A rationalization of the implanted magnetic moment will be presented as a function of several order parameters: the island dimension, shape, structure, and termination.
The implantation of magnetic moments in hydrogenated G-ene was pursued juxtaposing it to the chair isomer of G-ane, that is the most stable structure that is ought to form in large abundance and to be stable in thermodynamically driven reactions, for instance undergoing an annealing step after the hydrogenation process.40 Among stoichiometric G-ane compounds, (C1H1)n, the chair isomer is the most stable structure (Fig. 1a),41,97 as confirmed in literature where several other structures were considered.60 Therefore, it is likely to expect that, during the hydrogenation process, islands of this isomer can form in larger amount, or it can gradually grow at the expenses of other structures40 during annealing.
The structures considered hereafter are not composed by homogeneous coverages, rather by islands with isolated spots with different hydrogenation content, ranging from 2 to 50%. The rationalization of different magnetic properties was possible from the analysis of prototypical systems.
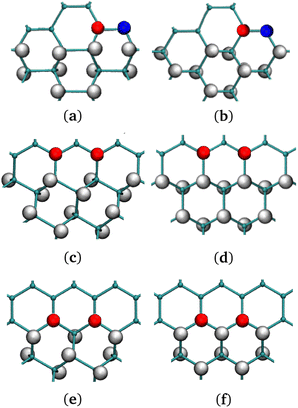 | ||
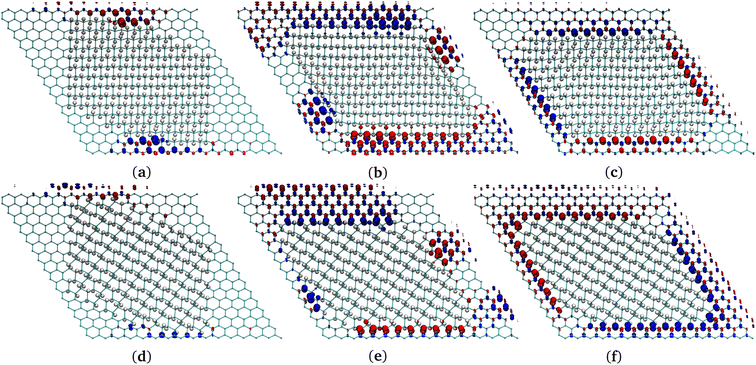
| Fig. 4 (a), (c), (e) Chair G-ane isomer at the interface with G-ene. (b), (d), (f) Boat G-ane isomer at the interface with G-ene. (a), (b) AC, (c), (d) ZZ-α, (e), (f) ZZ-β terminations of G-ane domain. Two carbon atoms belonging to the nearest neighbor row are shown: the red C atoms are part of sublattice A, the blue of the sublattice B. Check Fig. S9 in ESI† for the definition of a row. | ||
A set of island structures composed by the G-ane chair-type isomer (Fig. 1d) with AC, ZZ-α and -β edges was simulated. Being the sp3 domain constituted by 256 H, a direct comparison of the energies with the G-one structure containing the same number of H atoms is possible, ascertaining that the islands are far more stable than boat-type G-one (Fig. 1b) by about 8 a.u. (see Table 2).
| System | Isomer | Edge | Energy (a.u.) | Ref. |
|---|---|---|---|---|
| G-ane/G-ene | Chair | AC | −3063.710216 | Fig. 5a |
| G-ane/G-ene | Chair | ZZ-β | −3062.999279 | Fig. 5b |
| G-ane/G-ene | Chair | ZZ-α | −3063.709245 | Fig. 5c |
| G-ane/G-ene | Boat | AC | −3062.971278 | Fig. 5d |
| G-ane/G-ene | Boat | ZZ-β | −3062.21740 | Fig. 5e |
| G-ane/G-ene | Boat | ZZ-α | −3062.673169 | Fig. 5f |
| G-one | Chair | — | −3046.569877 | Fig. 1d |
| G-one | Boat | — | −3054.784962 | Fig. 1e |
The AC and the ZZ-α edges are the ones with the lowest energies which differ by only 0.06 kcal mol−1 (0.026 eV) in favor of the former. Such a result is of extreme importance, since it indicates that both are equally favorable at room temperature in a G-ane matrix,59,92,95,99 contrarily to the case of freestanding nanoribbons, where it was found that the ZZ edge is metastable and a planar reconstruction occurs leading to lower energy AC edges.98 The spin density is distributed along the ZZ-α edges and it is larger at the center of the row, decreasing towards the ends. From here on, only ZZ-α edges will be considered for the next systems under study. When dealing with 0D structures, several kinds of edges must coexist because the interface of a 0D island describes a closed path. As already mentioned, the edges reported in Fig. 4 are studied for a series of G-ane islands made of 256 H atoms and for each of them a prevalent edge type has been arranged at the interface (see Fig. 5 for complete island structure) and bound by different types of junctions.
In such a framework, it is interesting to notice that different island corners can be obtained. They are characterized by the 1,3 or the 1,4 patterning which have different effects on the propagation of the spin polarization present along the island sides. Such a behavior will be studied in detail in the next paragraph.
Indeed, it was found that a continuity in the 1,3 patterned C atoms across a sharp corner (Fig. S10c in ESI†) led to retention of the spin polarization. To confirm this outcome, several other junctions were considered. For instance, an obtuse angle between ZZ edges (Fig. S10d in ESI†) leads again to 1,4 pattern of the C atoms at the sp2/sp3 interface, forbidding a FM spin polarization. This type of junction becomes a point where the FM spin rows invert their polarity. AC (Fig. 4a and b) edges may be formed by the junction of ZZ rows (Fig. S10e in ESI†). They have the same feature of triggering the spin polarity inversion, but they are less efficient than the previous ones because they lead to the quenching of spin moment across them, lowering the total density of spin population per unit area.
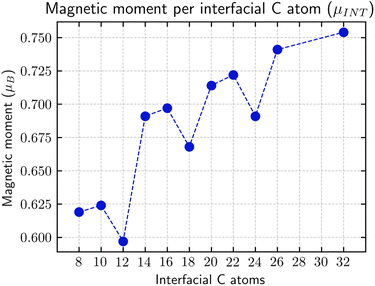 | ||
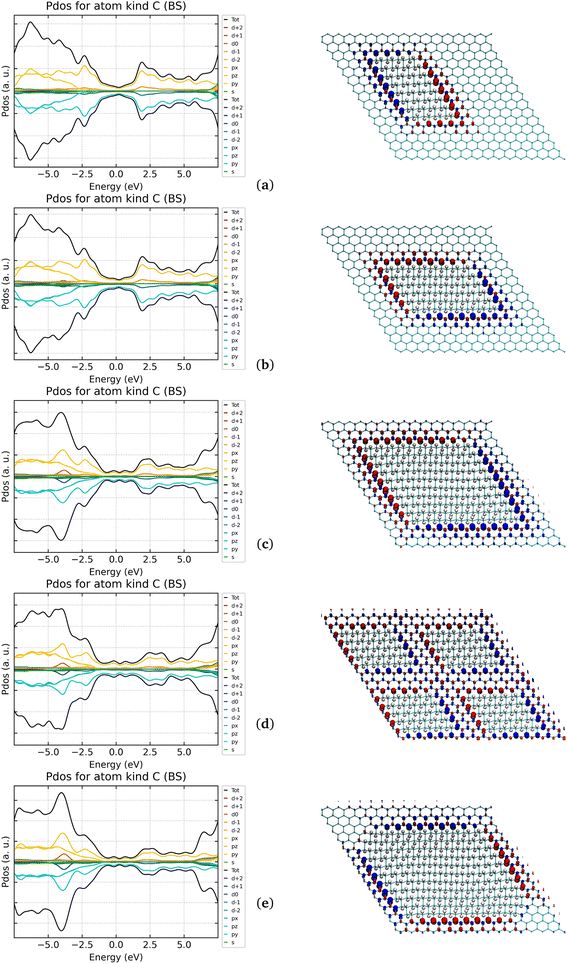
Fig. 6
α and β magnetic moment per interfacial C atom 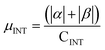 . The unit for magnetic moments is μB. Fig. S11 and S12 in ESI† show the systems analysed in this series, data are collected in Table 3. . The unit for magnetic moments is μB. Fig. S11 and S12 in ESI† show the systems analysed in this series, data are collected in Table 3. | ||
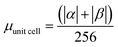 .
. 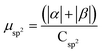 .
. 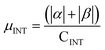 . The unit for magnetic moments is μB. See Table S7 in ESI for μα and μβ
. The unit for magnetic moments is μB. See Table S7 in ESI for μα and μβ
| Rings | H | Csp2 | CINT | μ | μ unit cell | μ sp2 | μ INT |
|---|---|---|---|---|---|---|---|
| 2 | 10 | 502 | 4 | 0 | 0 | 0 | 0 |
| 3 | 14 | 498 | 6 | 0 | 0 | 0 | 0 |
| 4 | 18 | 494 | 8 | 4.95 | 0.0193 | 0.0100 | 0.619 |
| 5 | 22 | 490 | 10 | 6.24 | 0.0244 | 0.0127 | 0.624 |
| 6 | 26 | 486 | 12 | 7.16 | 0.0280 | 0.0147 | 0.597 |
| 7 | 30 | 482 | 14 | 9.67 | 0.0378 | 0.0201 | 0.691 |
| 8 | 34 | 478 | 16 | 11.15 | 0.0436 | 0.0233 | 0.697 |
| 9 | 38 | 474 | 18 | 12.03 | 0.0470 | 0.0161 | 0.668 |
| 10 | 42 | 470 | 20 | 14.28 | 0.0558 | 0.0304 | 0.714 |
| 11 | 46 | 466 | 22 | 15.88 | 0.0620 | 0.0341 | 0.722 |
| 12 | 50 | 462 | 24 | 16.59 | 0.0648 | 0.0359 | 0.691 |
| 13 | 54 | 458 | 26 | 19.26 | 0.0752 | 0.0421 | 0.741 |
| 14 | 58 | 454 | 28 | — | — | — | — |
| 16 | 64 | 448 | 32 | 24.12 | 0.0942 | 0.0538 | 0.754 |
The only structure that did not converge was the 14 G-ane condensed rings nanoribbon, i.e., the one that has only two G-ene C rings separating the G-ane nanoribbon. The 15 C rings structure was not designed because it would reach one of the boundaries of the used carbon slab and would give rise to a 29 rings structure that exceed the designed series. A spin frustration at the junctions of two nanoribbons, too close to each other, could be claimed as the cause for such discontinuity.
The origin of the plateau value reached for n > 7 can be explained by the formation of a valence/conduction band. The C atoms at the edge (ZZ sp2/sp3 interface) theoretically possess a total magnetic moment of 1 μB, but, due to the periodic ripples induced by the interface, a large part of the energy degeneration in the Fermi region is removed. Such an effect is of extreme importance since it limits the increase of the instilled magnetic moment proportionally to the number of the Csp2 atoms.
Looking at the evolution of the DOS depending on the length of the G-ane nanoribbon, it can be observed that a Dirac cone-like structure is maintained for all the length values but with the difference that the Fermi energy is shifted from the Dirac point towards the occupied states. Such behavior is expected due to the break up of the G-ene π system because of the formation of σ C–H bonds which contribute to increasing the number of bands around Fermi and makes them asymmetrically populated with respect to it.
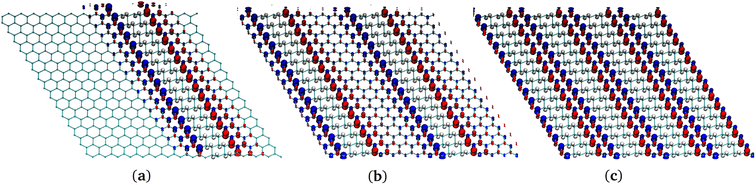 | ||
| Fig. 7 Comparison of structures of several G-ane/G-ene systems with nanoribbon patterns. (a) One nanoribbon. (b) Two nanoribbons. (c) Four nanoribbons. | ||
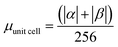 .
. 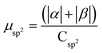 .
. 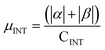 . The unit for magnetic moments is μB. See Table S8 in ESI for μα and μβ
. The unit for magnetic moments is μB. See Table S8 in ESI for μα and μβ
| H | Csp2 | CINT | μ | μ unit cell | μ sp2 | μ INT |
|---|---|---|---|---|---|---|
| 1 × 64 | 448 | 32 | 24.12 | 0.0942 | 0.0538 | 0.754 |
| 2 × 64 | 384 | 64 | 42.04 | 0.164 | 0.109 | 0.656 |
| 4 × 64 | 256 | 126 | 43.82 | 0.171 | 0.171 | 0.348 |
The design of the islands is based on the following insights to achieve the highest instilled magnetic moment in the G-ene portion of the material:
(i) ZZ-α sp2/sp3 interface (Fig. 4d);
(ii) Consider as many 1,3-type junctions to connect the ZZ-α sp2/sp3 interfaces to make a closed-path and generate a 0D structure;
(iii) Islands with sides greater than 4 and smaller than 14 G-ane rings in consideration of the computed dependence of the magnetic moment with the length of the interface;
(iv) The minimum distance between two ZZ-α sp2/sp3 interfaces, n, has to be set not lower than 3.
3.2.5.1 64H and 256H. The two systems in Fig. 8a and e were chosen to establish a direct energy comparison to the G-ane nanoribbons (Fig. 7a and c) as a function of the not hydrogenated/hydrogenated (sp2/sp3) ratio. The 256 H systems also allow a direct energy comparison with the most stable isomer of G-one, the boat-type. In both 64H and 256H cases, the islands showed to be much more stable than the correspondent nanoribbon (688 and 78 kcal mol−1, respectively) indicating that islands can effectively represent a stable alternative (see Table 5).
| H | Csp2 | Nanoribbon (a.u.) | Island (a.u.) | G-one boat (a.u.) |
|---|---|---|---|---|
| 64 | 448 | −2950.370277 | −2950.494546 | — |
| 256 | 56 | −3062.612797 | −3062.673169 | −3054.784962 |
However, the nanoribbons have shown to be able to stabilize 0.75 μB per interfacial CINT atom and 0.054 μB per Csp2 atom (64H system in Table 4). Such values are higher than those achieved for the islands: a larger spin polarization of 0.79 μB was achived for CINT but almost a half of the value, 0.034 μB, per Csp2 atom (64H system in Table 6). When looking at the 50% hydrogenated systems, the island has a higher value of retained magnetic moment per CINT, but the overall magnetic moment stabilized in the slab is higher for the ribbon (256H in Tables 4 and 6). Of course, if these data are compared with the ones that can be obtained with the homogeneous hydrogenation process of G-ene, i.e., with the G-one, it comes out that only a fraction of the magnetic moment per unit cell (or per Csp2) can be obtained by the heterogeneous hydrogenation of G-ene. Despite all this, such a fraction of instilled spin, being in the range of 5–11%, can still be suitable for spintronic applications. This is an appealing results because it clearly indicates that G-ane islands are by far the most thermodynamically stable systems compared to both G-one and G-ane nanoribbons. Because of the hydrogenation, a semioccupied band at the Fermi energy was observed for all the systems with a Dirac cone shifted of ∼0.2 eV at higher energy (Fig. S12 in ESI†).
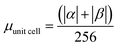 .
. 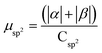 .
. 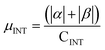 . The unit for magnetic moments is μB. See Table S9 in ESI for μα and μβ
. The unit for magnetic moments is μB. See Table S9 in ESI for μα and μβ
| H | Csp2 | CINT | μ | μ unit cell | μ sp2 | μ INT |
|---|---|---|---|---|---|---|
| 1 × 64 | 448 | 24 | 15.20 | 0.0590 | 0.034 | 0.633 |
| 1 × 96 | 416 | 28 | 17.82 | 0.0696 | 0.0428 | 0.636 |
| 1 × 200 | 312 | 40 | 25.00 | 0.0961 | 0.0789 | 0.801 |
| 4 × 50 | 312 | 80 | 29.75 | 0.116 | 0.0954 | 0.372 |
| 1 × 256 | 256 | 42 | 19.85 | 0.0775 | 0.0775 | 0.473 |
| G-one | 256 | 256 | 243.00 | 0.949 | 0.949 | 0.949 |
3.2.5.2 64His, 96His, 200His, and 256His. The island solution can be an effective strategy, showing how the magnetic moment could vary in function of the amount of hydrogenation is the next step. In Fig. 8, the systems where two descriptors change at the same time: (i) the number of CINT atoms at the sp2/sp3 interface; (ii) the extent of the sp2 portion between adjacent islands.
The computed results indicate that the μ can be increased by a constant value of ca. 0.63 μB per single CINT until a limiting distance among them is maintained (seven C rings in the 1 × 200His system). In other words the balance of the CINT/Csp2 ratio matters and when the distance between the CINT falls below seven C rings, the μ drops from 25 μB (1 × 200His) to 19.85 (1 × 256His). It is worth mentioning that another cause of the quenching of the magnetic moment is present in the 256His. Indeed, at the difference of all the other cases where the same junctions-type were used, the two 1,3 sharp corners had to be “smoothed” by the introduction of a small three-rings-long side connected to the adjacent ones by 1,4 junctions. The latter are known from previous paragraphs to quench the magnetic moment and, therefore, the obtained value of 0.0775 μB can be ascribed to that. No significant differences were observed for the DOS but the increase of the energy gap (ex G-ene Dirac cone) for the system with the highest hydrogenation coverage (0.06 and 0.11 eV for 200His and 256His, respectively. See Fig. 8).
3.2.5.3 200His (one island) & 200His (four islands). Among the single island models, the 200His shows the largest magnetic moment per unit cell, since the system in Fig. 8 was built to maximize the number of the C atoms at the sp2/sp3 interfaces at the detriment of their distances dividing the single island with four equivalent ones. The number of polarized C atoms was then doubled (from 40 to 80) and, consequently, the interfaces distances were halved (from n = 6 to 3). Indeed, the doubled number of CINT atoms did not lead to a doubled value of μ, since μINT dropped from 0.63 to 0.37 μB right because of the reduced distance between the “magnetic” interfaces. However, a further increase of μ was observed (from 25.00 to 29.75 μB) so that a value of 0.12 μB per cell was reached. The use of same number of atoms in the 1 × 200His and 4 × 50His cells allowed to directly estimate their enthalpic stability: Unfortunately, the former is far more stable than the latter of 346 kcal mol−1. Anyhow, the above results paved the way for the reach of best engineering between the number of CINT and the distance between the magnetic interfaces they belong to.
3.2.6.1 200His(1)@Au(111) (one island) & 200His(4)@Au(111) (four islands). A relaxation of the adsorbate for better interaction with the gold surface was observed. In particular, the evident ripples in the G-ane islands got significantly reduced leading to an overall 200His flattened structure. Such a reorganization maximized the adsorbate/substrate interaction which is witnessed by the stretching of the C–H bonds and, to a lesser extent, a shrinking of the C–C ones (see Table S10 and Fig. S13 in ESI†).
However, as a downside of longer C–H elongations, a quenching of the magnetic moment at the expenses of the respective carbon atoms was observed. This can be explained by the partial homolytic cleavage of the C–H bonds with the concurrent formation of the Au–H one, as a consequence of the strong affinity of the two elements. In the 200His(1)@Au(111) scenario the complete quenching interested not only the C atoms at both 1,3 and 1,4 junctions, where the C–H distances are larger, but also two/three more C atoms for single interfaces (island sides): the result is that four/five C atoms have a quenched magnetic moment versus a total of ten atoms that are polarized in the isolated scenario (see Fig. 8c and S14 in ESI†). Eventually, the magnetic moment retained is 2/3 of the latter (see Table 7) and it has to be compared to the 1/4 of the amount retained for G-one@Au(111).
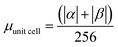 .
. 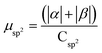 .
. 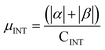 . The unit for magnetic moments is μB. See Table S9 in ESI for μα and μβ
. The unit for magnetic moments is μB. See Table S9 in ESI for μα and μβ
| Buffer | H | Csp2 | CINT | μ | μ unit cell | μ sp2 | μ INT |
|---|---|---|---|---|---|---|---|
| No | 200 | 312 | 40 | 9.95 | 0.0389 | 0.0319 | 0.249 |
| Yes | 200 | 312 | 40 | 14.08 | 0.0550 | 0.045 | 0.352 |
Such results indicate that a surface with less affinity towards the hydrogens would be better suited to maintain the magnetic moment in selectively hydrogenated G-ene derivatives and that no spin polarization could be likely obtained when the total number of C atoms for a single sp2/sp3 interface is smaller or equal to five. In this regard, the other promising system, 200His(4)@Au(111), which is formed by four islands with five Csp2 atoms per side and the same number of 1,2 and 1,4 junctions of the 200His(1), showed revealing results. As expected, a total quenching of the magnetic moment was then observed.
Such results gave a mixed picture. They confirmed that it was possible to retain a certain amount of magnetic moment for heterogeneous hydrogenated G-ene derivatives on a metal surface but at the same time suggested that this is possible if the number of C atoms at the sp2/sp3 interfaces are larger than a critical value. The latter consideration derives from the asymmetric Au–H interactions due to the G-ane island ripples.
3.2.6.2 200His@G-ene, 200His@Au(111)/G-ene. Taking advantage of the above results, a buffer layer of G-ene was introduced between the 200His systems and the Au(111) surface. As in G-one@Au(111)/G-ene where the magnetic moment was almost totally retained, the aim was to decouple the surface from the adsorbate to avoid strong interactions which could lead to a quenching of the magnetic moment. At the structural level, the ripples in the C atoms skeleton are still maintained even if to a smaller extent than the isolated scenario. The C–H bond variations, although present, are hence less pronounced than in the 200His(1)@Au(111). Consequently, some quenching of the magnetic moment was found even in this case. However, even if more limited than in the 200His(1)@Au(111) scenario, the original spin polarization of the C atoms at the sp2/sp3 interface was significantly retained: 0.35 μB for Au(111)/G-ene vs. 0.25 μB per interfacial C atom when the substrate is Au(111). Such a result is very promising since it suggests that the implantation of technologically relevant spin polarization can be achieved in such a kind of systems.
4 Conclusions
The quest for magnetic materials for spintronics has been pushed forward, seeking at implantation of stable magnetic moments on covalently hydrogenated graphene. The formation of covalent bonds between carbon atoms and other species (e.g., hydrogen and fluorine) strongly affect the electronic properties and local structure of the material (i.e. changing from sp2 to sp3 carbon hybridization). This process, however, does not explicitly instill unpaired electrons in the system, and, therefore, the counter-intuitive resulting establishment of localized spin moments in the new G-ene derivatives has been shown to be a valuable way to forward. We investigated several avenues to obtain, at the in silico level, a stable magnetic phase for hydrogenated G-ene. To overcome the magnetic instability which favors the diamagnetic states for hydrogenated G-ene derivatives, two main approaches have been tested: (i) the adsorption of hydrogenated G-ene layer on a substrate (gold and pristine G-ene, or the latter used as buffer layer on the former) to check whether the formation of new surface interactions could stabilize the FM phase; (ii) the partial patterned hydrogenation of carbon backbone by means of densely hydrogenated C atoms islands, forming locally a G-ane structure, surrounded by G-ene matrix. The first strategy was found to generate a strong surface–adsorbate interaction that basically reduces the magnetic moment of G-one, while the second one consisted in the formation of 0D hydrogenated structures. The latter disclosed new possibilities to obtain stable systems with the formation of a sizable magnetic moment at the sp2/sp3 interface portions of the material through the exploitation of several insights on its maximization that were here obtained. The magnetic moments are observed to couple by sizable antiferromagnetic interactions. The further step was the one where the synergic interplay of the two strategies adsorbing on Au(111) the best prototypes of 0D structures found during this study was observed. The 200 H island system was the 0D one chosen for adsorption on Au(111) and on Au(111)/G-ene. In both cases, the antiferromagnetic character was confirmed; in the latter, an almost complete retention of the magnetic moment was observed, while for the former a reduction of the 50% was computed instead. All the results presented demonstrate that G-ane islands are the most stable systems for the same number of H atoms and show a stable antiferromagnetic ground state. Our findings thus suggest that this novel and magneto-active G-ene derivative nanostructure could become achievable more easily than extended G-one or nanoribbons, with a strong potential for future spintronics applications with a variable spin-current density.Data availability
Data of the benchmark study, including input files, output files, and metadata,100 can be downloaded from the Novel Materials Discovery (NOMAD) Laboratory101 under the CC-BY-4.0 license. The scripts to process the raw data and obtain the figure of merit reported in this article are publicly available.102Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union through the Next Generation EU funds through the Italian MUR National Recovery and Resilience Plan, Mission 4 Component 2 – Investment 1.4 – National Center for HPC, Big Data and Quantum Computing – CUP B83C22002830001. The support of MUR through Progetto Dipartimenti di Eccellenza 2018–2022 (CUP B96C1700020008) and 2023–2027 (CUP B97G22000740001 – DICUS 2.0). The computing resources and the related technical support used for this work have been provided by CRESCO ENEAGRID High Performance Computing infrastructure and its staff.103 This work is partially supported by the IEMAP (Italian Energy Materials Acceleration Platform) project funded by MASE (formerly MiTE) Ministry under the international Mission Innovation initiative.104Notes and references
- R. Jansen, J. Phys. D: Appl. Phys., 2003, 36, 289–308 CrossRef.
- I. Zutic, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–386 CrossRef CAS.
- M. Z. Iqbal, M. W. Iqbal, J. H. Lee, Y. S. Kim, S. H. Chun and J. Eom, Nano Res., 2013, 6, 373–380 CrossRef CAS.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- B. Dieny, V. S. Speriosu, S. S. Parkin, B. A. Gurney, D. R. Wilhoit and D. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1297–1300 CrossRef CAS PubMed.
- S. Roche, J. Åkerman, B. Beschoten, J. C. Charlier, M. Chshiev, S. P. Dash, B. Dlubak, J. Fabian, A. Fert, M. Guimarães, F. Guinea, I. Grigorieva, C. Schönenberger, P. Seneor, C. Stampfer, S. O. Valenzuela, X. Waintal and B. Van Wees, 2D Materials, 2015, 2, 030202 CrossRef.
- Z. Zanolli, Sci. Rep., 2016, 6, 1–6 CrossRef PubMed.
- D. Pesin and A. H. MacDonald, Nat. Mater., 2012, 11, 409–416 CrossRef CAS PubMed.
- C. C. Lin, A. V. Penumatcha, Y. Gao, V. Q. Diep, J. Appenzeller and Z. Chen, Nano Lett., 2013, 13, 5177–5181 CrossRef CAS PubMed.
- M. Z. Iqbal, G. Hussain, S. Siddique and M. W. Iqbal, J. Magn. Magn. Mater., 2017, 432, 135–139 CrossRef CAS.
- A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Nano Lett., 2011, 11, 2634–2639 CrossRef CAS PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- M. Z. Iqbal, M. W. Iqbal, X. Jin, C. Hwang and J. Eom, J. Mater. Chem. C, 2015, 3, 298–302 RSC.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710 CrossRef CAS PubMed.
- N. M. Peres, F. Guinea and A. H. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–23 Search PubMed.
- Z. Zhang, A. Kutana and B. I. Yakobson, Nanoscale, 2015, 7, 2716–2722 RSC.
- A. H. Castro Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- P. R. Wallace, Phys. Rev., 1947, 71, 622–634 CrossRef CAS.
- M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 1–4 Search PubMed.
- T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Science, 2006, 313, 951–954 CrossRef CAS PubMed.
- H. Lee, K. Paeng and I. S. Kim, Synth. Met., 2018, 244, 36–47 CrossRef CAS.
- M. Pumera and Z. Sofer, Chem. Soc. Rev., 2017, 46, 4450–4463 RSC.
- L. Liao, H. Peng and Z. Liu, J. Am. Chem. Soc., 2014, 136, 12194–12200 CrossRef CAS PubMed.
- S. Agnoli and G. Granozzi, Surf. Sci., 2013, 609, 1–5 CrossRef CAS.
- J. Hong, S. Niyogi, E. Bekyarova, M. E. Itkis, P. Ramesh, N. Amos, D. Litvinov, C. Berger, W. A. De Heer, S. Khizroev and R. C. Haddon, Small, 2011, 7, 1175–1180 CrossRef CAS PubMed.
- E. J. Duplock, M. Scheffler and P. J. Lindan, Phys. Rev. Lett., 2004, 92, 1–4 CrossRef PubMed.
- L. Xie, X. Wang, J. Lu, Z. Ni, Z. Luo, H. Mao, R. Wang, Y. Wang, H. Huang, D. Qi, R. Liu, T. Yu, Z. Shen, T. Wu, H. Peng, B. Özyilmaz, K. Loh, A. T. Wee, A. Ariando and W. Chen, Appl. Phys. Lett., 2011, 98, 193113 CrossRef.
- W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794–807 CrossRef CAS PubMed.
- J. Wang, Y. Zhang, M. P. Sahoo, T. Shimada, T. Kitamura, P. Ghosez and T. Y. Zhang, Sci. Rep., 2018, 8, 1–9 Search PubMed.
- Y. Fei, S. Fang and Y. H. Hu, Chem. Eng. J., 2020, 397, 1–12 CrossRef.
- D. K. Samarakoon and X. Q. Wang, ACS Nano, 2010, 4, 4126–4130 CrossRef CAS PubMed.
- S. Ryu, M. Y. Han, J. Maultzsch, T. F. Heinz, P. Kim, M. L. Steigerwald and L. E. Brus, Nano Lett., 2008, 8, 4597–4602 CrossRef CAS PubMed.
- J. S. Bunch, S. S. Verbridge, J. S. Alden, A. M. Van Der Zande, J. M. Parpia, H. G. Craighead and P. L. McEuen, Nano Lett., 2008, 8, 2458–2462 CrossRef CAS PubMed.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- J. D. Jones, K. K. Mahajan, W. H. Williams, P. A. Ecton, Y. Mo and J. M. Perez, Carbon, 2010, 48, 2335–2340 CrossRef CAS.
- A. J. Giesbers, K. Uhlírová, M. Konečný, E. C. Peters, M. Burghard, J. Aarts and C. F. Flipse, Phys. Rev. Lett., 2013, 111, 166101 CrossRef CAS PubMed.
- D. Smith, R. T. Howie, I. F. Crowe, C. L. Simionescu, C. Muryn, V. Vishnyakov, K. S. Novoselov, Y.-J. Kim, M. P. Halsall, E. Gregoryanz and J. E. Proctor, ACS Nano, 2015, 9, 8279–8283 CrossRef CAS PubMed.
- M. H. Sluiter and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–7 CrossRef.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–4 CrossRef.
- F. Buonocore, A. Capasso and N. Lisi, Mater. Res. Express, 2014, 1, 15608 CrossRef CAS.
- O. Leenaerts, H. Peelaers, A. D. Hernández-Nieves, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–6 CrossRef.
- M. Pumera and C. H. An Wong, Chem. Soc. Rev., 2013, 42, 5987–5995 RSC.
- L. Feng and W. X. Zhang, AIP Adv., 2012, 2, 1–6 Search PubMed.
- R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Lægsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekær, Nat. Mater., 2010, 9, 315–319 CrossRef CAS PubMed.
- Y. Song, K. Qian, L. Tao, Z. Wang, H. Guo, H. Chen, S. Zhang, Y.-Y. Zhang, X. Lin, S. T. Pantelides, S. Du and H.-J. Gao, Small, 2022, 18, 2102687 CrossRef CAS PubMed.
- W. K. Lee, K. E. Whitener, J. T. Robinson and P. E. Sheehan, Adv. Mater., 2015, 27, 1774–1778 CrossRef CAS PubMed.
- J. Son, S. Lee, S. J. Kim, B. C. Park, H. K. Lee, S. Kim, J. H. Kim, B. H. Hong and J. Hong, Nat. Commun., 2016, 7, 1–7 Search PubMed.
- J. Berashevich and T. Chakraborty, Nanotechnology, 2010, 21, 1–5 CrossRef PubMed.
- R. R. Nair, M. Sepioni, I. L. Tsai, O. Lehtinen, J. Keinonen, A. V. Krasheninnikov, T. Thomson, A. K. Geim and I. V. Grigorieva, Nat. Phys., 2012, 8, 199–202 Search PubMed.
- J. Tuček, K. Holá, A. B. Bourlinos, P. Błoński, A. Bakandritsos, J. Ugolotti, M. Dubecký, F. Karlický, V. Ranc, K. Čépe, M. Otyepka and R. Zbořil, Nat. Commun., 2017, 8, 1–12 Search PubMed.
- A. Ney, P. Papakonstantinou, A. Kumar, N. G. Shang and N. Peng, Appl. Phys. Lett., 2011, 99, 2–5 CrossRef.
- J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870 CrossRef CAS PubMed.
- M. Wojtaszek, N. Tombros, A. Caretta, P. H. Van Loosdrecht and B. J. Van Wees, J. Appl. Phys., 2011, 110, 1–7 CrossRef.
- K. E. Whitener, J. Vac. Sci. Technol., A, 2018, 36, 05G401 CrossRef.
- B. Li, L. Zhou, D. Wu, H. Peng, K. Yan, Y. Zhou and Z. Liu, ACS Nano, 2011, 5, 5957–5961 CrossRef CAS PubMed.
- N. Watanabe, T. Nakajima and N. Ohsawa, Bull. Chem. Soc. Jpn., 1982, 55, 2029–2033 CrossRef CAS.
- D. K. Samarakoon and X.-Q. Wang, ACS Nano, 2009, 3, 4017–4022 CrossRef CAS PubMed.
- C. Zhou, S. Chen, J. Lou, J. Wang, Q. Yang, C. Liu, D. Huang and T. Zhu, Nanoscale Res. Lett., 2014, 9, 1–9 CrossRef PubMed.
- R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601–628 CrossRef CAS.
- A. Caneschi, D. Gatteschi and F. Totti, Coord. Chem. Rev., 2015, 289–290, 357–378 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. Vandevondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- R. Sabatini, T. Gorni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108 CrossRef.
- M. P. Teter, M. C. Payne and D. C. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 12255–12263 CrossRef PubMed.
- G. Santarossa, A. Vargas, M. Iannuzzi, C. A. Pignedoli, D. Passerone and A. Baiker, J. Chem. Phys., 2008, 129, 234703 CrossRef PubMed.
- I. Cimatti, L. Bondì, G. Serrano, L. Malavolti, B. Cortigiani, E. Velez-Fort, D. Betto, A. Ouerghi, N. B. Brookes, S. Loth, M. Mannini, F. Totti and R. Sessoli, Nanoscale Horiz., 2019, 4, 1202–1210 RSC.
- G. Serrano, L. Poggini, M. Briganti, A. L. Sorrentino, G. Cucinotta, L. Malavolti, B. Cortigiani, E. Otero, P. Sainctavit, S. Loth, F. Parenti, A.-L. Barra, A. Vindigni, A. Cornia, F. Totti, M. Mannini and R. Sessoli, Nat. Mater., 2020, 19, 546–551 CrossRef CAS PubMed.
- L. Bondì, S. Brooker and F. Totti, J. Mater. Chem. C, 2021, 9, 14256–14268 RSC.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–487 CrossRef CAS.
- G. Lippert, J. J. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140 Search PubMed.
- P. Kratzer and J. Neugebauer, Front. Chem., 2019, 7, 1–18 Search PubMed.
- S. Casolo, O. M. Løvvik, R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2009, 130, 1–10 CrossRef PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- L. Noodleman, C. Y. Peng, D. A. Case and J. M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244 CrossRef CAS.
- A. Bencini, F. Totti, C. A. Daul, K. Doclo, P. Fantucci and V. Barone, Inorg. Chem., 1997, 36, 5022–5030 CrossRef CAS.
- A. Bencini and F. Totti, J. Chem. Theory Comput., 2009, 5, 144–154 CrossRef CAS PubMed.
- M. Birowska, M. E. Marchwiany, C. Draxl and J. A. Majewski, Comput. Mater. Sci., 2021, 186, 109940 CrossRef CAS.
- F. Buonocore, A. Mosca Conte and N. Lisi, Phys. E, 2016, 78, 65–72 CrossRef CAS.
- M. Birowska, K. Milowska and J. A. Majewski, Acta Phys. Pol., A, 2011, 120, 845–848 CrossRef CAS.
- H. Şahin, C. Ataca and S. Ciraci, Appl. Phys. Lett., 2009, 95, 1–3 CrossRef.
- A. I. Podlivaev and L. A. Openov, Semiconductors, 2011, 45, 958–961 CrossRef CAS.
- L. A. Openov and A. I. Podlivaev, JETP Lett., 2009, 90, 459–463 CrossRef CAS.
- M. J. Schmidt and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–13 Search PubMed.
- V. Tozzini and V. Pellegrini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 22–25 CrossRef.
- M. Z. Flores, P. A. Autreto, S. B. Legoas and D. S. Galvao, Nanotechnology, 2009, 20, 1–6 CrossRef PubMed.
- A. G. Villalba, PhD thesis, Université Bourgogne Franche-Comté, 2017.
- A. D. Hernández-Nieves, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–9 CrossRef.
- J. H. Lee and J. C. Grossman, Appl. Phys. Lett., 2010, 97, 19–22 Search PubMed.
- S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–4 Search PubMed.
- P. Koskinen, S. Malola and H. Häkkinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 16–18 CrossRef.
- V. Georgakilas, J. A. Perman, J. Tucek and R. Zboril, Chem. Rev., 2015, 115, 4744–4822 CrossRef CAS PubMed.
- A. Albino, F. Buonocore, M. Celino, F. Totti, Dataset in NOMAD repository, 2024, DOI:10.17172/NOMAD/2024.01.09-2.
- M. Scheidgen, L. Himanen, A. N. Ladines, D. Sikter, M. Nakhaee, Á. Fekete, T. Chang, A. Golparvar, J. A. Márquez, S. Brockhauser, S. Brückner, L. M. Ghiringhelli, F. Dietrich, D. Lehmberg, T. Denell, A. Albino, H. Näsström, S. Shabih, F. Dobener, M. Kühbach, R. Mozumder, J. F. Rudzinski, N. Daelman, J. M. Pizarro, M. Kuban, C. Salazar, P. Ondračka, H.-J. Bungartz and C. Draxl, J. Open Source Softw., 2023, 8, 5388 CrossRef.
- https://github.com/aalbino2/CP2K_graphone_analysis .
- F. Iannone, F. Ambrosino, G. Bracco, M. D. Rosa, A. Funel, G. Guarnieri, S. Migliori, F. Palombi, G. Ponti, G. Santomauro and P. Procacci, 2019 International Conference on High Performance Computing and Simulation, 2019, pp. 1051–1052 Search PubMed.
- A. Aspuru-Guzik and K. Persson, Mission Innovation, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na01008b |
| This journal is © The Royal Society of Chemistry 2024 |