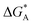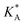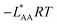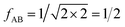Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting adsorption selectivities from pure gas isotherms for gas mixtures in metal–organic frameworks†
Arpan
Kundu‡
 a,
Kaido
Sillar‡
a,
Kaido
Sillar‡
 ab and
Joachim
Sauer
ab and
Joachim
Sauer
 *a
*a
aHumboldt Universität zu Berlin, Institut für Chemie, Unter den Linden 6, 10099 Berlin, Germany. E-mail: js@chemie.hu-berlin.de
bUniversity of Tartu, Institute of Chemistry, Ravila 14a, 50411, Tartu, Estonia
First published on 6th December 2019
Abstract
We perform Grand Canonical Monte Carlo simulations on a lattice of Mg2+ sites (GCMC) for adsorption of four binary A/B mixtures, CH4/N2, CO/N2, CO2/N2, and CO2/CH4, in the metal–organic framework Mg2(2,5-dioxidobenzedicarboxylate), also known as CPO-27–Mg or Mg–MOF-74. We present a mean field co-adsorption isotherm model and show that its predictions agree with the GCMC results if the same quantum chemical ab initio data are used for Gibbs free energies of adsorption at the individual sites and for lateral interaction energies between the same, A⋯A and B⋯B, and unlike, A⋯B, adsorbed molecules. We use both approaches to test the assumption underlying Ideal Adsorbed Solution Theory (IAST), namely approximating A⋯B interaction energies as the arithmetic mean of A⋯A and B⋯B interaction energies. While IAST works well for mixtures with weak lateral interactions, CH4/N2 and CO/N2, the deviations are large for mixtures with stronger lateral interactions, CO2/N2 and CO2/CH4. Motivated by the theory of London dispersion forces, we propose use of the geometric mean instead of the arithmetic mean and achieve substantial improvements. For CO2/CH4, the lateral interactions become anisotropic. To include this in the geometric mean co-adsorption model, we introduce an anisotropy factor. We propose a protocol, named co-adsorption mean field theory (CAMT), for co-adsorption selectivity prediction from known (experiment or simulation) pure component isotherms which is similar to the IAST protocol but uses the geometric mean to approximate mixed pair interaction energies and yields improved results for non-ideal mixtures.
1. Introduction
Porous media with well-defined pore structures have a high potential for the separation of gases by selective adsorption. Classical crystalline microporous materials, zeolites, are used since decades for such tasks, e.g., for air separation.1 With the synthesis of metal–organic frameworks (MOFs),2,3 new materials have become available with high adsorption capacities and tunable adsorption properties.4–6 Specifically, they have high potential for storage of energy carrying molecules (H2 and CH4)7,8 and for separation processes, such as CO2 and N2 removal for natural gas upgrade and CO2 capture from flue gas.9–11 Substituting natural gas for coal and post-combustion CO2 capture and storage (CCS) are key technologies to mitigate the environmental impact of burning fossil fuels.12The selection and rational design of improved materials with optimized properties for a specific separation target requires reliable predictions of co-adsorption isotherms and adsorption selectivities. Because isotherm measurements are much more demanding for mixtures than for single components and require specific equipment,13,14 more than 50 years after its invention, in the vast majority of cases, Ideal Adsorbed Solution Theory (IAST)15 is still used to predict co-adsorption isotherms for gas mixtures from pure gas data.16,17 Also when simulation methods are used, the availability of methods for predicting mixture isotherms from pure components will speed up computational screening for optimal materials in separations, e.g., ref. 18.
IAST assumes that mixture components behave like an ideal solution in the adsorbed phase – an approximation that is not always valid, for example when one component adsorbs more strongly than the other19 or is of very different size than the other.20 The ideal behavior of the adsorbed phase implies that the mixing energy is zero, which also defines the underlying approximation for the lateral interactions – the mixing energy can be zero only if the intermolecular interactions between the molecules of unlike components, EAB, are the average (arithmetic mean, AM) of the interactions between molecules of the individual mixture components A and B,21,22
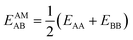 | (1) |
Here, we propose an improved method for predicting mixture isotherms from pure gas data that approximate the interaction energy between unlike molecules as the geometric mean (GM) of the interactions between molecules of the individual components,
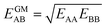 | (2) |
There are other ways of dealing with non-ideal mixing behavior, e.g., Real Adsorbed Solution Theory (RAST)26–28 makes use of activity coefficients to take lateral interactions into account, but requires experimental or simulated co-adsorption data, whereas we focus here on predictions based on pure gas components only. RAST is typically applied to mixtures with strong adsorbate–adsorbate interactions, comparable in strength with adsorbate–surface interactions, e.g., water–alcohol mixtures on microporous silica.28,29 Systems with strong lateral interactions are beyond the scope of our study.
We consider four binary gas mixtures: CO2/CH4 and N2/CH4 relevant for the natural gas upgrade, CO2/N2 relevant for flue gas separation for CCS, and CO/N2 for removal of toxic CO from gas mixtures (e.g., burnt air) which might be relevant for gas mask applications and syngas production and purification. As an adsorbent, we consider Mg2(dobdc)30–32 (dobdc4− = 2,5-dioxidobenzendicarboxylate), a MOF, also known as CPO-27–Mg and Mg–MOF-74, that is considered especially promising for CO2 adsorption because of its high concentration of accessible strong adsorption sites, “under-coordinated” (five-fold coordinated) Mg2+ ions. To these sites, CH4, N2, CO, and CO2 bind with 26, 29, 39, and 46 kJ mol−1, respectively (Table 1). Comparatively, the average lateral adsorbate–adsorbate energies are small, −0.55, −0.35, −0.34, and −2.81 kJ mol−1, respectively; only for CO2, they exceed the thermal energy at 298 K (−2.5 kJ mol−1).
| Ab initio | MF fit of ads. constant | MF fit of free energy | ||||||
|---|---|---|---|---|---|---|---|---|
| A | ΔEA | ΔGA | E AA = EavAA | ΔGA | −LAARTf | |||
a Zero point vibrational energy contributions are included.
b Used for IAST, Section 4.1.
c Used for CMFfit, Section 4.2.
d
Ref. 34–36.
e Calculated using eqn (21) from 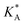 .
f See eqn (22), –LAART is comparable with EAA because N = 2 and EavAA = EAA as there is no anisotropy in pure gas lateral interactions.
g After fitting with continued fraction representation, −2.63 kJ mol−1, see Section S6 in the ESI. .
f See eqn (22), –LAART is comparable with EAA because N = 2 and EavAA = EAA as there is no anisotropy in pure gas lateral interactions.
g After fitting with continued fraction representation, −2.63 kJ mol−1, see Section S6 in the ESI.
|
||||||||
| CO | −39.0 | −1.11 | −0.34 | −1.11 | 1.5682 | −0.34 | −1.11 | −0.33 |
| N2 | −29.2 | 4.16 | −0.35 | 4.15 | 0.1872 | −0.33 | 4.16 | −0.32 |
| CH4 | −25.8 | 3.90 | −0.55 | 3.87 | 0.2097 | −0.46 | 3.89 | −0.46 |
| CO2 | −45.9 | −9.22 | −2.81 | −9.38 | 44.14 | −3.24g | −9.25 | −2.70 |
Although with increasing pressure also the adsorption sites at the dobdc linker molecules will become populated (our previous study33 on pure CO2 adsorption has shown that this will be the case for pressures higher than 0.05 atm) the present study considers a homogeneous lattice of Mg2+ adsorption sites as a model that captures essential features of MOFs with open metal ion sites.
For the CH4/N2, CO/N2, CO2/N2, and CO2/CH4 mixtures, we first predict co-adsorption isotherms and adsorption selectivities from quantum chemical ab initio calculations employing two methods:
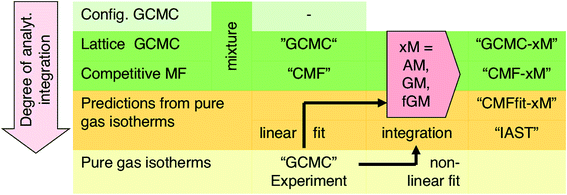
(i) Grand Canonical Monte Carlo (GCMC) simulations on a lattice of adsorption sites which use Gibbs free energies of adsorption as input for gas molecules at isolated individual sites and calculate the interaction energies for each configuration explicitly,33 both generated from quantum chemical ab initio calculations with chemical accuracy (4 kJ mol−1 or better).34–36 These results will serve as a benchmark for any other method used in this study.
(ii) Competitive mean-field (CMF) isotherm model that has clearly separated and physically meaningful parameters for molecule-surface and molecule–molecule (lateral) interactions.34–36 Before, we have used the mean field (Bragg–Williams) model for pure gases;34–36 here we extend it to mixture co-adsorption by including the interaction energy term between molecules of different gases in addition to the lateral interaction energies between the same gas molecules.37
For pure gases, we have shown before that MF theory which assumes an average value for lateral interaction energies not only yields isotherms in close agreement with experiments,34–36 but also in close agreement with the results of GCMC simulations on a lattice of adsorption sites.33 Here, for mixtures, we find the same level of agreement between the results of the analytical CMF equations and the benchmark GCMC simulations with the same ab initio data as the input.
Next, we use both GCMC and CMF co-adsorption isotherms and selectivities to test the AM approximation and the CMF results to test both the AM and GM approximations. For the adsorbed mixtures with very weak lateral interactions, CH4/N2 and CO/N2, we find that mixing energies are indeed negligible (less than 0.2 kJ mol−1) and, consequently, AM mixing is a good approximation and GM mixing has no advantage. For mixtures with stronger lateral interactions, CO2/N2 and CO2/CH4, isotherms obtained with AM mixing deviate substantially from the GCMC benchmarks and GM mixing is always an improvement, whereas for CO2/N2 with GM close agreement with the GCMC benchmark is reached, and for CO2/CH4, an “anisotropy” factor is needed to account for different mixed pair interactions in different directions of the adsorbate layer.
Based on the insight gained, we propose an improved protocol for predicting co-adsorption selectivities from measured (or calculated) pure gas adsorption isotherms. As with the classical IAST protocol, the starting point is fitting the pure component adsorption data with an isotherm model. For this we use the mean-field (Bragg–Williams) isotherm model. Co-adsorption data are then obtained with the CMF equations, using different mixing rules for unlike pair interactions. When AM mixing is used, it reproduces IAST,38 whereas improved results are obtained when GM mixing is applied. The final step is inclusion of an anisotropy factor which needs an atomistic model of adsorption structures. This is not an obstacle because structural optimization using force fields or density functional theory (DFT) has become routine.
This article is organized as follows. Section 2 describes ab initio calculations of Gibbs free energies for adsorption of N2, CO, CO2, and CH4 on Mg2+ sites and of molecule–molecule interaction energies in the adsorbate layers. Section 3 presents ab initio predictions of co-adsorption isotherms and selectivities using GCMC simulations and CMF equations including tests of the AM and GM approximations. Section 4 presents our geometric mean model for predicting co-adsorption isotherms and selectivities from fitted pure gas data as an alternative to IAST.
2. Ab initio calculation of adsorption structures and energies
The ab initio Gibbs free energies of adsorption for the gas components A and B, ΔGA and ΔGB, respectively, are taken from our previous studies34–36 and listed in Table 1. Chemical accuracy has been achieved for electronic energies by employing a quantum chemical hybrid method that uses Møller–Plesset second order perturbation theory (MP2)39 at the adsorption site and DFT+dispersion (PBE+D2) for the full periodic structures.40–43 For a smaller model of the adsorption site calculations are performed with Coupled Cluster theory, CCSD(T).39 Thermal effects and entropies for CO and N2 adsorption are obtained from vibrational partition functions with the anharmonic vibrational energies calculated for each vibrational mode separately.44–46 For adsorbed CH4 the partition function is calculated assuming that CH4 has retained all its rotational degrees of freedom upon adsorption34 while for CO2 only the vibrational mode that corresponds to the hindered rotation of CO2 is approximated by a one-dimensional free rotation.36For three of the four binary mixtures, Fig. 1 shows the adsorption structures with full occupation of the Mg2+ sites taken from previous PBE+D2 structural optimizations under periodic boundary conditions, see ref. 33–36. The figure shows the relevant interactions in the a,b-plane of the hexagonal pore. The distances in the z-direction, a unit cell length of 689 pm, are much larger and the corresponding interactions can be neglected. For pairs of adsorbed molecules taken from these periodic structures the lateral interaction energies are calculated using Coupled Cluster (CC) theory with complete basis set (CBS) extrapolation (CCSD(T)/CBS(D,T)). The pairs are isolated, i.e., the framework is not present in these calculations.
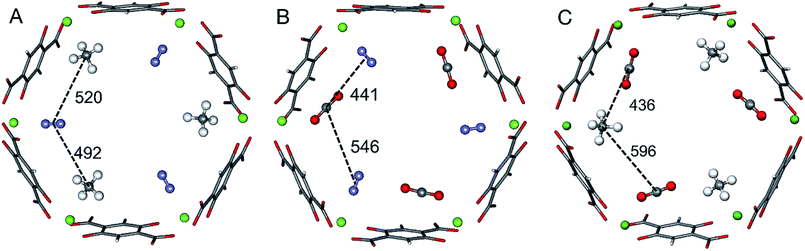 | ||
| Fig. 1 Adsorbate structures of CH4/N2 (A) CO2/N2 (B), and CO2/CH4 (C) mixtures in Mg2(dobdc). Distances between the centers of mass of the adsorbed molecules are given in pm. | ||
For the CO2/CH4 mixture the “mixed” term for the lateral interaction energies between unlike molecules is taken from our previous work,33 whereas for the other mixtures the CO⋯N2, CH4⋯N2, and CO2⋯N2 interaction energies are calculated in this work. Table 2 shows the results. All Mg2+ adsorption sites are equivalent and for adsorbed pure gases all interactions between adsorbed molecules are also equivalent, but with mixed adsorbates “symmetry breaking” occurs. The distances and the interaction energies between neighboring unlike molecules depend on the direction of the interactions, i.e. they are anisotropic. When a pair of unlike molecules gets closer in one direction, the lateral interaction between them gets stronger, whereas the interactions with a molecule in opposite direction gets more distant with a weaker interaction, see Fig. 1 and Table 2.
| A/B | CH4/N2 | CO/N2 | CO2/N2 | CO2/CH4 | |
|---|---|---|---|---|---|
| a Corresponds to IAST. b See eqn (9). c Effective lateral interaction energy, EGMAB/2, see Section 3.5, eqn (16) and (17). d Effective energy of mixing. e Corresponds to IAST; mixing energy is 0 kJ mol−1. f Effective LAB-parameter, LGMAB/2, see Section 4.4, eqn (30). g L parameter for mixing, defined as ΔLmix = LAB−(LAA + LBB)/2; see Table 1 for LAA and LBB parameters obtained from linear MF fitting. h In parenthesis, effective energy of mixing after considering fAB = 0.5. | |||||
| E AB | Short | −0.54 | −0.81 | −1.68 | −1.07 |
| Long | −0.40 | −0.14 | −0.48 | −0.22 | |
| E avAB(ab initio) | Average | −0.47 | −0.48 | −1.08 | −0.65 |
E
AMAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−0.45 | −0.35 | −1.58 | −1.68 | |
| ΔEmixb | −0.02 | −0.13 | 0.50 | 1.04 | |
| E GMAB | −0.44 | −0.34 | −0.99 | −1.24 (−0.62)c | |
| ΔEGMmix | 0.01 | 0.00 | 0.59 | 0.44 (1.06)d | |
−RT LAMAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
Fit | −0.39 | −0.33 | −1.51 | −1.58 |
| −RT LGMAB | Fit | −0.38 | −0.32 | −0.93 | −1.11 (−0.56)f |
−RT ΔLGMmix![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g g |
Fit | 0.01 | 0.00 | 0.58 | 0.47 (1.02)h |
3. Ab initio prediction of co-adsorption isotherms and selectivities
3.1. Grand canonical Monte Carlo simulation on a lattice of adsorption sites
We rely on our GCMC method on a lattice of sites33 to generate co-adsorption isotherms for the CH4/N2, CO/N2, CO2/N2, and CO2/CH4 mixtures. For pure gas (CO2, CH4) adsorption we have shown before that this method is reliable and yields isotherms in very close agreement with the experimental results when accurate (±1 kJ mol−1) ab initio Gibbs free energies are used as the input.33,36 The same can be expected for mixtures, and the lattice GCMC method has the additional advantage that the effect of different approximations for the lateral interactions can be tested.We consider a lattice that contains M Mg2+ adsorption sites (neglecting adsorption on the weaker linker sites). Each site can adsorb a gas molecule, either A or B from a binary gas mixture. For a particular lattice gas configuration i containing MA and MB adsorbed molecules of components A and B, respectively, there are MAA, MBB, and MAB interacting A⋯A, B⋯B, and A⋯B pairs, respectively, and the lattice gas Hamiltonian, Hi, which represents the total free energy of the configuration i is
| Hi = ΔGAMA + ΔGBMB + EAAMAA + EBBMBB + EABMAB; i = 1,2,…,3M | (3) |
As mentioned above, the lateral interaction energies are calculated for isolated pairs, i.e., the framework is not present in these calculations. Taking these energies from total energies for the full periodic structures would not be consistent with the use of constant ΔGA and ΔGB values in eqn (3), see also the ESI, Section S4.†
For a lattice gas model of moderate size with, e.g., M = 6 × 100 sites as used here, the number of possible configurations becomes enormously large – 2M and 3M for a pure gas and a binary mixture, respectively. Hence, adsorption isotherms cannot be calculated analytically from the partition function. A GCMC simulation on this lattice gas model samples only the important configurations at a constant chemical potential and temperature. From these configurations, adsorption isotherms are calculated as the ensemble average of the number of molecules adsorbed.33 Unlike the mean field approach introduced in Section 3.2, our GCMC simulations on a lattice of adsorption sites treat all the lateral interactions exactly, and we will refer to them as “GCMC” in the following, see Scheme 1.
Commonly, GCMC simulations are not performed on a lattice of sites but directly in configuration space which requires several orders of magnitude more energy evaluations. This is not affordable with ab initio, not even with DFT potential energy surfaces, and typically force fields are used. GCMC calculations and similar simulation techniques have been used with force fields before to test the accuracy of IAST.16,18,29,47–50
3.2. Mean-field approximation for a binary adsorbed mixture with lateral interactions
Since GCMC simulations are computationally very demanding, even if done on a lattice of sites, the question emerges if an average value for the lateral interaction energies can be used instead of their explicit evaluation for each of the configurations sampled. For pure gases this is a well-established approximation that leads to the analytical Bragg–Williams isotherm equations,51 which we have used in the past with much success for ab initio predictions.33–36Here, we extend the mean-field approximation to binary gas mixtures with components A and B. For the general case with many (m) components, see the ESI, Section S1.† The coverage dependent Gibbs free energy for component A in the mixture is
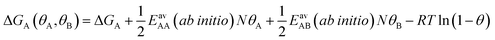 | (4) |
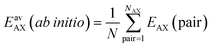 | (5) |
From eqn (4) we obtain the single component adsorption equilibrium constants for the mixture (see also Section S1 in the ESI†)
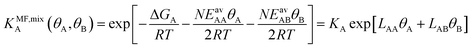 | (6) |
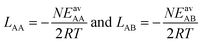 | (7) |
The surface coverage is obtained as
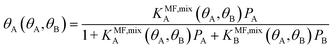 | (8) |
Under the limiting conditions of no lateral interactions, i.e., EavAA(ab initio) = EavAB(ab initio) = 0, eqn (8) reduces to the competitive Langmuir model of co-adsorption (KMF,mixc = Kc = exp[−ΔGc/RT], c = A, B). When lateral interactions are non-negligible, KMF,mixA and KMF,mixB become a function of the coverages and, hence, eqn (8) turns into a self-consistent equation where the coverage of each gas component, θA or B = f(θA,θB), is also a function of itself. We solve this CMF model using an iterative process with coverages from the competitive Langmuir model as an initial guess. Usually, a few iterations are sufficient to yield converged surface coverages (see also Fig. S1 in the ESI†).
3.3. Different combination rules for mixed interaction energies
The ideal behavior of the adsorbed phase assumed by IAST implies that the mixing energy,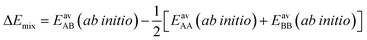 | (9) |
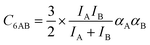 | (10) |
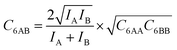 | (11) |
Our lattice GCMC method offers the unique possibility of examining the AM approximation without any additional assumptions. If in every step of the GCMC simulation, the A⋯B interaction energies are approximated as the AM of A⋯A and B⋯B pair interaction energies, we refer to it as “GCMC-AM”, see Scheme 1. In addition, we will use the analytical and computationally much more efficient competitive MF (CMF) model for testing the AM mixing rule and for comparing it with the GM mixing rule. We will insert EavAB values in the CMF equations, eqn (8), that are approximated according to eqn (1) and (2). We will refer to the results as “CMF-AM” and “CMF-GM”, respectively, see Scheme 1.
3.4. Ab initio lattice GCMC and CMF results for co-adsorption isotherms and selectivities
The adsorption selectivity coefficients sA,B are defined as the ratio of the mole fractions xc of different gas mixture components in the adsorbed phase divided by the respective mole fraction ratios in the gas phase, yc,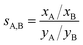 | (12) |
The selectivity of 1.1 calculated for a wide range of CH4/N2 mixture compositions and gas phase pressures shows that it will not be possible to separate nitrogen impurities from natural gas. For CO/N2, our ab initio lattice GCMC simulations yield a selectivity value of 8.4 which agrees well with the IAST selectivities of around 10 calculated for different CO/N2 mixtures based on measured pure gas data.17
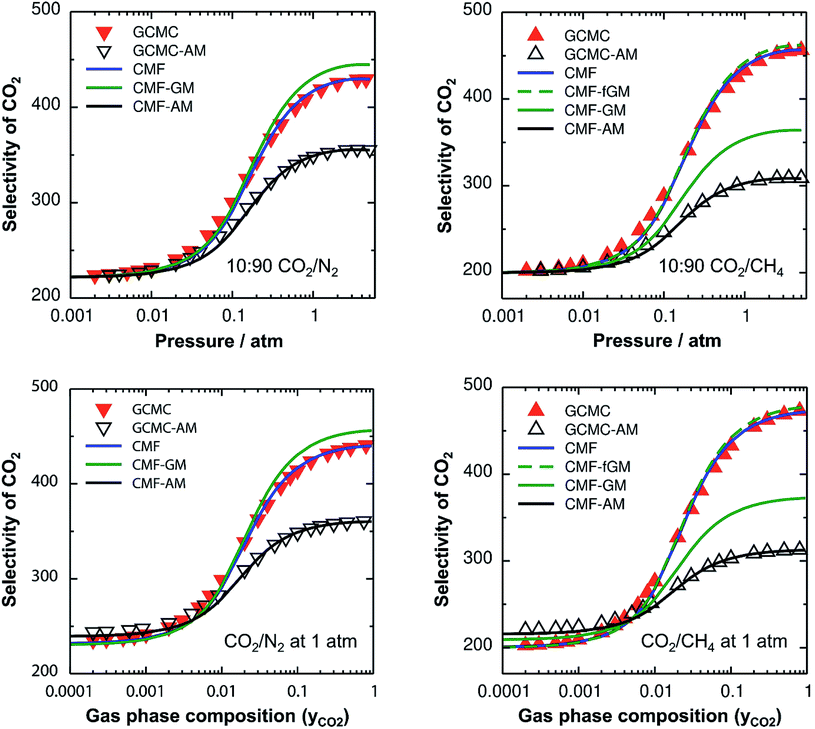
For the non-ideal CO2/N2 and CO2/CH4 mixtures, GCMC-AM substantially underestimates the selectivity for CO2 – the major component on the surface – by 16% and 32% for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 mixtures of CO2/N2 and CO2/CH4, respectively, in the pressure range between 0.5 and 5 atm, see Fig. 2, top. Correspondingly, the adsorbed amounts of the minor components, i.e., N2 and CH4 for CO2/N2 and CO2/CH4, respectively, are overestimated with the AM approximation. The reason is that the CO2⋯CO2 lateral interactions are stronger than the N2⋯N2 and CH4⋯CH4 ones, which makes the AM for the CO2⋯N2 and CO2⋯CH4 interactions, EAMAB, 46% and 158%, respectively, larger than the explicitly calculated EavAB(ab initio) values, see Table 2. Consequently, the stabilities of the minor components on the surface are overestimated which leads to the overestimation of their adsorbed amounts with the AM approximation. The dependence of the selectivity on the gas phase composition (bottom panels of Fig. 2) also shows that the AM approximation underestimates the GCMC CO2 selectivity for a high CO2 content, by 18% and 34% for CO2⋯N2 and CO2⋯CH4, respectively.
90 mixtures of CO2/N2 and CO2/CH4, respectively, in the pressure range between 0.5 and 5 atm, see Fig. 2, top. Correspondingly, the adsorbed amounts of the minor components, i.e., N2 and CH4 for CO2/N2 and CO2/CH4, respectively, are overestimated with the AM approximation. The reason is that the CO2⋯CO2 lateral interactions are stronger than the N2⋯N2 and CH4⋯CH4 ones, which makes the AM for the CO2⋯N2 and CO2⋯CH4 interactions, EAMAB, 46% and 158%, respectively, larger than the explicitly calculated EavAB(ab initio) values, see Table 2. Consequently, the stabilities of the minor components on the surface are overestimated which leads to the overestimation of their adsorbed amounts with the AM approximation. The dependence of the selectivity on the gas phase composition (bottom panels of Fig. 2) also shows that the AM approximation underestimates the GCMC CO2 selectivity for a high CO2 content, by 18% and 34% for CO2⋯N2 and CO2⋯CH4, respectively.
The effect of the AM mixing rule seen with lattice GCMC simulations (GCMC-AM in Fig. 2) is reproduced by the CMF model if the AM approximation is applied to calculate the average lateral interactions in eqn (8), CMF-AM. Because of this and because the CMF model is computationally much more efficient, in the following we will use the CMF to test the geometric mean approximation.
Fig. 2 shows the comparison of the AM and GM approximations for CMF selectivities, CMF-AM and CMF-GM, respectively. For CO2/N2 mixtures, CO2 selectivities obtained with GM are in close agreement with the CMF results. The reason is that the GM of the Eav parameters of CO2 and N2, EGMAB = −1.0 kJ mol−1 (see Table 2), is very close to the average of the directly calculated lateral interaction energies between CO2 and N2 molecules in the adsorbed phase, EavAB(ab initio) = −1.1 kJ mol−1.
For CO2/CH4, Fig. 2 shows an improvement of about 13% for the calculated selectivities when GM instead of AM mixing is used, but the deviations from the CMF results are still substantial, about 20%. The reason is that EGMAB = −1.24 kJ mol−1 gets closer to EavAB(ab initio) = −0.65 kJ mol−1 than EAMAB = −1.68 kJ mol−1, but the deviation is still 0.59 kJ mol−1. The origin of the remaining deviations observed with the CMF-GM model is the anisotropy of the lateral interaction energies (EAB) for “mixed” pairs as our ab initio calculations show. This anisotropy will be addressed in the next section.
Co-adsorption selectivity, nevertheless, is independent of this anisotropy if adsorbed molecules do not interact with each other on the surface, e.g., at a very low surface coverage. In this case, the co-adsorption selectivity becomes the ratio of zero coverage equilibrium constants for both components. Using the ab initio values for the latter, the calculated zero coverage CO2/N2 selectivity is 167 at 313 K and the CO2/CH4 selectivity is 199 at 298 K, which are in good agreement with the experimental IAST selectivities of ca. 175 and 210–220, respectively.52–54
3.5. Anisotropy factor
For the CO2/CH4 mixture, the geometric mean of the CO2⋯CO2 and CH4⋯CH4 interaction energies, EGMAB = −1.24 kJ mol−1, is almost twice as large as the average ab initio CO2⋯CH4 interaction energies, EavAB(ab initio) = −0.65 kJ mol−1 (Table 2). This can be explained by the “symmetry breaking” seen in Fig. 1 that yields a strongly interacting CO2⋯CH4 pair at short distance and a weakly interacting pair at long distance. The interaction energy of the former (−1.07 kJ mol−1) differs only 0.17 kJ mol−1 from the GM (−1.24 kJ mol−1) of the individual lateral interaction energies, whereas the interaction energy of the weakly interacting pair (−0.22 kJ mol−1) differs 1.02 kJ mol−1 and is even less than half of the CH4⋯CH4 interaction energy (−0.55 kJ mol−1).We may take this into account by defining effective pair interaction energies regarding the weakly interacting CO2⋯CH4 pairs as non-interacting. Assuming that there are nAA, nBB and nAB numbers of A⋯A, B⋯B and A⋯B pairs, respectively, with non-negligible interaction energies we get:
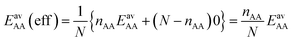 | (13) |
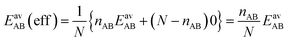 | (14) |
If we apply the geometric mean approximation for the average interaction energy of a mixed pair, i.e.,
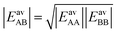 | (15) |
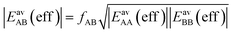 | (16) |
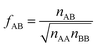 | (17) |
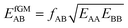 | (18) |
For the CO2/CH4, the long, weakly interacting (−0.22 kJ mol−1) CO2⋯CH4 pairs are regarded as non-interacting which means that there is only one interacting “mixed” pair, nAB = 1, whereas there are two interacting “same” pairs, nAA = nBB = 2, hence
After inclusion of the factor 1/2 for the CO2⋯CH4 interaction, we get EGMAB/2 = −0.62 kJ mol−1 which nicely agrees with the ab initio energy for the same interaction, EavAB(ab initio) = −0.65 kJ mol−1. Moreover, the effective mixing energy, ΔEGM/2mix = 1.06, calculated using the former, matches well with that for the “real mixture”, ΔEmix = 1.04 kJ mol−1, see Table 2. As Fig. 2 shows, the CMF calculations that account for the anisotropy factor fAB = 1/2, CMF-fGM, reproduce the target CMF and GCMC results.
4. Prediction of co-adsorption isotherms and selectivities from pure gas adsorption data
4.1. Ideal adsorbed solution theory (IAST)
Ideal adsorption solution theory (IAST)15 is the most widely used model for prediction of co-adsorption from pure gas adsorption isotherms.15,16 Solving the IAST equations involves integration over isotherms,15 see Section S5 of the ESI† for details. According to the standard protocol,38 first pure gas data points are fitted with an analytical isotherm model and subsequently the integration over isotherm expressions is done analytically.38For fitting the single component data points, we make use of the non-linear mean-field isotherm equation,36
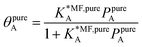 | (19) |
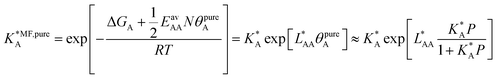 | (20) |
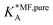 , on the surface coverage is approximated using a Langmuir isotherm. From the fitting parameters
, on the surface coverage is approximated using a Langmuir isotherm. From the fitting parameters 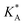 and
and 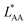 , the Gibbs free energies of adsorption and the average lateral interaction energies are obtained respectively, according to
, the Gibbs free energies of adsorption and the average lateral interaction energies are obtained respectively, according to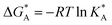 | (21) |
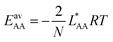 | (22) |
Table 1 shows the comparison of the fitted parameters with the ab initio data used for the GCMC simulations. For adsorbed gases with very weak lateral interactions (CO, N2, and CH4) there is agreement within 0.1 kJ mol−1; for CO2 with stronger lateral interactions (−2.8 kJ mol−1) the fit yields 0.4 kJ mol−1 (15%) stronger binding. The agreement can be improved by further expanding 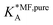 in continued fraction representation, see the ESI, Section S6.†
in continued fraction representation, see the ESI, Section S6.†
IAST predictions for mixture isotherms according to the standard protocol described here will be labelled “IAST” in the following, see Scheme 1. Any kind of pure component isotherms can be used, originating either from experiments16,38 or from simulations. The simulation method employed for the pure component isotherms is irrelevant, and it may range from ab initio GCMC on a lattice of sites (as we use in this work)34–36 to GCMC simulations in full configuration space using a force field, see, e.g., ref. 55.
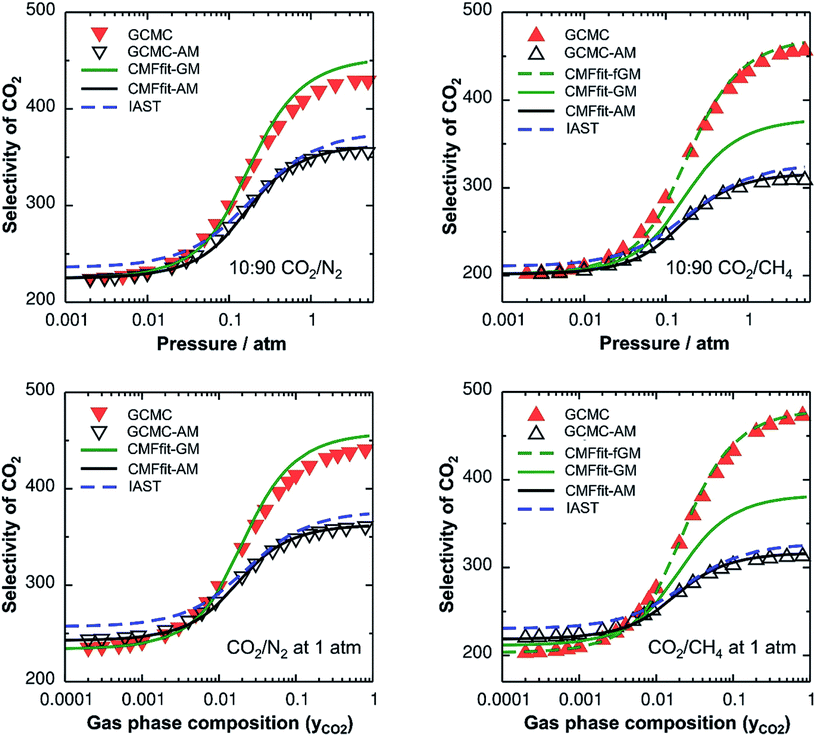
Since IAST shares the assumption of ideal mixtures with GCMC-AM and CMF-AM (Fig. 3), eqn (1), we should expect to get the same results. This is shown in Fig. 3 which will be discussed in more detail below.
4.2. Competitive mean field model with arithmetic mean approximation
The AM combination rule, together with the CMF model, opens another way of predicting co-adsorption isotherms and selectivities from measured or simulated pure component isotherms similar to IAST. Also here, the first step is to fit the isotherm data points with mean-field isotherm models. For a pure gas A, eqn (4) becomes,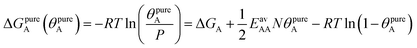 | (23) |
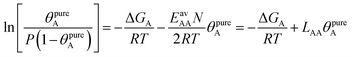 | (24) |
Table 1 shows that the linear, free energy fitting procedure, eqn (24), reproduces the pure component lateral interaction energies for adsorbed gases with very weak lateral interactions, i.e., for CO, N2, and CH4, within 0.1 kJ mol−1 of the directly calculated ab initio values, and within 0.2 kJ mol−1 for adsorbed gases with stronger lateral interactions, e.g. CO2.
In the second step, the fitted LAA and LBB interaction parameters are used to approximate LAB as the arithmetic mean, cf.eqn (1),
| LAMAB = (LAA + LBB)/2 | (25) |
With this, we have two different protocols for generating co-adsorption isotherms from pure component ones, both based on the assumption of ideal mixtures, IAST and CMFfit-AM. Since we use the same ab initio data as the input, they should yield the same results. While the IAST protocol does not require any explicit specification of the interactions between different adsorbed molecules, but involves an integration step, the CMFfit-AM protocol relies on the AM approximation for the interaction between pairs of unlike adsorbate molecules.
4.3. Results: IAST and CMF fit with the arithmetic mean mixing rule
4.4. Competitive mean field model with geometric mean approximation
In our CMF calculations with ab initio data (Section 3.4) the GM approximation for mixed terms proved to be superior to the AM approximation. This also suggests improved results when the CMF equations, eqn (6), are used with the GM of the fitted LAA and LBB interaction parameters,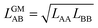 | (26) |
The anisotropy factor fAB, eqn (17), that has further improved the CMF-GM results for CO2/CH4 cannot be derived from pure gas adsorption data, neither from experimental nor from simulated ones. It requires input from adsorption structures for the mixture. The latter is only available from atomistic simulations, but high-level quantum chemical calculations as we perform in this study are not required. Computational methods that are easily available also for non-specialists like DFT(+dispersion) or even simple force fields, e.g., ref. 17, 24, and 25 are sufficient as long as they provide qualitatively correct adsorption structures. We will refer to such methods as “computational” in the following.
After identifying the location of the adsorption sites, one needs to carry out three DFT (or force field) optimization runs for the MOF structures with all adsorption sites filled with: (i) A, (ii) B, and (iii) half A and half B. In structure (iii), A and B molecules should alternate at the adsorption sites (see Fig. 1). Then lateral interaction energies for each “same” pair (AA, BB) and “mixed” (AB) pair must be calculated explicitly.
In Section 3.5 the numbers of interacting neighbors were determined by inspection of the structure of the adsorbate layer for the mixture and from these numbers, fAB was calculated using eqn (17). For a generally applicable protocol we recommend a different approach that is easier to implement into a computer code. Here, the anisotropy factor is calculated directly from the computed average lateral interaction energies. The GM approximation
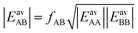 | (27) |
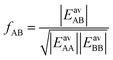 | (28) |
Not much is gained so far, because we need to know EavAB to calculate fAB. However, we may calculate fAB from the results of a simple computational approach mentioned above,
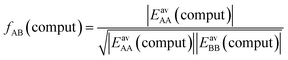 | (29) |
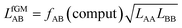 | (30) |
The fAB values calculated according to eqn (29) for CO2/N2 and CO2/CH4 are 1.09 and 0.52, respectively. The latter is in agreement with fAB = 0.5 obtained in Section 3.5 for CO2/CH4 from the numbers of non-interacting pairs. For the isotherms reported in Fig. 2 and 3 for CO2/CH4, we used fAB = 0.5.
Table 2 shows the GM mixed pair interaction energies, −RTLGMAB, as well as the GM mixing energies, −RTΔLGMmix. They have been obtained from single component LAA and LBB parameters that resulted from linear MF fitting of the GCMC isotherms for pure components. Table 2 shows that they are very close to the directly calculated EGMAB and ΔEGMmix values. We therefore expect that our “CMFfit-GM” and “CMFfit-fGM” co-adsorption isotherms show the same improvements over “CMFfit-AM” (Fig. 3) as Fig. 2 shows for the “CMF-GM” and CMF-fGM” compared to CMF-AM” – and this is indeed the case.
For CO2/N2 mixtures the “CMFfit-GM” predicted selectivities deviate only 4% from the GCMC reference values. This excellent agreement is reached because the GM of the L-parameters for CO2 and N2 (−0.9 kJ mol−1) is very close to the average ab initio lateral interaction energy, EavAB(ab initio) = −1.1 kJ mol−1, for a CO2⋯N2 pair, see Table 2. Moreover, the mixing energy calculated using these L-parameters is also within 0.1 kJ mol−1 of the ab initio mixing energy, ΔEmix.
For CO2/CH4, CMFfit-GM also improves the CO2 selectivities compared to CMFfit-AM, though the deviations from the reference GCMC results can be as large as 20%. The reason is that the geometric mean (−1.1 kJ mol−1) improves −RTLAB by 0.5 kJ mol−1 compared to the arithmetic mean (−1.6 kJ mol−1), yet it is almost double the ab initio CO2⋯CH4 lateral interaction energy, EavAB(ab initio) = −0.65 kJ mol−1. After including an anisotropy factor of 0.5, the −RTLAB-parameter (−0.56 kJ mol−1) is within 0.1 kJ mol−1 of the EavAB(ab initio) for CO2⋯CH4 interaction, and the mixing energy calculated using these L-parameters (−RTΔLmix) is in perfect agreement with the ab initio energy of mixing, ΔEmix. Fig. 3 shows that for CO2/CH4 the CMFfit-fGM results deviate by less than 1% from the GCMC reference values.
4.5. Co-adsorption mean field theory (CAMT)
For adsorbents with distinct adsorption sites and relatively weak lateral adsorbate–adsorbate interactions compared to adsorbate surface site interactions, we have shown that predictions of co-adsorption isotherms and adsorption selectivities from pure gas isotherms always improve when the GM instead of the AM mixing rule is applied, regardless whether the anisotropy factor is introduced or not. We have introduced GM mixing based on the London formula for dispersion, but intermolecular perturbation theory in combination with intermolecular multipole expansion tells us that also induction and electrostatic interaction terms contain products of multipole moments or multipole polarizabilities of the individual components. We therefore expect that the GM mixing will always be an improvement compared to the AM mixing assumed (implicitly) by IAST, even when applied to systems with stronger adsorbate–adsorbate interaction, for example hydrogen bonded water/alcohol, alcohol/alcohol or alcohol/aromatic mixtures in MOFs and zeolites.57We therefore recommend our computational protocol based on the GM mixing rule for general use when predicting co-adsorption isotherms from pure gas data. As IAST, our method which we name co-adsorption mean field theory (CAMT) needs fitted pure gas isotherms only, either from experiments or from simulation. The difference is that CAMT needs fitting with the mean field form that yields parameters for lateral interactions. CAMT involves the following steps:
(i) Mean field fitting of pure gas adsorption data, eqn (24), yielding Gibbs free energies for gas–surface interactions and gas–gas (A⋯A and B⋯B) interaction energies;
(ii) Competitive mean field calculation, eqn (6) and (8), of co-adsorption isotherms using pure gas data and A⋯B interaction energies approximated as the geometric mean of the single component A⋯A and B⋯B interaction energies, eqn (26).
Further improvement can be expected if a third, optional step is made which, however, requires input from computational methods:
(iii) Performing three structural optimizations using force fields or DFT for the adsorbent loaded both with the pure gases and the mixture, and calculation of the anisotropy factor in eqn (30) according to eqn (29). This does not necessarily require CCSD(T) calculations for the isolated pair interactions Eav (comput) at the periodic structures. As Table S4 in the ESI† shows, DFT-D calculations for the isolated pairs yield very similar values for fAB.
5. Summary and conclusions
We have used GCMC simulations on a lattice of Mg2+ adsorption sites with ab initio data as the input (eqn (3)) to predict co-adsorption isotherms and selectivities for CH4/N2, CO/N2, CO2/N2 and CO2/CH4 mixtures interacting with the Mg2+ ions of the Mg2(dobdc) MOF. We have also presented competitive mean field (CMF) equations that use average values for lateral interaction energies instead of calculating the lateral interactions for every single adsorbate configuration explicitly as GCMC simulations do. With the same ab initio data as the input, we have found excellent agreement between the predictions of the two methods and conclude that the computationally much more efficient CMF equations can be safely used to predict mixture isotherms.With both the GCMC and CMF methods we have tested the arithmetic mean (AM) of A⋯A and B⋯B adsorbate–adsorbate interactions as approximation for A⋯B interactions and obtained the same results, which also agreed with the standard IAST protocol for predicting co-adsorption isotherms from pure component isotherms. For the CH4/N2 and CO/N2 mixtures in which both gases have very weak lateral interactions, use of AM mixing or IAST shows very good agreement with the exact GCMC and CMF predictions, whereas for mixtures which contain the more strongly interacting CO2 (CO2/N2 and CO2/CH4) substantial deviations from ideal behavior are found.
If GM mixing is applied instead of AM mixing, as the laws of intermolecular interactions such as the London formula for dispersion suggest, agreement with the exact CMF (and GCMC) results is perfect for CO2/N2. For CO2/CH4 substantial improvement is reached, and the remaining deviation can be explained by the anisotropy of the lateral interactions in the mixed adsorbate layer. After introducing a factor (1/2 in this case) that accounts for this anisotropy, very good agreement is also reached for CO2/CH4.
For predicting co-adsorption isotherms and selectivities from pure gas data, we suggest a new computational protocol, co-adsorption mean field theory (CAMT) that like IAST starts from fitting isotherm expressions to pure gas adsorption data, but unlike IAST uses mean field theory for fitting and applies the GM mixing rule to approximate the interaction energies between different components in the CMF equations for the mixture.
Because of the generality of the GM for parameters describing intermolecular interactions, we expect an improvement compared to IAST in all cases in which adsorbate–adsorbate interactions are smaller than adsorbate–surface interactions. The anisotropy factor cannot be derived from pure gas data only; it requires atomistic structural optimizations for the pure gas and mixed adsorbate layers, using either force fields or DFT.
The present work has considered binary mixtures on homogeneous surfaces with identical surface sites. Future studies should aim at incorporating surface heterogeneity, for example linker sites for MOFs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the German Research Foundation (DFG) within the priority program 1570 “Porous media” and with a Reinhart Koselleck grant to JS, as well as by the Fonds of the Chemical Industry. AK has been a member of the International Max Planck Research School “Functional Interfaces in Physics and Chemistry”. KS is supported by the Estonian Ministry of Education and Research (IUT20-15 and PUT1541) and COST Action CM1405 “Molecules in Motion” (MOLIM).References
- J. N. Armor, in Materials Chemistry: An Emerging Discipline, Advances in Chemistry Series, ed. L. V. Interrante, L. A. Caspar and A. B. Ellis, American Chemical Society, Washington, 1995, vol. 245, p. 321 Search PubMed.
- J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3 CrossRef CAS.
- T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2012, 113, 734 CrossRef PubMed.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276 CrossRef CAS.
- H. K. Chae, D. Y. Siberio-Perez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523 CrossRef CAS PubMed.
- H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424 CrossRef CAS PubMed.
- L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC.
- R. B. Getman, Y.-S. Bae, C. E. Wilmer and R. Q. Snurr, Chem. Rev., 2012, 112, 703 CrossRef CAS PubMed.
- D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058 CrossRef PubMed.
- J. M. Huck, L.-C. Lin, A. H. Berger, M. N. Shahrak, R. L. Martin, A. S. Bhown, M. Haranczyk, K. Reuter and B. Smit, Energy Environ. Sci., 2014, 7, 4132 RSC.
- J. G. Vitillo, B. Smit and L. Gagliardi, Chem. Rev., 2017, 117, 9521 CrossRef CAS PubMed.
- R. S. Haszeldine, Science, 2009, 325, 1647 CrossRef CAS PubMed.
- O. Talu, Adv. Colloid Interface Sci., 1998, 76–77, 227 CrossRef CAS.
- J. I. Siepmann, J. F. Brennecke, D. T. Allen, M. T. Klein, P. E. Savage, G. C. Schatz and F. M. Winnik, J. Chem. Eng. Data, 2018, 63, 3651 CrossRef CAS.
- A. L. Myers and J. M. Prausnitz, AIChE J., 1965, 11, 121 CrossRef CAS.
- K. S. Walton and D. S. Sholl, AIChE J., 2015, 61, 2757 CrossRef CAS.
- E. D. Bloch, M. R. Hudson, J. A. Mason, S. Chavan, V. Crocellà, J. D. Howe, K. Lee, A. L. Dzubak, W. L. Queen, J. M. Zadrozny, S. J. Geier, L.-C. Lin, L. Gagliardi, B. Smit, J. B. Neaton, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 10752 CrossRef CAS PubMed.
- E. Haldoupis, S. Nair and D. S. Sholl, J. Am. Chem. Soc., 2012, 134, 4313 CrossRef CAS PubMed.
- J. A. Dunne, M. Rao, S. Sircar, R. J. Gorte and A. L. Myers, Langmuir, 1997, 13, 4333 CrossRef CAS.
- S. Sircar, AIChE J., 1995, 41, 1135 CrossRef CAS.
- E. A. Guggenheim, Mixtures: The Theory of the Equilibrium Properties of Some Simple Classes of Mixtures Solutions and Alloys, Oxford University Press, London, 1952 Search PubMed.
- K. Denbigh, The Principles of Chemical Equilibrium, Cambridge University Press, Cambridge, UK, 1981 Search PubMed.
- D. Berthelot, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1703 Search PubMed.
- S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128 CrossRef CAS.
- E. Haldoupis, J. Borycz, H. L. Shi, K. D. Vogiatzis, P. Bai, W. L. Queen, L. Gagliardi and J. I. Siepmann, J. Phys. Chem. C, 2015, 119, 16058 CrossRef CAS.
- E. Costa, J. L. Sotelo, G. Calleja and C. Marrón, AIChE J., 1981, 27, 5 CrossRef CAS.
- S. Sochard, N. Fernandes and J.-M. Reneaume, AIChE J., 2010, 56, 3109 CrossRef CAS.
- N. Mittal, P. Bai, J. I. Siepmann, P. Daoutidis and M. Tsapatsis, J. Membr. Sci., 2017, 540, 464 CrossRef CAS.
- P. Bai, M. Tsapatsis and J. I. Siepmann, Langmuir, 2012, 28, 15566 CrossRef CAS PubMed.
- P. D. C. Dietzel, V. Besikiotis and R. Blom, J. Mater. Chem., 2009, 19, 7362 RSC.
- P. D. C. Dietzel, Y. Morita, R. Blom and H. Fjellvåg, Angew. Chem., Int. Ed., 2005, 44, 6354 CrossRef CAS PubMed.
- N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504 CrossRef CAS PubMed.
- A. Kundu, K. Sillar and J. Sauer, J. Phys. Chem. Lett., 2017, 8, 2713 CrossRef CAS PubMed.
- K. Sillar and J. Sauer, J. Am. Chem. Soc., 2012, 134, 18354 CrossRef CAS PubMed.
- A. Kundu, G. Piccini, K. Sillar and J. Sauer, J. Am. Chem. Soc., 2016, 138, 14047 CrossRef CAS PubMed.
- K. Sillar, A. Kundu and J. Sauer, J. Phys. Chem. C, 2017, 121, 12789 CrossRef CAS.
- M. Jaroniec, M. Borówko and A. Patrykiejew, Surf. Sci., 1978, 78, L501 CrossRef.
- C. M. Simon, B. Smit and M. Haranczyk, Comput. Phys. Commun., 2016, 200, 364 CrossRef CAS.
- F. Jensen, Introduction to Computational Chemistry, Wiley, Chichester, 1999 Search PubMed.
- C. Tuma and J. Sauer, Chem. Phys. Lett., 2004, 387, 388 CrossRef CAS.
- S. Tosoni and J. Sauer, Phys. Chem. Chem. Phys., 2010, 12, 14330 RSC.
- M. Alessio, F. A. Bischoff and J. Sauer, Phys. Chem. Chem. Phys., 2018, 20, 9760 RSC.
- M. Alessio, D. Usvyat and J. Sauer, J. Chem. Theory Comput., 2019, 15, 1329 CrossRef PubMed.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2013, 9, 5038 CrossRef CAS PubMed.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479 CrossRef CAS PubMed.
- G. Piccini, M. Alessio, J. Sauer, Y. Zhi, Y. Liu, R. Kolvenbach, A. Jentys and J. A. Lercher, J. Phys. Chem. C, 2015, 119, 6128 CrossRef CAS.
- M. Heuchel, R. Q. Snurr and E. Buss, Langmuir, 1997, 13, 6795 CrossRef CAS.
- J. A. Swisher, L. C. Lin, J. Kim and B. Smit, AIChE J., 2013, 59, 3054 CrossRef CAS.
- E. O. Fetisov, M. S. Shah, J. R. Long, M. Tsapatsis and J. I. Siepmann, Chem. Commun., 2018, 54, 10816 RSC.
- R. Krishna, RSC Adv., 2015, 5, 52269 RSC.
- R. H. Fowler and E. A. Guggenheim, Statistical Thermodynamics: A Version of Statistical Mechanics for Students of Physics and Chemistry, Cambridge University Press, London, 1956 Search PubMed.
- J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Energy Environ. Sci., 2011, 4, 3030 RSC.
- D. Yu, A. O. Yazaydin, J. R. Lane, P. D. C. Dietzel and R. Q. Snurr, Chem. Sci., 2013, 4, 3544 RSC.
- Z. Bao, L. Yu, Q. Ren, X. Lu and S. Deng, J. Colloid Interface Sci., 2011, 353, 549 CrossRef CAS PubMed.
- J. Kim and B. Smit, J. Chem. Theory Comput., 2012, 8, 2336 CrossRef CAS PubMed.
- O. Hamdaoui and E. Naffrechoux, J. Hazard. Mater., 2007, 147, 381 CrossRef CAS PubMed.
- R. Krishna, J. M. van Baten and R. Baur, Microporous Mesoporous Mater., 2018, 267, 274 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Mean field approximation for lateral interactions in a multicomponent mixture. Derivation of the geometric mean mixing rule. Additional figures for ideal mixtures. Lateral interactions and the anisotropy factor. Details of ideal adsorption solution theory. Expansion of the mean field equilibrium constant for pure gas in continued fraction representation. See DOI: 10.1039/c9sc03008e |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2020 |