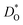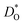Optimising oxygen diffusion in non-cubic, non-dilute perovskite oxides based on BiFeO3†
Haiwu
Zhang
 * and
Roger A.
De Souza
* and
Roger A.
De Souza
 *
*
Institute of Physical Chemistry, RWTH Aachen University, 52056 Aachen, Germany. E-mail: zhang@pc.rwth-aachen.de; desouza@pc.rwth-aachen.de; Fax: +49 241 8092128; Tel: +49 241 8094739
First published on 30th October 2019
Abstract
An ion-conducting crystal possessing non-cubic crystal symmetry and a non-dilute composition will in general display a multiplicity of different migration paths and different site energies for the mobile ions. Predicting the macroscopic rate of ion transport, and in particular, identifying substituent cations that optimise this rate, is therefore challenging. In this study, molecular dynamics simulations employing pair potentials were used to calculate the oxygen tracer diffusion coefficient  as a function of temperature in various substituted systems based on the rhombohedral perovskite oxide bismuth ferrite, BiFeO3. Substituent cations that maximise (or minimise)
as a function of temperature in various substituted systems based on the rhombohedral perovskite oxide bismuth ferrite, BiFeO3. Substituent cations that maximise (or minimise) 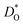 are identified. The results also reveal the limits of the standard crystal-chemical approach to maximising
are identified. The results also reveal the limits of the standard crystal-chemical approach to maximising 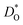 by matching the size of the substituent cation to that of the host's. The implications for the use of BiFeO3 as a high-performance oxide-ion conductor or as a multiferroic medium are discussed.
by matching the size of the substituent cation to that of the host's. The implications for the use of BiFeO3 as a high-performance oxide-ion conductor or as a multiferroic medium are discussed.
Despite their large ionic radius and their formal double charge, oxide ions can migrate at astonishing rates through certain close-packed oxide crystals. Indeed, the oxide-ion conductivity exhibited by various crystalline oxides (at T = 1000 K) is comparable to the ionic conductivity of one-molar aqueous solutions (at T = 298 K).1,2
One crystal structure that has attracted much interest in this regard is the ABO3 perovskite structure. The route to achieving high oxide-ion conductivity in perovskite systems such as (Na,Bi)TiO3, LaGaO3 or LaCoO3 (ref. 3–5) has been to generate a high concentration of mobile charge carriers (viz. oxygen vacancies) by substituting one or both of the host's constituent cations with subvalent species. To date, the choice of subvalent species has been guided by an empirical, crystal-chemical rule: the substituent cation(s) should be close in size to the respective host cation(s). The rationale behind this rule is that such size matching minimises the trapping of oxygen vacancies by the substituent cations.
It is becoming increasingly clear that this rationale, important though it is, is only part of the story of oxide-ion conduction in oxides.6 Subvalent cations have been found not only to trap oxygen vacancies, but also to affect the activation barriers for vacancy migration.7 Furthermore, with increasing vacancy concentration repulsive interactions between vacancies themselves become important. Consequently, the energy landscape through which the vacancies migrate is rather complex, and predicting the macroscopic conductivity of a substituted system is far from straightforward. This necessarily complicates the identification of optimal substituent cations.
A further complication arises in systems that exhibit distorted crystal structures. Many perovskite oxides, for example, do not adopt cubic symmetry at the temperatures of interest but rhombohedral or orthorhombic symmetry. The lowering of the symmetry away from cubic leads to a loss of symmetry equivalence: migration paths and/or crystallographic sites for oxide ions (oxygen vacancies) that are equivalent in the cubic structure are no longer equivalent in the distorted structure. The energy landscape thus becomes even more complex.
In this study, we use molecular dynamics (MD) simulations with empirical pair potentials to examine oxygen diffusion in a non-cubic, non-dilute perovskite. Some molecular static (MS) calculations are performed to illustrate particular points. Our principal aim is to identify the optimal substituents for oxygen diffusion in such a system, and in this way, to expose the limits of relying on size-matching arguments. We take bismuth ferrite (BiFeO3) as our model system, since it adopts rhombohedral symmetry both in experiment and in our MD simulations, and we substitute several percent of the host cations of perovskites with other cations, such that we are beyond the limit of a dilute solution (which is why we speak of substituents rather than dopants).
There is a second reason for studying oxide-ion transport in BiFeO3. It is a system for which oxide-ion transport should be maximised for certain applications and minimised for others. The use of BiFeO3 as a cathode in a solid oxide fuel cell, for example, requires high rates of oxide-ion transport, in order to minimise electrochemical losses.8 The use of BiFeO3 in multiferroic devices, however, requires low rates in order to minimise the (ionic) leakage current.9 Here, the choice of optimal substituent needs to be balanced against the ability to tune the ferroic properties. We examine, therefore, oxygen diffusion, and thus, the optimal substituents, in both positive and negative senses. We expect to gain deeper insights by looking at the whole story rather than at only half of it (i.e. only maximising the conductivity).
For both MD and MS simulations, the ions interacted with each other through long-range coulombic interactions and short-range interactions of the Buckingham form:
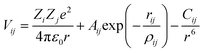 | (1) |
MD simulations were performed with the LAMMPS code with periodic boundary conditions.11 The simulation box consisted of 12 × 12 × 15 rhombohedral unit cells, giving a total of 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ions. Oxygen vacancies were randomly introduced into the cell at a site fraction of 1%. The charge of these vacancies for ‘pure’ and isovalent cation substituted systems was compensated by lowering the charge of all Fe3+ cations to Fe2.9398+. The site fraction of monovalent, divalent and trivalent cations was 3%, 6% and 6%, respectively. The systems were energy minimised in static calculations before the molecular dynamic simulations. At each temperature, the system was first equilibrated for 600 ps in the NpT ensemble followed by a data collection for 900 ps in the NVT ensemble, with the temperature being controlled by a Nose–Hoover thermostat.12 Further details are given as ESI (S2†). MS simulations were performed with the Mott–Littleton method,13 as implemented in the GULP code.14 More details about the calculation of
600 ions. Oxygen vacancies were randomly introduced into the cell at a site fraction of 1%. The charge of these vacancies for ‘pure’ and isovalent cation substituted systems was compensated by lowering the charge of all Fe3+ cations to Fe2.9398+. The site fraction of monovalent, divalent and trivalent cations was 3%, 6% and 6%, respectively. The systems were energy minimised in static calculations before the molecular dynamic simulations. At each temperature, the system was first equilibrated for 600 ps in the NpT ensemble followed by a data collection for 900 ps in the NVT ensemble, with the temperature being controlled by a Nose–Hoover thermostat.12 Further details are given as ESI (S2†). MS simulations were performed with the Mott–Littleton method,13 as implemented in the GULP code.14 More details about the calculation of 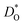 and ΔED can be found in our previous work.15
and ΔED can be found in our previous work.15
In order to emphasise the challenging nature of the problem and thus the need for MD simulations, we first examine the energy barriers for oxygen-vacancy migration in pure, rhombohedral BiFeO3. Although the rhombohedral structure has only a single crystallographic site for oxide ions, the distortion from the cubic form means that, rather than just one unique energy barrier, there are three. We used MS calculations to probe the relevant energy hypersurfaces in pure, rhombohedral BiFeO3. The resultant energy profiles are plotted in Fig. 1, and they yield activation energies of vacancy migration of 0.58, 0.60 and 0.81 eV, respectively. A simple question, then, is what is the effective activation energy for the long-range diffusion of oxygen? The value will be some weighted mean of the three individual barriers, depending, of course, on the relative values and on how the three paths are connected together in the structure. Determining the exact value requires, for instance, diffusion coefficients to be computed as a function of temperature, and one way of doing this is MD simulations.16 We have previously shown the benefits of using MD simulations to study quantitatively ion transport in other perovskites [SrTiO3, (Na,Bi)TiO3 and CH3NH3PbI3].15
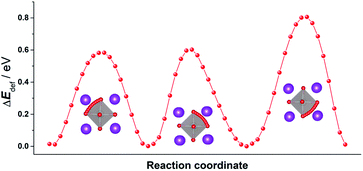 | ||
| Fig. 1 Three distinct energy profiles for oxide-ion migration in pure, rhombohedral BiFeO3. Key: Bi (purple); Fe (silver); O (red). The traced trajectories reveal that the migrating ion follows a curved pathway through a triangular aperture defined by two A-site cations and one B-site cation, bowing away from the edge of the BO6 octahedron, as observed previously.17 | ||
NB: upon substitution of the host's cations, the number of different energy barriers proliferates. There are now additional barriers for jumps around the substituent cation, as well as for jumps away from and towards the substituent cation—and the cation may influence barrier energies up to the third or even the fourth nearest-neighbour position. In addition, substituent cations will affect where the vacancies prefer to sit. MD simulations can capture all these features in a computationally efficient approach.
Let us start by using the standard size-matching rule to identify cations that should maximise the oxygen diffusivity. Examining ionic radii,12 one sees that the acceptor cations closest in size to Bi3+ (1.03 Å) are Na+ (1.02 Å), followed by Ca2+ (1.00 Å) and then Sr2+ (1.18 Å); and that the cations closest to high-spin Fe3+ (0.65 Å) are Ni2+ (0.69 Å) and Mg2+ (0.72 Å) (since ionic radii for twelve-fold coordination are not available for all the ions considered, we have used the values for six-fold coordination).18 According to the standard arguments, one would thus have two expectations for these species: (E1) they should display the lowest binding energies to oxygen vacancies, and consequently, (E2) they should give rise to the highest rates of oxygen diffusion.
If one wants to achieve the opposite goal of minimising the oxygen diffusivity, one would try first to lower the concentration of oxygen vacancies, e.g., through donor doping. If, however, the introduction of acceptor cations is unavoidable, as only they yield the required structural or ferroic properties, one would choose, with the crystal-chemical rule, cations with substantial mismatch, such as Ba2+ (1.38 Å) or Rb+ (1.52 Å) as A site substituents, or Mn2+ (0.83 Å) as a B site substituent. As isovalent species, Gd3+ (0.94 Å) for the A site or Lu3+ (0.86 Å) for the B site are possibilities. These species would be expected to bind oxygen vacancies strongly, and hence, to diminish strongly the rate of oxygen diffusion.
Having identified these cations, with the standard rule, as possible substituents, we now use atomistic simulations to examine in turn the two expectations, E1 and E2. Thus, we determine first, using MS calculations, the binding energy of an oxygen vacancy to a substituent cation, at infinite dilution, in rhombohedral BiFeO3. The binding energy (ΔEbind) is calculated according to the (self-explanatory) expression
| ΔEbind = ΔEassociate − (ΔEisolated cation + ΔEisolated vacancy) | (2) |
A negative value indicates that the associate is stable with respect to the component isolated defects. The results are plotted in Fig. 2a and b (for cations that prefer the Bi site or the Fe site, respectively; see Fig. S2†).
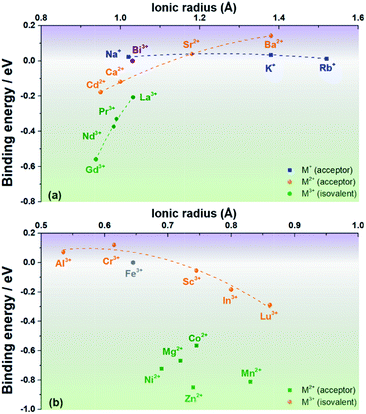 | ||
| Fig. 2 Binding energies of a cation substituent-oxygen vacancy associate as a function of ionic radius for cations that prefer (a) the Bi site and (b) the Fe site of rhombohedral BiFeO3. | ||
Fig. 2 shows that the first expectation is only partly fulfilled: Na+, Ca2+ and Sr2+ do indeed have small binding energies for oxygen vacancies, |ΔEbind| < 0.1 eV, but ΔEbind decreases (from positive to negative, i.e., from unbound to bound) in the order Sr2+ > Na+ > Ca2+, and not in the order of increasing mismatch. Furthermore, Ni2+ and Mg2+ have rather large binding energies, |ΔEbind| > 0.6 eV, despite their relatively small mismatch. In the opposite case of trying to maximise the binding energy, Ba2+ and Rb+, despite large degrees of mismatch, show relatively small binding energies. Mn2+, in contrast, shows an expected high binding energy, but curiously one that is comparable in magnitude to ΔEbind for Ni2+ and Mg2+.
In general, one sees in Fig. 2a that the dependence on ionic radius gets stronger with increasing substituent cation charge. Trivalent species show the strongest dependence, whereas univalent cations show hardly any dependence. This is interesting because the trivalent species (Gd3+, Nd3+, Pr3+ and La3+) are isovalent with the host Bi3+, ruling out any electrostatic interactions with oxygen vacancies. Similar behaviour is also seen in Fig. 1b for trivalent cations (Al3+, Cr3+, Sc3+, In3+ and Lu3+) substituting for the host Fe3+. Divalent cations on the B site show no discernible dependence on ionic radius.
On the basis of these results, one would expect the maximal oxygen diffusion coefficients to decrease in the order Sr2+ > Na+ > Ca2+ ≫ Ni2+, Mg2+. The minimal oxygen diffusion coefficients should decrease in the order Rb+ > Ba2+ ≫ Lu3+ > Gd3+ > Mn2+. In order to examine this second expectation (E2) we use MD simulations to calculate the oxygen tracer diffusivity in the substituted, rhombohedral BiFeO3 systems.
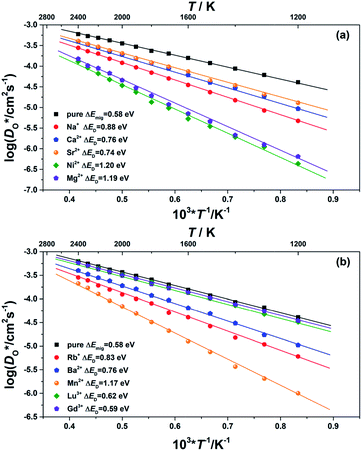
Although BiFeO3 shows rhombohedral (R3c) symmetry at room temperature and transforms to an orthorhombic structure (Pnma) at the Curie temperature TC = 1093 K,19–21 it remains in our simulations rhombohedral over the entire range of temperatures (1200 ≥ T/K ≥ 2400). This inconsistency has, in fact, two benefits for us: all diffusion data obtained refer to one structure (rhombohedral BiFeO3), and these data can be extrapolated down to the lower temperatures of experiment. The MD simulations yield the mean-square-displacement of the oxide ions as a function of time. From such data, the tracer diffusion coefficient of oxygen 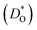 can be extracted (see Fig. 3).
can be extracted (see Fig. 3).
We first consider the diffusion data obtained for the ‘pure’ system, i.e. without any substituent species (the vacancies' charge being compensated by lowering the charge of all Fe cations slightly). The effective activation energy of migration of ΔEmig = 0.58 eV obtained from the MD simulations lies close to the two lowest barriers obtained from the MS calculations (see Fig. 1). It thus seems that the highest barrier (of 0.81 eV) is not traversed to a significant degree by the migrating oxide ions.
We consider this ‘pure’ system to be equivalent to a system containing ideal acceptor cations: such cations only introduce oxygen vacancies but they do not bind them nor do they change their migration barriers. In comparison with this system, all substituted BiFeO3 compositions show (Fig. 3) lower rates of oxygen diffusion and higher effective activation energies of diffusion. This is a very important result: it indicates that one cannot introduce vacancies into BiFeO3 through cation substitution and not affect the vacancies' dynamics.
We transformed our tracer diffusion coefficients into oxide-ion conductivities using the Nernst–Einstein equation, 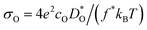 , with f* as the tracer correlation coefficient.22 Our computed conductivities are compared with data reported in the literature in Fig. S3.† In terms of activation enthalpies, we find for nominally undoped BiFeO3 very good agreement between our data (0.58 eV) and the data of Jun et al.23 (0.58 eV) and slightly worse agreement with the data from Chen et al. (0.5 eV).24 For Ca-substituted BiFeO3, our simulations give 0.74 eV, while experimental data25 yields 0.82 eV. For other data, the differences are much larger, but this can be attributed to either the complicated composition (the data from Wefring et al.26 refer to a solid solution of BiFeO3 with 10% (K0.5Bi0.5)TiO3); or to electronic conductivity (for Nb-substituted BiFeO3).23
, with f* as the tracer correlation coefficient.22 Our computed conductivities are compared with data reported in the literature in Fig. S3.† In terms of activation enthalpies, we find for nominally undoped BiFeO3 very good agreement between our data (0.58 eV) and the data of Jun et al.23 (0.58 eV) and slightly worse agreement with the data from Chen et al. (0.5 eV).24 For Ca-substituted BiFeO3, our simulations give 0.74 eV, while experimental data25 yields 0.82 eV. For other data, the differences are much larger, but this can be attributed to either the complicated composition (the data from Wefring et al.26 refer to a solid solution of BiFeO3 with 10% (K0.5Bi0.5)TiO3); or to electronic conductivity (for Nb-substituted BiFeO3).23
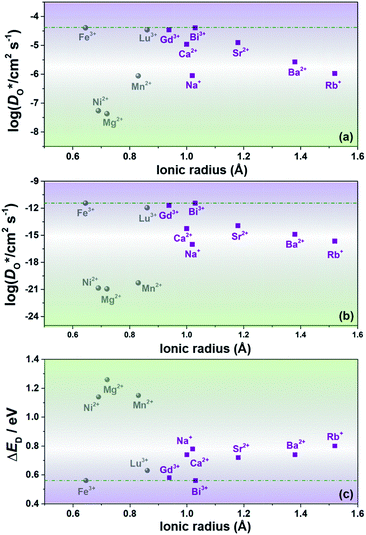
Since our interest in oxide-ion transport stems from the possible application of BiFeO3 as a fuel cell cathode or as a multiferroic medium, we extrapolate our MD data down to T = 1000 K and to T = 300 K, respectively, to reflect the appropriate operation temperatures. These data are shown in Fig. 4a and b, respectively; values of the effective activation energy of diffusion (ΔED) are plotted in Fig. 4c.
Let us first look in more detail at Fig. 4a, where the focus is on maximising 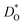 for SOFC application at T = 1000 K. If we look at the data from the viewpoint of the standard size-mismatch rule, we see that, even though Na+ has the smallest mismatch with Bi3+, the Na+-substituted material exhibits an oxygen tracer diffusivity at T = 1000 K that is a factor of 5 lower than that of the Ca2+-substituted material and a factor of 10 lower than that of the Sr2+-substituted material. Furthermore, we see that substituting Ni2+ or Mg2+ for Fe3+ reduces
for SOFC application at T = 1000 K. If we look at the data from the viewpoint of the standard size-mismatch rule, we see that, even though Na+ has the smallest mismatch with Bi3+, the Na+-substituted material exhibits an oxygen tracer diffusivity at T = 1000 K that is a factor of 5 lower than that of the Ca2+-substituted material and a factor of 10 lower than that of the Sr2+-substituted material. Furthermore, we see that substituting Ni2+ or Mg2+ for Fe3+ reduces 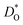 drastically, despite the low mismatch. In contrast, examining the data from the viewpoint of the binding energies, we find that Sr2+ is correctly identified as the best substituent, but Na+ is predicted to be better than Ca2+; Ni2+ and Mg2+ are correctly identified as inferior substituents because they display high ΔEbind, but again, the order is incorrect.
drastically, despite the low mismatch. In contrast, examining the data from the viewpoint of the binding energies, we find that Sr2+ is correctly identified as the best substituent, but Na+ is predicted to be better than Ca2+; Ni2+ and Mg2+ are correctly identified as inferior substituents because they display high ΔEbind, but again, the order is incorrect.
These problems are due to the two premises of the binding-energy approach, that an oxygen vacancy can escape from the vicinity of the substituent cation and migrate freely through the crystal; and that the barriers for vacancy migration remain unaffected by the presence of substituent cations. Both these premises are invalid for the materials considered here: in a concentrated solid solution, the vacancies are never free; and the migration barriers are altered considerably by the substituent cations. If the approach were correct, ΔED for the Sr2+-substituted material would simply be ΔEmig because the vacancies are not trapped by the substituent Sr2+ cations (Fig. 2). The value obtained from the MD simulations is ΔED = 0.74 eV, however, and substantially greater than ΔEmig (0.58 eV). The difference arises from the altered migration barriers and from the deviation from a dilute solution. Thus, Sr2+ has been identified as the best substituent for the wrong reasons.
In Fig. 4b the emphasis is on minimising 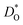 at T = 300 K for multiferroic applications. Compared to the pure material, the compositions with Mg2+, Ni2+ or Mn2+, can slow down the diffusion of oxygen by over ten orders of magnitude. The most surprising behaviour is perhaps that of the Gd3+- and Lu3+-substituted systems. Their tracer diffusivities are only slightly diminished, despite the high degrees of size mismatch, or equivalently, despite the large negative binding energies to an oxygen vacancy. Also surprising is Rb+ and Ba2+, in comparison with Na+, Sr2+, and Ca2+, having no strong effect on the tracer diffusivities. On the other hand, Mn2+ behaves as expected, both from the large mismatch and from the large negative binding energy for oxygen vacancies.
at T = 300 K for multiferroic applications. Compared to the pure material, the compositions with Mg2+, Ni2+ or Mn2+, can slow down the diffusion of oxygen by over ten orders of magnitude. The most surprising behaviour is perhaps that of the Gd3+- and Lu3+-substituted systems. Their tracer diffusivities are only slightly diminished, despite the high degrees of size mismatch, or equivalently, despite the large negative binding energies to an oxygen vacancy. Also surprising is Rb+ and Ba2+, in comparison with Na+, Sr2+, and Ca2+, having no strong effect on the tracer diffusivities. On the other hand, Mn2+ behaves as expected, both from the large mismatch and from the large negative binding energy for oxygen vacancies.
Conclusions
In summary, we have used MD simulations to identify those substituent cations that minimise or maximise the rate of oxygen diffusion in a non-cubic, non-dilute perovskite. Through comparisons with the predictions of the crystal-chemical rule we conclude that the rule does identify possible candidate compositions: the maximal oxygen diffusion coefficients are expected to decrease in the order Sr2+ > Na+ > Ca2+. The minimal oxygen diffusion coefficients should decrease in the order Rb+ > Ba2+ ≫ Ni2+, Mn2+ > Mg2+. Nevertheless, the identified compositions have to be subjected to detailed (experimental or computational) transport studies. In addition, the crystal-chemical rule evidently works better for maximisation rather than minimisation, although if the rule is valid, there should be no difference. The danger in relying on this crystal-chemical rule (and thus implicitly on the binding-energy argument) is that the reverse may be employed, albeit incorrectly: one could attribute the superior diffusivity of (Bi,Sr)FeO3, for example, to the low cation mismatch (with its low binding energy for vacancies), but this factor, as we have shown, plays no role in determining the oxygen diffusivity.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
H. Zhang thanks the Alexander von Humboldt Foundation for financial support. Simulations were performed with computing resources granted by RWTH Aachen University under project rwth0156.References
- (a) J. C. Boivin and G. Mairesse, Chem. Mater., 1998, 10, 2870–2888 CrossRef CAS; (b) J. B. Goodenough, Nature, 2000, 404, 821–823 CrossRef CAS PubMed; (c) J. B. Goodenough, Annu. Rev. Mater. Res., 2003, 33, 91–128 CrossRef CAS; (d) V. V. Kharton, F. M. B. Marques and A. Atkinson, Solid State Ionics, 2004, 174, 135–149 CrossRef CAS; (e) N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS; (f) L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387 RSC; (g) A. Orera and M. S. Islam, Chem. Mater., 2010, 22, 675–690 CrossRef CAS.
- (a) J. Maier, Angew. Chem., Int. Ed., 1993, 32, 313–456 CrossRef; (b) J. Maier, Angew. Chem., Int. Ed., 1993, 32, 528–542 CrossRef.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35 CrossRef CAS PubMed.
- T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801–3803 CrossRef CAS.
- K. Huang, R. S. Tichy and J. B. Goodenough, J. Am. Ceram. Soc., 1998, 81, 2565–2575 CrossRef CAS.
- (a) F. Shimojo, T. Okabe, F. Tachibana, M. Kobayashi and H. Okazaki, J. Phys. Soc. Jpn., 1992, 61, 2848–2857 CrossRef CAS; (b) M. Mayer and N. Nicoloso, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 1393–1398 Search PubMed; (c) A. D. Murray, G. E. Murch and C. R. A. Catlow, Solid State Ionics, 1986, 18, 196–202 CrossRef; (d) J. Koettgen, S. Grieshammer, P. Hein, B. O. H. Grope, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2018, 20, 14291–14321 RSC.
- (a) R. A. De Souza and M. Martin, Monatsh. Chem., 2009, 140, 1011 CrossRef; (b) M. Schie, R. Waser and R. A. De Souza, J. Phys. Chem. C, 2014, 118, 15185–15192 CrossRef CAS.
- (a) Y. J. Niu, W. Zhou, J. Sunarso, L. Ge, Z. H. Zhu and Z. P. Shao, J. Mater. Chem., 2010, 43, 9619–9622 RSC; (b) G. Catalan and J. F. Scott, Adv. Mater., 2009, 21, 2463–2485 CrossRef CAS.
- (a) J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Science, 2003, 299, 1719–1722 CrossRef CAS PubMed; (b) D. Lebeugle, D. Colson, A. Forget, M. Viret, A. M. Bataille and A. Gukasov, Phys. Rev. Lett., 2008, 100, 227602 CrossRef CAS PubMed.
- B. G. Dick JR and A. W. Overhauser, Phys. Rev., 1958, 112, 90 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- (a) S. Nose, J. Chem. Phys., 1984, 81, 511 CrossRef CAS; (b) W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- (a) S. P. Waldow and R. A. De Souza, ACS Appl. Mater. Interfaces, 2016, 8, 12246–12256 CrossRef CAS PubMed; (b) H. Zhang, A. H. H. Ramadan and R. A. De Souza, J. Mater. Chem. A, 2018, 6, 9116–9123 RSC; (c) D. Barboni and R. A. De Souza, Energy Environ. Sci., 2018, 11, 3266–32374 RSC.
- (a) E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 871–875 CrossRef CAS PubMed; (b) C. Tealdi, P. Mustarelli and M. S. Islam, Adv. Funct. Mater., 2010, 20, 3874–3880 CrossRef CAS; (c) E. Kendrick, M. S. Islam and P. R. Slater, Chem. Commun., 2008, 715–717 RSC; (d) D. Parfitt, A. Chroneos, A. Tarancon and J. A. Kilner, J. Mater. Chem., 2011, 21, 2183–2186 RSC.
- (a) M. S. Islam, J. Mater. Chem., 2000, 10, 1027–1038 RSC; (b) M. Cherry, M. S. Islam and C. R. A. Catlow, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS; (c) C. Baeumer, A. H. H. Ramadan, H. Du, K. Skaja, V. Feyer, P. Müller, A. Benedikt, J. C. Lin, J. Mayer, R. A. De Souza, C. M. Schneider, R. Waser and R. Dittmann, Nat. Commun., 2015, 6, 8610 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- R. Haumont, I. A. Kornev, S. Lisenkov, L. Bellaiche, J. Kreisel and B. Dkhil, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134108 CrossRef.
- V. F. Freitas, H. L. C. Grande, S. N. de Medeiros, I. A. Santos, L. F. Cotica and A. A. Coelho, J. Alloys Compd., 2008, 461, 48–52 CrossRef CAS.
- R. Palai, R. S. Katiyar, H. Schmid, P. Tissot, S. J. Clark, J. Robertson, S. A. T. Redfern, G. Catalan and J. F. Scott, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 014110 CrossRef.
- R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326–6342 CrossRef CAS.
- Y. Jun, W.-T. Moon, C.-M. Chang, H.-S. Kim, H. S. Ryu, J. W. Kim, K. H. Kim and S.-H. Hong, Solid State Commun., 2005, 135, 133–137 CrossRef CAS.
- W. Chen, A. J. Williams, L. Ortega-San-Martin, M. Li, D. C. Sinclair, W. Zhou and J. P. Attfield, Chem. Mater., 2009, 21, 2085–2093 CrossRef CAS.
- N. Masό and A. R. West, Chem. Mater., 2012, 24, 2127–2132 CrossRef.
- E. T. Wefring, M.-A. Einarsrud and T. Grande, Phys. Chem. Chem. Phys., 2015, 17, 9420 RSC.
Footnote |
† Electronic supplementary information (ESI) available: Details for potential parameters; crystal structure; the calculation of 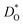 and ΔED; defect equations; dopant site-selectivity; oxide ion conductivity. See DOI: 10.1039/c9ta08980b and ΔED; defect equations; dopant site-selectivity; oxide ion conductivity. See DOI: 10.1039/c9ta08980b |
| This journal is © The Royal Society of Chemistry 2019 |