Evaluation of cation-exchanged zeolite adsorbents for post-combustion carbon dioxide capture†
Tae-Hyun
Bae
a,
Matthew R.
Hudson
bc,
Jarad A.
Mason
a,
Wendy L.
Queen
b,
Justin J.
Dutton
d,
Kenji
Sumida
a,
Ken J.
Micklash
d,
Steven S.
Kaye
d,
Craig M.
Brown
b and
Jeffrey R.
Long
*a
aDepartment of Chemistry, University of California, Berkeley and Materials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: jrlong@berkeley.edu
bNational Institute of Standards and Technology, Center for Neutron Research, Gaithersburg, MD 20899, USA
cDepartment of Materials Science and Engineering, University of Maryland, College Park, MD 20742, USA
dWildcat Discovery Technologies Inc., San Diego, CA 92121, USA
First published on 16th October 2012
Abstract
A series of zeolite adsorbents has been evaluated for potential application in post-combustion CO2 capture using a new high-throughput gas adsorption instrument capable of measuring 28 samples in parallel. Among the zeolites tested, Ca-A exhibits the highest CO2 uptake (3.72 mmol g−1 and 5.63 mmol cm−3) together with an excellent CO2 selectivity over N2 under conditions relevant to capture from the dry flue gas stream of a coal-fired power plant. The large initial isosteric heat of adsorption of −58 kJ mol−1 indicates the presence of strong interactions between CO2 and the Ca-A framework. Neutron and X-ray powder diffraction studies reveal the precise location of the adsorption sites for CO2 in Ca-A and Mg-A. A detailed study of CO2 adsorption kinetics further shows that the performance of Ca-A is not limited by slow CO2 diffusion within the pores. Significantly, Ca-A exhibited a higher volumetric CO2 uptake and CO2/N2 selectivity than Mg2(dobdc) (dobdc4− = 1,4-dioxido-2,5-benzenedicarboxylate; Mg-MOF-74, CPO-27-Mg), one of the best performing adsorbents. The exceptional performance of Ca-A was maintained in CO2 breakthrough simulations.
Broader contextThe development of a cost-effective CO2 capture system is critical to reducing global CO2 emissions in the short-term as power plants continue to burn fossil fuels. While current CO2 capture technologies are too costly for widespread application in the absence of a large tax on CO2 emissions, solid adsorbent based systems have demonstrated potential toward reducing cost and improving performance compared to existing systems that rely on aqueous amine solutions. In particular, zeolites are inexpensive porous materials that are already produced on a large scale for many commercial applications. However, their detailed adsorption performance at conditions relevant to CO2 capture has not been fully characterized for many zeolites in their pure form, making comparisons to other solid adsorbents difficult. Here, a custom high-throughput gas adsorption instrument is used to rapidly evaluate the CO2 capture potential of different cation-exchanged zeolites. |
Introduction
As concerns over the impact of rising concentrations of atmospheric carbon dioxide on climate change continue to mount, there is an urgent need for the development and implementation of technologies that mitigate CO2 emissions from anthropogenic sources.1 Carbon capture and sequestration (CCS) has been proposed as a means of limiting CO2 emissions from large stationary sources, such as fossil fuel-burning power plants.2 Specifically, retrofitting existing power plants for post-combustion CO2 capture, wherein the CO2 is selectively removed from a flue gas stream and permanently sequestered in underground geological formations, is a near-term scenario under which CCS could be rapidly deployed.3,4 Here, the captured CO2 must have a high purity in order to make its compression, transport, and injection underground economical. For coal-fired power plants, the largest flue gas components by volume are N2 (70–75%), CO2 (15–16%), H2O (5–7%) and O2 (3–4%), with a total pressure near 1 bar and temperatures between 40 and 60 °C.5 It should be noted that, although separating CO2 from N2 is the main challenge in post-combustion CO2 capture, the effects of other flue gas components must also be taken into consideration when evaluating the separation performance of a material for realistic applications.In conventional CO2 removal technologies employing aqueous alkanolamine solutions (amine scrubbers), the primary cost of the capture process is associated with the thermal energy required for regenerating the absorbent following saturation with CO2.6 Indeed, it has been reported that the energy penalty for regenerating the capture media is about 30% of the output of the power plant, most of which is associated with heating the large amount of water present to the regeneration temperature.2,3 Thus, materials that feature a lower energy penalty for regeneration, while maintaining high CO2 adsorption capacity and selectivity over the other components in the flue gas, are crucial for improving the commercial viability of CCS.
Recently, there has been significant interest in developing porous solid adsorbents that selectively take up large amounts of CO2 under the conditions applicable to CCS.7–10 Such adsorbents are particularly promising for post-combustion CO2 capture due to their significantly lower heat capacity compared to aqueous solutions, which is expected to reduce the amount of energy required for regeneration. In addition, capacity loss upon cycling and corrosion issues resulting from the use of aqueous amines could potentially be reduced by employing solid adsorbents. For applications in post-combustion CO2 capture, the materials should be designed to have a high adsorption capacity and selectivity for CO2 at a temperature near 40 °C and a partial pressure of near 0.15 bar.
Indeed, many porous solids have displayed promising CO2 adsorption properties for post-combustion capture applications. For example, mesoporous silica functionalized with a high density of alkylamines has shown a high CO2 adsorption capacity at low partial pressures owing to the presence of strong chemical interactions between CO2 and amine groups grafted to the silica surface.11–15 However, CO2 diffusion in these materials is often hindered by the organic groups present in the mesopores, resulting in long times for reaching equilibrium at a given partial pressure.12 Recently, metal–organic frameworks have been investigated as capture materials due to their large surface area and tunable pore surfaces, which together can facilitate selective binding of CO2 at high capacity.16–28 In particular, frameworks containing coordinatively unsaturated metal sites that can selectively interact with CO2 molecules have shown very high CO2 adsorption capacities at low pressure.24,29–31 In addition, alkylamine groups have been successfully introduced post-synthetically into several metal–organic frameworks as a means of further increasing the strength and selectivity of CO2 binding.32–35
The separation performance of metal–organic frameworks has often been compared to that of zeolites, which represent a conventional class of adsorbents for many gas and hydrocarbon separations.31,36–38 Despite the fact that zeolites are widely used as adsorbents for industrial gas separations, there is surprisingly little detailed information available on the CO2 adsorption properties of most zeolites, especially at conditions relevant to post-combustion capture (0.15 bar and 40–50 °C). Furthermore, many studies have utilized pelletized zeolite molecular sieves, which contain 10–20% of binders, rather than pure zeolite powders.39–45 As a result, these studies significantly underestimate the true performance of zeolites, making comparison to other solid adsorbents difficult. In particular, zeolite Na-X (or 13X) is considered to be one of the best performing zeolites for CO2 capture and is widely used as a benchmark for evaluating the performance of new solid adsorbents. Since zeolites have several advantages over metal–organic frameworks as adsorbents, including high stability and low production cost, it is important to thoroughly evaluate their CO2 adsorption performance under flue gas conditions to establish the most promising candidates for post-combustion CO2 capture and to direct future efforts in the discovery of improved materials.
The performance of adsorbents is generally evaluated using gas adsorption isotherms measured over a range of relevant temperatures and pressures. Acquiring adsorption isotherms for many samples at several temperatures, however, is extremely time-consuming and limits the ability to screen new materials rapidly. Hence, the utilization of an adsorption analyzer capable of measuring multiple samples simultaneously could greatly accelerate the screening process.
Herein, we evaluate a series of cation-exchanged zeolites for potential application in post-combustion CO2 capture using a custom-built high-throughput gas adsorption analyzer. Based on the CO2 and N2 adsorption isotherms obtained, the separation performance of the zeolites is evaluated in detail by determining CO2 adsorption capacities and CO2/N2 selectivity. Adsorption kinetics, an important consideration in designing a fixed-bed adsorber, are also investigated. Finally, the best performing zeolite from these analyses is directly compared with Mg2(dobdc) (dobdc4− = 1,4-dioxido-2,5-benzenedicarboxylate; Mg-MOF-74, CPO-27-Mg), one of the best reported solid adsorbents for post-combustion CO2 capture.
Experimental
Preparation and characterization of zeolites
Zeolites Na-A (LTA) and Na-X (FAU) were purchased as powders from Sigma-Aldrich. Ion-exchange was performed to generate aluminosilicate zeolites containing divalent extra-framework cations. Zeolites A and X (1.0 g, hydrated) were dispersed in 20 mL of aqueous (0.5 M) Mg(NO3)2 or Ca(NO3)2 solutions and stirred for 15 h at 60 °C. After collecting the solid by centrifugation, the ion-exchange procedure was repeated. Then, the solids were washed 5 times with 40 mL aliquots of deionized water and dried at 80 °C. The degree of ion-exchange was estimated by measuring the elemental composition (see Table S1†). Pure-silica (PS) MFI zeolite was synthesized hydrothermally, as previously reported,46,47 using tetraethylorthosilicate (TEOS, 98%, Acros) and tetrapropylammonium bromide (TPABr, 98%, Acros) as the silica source and structure directing agent, respectively. A 200 mL solution with a molar ratio of 1.0 TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 TPABr
0.1 TPABr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 NaOH
0.1 NaOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98 H2O was aged at 50 °C for 3 days and allowed to be crystallized at 110 °C over the course of another 3 days. The PS-MFI particles were repeatedly centrifuged and washed 5 times with 40 mL aliquots of deionized water to remove the extra structure directing agents, and then dried at 80 °C. Finally, calcination was performed at 550 °C for 8 h in air to remove any remaining structure-directing agent from the pores. All zeolites prepared, PS-MFI (SiO2), Na-A (NaAlSiO4),48 Mg-A (Na0.48Mg0.26AlSiO4), Ca-A (Na0.28Ca0.36AlSiO4), Na-X (NaAlSi1.18O4.36),49 Mg-X (Na0.38Mg0.31AlSi1.18O4.36) and Ca-X (Na0.06Al0.47Si1.18O4.36), were activated by heating at 250 °C for 24 h under a continuous nitrogen flow prior to gas adsorption measurements.
98 H2O was aged at 50 °C for 3 days and allowed to be crystallized at 110 °C over the course of another 3 days. The PS-MFI particles were repeatedly centrifuged and washed 5 times with 40 mL aliquots of deionized water to remove the extra structure directing agents, and then dried at 80 °C. Finally, calcination was performed at 550 °C for 8 h in air to remove any remaining structure-directing agent from the pores. All zeolites prepared, PS-MFI (SiO2), Na-A (NaAlSiO4),48 Mg-A (Na0.48Mg0.26AlSiO4), Ca-A (Na0.28Ca0.36AlSiO4), Na-X (NaAlSi1.18O4.36),49 Mg-X (Na0.38Mg0.31AlSi1.18O4.36) and Ca-X (Na0.06Al0.47Si1.18O4.36), were activated by heating at 250 °C for 24 h under a continuous nitrogen flow prior to gas adsorption measurements.
High-throughput gas adsorption analysis
All zeolites were loaded in a custom-built high-throughput gas adsorption analyzer designed and built by Wildcat Discovery Technologies Inc.50 (see Fig. S1 in the ESI†) that is capable of measuring single-component isotherms for up to 28 samples simultaneously. The operation of the system is based on a volumetric adsorption analysis in which the amount of gas uptake in adsorbents is calculated by subtracting the amount of gas in the bulk phase at equilibrium from the initial amount of gas dosed. The free space not occupied by the adsorbent in each sample well is initially measured by dosing a known amount of He. For adsorption measurements, all volumes are fully evacuated, and the dosing chambers are then pressurized to a specified pressure with adsorbate. After a series of valves between the dosing manifold and the dosing chambers are closed, valves connected to sample wells are opened in order to dose known amounts of gas to all adsorbents simultaneously. After waiting for the pressures measured in each dosing chamber to stabilize, the amounts of gases in the bulk phase at equilibrium can be calculated from the equilibrium pressures. The temperatures in the sample wells are controlled by a heating nest located at the bottom of the sample assemblies. In addition to equilibrium gas adsorption isotherms, adsorption kinetics can be measured with this instrument. The system is operated automatically using pre-programmed commands and methods.Before measuring adsorption isotherms, all samples were reactivated at 120 °C under vacuum for 10 h. Then, CO2 and N2 adsorption isotherms were measured over a range of temperatures and pressures. Once an adsorption measurement was completed, all zeolites were regenerated in the instrument by heating at 70 °C for 3 h under dynamic vacuum prior to the next series of measurements.
Evaluation of CO2 capture performance
To evaluate the CO2 capture performance for each zeolite, recorded CO2 and N2 isotherms were fit with adsorption models. Simple adsorption models, such as the single-site Langmuir (SSL) model, often do not adequately describe CO2 adsorption on heterogeneous surfaces. As such, a dual-site Langmuir (DSL) model was used to describe the CO2 adsorption of aluminosilicate zeolites over the entire pressure range: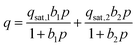 | (1) |
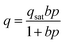 | (2) |
In this work, N2 adsorption was not measured at high pressures making it difficult to estimate the saturation loadings for N2. Thus, it is assumed that all adsorption sites in a zeolite are equally accessible to both CO2 and N2. Namely, the saturation capacity for CO2 (qsat,1 plus qsat,2 in DSL model) is equal to that for N2. According to a recent study, CO2 and N2 saturation capacities are fairly close to each other in many aluminosilicate zeolites, such that the ratio of qsat,N2 to qsat,CO2 for Na-A is about 1.03.31 This assumption is also likely reasonable for microporous metal–organic frameworks since the ratios reported are 0.84 and 1 for Mg2(dobdc) and MOF-177, respectively.31 The impact of errors resulting from this assumption are discussed in detail in the ESI.†
To estimate the CO2/N2 separation performance of each zeolite under conditions relevant to post-combustion CO2 capture, ideal adsorbed solution theory (IAST) was used to calculate CO2 and N2 selectivities. The detailed methodology for calculating the amount of CO2 and N2 adsorption from a mixture is described elsewhere.51 The accuracy of the IAST procedure has already been established for adsorption of a wide variety of gas mixtures in many different zeolites.52,53 The adsorption selectivity is defined as
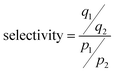 | (3) |
Isosteric heats of adsorption for CO2 were calculated using the SSL or DSL isotherm fits at 25, 40, and 55 °C. Two different methods for the calculation of isosteric heats of adsorption, Qst, from dual-site Langmuir models have been proposed.31,54 Since both methods give the same result, the method suggested by Mathias et al. was used here due to the simplicity of the calculation.54
Simulation of breakthrough in a fixed-bed adsorber
The performance of materials in a fixed-bed adsorber was predicted using a mathematical model. Assuming plug flow of a gas mixture through a fixed-bed maintained under isothermal conditions and negligible pressure drop, the partial pressures in the gas phase at any position and instant of time are obtained by solving the following set of partial differential equations for each of the species i in the gas mixture:55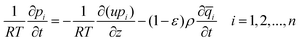 | (4) |
![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) i is the average loading within the zeolite crystals.
i is the average loading within the zeolite crystals.
Since the primary objective of this work is to compare the properties of adsorbents, rather than detailed process design, it is assumed that there are no intracrystalline diffusion limitations and that thermodynamic equilibrium prevails everywhere within the bed. The equilibrium loadings, qi, were estimated using a mixed-gas dual-site Langmuir model:
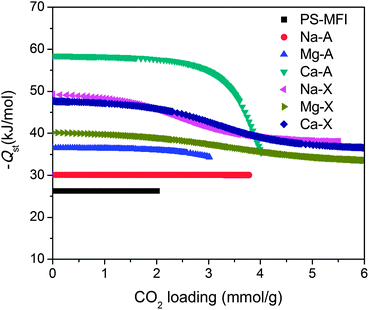
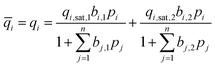 | (5) |
Equilibrium loadings calculated by eqn (5) are most accurate when the saturation loadings for different adsorbates are close to each other, which is the case here. Eqn (4) and (5) were solved based on methods described in the literature in order to simulate breakthrough curves for CO2 and N2 under relevant flue gas conditions.56,57 It is worth noting that when the differences in saturation loadings for species are large, such as for a CO2–H2 mixture, utilization of eqn (5) may result in a significant error. In such a case, combining eqn (4) and IAST has been proposed as a means of estimating qi,55 but this is not necessary for studying CO2 and N2 mixtures.
Diffraction data collection and structure determinations
Synchrotron X-ray diffraction (XRD) measurements were carried out at the Advanced Photon Source (APS) on the 1-BM-C materials diffractometer (E ≈ 20 keV, λ = 0.61072 Å) for zeolites Ca-A (12.5 mg) and Mg-A (14.4 mg) at approximately 100 K. Neutron powder diffraction (NPD) measurements on Ca-A (1.084 g) and Mg-A (1.321 g) at approximately 10 K and on Ca-A at 298 K were collected at the NIST Center for Neutron Research (NCNR) on the high-resolution diffractometer BT1 using a Ge(311) monochromator (λ = 2.0787(2) Å) and in-pile collimation of 60 min of arc. Activated (dehydrated) Ca-A and Mg-A samples were transferred into quartz capillaries for the XRD measurements and into cylindrical vanadium cans for NPD measurements within a helium glove box. In each instance after collecting data on the bare sample, the sample was dosed at ca. 250–300 K with an amount of CO2, calculate based on the total number of 8-ring sites per unit cell, using a custom built gas dosing manifold of known volume.All XRD and NPD data were analyzed using the Rietveld method, as implemented in EXPGUI/GSAS.58,59 Cation positions and occupancies were determined from the bare framework data, and the occupancies were subsequently carried over into CO2-dosed data refinements. Due to the difference in sodium cross-section and scattering lengths in X-ray versus neutron data, the XRD data was used to confirm the starting geometry and occupancy for the second sodium site (Na2) in Mg-A, in which Na2 is disordered within the center of the 8-ring pore window. The location of Na2 was then fixed at the resulting position for CO2-dosed NPD refinements. From both the bare XRD and NPD refinements, residual water was determined to be located in the central β cage near the divalent cations in both Ca-A and Mg-A. This was modeled as uniform scattering density and fixed from the initial structural refinements for the CO2-dosed refinements.
Results and discussion
Validation of the high-throughput gas adsorption system
To ensure the accuracy of the adsorption isotherm measurements on the new high-throughput instrument, the data obtained for Ca-A (or 5A) and PS-MFI were compared with data measured on a conventional gas adsorption analyzer. For this purpose, CO2 and N2 adsorption isotherms were measured at 25 °C using the high-throughput instrument and a Micromeritics ASAP® 2020 gas adsorption analyzer. Fig. 1 compares the isotherms obtained from the two instruments, demonstrating that the CO2 and N2 uptake measured on the high-throughput instrument is in good agreement with that measured by the ASAP® 2020 analyzer. It is important to note that while PS-MFI has a homogeneous surface lacking strong adsorption sites for CO2, zeolite Ca-A has strong adsorption sites that lead to significantly steeper CO2 adsorption at low pressures. In both cases, the difference in CO2 adsorption isotherms obtained from both instruments is within the error associated with the technique, and the high-throughput instrument is fully capable of measuring accurate adsorptions isotherms for both strongly and moderately adsorbing materials.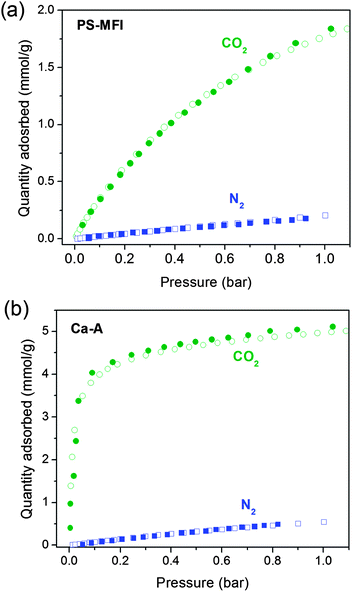 | ||
| Fig. 1 Pure component CO2 (green circles) and N2 (blue squares) gas adsorption isotherms for (a) PS-MFI and (b) Ca-A, as measured at 25 °C using the high-throughput gas adsorption analyzer (solid symbols) and, for comparison, a Micromeritics ASAP® 2020 gas adsorption analyzer (open symbols). | ||
CO2 and N2 adsorption in zeolites
Fig. 2 shows the CO2 and N2 adsorption isotherms measured on the high-throughput instrument for all of the zeolites assessed in this study at 25, 40, and 55 °C (only CO2 was measured at 55 °C). All 35 isotherms were obtained within just 3 days, illustrating the powerful performance of the high-throughput system. If the isotherms were instead measured in a serial manner with a typical adsorption analyzer, data acquisition would be expected to take at least 15 to 20 days. Significantly, the amount of CO2 adsorbed in several zeolites is higher than data reported in the literature under the same conditions. For example, the CO2 loadings in Na-X measured in this work are higher than literature reports where pelletized molecular sieves containing substantial amounts of binders were used as the samples instead of pure zeolite powders.39,40,42 The CO2 loadings in zeolite Ca-A are also higher than some reported data for the same reason.42,43,45,60,61 It is worth emphasizing that comparing CO2 adsorption isotherms obtained from pelletized zeolites to other unprocessed adsorbents, like metal–organic frameworks, should be avoided since the isotherms do not represent the intrinsic properties of the pure zeolites. In contrast, the gas uptake results in this work can be compared with studies of other adsorbents since pure zeolite powders were used as samples.62 It should be noted that, in some previous studies,63,64 CO2 uptakes in binderless or pure zeolites have been reported to be lower than those in the present work, presumably due to the differences in elemental compositions and the amount of crystal defects in zeolites.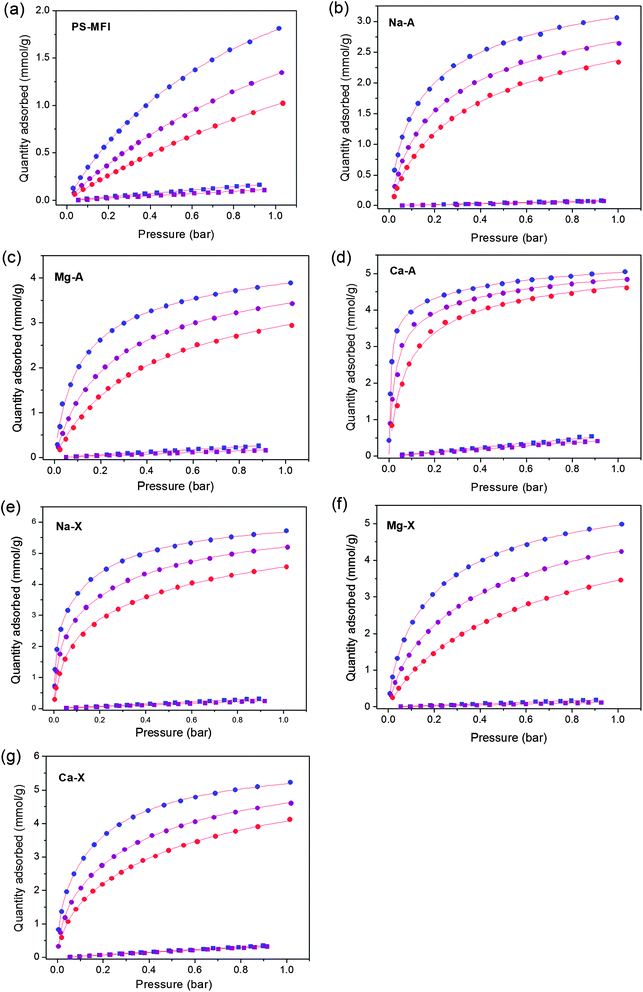 | ||
| Fig. 2 Pure component CO2 (circles) and N2 (squares) adsorption isotherms for (a) PS-MFI, (b) Na-A, (c) Mg-A, (d) Ca-A, (e) Na-X, (f) Mg-X and (g) Ca-X at 25 (blue), 40 (purple) and 55 (red) °C. Solid red lines correspond to DSL or SSL fits at each temperature (see text for details). | ||
In order to evaluate the CO2 capture performance of each zeolite, DSL or SSL fitting models were used to accurately describe the CO2 and N2 adsorption isotherms obtained at various temperatures. All fitted parameters are summarized in Tables S2–S6.† As expected, the pure silica zeolite PS-MFI showed a significantly lower CO2 adsorption capacity at low pressure due to the weak interactions between the inert silica surfaces and CO2 molecules. Additionally, zeolite Ca-A showed the steepest increase in CO2 uptake at low pressure, while the CO2 uptake at 1 bar was highest in Na-X. For comparison of the adsorption properties of the zeolites at conditions relevant to post-combustion capture from a dry flue gas, CO2 capacities at 0.15 bar and N2 capacities at 0.75 bar at 40 °C are listed for each material in Table S7.†
For a CO2 capture process, the amount of CO2 adsorbed from an actual flue gas mixture is more important, but difficult to measure experimentally. Therefore, the amounts of CO2 and N2 adsorbed from a hypothetical gas mixture consisting of 0.15 bar CO2 and 0.75 bar N2 at 40 °C were predicted by IAST, affording the results listed in Table 1. The CO2/N2 selectivities estimated by IAST are significantly different from those calculated from single-component CO2 and N2 isotherms (see Table S7†), since the latter does not consider the effect of gas molecules competing for adsorption sites on the pore surfaces. For all zeolites, the IAST CO2/N2 selectivity at 25 °C (see Table S8†) is higher than that measured at 40 °C, indicating that room temperature gas adsorption measurements overestimate the performance of adsorbents for post-combustion CO2 capture. This serves to emphasize the need to perform adsorption experiments at temperatures relevant to the desired application. In addition to its low CO2 adsorption capacity, PS-MFI exhibited the worst performance with respect to CO2/N2 selectivity and captured CO2 purity. Significantly, Ca-A, Na-X, and Na-A showed excellent CO2/N2 selectivities (over 200) resulting in high purities of 98% for the captured CO2. Note that the CO2/N2 selectivity of Na-X reported here is higher than the value in the literature where adsorption isotherms obtained from pelletized zeolites were used for the calculation.31 Interestingly, Ca-A exhibits the highest CO2 adsorption capacity at a partial pressure relevant for a post-combustion flue gas, even though the total pore volume available is less than in zeolite Na-X.65,66 Since the crystallographic density of zeolite Ca-A (1.514 g cm−3)48 is greater than Na-X (1.426 g cm−3),49 the difference in volumetric adsorption capacities between the materials is even greater than for the gravimetric capacity.
| Zeolite | Total gas uptake | CO2 purity (%) | CO2/N2 selectivity | |
|---|---|---|---|---|
| (mmol g−1) | (mmol cm−3) | |||
| PS-MFI | 0.371 | 0.667 | 78 | 18 |
| Na-A | 1.40 | 2.12 | 98 | 200 |
| Mg-A | 1.80 | 2.58 | 95 | 90 |
| Ca-A | 3.81 | 5.77 | 98 | 250 |
| Na-X | 3.38 | 4.82 | 98 | 310 |
| Mg-X | 2.01 | 2.67 | 97 | 170 |
| Ca-X | 2.65 | 3.71 | 96 | 120 |
The trends in the selectivity and the CO2 adsorption capacity at 0.15 bar for the different zeolites can be explained in part by examining the differences in the strength of the interaction of CO2 with the pore surface of each zeolite. As such, isosteric heats of adsorption, Qst, were calculated using the Clausius–Clapeyron equation and the fits for CO2 adsorption isotherms at 25, 40, and 55 °C. As shown in Fig. 3, Ca-A has by far the highest isosteric heat of adsorption at low CO2 loading. Furthermore, Qst for Ca-A remained constant near −58 kJ mol−1 before dropping off after a loading of near 3.2 mmol g−1, indicating that the strong interaction between CO2 and framework is maintained until a large number of accessible strong adsorption sites are saturated. The high CO2 adsorption capacity observed in Ca-A at 0.15 bar of CO2 is a direct result of this Qst behavior. In contrast, the lower Qst for PS-MFI, Na-A, and Mg-A result in relatively low CO2 uptakes at 0.15 bar, and, accordingly, lower selectivities. Note that the Qst values calculated from CO2 adsorption isotherms for pure Na-X and Ca-A powders in this work are higher than those calculated previously from data obtained using pelletized zeolites.40,45 Based on the measured CO2 capacities and IAST analysis, Ca-A appears to be the best candidate for application in post-combustion CO2 capture among the zeolites tested.
 | ||
| Fig. 3 Isosteric heats of adsorption, Qst, as a function of CO2 loading for zeolites. | ||
In addition to evaluating the equilibrium CO2 adsorption capacity and selectivity, the consideration of the kinetics of CO2 adsorption is also an important property when evaluating the performance of an adsorbent for post-combustion CO2 capture. Indeed, if CO2 diffusion through the pores is extremely slow, as has been observed in mesoporous silicas with high alkylamine loadings,12 the time required for each adsorption–desorption cycle will be increased, resulting in inefficient process rates and greater capture costs. Thus, intracrystalline CO2 diffusion rates should be high so as not to be a limiting factor in the overall performance of a CO2 capture process.
In this work, the rate of CO2 uptake was measured by monitoring the bulk phase pressure as a function of time after dosing the samples. As shown in Fig. 4, all zeolites except Na-A, which possesses the smallest pore windows (ca. 4 Å), showed rapid CO2 uptake, such that fractional uptakes were 97% or higher within 2 min of dosing CO2 into the zeolites. Although more detailed quantitative studies are necessary to compare the diffusion rates in different materials, this qualitative investigation may imply that the application of all zeolites except Na-A in CO2 adsorption processes will not be limited by slow CO2 diffusion in the pore channels.
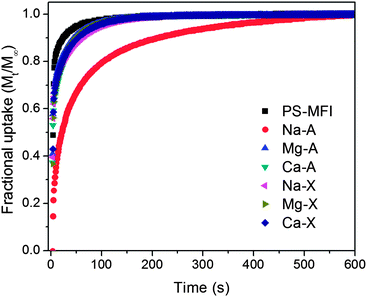 | ||
| Fig. 4 Fractional CO2 uptake as a function of time measured at 40 °C and 1 bar dosing pressure. | ||
Structural determination by X-ray and neutron powder diffraction
In order to understand the exceptional CO2 adsorption performance of Ca-A, X-ray and neutron diffraction studies were used to elucidate the detailed mechanism of CO2 adsorption in the zeolite. It is well-known that the majority of extra-framework Na+ cations are located at two sites in zeolite Na-A: (1) near the center of the 8-membered ring windows, and (2) near the 6-membered ring windows.67,68 Moreover, it has been previously shown that exchanging Ca2+ for Na+ results in the complete removal of Na+ from the 8-ring window site, with Ca2+ and any remaining Na+ cations occupying sites near the 6-ring windows.69 While the composition of the Ca-A sample used in this work is different than that in previously reported structural studies, neutron powder diffraction measurements and subsequent Rietveld refinements performed here reveal similar locations for the extra-framework cations. Indeed, Na+ is located just outside the 6-ring window of the β-cage, while Ca2+ is located in the plane of the 6-ring. As expected, the cations are disordered over the 6-rings such that a given 6-ring site may contain either a Ca2+ or Na+, but the refined site occupancies are in agreement with elemental analysis results. It is also important to note that Fourier difference maps do not show any residual electron density in the 8-ring windows, indicating complete removal of the Na+ cations from the 8-ring sites.Neutron powder diffraction data were further collected at sequential, in situ loadings of 0.75 and 1.5 CO2 molecules per 8-ring site (corresponding to loadings of 1.3 and 2.7 mmol g−1, respectively). Fourier difference maps revealed the adsorbed CO2 site positions, and Rietveld refinements provided a final determination of atomic coordinates and CO2 occupancy as a function of gas loading. At low loadings, CO2 adsorption occurs at two distinct sites, situated between two extra-framework cations at neighboring 6-rings (site A in Fig. 5) or at the center of the 8-ring (site B), a site similar to that previously observed in chabazites.70 Adsorption occurs simultaneously at each site with refined occupancies of 12.8% and 24.2% at the 0.75 loading for sites A and B, respectively, as measured at 10 K. Doubling the concentration of CO2 from 0.75 to 1.5 CO2 per 8-ring results in a near doubling of the occupancies at both sites A and B to 27.9% and 48.4%, respectively. Site B appears to be the stronger adsorption site based on the occupancy factors, since an equal affinity would be expected to lead to an equivalent population of the two sites.
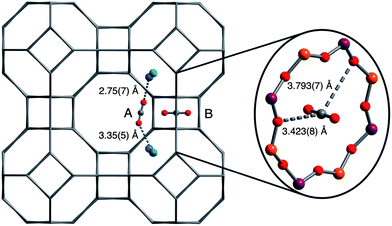 | ||
| Fig. 5 Structures associated with CO2 adsorption at sites A and B in zeolite Ca-A, as determined from neutron powder diffraction measurements at 10 K. Gray, red, blue, green, orange, and purple spheres represent C, O, Na, Ca, Al, and Si atoms, respectively. Note that cations in the 6-ring sites are disordered such that a given CO2 at site A may interact with two Na+ atoms, two Ca2+ atoms, or one Na+ atom and one Ca2+ atom (as depicted). A molecule of CO2 adsorbed in an 8-ring (site B) is shown at the right. | ||
Extracting the details of the CO2 binding at site A is complicated by the disorder of the extra-framework Ca2+ and Na+ cations over the 6-rings, wherein a given CO2 molecule at site A may interact with two Ca2+ ions, two Na+ ions, or one Ca2+ ion and one Na+ ion. Nevertheless, CO2 was observed in an end-on coordination geometry via both oxygen atoms to bridge two cations with an average Mn+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance of 3.35(5) and 2.75(7) Å for Ca2+ and Na+, respectively. In a manner similar to that recently observed for zeolite SSZ-13,70 CO2 adsorption also occurs at the center of the 8-ring windows, with the CO2 carbon centered in the window and interacting with the surrounding oxygen atoms of the 8-ring. Here, the closest CO2-framework interactions include C–O1 and C–O2, which are 3.423(8) and 3.793(7) Å, respectively. In addition, a reduction in the unit cell volume with increasing CO2 loading was observed as a result of a decrease in the size of the 8-ring window apertures via changes in the Si–O–Al angles. Data were also measured at 298 K for the higher loading, and the CO2 adsorption capacities and site geometries as well as extra-framework cation site geometries are extremely similar to those measured at 10 K, indicating that temperature does not significantly affect the site distribution or bonding characteristics in this system.
O distance of 3.35(5) and 2.75(7) Å for Ca2+ and Na+, respectively. In a manner similar to that recently observed for zeolite SSZ-13,70 CO2 adsorption also occurs at the center of the 8-ring windows, with the CO2 carbon centered in the window and interacting with the surrounding oxygen atoms of the 8-ring. Here, the closest CO2-framework interactions include C–O1 and C–O2, which are 3.423(8) and 3.793(7) Å, respectively. In addition, a reduction in the unit cell volume with increasing CO2 loading was observed as a result of a decrease in the size of the 8-ring window apertures via changes in the Si–O–Al angles. Data were also measured at 298 K for the higher loading, and the CO2 adsorption capacities and site geometries as well as extra-framework cation site geometries are extremely similar to those measured at 10 K, indicating that temperature does not significantly affect the site distribution or bonding characteristics in this system.
In order to better understand the high CO2 adsorption capacity of Ca-A at low pressures as compared to other cation-exchanged zeolites, a combination of X-ray and neutron powder diffraction data were also collected and analyzed for Mg-A. In agreement with previous diffraction studies,71 Mg2+ cations were found exclusively at the 6-ring sites, while Na+ cations were located at both the 6- and 8-ring windows. Significantly, 50% of all 8-ring sites were found to still contain Na+ cations, making these sites inaccessible for CO2 adsorption. At a low CO2 loading of 0.5 CO2 molecules per 8-ring site (1.0 mmol g−1), CO2 adsorption appears to occur preferentially at site A, bridging two extra-framework Mg2+ and/or Na+ cations with average Mn+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances of 3.12(6) and 2.67(6) Å, respectively, due to the partial blocking of site B. While CO2 adsorption does occur significantly at vacant 8-ring sites at higher loadings, only half of all 8-rings are available to act as strong CO2 binding sites. It is also important to note that less divalent cations are present at the 6-ring sites due to the smaller degree of ion exchange in Mg-A than in Ca-A. While it is difficult to determine the relative importance of each of these differences, the inferior CO2 adsorption performance of Mg-A compared to Ca-A, and the lower overall isosteric heat in Mg-A is likely due to a combination of (1) Na+ cations blocking access to 8-ring sites and increasing the overall 8-ring window diameter, (2) different ratios of M2+
O distances of 3.12(6) and 2.67(6) Å, respectively, due to the partial blocking of site B. While CO2 adsorption does occur significantly at vacant 8-ring sites at higher loadings, only half of all 8-rings are available to act as strong CO2 binding sites. It is also important to note that less divalent cations are present at the 6-ring sites due to the smaller degree of ion exchange in Mg-A than in Ca-A. While it is difficult to determine the relative importance of each of these differences, the inferior CO2 adsorption performance of Mg-A compared to Ca-A, and the lower overall isosteric heat in Mg-A is likely due to a combination of (1) Na+ cations blocking access to 8-ring sites and increasing the overall 8-ring window diameter, (2) different ratios of M2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ at the 6-ring sites, and (3) differences in the interactions of CO2 with an Mg2+ ion versus the larger Ca2+ ion. Efforts to increase the incorporation of Mg2+ to a level similar to Ca2+ are in progress and should allow for a better understanding of the precise CO2 adsorption mechanisms responsible for the different CO2 adsorption properties of each zeolite. Moreover, in view of the lighter weight and higher charge density of the Mg2+ ion relative to a Ca2+ ion, it is possible that the CO2 capture performance of Mg-A could surpass that of Ca-A if a fully exchanged form of the zeolite can be obtained.
Na+ at the 6-ring sites, and (3) differences in the interactions of CO2 with an Mg2+ ion versus the larger Ca2+ ion. Efforts to increase the incorporation of Mg2+ to a level similar to Ca2+ are in progress and should allow for a better understanding of the precise CO2 adsorption mechanisms responsible for the different CO2 adsorption properties of each zeolite. Moreover, in view of the lighter weight and higher charge density of the Mg2+ ion relative to a Ca2+ ion, it is possible that the CO2 capture performance of Mg-A could surpass that of Ca-A if a fully exchanged form of the zeolite can be obtained.
Relative performance of Ca-A and Mg2(dobdc)
The evaluation of this series of zeolites shows that Ca-A is currently the most promising candidate for post-combustion CO2 capture. Hence, it is useful to compare the properties of Ca-A with Mg2(dobdc), which is currently one of the best and most studied metal–organic frameworks for this application. Previously, we reported a detailed evaluation of the CO2 capture performance of Mg2(dobdc).31 Owing primarily to its larger surface area and a high density of exposed Mg2+ cations that act as strong CO2 adsorption sites, Mg2(dobdc) has a higher gravimetric CO2 uptake than zeolite Ca-A at all pressures. For example, at 0.15 bar of CO2 and 40 °C, the gravimetric CO2 uptake for Mg2(dobdc) and Ca-A is 5.57 and 3.72 mmol g−1, respectively. However, it is also important to take into account the significant difference in crystal densities between Mg2(dobdc) (0.911 g cm−3)29 and Ca-A (1.514 g cm−3) when comparing their CO2 capture performance, since the volumetric capacity is also an important consideration when designing a fixed-bed adsorber. Indeed, Fig. 6b demonstrates that Ca-A has a higher volumetric CO2 uptake (5.63 mmol cm−3) than Mg2(dobdc) (5.07 mmol cm−3) at 0.15 bar and 40 °C. The low-coverage isosteric heat of adsorption for CO2 in Ca-A (−58 kJ mol−1) is also higher than that of Mg2(dobdc) (−42 kJ mol−1). As a direct results, Ca-A has a higher IAST selectivity for CO2 over N2 of ca. 250, compared to the value of ca. 175 obtained for Mg2(dobdc). These selectivity values translate into CO2 purities of 98% and 97% in the adsorbed phases for Ca-A and Mg2(dobdc), respectively. Consequently, zeolite Ca-A has a greater volumetric CO2 adsorption capacity and CO2/N2 selectivity than Mg2(dobdc) at conditions relevant to post-combustion CO2 capture.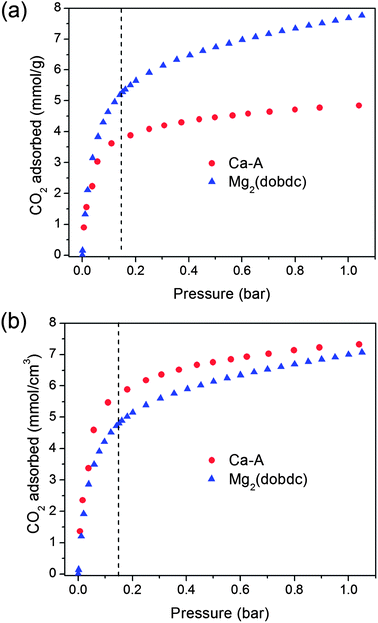 | ||
| Fig. 6 (a) Gravimetric and (b) volumetric CO2 adsorption capacities in zeolite Ca-A and Mg2(dobdc) at 40 °C. | ||
In addition to CO2 uptake and selectivity, the working capacity, corresponding to the actual amount of CO2 captured in an adsorption–desorption cycle, is a critical parameter in evaluating the potential performance of an adsorbent in a real process. Temperature-swing adsorption (TSA) is a particularly promising process for post-combustion CO2 capture, owing to difficulties with compressing or applying a vacuum to large volumes of a low-pressure flue gas stream, as would be required for pressure-swing or vacuum-swing adsorption.31,72 As such, the working capacity was estimated for Ca-A based on an idealized TSA cycle, where the working capacity corresponds to the difference between the amount of CO2 adsorbed at 0.15 bar and 40 °C and the amount of CO2 adsorbed at 1 bar and the desorption temperature. Here, a CO2 adsorption isotherm at 170 °C, the highest temperature reliably attainable in the high-throughput gas adsorption analyzer, was measured in order to estimate the working capacity (see Fig. 7). The resulting working capacity for Ca-A is 4.22 mmol cm−3 (2.79 mmol g−1), which is higher by volume than that obtained for Mg2(dobdc) (3.88 mmol cm−3 and 4.26 mmol g−1) under the same conditions. The working capacity of Ca-A, which has excellent thermal stability, could be further enhanced simply by increasing the desorption temperature.
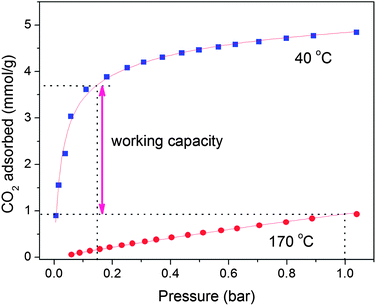 | ||
| Fig. 7 Working capacity of zeolite Ca-A in a simulated TSA process in which the adsorbed CO2 is desorbed at 170 °C. | ||
While capacities and selectivities are useful for the initial evaluation of adsorbents, in a real post-combustion CO2 capture process, the flue gas will likely pass over a large fixed-bed packed with the solid adsorbent. Breakthrough measurements with a gas mixture can provide a useful indication of the performance of an adsorbent in such a system. However, accurate measurements of this type are challenging, since variations in particle size and column packing can lead to difficulties in directly comparing breakthrough measurement results for different samples. Thus, breakthrough simulations, a convenient alternative, were performed for all of the zeolites studied here and for Mg2(dobdc), assuming a 0.15 bar CO2 and 0.75 bar N2 feed gas mixture at 40 °C (see Fig. S6†).55 The results for the most promising adsorbents, Ca-A and Mg2(dobdc), are plotted in Fig. 8, together with the breakthrough performance of PS-MFI for comparison. As expected, due to its lack of strong CO2 adsorption sites, CO2 breakthrough in PS-MFI occurs rapidly. In contrast, Ca-A and Mg2(dobdc) display significantly longer breakthrough times due to their high CO2 loading capacities at 0.15 bar CO2. Importantly, Ca-A shows an enhanced breakthrough performance compared to Mg2(dobdc) owing to the fact that the volumetric CO2 uptake has a greater influence than the gravimetric uptake in determining the performance in a fixed-bed adsorber. In addition, Ca-A adsorbs more CO2 (5.5 mmol cm−3) than Mg2(dobdc) (4.9 mmol cm−3) prior to breakthrough, which is defined here as when the CO2 concentration at the outlet is greater than 1 mol%.
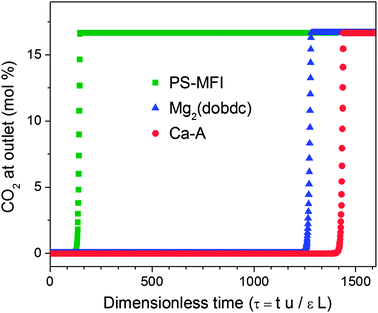 | ||
| Fig. 8 Simulated breakthrough curves for PS-MFI, Ca-A and Mg2(dobdc) at 40 °C with a gas mixture of 0.15 bar CO2 and 0.75 bar N2. | ||
Beyond its outstanding performance for post-combustion CO2 capture, zeolite Ca-A has several other advantages over metal–organic frameworks. Specifically, the precursor, zeolite LTA, can already be synthesized on a large scale from abundant mineral sources under mild conditions (as low as 60 °C in aqueous media) without the use of structure-directing agents or organic solvents.73 Thus, the production cost for zeolite Ca-A is expected to be far lower than that of Mg2(dobdc), which is not yet industrially produced on a large scale. Furthermore, zeolite LTA is a robust microporous solid which is widely used in many industrial separation processes as well as catalytic chemical reactions.74,75 As a result, many properties required for large-scale industrial operations, such as long-term stability and regenerability, are already well-established for zeolite Ca-A. Owing to its successful applications in many large-scale processes, Ca-A may be applied to post-combustion CO2 capture more easily than metal–organic frameworks, which have yet to be used in large-scale commercial applications.
Conclusions
The foregoing results provide an initial demonstration of the efficacy of a new high-throughput gas adsorption analyzer, capable of measuring 28 samples in parallel, through evaluation of the CO2 and N2 gas adsorption properties of a series of cation-exchanged zeolites. Among the materials assessed, Ca-A exhibits exceptional performance characteristics for the capture of CO2 from the dry flue gas of a coal-fired power plant, displaying a highly selective uptake of 5.63 mmol cm−3 (3.72 mmol g−1) of CO2 at 0.15 bar and 40 °C and rapid adsorption kinetics. These characteristics, together with the stability and ready availability of the material, suggest that zeolite Ca-A is the best current option for such an application. Results from X-ray and neutron powder diffraction experiments indicate its superior performance to arise from the strong binding of CO2 at two sites: within 8-ring windows of the framework and between two extra-framework cations located at neighboring 6-rings. Future efforts will focus on attempting to further improve upon the observed performance characteristics by adjusting the extent of exchange of Mg2+ or Ca2+ ions for the Na+ cations in zeolite LTA. In addition, a systematic study will be performed to investigate the relationship between elemental composition of aluminosilicate zeolites and their CO2 adsorption properties.Acknowledgements
This research was funded by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy (DoE). Use of the Advanced Photon Source (APS), an Office of Science User Facility operated for the U.S. DoE Office of Science by Argonne National Laboratory, was supported by the U.S. DoE under Contract DE-AC02-06CH11357. We thank Dr Greg Halder for help with the diffraction data collection on 1-BM-C at the APS and Dr Trudy Bolin and Dr Michael Pape for the use of the helium glovebox in APS Sector 9. We also thank NSF for providing graduate fellowship support for J.A.M., and the NIST National Research Council Postdoctoral Fellowship Research Associate program for support of M.R.H. and W.L.Q.Notes and references
- M. Z. Jacobson, Energy Environ. Sci., 2009, 2, 148–173 RSC.
- R. S. Haszeldine, Science, 2009, 325, 1647–1652 CrossRef CAS.
- J. D. Figueroa, T. Fout, S. Plasynski, H. McIlvried and R. D. Srivastava, Int. J. Greenhouse Gas Control, 2008, 2, 9–20 CrossRef CAS.
- S. M. Klara, R. D. Srivastava and H. G. McIlvried, Energy Convers. Manage., 2003, 44, 2699–2712 CrossRef CAS.
- E. J. Granite and H. W. Pennline, Ind. Eng. Chem. Res., 2002, 41, 5470–5476 CrossRef CAS.
- G. T. Rochelle, Science, 2009, 325, 1652–1654 CrossRef CAS.
- D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082 CrossRef CAS.
- S. Choi, J. H. Drese and C. W. Jones, ChemSusChem, 2009, 2, 796–854 CrossRef CAS.
- L.-C. Lin, A. H. Berger, R. L. Martin, J. Kim, J. A. Swisher, K. Jariwala, C. H. Rycroft, A. S. Bhown, M. W. Deem, M. Haranczyk and B. Smit, Nat. Mater., 2012, 11, 633–641 Search PubMed.
- F. Akhtar, Q. Liu, N. Hedin and L. Bergstrom, Energy Environ. Sci., 2012, 5, 7664–7673 RSC.
- J. C. Hicks, J. H. Drese, D. J. Fauth, M. L. Gray, G. Qi and C. W. Jones, J. Am. Chem. Soc., 2008, 130, 2902–2903 CrossRef CAS.
- J. H. Drese, S. Choi, R. P. Lively, W. J. Koros, D. J. Fauth, M. L. Gray and C. W. Jones, Adv. Funct. Mater., 2009, 19, 3821–3832 CrossRef CAS.
- W. Li, P. Bollini, S. A. Didas, S. Choi, J. H. Drese and C. W. Jones, ACS Appl. Mater. Interfaces, 2010, 2, 3363–3372 CrossRef CAS.
- S. Choi, M. L. Gray and C. W. Jones, ChemSusChem, 2011, 4, 628–635 CrossRef CAS.
- S. Choi, J. H. Drese, P. M. Eisenberger and C. W. Jones, Environ. Sci. Technol., 2011, 45, 2420–2427 CrossRef CAS.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef.
- S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS.
- R. Matsuda, R. Kitaura, S. Kitagawa, Y. Kubota, R. V. Belosludov, T. C. Kobayashi, H. Sakamoto, T. Chiba, M. Takata, Y. Kawazoe and Y. Mita, Nature, 2005, 436, 238–241 CrossRef CAS.
- A. R. Millward and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 17998–17999 CrossRef CAS.
- G. Ferey, Chem. Soc. Rev., 2008, 37, 191–214 RSC.
- R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981 CrossRef.
- P. L. Llewellyn, S. Bourrelly, C. Serre, A. Vimont, M. Daturi, L. Hamon, G. De Weireld, J. S. Chang, D. Y. Hong, Y. K. Hwang, S. H. Jhung and G. Ferey, Langmuir, 2008, 24, 7245–7250 CrossRef.
- J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- A. O. Yazaydin, R. Q. Snurr, T. H. Park, K. Koh, J. Liu, M. D. LeVan, A. I. Benin, P. Jakubczak, M. Lanuza, D. B. Galloway, J. J. Low and R. R. Willis, J. Am. Chem. Soc., 2009, 131, 18198–18199 CrossRef CAS.
- S. Keskin, T. M. van Heest and D. S. Sholl, ChemSusChem, 2010, 3, 879–891 CrossRef CAS.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T. H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781 CrossRef CAS.
- J. R. Li, J. Sculley and H. C. Zhou, Chem. Rev., 2012, 112, 869–932 CrossRef CAS.
- S. Xiang, Y. He, Z. Zhang, H. Wu, W. Zhou, R. Krishna and B. Chen, Nat. Commun., 2012, 3, 954 Search PubMed.
- D. Britt, H. Furukawa, B. Wang, T. G. Glover and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20637–20640 CrossRef CAS.
- S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2008, 130, 10870–10871 CrossRef CAS.
- J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Energy Environ. Sci., 2011, 4, 3030–3040 RSC.
- A. Demessence, D. M. D'Alessandro, M. L. Foo and J. R. Long, J. Am. Chem. Soc., 2009, 131, 8784–8785 CrossRef CAS.
- T. M. McDonald, D. M. D'Alessandro, R. Krishna and J. R. Long, Chem. Sci., 2011, 2, 2022–2028 RSC.
- S. Choi, T. Watanabe, T.-H. Bae, D. S. Sholl and C. W. Jones, J. Phys. Chem. Lett., 2012, 3, 1136–1141 Search PubMed.
- T. M. McDonald, W. R. Lee, J. A. Mason, B. M. Wiers, C. S. Hong and J. R. Long, J. Am. Chem. Soc., 2012, 134, 7056–7065 CrossRef CAS.
- R. Krishna and J. A. van Baten, Langmuir, 2010, 26, 3981–3992 CrossRef CAS.
- Z. R. Herm, J. A. Swisher, B. Smit, R. Krishna and J. R. Long, J. Am. Chem. Soc., 2011, 133, 5664–5667 CrossRef CAS.
- R. Krishna and J. M. van Baten, Phys. Chem. Chem. Phys., 2011, 13, 10593–10616 RSC.
- J.-S. Lee, J.-H. Kim, J.-T. Kim, J.-K. Suh, J.-M. Lee and C.-H. Lee, J. Chem. Eng. Data, 2002, 47, 1237–1242 CrossRef CAS.
- S. Cavenati, C. A. Grande and A. E. Rodrigues, J. Chem. Eng. Data, 2004, 49, 1095–1101 CrossRef CAS.
- Y. Belmabkhout, G. Pirngruber, E. Jolimaitre and A. Methivier, Adsorption, 2007, 13, 341–349 CrossRef CAS.
- Y. Wang and M. D. LeVan, J. Chem. Eng. Data, 2009, 54, 2839–2844 CrossRef CAS.
- Z. Liu, C. A. Grande, P. Li, J. Yu and A. E. Rodrigues, Sep. Sci. Technol., 2011, 46, 434–451 Search PubMed.
- P. Li and F. H. Tezel, J. Chem. Eng. Data, 2008, 53, 2479–2487 Search PubMed.
- L. M. Mulloth and J. E. Finn, Carbon Dioxide Adsorption on a 5A Zeolite Design for CO2 Removal in Spacecraft Cabins, NASA/TM-1998-208752, NASA Ames Research Center, Moffett Field, CA, 1998 Search PubMed.
- T. H. Bae, J. Q. Liu, J. S. Lee, W. J. Koros, C. W. Jones and S. Nair, J. Am. Chem. Soc., 2009, 131, 14662–14663 CrossRef CAS.
- T. H. Bae, J. Q. Liu, J. A. Thompson, W. J. Koros, C. W. Jones and S. Nair, Microporous Mesoporous Mater., 2011, 139, 120–129 CrossRef CAS.
- R. F. Lobo, Handbook of Zeolite Science and Technology, M. Dekker, New York, 2003, ch. 3 Search PubMed.
- D. H. Olson, J. Phys. Chem., 1970, 74, 2758–2764 CrossRef CAS.
- B. Li, S. S. Kaye, C. Riley, D. Greenberg, D. Galang and M. S. Bailey, ACS Comb. Sci., 2012, 14, 352–358 Search PubMed.
- A. L. Myers and J. M. Prausnitz, AIChE J., 1965, 11, 121–127 CrossRef CAS.
- R. Krishna, S. Calero and B. Smit, Chem. Eng. J., 2002, 88, 81–94 CrossRef CAS.
- R. Krishna and J. M. van Baten, Chem. Eng. J., 2007, 133, 121–131 CrossRef CAS.
- P. M. Mathias, R. Kumar, J. D. Moyer, J. M. Schork, S. R. Srinivasan, S. R. Auvil and O. Talu, Ind. Eng. Chem. Res., 1996, 35, 2477–2483 Search PubMed.
- R. Krishna and J. R. Long, J. Phys. Chem. C, 2011, 115, 12941–12950 CrossRef CAS.
- D. M. Ruthven, Pressure Swing Adsorption, VCH Publishers, New York, 1994 Search PubMed.
- R. T. Yang, Gas Separation by Adsorption Processes, Imperial College Press, Singapore, 1997 Search PubMed.
- A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Almos National Laboratory Report LAUR, 86, 784, 1994 Search PubMed.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- J. Merel, M. Clausse and F. Meunier, Ind. Eng. Chem. Res., 2007, 47, 209–215 Search PubMed.
- S. Pakseresht, M. Kazemeini and M. M. Akbarnejad, Sep. Purif. Technol., 2002, 28, 53–60 CrossRef CAS.
- D. Saha, Z. Bao, F. Jia and S. Deng, Environ. Sci. Technol., 2010, 44, 1820–1826 CrossRef CAS.
- J. A. C. Silva, K. Schumann and A. E. Rodrigues, Microporous Mesoporous Mater., 2012, 158, 219–228 Search PubMed.
- R. V. Siriwardane, M.-S. Shen, E. P. Fisher and J. A. Poston, Energy Fuels, 2001, 15, 279–284 CrossRef CAS.
- J. L. Stakebake and J. Fritz, J. Colloid Interface Sci., 1985, 105, 112–118 Search PubMed.
- U. D. Joshi, P. N. Joshi, S. S. Tamhankar, V. V. Joshi, C. V. Rode and V. P. Shiralkar, Appl. Catal., A, 2003, 239, 209–220 CrossRef CAS.
- J. M. Adams, D. A. Haselden and A. W. Hewat, J. Solid State Chem., 1982, 44, 245–253 CrossRef CAS.
- J. J. Pluth and J. V. Smith, J. Am. Chem. Soc., 1980, 102, 4704–4708 CrossRef CAS.
- J. M. Adams and D. A. Haselden, J. Solid State Chem., 1984, 51, 83–90 CrossRef CAS.
- M. R. Hudson, W. L. Queen, J. A. Mason, D. W. Fickel, R. F. Lobo and C. M. Brown, J. Am. Chem. Soc., 2012, 134, 1970–1973 CrossRef CAS.
- J. M. Adams and L. V. C. Rees, J. Solid State Chem., 1986, 62, 184–190 Search PubMed.
- M. Ishibashi, H. Ota, N. Akutsu, S. Umeda, M. Tajika, J. Izumi, A. Yasutake, T. Kabata and Y. Kageyama, Energy Convers. Manage., 1996, 37, 929–933 CrossRef CAS.
- H. E. Robson, Verified Syntheses of Zeolitic Materials, Elsevier, Amsterdam, 2001 Search PubMed.
- P. Payra and P. K. Dutta, Handbook of Zeolite Science and Technology, M. Dekker, New York, 2003, ch. 1 Search PubMed.
- S. Sircar and A. L. Myers, Handbook of Zeolite Science and Technology, M. Dekker, New York, 2003, ch. 22 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Characterization of zeolites, calculations, fitting parameters, breakthrough simulations, tables of refinement details. See DOI: 10.1039/c2ee23337a |
| This journal is © The Royal Society of Chemistry 2013 |
