Constructing asymmetric gradient structures to enhance the energy storage performance of PEI-based composite dielectrics†
Dong
Yue
ab,
Wenchao
Zhang
*ab,
Puzhen
Wang
ab,
Yong
Zhang
ab,
Yu
Teng
ab,
Jinghua
Yin
 ab and
Yu
Feng
ab and
Yu
Feng
 *ab
*ab
aKey Laboratory of Engineering Dielectrics and Its Application, Ministry of Education, Harbin University of Science and Technology, Harbin, 150080, P.R. China. E-mail: zhangwenchao@hrbust.edu.cn; fengyu@hrbust.edu.cn
bSchool of Electrical and Electronic Engineering, Harbin University of Science and Technology, Harbin, 150080, P.R. China
First published on 17th November 2023
Abstract
Enhancing the high electric field resistance and energy storage capacity of polymer dielectrics has been a long-standing challenge for the iterations of power equipment. Synergistic inhibition of carrier injection and transport is vital to energy storage performance improvement. Herein, promising polymer polyetherimide (PEI) was employed as a matrix and wider bandgap boron nitride nanosheets (BNNSs) were used as a reinforcing filler. Utilizing high-throughput stochastic breakdown simulations with the distribution characteristics of BNNSs as parameters, a series of topological gradient structures with the potential to enhance performance were obtained, thereby shortening the experimental cycle. Changing the BNNS distribution of symmetric/asymmetric and positive/inverse gradients, as well as the total and gradient contents of BNNSs, means that the position and condition of the surface barrier layer and central hinder layer change, which influences the energy storage performance of the polymer at room temperature and high temperature. Remarkably, the asymmetric gradient structure composite dielectrics exhibited excellent performances. Among them, the PEI-based composite dielectric with 2 vol% BNNS asymmetric inverse gradient distribution (gradient content of 1 vol%) achieved energy densities of 8.26 and 4.78 J cm−3 at room temperature and 150 °C, respectively. The asymmetric gradient structure design strategy holds great promise for optimizing the energy storage capacity of polymer dielectric capacitors.
New conceptsThis work demonstrates a novel design approach for polymer dielectrics with asymmetric gradient structures. By adjusting the distribution characteristics of inorganic fillers, while considering the carrier injection and transport mechanisms, the surface barrier layer and internal hinder layer in different positions and states can be constructed. The combination of simulation and experiment intelligently and effectively selects the optimal range of parameters and results in a asymmetric gradient composite dielectric with significantly improved energy storage performance. This route holds potential for application in more polymer systems and provides a new composite structure preparation strategy for electrical equipment operating in different environments. |
1. Introduction
Breakthrough and proliferation of energy storage technology will enable energy distribution and adaptation across time and space, which is revolutionary for the generation and consumption of energy.1–3 Dielectric capacitors possess a high power density and rapid charge/discharge ability within a short time, making them extensively applicable in domains such as high-power electronic devices, new energy vehicles, and grid storage systems.4–6 Compared to inorganic dielectric capacitors, polymer dielectric capacitors exhibit characteristics such as high breakdown strength (Eb), low dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), and excellent processability, providing a broader scope for the structural design of dielectric film capacitors.7–9 However, polymer dielectric capacitors suffer from relatively low energy storage density (Ue), which limits their practical applications. The most typical representative of commercial dielectric capacitors, biaxially oriented polypropylene (BOPP), exhibits an Ue of only 2–3 J cm−3, impeding the development of dielectric film capacitors towards miniaturization and integration. In practical applications, linear dielectrics are desirable since the stored energy in them can be discharged to the utmost extent. The Ue of a dielectric capacitor in the linear approximation is given by Ue = 1/2ε0εrEb2 with ε0 as the vacuum dielectric constant (8.85 × 10−12 F m−1) and εr as the relative dielectric constant. It can be seen that the Ue of the dielectric depends on both εr and Eb. In addition, in linear dielectrics, the Ue is positively correlated with the square of the Eb, which indicates that the Eb has a greater driving effect on the Ue than the εr.
δ), and excellent processability, providing a broader scope for the structural design of dielectric film capacitors.7–9 However, polymer dielectric capacitors suffer from relatively low energy storage density (Ue), which limits their practical applications. The most typical representative of commercial dielectric capacitors, biaxially oriented polypropylene (BOPP), exhibits an Ue of only 2–3 J cm−3, impeding the development of dielectric film capacitors towards miniaturization and integration. In practical applications, linear dielectrics are desirable since the stored energy in them can be discharged to the utmost extent. The Ue of a dielectric capacitor in the linear approximation is given by Ue = 1/2ε0εrEb2 with ε0 as the vacuum dielectric constant (8.85 × 10−12 F m−1) and εr as the relative dielectric constant. It can be seen that the Ue of the dielectric depends on both εr and Eb. In addition, in linear dielectrics, the Ue is positively correlated with the square of the Eb, which indicates that the Eb has a greater driving effect on the Ue than the εr.
Adding inorganic materials with different physical and chemical properties into the polymer matrix serves as a common strategy for reinforcement.10 Non-0D filler orientation in the matrix can further optimize the performance by mitigating electric field distortion and increasing breakdown path tortuosity.11 Notably, 2D nanosheet inorganic fillers such as boron nitride (BN) and molybdenum sulfide (MoS2) exhibit a remarkable ability to block the breakdown path in a wider region.12,13 Nevertheless, it is difficult to inhibit both carrier injection and transport in this approach, resulting in limited performance improvements. Despite efforts to modify the surface of inorganic fillers to further improve Ue by strengthening the organic–inorganic interface, these often come at the cost of cumbersome processes. The multi-layer structure design strategy provides more imagination for performance improvement.14–18 The layer structure design can give different functional properties to each layer, and the mesoscopic interface formed between the adjacent layers can also block the breakdown path, twisting the breakdown path between layers. Bai et al.19 proposed a sandwich-structured polymer composite dielectric composed of a polarization layer and an insulating layer, with the multi-layer structure and filler synergy achieving the Ue enhancement. Jiang et al.20 introduced a structured design of multilayered polymer composite dielectrics capable of integrating the inhibited effects of dielectric/electrode and dielectric/dielectric interfaces on charge injection and migration, remarkably enhancing the Eb and Ue. However, another challenge was exposed, as the dielectric performance varies when adjacent layers have different functionalities, resulting in a dielectric mismatch between layers. This leads to local electric field distortion and severe carrier transport. The multi-layer gradient structure refines the spatial distribution and breaks this barrier.21–23 Jiang et al.24 designed the gradient distribution strategy of BaTiO3 in the P(VDF–HFP) matrix by using the improved electrospinning process. The gradient structure effectively delayed the breakdown path development. Our previous work has also demonstrated that the gradient structure greatly improved the energy storage performance of the polymer.25,26
Hence, in this paper, a performance enhancement strategy by adjusting the BNNS distribution characteristics in the PEI matrix is proposed. It is proven that the function of the surface barrier layer and central hinder layer at both carrier injection and transport is to reduce the distance between the functional layers, which can lower the carrier acceleration distance and energy after acceleration. Importantly, the composite dielectrics with an asymmetric inverse structure exhibit higher withstand breakdown and energy storage capacity, and present outstanding performance even at high temperature. This work pointed out the importance of a topological gradient structure and different functional layer positions. It does not involve more complicated processes of inorganic filler modification or lengthy technical challenges in new monomer development, and provides a new design route for the development and mass production of high-energy storage polymer dielectrics.
2. Experimental section
2.1 Materials
Polyetherimide (PEI) was provided by PolyK Technologies. Boron nitride nanosheets (BNNSs) were provided by Nanjing Suzhan Intelligent Technology Co., Ltd. 1-Methyl-2-pyrrolidinone (NMP) was provided by Tianjin Bailunsi Biotechnology Co., Ltd.2.2 Preparation of the polymer dielectrics
As shown in Fig. S1 (in the ESI†), a certain amount of BNNSs was taken and dispersed in the NMP solution by sonication. Then, the PEI particles were added to the above dispersion in proportion, heated and stirred until completely dissolved. The obtained mixed solution was placed in a vacuum oven to discharge the bubbles. The mixed solutions with different BNNS contents were transferred to syringes, and the mixed solutions underwent high-speed directional electrospinning in the designed gradient order layer by layer at an electric field of 0.2 kV mm−1 and the directional rotary receiver speed of 2000 rpm. The as-spun fiber mats were dried to remove the organic solvents. They were hot-pressed at 220 °C for 5 min under a pressure of 15 MPa and then quenched in ice water to finally obtain dense gradient composite dielectrics.2.3 Microstructure characterization and performance measurement
The morphology and elemental mapping of nanosheets were measured by transmission electron microscopy (TEM, FEI Tecnai G2 F20). The cross-sectional morphology and elemental mapping of the polymer composite dielectrics were characterized by scanning electron microscopy (SEM, Hitachi SU8020). The phase structure of the nanosheets and polymer composite dielectrics was measured by X-ray diffraction (XRD, PANalytical Empyrean). The chemical construction of the polymer composite dielectrics was characterized by Fourier transform infrared spectroscopy (FT-IR, Bruker Vector-22). The luminescence intensity of the polymer composite dielectrics was measured with a photoluminescence test system (PL, FLS1000). The Al electrodes (9 mm and 3 mm in diameter) were evaporated on two sides of the polymer composite dielectrics for the following electric measurements. The dielectric constant, dielectric loss, and AC conductivity measurements of the polymer composite dielectrics were performed using a Concept 40 broadband dielectric spectrometer at room temperature and high temperature from 1 Hz to 106 Hz. The breakdown and energy storage performances of the polymer composite dielectrics at room temperature and high temperature were investigated using a DC breakdown test system (a voltage ramp of 500 V s−1) and a ferroelectric polarized loop test system (at 102 Hz) from PolyK Technologies, respectively.2.4 Stochastic breakdown model
A modified stochastic model27 was employed based on the one proposed by Niemeyer et al.28 to study the internal electric field distribution and breakdown path development of the polymer dielectrics under the applied electric field. In the stochastic breakdown model, the breakdown probability P(r) is written as: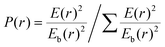 | (1) |
3. Results and discussion
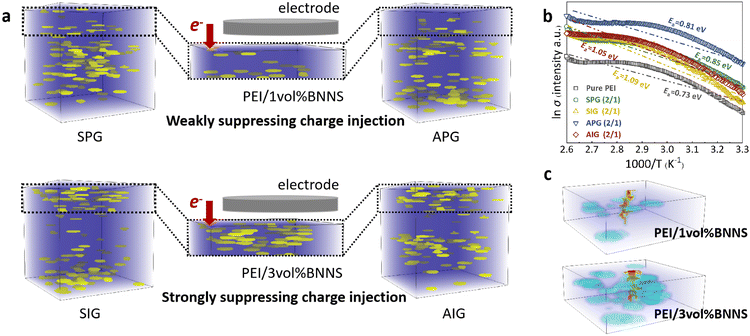
Fig. 1a depicts the schematics of the different topological gradient structures. Through adjustment of the BNNS distribution within the matrix, a symmetric positive or inverse gradient structure is formed, with the content changing from both sides towards the center gradient. Additionally, an asymmetric positive or inverse gradient structure is created, with the content increasing or decreasing from the top towards the center gradient, and continuing to increase or decrease from the center towards the bottom content. Before the experiment began, high-throughput stochastic breakdown simulation was used to verify the feasibility of the experiment design and find the optimal parameter range to shorten the experiment cycle. The total content and gradient content of BNNSs are set at 0.5, 1, 1.5, 2, 2.5, 3, 3.5, and 4 vol%, respectively, to achieve 144 various topological gradient structures. Subsequently, it is named by combining the symmetric/asymmetric (S/A), positive/inverse (P/I), gradient (G), and total content and gradient content of BNNSs. For example, the AIG (2/1) composite dielectric refers to an asymmetric inverse gradient composite dielectric with a BNNSs total content of 2 vol% and a BNNSs gradient content of 1 vol%. Fig. S2–S5 (in the ESI†) show the simulated temporal development of the breakdown fraction of different PEI-based composite dielectrics, while Fig. 1b shows the improvement or decline degree of all composite structures compared with the PEI matrix. The breakdown path development is obviously restricted via constructing a 3D topological structure, resulting in varying degrees of improvement of breakdown performance. Meanwhile, the improvement in the breakdown performance is weak at small or large total content of BNNSs, and the difference in improvement between adjacent gradient contents of BNNSs is indistinguishable. Hence, the total content and gradient content of BNNSs were considered 1, 2, and 3 vol% in the subsequent experiments, respectively. The improvement mechanism of the topological gradient structure with respect to the energy storage performance was investigated across four dimensions: total content and gradient content of BNNSs, symmetric gradient and asymmetric gradient, positive gradient and inverse gradient.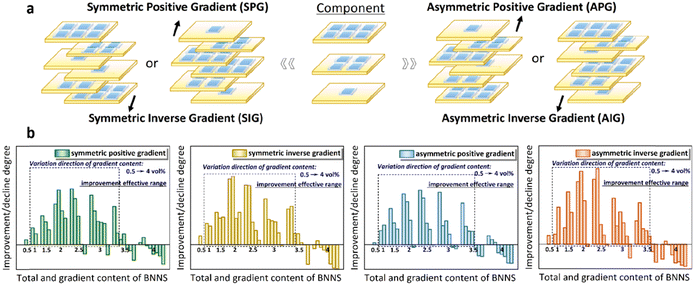 | ||
| Fig. 1 (a) Design concept of PEI-based composite dielectrics with different topological gradient structures. (b) Improvement or decline degree of all composite structures compared with the matrix. | ||
Fig. 2a shows the TEM image of BNNSs, which can be seen to exhibit a distinct 2D sheet structure with a size of about 100 nm. Elemental mappings show the distribution of B and N elements, which is in perfect agreement with that in the selected scan area, as shown in Fig. 2b–d. The AFM image shows that the thickness of BNNSs is ∼10 nm (Fig. S6 in the ESI†). It can be observed from the XRD pattern that the diffraction peaks corresponding to BNNSs at 26.5°, 41.6°, and 55° correspond to (002), (100), and (004) crystal planes, respectively (Fig. S7 in the ESI†). The SEM images of PEI-based composite dielectrics with different topological gradient structures are shown in Fig. 2e. The alternating high-speed directional electrospinning process enables precise control over the components of the topological gradient structure owing to manipulating the spinning time of each layer, while ensuring consistent hot-pressing conditions. All PEI-based composite dielectrics have a thickness of ∼12 μm, exhibit a high-density structure and lack evident defects such as stratification or holes. Elemental mappings were performed to visually observe the distribution characteristics of BNNSs in different gradient structures, as shown in Fig. 2e. BNNSs doping content in the symmetric positive gradient structure increases from both sides to the center, forming a “Λ” shape; BNNSs doping content in the symmetric inverse gradient structure decreases from both sides to the center, forming a “V” shape; BNNSs doping content in the asymmetric positive gradient structure first increases from the top to the center, then rapidly decreases, and increases again from the center to the bottom; BNNSs doping content in the asymmetric inverse structure demonstrates an inverse pattern, and BNNSs doping content decreases from the top to the center, followed by a rapid increase, and then another decrease from the center to the bottom. The elemental mapping results confirm that the prepared PEI-based composite dielectrics with different gradient structures conform to the expected design and distribution characteristics.
 | ||
| Fig. 2 The TEM image (a) and elemental mappings (b)–(d) of the BNNSs. (e) The cross-sectional SEM images and elemental mappings of the gradient composite dielectrics. | ||
The XRD patterns of all PEI-based composite dielectrics show comparable structural characteristics (Fig. S8 in the ESI†). The broad scattering peak observed around 2θ = 23° corresponds to the characteristic diffraction peak of the PEI matrix. With an increase in the BNNSs total content, the peak position of PEI-based composite dielectrics gradually shifts to the left. According to Bragg's law:
nλ = 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
Fig. S10 (in the ESI†) shows the εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curves with respect to frequency for pure PEI and PEI-based composite dielectrics. The εr of all dielectrics continuously decreases with increasing frequency, which is attributed to the dipole orientation polarization having difficulty keeping up with the external electric field at high frequency, resulting in an inability to establish polarization in time. The tan
δ curves with respect to frequency for pure PEI and PEI-based composite dielectrics. The εr of all dielectrics continuously decreases with increasing frequency, which is attributed to the dipole orientation polarization having difficulty keeping up with the external electric field at high frequency, resulting in an inability to establish polarization in time. The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ tends to first decrease and then increase with increasing frequency as the change time of the electric field becomes shorter as the frequency increases, making it difficult for the electrons in the dielectric to move with it. However, the inherent loss increases as the frequency continues to increase, leading to a gradual rise in tan
δ tends to first decrease and then increase with increasing frequency as the change time of the electric field becomes shorter as the frequency increases, making it difficult for the electrons in the dielectric to move with it. However, the inherent loss increases as the frequency continues to increase, leading to a gradual rise in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ.30 The εr and tan
δ.30 The εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 102 Hz of all dielectrics were extracted, and a histogram was plotted, as shown in Fig. 3. Compared with pure PEI, PEI-based composite dielectrics with gradient structures exhibit varying degrees of enhancement in εr, which is attributed to the enhanced interface polarization provided by the micro-interface between the filler and matrix and the mesoscopic interface of the layer structure. The εr of the gradient composite dielectrics increases constantly with the increase in the total content of BNNSs. The total content plays a decisive role in increasing the εr with the same filler and layer numbers. Furthermore, increasing the total content means a higher number of BNNSs in the gradient composite dielectric and an increase in the interface numbers between the organic and inorganic phases, which improves the interfacial polarization. With the gradient content of BNNSs increasing, the εr of the gradient composite dielectric initially increases and then decreases because the component units with a higher gradient content often contain single-layer PEI-based composite dielectrics with a higher BNNSs content, which can contribute to higher polarization (Fig. S11 in the ESI†). However, the excessively high gradient content compelled a dense distribution of BNNSs, leading to larger interfacial charge accumulation and charge obstruction within the dielectric, which decreases the εr.
δ at 102 Hz of all dielectrics were extracted, and a histogram was plotted, as shown in Fig. 3. Compared with pure PEI, PEI-based composite dielectrics with gradient structures exhibit varying degrees of enhancement in εr, which is attributed to the enhanced interface polarization provided by the micro-interface between the filler and matrix and the mesoscopic interface of the layer structure. The εr of the gradient composite dielectrics increases constantly with the increase in the total content of BNNSs. The total content plays a decisive role in increasing the εr with the same filler and layer numbers. Furthermore, increasing the total content means a higher number of BNNSs in the gradient composite dielectric and an increase in the interface numbers between the organic and inorganic phases, which improves the interfacial polarization. With the gradient content of BNNSs increasing, the εr of the gradient composite dielectric initially increases and then decreases because the component units with a higher gradient content often contain single-layer PEI-based composite dielectrics with a higher BNNSs content, which can contribute to higher polarization (Fig. S11 in the ESI†). However, the excessively high gradient content compelled a dense distribution of BNNSs, leading to larger interfacial charge accumulation and charge obstruction within the dielectric, which decreases the εr.
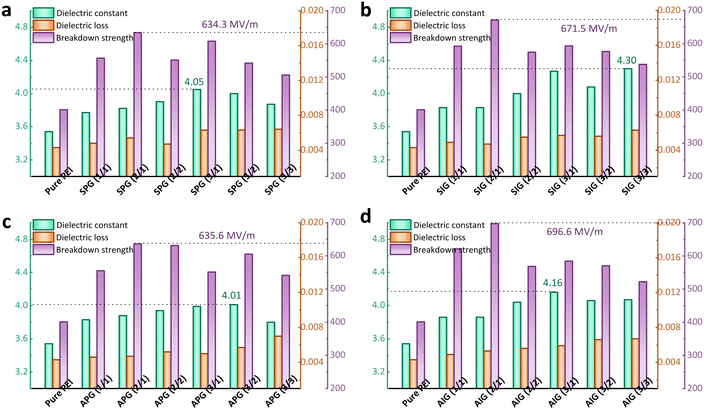 | ||
| Fig. 3 The dielectric constant and dielectric loss at 102 Hz, as well as the breakdown strength of (a) SPG, (b) SIG, (c) APG, and (d) AIG composite dielectrics. | ||
It is noted that the SIG (3/3) composite dielectric with symmetric inverse gradient obtains the highest εr of 4.30 at 102 Hz, which is 1.2 times that of pure PEI. The distinction from the above conclusion is that the symmetric inverse gradient structure leads to the dispersion of BNNSs on both sides of the gradient composite dielectric. This distribution lowers the probability of agglomeration and charge accumulation, resulting in a more homogeneous electric field within the composite dielectric. Furthermore, the inverse gradient makes the outermost region near the upper electrode have a higher BNNSs content, which makes the surface of the gradient composite dielectric have a higher responsiveness to the electric field. This has also been demonstrated in asymmetric gradient composite dielectrics, i.e., the εr of AIG composite dielectrics is higher than that of APG composite dielectrics. The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and AC conductivity (σ) of all gradient composite dielectrics are maintained at a lower level owing to the wider band gap, lower tan
δ and AC conductivity (σ) of all gradient composite dielectrics are maintained at a lower level owing to the wider band gap, lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, polar B–N chemical bond, and nanosheet structure (Fig. S10 and S12 in the ESI†).
δ, polar B–N chemical bond, and nanosheet structure (Fig. S10 and S12 in the ESI†).
The two-parameter Weibull statistical distribution function was used to calculate the characteristic breakdown strength based on the cumulative breakdown probability, and the equation can be described as follows:
ln(−ln(1 − P(E))) = β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(E) − β ln(E) − β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Eb) ln(Eb) | (3) |
At the same total content and gradient content of BNNSs, the Eb of PEI-based composite dielectrics with the inverse gradient is higher than that with the positive gradient. The inverse gradient structure makes the BNNSs content decrease gradually from the upper surface to the center. As a result, large quantities of BNNSs are distributed near the surface contacting the electrode, which effectively raises the injection barrier height. The Eb of a reasonable asymmetric gradient structure will also be higher than that of a symmetric gradient structure under the same conditions. After the carrier crosses the barrier and is injected into the interior, the voltage sustained inside gradually increases as the acting time of the applied electric field increases, which causes an increase in the carrier migration rate. The breakdown path develops to the region near the bottom electrode inevitably weakening the contribution of the inorganic hinder layer. Hence, it can achieve better breakdown performance by effectively blocking carrier transport in the early and middle stages. Correspondingly, the asymmetric inverse gradient structure adjusts the BNNSs content distribution to inhibit the breakdown path development on the upper surface and in the center during the carrier's early and middle transport processes, and maximally inhibits the carrier migration rate. Among all the topological gradient dielectrics, the AIG (2/1) composite dielectric obtains the highest Eb of 696 MV m−1, which surpasses the Eb of SIG (2/1) and APG (2/1) composite dielectric, significantly enhancing the withstanding high electric field capability of polymer dielectric. At the same time, Fig. S13 (in the ESI†) also shows that all PEI-based composite dielectrics with a gradient structure exhibit high β values (>10), indicating higher performance reliability, which reflects the excellent compactness achieved by the alternate high-speed electrospinning process combined with the hot-pressing process.
The typical electric displacement dependence of applied electric field (D–E) loops of pure PEI and gradient composite dielectrics with elevated electric fields is shown in Fig. S16–S19 (in the ESI†). The relationship between the polarization strength and electric field is approximately linear, and the topological gradient structure significantly optimizes the polarization and withstanding electric field capabilities of the PEI matrix. The Ue and the corresponding energy storage efficiency (η) of the polymer dielectrics were calculated through the D–E loops and are shown in Fig. 4. Based on the synergistic enhancement of εr and Eb, PEI-based composite dielectrics with a gradient structure achieve higher Ue. Furthermore, the improvement in Ue of gradient composite dielectrics is closely related to the enhancement of Eb since the square of the Eb has a positive correlation with the Ue, and the nanosheets limit the enhancement of polarization by restricting the end group steering of the PEI matrix. The AIG (2/1) composite dielectric achieved the highest Ue of 8.26 J cm−3, which is 2.98 times that of pure PEI (2.77 J cm−3). More precisely, the excellent ability to inhibit carrier injection and transport simultaneously, as well as the response ability of a higher BNNSs content near the upper electrode to the electric field, promotes the Ue of the AIG (2/1) composite dielectric significantly. The η of all polymer dielectrics gradually decreases with increasing electric field since the energy loss is caused by the space charge effect. Because of a certain degree of correlation between the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and η of the polymer,36 most gradient composite dielectrics maintain a higher η of ∼90% benefit from the lower tan
δ and η of the polymer,36 most gradient composite dielectrics maintain a higher η of ∼90% benefit from the lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. Nevertheless, certain composite dielectrics exhibit lower η, with some experiencing an unavoidable decline under high electric fields, while others are due to their gradient composition. The single-layer PEI-based composite dielectric with a higher BNNSs content leads to higher polarization, and the tan
δ. Nevertheless, certain composite dielectrics exhibit lower η, with some experiencing an unavoidable decline under high electric fields, while others are due to their gradient composition. The single-layer PEI-based composite dielectric with a higher BNNSs content leads to higher polarization, and the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ also increases (Fig. S11 in the ESI†). Consequently, the gradient structure containing the single-layer composite dielectric with a higher BNNSs content exhibits a slightly lower η, but still higher than ∼85%.
δ also increases (Fig. S11 in the ESI†). Consequently, the gradient structure containing the single-layer composite dielectric with a higher BNNSs content exhibits a slightly lower η, but still higher than ∼85%.
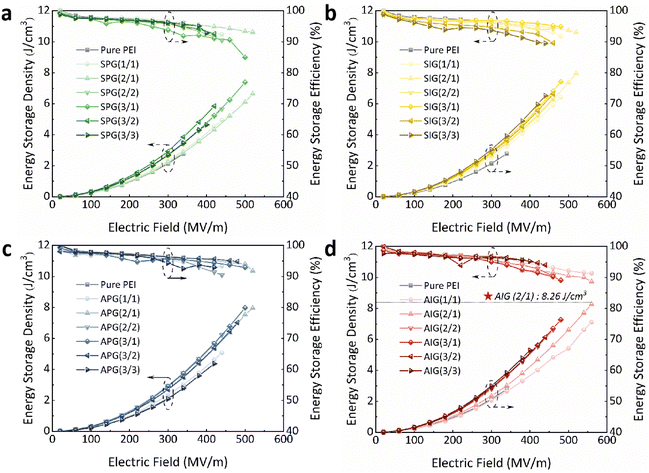 | ||
| Fig. 4 The energy storage density and efficiency as a function of the electric field of (a) SPG, (b) SIG, (c) APG, and (d) AIG composite dielectrics. | ||
To enhance the understanding of the mechanism behind carrier injection and transport inhibition by the topological gradient structure, a schematic of the metal electrode/dielectric interface was plotted, as shown in Fig. 5a. Taking the best performance series as examples, including SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics, irrespective of whether it is symmetric or asymmetric, the BNNSs content near the electrode/dielectric surface for the positive gradient composite dielectric is 1 vol%, while that of the inverse gradient composite dielectric is 3 vol%. The Eb values of both PEI/1 vol% BNNSs (505.5 MV m−1) and PEI/3 vol% BNNSs (546.4 MV m−1) composite dielectrics are higher than that of pure PEI (400.5 MV m−1). Therefore, the barrier height can be raised and charge injection can be slowed down by using the PEI/1 vol% BNNSs or PEI/3 vol% BNNSs composite dielectric as a surface barrier layer. Furthermore, the PEI/3 vol% BNNSs composite dielectric has a higher Eb than the PEI/1 vol% BNNSs composite dielectric, thus the inverse gradient structure can effectively inhibit carrier injection.
When carriers are injected across the barrier height into the interior of the dielectric, the breakdown path develops slowly owing to the lower electric field and fewer carriers in the early transport process. Therefore, the surface barrier layer can secondarily block the breakdown path development in the early stage of carrier transport. The conductivity activation energy (Ea) can reflect the minimum energy barrier that the carrier needs to overcome during the early stage of transport. The conductive activation energy of the pure PEI and gradient composite dielectrics was obtained using a dielectric spectrometer at varied temperatures.37,38Fig. 5b shows the dependence of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ on 1000/T for pure PEI and gradient composite dielectrics at 102 Hz, which is well described using the Arrhenius equation.39 According to Arrhenius’ law, the σ depends strongly on the temperature (T), and the dependence equation can be written as follows:
σ on 1000/T for pure PEI and gradient composite dielectrics at 102 Hz, which is well described using the Arrhenius equation.39 According to Arrhenius’ law, the σ depends strongly on the temperature (T), and the dependence equation can be written as follows:
σ(T) = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kT) exp(−Ea/kT) | (4) |
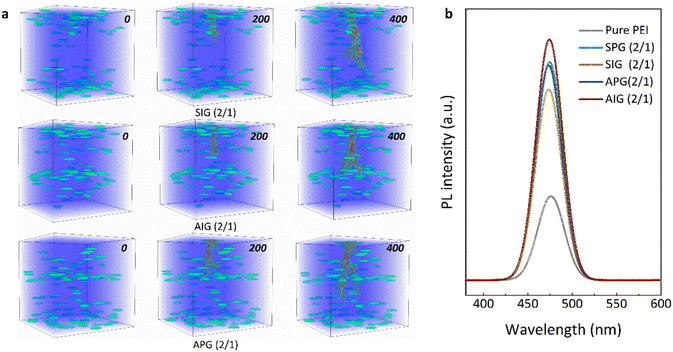
The stochastic breakdown model was employed to simulate the breakdown path development of pure PEI, and SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics and further find out the strengthening effect on the inhibition of carrier transport, as shown in Fig. 6a and Fig. S20 (in the ESI†). Compared with SIG (2/1) and AIG (2/1) composite dielectrics, the surface barrier layer of the SPG (2/1) and APG (2/1) composite dielectrics has a weaker blocking effect on carrier transport in the early stage, which accelerates breakdown path development. With the increasing electric field, as the breakdown path develops towards the central region, the central hinder layer in the asymmetric gradient structure exhibits a stronger block effect, which shows that the breakdown path pattern of APG and AIG composite dielectrics becomes divergent. The surface barrier layer of the AIG (2/1) composite dielectric has blocked and slowed down the carrier, resulting in a more divergent breakdown path when it reaches the dielectric center and touches the hinder layer. Since both the surface barrier layer and center hinder layer can block and slow down the carriers, the component units of the AIG (2/1) composite dielectric reduce the distance between the surface barrier layer and central hinder layer, and make them appear in the early and middle stages of the carrier transport. Thus, it reduces the free acceleration distance of the carriers and lowers the carrier energy. In contrast, the component units of the SIG (2/1) composite dielectric enlarged the distance between the surface barrier layer and the central hinder layer, which makes the free acceleration distance of the carrier longer and the accelerated energy higher.40 In addition, by comparing the photoluminescence (PL) spectra of pure PEI, and SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics, the effect of the central hinder layer on carrier transport was further analyzed, as shown in Fig. 6b. A low PL intensity indicates stronger PL quenching, which in turn indicates higher carrier mobility.41 It can be seen that the pure PEI has a lower intensity, indicating the highest internal carrier mobility, while the AIG (2/1) composite dielectric has the highest intensity and lowest carrier mobility. It is noted that the SIG (2/1) composite dielectric shows a lower intensity compared with other gradient composite dielectrics, indicating that the component units cannot effectively block carrier transport. These results show that the appropriate construction of the asymmetric gradient structure can effectively inhibit carrier injection and transport simultaneously.
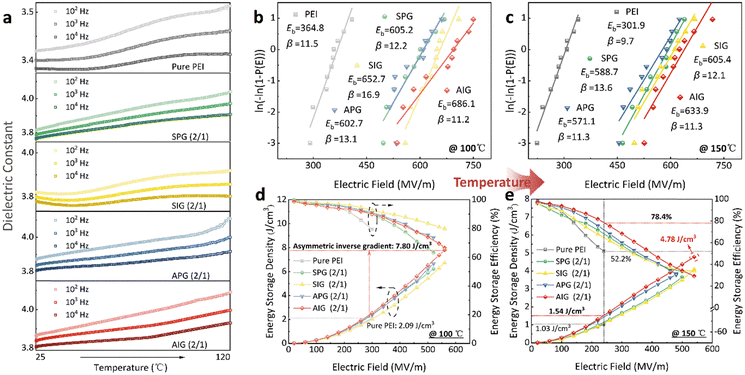
As the most widely used commercial dielectric capacitor, the optimal working temperature of BOPP is only 70 °C. When the temperature exceeds 105 °C, the insulation performance of BOPP will decrease dramatically. Mitigating temperature rises requires additional cooling devices, adding space and cost. It is urgent to consider the effect of high temperature on high-energy storage polymer-based composite dielectrics to meet applications in high-temperature environments in fields such as aerospace and new energy vehicles. Therefore, the topological gradient structure series with the best performance at room temperature was selected to further analyze the dielectric and energy storage performances at high temperatures. Fig. 7a and Fig. S21 (ESI†) show the εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of pure PEI, SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics at different frequencies as a function of temperature. As the temperature increases, the thermal motion of molecules inside the polymer dielectrics gains reinforcement, weakening the interaction force between molecules and resulting in an increasing polarization degree. Meanwhile, the electric field changes faster with the increased temperature, which corresponds to the dipole moment turnover rate slowing down. This makes the εr growth rate at high frequency lower than that at low frequency. Compared with the positive gradient structure, a large number of BNNSs in the inverse gradient structure are concentrated on both sides of the dielectric, effectively slowing down the thermal motion of the molecules inside the dielectric, resulting in a lower change in εr with temperature, particularly evident in the SIG (2/1) composite dielectric. In addition, as the temperature increases, the tan
δ of pure PEI, SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics at different frequencies as a function of temperature. As the temperature increases, the thermal motion of molecules inside the polymer dielectrics gains reinforcement, weakening the interaction force between molecules and resulting in an increasing polarization degree. Meanwhile, the electric field changes faster with the increased temperature, which corresponds to the dipole moment turnover rate slowing down. This makes the εr growth rate at high frequency lower than that at low frequency. Compared with the positive gradient structure, a large number of BNNSs in the inverse gradient structure are concentrated on both sides of the dielectric, effectively slowing down the thermal motion of the molecules inside the dielectric, resulting in a lower change in εr with temperature, particularly evident in the SIG (2/1) composite dielectric. In addition, as the temperature increases, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of pure PEI and gradient structure composite dielectrics increases at all frequencies owing to the enhanced polarization effect, which may affect the energy storage efficiency at high temperatures.
δ of pure PEI and gradient structure composite dielectrics increases at all frequencies owing to the enhanced polarization effect, which may affect the energy storage efficiency at high temperatures.
The Eb values of pure PEI, and SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics at 100 °C and 150 °C are shown in Fig. 7b and c, respectively. Compared with room temperature, the Eb of all dielectrics has different degrees of decline. However, compared with pure PEI, the Eb decline rate of the composite dielectric is lower. This is attributed to the fact that BNNSs have a higher thermal conductivity, because of which, they can quickly dissipate the heat generated by the loss under high temperatures and high electric fields. As the temperature further increases to 150 °C, the Eb of all polymer dielectrics decreases rapidly. The interface structure of BNNSs and the PEI matrix is prone to damage at high temperatures owing to the larger thermal expansion coefficient of the BNNSs. It is noted that the gradient composite dielectric still maintains a higher Eb at high temperatures, which is conducive to improving high-temperature energy storage performance. For example, the AIG (2/1) composite dielectric achieves a highest Eb of 686.1 MV m−1 and 633.9 MV m−1 at 100 °C and 150 °C, respectively. Finally, the high-temperature energy storage performance of several dielectrics was tested. The Ue and η of pure PEI, and SPG (2/1), SIG (2/1), APG (2/1), and AIG (2/1) composite dielectrics at 100 °C and 150 °C are shown in Fig. 7d and e, respectively. Combined with the dielectric and breakdown performances of the gradient composite dielectric under high temperatures, unsurprisingly, the AIG (2/1) composite dielectric achieves excellent energy storage performance with the highest Ue of 7.80 J cm−3 at 560 MV m−1 and 100 °C, which is 3.7 times that of pure PEI. In addition, the Ue of the AIG (2/1) composite dielectric can reach 4.78 J cm−3 at 150 °C, which is much higher than those of the dielectrics reported in previous studies.42–45 When compared with pure PEI in the same electric field (240 MV m−1), the Ue and η of the AIG (2/1) composite dielectric can reach 1.54 J cm−3 and 78.4%, respectively, which are significantly higher than those of pure PEI (1.03 J cm−3 and 52.4%). By using a simple preparation strategy of alternate electrospinning process, the distribution characteristics of BNNSs can be regulated to achieve higher breakdown strength and energy storage performances at room temperature and high temperature without additional interface modification or processing technology.
4. Conclusions
In summary, an intelligent and effective design route was demonstrated to develop PEI-based composite dielectric capacitors with higher breakdown strength and excellent energy storage performance working at room temperature to 150 °C based on stochastic breakdown simulation and adjustment of filler distribution characteristics. After the high-throughput simulation shortened the experiment cycle, by adjusting the asymmetric gradient distribution of BNNSs, constructing the surface barrier layer and central hinder layer, the breakdown strength and energy storage density were substantially enhanced. Higher energy storage density values of 8.26 J cm−3 and 4.78 J cm−3 were achieved at room temperature and 150 °C, respectively. Reducing the distance between the surface barrier layer and central hinder layer and increasing the height of the carrier injection barrier, as well as reducing the free acceleration distance of the carrier and minimizing the carrier energy, are the keys to significantly improving the performance. This work provides a strategy with simple and quantifiable production for high-energy storage dielectric capacitors.Author contributions
Dong Yue: writing – original draft, writing – review & editing, software, and formal analysis. Wenchao Zhang: conceptualization and supervision. Puzhen Wang: validation. Yong Zhang: formal analysis. Yu Teng: investigation. Jinghua Yin: methodology. Yu Feng: conceptualization, supervision, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Thanks to Prof. Sergey Maksimenko from the Belarusian State University for the physical model. This work was supported by the National Natural Science Foundation of China (No. 52177017), the National Key R&D Program of China (2022YFB2502602), the Natural Science Foundation of Heilongjiang Province of China (No. YQ2021E036), and the University Nursing Program for Young Scholars with Creative Talents in Heilongjiang Province (No. UNPYSCT-2020177).References
- J. Chen, Y. Zhou, X. Huang, C. Yu, D. Han, A. Wang, Y. Zhu, K. Shi, Q. Kang, P. Li, P. Jiang, X. Qian, H. Bao, S. Li, G. Wu, X. Zhu and Q. Wang, Nature, 2023, 615, 62–66 CrossRef CAS PubMed.
- D. Yue, J. H. Yin, W. C. Zhang, X. X. Cheng, M. H. Zhang, J. J. Wang and Y. Feng, Adv. Funct. Mater., 2023, 33, 2300658 CrossRef CAS.
- Q. Li, L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, U. Li, E. Iagodkine, A. Haque, L. Q. Chen, N. Jackson and Q. Wang, Nature, 2015, 523, 576–579 CrossRef CAS PubMed.
- R. Wang, Y. Zhu, J. Fu, M. Yang, Z. Ran, J. Li, M. Li, J. Hu, J. He and Q. Li, Nat. Commun., 2023, 14, 2406 CrossRef CAS PubMed.
- M. Zhang, B. Li, J. J. Wang, H. B. Huang, L. Zhang and L. Q. Chen, Adv. Mater., 2021, 33, e2008198 CrossRef PubMed.
- N. Meng, X. Ren, G. Santagiuliana, L. Ventura, H. Zhang, J. Wu, H. Yan, M. J. Reece and E. Bilotti, Nat. Commun., 2019, 10, 4535 CrossRef PubMed.
- Z. Bao, S. Ding, Z. Dai, Y. Wang, J. Jia, S. Shen, Y. Yin and X. Li, Mater. Horiz., 2023, 10, 2120–2127 RSC.
- Z. H. Shen, J. J. Wang, J. Y. Jiang, S. X. Huang, Y. H. Lin, C. W. Nan, L. Q. Chen and Y. Shen, Nat. Commun., 2019, 10, 1843 CrossRef PubMed.
- Q. K. Feng, S. L. Zhong, J. Y. Pei, Y. Zhao, D. L. Zhang, D. F. Liu, Y. X. Zhang and Z. M. Dang, Chem. Rev., 2022, 122, 3820–3878 CrossRef CAS PubMed.
- H. Li, D. Ai, L. Ren, B. Yao, Z. Han, Z. Shen, J. Wang, L. Q. Chen and Q. Wang, Adv. Mater., 2019, 31, e1900875 CrossRef PubMed.
- X. Zhang, J. Jiang, Z. Shen, Z. Dan, M. Li, Y. Lin, C. W. Nan, L. Chen and Y. Shen, Adv. Mater., 2018, 30, e1707269 CrossRef PubMed.
- J. Li, X. Liu, Y. Feng and J. Yin, Prog. Polym. Sci., 2022, 126, 101505 CrossRef CAS.
- P. Wang, L. Yao, Z. Pan, S. Shi, J. Yu, Y. Zhou, Y. Liu, J. Liu, Q. Chi, J. Zhai and Q. Wang, Adv. Mater., 2021, 33, e2103338 CrossRef PubMed.
- R. Guo, H. Luo, M. Yan, X. Zhou, K. Zhou and D. Zhang, Nano Energy, 2021, 79, 105412 CrossRef CAS.
- Y. Niu, J. Dong, Y. He, X. Xu, S. Li, K. Wu, Q. Wang and H. Wang, Nano Energy, 2022, 97, 107215 CrossRef CAS.
- H. Chen, Z. Pan, Y. Cheng, X. Ding, J. Liu, Q. Chi, M. Yang, J. Yu and Z.-M. Dang, J. Mater. Chem. A, 2022, 10, 1579–1587 RSC.
- W. Zhang, F. Guan, M. Jiang, Y. Li, C. Zhu, D. Yue, J. Li, X. Liu and Y. Feng, Composites, Part A, 2022, 159, 107018 CrossRef CAS.
- L. Sun, Z. Shi, B. He, H. Wang, S. Liu, M. Huang, J. Shi, D. Dastan and H. Wang, Adv. Funct. Mater., 2021, 31, 2100280 CrossRef CAS.
- H. Bai, K. Zhu, Z. Wang, B. Shen and J. Zhai, Adv. Funct. Mater., 2021, 31, 2102646 CrossRef CAS.
- J. Jiang, Z. Shen, J. Qian, Z. Dan, M. Guo, Y. He, Y. Lin, C.-W. Nan, L. Chen and Y. Shen, Nano Energy, 2019, 62, 220–229 CrossRef CAS.
- H. Bai, G. Ge, F. Yan, K. Zhu, J. Lin, C. Shi, J. Qian, Z. Wang, B. Shen and J. Zhai, Energy Storage Mater., 2022, 46, 503–511 CrossRef.
- J. Jiang, Z. Shen, X. Cai, J. Qian, Z. Dan, Y. Lin, B. Liu, C. W. Nan, L. Chen and Y. Shen, Adv. Energy Mater., 2019, 9, 1803411 CrossRef.
- C. Huang, L. Zhang, S. Liu, Y. Wang, N. Wang and Y. Deng, Chem. Eng. J., 2021, 411, 128585 CrossRef CAS.
- Y. Jiang, X. Zhang, Z. Shen, X. Li, J. Yan, B. W. Li and C. W. Nan, Adv. Funct. Mater., 2019, 30, 1906112 CrossRef.
- Y. Shang, Y. Feng, C. Zhang, T. Zhang, Q. Lei and Q. Chi, J. Mater. Chem. A, 2022, 10, 15183–15195 RSC.
- Y. Feng, J.-P. Xue, T.-D. Zhang, Q.-G. Chi, J.-L. Li, Q.-G. Chen, J.-J. Wang and L.-Q. Chen, Energy Storage Mater., 2022, 44, 73–81 CrossRef.
- D. Yue, Y. Feng, X. X. Liu, J. H. Yin, W. C. Zhang, H. Guo, B. Su and Q. Q. Lei, Adv. Sci., 2022, 9, 2105773 CrossRef CAS PubMed.
- L. Niemeyer, L. Pietronero and H. J. Wiesmann, Phys. Rev. Lett., 1984, 52, 1033–1036 CrossRef.
- J. J. Wang, X. Q. Ma, Q. Li, J. Britson and L.-Q. Chen, Acta Mater., 2013, 61, 7591–7603 CrossRef CAS.
- Y. Li, J. Yin, Y. Feng, J. Li, H. Zhao, C. Zhu, D. Yue, Y. Liu, B. Su and X. Liu, Chem. Eng. J., 2022, 429, 132228 CrossRef CAS.
- J. Chen, Z. Shen, Q. Kang, X. Qian, S. Li, P. Jiang and X. Huang, Sci. Bull., 2022, 67, 609–618 CrossRef CAS PubMed.
- F. Liu, Q. Li, Z. Li, Y. Liu, L. Dong, C. Xiong and Q. Wang, Compos. Sci. Technol., 2017, 142, 139–144 CrossRef CAS.
- J. Li, X. Liu, Y. Feng, D. Chen, Y. Li, D. Yue, B. Huang and J. Yin, Energy Storage Mater., 2023, 54, 605–614 CrossRef.
- Prateek, V. K. Thakur and R. K. Gupta, Chem. Rev., 2016, 116, 4260–4317 CrossRef CAS PubMed.
- H. Li, T. Yang, Y. Zhou, D. Ai, B. Yao, Y. Liu, L. Li, L. Q. Chen and Q. Wang, Adv. Funct. Mater., 2020, 31, 2006739 CrossRef.
- M. Guo, J. Jiang, Z. Shen, Y. Lin, C.-W. Nan and Y. Shen, Mater. Today, 2019, 29, 49–67 CrossRef CAS.
- H. Li, M. R. Gadinski, Y. Huang, L. Ren, Y. Zhou, D. Ai, Z. Han, B. Yao and Q. Wang, Energy Environ. Sci., 2020, 13, 1279–1286 RSC.
- L. Zhang, X. Lu, X. Zhang, L. Jin, Z. Xu and Z. Y. Cheng, Compos. Sci. Technol., 2018, 167, 285–293 CrossRef CAS.
- Y. Feng, W. L. Li, Y. F. Hou, Y. Yu, W. P. Cao, T. D. Zhang and W. D. Fei, J. Mater. Chem. C, 2015, 3, 1250–1260 RSC.
- M. Feng, Y. Feng, C. Zhang, T. Zhang, Q. Chen and Q. Chi, Mater. Horiz., 2022, 9, 3002–3012 RSC.
- G. Liu, Q. Lei, Y. Feng, C. Zhang, T. Zhang, Q. Chen and Q. Chi, InfoMat, 2023, 5, e12368 CrossRef CAS.
- L. Ren, L. Yang, S. Zhang, H. Li, Y. Zhou, D. Ai, Z. Xie, X. Zhao, Z. Peng, R. Liao and Q. Wang, Compos. Sci. Technol., 2021, 201, 108528 CrossRef CAS.
- Y. Wang, J. Zhou, A. C. Konstantinou, M. A. Baferani, K. Davis-Amendola, W. Gao and Y. Cao, Small, 2023, 19, 2208105 CrossRef CAS PubMed.
- M.-Z. Fan, B.-Z. Sun, J.-Y. Jiang, J.-Y. Pan and P.-H. Hu, Rare Met., 2023, 42, 1912–1922 CrossRef CAS.
- J. Liu, L. Ji, J. Yu, S. Ding, S. Luo, B. Chu, J. Xu, R. Sun and S. Yu, Chem. Eng. J., 2023, 456, 140950 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00907f |
| This journal is © The Royal Society of Chemistry 2024 |