Open Access Article
Open Access ArticleCorrection for neutron self-shielding and gamma-ray self-absorption in prompt-gamma activation analysis for large and irregularly shaped samples†
László
Szentmiklósi
 *,
Zoltán
Kis
*,
Zoltán
Kis
 ,
Boglárka
Maróti
,
Boglárka
Maróti
 and
László Zoltán
Horváth
and
László Zoltán
Horváth
Nuclear Analysis and Radiography Department, Centre for Energy Research, 29-33 Konkoly-Thege Miklós Street, 1121 Budapest, Hungary. E-mail: szentmiklosi.laszlo@energia.mta.hu
First published on 22nd October 2020
Abstract
Prompt-gamma activation analysis (PGAA) is a useful method to determine the elemental composition of bulky samples, where non-destructivity, representativity, and high metrological quality are of great importance. Voluminous samples significantly attenuate both the exciting neutron beam and the emerging gamma radiation within the sample. We have developed a generally applicable correction for the neutron self-shielding and gamma-ray self-absorption effect for large and irregularly shaped samples, based on digital geometry data and Monte Carlo simulations. The numerical correction gives results that agree well with those from destructive sampling.
Introduction
Prompt-gamma activation analysis (PGAA)1,2 is an elemental analysis method based on radiative neutron capture, also known as (n,γ) reaction.3 While the sample is irradiated with a beam of slow neutrons, gamma rays with up to 11 MeV energy emerge from the neutron capture reaction. These gamma rays are characteristic of the emitting nucleus, so the elements are identified based on the gamma-ray energies while the elemental amounts within the irradiated volume are proportional to the areas of the analytical gamma-ray peaks. Using a spectroscopic library,4 PGAA is capable of quantifying major and minor components as well as several trace elements.The commonly used analytical techniques for elemental analysis either require destructive sampling, powdering, or even dissolution (e.g. Atomic Absorption Spectrometry (AAS), and Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES) or Mass Spectrometry (ICP-MS)), or their probing volumes are limited both laterally and in depth (e.g. X-ray Fluorescence (XRF), Particle-Induced X-ray Emission (PIXE), Laser-Induced Breakdown Spectrometry (LIBS), and Laser-Ablation Inductively Coupled Plasma Mass Spectrometry (LA-ICP-MS)). These shortcomings ultimately lead to a reduced representativity of the results and make them prone to bias due to the ignoring of inhomogeneities or surface-related contaminations.
Neutrons and energetic gamma rays have, however, much larger penetration depths, up to a few mm or even cm, so they are suitable for measuring the bulk composition of silicate-based samples, such as whole-rock geological samples, meteorites, paleontological samples, prehistoric stone tools, obsidian cores, and ceramics non-destructively. Thanks to the complete uncertainty budget, the results have high metrological value. Both the neutron beam and the gamma detector's acceptance angle can be collimated, so an object can be measured at many positions of interest by scanning, if it is assumed to be inhomogeneous.
When analysing large samples, a complex chain of interactions takes place between the impinging neutrons, the emerging gamma rays and the matter that attenuates the intensities and shifts the energy distributions of both radiation types within the sample.5 The extent of these matrix effects depends on the matrix composition.6,7
The fundamental equation of PGAA contains a double integral which is a function of the irradiated volume and the neutron energy distribution, and the basic variables in the integrand are assumed to be position and/or energy dependent:2
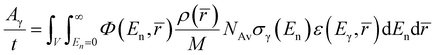 | (1) |
In the practical analysis of homogeneous and regularly shaped samples, however, this is usually simplified to eqn (2) and the negative bias on the resulting masses due to the internal absorption effects is compensated for by using the fn and fγ integral neutron self-shielding and gamma-ray self-absorption factors:
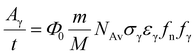 | (2) |
In these equations, Aγ is the measured peak area in the gamma-ray spectrum at energy Eγ during measurement time t, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) is a position vector, ρ(
is a position vector, ρ(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) is the local mass density of the element of interest, Φ(En,
) is the local mass density of the element of interest, Φ(En,![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) is the local energy-differential neutron flux, m is the mass of the element to be quantified (within the illuminated volume V), M is its molar mass, and NAv is the Avogadro constant. σγ is the so-called partial gamma-ray production cross-section, a compound nuclear constant defined as the product of the thermal neutron capture cross-section (σ0), the isotopic abundance (Θ), and the emission probability (Pγ) of the gamma rays with energy Eγ: σγ = σ0ΘPγ. εγ denotes the counting efficiency of the detector at the specified gamma energy and in the given experimental geometry. Φ0 is the so-called thermal-equivalent flux of the impinging neutrons, defined as
) is the local energy-differential neutron flux, m is the mass of the element to be quantified (within the illuminated volume V), M is its molar mass, and NAv is the Avogadro constant. σγ is the so-called partial gamma-ray production cross-section, a compound nuclear constant defined as the product of the thermal neutron capture cross-section (σ0), the isotopic abundance (Θ), and the emission probability (Pγ) of the gamma rays with energy Eγ: σγ = σ0ΘPγ. εγ denotes the counting efficiency of the detector at the specified gamma energy and in the given experimental geometry. Φ0 is the so-called thermal-equivalent flux of the impinging neutrons, defined as 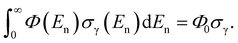 The neutron self-shielding factor, fn, depends on the energy distribution of the traversing beam, while the gamma-ray self-absorption factor, fγ, is a function of the gamma energy. For point-like samples, fn and fγ tend to unity. For real samples, fn is a common mass scaling factor for all gamma lines, unlike fγ, which affects low- and high-energy gammas to different extents. Since we obtain the mass of an element as the weighted average of those determined from several individual analytical lines, an adequate fγ curve is essential to make the element mass values from the several lines self-consistent.
The neutron self-shielding factor, fn, depends on the energy distribution of the traversing beam, while the gamma-ray self-absorption factor, fγ, is a function of the gamma energy. For point-like samples, fn and fγ tend to unity. For real samples, fn is a common mass scaling factor for all gamma lines, unlike fγ, which affects low- and high-energy gammas to different extents. Since we obtain the mass of an element as the weighted average of those determined from several individual analytical lines, an adequate fγ curve is essential to make the element mass values from the several lines self-consistent.
Both the ISO ‘Guide to the Expression of Uncertainty in Measurement’ (GUM) and the Eurachem/Citac ‘Quantifying Uncertainty in Analytical Measurement’ (QUAM) guidelines explicitly state that known biases of an analytical method must be corrected for. The f factors in eqn (2) can be obtained either experimentally by calibration8,9 for liquids or disposable mixtures of powders, or can be approximated analytically10 (based on the Beer–Lambert law and assuming monoenergetic radiation) or calculated numerically11 in the case of some regular sample shapes. However, until now no rigorous solution was routinely applicable to the non-destructive analysis of irregularly shaped large samples with unknown compositions.
In this work, we significantly widen the practical applicability of the prompt-gamma activation analysis technique by presenting a general approach based on eqn (1) to address the attenuation effects of large and/or complex-shaped samples. This was achieved by taking advantage of surface and volumetric imaging techniques, as well as Monte Carlo computer simulations.12 The geometries of the objects were captured using 3D structured-light optical scanning or were taken from X-ray/neutron tomography. The layout of the NIPS-NORMA instrument, as well as the placement of the analyte, has been implemented in the MCNP6.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 simulation environment where the interaction of the radiation was modelled, and finally, the required correction factors were deduced.
13 simulation environment where the interaction of the radiation was modelled, and finally, the required correction factors were deduced.
Experimental
Samples
PGAA's most appreciated advantages are non-destructivity, bulk representativity, and high metrological quality, which are utilized in the analysis of whole-rock geological samples, meteorites, paleontological samples, prehistoric stone tools, obsidian cores, and ceramics, as well as complex objects made from composite materials.We have therefore chosen a massive composite rock fragment, a red nodular chert embedded in white-rose limestone, to demonstrate an extreme case from our recent analytical practice. It has dimensions of 124 mm × 61 mm × 156 mm, a total volume of 426 cm3, and a mass of 1025 g, giving an average density of 2.40 g cm−3. Composition-wise, it contains amorphous/cryptocrystalline SiO2 and fine-crystalline CaCO3 with a minor Fe content. It is known that iron is inhomogeneously incorporated at the microscale during sedimentation and is responsible for the uneven red or rose coloration of the limestone rock. The slight variation of the macroscale iron-content within the 0.3–0.4 m% range has however no practical influence on the attenuation features of the object. The yellowish weathered cortex makes the outer layers different from the bulk, so results from any competing surface-confined techniques could be bulk representative only after surface cleaning, which is often not approved for real samples due to their uniqueness.
Unlike geological samples, industrial products often have well-controlled homogeneity, shape, and external dimensions. We, therefore, carried out a validation experiment on a large Ca–Al-silicate pavement stone block with dimensions of 60 × 100 × 200 mm3, i.e. total volume of 1200 cm3, mass of 2580 g, and bulk density of 2.15 g cm−3.
Digital sample geometry
To accurately determine the geometries of the samples, we applied 3D structured-light optical scanning, using a RangeVision SMART scanner. It has 0.15 mm spatial accuracy and is capable of creating photorealistic digital models within 10 minutes. The complex outer surfaces of both objects were approximated with 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 vertices.
000 vertices.
From these data, one can obtain any linear dimensions, the centre of gravity (if the macroscopic mass density is position-independent) to check its balance, the total volume, and a bounding box for collision-protection during the automated sample manipulations within the sample chamber.
Since the homogeneity of geological samples, in general, cannot be assumed, we carried out neutron and X-ray tomography experiments on the object at the RAD station14 of the Budapest Neutron Centre to map its internal structure. It was found that although there are two distinct materials in the sample visible to the naked eye, the neutron15 and photon attenuation16 properties, i.e. the linear attenuation coefficients, are by chance almost equal all over the object (see Fig. 1).
 | ||
| Fig. 1 The textured 3D surface mesh of the pavement stone validation object as well as the stone geological object. The neutron and X-ray tomograms of the latter are also shown after registration in VGStudio MAX. The CT data cuts revealed no internal structures. The 3D photorealistic digital models of the measured objects are available as ESI 1 and 2.† | ||
These volumetric CT data can also be used for defining the geometry, as an alternative to 3D scanning. Volume rendering software, such as VGStudio MAX 3.2, can determine the surface at a given grayscale threshold and construct a similar triangular surface mesh.
The ratio of the measured weight and the digital volume readily defines the average density, a vital parameter of the subsequent calculations.
Prompt-gamma experiment
The prompt-gamma measurements were carried out at the NIPS-NORMA station17 of the Budapest Neutron Centre. This experimental facility consists of a Compton-suppressed n-type coaxial HPGe (Canberra GR 2318/S) gamma detector placed within a 10–15 cm thick lead shielding, a downstream placed neutron imaging camera, an xyzω sample stage, and a sample chamber of 200 × 200 × 200 mm3 internal dimensions made of AlMgSi alloy and lined with 6Li-polymer neutron shielding. The setup was carefully calibrated for point-source gamma-ray detection efficiency18 and non-linearity19 of the energy response. The prompt-gamma spectra were evaluated with the gamma spectrometry software Hypermet-PC,20 while the elemental concentrations were calculated with the Excel macro ProSpeRo.21The pavement stone validation object was placed perpendicular to the impinging neutron beam and was irradiated for 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s at the half point of its full height with a beam spot of 10 mm (w) × 20 mm (h), at three horizontal positions, i.e. Y = 25 mm, 50 mm and 75 mm from the vertical edge. These are labelled as Pos A–Pos C, respectively. The count rates were between 400 and 500 cps. With this experiment, we aimed to demonstrate that the physics is well handled by our method during upscaling to a large, regularly shaped object.
000 s at the half point of its full height with a beam spot of 10 mm (w) × 20 mm (h), at three horizontal positions, i.e. Y = 25 mm, 50 mm and 75 mm from the vertical edge. These are labelled as Pos A–Pos C, respectively. The count rates were between 400 and 500 cps. With this experiment, we aimed to demonstrate that the physics is well handled by our method during upscaling to a large, regularly shaped object.
The irregularly shaped stone object was placed at the centre of the sample stage at an approximately 30 degree angle relative to the beam axis and exposed to a cold neutron beam (thermal equivalent flux: 2.7 × 107 cm−2 s−1, beam cross-section: 10 × 10 mm2) for 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 s, producing a count rate of 470–970 cps in the spectrum. This sample was measured at four positions, with 20 mm vertical increments from the bottom, labelled as Pos 1 to Pos 4 (Z = 20, 40, 60, and 80 mm). Pos 1 and 2 targeted the limestone part, and Pos 4 the chert part, while Pos 3 contained contributions from both parts.
500 s, producing a count rate of 470–970 cps in the spectrum. This sample was measured at four positions, with 20 mm vertical increments from the bottom, labelled as Pos 1 to Pos 4 (Z = 20, 40, 60, and 80 mm). Pos 1 and 2 targeted the limestone part, and Pos 4 the chert part, while Pos 3 contained contributions from both parts.
The physical source of the analytical information, i.e. the geometrical intersection of the neutron beam and the gamma collimator's solid angle, is a fixed volume in space and is called the isovolume.22 In our case, it was a chord-like volume, and we moved the object relative to it. For the pavement stone sample, the material's thickness towards the neutron beam was constant at all measured points and only the attenuation of gamma rays towards the gamma detector varied. In contrast, the stone object's thickness differed significantly along the neutron beam (shorter or longer chord) as well as towards the gamma detector (thinner or thicker rock layers) for the different measurement positions, so both the spatial distribution of the prompt-gamma production and the lateral self-absorption effects varied.
A second approach to method validation has been that the geological rock object was destructively sampled after the measurement. To mitigate the effect of a potential inhomogeneity, we took samples from both limestone and chert parts at positions strictly coincident with the neutron beam spot positions Pos 1–4. These samples were crushed, powdered, sealed into Teflon bags, and analysed using our validated standard procedure.23 The base analytical method has been described in ref. 21, while a detailed discussion of the uncertainty budget of the calculation is available in ref. 24.
Monte Carlo simulations
The interaction of ionizing radiation with objects cannot be rigorously calculated with closed analytical formulae. In these cases, one can apply the Monte Carlo technique, where a mathematical model and computer-generated random numbers are used to describe the neutron, photon, or electron transport throughout the material at the event-level. The law of large numbers ensures that a statistical manifold of these individual interactions will truly represent the overall physical effect. To model the interactions, this software uses a comprehensive data library of nuclear reaction cross-sections for many isotopes, elements, particle types, and energies.We used MCNP version 6.2 along with the nuclear data library Lib80x25 (based on ENDF/B-VIII.0) in our calculations. The geometry of the NIPS-NORMA setup was defined using simple solids to represent various geometrical objects, while the sample was constructed from voxels, just like the detailed patient models in medical physics.26
A conversion utility has been programmed in C# language to convert a surface mesh to voxels, using the geometry3Sharp open-source library for geometric computing.27 The voxels from the triangular surface were constructed using the Generalized Winding Numbers method.28 The other functionality of this utility is to merge voxels of a high-definition 3D tomogram, loaded in the form of a TIFF image stack. The TIFF files were handled with the LibTIFF.NET library.29 In both cases, we have chosen 1 × 1 × 1 mm3 unit cells for output, as this was found to be the right balance between the computational efficiency and the true representation of the object geometry.
Finally, for the “diluted sample case” calculations, adequate material (or air) was assigned to each of the voxels, and the voxels were written into a formatted text file according to the MCNP6 layout. This keeps the option open to handle any inhomogeneous objects in the future if segmented CT data can be used for a non-binary material assignation. The sample description was linked to the main simulation file with the READ FILE keyword. The energy distribution of the impinging neutron beam was taken from ref. 30.
The direct modeling of the whole radiative neutron capture process by MNCP is computationally inefficient and, due to the lack of high-quality gamma-emission data, analytically imprecise, so a two-step process was used. Spatially resolved data for the neutron field and the capture rate of the relevant isotopes were extracted first using the F4 mesh tally feature of MCNP6.
The local capture rate is not solely dependent on the local number of neutrons, as the more energetic neutrons reach deeper layers at a higher survival rate, but they induce a lower reaction rate due to the 1/v law of neutron capture.31 The volume integral of the F4 capture-rate mesh tally values (subscript r) relative to that for an assumed “diluted sample case” (subscript d), where the modification of the transmitted beam is negligible, provided the neutron self-shielding coefficient, fn.
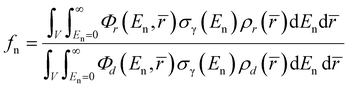 | (3) |
Calculations with various reduced densities showed that the reduction of the macroscopic material density by a factor of 1000 already resulted in a converging fn factor. The capture rate abundances per started neutron at the nodes of the orthogonal mesh, R(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ), are directly related to the emission rates of prompt-gammas by an isotope of interest and form the discretized starting point for dealing with the attenuation of the emitted photons. In the second step of the correction method, this discretized distribution was used as weighting factors to generate the prompt gamma rays and they were propagated through the experimental geometry. The intensities of the analytical peaks in the energy spectrum, representing the energy deposition in the active volume of the HPGe detector crystal (F8 tally), were compared to another artificial case where the object was filled with air, i.e. the absorption of the gamma rays is negligible (subscript a). This proportion gave the gamma self-absorption factor, fγ.
), are directly related to the emission rates of prompt-gammas by an isotope of interest and form the discretized starting point for dealing with the attenuation of the emitted photons. In the second step of the correction method, this discretized distribution was used as weighting factors to generate the prompt gamma rays and they were propagated through the experimental geometry. The intensities of the analytical peaks in the energy spectrum, representing the energy deposition in the active volume of the HPGe detector crystal (F8 tally), were compared to another artificial case where the object was filled with air, i.e. the absorption of the gamma rays is negligible (subscript a). This proportion gave the gamma self-absorption factor, fγ.
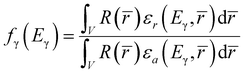 | (4) |
In eqn (4), εr and εa stand for the pointwise detection efficiency, and they have the attenuation effect incorporated. The product of fn and fγ has to be pasted into the appropriate column of the ProSpeRo, overriding the default correction factors which are only valid for slab geometry.
The MCNP simulations were executed on an Intel i9-7940X 3.1 GHz workstation, for a few hours each, until convergence was reached.
Results and discussion
Validation experiment
The calculated neutron capture rate field for a nominally 10 × 20 mm2 pencil beam incident on the pavement stone at Pos A is shown in Fig. 2. | ||
| Fig. 2 The visualization of the calculated capture rate field for the 25 mm position of the pavement stone (Pos A), with a vertical cutting plane at the beam center. Neutrons reach the sample from the right, as shown by the red arrow. Additional plots are shown in ESI 3.† | ||
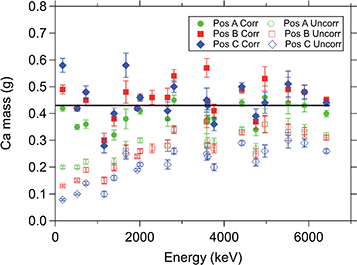
Using these capture rates we generated prompt gammas at several energies and propagated them in the experimental geometry until they reached the HPGe detector and gave rise to the spectrum counts. Since the thickness of the object and the irradiation conditions were constant, the masses within the isovolume were expected to be equal at all three positions. We have chosen the element calcium to verify this, as it is an easily measurable and multiline element with analytical lines covering a wide range of gamma-ray energies from 175 keV to 6420 keV, i.e. very useful to verify the consistency of the correction versus gamma energy.
After making the suitable corrections, a good overall agreement was found between different gamma lines in the same spectrum, as well as between spectra taken at the three different positions. Masses of Ca before and after correction are illustrated in Fig. 3.
Analysis of the stone object
The correction method was finally applied to the stone object that had a complex geometry. The neutron field and the neutron capture rates for the 40Ca isotope simulated for a 10 × 10 mm2 beam at Pos 1 of the stone are shown in the top panel of Fig. 4. The neutron capture rate is proportional to the product of the point-wise and energy-dependent neutron intensity, the local atomic density, and the neutron capture cross-section. The horizontal and vertical cutting planes are coincident with the beam axis. Here we used a 4% threshold to visualize the neutron field, while a lower 1%-cut was used on the capture rates to highlight the contributions of the scattered neutrons (in dark blue) outside the directly irradiated volume. When calculating the position-dependent gamma emission rates based on eqn (1), we can accurately account for both the neutron scattering and the beam hardening effect32 too, unlike the conventional Beer–Lambert-formula-based approach.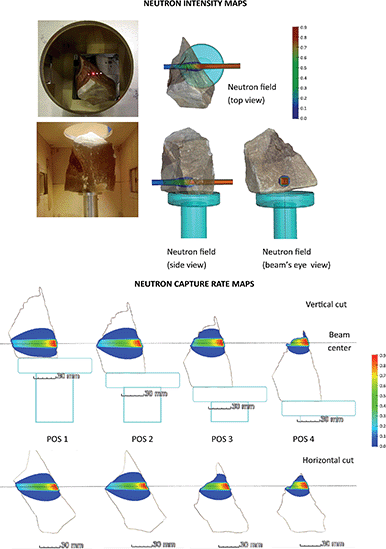 | ||
| Fig. 4 A photo of the object in the sample chamber (top left), the neutron field at the bottom position of the stone object, Pos 1 (top right), and the capture reaction rate map of the 40Ca isotope for all four measurement positions (bottom), indicating the local source strength of the prompt-gamma rays. Note the dark blue area around the direct beam, where only scattered neutrons are present. The experimental measurement positions are indicated in the photo by laser beam spots. Additional plots are shown in ESI 3.† | ||
The calculated integral neutron self-shielding factors are tabulated in Table 1.
| Pos 1 | Pos 2 | Pos 3 | Pos 4 | |
|---|---|---|---|---|
| Beam transmission thickness (mm) | 60 | 53 | 37 | 20 |
| f n factors | 0.603 | 0.642 | 0.757 | 0.861 |
Since the front plane of the sample was by chance almost vertical and the gamma detector observed the first 3 cm of the thickness in this configuration, similar amounts of the material produced the analytical signal. Therefore, the registered gamma spectra, experimental total count rates, calculated reaction rate profiles and gamma attenuation curves (Fig. 5) were almost identical for Pos 1 and Pos 2, irrespective of the remaining, unobserved, sample thickness.
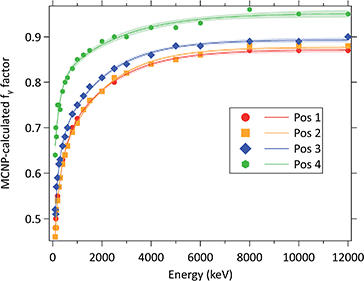 | ||
| Fig. 5 The MCNP6-simulated gamma attenuation curves and their 1-sigma confidence bands for the stone sample at the four measurement positions, Pos 1–4. | ||
When these attenuation curves were applied to the measured raw peak areas, and subsequently the masses within the irradiated volumes, a very good self-consistency for the whole range of gamma-ray energies was obtained, as shown in Fig. 6. The position dependence shows the changing elemental composition with height.
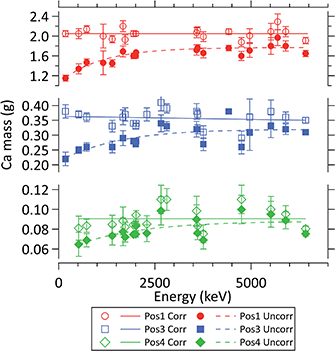 | ||
| Fig. 6 The corrected (open symbols) and uncorrected (closed symbols) masses of the element Ca in the active measurement volume. The corrected mass values from analytical peaks at various gamma energies show no energy-dependent tendency and agree within the 1-sigma statistical uncertainty, calculated as described in ref. 24. The interpolation curves were determined with a nonlinear weighted least-squares fit. | ||
Fig. 5 and 6 illustrate that biases up to 50% occur at low energies and could be successfully corrected for. This becomes important when elements are analysed which have predominantly or exclusively low-energy lines, such as gadolinium, samarium, or boron. The corrected boron contents showed a much better agreement with the flat powder sample results. For instance, the uncorrected boron content of Pos 4 was 33.5 ppm ± 1.1% which after correction became 38.6 ppm ± 1.1%.
The typical relative 1-sigma uncertainties can be as low as 2–3%, similarly to our standard PGAA method; hence, for several elements their previously discarded analytical lines could now be considered. The corrected concentrations, together with their 1-sigma uncertainties, are listed in Table 2. The agreement of the compositions from the bulk measurements and the powder samples shows the potential of the proposed approach.
| Pos 1 | Powder Pos 1 | Pos 2 | Powder Pos 2 | Pos 3 | Powder Pos 3 | Pos 4 | Powder Pos 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m% | rel unc% | m% | rel unc% | m% | rel unc% | m% | rel unc% | m% | rel unc% | m% | rel unc% | m% | rel unc% | m% | rel unc% | |
| H | 0.124 | 0.9 | 0.161 | 1.4 | 0.125 | 1.8 | 0.144 | 1.3 | 0.141 | 0.9 | 0.138 | 1.2 | 0.137 | 1.2 | 0.134 | 1.2 |
| B | 18.0 ppm | 0.8 | 22.6 ppm | 1.4 | 19.5 ppm | 0.9 | 23.8 ppm | 1.3 | 36.7 ppm | 0.9 | 37.1 ppm | 1.2 | 38.6 ppm | 1.1 | 38.4 ppm | 1.6 |
| C | 5.8 | 5.3 | 6 | 16 | 5.4 | 6.0 | 6 | 12 | <3.5 (DL) | <3.5 (DL) | <3.5 (DL) | <3.5 (DL) | ||||
| O | 49.9 | 5 | 50 | 5 | 49.5 | 5 | 51 | 5 | 48.2 | 5 | 53 | 5 | 47 | 5 | 53 | 5 |
| Al | 2.13 | 1.8 | 0.8 | 7.8 | 0.85 | 2.0 | 0.69 | 4 | 0.67 | 2.1 | 0.49 | 2.4 | 0.56 | 2.3 | 0.49 | 2.3 |
| Si | 21.2 | 1.6 | 21.4 | 2.05 | 22.4 | 1.8 | 21.8 | 1.9 | 43 | 1.1 | 45 | 1.3 | 44 | 1.3 | 45 | 1.4 |
| Cl | <30 ppm (DL) | 28 | 15 | <30 ppm (DL) | 25 | 16 | 30 ppm | 5 | 40 ppm | 5 | 32 ppm | 5 | 43 ppm | 4 | ||
| K | 0.243 | 2.2 | 0.26 | 2.6 | 0.25 | 2.2 | 0.24 | 2.6 | 0.232 | 1.9 | 0.18 | 2.2 | 0.207 | 2.2 | 0.192 | 1.9 |
| Ca | 20 | 2.4 | 21 | 2.4 | 20 | 2.7 | 19 | 2.4 | 3.8 | 3.1 | 0.27 | 3.1 | 1.46 | 2.6 | 0.57 | 2.6 |
| Ti | 280 ppm | 2.9 | 350 ppm | 3.5 | 290 ppm | 3.0 | 310 ppm | 3.2 | 260 ppm | 2.9 | 210 ppm | 3.1 | 220 ppm | 3.1 | 220 ppm | 2.6 |
| Mn | 0.055 | 2.4 | 0.053 | 2.3 | 0.051 | 3.9 | 0.049 | 2.2 | 90 ppm | 10 | 20 ppm | 5 | 180 ppm | 3.1 | 24 ppm | 9.2 |
| Fe | 0.31 | 2.2 | 0.44 | 6.1 | 0.36 | 2.9 | 0.39 | 6 | 0.32 | 2.6 | 0.27 | 2.9 | 0.30 | 2.6 | 0.33 | 3.3 |
| Sm | 0.96 ppm | 2.2 | 1.14 ppm | 2.9 | 0.99 ppm | 2.0 | 1.10 ppm | 2.2 | 0.62 ppm | 2.4 | 0.54 ppm | 2.1 | 0.55 ppm | 2.8 | 0.38 ppm | 2.3 |
| Gd | 1.5 ppm | 7.1 | 1.5 ppm | 5.9 | 1.5 ppm | 9 | 1.4 ppm | 7.1 | 0.8 ppm | 7 | 0.6 ppm | 6 | 0.7 ppm | 5 | 0.5 ppm | 18 |
Conclusions
We worked out a comprehensive correction method to handle the negative matrix effect of PGAA – related to the neutron self-shielding and gamma self-absorption – for voluminous and/or complex-shaped samples. It relies on the geometrical data obtained by 3D scanning that were input into the MCNP simulation model of the Budapest NIPS-NORMA facility, implementing the real experimental sample geometry. Neutrons with known energy- and directional-distributions were propagated through the object and the neutron field, and the capture rates of selected elements were mapped with 3D mesh tallies. In a second step, these were used to define a distributed source of the emerging capture gamma rays with characteristic energies, and to simulate their attenuations while propagating towards the Compton-suppressed HPGe detector.The method was applied to a rectangular pavement stone of 2.6 kg and a whole-rock geological sample of about 1 kg, to determine their elemental compositions non-destructively. Good general consistency was found between the sets of the measurement positions, as well as with the destructively obtained powder samples analysed with our validated standard procedure. This can justify the use of PGAA as a highly representative analytical technique when large geological, cosmochemical, paleontological, and heritage science objects are to be characterized. A similar procedure can be adapted to other beamline experiments, e.g. neutron imaging, PIXE or synchrotron XRF.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support of the János Bolyai Research Fellowship of the Hungarian Academy of Sciences, and Projects K 124068 and NN 127102 of the National Research, Development and Innovation Fund of Hungary. We thank Veronika Szilágyi for the geological characterization of the presented bulk stone sample, and Jesse L. Weil for his advice on the manuscript.References
- R. L. Paul and R. M. Lindstrom, Prompt Gamma-Ray Activation Analysis: Fundamentals and Applications, J. Radioanal. Nucl. Chem., 2000, 243(1), 181–189 CrossRef CAS.
- G. L. Molnár, Handbook of Prompt Gamma Activation Analysis, Kluwer Academic Publisher Dordrecht, Boston, London: Budapest, 2004, pp. 1–423, DOI:10.1007/978-0-387-23359-8.
- N. Bohr, Neutron Capture and Nuclear Constitution, Nature, 1936, 137(3461), 344–348, DOI:10.1038/137344a0.
- Z. Révay, R. B. Firestone, T. Belgya and G. L. Molnár, Prompt Gamma-Ray Spectrum Catalog, in Handbook of Prompt Gamma Activation Analysis, ed. G. L. Molnár, Kluwer Academic Publishers, Dordrecht, Boston, London, 2004, pp. 173–364, DOI:10.1007/978-0-387-23359-8_7.
- I. E. Stamatelatos, F. Tzika, T. Vasilopoulou and M. J. J. Koster-Ammerlaan, Large Sample Neutron Activation Analysis of a Ceramic Vase, J. Radioanal. Nucl. Chem., 2010, 283(3), 735–740, DOI:10.1007/s10967-010-0454-3.
- R. M. W. Overwater, P. Bode and J. J. M. Degoeij, Gamma-Ray Spectroscopy of Voluminous Sources - Corrections for Source Geometry and Self-Attenuation, Nucl. Instrum. Methods Phys. Res., Sect. A, 1993, 324(1–2), 209–218 CrossRef.
- M. Blaauw and E. A. M. Mackey, Neutron Self-Shielding in Hydrogenous Samples, J. Radioanal. Nucl. Chem., 1997, 216(1), 65–68 CrossRef CAS.
- R. Acharya, Prompt Gamma-Ray Neutron Activation Analysis Methodology for Determination of Boron from Trace to Major Contents, J. Radioanal. Nucl. Chem., 2009, 281(2), 291–294, DOI:10.1007/s10967-009-0100-0.
- R. K. Harrison and S. Landsberger, Determination of Boron over a Large Dynamic Range by Prompt-Gamma Activation Analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267(3), 513–518, DOI:10.1016/j.nimb.2008.11.057.
- R. F. Fleming, Neutron Self-Shielding Factors for Simple Geometrics, Int. J. Appl. Radiat. Isot., 1982, 33(11), 1263–1268, DOI:10.1016/0020-708X(82)90247-2.
- M. Blaauw, I. H. Degenaar, C. Yonezawa, H. Matsue and J. J. M. De Goeij, Validation Experiment for Large-Sample Prompt-Gamma Neutron Activation Analysis, J. Radioanal. Nucl. Chem., 2007, 271(3), 745–750, DOI:10.1007/s10967-007-0336-5.
- I. Lux and L. Koblinger, Monte Carlo Particle Transport Methods, CRC Press, 1991 Search PubMed.
- T. Goorley, M. James, T. Booth, F. Brown, J. Bull, L. J. Cox, J. Durkee, J. Elson, M. Fensin, R. A. Forster, J. Hendricks, H. G. Hughes, R. Johns, B. Kiedrowski, R. Martz, S. Mashnik, G. McKinney, D. Pelowitz, R. Prael, J. Sweezy, L. Waters, T. Wilcox and T. Zukaitis, Features of MCNP6, Ann. Nucl. Energy, 2016, 87, 772–783, DOI:10.1016/J.ANUCENE.2015.02.020.
- Z. Kis, L. Szentmiklósi, T. Belgya, M. Balaskó, L. Z. Horváth and B. Maróti, Neutron Based Imaging and Element-Mapping at the Budapest Neutron Centre, Phys. Procedia, 2015, 69, 40–47, DOI:10.1016/j.phpro.2015.07.005.
- V. F. Sears, Neutron Scattering Lengths and Cross Sections, Neutron News, 1992, 3(3), 26–37 CrossRef.
- J. H. Hubbell and S. M. Seltzer, Tables of X-Ray Mass Attenuation Coefficients and Mass-Energy Absorption Coefficients from 1 keV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric, Interest, 2020 Search PubMed , http://physics.nist.gov/xaamdi.
- Z. Kis, L. Szentmiklósi and T. Belgya, NIPS–NORMA Station—A Combined Facility for Neutron-Based Nondestructive Element Analysis and Imaging at the Budapest Neutron Centre, Nucl. Instrum. Methods Phys. Res., Sect. A, 2015, 779, 116–123, DOI:10.1016/j.nima.2015.01.047.
- G. L. Molnár, Z. Révay and T. Belgya, Wide Energy Range Efficiency Calibration Method for Ge Detectors, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 489(1–3), 140–159, DOI:10.1016/S0168-9002(02)00902-6.
- B. Fazekas, Z. Révay, J. Östör, T. Belgya, G. Molnár and A. Simonits, A New Method for Determination of Gamma-Ray Spectrometer Non- Linearity, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 422(1–3), 469–473 CrossRef CAS.
- Z. Révay, T. Belgya and G. L. Molnár, Application of Hypermet-PC in PGAA, J. Radioanal. Nucl. Chem., 2005, 265(2), 261–265, DOI:10.1007/s10967-005-0818-2.
- Z. Révay, Determining Elemental Composition Using Prompt γ Activation Analysis, Anal. Chem., 2009, 81(16), 6851–6859, DOI:10.1021/ac9011705.
- R. Schulze, L. Szentmiklósi, P. Kudejova, L. Canella, Z. Kis, T. Belgya, J. Jolie, M. Ebert, T. Materna, K. T. Biró and Z. Hajnal, The ANCIENT CHARM Project at FRM II: Three-Dimensional Elemental Mapping by Prompt Gamma Activation Imaging and Neutron Tomography, J. Anal. At. Spectrom., 2013, 28(9), 1508–1512, 10.1039/c3ja50162k.
- K. Gméling, A. Simonits, I. Sziklai László and D. Párkányi, Comparative PGAA and NAA Results of Geological Samples and Standards, J. Radioanal. Nucl. Chem., 2014, 300(2), 507–516, DOI:10.1007/s10967-014-3032-2.
- Z. Révay, Calculation of Uncertainties in Prompt Gamma Activation Analysis, Nucl. Instrum. Methods Phys. Res., Sect. A, 2006, 564(4–6), 688–697 CrossRef.
- J. Lloyd Conlin, W. Haeck, D. Neudecker, D. Kent Parsons and M. C. White, LA-UR-18–24034: Release of ENDF/B-VIII.0-Based ACE Data Files, Los Alamos, 2018 Search PubMed.
- I. G. Zubal, C. R. Harrell, E. O. Smith and A. L. SmithTwo Dedicated Software, Voxel-Based, Anthropomorphic (Torso and Head) Phantoms, in Proc. Int. Workshop on Voxel Phantom Development, National Radiological Protection Board, Chilton, UK, 1995, pp. 105–111 Search PubMed.
- GradientSpace, geometry3sharp, 2020, https://github.com/gradientspace/geometry3Sharp Search PubMed.
- A. Jacobson, L. Kavan and O. Sorkine-Hornung, Robust Inside-Outside Segmentation Using Generalized Winding Numbers, ACM Trans. Graph., 2013, 32(4), 1–12 CrossRef.
- Bitmiracle, LibTIFF.NET, 2020, https://bitmiracle.com/libtiff/ Search PubMed.
- T. Belgya, Z. Kis and L. Szentmiklósi, Neutron Flux Characterization of the Cold Beam PGAA-NIPS Facility at the Budapest Research Reactor, Nucl. Data Sheets, 2014, 119, 419–421, DOI:10.1016/j.nds.2014.08.118.
- G. Breit and E. Wigner, Capture of Slow Neutrons, Phys. Rev., 1936, 49(7), 519–531, DOI:10.1103/PhysRev.49.519.
- F. Kharfi, M. Bastuerk and A. Boucenna, Characterization of Weak, Fair and Strong Neutron Absorbing Materials by Means of Neutron Transmission: Beam Hardening Effect, Nucl. Instrum. Methods Phys. Res., Sect. A, 2006, 565(2), 416–422, DOI:10.1016/j.nima.2006.06.042.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00364f |
| This journal is © The Royal Society of Chemistry 2021 |