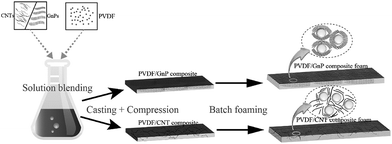
A versatile foaming platform to fabricate polymer/carbon composites with high dielectric permittivity and ultra-low dielectric loss†
Biao
Zhao‡
 ,
Mahdi
Hamidinejad‡
,
Mahdi
Hamidinejad‡
 ,
Chongxiang
Zhao
,
Ruosong
Li
,
Sai
Wang
,
Yasamin
Kazemi
and
Chul B.
Park
,
Chongxiang
Zhao
,
Ruosong
Li
,
Sai
Wang
,
Yasamin
Kazemi
and
Chul B.
Park
 *
*
Microcellular Plastics Manufacturing Laboratory, Department of Mechanical and Industrial Engineering, University of Toronto, 5 King's College Road, Toronto M5S 3G8, Canada. E-mail: park@mie.utoronto.ca; Fax: +1-416-978-7753; Tel: +1-416-978-3053
First published on 20th August 2018
Abstract
There is an urgent need for dielectric-based capacitors to manage the increase in storage systems related to renewable energy production. Such capacitors must have superior qualities that include light weight, a high dielectric constant, and ultra-low dielectric loss. Poly(vinylidene fluoride) (PVDF)/carbon (carbon nanotube (CNT) or graphene nanoplatelet (GnP)) nanocomposite foams are considered promising alternatives to solid PVDF/carbon nanocomposites. This is because they have excellent dielectric properties, which are due to the preferred orientation of their carbon materials occurring in the foaming process. In the PVDF/carbon foams, their microcellular structure significantly influenced their electrical conductivity and dielectric properties. In the PVDF/CNT composite foams, the electrical conductivity was increased by an increased degree of foaming that was below a critical foaming degree. The CNTs even formed conductive networks and this caused current leakage. Thus, in the PVDF/CNT foam sample with an expansion ratio of 4.0 where a high dielectric constant of 80.6 was obtained, a relatively high dielectric loss of 3.51 was observed at the same time. In the PVDF/GnP composite foams, the presence of a microcellular structure forcefully increased the distance between GnPs. This induced and produced the insulating quality of the PVDF/GnP foams. In addition, the parallel graphene nanoplatelets that accompanied this process were close together, and they isolated the polymer layer, or air, as a medium between themselves. An unprecedentedly high dielectric constant of 112.1 and an ultra-low dielectric loss of 0.032 at 100 Hz were obtained from the PVDF/GnP composite foam with a high expansion ratio of 4.4 due to charge accumulation at the aligned conductive filler/insulating polymer (or air bubble) interface.
1. Introduction
Due to population growth, global warming, and the energy crisis, the development of renewable, cost-effective and green energy techniques to supply future generations with renewable energy is both challenging and urgent.1 Of the various energy storage systems that exist, dielectric capacitors with an ultrafast charging–discharging ability have fast become one of the most important new technologies. They could greatly benefit the high-performance power electronics used in military power systems, hybrid electric vehicles, and in some portable electronics.2,3 Ceramic-based dielectric materials, such as SrTiO3,4 SiC,5 and BaTiO3,6 have high dielectric constant values, which is why they play a major role in current practical applications. However, their numerous serious defects, which include an insurmountable brittleness and a low electrical breakdown strength, have hindered the development of dielectric materials.7–9 Compared to conventional ceramic-based dielectric materials, polymer-based dielectric materials have several advantages: large-scale processability, mechanical flexibility, light weight, low cost, and high electrical breakdown strength. However, most polymers' dielectric constant is low compared to the dielectric constant of inorganic ceramics. For example, polypropylene, polystyrene, polyacrylates, and polymethacrylates usually have dielectric constant values between 2 and 5.10To address these issues, significant efforts have been made to create polymer-based dielectric materials with high permittivity. One effective strategy has been to introduce high-dielectric-constant (high-k) ceramics into the polymer matrix, and this strategy has been extensively investigated in the past few decades.11–14 However, it was reported that these composites always possess a high concentration of ceramic particles, which severely damaged the polymer composites' processability and mechanical flexibility. In addition, the poor compatibility between the inorganic fillers and the organic polymer matrix resulted in weak interfacial adhesion and aggregation. This led to a high dielectric loss and a further decrease in the breakdown strength.3
Given the noted EMI shielding properties of polymer/Cu and polymer/Ag composites, we concluded that adding conductive metal nanoparticles to a conductive polymer could effectively enhance its EMI shielding properties. However, we also observed that the dissipation mechanism of these two composites stemmed from dielectric loss or conduction loss due to their lack of magnetic constituents, and that this somehow hampered their usage. In our study, we added the dual loss mechanisms of Ni chains and combined their conduction loss and magnetic loss into the PVDF matrix to examine their electrical conductivity, EMI shielding, and permittivity.15
When a conductive filler is added to a polymer matrix, under an alternating electromagnetic field, charge accumulation between the conductive filler and the polymer matrix would take place. In this situation, numerous nanocapacitors are formed in which the conductive fillers and the polymer matrix are considered as electrodes and a dielectric, respectively. When the content of the conductive filler is less than the percolation threshold, the dielectric constant is enhanced dramatically with an increased filler content, while the dielectric loss is moderately increased. Finally, we may obtain a supercapacitor. However, when the content of the conductive filler is very close to or above the percolation threshold, conductive networks are generated and, thus, significant dielectric loss caused by leakage conduction loss from the capacitors would occur. Consequently, the breakdown of capacitors would occur, and the leakage conduction loss would be beneficial for the EMI shielding properties. Thus, selecting a reasonable content of the conductive filler is the crucial step to determine the application (i.e., capacitor application or EMI-shielding application) of the polymer–conductive filler composites.
In recent years, one-dimensional (1-D) and two-dimensional (2-D) carbon nanomaterials with large aspect ratios have become potential candidates for preparing high-k nanocomposites. Carbon nanotubes (CNTs) and graphene nanoplatelets (GnPs) have been used most frequently for this. In light of the percolation phenomenon, it is well accepted that a sudden increase in the composites' permittivity about one or even several orders of magnitude occurs when the loading of conducting nanomaterials reaches a critical value, i.e., the percolation threshold.13,14 We noted that a large number of conductive networks would form in the composites if the percolation threshold was exceeded. Therefore, to obtain a high permittivity, the amount of conducting nanomaterials in the polymer matrix composites should be near the percolation threshold without exceeding it. This means that the polymer composites with conducting fillers should still act as insulators under this condition. Due to the excellent conductivity of carbon nanomaterials (CNTs or GnPs), a high dielectric constant is easily obtained near the percolation threshold in carbon nanomaterial/polymer composites. However, the formation of conductive channels also increases the leakage current, which causes a high dielectric loss and a low breakdown strength.16,17 This dilemma seriously hampers the development of carbon polymer dielectric composites. Thus, the core question is how to separate the adjacent carbon materials (CNTs or GnPs).
Recently, Ameli et al. investigated the dielectric properties of polypropylene (PP)–MWCNT nanocomposite foams.18,19 They found that adding a microcellular structure effectively improved the dielectric constant and decreased the dielectric loss. They reported a real permittivity of 30 and a dielectric loss of 0.07 for the PP–0.34 vol% MWCNT foams.18 In addition, a microcellular PP–1.25 vol% MWCNT had a dielectric permittivity of 57.2 and a dielectric loss of 0.05.19 In our study, PVDF was used as the polymer matrix. This was because of the strong electric dipole moment of its molecular chains and its high dielectric constants in the range of 8–10.20 Also, the carbon materials (CNTs or GnPs) acted as conductive fillers as we investigated the correlation between a microcellular structure and dielectric properties. Amazingly, an unprecedentedly high real permittivity with an extremely low loss-tangent value was obtained from the foamed PVDF/GnP composites.
2. Experimental section
The preparation of PVDF/carbon composite foams is a two-step process involving fabrication of PVDF/carbon solid composites and foaming of PVDF/carbon solid composites. The PVDF/carbon (CNT or GnP) solid composites were prepared by solvent casting. This was followed by compression-molding, which is similar to a method previously reported to fabricate PVDF/Ni and PVDF/carbon/Ni composite films.21,22 Then, we used a homemade batch foaming device to prepare the PVDF/carbon composite foams.23 Finally, the electrical conductivity and broadband dielectric spectroscopy measurements of the PVDF/carbon composite foams were carried out using an Alpha-N analyzer from Novocontrol Technologies GmbH & Co. KG. The detailed experiment process is shown in the ESI.†3. Results and discussion
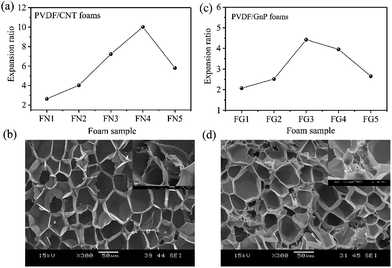
Fig. 1 shows the PVDF/carbon (CNT or GnP) foams' fabrication process. First, both the PVDF particles and the carbon materials (CNTs or GnPs) were added to the DMF solvents and evenly blended. Second, the PVDF/carbon solid composites were fabricated through casting and compression processes. Third, we used a homemade batch foaming device to foam the PVDF/carbon solid composites. Thus, the PVDF/carbon (CNT or GnP) foams were successfully fabricated.Fig. 2 and S(5–7)† show the cellular properties (the expansion ratio, cell morphology and cell density) of various PVDF/CNT and PVDF/GnP composite foams. As shown in Fig. 2(a and c), the expansion ratios of both PVDF/CNT and PVDF/GnP composite foams firstly increased and then decreased with increasing the saturation temperature as observed in the literature.24 It is noteworthy that both PVDF/CNT and PVDF/GnP composite foams display a similar cell density (Fig. S7†), indicating a negligible effect of the cell density on the expansion ratio.25 For the PVDF/CNT composite foams (Fig. S5†), the cell size gradually increased from the FN1 to the FN4 sample, and then it decreased in the FN5 sample. We believe that these changes were the result of variations in the crystal structure of the PVDF matrix, which had been treated at different saturation temperatures.17,26–28 We also investigated the cell morphology of the PVDF/GnP composite foams, and Fig. S6† shows the results. Compared with the four other foam samples, the FG3 sample had the highest cell size. This variation of expansion ratio and morphological foam properties provided a complete platform by which the dielectric properties of the PVDF/carbon composite foams can be tuned.
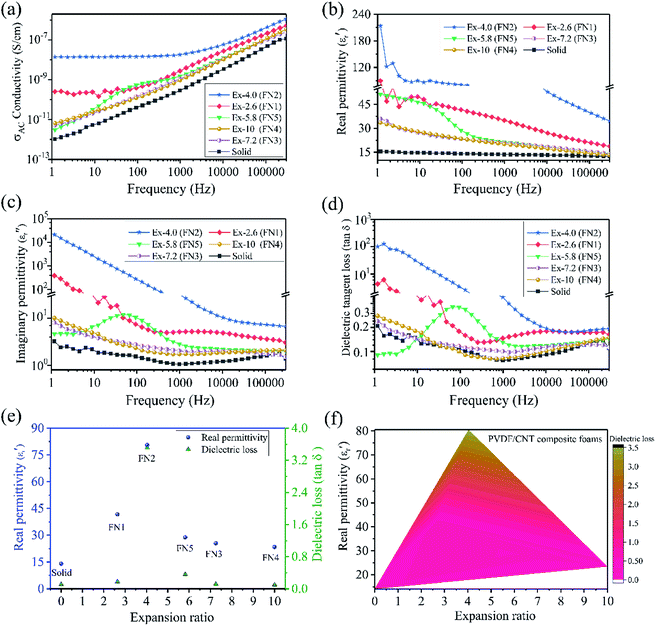
Fig. 3a shows the dependence of the alternating current (AC) conductivity as a function of the frequency of the solid and foamed PVDF/CNT composites. Compared with the solid PVDF/CNT composite, all the PVDF/CNT composite foams had much higher electrical conductivity. This shows that the foaming process could increase the electrical conductivity of the PVDF/CNT composites. This phenomenon is in good agreement with other polymer/CNT foams, such as epoxy/CNT foams,29 PMMA/Fe3O4@MWCNT nanocomposite foams,30 PP/CNT nanocomposite foams,17 and waterborne polyurethane (WPU)/MWCNT foams.31 This might be attributed to the generation of the conductive CNT pathways during the foaming process. Due to the foaming action, the conductive fillers were re-oriented during cell growth and a low void fraction caused a slight filler orientation and relocation. Thus, the slight orientation of the conductive fillers at an appropriate void fraction in foams can increase their conductivity.32 It is noteworthy that the AC conductivity of the solid PVDF/CNT nanocomposite and the FN3–FN5 (a relatively high expansion ratio) foam samples demonstrated a strong dependence on the frequency because of the insulation properties. However, in the FN1 and FN2 (a small expansion ratio) foam samples, the AC conductivities displayed not only a monotonic increase, but also a typical frequency-independence within the low frequency range. This represents a typical transitional percolation behavior from insulation to conduction,33 which indicates that the conductive network was formed in the PVDF polymer matrix. It is well known that this can occur in polymer nanocomposites either through direct “contact” between the conductive fillers or by the “tunneling” of electrons between sufficiently close conductive particles.34 In the former case, the conductive fillers physically establish contact with one another to produce a conductive network, and the electrons can move in the same way they do in a typically and inherently conducting material. However, in the “tunneling” model, the electrons can literally tunnel between two sufficiently close conductive fillers, which are separated by a thin layer of polymer.35 In these PVDF/CNT composite foams, as Fig. 2a shows, the FN1 and FN2 foam samples with a relatively low expansion ratio are in close proximity to and have established some links between the adjacent MWCNTs (Fig. S8(a and b)†). However, in the FN3 foam sample with its high expansion ratio, as the expansion ratio increased, the CNT particles became more perpendicular to the radial direction. Consequently, the CNTs became more parallel with respect to each other regardless of the initial orientation.32,36 The distance between adjacent MWCNTs is too far for an electron to jump. Thus, the FN3–FN5 foam samples with a high expansion ratio had a frequency-dependent AC conductivity, which meant it had insulation properties.
The variation in real permittivity (ε′), imaginary permittivity (ε′′), and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε = ε′′/ε′) of the PVDF/CNT composite foams as a function of the frequency at 300 K is shown in Fig. 3b–d. Compared with the solid PVDF/CNT composite, all the composite foams had enhanced real permittivity (ε′) values. These were the result of a good dispersion state and a certain degree of the CNT alignment, as well as a much higher electrical conductivity (Fig. 3a). This was especially so in the FN1 and FN2 foam samples with a low expansion ratio where, due to enormous interfacial areas (interfacial polarization) and the nearness of the adjacent CNTs, the activation energy (Ea) was decreased.7,37 Thus, the resultant nanocomposite foams' real permittivity was high. Moreover, the dielectric constant decreased dramatically with increased frequency. This was because polarization cannot catch up with the varied electromagnetic fields under high frequency conditions.38 We note that, in the meantime, the samples' imaginary permittivity (Fig. 3c) and dielectric loss (Fig. 3d) were both largely increased. The significant increase of dielectric loss in the FN1 and FN2 foams should be attributed to the CNT agglomerates' percolation network, which caused a dramatic increase in the leakage of currents.39 To clearly show how the foaming method affected the dielectric constant of the PVDF/CNT nanocomposite, we extracted the dielectric constant and the dielectric loss of the solid and foamed PVDF/CNT nanocomposites at 100 Hz. Fig. 3e shows the results. The dielectric constant values of the FN1 (41.7) and FN2 (80.6) foams were increased by nearly three times and six times, respectively, compared to that of their solid counterpart (14.1). The values for the other three foam samples were increased to almost double that of the solid sample. The above results indicated that this foaming platform can effectively improve the dielectric constant of a PVDF/CNT nanocomposite. Compared with other polymer-based composites, such as cellulose/Ag nanofiber (12.9),40 cyanoethyl pullulan polymer/rGO/CNT (32),41 and polypropylene/MWCNT (30),17 the FN2 foam was the most competitive. However, the FN2 and FN1 foams had not only a high dielectric constant, but also a high dielectric loss. Such factors could hamper dielectric-based capacitor applications. It is worth pointing out that when the expansion ratio of the PVDF/CNT composite foam was as high as 4 (FN2 sample), the electrical conductivity, the real permittivity, and the dielectric tangent loss were very high. But as the CNTs were separated by increasing or decreasing the expansion ratio, the conductivity, the real permittivity, and the dielectric tangent loss became low. These numbers are all acceptable and the acceptable window of the expansion ratio was very large. Furthermore, we plotted the real permittivity and the dielectric loss versus the expansion ratio, and the result is shown in Fig. 3f. This correlation amongst the real permittivity, the dielectric loss and the expansion ratio of the foamed PVDF/CNT composites paves a novel way to design such PVDF/CNT composite foams applied in dielectric-based capacitor applications.
δε = ε′′/ε′) of the PVDF/CNT composite foams as a function of the frequency at 300 K is shown in Fig. 3b–d. Compared with the solid PVDF/CNT composite, all the composite foams had enhanced real permittivity (ε′) values. These were the result of a good dispersion state and a certain degree of the CNT alignment, as well as a much higher electrical conductivity (Fig. 3a). This was especially so in the FN1 and FN2 foam samples with a low expansion ratio where, due to enormous interfacial areas (interfacial polarization) and the nearness of the adjacent CNTs, the activation energy (Ea) was decreased.7,37 Thus, the resultant nanocomposite foams' real permittivity was high. Moreover, the dielectric constant decreased dramatically with increased frequency. This was because polarization cannot catch up with the varied electromagnetic fields under high frequency conditions.38 We note that, in the meantime, the samples' imaginary permittivity (Fig. 3c) and dielectric loss (Fig. 3d) were both largely increased. The significant increase of dielectric loss in the FN1 and FN2 foams should be attributed to the CNT agglomerates' percolation network, which caused a dramatic increase in the leakage of currents.39 To clearly show how the foaming method affected the dielectric constant of the PVDF/CNT nanocomposite, we extracted the dielectric constant and the dielectric loss of the solid and foamed PVDF/CNT nanocomposites at 100 Hz. Fig. 3e shows the results. The dielectric constant values of the FN1 (41.7) and FN2 (80.6) foams were increased by nearly three times and six times, respectively, compared to that of their solid counterpart (14.1). The values for the other three foam samples were increased to almost double that of the solid sample. The above results indicated that this foaming platform can effectively improve the dielectric constant of a PVDF/CNT nanocomposite. Compared with other polymer-based composites, such as cellulose/Ag nanofiber (12.9),40 cyanoethyl pullulan polymer/rGO/CNT (32),41 and polypropylene/MWCNT (30),17 the FN2 foam was the most competitive. However, the FN2 and FN1 foams had not only a high dielectric constant, but also a high dielectric loss. Such factors could hamper dielectric-based capacitor applications. It is worth pointing out that when the expansion ratio of the PVDF/CNT composite foam was as high as 4 (FN2 sample), the electrical conductivity, the real permittivity, and the dielectric tangent loss were very high. But as the CNTs were separated by increasing or decreasing the expansion ratio, the conductivity, the real permittivity, and the dielectric tangent loss became low. These numbers are all acceptable and the acceptable window of the expansion ratio was very large. Furthermore, we plotted the real permittivity and the dielectric loss versus the expansion ratio, and the result is shown in Fig. 3f. This correlation amongst the real permittivity, the dielectric loss and the expansion ratio of the foamed PVDF/CNT composites paves a novel way to design such PVDF/CNT composite foams applied in dielectric-based capacitor applications.
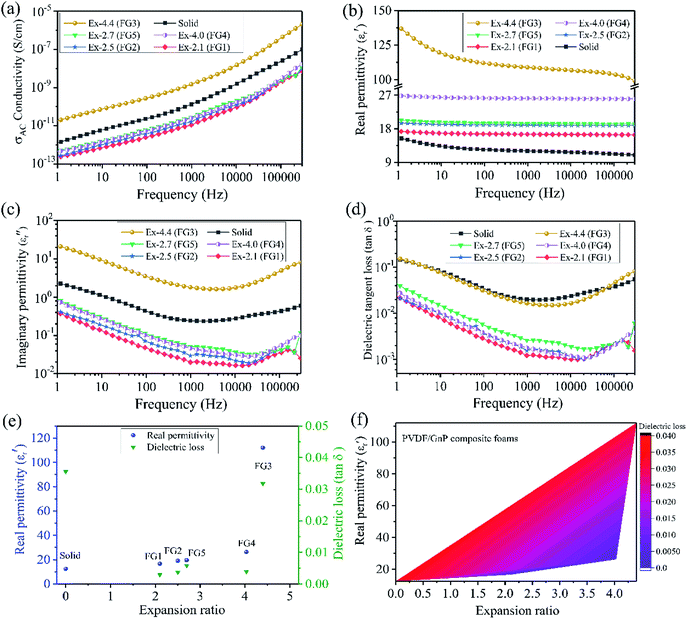
Fig. 4b–d show the frequency-dependent real permittivity (ε′), the imaginary permittivity (ε′′), and the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε) for the solid and foamed PVDF/GnP composites. Astonishingly, all of the PVDF/GnP composite foams displayed a much higher dielectric constant than that of their solid counterpart (Fig. 4b). The Maxwell–Wagner–Sillars (MWS) polarization, which is also called interfacial polarization, for heterogeneous systems plays a very important role in improving the dielectric constant.42,43 The MWS effect is associated with the entrapment of the free charges between the insulator/conductor interfaces. Moreover, the large number of nanocapacitors that form between two parallel GnPs would also enhance the dielectric constant. Furthermore, the FG3 foam had the highest dielectric constant value of the five composite foams, which was due to its relatively high electrical conductivity, and more parallel nanocapacitors. Correspondingly, the imaginary permittivity (Fig. 4c) and the dielectric loss (Fig. 4d) of both the solid and foamed PVDF/GnP composites had low values because of the insulation properties. Moreover, we compared both the dielectric constant and dielectric loss of the solid and PVDF/GnP composite foams at 100 Hz. Fig. 4e shows the results. It is noteworthy that the dielectric constant values of all the foam samples had been significantly increased when compared with the solid sample. Specifically, for the FG3 with the highest expansion ratio, the dielectric constant improved nearly one order of magnitude, and a value of 112.1 was obtained. In addition, it is inspiring that the dielectric loss had ultra-low values of less than 0.05. This meets the requirements for the miniaturization of dielectric capacitors.2 In comparison with the CNT case, the GnP particles cannot easily establish a good contact surface area with each other and, therefore, dielectric loss was not high. So, the maximum dielectric tangent loss was still very low (0.032) at the maximum expansion ratio, which is a unique feature of the GnP case. The dielectric tangent loss numbers were all outstanding and the acceptable window of the expansion ratio was much larger than in the CNT case. Unlike the CNT case, there was no optimal expansion ratio at which the percolation of the GnPs was achieved (Fig. 4a).
δε) for the solid and foamed PVDF/GnP composites. Astonishingly, all of the PVDF/GnP composite foams displayed a much higher dielectric constant than that of their solid counterpart (Fig. 4b). The Maxwell–Wagner–Sillars (MWS) polarization, which is also called interfacial polarization, for heterogeneous systems plays a very important role in improving the dielectric constant.42,43 The MWS effect is associated with the entrapment of the free charges between the insulator/conductor interfaces. Moreover, the large number of nanocapacitors that form between two parallel GnPs would also enhance the dielectric constant. Furthermore, the FG3 foam had the highest dielectric constant value of the five composite foams, which was due to its relatively high electrical conductivity, and more parallel nanocapacitors. Correspondingly, the imaginary permittivity (Fig. 4c) and the dielectric loss (Fig. 4d) of both the solid and foamed PVDF/GnP composites had low values because of the insulation properties. Moreover, we compared both the dielectric constant and dielectric loss of the solid and PVDF/GnP composite foams at 100 Hz. Fig. 4e shows the results. It is noteworthy that the dielectric constant values of all the foam samples had been significantly increased when compared with the solid sample. Specifically, for the FG3 with the highest expansion ratio, the dielectric constant improved nearly one order of magnitude, and a value of 112.1 was obtained. In addition, it is inspiring that the dielectric loss had ultra-low values of less than 0.05. This meets the requirements for the miniaturization of dielectric capacitors.2 In comparison with the CNT case, the GnP particles cannot easily establish a good contact surface area with each other and, therefore, dielectric loss was not high. So, the maximum dielectric tangent loss was still very low (0.032) at the maximum expansion ratio, which is a unique feature of the GnP case. The dielectric tangent loss numbers were all outstanding and the acceptable window of the expansion ratio was much larger than in the CNT case. Unlike the CNT case, there was no optimal expansion ratio at which the percolation of the GnPs was achieved (Fig. 4a).
The conductivity, the real permittivity, and the dielectric tangent loss became relatively larger with an increased expansion ratio. Because of the limited expanding ability of the GnP samples (Fig. 4e), we could not achieve a very high expansion ratio from the GnP samples. Furthermore, as the expansion ratio was increased, the GnP particles would become more perpendicular to the radial direction as in the case of the CNTs.34 Consequently, the GnPs became more parallel with respect to each other regardless of the initial orientation.35 One can note that a large expansion ratio brings the platelets closer in general as well. Consequently, the real permittivity increased. For FG3, the generation of a microcellular structure produced numerous parallel-plate nanocapacitors consisting of GnP pairs as electrodes with the insulating polymer as nanodielectrics. In addition, the increased dielectric constant of the FG3 foam sample also resulted from several factors. FG3 had the highest expansion ratio amongst all the samples. As the degree of foaming increases, the GnPs will be oriented more perpendicular to the radial direction, regardless of their initial orientation. So, initially non-parallel GnPs will become more parallel with respect to each other. Because of the highest expansion ratio of the FG3 foam sample, the GnP–polymer interfaces and the number of nanocapacitors significantly increased. This also decreased the interspace distances between the adjacent GnPs because the polymer melt was compressed between the two growing cells. All these factors led to a higher interface polarization density and dielectric permittivity. Thus, the FG3 foam sample possessed the highest dielectric constant. Fig. 4f presents the correlation between the real permittivity, the dielectric loss and the expansion ratio of the foamed PVDF/GnP composites. Intriguingly, based on this unique two-dimensional contour of the real permittivity and dielectric loss as a function of the expansion ratio, one can design suitable PVDF/GnP composite foams with a high real permittivity and a low dielectric loss.
Table 1 and Fig. 5 show the dielectric properties of various polymer nanocomposites. Our PVDF/carbon composite foams had superior properties of a high dielectric constant and a low dielectric loss. They also save materials. In particular, from Fig. 5, one can clearly notice that the FG3 foam had a high dielectric permittivity and an ultra-low dielectric loss compared with other nanocomposites, which means that it holds much promise for use in electronic capacitor applications.
| Polymer matrix | Nano-filler | Dielectric constant | Dielectric loss | Frequency (Hz) | Ref. |
|---|---|---|---|---|---|
| Cyanate ester | 2 wt% MWCNTs | 103 | 2.5 | 100 | 44 |
| Polypropylene foam | 0.34 vol% MWCNTs | 30 | 0.06 | 100 | 17 |
| Cyanoethyl pullulan polymer | 0.06 wt% (CNT + reduced graphene oxide) | 32 | 0.05 | 100 | 41 |
| Polyimide polymer | 2.7 wt% reduced graphene oxide | 31 | 1.57 | 100 | 45 |
| Poly(vinylidene fluoride-co-trifluoroethylene) | 2 wt% CNTs | 102 | 0.36 | 100 | 46 |
| Poly(vinylidene fluoride) | 1.3 vol% acetylene-black | 56 | 1.2 | 100 | 47 |
| Poly(vinylidene fluoride) | 27 vol% nanocrystalline nickel | 2050 | 10 | 100 | 48 |
| Poly(vinylidene fluoride) | 1.57 wt% SiC | 24 | 0.1 | 100 | 49 |
| Poly(vinylidene fluoride) | 0.5 vol% MWCNTs | 756 | 7 × 104 | 100 | 50 |
| Polypropylene | 3 wt% MWCNTs | 21 | 0.06 | 100 | 51 |
| Poly(vinylidene fluoride) | 0.5 wt% MWCNTs | 46.5 | 1240 | 100 | 52 |
| Hyperbranched polyaniline | 0.5 wt% MWCNTs | 100 | 355 | 100 | 53 |
| Cyanate ester | 1 wt% MWCNTs | 117 | 335 | 100 | 54 |
| Polypropylene foam | 1.25 vol% MWCNTs | ∼57.2 | ∼0.05 | 100 | 18 |
| Poly(vinylidene fluoride) | 1.25 vol% MWCNTs | ∼270 | ∼0.8 | 100 | 55 |
| Poly(vinylidene fluoride) | 8 vol% modified MWCNTs | ∼900 | ∼2 | 100 | 56 |
| Poly(vinylidene fluoride) | 1.78 wt% CNT + 4.82 wt% SiC | 894 | 0.39 | 100 | 57 |
| Poly(vinylidenefluoride-co-trifluoroethylene) | 0.1 wt% single-walled CNTs | 284 | ∼1.0 | 1000 | 58 |
| poly(vinylidene fluoride) | 0.13 vol% acid-treated CNTs | ∼217 | ∼0.4 | 1000 | 59 |
| Poly(vinylidene fluoride) foam | 0.2 wt% MWCNTs | 40.7 | 0.18 | 100 | FN1 |
| Poly(vinylidene fluoride) foam | 0.2 wt% MWCNTs | 80.6 | 3.51 | 100 | FN2 |
| Poly(vinylidene fluoride) foam | 2 wt% GnPs | 112.1 | 0.032 | 100 | FG3 |
| Poly(vinylidene fluoride) foam | 2 wt% GnPs | 26.2 | 0.0039 | 100 | FG4 |
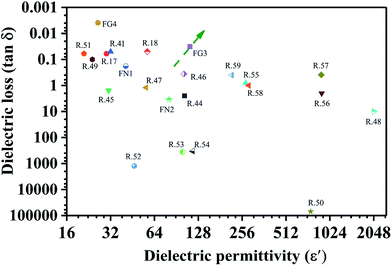 | ||
| Fig. 5 The dielectric properties of various polymer nanocomposites containing carbon fillers (CNTs or graphene) at a frequency of 100 Hz (R is the abbreviation of reference). | ||
Fig. 6 shows how the cellular growth affected the orientations of the carbon materials and the dielectric constant in the PVDF/carbon composite foams. In the PVDF/CNT foams, when the microcellular structures were first introduced into the PVDF system, they induced the CNTs to subtly orient themselves around the cells to shorten the distance between them. However, when the degree of foaming was increased beyond the critical value, the CNTs became fully oriented in alignment with the periphery of the cells, and their serious stretching resulted in their dilution, which meant that they had lost their interconnections. It has been demonstrated that neither a fully isotropic distribution nor a complete alignment of CNTs with the cells is the best orientation to achieve the highest conductivity.60,61 The FN2 foam had a high dielectric constant and this can be described in terms of Maxwell–Wagner–Sillars (MWS) polarization, nanocapacitor formation (CNTs as the electrodes, and a bubble and polymer as the dielectrics), and the percolation behavior.62,63
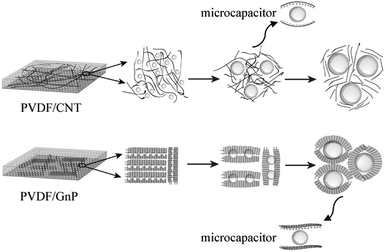 | ||
| Fig. 6 Schematic diagram of cellular growth and the improved dielectric constant mechanism in the PVDF/carbon composite foams. | ||
With respect to the PVDF/GnP composite foams, it appears that adding a blowing gas and thereby a microcellular structure to the composites separated the adjacent GnPs, and this decreased the interconnectivity of GnPs, i.e., the electrical conductivity of the composites (Fig. 4a). But as the degree of foaming increased, the GnPs oriented more perpendicular to the radial direction34 and the interconnectivity was improved while maintaining the insulating nature. The FG3 foam possessed a high dielectric constant and an ultra-low dielectric loss (Fig. 4c and d). In addition to the Maxwell–Wagner–Sillars (MWS) polarization contribution to the dielectric constant, the formation of a larger number of nanocapacitors in the nanocomposite foams (conductive GnPs as the electrodes; an insulating bubble and polymer as the dielectrics) played a major role in improving the dielectric constant.32,43 More precisely, the graphene nanoplatelets were parallel to each other and were isolated by the polymer layer, or air, as a medium between them, as Fig. 5 shows. We believe that the excellent GnP dispersion and the existence of many nanocapacitors in the PVDF polymer foams aid in achieving a high dielectric constant, but with a low GnP loading and an ultra-low dielectric loss.43
4. Conclusions
In summary, we have reported, for the first time, the fabrication of PVDF/carbon (CNT or GnP) nanocomposite foams with an enhanced dielectric constant. We effectively tuned the electrical conductivity and dielectric constant by controlling the microcellular structure. For the PVDF/CNT foams, the electrical conductivity was increased by increasing the foaming degree (that is, the expansion ratio). This was caused by a CNT array orientation, which was brought about by cell force, when the foaming degree was below the critical value. Otherwise, it would have decreased with increased foaming degree. We attributed the highest dielectric constant in the FN2 sample to the Maxwell–Wagner–Sillars polarization, the nanocapacitors, and the percolation behavior. In the PVDF/GnP composites, foaming significantly enhanced the dielectric constant and decreased the dielectric loss, while the insulating nature of the samples was maintained. This resulted in an excellent dielectric property combination. For instance, the FG3 foam sample had the highest expansion ratio, the highest dielectric constant (112.1) and a low dielectric loss of 0.032 at 100 Hz, which resulted from the Maxwell–Wagner–Sillars polarization, and a larger number of nanocapacitors. This novel methodology promises to lead the way to a new design for lightweight energy storage capacitors, which are made from polymer/carbon foams, and which have a high dielectric constant and an ultra-low dielectric loss.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge Solvay's donation of PVDF, NanoXplore's donation of graphene nanoplatelets, and the financial support of the Consortium for Cellular and Microcellular Plastics (CCMCP).References
- Z. L. Wang and J. Song, Science, 2006, 312, 242 CrossRef CAS.
- Z.-M. Dang, J.-K. Yuan, J.-W. Zha, T. Zhou, S.-T. Li and G.-H. Hu, Prog. Mater. Sci., 2012, 57, 660–723 CrossRef CAS.
- X. Zhang, Y. Shen, Q. Zhang, L. Gu, Y. Hu, J. Du, Y. Lin and C.-W. Nan, Adv. Mater., 2015, 27, 819–824 CrossRef CAS.
- J. H. Haeni, P. Irvin, W. Chang, R. Uecker, P. Reiche, Y. L. Li, S. Choudhury, W. Tian, M. E. Hawley, B. Craigo, A. K. Tagantsev, X. Q. Pan, S. K. Streiffer, L. Q. Chen, S. W. Kirchoefer, J. Levy and D. G. Schlom, Nature, 2004, 430, 758 CrossRef CAS PubMed.
- R. Zhang, L. Gao, H. Wang and J. Guo, Appl. Phys. Lett., 2004, 85, 2047–2049 CrossRef CAS.
- J.-Y. Hong and H.-Y. Lu, J. Am. Chem. Soc., 2014, 97, 2256–2263 CAS.
- Z.-M. Dang, M.-S. Zheng and J.-W. Zha, Small, 2016, 12, 1688–1701 CrossRef CAS.
- H. Lv, Y. Guo, G. Wu, G. Ji, Y. Zhao and Z. J. Xu, ACS Appl. Mater. Interfaces, 2017, 9, 5660–5668 CrossRef CAS.
- H. Lv, G. Ji, X. Liang, H. Zhang and Y. Du, J. Mater. Chem. C, 2015, 3, 5056–5064 RSC.
- Y. Qiao, M. S. Islam, K. Han, E. Leonhardt, J. Zhang, Q. Wang, H. J. Ploehn and C. Tang, Adv. Funct. Mater., 2013, 23, 5638–5646 CrossRef CAS.
- Z.-M. Dang, T. Zhou, S.-H. Yao, J.-K. Yuan, J.-W. Zha, H.-T. Song, J.-Y. Li, Q. Chen, W.-T. Yang and J. Bai, Adv. Mater., 2009, 21, 2077–2082 CrossRef CAS.
- Z.-M. Dang, H.-Y. Wang, Y.-H. Zhang and J.-Q. Qi, Macromol. Rapid Commun., 2005, 26, 1185–1189 CrossRef CAS.
- N. Xu, L. Hu, Q. Zhang, X. Xiao, H. Yang and E. Yu, ACS Appl. Mater. Interfaces, 2015, 7, 27373–27381 CrossRef CAS PubMed.
- D. He, Y. Wang, S. Song, S. Liu and Y. Deng, ACS Appl. Mater. Interfaces, 2017, 9, 44839–44846 CrossRef CAS PubMed.
- B. Zhao and C. B. Park, J. Mater. Chem. C, 2017, 5, 6954–6961 RSC.
- H. Lv, Y. Guo, Y. Zhao, H. Zhang, B. Zhang, G. Ji and Z. J. Xu, Carbon, 2016, 110, 130–137 CrossRef CAS.
- Y. Y. Huang and E. M. Terentjev, Adv. Funct. Mater., 2010, 20, 4062–4068 CrossRef CAS.
- A. Ameli, M. Nofar, C. B. Park, P. Pötschke and G. Rizvi, Carbon, 2014, 71, 206–217 CrossRef CAS.
- A. Ameli, S. Wang, Y. Kazemi, C. B. Park and P. Pötschke, Nano Energy, 2015, 15, 54–65 CrossRef CAS.
- Prateek, V. K. Thakur and R. K. Gupta, Chem. Rev., 2016, 116, 4260–4317 CrossRef CAS PubMed.
- B. Zhao, C. Zhao, R. Li, S. M. Hamidinejad and C. B. Park, ACS Appl. Mater. Interfaces, 2017, 9, 20873–20884 CrossRef CAS.
- B. Zhao, S. Wang, C. Zhao, R. Li, S. M. Hamidinejad, Y. Kazemi and C. B. Park, Carbon, 2018, 127, 469–478 CrossRef CAS.
- B. Zhao, C. Zhao, C. Wang and C. B. Park, J. Mater. Chem. C, 2018, 6, 3065–3073 RSC.
- H. E. Naguib, C. B. Park and N. Reichelt, J. Appl. Polym. Sci., 2003, 91, 2661–2668 CrossRef.
- H. E. Naguib, C. B. Park and P. C. Lee, J. Cell. Plast., 2003, 39, 499–511 CrossRef CAS.
- L. Wang, R. E. Lee, G. Wang, R. K. M. Chu, J. Zhao and C. B. Park, Chem. Eng. J., 2017, 327, 1151–1162 CrossRef CAS.
- Y. Guo, N. Hossieny, R. K. M. Chu, C. B. Park and N. Zhou, Chem. Eng. J., 2013, 214, 180–188 CrossRef CAS.
- M. Nofar, A. Ameli and C. B. Park, Polymer, 2015, 69, 83–94 CrossRef CAS.
- J. Li, G. Zhang, H. Zhang, X. Fan, L. Zhou, Z. Shang and X. Shi, Appl. Surf. Sci., 2018, 428, 7–16 CrossRef CAS.
- H. Zhang, G. Zhang, J. Li, X. Fan, Z. Jing, J. Li and X. Shi, Composites, Part A, 2017, 100, 128–138 CrossRef CAS.
- Z. Zeng, H. Jin, M. Chen, W. Li, L. Zhou and Z. Zhang, Adv. Funct. Mater., 2016, 26, 303–310 CrossRef CAS.
- S. Wang, A. Ameli, V. Shaayegan, Y. Kazemi, Y. Huang, H. E. Naguib and C. B. Park, Polymers, 2018, 10, 261 CrossRef.
- Z. M. Dang, L. Wang, Y. Yin, Q. Zhang and Q. Q. Lei, Adv. Mater., 2007, 19, 852–857 CrossRef CAS.
- N. Yousefi, X. Sun, X. Lin, X. Shen, J. Jia, B. Zhang, B. Tang, M. Chan and J.-K. Kim, Adv. Mater., 2014, 26, 5480–5487 CrossRef CAS.
- J. Gao and Y.-L. Loo, Adv. Funct. Mater., 2015, 25, 105–110 CrossRef CAS.
- V. Shaayegan, A. Ameli, S. Wang and C. B. Park, Composites, Part A, 2016, 88, 67–74 CrossRef CAS.
- J.-K. Yuan, S.-H. Yao, Z.-M. Dang, A. Sylvestre, M. Genestoux and J. Bai, J. Phys. Chem. C, 2011, 115, 5515–5521 CrossRef CAS.
- J. Q. Huang, P. Y. Du, L. X. Hong, Y. L. Dong and M. C. Hong, Adv. Mater., 2007, 19, 437–440 CrossRef CAS.
- M. Li, X. Huang, C. Wu, H. Xu, P. Jiang and T. Tanaka, J. Mater. Chem., 2012, 22, 23477–23484 RSC.
- S. Ji, J. Jang, E. Cho, S.-H. Kim, E.-S. Kang, J. Kim, H.-K. Kim, H. Kong, S.-K. Kim, J.-Y. Kim and J.-U. Park, Adv. Mater., 2017, 29, 1700538 CrossRef.
- J.-Y. Kim, T. Kim, J. W. Suk, H. Chou, J.-H. Jang, J. H. Lee, I. N. Kholmanov, D. Akinwande and R. S. Ruoff, Small, 2014, 10, 3405–3411 CrossRef CAS.
- J. C. Dyre and T. B. Schrøder, Rev. Mod. Phys., 2000, 72, 873–892 CrossRef.
- F. He, S. Lau, H. L. Chan and J. Fan, Adv. Mater., 2009, 21, 710–715 CrossRef CAS.
- C. Han, A. Gu, G. Liang and L. Yuan, Composites, Part A, 2010, 41, 1321–1328 CrossRef.
- G. Tian, J. Song, J. Liu, S. Qi and D. Wu, Soft Mater., 2014, 12, 290–296 CrossRef CAS.
- S. Zhang, N. Zhang, C. Huang, K. Ren and Q. M. Zhang, Adv. Mater., 2005, 17, 1897–1901 CrossRef CAS.
- Q. Chen, P. Du, L. Jin, W. Weng and G. Han, Appl. Phys. Lett., 2007, 91, 022912 CrossRef.
- M. Panda, V. Srinivas and A. K. Thakur, Appl. Phys. Lett., 2008, 92, 132905 CrossRef.
- A. B. Dichiara, J. Yuan, S. Yao, A. Sylvestre, L. Zimmer and J. Bai, J. Mater. Chem. A, 2014, 2, 7980–7987 RSC.
- M. Arjmand and U. Sundararaj, Polym. Compos., 2016, 37, 299–304 CrossRef CAS.
- C.-R. Yu, D.-M. Wu, Y. Liu, H. Qiao, Z.-Z. Yu, A. Dasari, X.-S. Du and Y.-W. Mai, Compos. Sci. Technol., 2011, 71, 1706–1712 CrossRef CAS.
- M. Khajehpour, M. Arjmand and U. Sundararaj, Polym. Compos., 2016, 37, 161–167 CrossRef CAS.
- Z. Qiang, G. Liang, A. Gu and L. Yuan, J. Nanopart. Res., 2014, 16, 2391 CrossRef.
- X. Zhang, G. Liang, J. Chang, A. Gu, L. Yuan and W. Zhang, Carbon, 2012, 50, 4995–5007 CrossRef CAS.
- L. Wang and Z.-M. Dang, Appl. Phys. Lett., 2005, 87, 042903 CrossRef.
- Z. M. Dang, L. Wang, Y. Yin, Q. Zhang and Q. Q. Lei, Adv. Mater., 2007, 19, 852–857 CrossRef CAS.
- J. Yuan, S. Yao, W. Li, A. Sylvestre and J. Bai, J. Phys. Chem. C, 2014, 118, 22975–22983 CrossRef CAS.
- K. Y. Cho, Y.-J. Lee, H.-J. Kim, H. G. Yoon, S. S. Hwang, Y.-K. Han and K.-Y. Baek, Polymer, 2015, 77, 55–63 CrossRef CAS.
- G. S. Kumar, D. Vishnupriya, K. S. Chary and T. U. Patro, Nanotechnology, 2016, 27, 385702 CrossRef.
- F. Du, J. E. Fischer and K. I. Winey, Phys. Rev. B, 2005, 72, 121404 CrossRef.
- A. Ameli, P. U. Jung and C. B. Park, Carbon, 2013, 60, 379–391 CrossRef CAS.
- Z. M. Dang, Y. H. Lin and C. W. Nan, Adv. Mater., 2003, 15, 1625–1629 CrossRef CAS.
- C. W. Nan, Y. Shen and J. Ma, Annu. Rev. Mater. Res., 2010, 40, 131–151 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta05556d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |