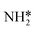Elementary kinetics of nitrogen electroreduction to ammonia on late transition metals†
Gholamreza
Rostamikia
a,
Sharad
Maheshwari
b and
Michael J.
Janik
 *b
*b
aUniversity of North Carolina – Wilmington, Department of Chemistry and Biochemistry, Wilmington, NC, USA
bThe Pennsylvania State University, Department of Chemical Engineering, University Park, PA, USA. E-mail: mjanik@psu.edu; Fax: +(814)865 7846; Tel: +(814)863 9366
First published on 28th November 2018
Abstract
Developing small scale nitrogen to ammonia conversion devices could greatly help sustainable agriculture. The lack of effective cathode materials for reduction of nitrogen to ammonia puts a major limitation on developing small scale electrochemical ammonia production devices that can operate at low pressures and temperatures. In this study, the electrochemical nitrogen reduction reaction (NRR) mechanism is investigated over late transition metals. Activation barriers for possible rate limiting steps are calculated using density functional theory (DFT) methods and are converted to potential dependent electrochemical barriers. Associative and dissociative paths are evaluated and the associative path shows lower barriers on all metals considered at NRR potentials. Brønsted–Evans–Polanyi (BEP) relationships are evaluated for rate limiting steps and a “kinetic volcano” is demonstrated for catalyst optimization. Rhodium (Rh) and iron (Fe) appear to have the lowest kinetic barriers to convert N2 to NH3. A large over-potential, however, is required to convert nitrogen to ammonia over all the surfaces considered. The hydrogen evolution reaction (HER) has a lower activation barrier compared to NRR, demonstrating the kinetic selectivity challenge.
1. Introduction
The Haber–Bosch process has enabled our world to feed 7 billion people.1 Invention of this process enabled mass production of ammonia, a fertilizer ingredient that helped population growth to current levels. Although the Haber–Bosch process is well optimized, it requires high pressure and temperature and cannot be used for small scale ammonia production. Hydrogen gas and nitrogen react at high pressures and temperatures over an iron catalyst to produce ammonia:| N2 + 3H2 → 2NH3 | (1) |
This process requires a large infrastructure and capital investment. Development of small scale ammonia production devices, powered by renewable sources and operating at ambient pressure and temperature, can greatly help sustainable agriculture.
Electrochemical reduction of nitrogen to ammonia has gained interest in the past few decades.2,3 In this process, nitrogen can reduce to ammonia in an aqueous environment at the cathode using 6 electrons and water as the source of hydrogen:
| N2 + 6H2O + 6e− → 2NH3 + 6OH− | (2) |
The poor performance of the cathode electrocatalyst puts a major limitation on practicality of these devices. Multiple recent studies point out that, due to low catalytic activity, large overpotentials are required to reduce nitrogen to ammonia.4,5 The undesirable hydrogen evolution reaction (HER) also greatly reduces the Faradaic efficiency to less than 10% at ambient conditions:4,6–8
| 2H+ + 2e− + * → H2 + * | (3) |
Multiple materials9,10 including metals, alloys,11 enzymes12 and metal nitrides13 have been tested for NRR, however, all tested materials suffer from low selectivity and activity for this reaction. Lan et al. tested platinum for the reduction reaction and observed a large overpotential and a Faradaic efficiency below 1% in the presence of water; 99% of the electricity was used to produce hydrogen rather than ammonia.6 Qing et al. reported a 2.1% faradaic efficiency at 220 °C using platinum electrodes.8 Cook et al. tested ruthenium for this reaction and reported an extremely low faradaic efficiency of 0.0015%.14 Kordali et al. also tested ruthenium and reported a faradaic efficiency less than 1% for nitrogen reduction.15 Iron has been tested at ambient pressure, showing low current efficiencies.16 Licht et al. used an Fe2O3 cathode catalyst in a molten electrolyte cell and reported 35% electrolysis efficiency, though requiring an elevated temperature of around 200 °C.7
Low NRR activity and selectivity makes experimental determination of mechanism, or even relative activity of different catalysts, difficult to determine. NRR is a complex reaction that goes through at least 6 elementary steps. Due to the complexity of NRR and experimental limitations to identify reaction intermediates, electronic structure calculations have been used to help explain the reaction mechanism and limiting steps.4,5,17–19 Montoya et al. used DFT calculations of elementary step reaction free energies to determine possible rate limiting steps.4 Their findings illustrate that late transition metal catalysts such as platinum, palladium, nickel, cobalt and ruthenium are limited by the reductive adsorption of nitrogen on the surface
| N2(gas) + * + H+(aq) + e− → N2H* | (4) |
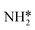
 | (5) |
These findings are solely based on elementary step thermodynamics, embedding the assumption that activation barriers of these reactions correlate with the reaction energies across different metals.
Herein, we use density functional theory (DFT) methods to explicitly evaluate the elementary reaction barriers of NRR on late transition metal surfaces. A (111) surface is used to model the reaction steps on FCC metals with comparison to barriers on iron (110 surface) and ruthenium (0001) surfaces. Activation energies of the initial reductive adsorption of nitrogen are calculated and compared with nitrogen dissociation barriers. We then consider the barriers to reactions (4) and (5) above, as these were proposed to be the rate limiting steps across many metals based on elementary step reaction energies,4,5 and had the highest DFT-calculated barriers on the Fe(100) surface.20 We evaluate the reliability of Brønsted–Evans–Polanyi (BEP) relationships that correlate activation barriers with corresponding reaction energies across fcc (111) surfaces. Though these correlations only roughly hold, they are used to show a “kinetic volcano” in which the trade-off between strong and weak surface–nitrogen binding is seen to optimize the elementary reaction kinetics. NRR barriers are compared with HER barriers to quantify the challenge in developing a selective NRR electrocatalyst.
2. Computational methods
All calculations were performed using the ab initio total-energy and molecular-dynamics Vienna ab initio simulation program (VASP) developed at the Institute for Material Physics at the University of Vienna.21–23 The electronic structure was represented using the Perdew-Wang24 form of the generalized gradient approximation (GGA) and the projector augmented wave method. Exchange and correlation energies of iron were calculated using the Perdew, Burke, and Ernzerhof (PBE) functional25 described by GGA. A cut off energy of 450 eV was used for the plane wave basis set. A 5 × 5 × 1 Monkhorst–Pack mesh was used for sampling of the first Brillouin zone.26 For all metals, other than iron and nickel, calculations were spin-restricted. During structural optimizations, the forces on all atoms were reduced to less than 0.05 eV Å−1. The climbing image nudged elastic band (CI-NEB) method was used to isolate the transition states.27,28 In each transition state search, four images were used between the initial and final state. An image with highest energy and an absolute tangential force of less than 0.05 eV Å−1 was identified as the transition state and was confirmed to have a single imaginary harmonic vibrational frequency. The harmonic oscillator approximation was used to calculate vibrational modes and to determine the zero-point vibrational frequency (ZPVE) and vibrational entropic corrections to the total energy. Surfaces of M(111) metals (M = Pt, Pd, Ni, Rh, Cu and Ir), Ru(0001) and Fe(110) were modeled using 3 × 3 four layer slabs with the bottom two layers constrained and top two layers allowed to relax. A 15 Å vacuum space was inserted between the periodic surface slabs and dipole corrections were added in the surface normal direction to remove unphysical periodic dipole interactions.To evaluate the activation barrier for the initial reductive adsorption of nitrogen (eqn (4)), the barrier of the non-electrochemical hydrogenation step was calculated:
| N2(gas) + H2O + H* → N2H* + H2O | (6) |
A Heyrovsky-like mechanism was assumed for the proton transfer where the reaction is assisted with a water molecule. Barriers are referenced to gas phase N2, as molecular nitrogen binds very weakly to the majority (other than Fe) surfaces considered herein. The energy of the transition state for reaction (6) was referenced to the free energy of gas phase nitrogen and aqueous phase water at 298 K.
| Ga1 = GTS − GH* − GH2O(aq) − GN2(gas) | (7) |
This non-electrochemical activation barrier was converted to the potential dependent electrochemical barrier of reaction (4) using our previously developed method:29
| Ga1(U) = Ga1(U0) + β(U − U0) | (8) |
For most electrochemical systems, β falls in the range of 0.3–0.7.30 An approximate value of β = 0.5 is used in all calculations to estimate the potential dependent activation barriers.
Similarly, the activation barrier (Ga2) for the reductive hydrogenation of NH* species (reaction (5)) is calculated using the non-electrochemical barrier for:
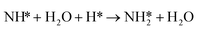 | (9) |
To confirm the dominant reaction path, the activation barrier of N2 dissociation is calculated:
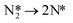 | (10) |
The transition state energy is referenced to the free energy of nitrogen in the gas phase
| Ga3 = GTS − G* − GN2(gas) | (11) |
The hydrogen evolution reaction (reaction (3)) can be written as following two elementary steps:
| H+ + e− + * → H* | (12) |
| 2H* → H2(gas) + * | (13) |
| H* + H2O → H2O + H* | (14) |
The activation barrier is then made potential dependent equivalently to eqn (8). Similarly, the activation barrier for the Tafel step (eqn (13)) is also calculated using VASP on a 3 × 3 surface cell
| 2H* → H2(gas) + * | (15) |
3. Results and discussion
Density functional theory calculations are used to determine the elementary barriers in the NRR reaction on late transition metal surfaces. We first consider the relative barriers for N2 dissociation and N2 reduction to N2H* to demonstrate that the associative path is dominant (section 3.1). In section 3.2, we report the barriers for NH* reduction to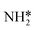 , and compare these barriers with N2H* formation barriers to illustrate the trade-offs in elementary step kinetics in optimizing NRR catalysts. We then compare the elementary barriers for NRR with those for HER on the same metals calculated with the same methods in order to quantify the NRR selectivity challenge based on elementary kinetics (section 3.3).
, and compare these barriers with N2H* formation barriers to illustrate the trade-offs in elementary step kinetics in optimizing NRR catalysts. We then compare the elementary barriers for NRR with those for HER on the same metals calculated with the same methods in order to quantify the NRR selectivity challenge based on elementary kinetics (section 3.3).
3.1. Elementary barriers for initial associative and dissociative paths
Little experimental evidence is available regarding the reaction path and limiting steps of electrochemical nitrogen reduction. However, DFT reaction free energies suggest that the initial step of reductive adsorption of N2 (eqn (4)) is limiting across most late transition metals and the associative reaction path is favorable. Based on the elementary step thermodynamic data, it is proposed that the N2 molecule will not initially dissociate on the surface, instead hydrogenating to form N2H*.4 As this conclusion has been reached without availability of DFT barriers, we first assess the relative barriers of initial dissociation and reduction of N2 to N2H*. Fig. 1 illustrates the configuration of reactants, products and transition states for N2 reduction on the Pt(111) surface. Images of all structures on all surfaces considered are included in the ESI.† N2H* has a strong preference to bind parallel to the surface, with an “end-on” adsorption 0.3 eV higher in energy on Pt(111) and 0.75 eV higher on Fe(110). We have therefore chosen to orient N2 parallel to the surface in the initial state to facilitate location of the optimal parallel orientation of the N2–H* formation transition state. N2 binds very weakly to all non-Fe surfaces considered (and adsorbs parallel on Fe surfaces), and our activation barriers are reported with reference to the gas phase N2 energy due to expected low coverage of adsorbed molecular N2. The energy of the initial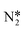 state, therefore, does not enter into the reported results. The potential dependent activation barriers for N2 reductive adsorption, across low-index surfaces of a series of late transition metals, were calculated at 0 V-RHE using eqn (8) and are compared with N2 dissociation barriers.
state, therefore, does not enter into the reported results. The potential dependent activation barriers for N2 reductive adsorption, across low-index surfaces of a series of late transition metals, were calculated at 0 V-RHE using eqn (8) and are compared with N2 dissociation barriers.
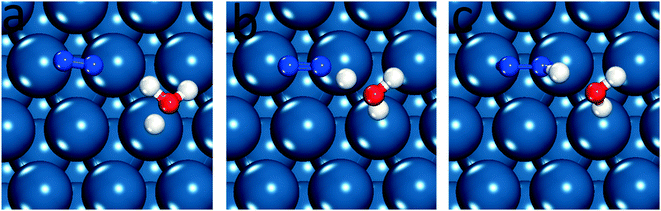 | ||
| Fig. 1 Equilibrium and transition states for N2 reduction to N2H* on Pt(111), (a) initial state, (b) transition state and (c) final state. | ||
Fig. 2 plots N2 reduction and dissociation barriers against the N* binding energy (relative to gas phase 1/2 N2). As the N2H* binding energy correlates well with the N* binding energy,5 this represents a BEP plot with the x-axis giving a surrogate measure of the reaction energy for reduction, and a direct measure of the reaction energy for dissociation. The BEP relationship holds very well for N2 dissociation on (111) surfaces of FCC metals.32 The values calculated here are in good agreement with previously reported N2 dissociation barriers on similar surfaces.32–35 For the FCC metals, the N2 dissociation barriers range from 2.03 eV for the Ni(111) surface to 4.36 eV for the Cu(111) surface. Fe and Ru bind N* stronger such that the N2 dissociation barrier is 1.72 eV on the Ru(0001) surface and 0.59 eV on the Fe(110) surface.
The BEP relationship for N2 reduction does not hold well, as the barriers show only a rough linear correlation with the nitrogen binding energy for FCC metals. For FCC metals, reductive N2 adsorption barriers range from 1.36 eV on the Rh(111) surface to 2.57 eV on the Cu(111) surface at 0 V-RHE. For the FCC metals, the N2 dissociation barrier is significantly higher than the reductive N2 adsorption barrier at 0 V-RHE. The smallest difference is on the Rh(111) surface where the N2 dissociation barrier is 1.05 eV higher. Decreasing the potential will further decrease the reductive N2 adsorption barrier (viaeqn (8)), and, therefore, the reductive N2 adsorption barrier is lower than the dissociation barrier at all NRR conditions on all these FCC(111) surfaces. We reach the same conclusion based on reaction energies alone,4 that ambient condition NRR will follow an associative mechanism. This conclusion must be qualified by noting that the results presented consider only low index facets, whereas N2 dissociation would be more facile on stepped surfaces. As we also have not considered N2H* formation at steps, the results presented here are only directly applicable to the low index surfaces considered.
For Ru(0001) surface, the N2 dissociation barrier is 0.08 eV higher than the reductive N2 adsorption barrier at 0 V-RHE. Alternatively, for Fe(110) surface, the N2 dissociation barrier is 0.22 eV lower than the reductive N2 adsorption barrier at 0 V-RHE. Reductive overpotentials will lead to preferential initial reduction rather than dissociation, though the two mechanisms will be competitive at typical NRR conditions.
As the N2 reduction barriers do not correlate well with N* binding energies, we considered a more direct BEP correlation with the product formation N2H* energy. Fig. 3 shows a more reliable correlation for the FCC metals (R2 = 0.83 compared to 0.66 using N* binding energies). We use N2H* binding energy, rather than N* binding energy, as our descriptor for predicting activation barriers due to this stronger correlation. The non-FCC Ru(0001) and Fe(110) surfaces show considerable deviation relative to the FCC(111) trend.
3.2. NH* to 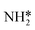 reduction and kinetic trade-offs in NRR catalyst optimization
reduction and kinetic trade-offs in NRR catalyst optimization
Montoya et al. calculated the ΔG of all NRR elementary steps on (111) and (211) surfaces of many transition metals.4 Based on the elementary step thermodynamics, they suggest that most late transition metals were limited by the initial reductive hydrogenation of nitrogen on the surface, in agreement with the large barriers for this step reported in the previous section. Elementary step thermodynamics suggested that NRR might be limited by hydrogenation of NH* on strongly binding transition metals: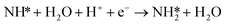 | (16) |
We therefore determined the activation barrier for the NH* reduction. Fig. 4 illustrates the preferred adsorption configuration of the initial state, transition state and final state on the Pt(111) surface.
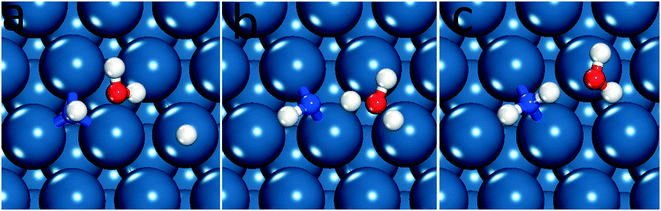 | ||
| Fig. 4 Reaction path for NH* hydrogenation on the Pt(111) surface, (a) initial state, (b) transition state and (c) final state. | ||
On Pt(111) the dissociating O–H bond of H2O is extended from 0.98 Å in the initial state to 1.02 Å in the transition state. The forming N–H bond distance is 1.76 Å as the H is shared between O and N at the transition state. Similarly, the transition state for NH* hydrogenation was located for the same surfaces used in the previous section. The NH* reduction barriers are plotted along with the 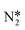 reduction barriers at 0 V-RHE in Fig. 5. All non-electrochemical (hydrogenation) barriers and U0 values are given in the ESI.†
reduction barriers at 0 V-RHE in Fig. 5. All non-electrochemical (hydrogenation) barriers and U0 values are given in the ESI.†
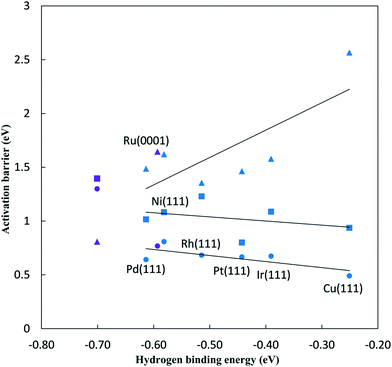
The reductive N2 adsorption and NH* reduction barriers are plotted against the N2H* binding energy at 0 V-RHE in Fig. 5. For FCC metals, NH* reduction barriers range from 0.8 eV for the Pt(111) surface to 1.23 eV for the Rh(111) surface at 0 V-RHE (R2 = 0.37). Fe(110) has a large barrier for NH* reduction as iron binds NH* strongly. Surfaces with stronger N2H* binding, generally, have higher barriers for NH* reduction This is in contrast with the N2H* formation, such that the slopes of barriers for N2 reduction against the N2H* binding (0.93) is positive and sharper than that for NH* reduction (−0.21).
For all FCC surfaces, the reductive N2 adsorption has a higher barrier than NH* reduction and, therefore, limits the overall NRR rate. This is consistent with conclusions based on elementary step thermodynamics.4
Initial N2 reduction and NH* reduction have been considered rate limiting steps for the NRR based on the thermodynamic equilibrium data and limiting potentials. By considering these steps as kinetic rate limiting steps for the NRR, Fig. 5 represents a kinetic volcano for the NRR. Though the data in this figure are barriers at 0 V-RHE, both data sets would move down in barrier equivalently if potential was lowered, provided both steps had the same symmetry coefficient. The rate limiting step is determined by the higher barrier between N2 and NH* reduction steps. Therefore, the crossing point of the kinetic volcano would optimize the NRR rate. For the FCC metals, these lines do not cross suggesting that a stronger binding transition metal is required to lower the effective barrier on FCC metals. This is consistent with the purely “thermodynamic volcano”, which indicates that the optimal catalyst bind slightly stronger to reaction intermediates.4 Based on the thermodynamic volcano, this crossing point falls between ruthenium and rhenium which both bind stronger to reaction intermediates than the FCC(111) surfaces we considered. Alternatively, if we consider the Fe(110) surface in the correlations, the crossing point falls between ruthenium and rhodium on the right and iron on the left side suggesting that an optimal transition metal binds stronger than ruthenium and rhodium and weaker than iron to the reaction intermediates. However, data scatter from the correlations and error associated with the reaction path are significant, and if we examine the DFT barriers directly rather than the correlations, it would be difficult to differentiate between ruthenium, iron, rhodium and even platinum. Kinetic volcano and elementary thermodynamics are in qualitative agreement and both suggest that for strong binding catalysts, such as iron, the reaction is limited by NH* reduction, and weak binding catalysts are limited by initial N2 to N2H* reduction. If we assume that data scattered from the correlations are less reliable than the correlations themselves, we conclude that an optimal catalyst binds N2H* stronger than ruthenium and weaker than iron. Alloying to weaken N2H* binding on Fe might reduce the overpotentials required for the N2 reduction.
The kinetic volcano suggests that the barrier for the rate limiting step at 0 V-RHE will be 1.15 eV on the optimal catalyst, which is a significant barrier in line with the low NRR activity on all tested metals at room temperature. The effective NRR barriers range from 1.36 eV on the Rh(111) surface to 2.57 eV on the Cu(111) surface at 0 V-RHE, suggesting that none of these transition metals can effectively convert nitrogen to ammonia at 0 V-RHE (Table 1). Therefore, large overpotentials are required to produce ammonia on all these transition metals. Decreasing the electrode potential reduces the effective NRR barrier, with the barrier decreasing by 0.5 eV if the voltage is lowered by 1 V if a β of 0.5 is assumed. The overpotential required to decrease the effective NRR barrier to a reasonable value of 0.4 eV is calculated from eqn (9) and is presented in Table 2. The required overpotential for N2 reduction varies from 1.91 V for Rh(111) surface to 4.33 V for Cu(111) surface. These large overpotentials suggest that nitrogen reduction on all these surfaces is very inefficient and energy intensive. Experimental results also show that NRR has a low rate at small overpotentials over various transition metal surfaces.1,15,36
| Surface | 0 V-RHE barrier (eV) | Overpotential (V-RHE) |
|---|---|---|
| Pt(111) | 1.46 | −2.13 |
| Ir(111) | 1.58 | −2.36 |
| Rh(111) | 1.36 | −1.91 |
| Cu(111) | 2.57 | −4.33 |
| Ni(111) | 1.62 | −2.44 |
| Pd(111) | 1.49 | −2.17 |
| Fe(110) | 1.39 | −1.99 |
| Surface | G a,H (eV) at 0 V RHE |
|---|---|
| Pt(111) | 0.25 |
| Ir(111) | 0.78 |
| Rh(111) | 0.94 |
| Cu(111) | 1.13 |
| Ni(111) | 0.98 |
| Pd(111) | 0.76 |
| Ru(0001) | 1.06 |
| Fe(110) | 1.08 |
3.3. Hydrogen evolution reaction (HER) competition with N2 reduction
In addition to large overpotentials and low catalytic activity, the NRR reaction is challenged by poor selectivity due to the competing HER. The potential dependent proton adsorption barriers and hydrogen evolution barriers (Tafel reaction) are calculated in order to quantify the relative barriers to nitrogen reduction.4. Summary and conclusions
Previous DFT studies have suggested rate limiting steps and reaction paths for NRR on late transition metals, but did so based on elementary step thermodynamics without explicit consideration of potential dependent barriers for electrochemical steps. Elementary activation barriers were reported for initial N2 reduction, N2 dissociative adsorption, reduction of surface bound NH*, and the Volmer and Tafel steps of HER. Low index surfaces of late transition metals were considered. A “kinetic volcano” was developed for nitrogen reduction over (111) surfaces of FCC metals. The qualitative conclusions reached based on elementary kinetics match those based on elementary step thermodynamics – that weakly binding metals are limited by initial N2 activation and strongly binding metals are limited by reduction of surface bound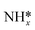 species. Kinetic barriers suggest large overpotentials for NRR, suggesting low activity and high overpotentials of all late transition metals (or at least their low index facets). NRR barriers are greater than 1 eV on all surfaces considered, significantly exceeding those for HER calculated with the same approach. The low activity due to high NRR barriers and low selectivity due to lower HER barriers demonstrate the extreme challenge in developing active and selective NRR electrocatalysts.
species. Kinetic barriers suggest large overpotentials for NRR, suggesting low activity and high overpotentials of all late transition metals (or at least their low index facets). NRR barriers are greater than 1 eV on all surfaces considered, significantly exceeding those for HER calculated with the same approach. The low activity due to high NRR barriers and low selectivity due to lower HER barriers demonstrate the extreme challenge in developing active and selective NRR electrocatalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The US Department of Energy, Office of Science, Basic Energy Sciences, Catalysis Science Program supported this work, under award # DE-SC0016529. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575. SM acknowledges training provided by the Computational Materials Education and Training (CoMET) NSF Research Traineeship (grant number DGE-1449785).References
- J. N. Renner, L. F. Greenlee, K. E. Ayres and A. M. Herring, Electrochem. Soc. Interface, 2015, 24, 51–57 CrossRef CAS.
- J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. M. Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360, 6391 Search PubMed.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500 CrossRef.
- J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186 CrossRef CAS PubMed.
- E. Skulason, T. Bligaard, S. Gudmundsdottir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jonsson and J. K. Norskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC.
- R. Lan, J. T. S. Irvine and S. Tao, Sci. Rep., 2013, 3, 1145 CrossRef PubMed.
- S. Licht, B. Cui, B. Wang, F.-F. Li, J. Lau and S. Liu, Science, 2014, 345, 637–640 CrossRef CAS PubMed.
- G. Qing, R. Kikuchi, S. Kishira, A. Takagaki, T. Sugawara and S. T. Oyama, J. Electrochem. Soc., 2016, 163, E282–E287 CrossRef CAS.
- G.-F. Chen, S. Ren, L. Zhang, H. Cheng, Y. Luo, K. Zhu, L.-X. Ding and H. Wang, Small Methods, 2018, 1800337 CrossRef.
- X. Cui, C. Tang and Q. Zhang, Adv. Energy Mater., 2018, 8, 1800369 CrossRef.
- R. Manjunatha and A. Schechter, Electrochem. Commun., 2018, 90, 96–100 CrossRef CAS.
- R. D. Milton, S. Abdellaoui, N. Khadka, D. R. Dean, D. Leech, L. C. Seefeldt and S. D. Minteer, Energy Environ. Sci., 2016, 9, 2550–2554 RSC.
- X. Yang, J. Nash, J. Anibal, M. Dunwell, S. Kattel, E. Stavitski, K. Attenkofer, J. G. Chen, Y. Yan and B. Xu, J. Am. Chem. Soc., 2018, 140, 13387–13391 CrossRef CAS PubMed.
- R. L. Cook and A. F. Sammells, Catal. Lett., 1988, 1, 345–349 CrossRef CAS.
- V. Kordali, G. Kyriacou and C. Lambrou, Chem. Commun., 2000, 1673–1674, 10.1039/B004885M.
- S. Grayer and M. Halmann, J. Electroanal. Chem. Interfacial Electrochem., 1984, 170, 363–368 CrossRef CAS.
- S. Back and Y. Jung, Phys. Chem. Chem. Phys., 2016, 18, 9161–9166 RSC.
- A. L. Garden and E. Skúlason, J. Phys. Chem. C, 2015, 119, 26554–26559 CrossRef CAS.
- L. Rao, X. Xu and C. Adamo, ACS Catal., 2016, 6, 1567–1577 CrossRef CAS.
- S. Maheshwari, G. Rostamikia and M. J. Janik, J. Chem. Phys., 2018, 150, 041708 CrossRef.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Rostamikia, A. J. Mendoza, M. A. Hickner and M. J. Janik, J. Power Sources, 2011, 196, 9228–9237 CrossRef CAS.
- A. Bard, L. Faulkner, A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2001, p. 2002 Search PubMed.
- A. C. Lausche, A. J. Medford, T. S. Khan, Y. Xu, T. Bligaard, F. Abild-Pedersen, J. K. Nørskov and F. Studt, J. Catal., 2013, 307, 275–282 CrossRef CAS.
- T. R. Munter, T. Bligaard, C. H. Christensen and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 5202–5206 RSC.
- C. H. Christensen and J. K. Nørskov, J. Chem. Phys., 2008, 128, 182503 CrossRef PubMed.
- J. A. Herron, P. Ferrin and M. Mavrikakis, J. Phys. Chem. C, 2015, 119, 14692–14701 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L. B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl and C. J. H. Jacobsen, J. Catal., 2002, 209, 275–278 CrossRef.
- R. Lan and S. Tao, RSC Adv., 2013, 3, 18016–18021 RSC.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- K. Nobuhara, H. Kasai, W. A. Diño and H. Nakanishi, H2 dissociative adsorption on Mg, Ti, Ni, Pd and La Surfaces, 2004 Search PubMed.
- C. T. Rettner, H. A. Michelsen and D. J. Auerbach, J. Chem. Phys., 1995, 102, 4625–4641 CrossRef CAS.
- W. Dong, G. Kresse and J. Hafner, J. Mol. Catal. A: Chem., 1997, 119, 69–76 CrossRef CAS.
- N. B. Arboleda and H. Kasai, Surf. Interface Anal., 2008, 40, 1103–1107 CrossRef CAS.
- W. Dong and J. Hafner, H2 dissociative adsorption on Pd(111), 1997 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cy01845f |
| This journal is © The Royal Society of Chemistry 2019 |