Nanoconfinement greatly speeds up the nucleation and the annealing in single-DNA collapse

Abstract

Manipulating and measuring single-molecule dynamics and reactions in nanofluidics is a rapidly growing field with broad applications in developing new biotechnologies, understanding nanoconfinement effects in vivo, and exploring new phenomena in confinement. In this work, we investigate the kinetics of DNA collapse in nanoslits using single T4-DNA (165.6 kbp) and λ-DNA (48.5 kbp), with particular focus on the measurement of the nucleation and annealing times. Fixing the ethanol concentration at 35% and varying the slit height from 2000 to 31 nm, the nucleation time dramatically decreases from more than 1 hour to a few minutes or less. The increased collapsed rate results from the larger free energy experienced by coiled DNA in confinement relative to compacted DNA. Our results also shed light on other conformational transitions in confinement, such as protein folding.

---

1. Introduction

Nanofluidics provides a platform to explore new phenomena in nanoconfinement,^1–4 develop biotechnologies to manipulate and measure biomolecules,^5–8 as well as understand nanoconfinement effects by membranes and cytoskeleton in vivo.⁹ The effects of nanoconfinement are usually caused by spatial constraint,¹⁰ high surface–volume ratio,¹ and altered hydrodynamics as well as transport properties.¹ Nanoconfinement may greatly affect conformation,¹⁰ dynamics¹⁰ and reactions^11,12 of molecules, or provide conveniences in observing conformations and reactions¹³ through molecular stretching.

DNA molecules in nanofluidic devices have been extensively investigated to develop genome mapping technology, explore new scaling regimes of confined polymers,^14–17 and discover novel ways of manipulating single DNA molecules.^7,18–20 Quantitative data for the equilibrium conformation and dynamics of DNA in nanofluidics with well-defined geometries has led to great successes in critical examinations of classic theories about confined polymers and the improvement of those theories.^10,14,15,21 In this work, we attempt to extend such quantitative analysis from DNA equilibrium properties to non-equilibrium properties; more specifically, toward describing DNA collapse in nanofluidics. We note that other non-equilibrium DNA behaviors in nano-confinement have also been investigated previously.^22–26 The DNA collapse we investigate here is a kinetic process, the effect of nanoconfinement on DNA collapse can provide more general insights about how confinement affects reaction rates. In addition, DNA collapse can be used to reversibly control gene expression.²⁷In vivo, DNA collapse is necessary for dense packaging of the genome.

DNA collapse in confinement has been explored in several experiments. In these experiments, the DNA size rapidly decreases after adding condensing agents (e.g. crowders,³ proteins,^28,29 and cationic surfactant¹³). While these studies used nanofluidic confinement to visualize the collapse process, they did not study the nucleation and annealing processes, which will be described shortly, and the effect of nanoconfinement on these processes.

In this work, we subject DNA to poor solvent conditions, using a buffer based on a 35% ethanol solution, which is marginally sufficient to initiate DNA collapse in bulk and allows us to study the process in detail. Accordingly, the nucleation can take more than 1 hour³⁰ and the change in nucleation time in nanoconfinement can be readily measured.

2. Materials and methods

2.1 Overview of our experimental setup

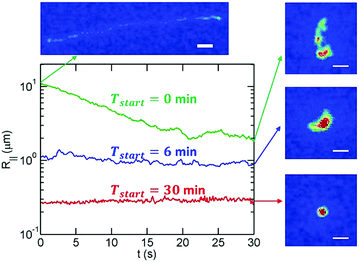
Fig. 1 shows the overview of our experimental system to study DNA collapse. We drive a DNA molecule into a nanoslit, i.e. a shallow region confined by two parallel walls, by an electric field, and then turn off the electric field immediately after the DNA enters the slit. The DNA molecules are initially stretched by the electric field gradient at the entrance to the slit, which will be discussed in more detail below. A DNA molecule eventually collapses from an extended to a compact conformation due to the concentration of ethanol in the buffer. To obtain quantitative information about the collapse kinetics, we use fluorescent microscopy to record the DNA conformation in the nanoslits. The fluorescence intensity profile is used to calculate the in-plane radius of gyration R_‖. In addition, we also calculate the apparent aspect ratio R_M/R_m of every conformation, where R_M and R_m are the major and minor principal axes of DNA conformations, respectively. Here, we define and 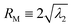, where λ₁ and λ₂ are the large and small eigenvalues of the radius of gyration tensor,³¹ respectively. To obtain the relaxation time of a DNA molecule, we calculate the self-correlation time τ_relax for the direction of the major principal axis of the gyration tensor.³¹ We use an exponential function to fit the self-correlation C(t) starting from C(t) ∼ 0.3. We calculate the relaxation time only for coiled conformations, not for globular conformations. See the ESI† for more details about the calculation of R_‖ and τ_relaxvia image analysis.

Fig. 1 Overview of our experimental system to study DNA collapse in slits. DNA molecules are driven into a nanoslit (two parallel walls with a gap in z-direction) by an electric field. The electric field is turned off once a DNA molecule enters a nanoslit. The DNA conformation projected on the x–y plane (R_‖) is recorded by fluorescent microscopy with a camera.

2.2 Nanoslit fabrication and DNA sample preparation

The nanoslits are fabricated from fused-silica wafers (Mark Optics) using two layers of contact photolithography and reactive ion etching (CHF3/O2). The detail of nanoslit fabrication was described previously.³² The slit height h is 31, 89, 250, 549, or 2000 nm. We also perform DNA collapse experiments in bulk using a channel with the height of 100 μm.

In our experiments, λ-DNA (48.502 kbp, New England Biolabs) or T4 DNA (165.6 kbp, Nippon gene) suspended at a concentration of 0.69 μg mL⁻¹ is stained with YOYO-1 (Invitrogen) intercalating dye at a base pair to dye ratio of 4 : 1 and allowed to sit overnight. YOYO-1 staining significant increases DNA length,³³ yielding λ-DNA with a length ∼22 μm and T4-DNA with a length of ∼75 μm. Immediately before experiments, DNA samples are diluted to produce workable concentrations of DNA. The ethanol concentration is always 35% for slit experiments, but varies for the bulk experiments as shown in Fig. 4. The experimental buffer consisted of 1.5 × TBE (134 mM Tris base, 134 mM boric acid, and 3 mM EDTA), 4 vol% β-mercaptoethanol (BME, Cabiochem) and ethanol. The ionic strength is approximately 57 mM.³¹

2.3 Data acquisition and analysis

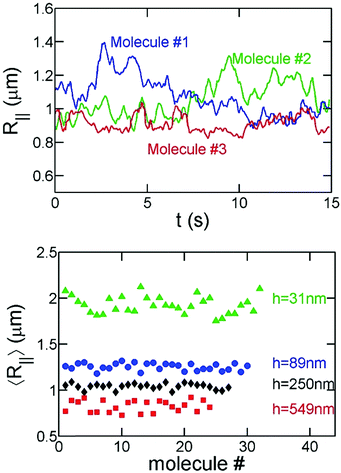
In order to avoid photobleaching over the experiment's duration, we turn on the fluorescent lamp and record 15–30 seconds of video every few minutes until a molecule has fully collapsed. Note that the slit confinement restricts DNA motion in the z-direction, and hence DNA molecules stay in focus during the imaging period. Sample experimental videos are included in the ESI.† For the bulk/free space experiments, DNA molecules move out of focus in a few seconds as indicated by the decrease of the total fluorescence intensity of an individual DNA. Accordingly, for the bulk experiments, we measure the hydrodynamic size of DNA based on the in-plane (X–Y) diffusivity as described below.

Fig. 2 shows examples of the time evolution of R_‖ for a T4-DNA molecule at different time intervals. We analyze about 20–30 different molecules for each channel height h at various times T_start. We find that the variance of R_‖ among these molecules is small (Fig. 3). We further average R_‖ for these molecules with the same h and T_start. Eventually, we obtain the time evolution of R_‖ for each slit height as shown in Fig. 5. Similar data analysis is also applied to obtain the apparent aspect ratio R_M/R_m.

Fig. 2 The time evolution of R_‖ for T4-DNA in a nanoslit with h = 89 nm and 35% ethanol. The top image shows a stretched DNA molecule induced by the electric field that drives the DNA into a nanoslit. In order to avoid photobleaching over the long-time experiments, we turn on the fluorescent lamp and take 15–30 s video every few minutes until a molecule has fully collapsed. The green, blue, and red curves correspond to videos taken at the times T_start = 0, 6, 30 min, respectively. The scale bars are 2 μm.

Fig. 3 Comparison of R_‖ for different T4-DNA molecules. (top) Three curves correspond to videos taken for three different DNA molecules with h = 250 nm and 35% ethanol at T_start = 2 min. (bottom) Each data point correspond to R_‖ for a T4-DNA molecule averaged over 15–30 s. Different symbols correspond to different slit heights. All data points are measured at the same T_start = 2 min.

Direct calculation of the DNA size from the intensity profile is limited in resolution and accuracy due to the point-spread function of the microscope.³¹ This problem is more profound when DNA assumes a highly compact conformation. As a result, we also measure the DNA diffusion coefficient D, and then calculate the DNA hydrodynamic radius through R_h = k_BT/(6πηD). The viscosity η for different ethanol concentrations are determined by measuring the mean squared displacement of polystyrene beads of known radius. We use this method for our measurement of DNA size in bulk, i.e. free space.

It is worth mentioning that a given DNA molecule is stretched by the electric field when driven into a nanoslit as shown by the top-left image in Fig. 2. The green curve in Fig. 2 indicates that the effect of initial stretching in T4-DNA vanishes after about 20 seconds for the slit height of 89 nm. Our previous experiments³⁴ systematically measured the duration τ_str for a stretched DNA molecule to reach its equilibrium conformation in a nanoslit and found the empirical formula τ_str ∼ L_DNA^2.2h^−0.5. We estimate that the effect of initial stretching by the electric field will vanish in less than 1 minute for all slit heights used in the current study.

The electric field that is used to drive DNA into a nanoslit may introduce concentration polarization at the microchannel–nanochannel–microchannel interfaces wherein the concentrations of ions in the buffer do not distribute homogenously.³⁵ Prior work has shown that concentration polarization primarily depends on an inverse Dukhin number Fhzc/σ, where F is Faraday's constant, h is the slit height, z is the valence of the ion, c is the concentration of the ion, and σ is the surface charge density of slit walls.³⁵ Substituting z = 1, c ≈ 57 mM, and σ ≈ 60 mC m⁻²,³⁶ we obtain the inverse Dukhin numbers of approximately 183, 50, 23, 8.2 and 2.8 for h = 2000, 549, 250, 89 and 31 nm, respectively. These inverse Dukhin numbers are greater than unity, which suggests that concentration polarization is not significant in our experiments.

3. Results and discussions

3.1 DNA collapse in free space

We first present our experimental results of DNA collapse in free space. The free-space experiments are used to estimate the critical ethanol concentration for DNA collapse, and later we pick an ethanol concentration in the vicinity of the critical concentration so that the duration of DNA collapse is sufficiently long and we can measure the effect of confinement on DNA collapse more conveniently.

Fig. 4a shows the time evolution of the hydrodynamic radius, R_h, of T4-DNA for a range of ethanol concentration c_ethanol from 0% to 60%. For c_ethanol ≲ 30%, T4-DNA molecules always assume coiled conformations in 24 hours and show significant conformational fluctuations (Fig. 4b). Accordingly, we consider that T4-DNA or λ-DNA collapse do not take place for c_ethanol ≲ 30%. Note that the typical relaxation time of DNA conformations is on the order of seconds and our maximal observation time 24 hours is many orders of magnitude longer than the relaxation time. For 30% ≲ c_ethanol ≲ 45%, T4-DNA molecules collapse towards globular conformations (Fig. 4b). For globular conformations, we can still observe conformational fluctuations, such as a short DNA fragment occasionally stretching out from a globular conformation (see experimental videos in ESI†). For c_ethanol ≳ 45%, T4-DNA molecules eventually reach more compact conformations with little conformational fluctuations (Fig. 4b). These compact conformations are expected to be toroidal based on previous experimental^37,38 and simulation^39,40 studies of condensed DNA. The duration until DNA collapse depends on the ethanol concentration. For 30% ≲ c_ethanol ≲ 50%, DNA collapse takes hours.

Fig. 4 (a) Time evolution of hydrodynamic size R_h (based on a diffusivity measurement) of T4 DNA in solution with different ethanol concentrations. (b) Experimental images of T4-DNA molecules in three states: a coil, a globule and a toroid.

Single-molecule DNA collapse under a wide range of ethanol concentration has also been investigated using magnetic tweezers and Atomic Force Microscopy (AFM) by Wang et al.³⁷ They found that λ-DNA collapse occurs within a few hours incubation time for c_ethanol ≳ 30%, and the condensed λ-DNA structures become more compact with the increasing ethanol concentration. At c_ethanol = 50%, they found that DNA reaches condensed states between two and three hours. All of these observations are in agreement with our results.

Based on these results for DNA in bulk, we pick the ethanol concentration of 35% for nanoslit experiments. With 35% ethanol, T4-DNA is fully collapsed after about 220 minutes and eventually reaches globular conformations.

3.2 DNA collapse in nanoslits

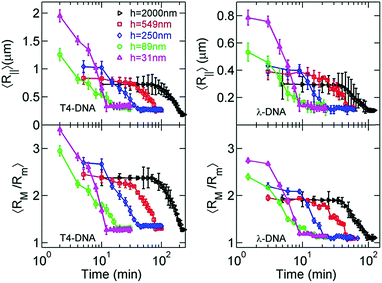
Now, we move to the experimental results of DNA collapse in nanoslits using the fixed ethanol concentration of 35%. To monitor the conformation change during DNA collapse, we calculate both the average in-plane radius of gyration 〈R_‖〉 and the apparent aspect ratio 〈R_M/R_m〉 of single DNA conformations based on the DNA intensity profiles, as shown in Fig. 5. Recall that R_M and R_m are the major and minor principal axes of DNA conformation.⁴¹ The observations of 〈R_‖〉 (two top plots in Fig. 5) and 〈R_M/R_m〉 (two bottom plots in Fig. 5) are consistent with each other. During DNA collapse, the DNA size becomes smaller and the apparent aspect ratio decreases towards unity, which indicates nearly isotropic conformations.

Fig. 5 In-plane radius of gyration 〈R_‖〉 (top) and apparent aspect ratio of conformation 〈R_M/R_m〉 (bottom) as a function of the incubation time in 35% ethanol for T4 DNA (left) and λ-DNA (right) confined to different slit channels. We calculate 〈R_‖〉 and 〈R_M/R_m〉 based on the DNA intensity profile. The error bars indicate the standard deviations among the 〈R_‖〉_interval of 20–30 DNA molecules under a certain condition, where 〈R_‖〉_interval is the average size of a given DNA over an interval of 15–30 seconds.

With the decrease of the slit height from h = 2000 nm to h = 31 nm, the collapse time decreases from more than one hour to about 10 minutes. To elaborate the process of DNA collapse, we re-plot the time evolution of 〈R_‖〉 for T4-DNA in Fig. 6 but with a linear time-scale for h = 2000 nm, h = 250 nm, and h = 31 nm. For h = 2000 nm, the collapse process exhibits three stages: a nucleation state where 〈R_‖〉 remains approximately constant, an annealing stage where 〈R_‖〉 rapidly decreases, and a final stage where the DNA is collapsed. These stages are similar to those observed in previous experiments of single-DNA collapse.³⁰ The nucleation in our experiments is reasonable considering that the DNA–DNA attraction induced by 35% ethanol is marginally larger than the critical attraction and the condensed state is stable only when its size exceeds a certain value, i.e. the nucleation size. We define the nucleation time τ_nucl for the first stage and the annealing time τ_anneal for the second stage as shown in Fig. 6a. We also define the collapse time τ_collapse = τ_nucl + τ_anneal for the entire process.

Fig. 6 Plot of 〈R_‖〉 for T4-DNA in (same as in Fig. 5), but with a linear scale for the incubation time for (a) h = 2000 nm, (b) h = 250 nm, and (c) h = 31 nm. For (a), the collapse process exhibits three stages. The intersection of the two green lines is used to determine the nucleation time. Three inset images in (b) show one T4-DNA molecule at t = 10, 25 and 70 min. The error bars indicate the standard deviations among the 〈R_‖〉_interval of 20–30 DNA molecules under a certain condition, where 〈R_‖〉_interval is the average size of a given DNA over an interval of 15–30 seconds.

Now we proceed to more quantitative analysis of the time scales τ_nucl, τ_anneal, and τ_collapse for DNA collapse. We determine τ_collapse as follows. We calculate the average value and standard deviation of R_‖ over the time interval that the DNA is clearly in the collapsed stage 3; e.g. t ≥ 230 minutes for T4-DNA with h = 2000 nm, and t ≥ 14 minutes for T4-DNA with h = 31 nm. We refer the average value as 〈R₃〉 and the standard deviation as σ₃. Then, τ_collapse is defined as the earliest time that R_‖ is less than 〈R₃〉 + σ₃. The collapse times are listed in Table 1 and plotted in Fig. 7. We determine τ_nucl as follows. We approximate that the evolution of R_‖ in stage 1 and stage 2 can be fit by two straight lines, respectively, and the intersection of these two straight lines correspond to τ_nucl. We adjust the lines to minimize the error in the fit (details provided in the ESI†). This method yields τ_nucl = 70 min for h = 2000 nm, τ_nucl = 35 min for h = 549 nm, and τ_nucl = 10 min for h = 250 nm in the case of T4-DNA. We stress that this is an approximate method to estimate the time at which the DNA transitions from stage 1 to stage 2 that we define as τ_nucl. For T4-DNA with h = 89 nm and h = 31 nm, there is no clear distinction between stages 1 and 2, which can be caused by three possible reasons: (i) no nucleation exists for these two slit heights (see more discussion in Section 3.3); (ii) the nucleation is less than a few minutes, which cannot be resolved by our data sampling rate; (iii) the nucleation is less than a few minutes, and the plateau in the evolution of 〈R_‖〉 is convoluted with the initial DNA stretching due to the electric field (see Fig. 2 for an example). The third possible reason is unlikely, because the effect of the initial DNA stretching vanishes in less than one minute as discussed in the methods section. It is worth pointing out that the data in Fig. 6 show a clear trend that the nucleation time is shorter for a smaller slit height from h = 2000 nm to 89 nm, and the transition from stage 2 to 3 is clearly seen. The speeds of DNA collapse for h = 89 nm and h = 31 nm are close and so it is unclear which one is faster. Note that it is also difficult to precisely identify the spatial location of the nucleation core directly from image analysis, because the high-intensity spots seen in nucleation cores are hard to distinguish from similar spots caused by thermal fluctuations in the projected DNA conformation (see an example of the coil in Fig. 4b and more images in the ESI†). Only in a few experiments are we able to observe the nucleation process as shown by the imaging of Fig. 6b. In the previous AFM experiments by Wang et al.,³⁷ DNA collapse sometimes starts from non-local contacts of DNA segments, which are separated by a big loop that assumes a loose conformation. If the nucleation occurs due to non-local contacts, it is even more difficult to identify the nucleation core location from the image analysis.

Table 1 The time scales for the collapse of T4-DNA and λ-DNA. The data for λ-DNA are shown in square brackets. A nucleation time of 0 min is assigned if there is no clear transition from stage 1 to stage 2

	τ collapse (min)	τ nucl (min)	τ anneal (min)
h = 2000 nm	220 [95]	70 [35]	150 [60]
h = 549 nm	80 [45]	35 [24]	45 [21]
h = 250 nm	45 [21]	10 [9]	35 [12]
h = 89 nm	16 [12]	0 [0]	16 [12]
h = 31 nm	12 [9]	0 [0]	12 [9]

---

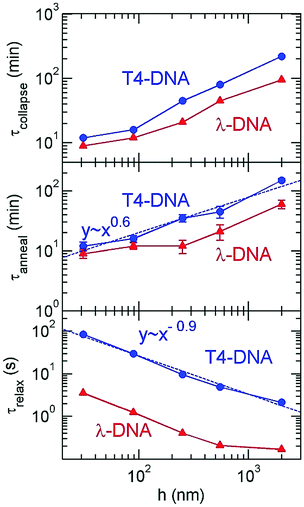Fig. 7 The collapse time, annealing time and rotational relaxation time as a function of the slit height for T4 DNA and λ-DNA.

The five slit heights in our experiments vary from h = 2000 nm to h = 31 nm. To evaluate the strength of confinement by these slits, we compare the slit height with the DNA persistence length in 35% ethanol and the DNA size in bulk. The DNA persistence length decreases from L_p ≈ 50 nm to L_p ≈ 22 nm after adding 35% ethanol, which was determined by previous experiments by Wang et al.³⁷ The smallest slit height h = 31 nm is close to L_p ≈ 22 nm. To calculate the size of DNA coils in bulk, we first analyze the effective DNA diameter w in 35% ethanol. The value of w should be close to zero, because 35% ethanol concentration is close to the critical value for DNA collapse, and the solvent quality is close to the θ-condition. As such, we approximate YOYO-1 stained DNA in 35% ethanol as a wormlike chain with L_p ≈ 22 nm and w ≈ 0 nm. We obtain λ-DNA size 〈R^λ-DNA_‖,bulk〉 ≈ 0.33 μm and T4-DNA size 〈R^T4-DNA_‖,bulk〉 ≈ 0.61 μm after using L^λ-DNA ≈ 22 μm, L^T4-DNA ≈ 75 μm and applying the theoretical formula , where is used for the in-plane rather than three dimensional radius of gyration. The largest slit height h = 2000 nm is about six times of 〈R^λ-DNA_‖,bulk〉 ≈ 0.33 μm, and hence λ-DNA experiences negligible confinement, and the initial λ-DNA size for h = 2000 nm is 〈R_‖〉 ≈ 0.30 μm, which is close to 〈R^λ-DNA_‖,bulk〉. For T4-DNA, The largest slit height h = 2000 nm is about three times of 〈R^T4-DNA_‖,bulk〉 ≈ 0.61 μm, and T4-DNA experiences weak confinement. The initial T4-DNA size for h = 2000 nm is 〈R_‖〉 ≈ 0.72 μm, which is larger than 〈R^T4-DNA_‖,bulk〉 due to DNA compression by slit walls. Note that our previous experiment³¹ obtained the λ-DNA size 〈R^λ-DNA_‖,bulk〉 ≈ 0.52 μm in the absence of ethanol, which is larger than 0.33 μm in the current study.

Our experiments employ two types of DNA molecules: T4-DNA with L ≈ 75 μm and λ-DNA with L ≈ 22 μm. Despite of the difference in the contour length by a factor of 3.41, both DNA molecules exhibit the same trend in confinement. Quantitatively, the difference in the contour length leads to the differences in confinement free energy and the relaxation time τ_relax, and then the difference in time scales of DNA collapse. Based on the blob-model scaling τ_relax ∼ L^−5/2 in confinement,³¹ the relaxation of T4-DNA is expected to be slower than λ-DNA by a factor of 21, which is close to τ^T4-DNA_relax/τ^λ-DNA_relax ≈ 24 observed in our experimental measurement of rotational relaxation time over the range from h = 31 nm to 549 nm. The relaxation time of T4-DNA appears to follow a scaling τ_relax ∼ h^−0.9 from h = 31 to 2000 nm, while the relaxation time of λ-DNA significantly deviates from this scaling at h = 2000 nm, because λ-DNA experiences negligible confinement at h = 2000 nm due to the insufficiency in the contour length. Although T4-DNA and λ-DNA differ in the relaxation time by a factor of about 24, the difference in the collapse time is only by a factor of about 1.8, and the difference in the annealing times is by a factor of about 2.1 (see ESI†). As previously investigated by Yoshinaga,⁴² the annealing speed may be determined by the motion of the collapsed domain or the coil domain depending on the stage of collapse process. If it is the former, the annealing time is insensitive to the chain length, while if it is the latter, the annealing time is related to the relaxation time of the entire length. The mixture of both motions in the collapse process may result in a weak dependence of the annealing time or collapse time on the chain length.

3.3 Discussion about how confinement speeds up DNA collapse

Now we proceed to the theoretical explanation for the effect of confinement on DNA collapse. We highlight that as the slit becomes shallower, the relaxation dramatically slows down, but conversely the collapse kinetics greatly speeds up (Fig. 7). These two trends indicate that the faster collapse in confinement is driven by the effect of confinement on the free energy landscape and not by hydrodynamic effects. Fig. 8 illustrates the effect of confinement on the free energy landscape with respect to the compactness of DNA conformations. DNA collapse corresponds to a transition from a coiled conformation to a globular conformation. The confinement free energy experienced by the coiled conformation F^slit_coil is larger than the one by the globular conformation F^slit_globule, because the coiled conformation is larger and more likely to be restricted by slit walls. The difference ΔF_slit = F^slit_coil − F^slit_globule reshapes the free energy landscape and thermodynamically promotes the coil-globule transition in confinement. In our previous simulation study,⁴³ we have calculated the free energy landscape for the coil-globule transition in slit confinement using computer simulations and obtained similar curves as shown in Fig. 8. More generally, confinement promotes any reaction or conformation change that compacts the polymer conformation, such as protein folding^44,45 and knot formation in confinement.⁴⁶

Fig. 8 Illustration of the effect of confinement on the free energy landscape with respect to the compactness of DNA conformation. DNA collapse corresponds to the transition from the left to the right with the increase of the compactness of DNA conformations. Because confinement significantly increases the free energy of the coiled conformation, the energy barrier separating the coil and globule shape is reduced in the shallow slit.

Due to the existence of plateaus in the time evolution of 〈R_‖〉, we expect that there is a free energy barrier along the path of DNA collapse. The free energy barrier is akin to that found in typical crystallization of small molecules, namely that the small nuclei are unstable due to a relatively large surface energy. Here, the surface energy refers to an energy increase because the surface monomers have a smaller number of attractive neighbors than the monomers in the core. The dependence of confinement free energy on the compactness of DNA conformation also reduces the free energy barrier for DNA collapse. The reduction of free energy barrier by confinement can explain our observation that the nucleation process becomes shorter or disappears in shallower slits.

Our experimental data can be understood quantitatively to a certain extent. We focus on the data of T4-DNA rather than λ-DNA, because T4-DNA is longer and it suffers less finite-length effects when applying scaling relationships. We estimate the confinement free energy per unit length f_confine by the scaling relationship¹⁵

where k_B is the Boltzmann constant, and T is the temperature. Substituting L_p ≈ 22 nm and h = 31, 89, 250, 549 and 2000 nm, we have the confinement free energy per unit length as 75, 9.1, 1.2, 0.24, and 0.018k_BT μm⁻¹. To proceed with the quantitative estimation using limited data points, we adopt a crude approximation for the nucleation time

τ_nucl ∼ τ_relax exp(F^slit_barrier/k_BT), (2)

F^slit_barrier = F^bulk_barrier + f_confineL_nucl (3)

where F^bulk_barrier is the barrier in bulk, and L_nucl is the DNA contour length inside the nucleation core and is assumed to be unchanged with confinement. From h = 2000 nm to h = 549 nm, the relaxation time increases from 2.15 to 4.97 seconds by a factor of 2.31, and the nucleation time decreases from 70 to 35 min by a factor of 2. Accordingly, we have (f^h=549nm_confine − f^h=2000nm_confine) L_nucl ≈ ln(2 × 2.31)k_BT. Eventually, we obtain L_nucl ≈ 6.9 μm. Due to the confinement free energy experienced by the DNA fragment with a length of 6.9 μm, the free energy barrier of nucleation is lowered by f^h=2000nm_confineL_nucl ≈ 0.1k_BT for h = 2000 nm, and by f^h=549nm_confineL_nucl ≈ 1.65k_BT for h = 549 nm. The nucleation size of 6.9 μm is reasonable considering that the nucleation is a fraction of λ-DNA length of 22 μm. For example, the first image of Fig. 6b contains a nucleation core with DNA contour length of about 8.6 μm based on the analysis of the intensity profile.

We also adopt a crude approximation to quantitatively analyze the annealing time. We assume the annealing speed is proportional to the slope of free energy landscape as labeled in Fig. 8:

τ_anneal ∼ τ_relax/ε_slit, (4)

ε_slit = ε_bulk + (π²/3)h⁻²L_p (5)

where ε_slit is the decrease of the free energy during DNA collapse after crossing the free energy barrier. This formula is similar with the one proposed by Yoshinaga:⁴²τ_anneal ∼ η/ε, while we replace η by τ_relax. This model views DNA collapse as a ball moving downhill with the resistance produced by the solvent. We assume that ε_bulk is much smaller than the second term in eqn (5) and is dropped, because we use an ethanol concentration close to the critical value for DNA collapse. Hence, we further simplify the annealing time to

τ_anneal ∼ τ_relax/h⁻². (6)

Using the de Gennes scaling τ_relax ∼ h^−7/6, we obtain τ_anneal ∼ h^5/6. Considering that many assumptions are made, the predicted exponent of 5/6 agrees fairly well with the exponent 0.6 ± 0.2 obtained by the fit to our experiment results of τ_anneal. In particular, we ignore ε_bulk in eqn (5). The mixture of ε_bulk ∼ h⁰ and (π²/3)h⁻²L_p would result in an apparent scaling exponent larger than −2, and then an exponent in τ_anneal less than 5/6.

Previous simulations by Das and Chakraborty have also quantitatively investigated the effect of slit confinement on polymer collapse, however, only for short flexible chains.⁴⁷ After including hydrodynamic interactions, the slit confinement can speed up polymer collapse by a factor from 2.5 to 4 for the chain length from 80 to 200. If we extrapolate the confinement effect to longer chains, it may explain our experimental observation that the slit confinement speeds up DNA collapse by 18 times. Recall that T4-DNA used in our experiments has a contour length ∼75 μm, which is about 3400 times of DNA the persistence length ∼22 nm in 35% ethanol.

3.4 Discussion about the surface charge of the slit walls

In addition to the steric repulsion, the slit walls also affect DNA behavior through the surface charge.³⁶ The silica nanoslits used here have negative surface charges. The electrostatic repulsion between slit walls and DNA makes the accessible height by DNA less than the actual slit height, i.e. h_actual = h − 2δ, where δ is the effective thickness of the surface layer inaccessible by DNA. The calculation of δ is rather complicated, but δ depends on the Debye length and is on the order of nanometres in our studies.^2,48 Accordingly, we expect the difference between h_actual and h is small in our studies and does not affect our overall conclusions.

The counterions (more specifically, H⁺ in the current study) of surface charge also change the pH value of the buffer in nanoslits. Previous experiments by Bottenus et al.⁴⁹ measured the change in the pH value in nanochannels over a range of buffer conditions. In a channel with a cross-section of 100 nm × 400 nm, the pH value shift is about 0.2 at an ionic strength of 57 mM.⁴⁹ This prior work suggests that the changes in pH value for h = 2000, 549, 250 and 89 nm are smaller than or around 0.2. Such a small change in pH value should not change DNA properties, such as charge density.

4. Conclusions

In summary, single molecule experiments show that nanoconfinement greatly speeds up the nucleation and the annealing of single-DNA collapse, despite the fact that DNA dynamics is slowed down by confinement. If we view DNA collapse as a reaction from a metastable coiled state to a globule state, then nanoconfinement can be considered as a catalyst to accelerate this reaction by reshaping the free energy landscape and promoting smaller conformations. What is different from a traditional catalyst is that the relative free energy between the coil (reactant) and the globule (product) is also altered by confinement. However, if DNA is driven into confinement before reaction and driven out of confinement after reaction, then confinement essentially acts as a catalyst by changing the free energy barrier. Such catalysis by confinement may be used by cells to speed up protein folding. Experiments^44,50 and simulations⁴⁵ suggest that the nanocage-confinement by chaperonin may be a key factor, among others,⁵¹ facilitating protein folding. Confinement is also suggested to affect other conformation transitions, e.g. DNA denaturation,⁵² polymer looping⁵³ and protein dimerization.⁵⁴ The direct visualization of long DNA in our experiment allows for quantitative measurements and sheds light on conformation transitions in confinement.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Singapore-MIT Alliance for Research and Technology (SMART) and the National Science Foundation (NSF) grant CBET-1602406.

References

1. R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839.
2. W. Reisner, J. N. Pedersen and R. H. Austin, Rep. Prog. Phys., 2012, 75, 106601.
3. C. Zhang, P. G. Shao, J. A. van Kan and J. R. van der Maarel, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16651.
4. D. J. Mai, C. Brockman and C. M. Schroeder, Soft Matter, 2012, 8, 10560.
5. E. T. Lam, A. Hastie, C. Lin, D. Ehrlich, S. K. Das, M. D. Austin, P. Deshpande, H. Cao, N. Nagarajan, M. Xiao and P. Y. Kwok, Nat. Biotechnol., 2012, 30, 771.
6. R. Marie, J. N. Pedersen, D. L. Bauer, K. H. Rasmussen, M. Yusuf, E. Volpi, H. Flyvbjerg, A. Kristensen and K. U. Mir, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4893–4898.
7. W. Reisner, N. B. Larsen, H. Flyvbjerg, J. O. Tegenfeldt and A. Kristensen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 79–84.
8. W. Reisner, N. B. Larsen, A. Silahtaroglu, A. Kristensen, N. Tommerup, J. O. Tegenfeldt and H. Flyvbjerg, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13294–13299.
9. H.-X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375.
10. W. Reisner, K. J. Morton, R. Riehn, Y. M. Wang, Z. Yu, M. Rosen, J. C. Sturm, S. Y. Chou, E. Frey and R. H. Austin, Phys. Rev. Lett., 2005, 94, 196101.
11. A. Küchler, M. Yoshimoto, S. Luginbühl, F. Mavelli and P. Walde, Nat. Nanotechnol., 2016, 11, 409.
12. T. E. Sintra, S. P. Ventura and J. A. Coutinho, J. Mol. Catal. B: Enzym., 2014, 107, 140.
13. G. Henkin, D. Berard, F. Stabile, M. Shayegan, J. S. Leith and S. R. Leslie, Anal. Chem., 2016, 88, 11100.
14. Y. Wang, D. R. Tree and K. D. Dorfman, Macromolecules, 2011, 44, 6594.
15. L. Dai, J. R. C. Van der Maarel and P. S. Doyle, Macromolecules, 2014, 47, 2445.
16. L. Dai, C. B. Renner and P. S. Doyle, Adv. Colloid Interface Sci., 2016, 232, 80.
17. L. Dai, D. R. Tree, J. R. C. van der Maarel, K. D. Dorfman and P. S. Doyle, Phys. Rev. Lett., 2013, 110, 168105.
18. D. J. Berard, F. Michaud, S. Mahshid, M. J. Ahamed, C. M. McFaul, J. S. Leith, P. Bérubé, R. Sladek, W. Reisner and S. R. Leslie, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13295.
19. A. R. Klotz, M. Mamaev, L. Duong, H. W. de Haan and W. W. Reisner, Macromolecules, 2015, 48, 4742.
20. J.-W. Yeh, A. Taloni, Y.-L. Chen and C.-F. Chou, Nano Lett., 2012, 12, 1597.
21. C. Zhang, F. Zhang, J. A. van Kan and J. R. C. van der Maarel, J. Chem. Phys., 2008, 128, 225109.
22. J. Tang, D. W. Trahan and P. S. Doyle, Macromolecules, 2010, 43, 3081–3089.
23. A. C. Klepinger, M. K. Greenier and S. L. Levy, Macromolecules, 2015, 48, 9007–9014.
24. A. Khorshid, S. Amin, Z. Zhang, T. Sakaue and W. W. Reisner, Macromolecules, 2016, 49, 1933–1940.
25. M. J. Ahamed, S. Mahshid, D. J. Berard, F. O. Michaud, R. Sladek, W. W. Reisner and S. R. Leslie, Macromolecules, 2016, 49, 2853–2859.
26. D. Kim, C. Bowman, J. T. Del Bonis-O'Donnell, A. Matzavinos and D. Stein, Phys. Rev. Lett., 2017, 118, 048002.
27. A. Estevez-Torres and D. Baigl, Soft Matter, 2011, 7, 6746.
28. C. Zhang, D. Guttula, F. Liu, P. P. Malar, S. Y. Ng, L. Dai, P. S. Doyle, J. A. van Kan and J. R. van der Maarel, Soft Matter, 2013, 9, 9593.
29. C. Zhang, K. Jiang, F. Liu, P. S. Doyle, J. A. van Kan and J. R. van der Maarel, Lab Chip, 2013, 13, 2821.
30. K. Yoshikawa and Y. Matsuzawa, J. Am. Chem. Soc., 1996, 118, 929.
31. J. Tang, S. L. Levy, D. W. Trahan, J. J. Jones, H. G. Craighead and P. S. Doyle, Macromolecules, 2010, 43, 7368.
32. E. A. Strychalski, S. L. Levy and H. G. Craighead, Macromolecules, 2008, 41, 7716.
33. K. Günther, M. Mertig and R. Seidel, Nucleic Acids Res., 2010, 38, 6526.
34. A. Balducci, C.-C. Hsieh and P. Doyle, Phys. Rev. Lett., 2007, 99, 238102.
35. T. A. Zangle, A. Mani and J. G. Santiago, Chem. Soc. Rev., 2010, 39, 1014.
36. D. Stein, M. Kruithof and C. Dekker, Phys. Rev. Lett., 2004, 93, 035901.
37. Y. Wang, S. Ran, B. Man and G. Yang, Soft Matter, 2011, 7, 4425.
38. V. A. Bloomfield, Curr. Opin. Struct. Biol., 1996, 6, 334.
39. A. Montesi, M. Pasquali and F. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021916.
40. H. Noguchi, S. Saito, S. Kidoaki and K. Yoshikawa, Chem. Phys. Lett., 1996, 261, 527.
41. C. C. Hsieh, A. Balducci and P. S. Doyle, Nano Lett., 2008, 8, 1683.
42. N. Yoshinaga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061805.
43. L. Dai, C. B. Renner, J. Yan and P. S. Doyle, Sci. Rep., 2015, 5, 18438.
44. A. Brinker, G. Pfeifer, M. J. Kerner, D. J. Naylor, F. U. Hartl and M. Hayer-Hartl, Cell, 2001, 107, 223.
45. J. Mittal and R. B. Best, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20233.
46. L. Dai, C. B. Renner and P. S. Doyle, Macromolecules, 2015, 48, 2812–2818.
47. S. Das and S. Chakraborty, J. Chem. Phys., 2010, 133, 174904.
48. G. K. Cheong, X. Li and K. D. Dorfman, Phys. Rev. E, 2017, 95, 022501.
49. D. Bottenus, Y.-J. Oh, S. M. Han and C. F. Ivory, Lab Chip, 2009, 9, 219–231.
50. Y.-C. Tang, H.-C. Chang, A. Roeben, D. Wischnewski, N. Wischnewski, M. J. Kerner, F. U. Hartl and M. Hayer-Hartl, Cell, 2006, 125, 903.
51. A. I. Jewett and J.-E. Shea, Cell. Mol. Life Sci., 2010, 67, 255.
52. H. Li, Z. Wang, N. Li, X. He and H. Liang, J. Chem. Phys., 2014, 141, 044911.
53. J. Shin, A. G. Cherstvy and R. Metzler, ACS Macro Lett., 2015, 4, 202.
54. W. Wang, W.-X. Xu, Y. Levy, E. Trizac and P. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5517.

---

Footnote

† Electronic supplementary information (ESI) available: More information about experiments, data analysis and images and videos of DNA collapse. See DOI: 10.1039/c7sm01249g

---