Cavitation to fracture transition in a soft solid
Abstract
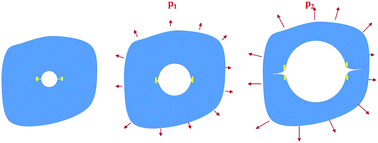
When a soft solid such as rubber, gel and soft tissue is subject to hydrostatic tension, a small cavity inside the solid expands. For a neo-Hookean solid, when the hydrostatic tension approaches a critical value: 2.5 times its shear modulus, the initially small cavity can expand unboundedly. Such a phenomenon is usually referred to as cavitation instability in soft solids. Several recent experiments have shown that fractures may occur in the material when the hydrostatic tension is far below the critical value. In this article, we study a spherical cavity with a ring crack on its wall and inside a neo-Hookean elastomer subject to hydrostatic tension. We compute the energy release rate associated with the extension of the ring crack, for both pressure-control and (cavity) volume-control loading modes. We find that for the pressure-control mode, the energy release rate increases with the increase of the crack size as well as the magnitude of pressure; for the (cavity) volume-control mode, with a fixed cavity volume, the energy release rate increases with the increase of the crack size when the crack is short; the energy release rate maximizes for an intermediate crack size, and decreases with the increase of crack size when the crack is long. The results obtained in this article may be helpful for understanding cavitation-to-fracture transition in soft solids subject to different loading conditions.


 Please wait while we load your content...
Please wait while we load your content...