Open Access Article
Open Access ArticleStretching self-entangled DNA molecules in elongational fields†
C. Benjamin
Renner
and
Patrick S.
Doyle
*
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: pdoyle@mit.edu
First published on 2nd February 2015
Abstract
We present experiments of self-entangled DNA molecules stretching under a planar elongational field, and their stretching dynamics are compared to identical molecules without entanglements. Self-entangled molecules stretch in a stage-wise fashion, persisting in an “arrested” state for decades of strain prior to rapidly stretching, slowing down the stretching dynamics by an order of magnitude compared to unentangled molecules. Self-entangled molecules are shown to proceed through a transient state where one or two ends of the molecule are protruding from an entangled, knotted core. This phenomenon sharply contrasts with the wide array of transient configurations shown here and by others for stretching polymers without entanglements. The rate at which self-entangled molecules stretch through this transient state is demonstrably slower than unentangled molecules, providing the first direct experimental evidence of a topological friction. These experimental observations are shown to be qualitatively and semi-quantitatively reproduced by a dumbbell model with two fitting parameters, the values of which are reasonable in light of previous experiments of knotted DNA.
1 Introduction
Advances in nanofabrication, microscopy, and molecular biology have both motivated and enabled the direct observation of the static and dynamic properties of single DNA molecules. These experiments help guide applications such as direct linear analysis1 or nanopore translocation2 for sequencing genomes. Experiments on single DNA molecules have a rich history in addressing a number of fundamental questions in polymer physics.3–5 Optical tweezers have been used to stretch molecules,6 and the data were well described by the theory of Marko and Siggia for semiflexible chains.7 A wide range of microfluidic devices have been designed to actively manipulate DNA molecules with hydrodynamic flows or electric fields for analysis8,9 such as t-junctions,10 cross-slots,11–13 posts,14–16 contractions,17–19 and nano-scale slits20,21 and channels.22 In particular, cross-slot microfluidic devices have been used as a way to stretch molecules without bulky probes for detection of specific DNA sequences23 or to understand the subsequent relaxation of polymers in slits24 or collapse of polymers in poor solvents.25 These devices have also been used to study the transient dynamics of polymer molecules in well-controlled elongational flows/fields, and experiments have revealed surprising configurational diversity26,27 and hysteresis in the coil–stretch transition.28One of the most dramatic findings of such experiments is that polymer molecules unraveling in elongational flows do so at distinct rates that are largely controlled by a diverse set of transient configurations,26,27 referred to as molecular individualism.29 These transient configurational classes, dumbbells, half-dumbbells, kinks, hairpins/folds, and coils, were investigated in the simulations of Larson and coworkers.30 They showed that a bead-spring polymer model with only polymer connectivity, hydrodynamic drag of the solvent, and Brownian fluctuations can recreate the qualitative features of DNA experiments. From an applications perspective, the intrinsic variance in the rate of stretching DNA molecules due to molecular individualism has complicated the design of flow-based stretching devices for DNA analysis. In response, cross-linked gels31 or post array32 “preconditioning” devices have been developed to reduce this variability.
More recently, there has been a focus on how the topology of a polymer molecule can affect polymer properties.33 Topological entanglements are found in biological contexts;34 knots occur in DNA confined to the tight spaces of viral capsids35,36 as well as in folded proteins.37 Simulations have investigated the statistics of knots on polymers in confining geometries at equilibrium.38–40 In dynamical processes, simulations have indicated knots can significantly slow the ejection of viral DNA,41 slow or jam the sequencing of DNA through nanopores,42 and reduce the rate at which a protein is digested by the proteasome.43 Theory suggested that topological entanglements can arrest the swelling of polymer globules,44 and simulations supported this idea.45,46 More recently, Tang et al. reported an experimental technique for compressing DNA with electric fields and demonstrated an arrested state prior to expanding back to a swollen coil, which they attributed to self-entanglements.47
In this work, we present experiments in which DNA molecules are initially preconditioned to a self-entangled state and are then subjected to a planar elongational field. We compare these results with DNA molecules which are stretched in a planar elongational field starting from an equilibrium (unentangled) state. We find substantial differences between these two cases, and we quantify these differences by analyzing their different rates of stretching. Finally, we present a simple model that is shown to semi-quantitatively capture the mean stretching behavior of the self-entangled molecules in our experiments.
2 Experimental methods
The experimental buffer consisted of 4% (vol) β-mercaptoethanol (BME, Cabiochem), 0.1% 10 kDa polyvinylpyrrolidone (PVP, Polysciences) in 0.5× Tris–borate–EDTA (TBE, Accugene). T4GT7 DNA (165.6 kbp, Wako) and λ-DNA (48.502 kbp, New England Biolabs) were fluorescently labeled with YOYO-1 intercalating dye (Invitrogen) at a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base pair to dye ratio in the experimental buffer, leading to a final contour length of 75 μm, 38% larger than bare DNA.48 This mixture was allowed to stain for 12–48 hours prior to viewing. Cross-slot channels, 1.65 μm in height, were manufactured in PDMS (Sylgard 184, Dow Corning) using soft lithography on a silicone master template (SU8-2 photoresist). Channels were soaked overnight in the experimental buffer at 40 °C to mitigate permeation-driven flow,31 quickly rinsed with RO water, dried with argon, and sealed to a glass cover slide. Stained DNA solutions were diluted in the experimental buffer 10 to 25-fold for optimal viewing concentrations and loaded in the channel reservoirs. The channel was flushed with buffer for a minimum of 30 minutes prior to collecting data via the application of a moderate (∼50 V) electric potential at the reservoirs.
1 base pair to dye ratio in the experimental buffer, leading to a final contour length of 75 μm, 38% larger than bare DNA.48 This mixture was allowed to stain for 12–48 hours prior to viewing. Cross-slot channels, 1.65 μm in height, were manufactured in PDMS (Sylgard 184, Dow Corning) using soft lithography on a silicone master template (SU8-2 photoresist). Channels were soaked overnight in the experimental buffer at 40 °C to mitigate permeation-driven flow,31 quickly rinsed with RO water, dried with argon, and sealed to a glass cover slide. Stained DNA solutions were diluted in the experimental buffer 10 to 25-fold for optimal viewing concentrations and loaded in the channel reservoirs. The channel was flushed with buffer for a minimum of 30 minutes prior to collecting data via the application of a moderate (∼50 V) electric potential at the reservoirs.
A planar elongational field may be used to linearize a charged macromolecule such as DNA,12,49,50 and the kinematics of this field are described by the following equation:
Vx = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) x; Vy = − x; Vy = −![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) y y | (1) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is the strain rate of the field. We used a cross-slot device to generate a homogeneous elongational field within a ∼100 × 100 μm field of view. The strain rate was controlled by varying the voltages applied at the reservoirs. Molecules were trapped at the metastable stagnation point at the center of the field by manually perturbing the potential (∼2 V) of the right reservoir. See the ESI† for device layout and strain rate calibration curve.
is the strain rate of the field. We used a cross-slot device to generate a homogeneous elongational field within a ∼100 × 100 μm field of view. The strain rate was controlled by varying the voltages applied at the reservoirs. Molecules were trapped at the metastable stagnation point at the center of the field by manually perturbing the potential (∼2 V) of the right reservoir. See the ESI† for device layout and strain rate calibration curve.
For a molecule in an elongational flow or field, the relevant dimensionless group is the Deborah number, De ≡ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) λ, where λ is the longest relaxation time of the polymer molecule. In such fields, a polymer will undergo the coil–stretch transition at Dec ≈ 0.5, and the critical strain rate for the onset of this transition is
λ, where λ is the longest relaxation time of the polymer molecule. In such fields, a polymer will undergo the coil–stretch transition at Dec ≈ 0.5, and the critical strain rate for the onset of this transition is 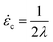 . The longest relaxation time of DNA was measured as λ = 2.6 s by fitting the long time decay of the autocorrelation function of orientation angles of DNA molecules at equilibrium51 (see ESI†).
. The longest relaxation time of DNA was measured as λ = 2.6 s by fitting the long time decay of the autocorrelation function of orientation angles of DNA molecules at equilibrium51 (see ESI†).
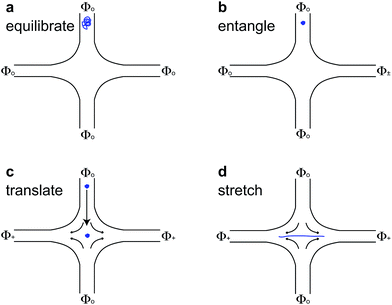
For molecules with unentangled initial conditions, the molecule was brought to the stagnation point and there allowed to relax for ∼30 s > 10λ, allowing the molecule to thoroughly sample its equilibrium configurations. The elongational field was then turned on, and the molecule was stretched. The procedures for generating the initial self-entangled molecular states are more complex and are shown in Fig. 1. For a self-entangled initial condition, the molecule was brought to a channel arm and allowed to relax for ∼30 s. An AC square-wave electric field of strength Erms = 200 V cm−1 and frequency f = 10 Hz was applied for 30 s to compress and self entangle a molecule in a fashion demonstrated by Tang et al.47 After entanglement, the reservoir potentials were switched to generate an elongational field, and the molecule was quickly (<5 s) swept into the straining region of the device. The molecule was held in this region until it stretched.
3 Results and discussion
3.1 Differences due to entanglements
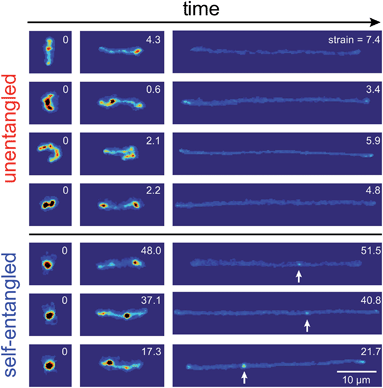
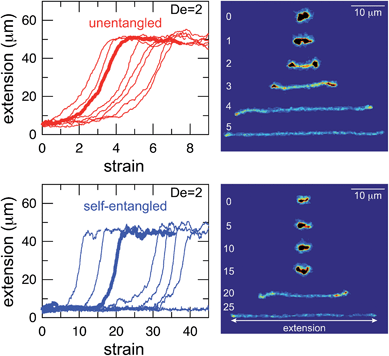
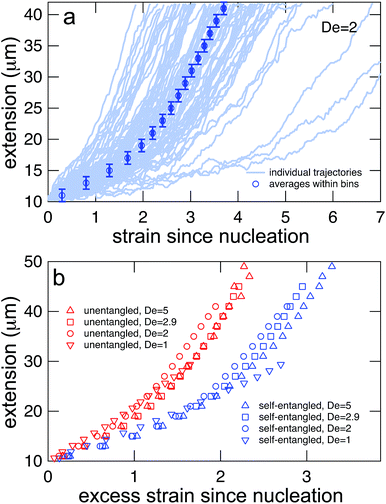
Representative snapshots of the initial, transient, and fully stretched configurations of both initially unentangled and self-entangled molecules are shown in Fig. 2. Several stark differences between the stretching processes for each type of molecule are immediately apparent. The initial configurations for unentangled molecules are visually diverse and somewhat anisotropic since the molecules are exploring the full configurational space of a polymer in a good solvent prior to the onset of the field. The initial conditions of the self-entangled molecules are highly isotropic “globules,” and the important differences between their individual configurations exist at a length scale smaller than can be resolved by fluorescence microscopy. It is important to emphasize that the subsequent differences in stretching behavior of unentangled and self-entangled molecules arise solely due to these differences in the initial conditions. The so-called “half-dumbbell”, “kink”, “hairpin/fold”, and “dumbbell” configurations emerge as transient configurations of unentangled molecules. This phenomenon as well as the corresponding differences in the rates of stretching grouped by transient configurational class is the key concept behind molecular individualism. The transient configurations of self-entangled molecules are less diverse, all consisting of a knotted core from which one or two ends of the chain unravel. The differences between initially unentangled and self-entangled molecules even persist in their fully stretched conformations. While absent in the vast majority of unentangled molecules, a region of increased fluorescence (indicated with arrows) can be seen in the stretched conformation of an initially self-entangled molecule. These regions are persistent and suggest that a topological knot has been pulled tight in the chain. See the ESI† for movies initially unentangled and self-entangled molecules stretching.Selected trajectories of extension versus strain are plotted for both initially unentangled and self-entangled DNA molecules in Fig. 3. The trajectories of initially unentangled molecules demonstrate that their stretching dynamics are progressive – the molecule orients, aligns, and immediately begins stretching until fully extended. Initially self-entangled molecules exhibit stage-wise stretching dynamics – the molecule persists in a low extension arrested state before rapidly stretching. The snapshots corresponding to the bolded trajectory in each plot are shown on the right further illustrate this point. The unentangled molecule immediately begins stretching, and within 2 units of strain, the transient “dumbbell” configuration can be easily seen. The self-entangled molecule persists in its arrested state until a strain of 15. At a strain of 15, the nascent ends of the molecule can be seen to first clearly protrude from the highly knotted core. This event immediately precedes the onset of a comparably rapid stretching phase of this molecule, indicative of a nucleation phenomenon. Nearly all molecules in experiments follow this general nucleation then stretch behavior, a phenomenon with qualitative similarities to the onset of stretching in collapsed polymers in elongational flows.52,53
In Fig. 4, stretching trajectories are shown for both unentangled (red) and self-entangled (blue) molecules unraveling in elongational fields of De = 1, 2, 2.9, and 5. The immediate difference in time scales associated with stretching the two populations is evident at all field strengths, indicating that even at relatively strong fields of De = 5, the presence of topological restrictions can dramatically slow the stretching process. At all field strengths, the trajectories clearly indicate significant dispersity in the times to reach a fully stretched conformation for both initially unentangled and self-entangled molecules. For unentangled molecules, this dispersity is referred to as molecular individualism and can be largely associated with the differences in transient configurations. For initially self-entangled molecules, the variation in the time to fully stretch a molecule arises almost entirely from the different lengths of time spent in the arrested state.
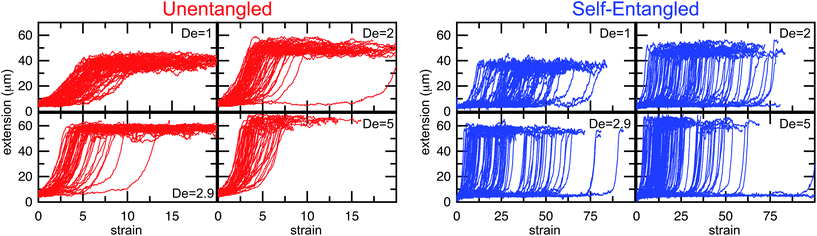 | ||
| Fig. 4 Extension vs. strain trajectories for initially unentangled (left) or self-entangled (right) DNA for all Deborah numbers (De = 1, 2, 2.9, and 5) in this study. | ||
3.2 Stage-wise decomposition of trajectories
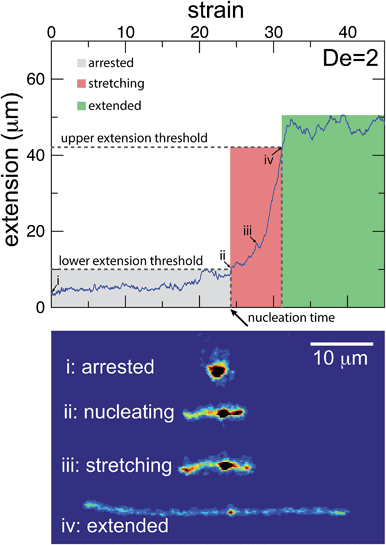
The images and trajectories in Fig. 2–4 all indicate a stage-wise stretching of a self-entangled molecule. In general, each trajectory can be decomposed into three distinct stages: a metastable arrested state, a transient stretching phase, and an extended steady state, shown in Fig. 5. We now present the method by which we algorithmically defined these stages for all experimental trajectories.The arrested state is the initial phase of a molecule, and the molecule is considered to remain in this state until its extension permanently passes a lower extension threshold. The duration of the arrested state is deemed the nucleation time, denoted tnuc, since the end of the arrested state corresponds to the nucleation events described in the previous section. To best delineate the arrested state from the stretching phase, the value for the lower extension threshold should be chosen to be the smallest extension where molecules all immediately stretch upon passing the threshold for the last time. A value of 10 μm was found to be suitable for our ensemble of experimental data.
The stretching phase of the molecule begins at the end of the arrested state and continues until the extension of the molecule passes an upper extension threshold. The value of the upper extension threshold is again chosen so that all molecules in the ensemble continue to stretch rapidly. As the steady state extension of DNA is a function of De, this parameter, too, is a function of De. Values for the upper extension threshold of 30, 42, 46, and 50 μm for De = 1, 2, 2.9, and 5 were used in the following analysis. Both the upper and lower extension thresholds were chosen empirically to best segregate the phases.
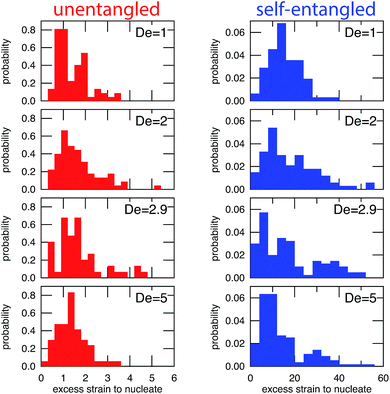
In Fig. 6, the distributions of nucleation times are shown for both unentangled and self-entangled molecules. The x-axes of these distributions are scaled by the here-called “excess strain” rate. The strain, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) t, time scaled by the strain rate, relates the exponential increase in separation between tracers along streamlines in an elongational field, x(t + δt) = x(t)exp(
t, time scaled by the strain rate, relates the exponential increase in separation between tracers along streamlines in an elongational field, x(t + δt) = x(t)exp(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) δt). The excess strain, (
δt). The excess strain, (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) −
− ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c)t, time scaled by the strain rate exceeding the onset of the coil–stretch transition, relates the exponential increase in separation between two points connected by a Hookean spring with the same entropic elasticity as the DNA molecule, x(t + δt) = x(t)exp((
c)t, time scaled by the strain rate exceeding the onset of the coil–stretch transition, relates the exponential increase in separation between two points connected by a Hookean spring with the same entropic elasticity as the DNA molecule, x(t + δt) = x(t)exp((![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) −
− ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c)δt). This quantity has been shown to reasonably scale the stretching kinetics in experiments26,27 and nucleation-type behavior of the coil stretch transition in simulations.54 In Fig. 6, the x-axes thus correspond to the amount of excess strain accumulated until the nucleation event occurs at tnuc, i.e. (
c)δt). This quantity has been shown to reasonably scale the stretching kinetics in experiments26,27 and nucleation-type behavior of the coil stretch transition in simulations.54 In Fig. 6, the x-axes thus correspond to the amount of excess strain accumulated until the nucleation event occurs at tnuc, i.e. (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) −
− ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c)tnuc.
c)tnuc.
For initially unentangled molecules, the “nucleation time,” also called the transition time by others,54 represents the time required for a molecule to begin to align, orient, and immediately stretch to the lower extension threshold. Although this process is fundamentally different than the nucleation-type events seen in initially self-entangled molecules, we will use the term “nucleation time,” still the time required to pass the 10 μm lower extension threshold, for the sake of consistency. The distributions of nucleation times for unentangled molecules appear to be properly scaled by the excess strain, in agreement with the simulations results of Cifre and de la Torre.54 For all field strengths, ∼1.5 “excess strain” is the characteristic quantity required to nucleate the unentangled molecules, and ∼3 “excess strain” is approximately the characteristic width of the distributions. The simulations of Cifre and de la Torre54 found (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) −
− ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c)〈ttrans〉 = 3.23 ± 0.04, where (
c)〈ttrans〉 = 3.23 ± 0.04, where (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) −
− ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c)〈ttrans〉 is analogous to the nucleation time of an unentangled molecule. This result appeared universal for ideal chains or chains with excluded volume as well as chains with and without hydrodynamic interactions. However, the results of these simulations show some disagreement with our result of 1.5, the reason for which is not immediately clear.
c)〈ttrans〉 is analogous to the nucleation time of an unentangled molecule. This result appeared universal for ideal chains or chains with excluded volume as well as chains with and without hydrodynamic interactions. However, the results of these simulations show some disagreement with our result of 1.5, the reason for which is not immediately clear.
For initially self-entangled molecules, the nucleation time represents the time for the ends of the molecule to free themselves from an entangled core a sufficient distance to initiate stretching. The distributions of nucleation times for initially self-entangled molecules are similarly scaled by the excess strain rate, and interestingly, this quantity appears to be able to reasonably scale these distributions as well, although the physical reason is not as clear. For all field strengths, ∼15 excess strain is required to stretch these tangled globules and the width of the distributions is ∼30 excess strain. These quantities are an order of magnitude larger than their counterparts in initially unentangled molecules, underscoring the fundamentally different physics in the arrested state that is present in the self-entangled molecules.
We now turn our attention to the stretching phase. The distributions of nucleation times in Fig. 6 are useful in quantifying the differences between the initially unentangled and self-entangled populations, but the main result, the existence of a the arrested state in self-entangled molecules, is already apparent when viewing the images in Fig. 2 or the trajectories in Fig. 3 and 4. Less obvious, however, are the differences in the rapid stretching phase between the two populations. Using the decomposition criteria described in Fig. 5, the stretching phase of each molecule can be separated from the prior nucleation process. This decomposition affords the ability to independently analyze this phase.
In Fig. 7a, trajectories of the stretching phase for initially self-entangled molecules are shown at a field strength of De = 2. From the ensemble of trajectories, a master stretching curve was created by sorting the extensions of the molecules into 2 μm bins and calculating the average strain of all trajectories as they pass through each bin. Such a master curve is shown superimposed over the underlying trajectories in Fig. 7a.
The process of generating master stretching curves was repeated for all initial conditions and field strengths. These curves are plotted versus excess strain in Fig. 7b. The affect of varying the lower and upper extension thresholds is shown in the ESI.† For both initially unentangled and self-entangled molecules, the master curves collapse when scaled by the excess strain, consistent with previous experiments of unentangled molecules in extensional flows.27 Interestingly, initially self-entangled molecules stretch ∼50% more slowly than initially unentangled molecules. Initially self-entangled molecules appear to have a localized, knotted core that shrinks and is tightened during stretching, as can be seen in Fig. 2, 3b, and 5. However, such a structure is very rare in stretching unentangled molecules. It follows that the difference in the rate of stretching between initially unentangled and self-entangled molecules corresponds to this topological difference. In other words, pulling the strands through a tangled core introduces and additional “topological friction” into the stretching process. The concept that knots can introduce an effective topological friction has been seen in computer simulations of knots slowing (or even jamming) the translocation of DNA through nanopores,42 the ejection of viral capsids,41 and the pulling of knotted proteins through the proteasome.43 To our knowledge, the results in Fig. 7b are the first direct experimental observation that is suggestive of the phenomena of topological friction due to a knotted domain at the molecular scale.
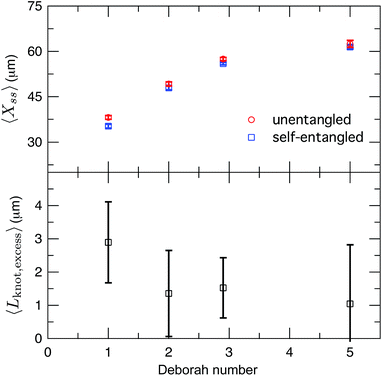
After exiting the stretching window, a molecule will remain in an extended state as long as the elongational field is applied. Once extended, initially self-entangled molecules frequently have a localized area of increased fluorescence along the contour, like those shown in Fig. 2. These regions are likely localized knots. We estimated the amount of contour stored in the knots by comparing the ensemble average steady state extensions, 〈Xss〉 of initially unentangled and self-entangled molecules, shown in Fig. 8a. The trend of increasing molecular extension with increasing field strength is expected and readily seen. For all field strengths, the initially self-entangled molecules exhibit lower 〈Xss〉 due to the finite amount of contour length stored within localized knots on the stretched chains. The difference in the steady state extension between initially unentangled and self-entangled ensembles is the excess knot length, 〈Lknot,excess〉 = 〈Xss,unentangled〉 − 〈Xss,entangled〉, shown in Fig. 8b. This quantity was first introduced as a length reduction due to a knot in a perfectly tightened string55 and has been used to characterize the size of knots in the experiments of Bao et al.56 In Fig. 8b, 〈Lknot,excess〉 is plotted versus De. A gradual decrease of 〈Lknot,excess〉 is seen as De increases, consistent with the notion of tightening a knot. Over the range of field strengths in this study, 〈Lknot,excess〉 varies approximately from 1 to 3 μm. These data can be compared to the excess knot lengths found by Bao et al.56 of ∼0.25–0.55 μm found for the 31, 41, 51, 52, and 71 knots held at tension of 0.1–2 pN, suggesting that the interior knots may be quite complex in our experiments. The large amount of extra knot length we observe in our experiments may also be an important factor in our ability to measure a strong signature of topological friction in Fig. 7b. Overall, the data in Fig. 8 verify the notion of a topological knot containing some finite amount of chain contour.
If the applied field is switched off, the molecule will relax back to the equilibrium coil. Images of a relaxing molecule are shown in Fig. 9. On average, the molecules that begin with interior bright spots relax more quickly than molecules without. This increase in the rate of relaxation contrasts with the slowing of stretching in initially self-entangled globules, shown in Fig. 7. Both observations, however, can be qualitatively explained by the electrostatic interactions within the vicinity of the knot. Stretching a knotted chain requires the knot to be pulled “tight”, and the electrostatic repulsions in the vicinity of the knot will act to slow the stretching process. Similarly, when tension is released from a tightened knot, the electrostatic interactions seek to swell the knotted core. Swelling can only be achieved by retraction of the ends of the molecule, and this will increase the observed rate at which the extension of the molecule relaxes. These observations further reinforce the notion that localized knots are frequently present upon stretching self-entangled molecules.
 | ||
| Fig. 9 Relaxation of a stretched DNA molecule. Selected snapshots for an initially unentangled and self-entangled molecule relaxing after the shutoff of the field. | ||
3.3 Modeling stretching dynamics of entangled DNA
The preceding discussion has emphasized key differences in stretching of initially self-entangled and unentangled DNA, both qualitative (initial, transient, and stretched configurations) and quantitative (nucleation times and stretching rates) in nature. Here, we lay out a physical framework that is consistent with these observations, and show that a simple dumbbell model motivated by this framework can semi-quantitatively capture the mean nucleation times and stretching curves for the experimental data.Consider a highly self-entangled blob. The topological entanglements can be thought to form a transient network structure. In order to stretch such a blob, this network must be resolved by transporting contour from a centrally entangled region to an unentangled region near the ends of the molecule. We suggest that this transport can occur via two mechanisms: (i) diffusive release of entanglements via cooperative motions of the DNA ends and entangled loops and (ii) convective transport of contour to the ends via pulling contour out of the central entangled region. This process will result in the gradual “softening” of an initially inextensible blob until soft enough to be extended by the flow, which could reproduce the initial arrested state.
We will seek to model this process by the stretching of a single non-Brownian dumbbell. The contour of the molecule is partitioned into both “free” and “entangled” regions such that Lf + Le = Lc, where Lf, Le, and Lc are the contour lengths of the free portion, entangled portion, and entire molecule, respectively. We will consider only the free portion of the molecule as being able to directly interact with the external field. The beads of the dumbbell, therefore, have drag coefficients that vary as  . Here, ζ = 4Hλ is the total drag on the DNA molecule at equilibrium and
. Here, ζ = 4Hλ is the total drag on the DNA molecule at equilibrium and 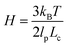 is spring constant of the total molecule.49
is spring constant of the total molecule.49
Given the concept of a varying length of extensible contour, the Deborah number, De = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) λ, cannot describe the transient dynamics of an entangled strand; the relaxation time, λ is that of unentangled state. We therefore define a “free” Deborah number as
λ, cannot describe the transient dynamics of an entangled strand; the relaxation time, λ is that of unentangled state. We therefore define a “free” Deborah number as
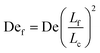 | (2) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , De is constant while Def changes in time as Lf changes from a small fraction of Lc to nearly the entire contour length of the molecule as contour is progressively freed. Given an initially highly entangled state, Lf ≈ 0, Def will progress from Def ≈ 0 at time t = 0 to Def = De as time t → ∞. The dumbbell will persist in a low extension (coiled) state until Def ≈ 0.5, giving rise to an apparent arrested state.
, De is constant while Def changes in time as Lf changes from a small fraction of Lc to nearly the entire contour length of the molecule as contour is progressively freed. Given an initially highly entangled state, Lf ≈ 0, Def will progress from Def ≈ 0 at time t = 0 to Def = De as time t → ∞. The dumbbell will persist in a low extension (coiled) state until Def ≈ 0.5, giving rise to an apparent arrested state.
We now turn to the specifics of the model that give rise to the evolution equation of the total extension of the molecule. The initially entangled state is considered to have an extension between the ends of Xknot = 1.6 μm (experimental diameter of gyration), and we assume that the extension in this region does not change. We consider the free contour on each end to be tethered to this inextensible core. The cumulative extension of both ends from their tethers is R, and the total extension of the molecule is R + Xknot. By neglecting inertia, the evolution equation for the dumbbell becomes
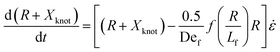 | (3) |
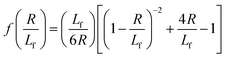 | (4) |
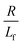 . The first term in the right hand side of eqn (3) corresponds to the affine deformation of two points separated by R + Xknot, and the second term slows this deformation rate due to a nonlinear spring of fractional extension
. The first term in the right hand side of eqn (3) corresponds to the affine deformation of two points separated by R + Xknot, and the second term slows this deformation rate due to a nonlinear spring of fractional extension 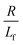 .
.
In order to solve eqn (3), an expression for Lf(t) is needed. We consider two factors can free entangled contour from the knotted core: (i) cooperative diffusion of the ends and knot and (ii) “pulling” of the ends out of the globule by the external flow. While both factors (particularly (i)) are quite complex in reality, we considered the simplest estimates of each for the purpose of this model, described as follows.
We estimate the rate of diffusive release of entangled contour to the free ends as
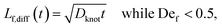 | (5) |
We estimate the rate at which contour is pulled out of the entangled center due to the field is
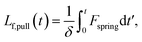 | (6) |
The total contour that has been freed from the initially entangled globule is then written as
| Lf(t) = min(Lf,diff(t) + Lf,pull(t), Lc − Xknot), | (7) |
Eqn (7) was solved simultaneously with eqn (5) and (6)via a midstepping Euler integration scheme. The resulting stretching curves are shown in Fig. 10a. These curves qualitatively reproduce three key experimental findings. (1) Each curve persists in an arrested state for some time. (2) The duration of the arrested state decreases as De increases. (3) The arrested state is followed by a rapid stretching phase.
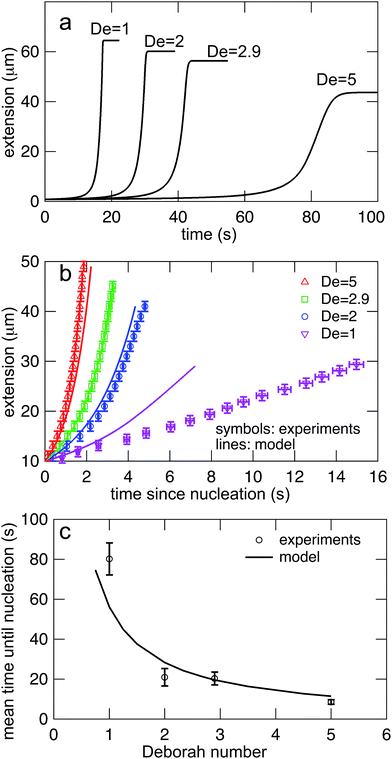 | ||
| Fig. 10 (a) Stretching curves for generated by the model all Deborah numbers (De = 1, 2, 2.9, and 5) in this study with δ = 0.5ζ and Dknot = 22 μm2 s−1. Note the presence of an arrested state followed by a rapid stretching phase and finally a fully extended state. (b) Comparison of the rates of stretching for curves in the model vs. the experimental data from Fig. 7b. Error bars represent the bin widths (y-axis) and 95% confidence intervals around the mean (x-axis). (c) Comparison of the nucleation times from the model vs. the mean nucleation time from the data in Fig. 6. Error bars represent 95% confidence intervals around the mean (y-axis). | ||
The values of δ = 0.5ζ and Dknot = 22 μm2 s−1 were chosen to best match the ensemble average nucleation times and the master stretching curves from experiments. The results from the model are compared to the experimental results for average nucleation times and master stretching curves in Fig. 10b and c. The model does predict a slowed rate of stretching, seen in Fig. 10b. It captures the slowed rate of stretching well at high De, but fails to capture the experimental curve at De = 1. This discrepancy is likely due to the documented difficulty in a simple dumbbell model in capturing polymer dynamics over ranges of De (regardless of entanglements); additional complexity such as configurationally dependent drag is often needed to capture this behavior.57 The model and experiment find good agreement for the average nucleation time over the entire range of field strengths, De = 1, 2, 2.9, and 5, seen in Fig. 10c. This quantity depends only on the rate of diffusive release of the contour coupled with convective release due to flow on a globule of low and nearly constant extension, further supporting the notion that configurationally dependent drag causes the discrepancy in Fig. 10b.
Given the simplicity of the dumbbell model, the results in Fig. 10 are encouraging. We now turn to discuss the limitations of this modeling approach. Foremost, by seeking to capture average properties, this model ignores the wealth of information encoded in the distributions of nucleation times or stretching rates. This issue seems likely intractable by any model of such simplicity. Fine-scaled simulations by Larson and others30 were the first successful attempt to recreate the qualitative configurational classes seen in the molecular individualism experiments.26,27 We expect that even finer-grained simulations that preserve the topology of individual entanglements will be necessary to make further progress into our experimental work. Also, the assumptions of constant diffusion coefficients and friction coefficients for the diffusive and convective transport of contour out of the entangled structure are oversimplifications. Both the rate of disentangling and the friction of pulling an end through an entangled core should be functions of the entangled state, but the functional dependence of each is likely complex and not presently clear.
We now seek to put the values of δ = 0.5ζ and Dknot = 22 μm2 s−1 in proper context. With similar experimental conditions, Tang et al.47 found the relaxation of an initially entangled molecule to the equilibrium state to proceed via a two stage process with average durations of 19.7 s and 20 s, giving a total disentanglement time of ∼40 s. From our model, the value of Dknot = 22 μm s−1 would give a characteristic time of 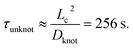 While this discrepancy appears large at first, it can be understood in context of experimental results. The 40 s disentanglement time of Tang et al.47 corresponds to the average time when the fluctuations and size of the molecule are indistinguishable from the equilibrium state under no external forces. In Fig. 10, the experimental nucleation time for De = 1 is ∼80 s. These results suggest that in the process of disentangling a molecule under no field, there exists a period of time where measurements of the molecule approach their equilibrium values, yet entanglements significant enough to affect an out of equilibrium process remain. This observation underscores the well-established fact that dynamical measurements, such as stretching a molecule in an elongational field, can provide a wealth of information beyond that provided by experiments at equilibrium.
While this discrepancy appears large at first, it can be understood in context of experimental results. The 40 s disentanglement time of Tang et al.47 corresponds to the average time when the fluctuations and size of the molecule are indistinguishable from the equilibrium state under no external forces. In Fig. 10, the experimental nucleation time for De = 1 is ∼80 s. These results suggest that in the process of disentangling a molecule under no field, there exists a period of time where measurements of the molecule approach their equilibrium values, yet entanglements significant enough to affect an out of equilibrium process remain. This observation underscores the well-established fact that dynamical measurements, such as stretching a molecule in an elongational field, can provide a wealth of information beyond that provided by experiments at equilibrium.
The value of δ = 0.5ζ means that pulling contour out of the entangled glob experiences an additional friction of approximately half the total friction coefficient of the molecule. This value appears eminently reasonable given the cooperative nature of pulling segments through a topological knot. Our value of δ can be estimated with units as 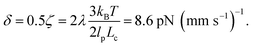 In experiments where knots of specific topologies were tied with optical tweezers, Bao et al.56 were able to directly measure the friction coefficients of knots via the diffusivities of the knot along an extended contour. They found frictions of ∼3–8 pN (mm s−1)−1 for the 31, 41, 51, 52, and 71 knots, and it is interesting to note the similarity between our results and their measured friction coefficients.
In experiments where knots of specific topologies were tied with optical tweezers, Bao et al.56 were able to directly measure the friction coefficients of knots via the diffusivities of the knot along an extended contour. They found frictions of ∼3–8 pN (mm s−1)−1 for the 31, 41, 51, 52, and 71 knots, and it is interesting to note the similarity between our results and their measured friction coefficients.
4 Conclusion
We have presented a systematic study comparing the rates at which initially unentangled and self-entangled DNA molecules stretch while in elongational fields. These experiments revealed two striking qualitative differences between their stretching pathways. For initially self-entangled molecules, there exists and initial topologically stabilized arrested state leading to nucleation-type behavior after which molecules stretch at a slowed rate due to interior knots. The herein observed slowed rate of stretching represents the first direct experimental evidence of a topological friction in polymer molecules, seen recently in computer simulations of driven knots.58 We systematically characterized the nucleation times and stretching rates over a variety of field strengths. Guided by this experimental data, we developed a simple dumbbell model which consists of a gradually softening spring due to diffusive and convective release of contour from the knot. This model is able to semi-quantitatively capture both the average nucleation time and stretching dynamics of an initially self-entangled molecule, reinforcing the key physics in play. Looking forward, we anticipate this approach will stimulate future work on expanding the model in more detail, possibly through the use of fine-grained dynamical computer simulations. From an experimental point of view, we hope our work motivates further experimental studies of knotted polymers, such as knotted DNA in nano-scale confining geometries or knotted DNA driven through nanopores.Acknowledgements
This work is supported by the Singapore-MIT Alliance for Research and Technology (SMART) and National Science Foundation (NSF) grant CBET-1335938.References
- Y. Michaeli and Y. Ebenstein, Nat. Biotechnol., 2012, 30, 762–763 CrossRef CAS PubMed.
- J. Clarke, H.-C. Wu, L. Jayasinghe, A. Patel, S. Reid and H. Bayley, Nat. Nanotechnol., 2009, 4, 265–270 CrossRef CAS PubMed.
- E. Shaqfeh, J. Non-Newtonian Fluid Mech., 2005, 130, 1–28 CrossRef CAS PubMed.
- M. D. Graham, Annu. Rev. Fluid Mech., 2011, 43, 273–298 CrossRef.
- A. B. Marciel and C. M. Schroeder, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 556–566 CrossRef CAS.
- S. Smith, L. Finzi and C. Bustamante, Science, 1992, 258, 1122–1126 CAS.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- K. D. Dorfman, Rev. Mod. Phys., 2010, 82, 2903 CrossRef CAS.
- D. J. Mai, C. Brockman and C. M. Schroeder, Soft Matter, 2012, 8, 10560–10572 RSC.
- J. Tang and P. S. Doyle, Appl. Phys. Lett., 2007, 90, 224103 CrossRef PubMed.
- Y.-J. Juang, S. Wang, X. Hu and L. Lee, Phys. Rev. Lett., 2004, 93, 268105 CrossRef.
- A. G. Balducci, J. Tang and P. S. Doyle, Macromolecules, 2008, 41, 9914–9918 CrossRef CAS.
- S. Gerashchenko and V. Steinberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 040801 CrossRef.
- G. C. Randall and P. S. Doyle, Phys. Rev. Lett., 2004, 93, 058102 CrossRef.
- G. C. Randall and P. S. Doyle, Macromolecules, 2006, 39, 7734–7745 CrossRef CAS.
- J. Ou, J. Cho, D. W. Olson and K. D. Dorfman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061904 CrossRef.
- E. Y. Chan, N. M. Goncalves, R. A. Haeusler, A. J. Hatch, J. W. Larson, A. M. Maletta, G. R. Yantz, E. D. Carstea, M. Fuchs and G. G. Wong, et al. , Genome Res., 2004, 14, 1137–1146 CrossRef CAS PubMed.
- G. C. Randall, K. M. Schultz and P. S. Doyle, Lab Chip, 2006, 6, 516–525 RSC.
- J. M. Kim and P. S. Doyle, Lab Chip, 2007, 7, 213–225 RSC.
- A. Balducci, P. Mao, J. Han and P. Doyle, Macromolecules, 2006, 43, 6273–6281 CrossRef.
- J.-W. Yeh, A. Taloni, Y.-L. Chen and C.-F. Chou, Nano Lett., 2012, 12, 1597–1602 CrossRef CAS PubMed.
- W. Reisner, K. J. Morton, R. Riehn, Y. M. Wang, Z. Yu, M. Rosen, J. C. Sturm, S. Y. Chou, E. Frey and R. H. Austin, Phys. Rev. Lett., 2005, 94, 196101 CrossRef.
- R. Dylla-Spears, J. E. Townsend, L. Jen-Jacobson, L. L. Sohn and S. J. Muller, Lab Chip, 2010, 10, 1543–1549 RSC.
- A. Balducci, C. Hsieh and P. Doyle, Phys. Rev. Lett., 2007, 99, 238102 CrossRef CAS.
- W. Xu and S. J. Muller, Lab Chip, 2012, 12, 647–651 RSC.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS.
- D. E. Smith and S. Chu, Science, 1998, 281, 1335–1340 CrossRef CAS.
- C. M. Schroeder, H. P. Babcock, E. S. Shaqfeh and S. Chu, Science, 2003, 301, 1515–1519 CrossRef CAS PubMed.
- P. G. de Gennes, Science, 1997, 276, 1999–2000 CrossRef CAS.
- R. Larson, H. Hu, D. Smith and S. Chu, J. Rheol., 1999, 43, 267 CrossRef CAS.
- G. Randall and P. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10813 CrossRef CAS PubMed.
- A. Balducci and P. Doyle, Macromolecules, 2008, 41, 5485–5492 CrossRef CAS.
- C. Micheletti, D. Marenduzzo and E. Orlandini, Phys. Rep., 2011, 504, 1–73 CrossRef CAS PubMed.
- D. Meluzzi, D. E. Smith and G. Arya, Annu. Rev. Biophys., 2010, 39, 349–366 CrossRef CAS PubMed.
- J. Arsuaga, M. Vázquez, S. Trigueros, D. Sumners and J. Roca, et al. , Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5373 CrossRef CAS PubMed.
- J. Arsuaga, M. Vazquez, P. McGuirk, S. Trigueros, D. Sumners and J. Roca, et al. , Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9165 CrossRef CAS PubMed.
- W. Taylor, Nature, 2000, 406, 916–919 CrossRef CAS PubMed.
- C. Micheletti and E. Orlandini, Macromolecules, 2012, 45, 2113–2121 CrossRef CAS.
- C. Micheletti and E. Orlandini, Soft Matter, 2012, 8, 10959–10968 RSC.
- L. Dai, J. R. van der Maarel and P. S. Doyle, ACS Macro Lett., 2012, 1, 732–736 CrossRef CAS.
- D. Marenduzzo, C. Micheletti and E. Orlandini, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20081–20086 CrossRef CAS PubMed.
- A. Rosa, M. Di Ventra and C. Micheletti, Phys. Rev. Lett., 2012, 109, 118301 CrossRef CAS.
- L. Huang and D. E. Makarov, J. Chem. Phys., 2008, 129, 121107 CrossRef PubMed.
- Y. Rabin, A. Grosberg and T. Tanaka, Europhys. Lett., 1995, 32, 505 CrossRef CAS.
- N. Lee, C. Abrams, A. Johner and S. Obukhov, Phys. Rev. Lett., 2003, 90, 225504 CrossRef.
- N. Lee, C. Abrams, A. Johner and S. Obukhov, Macromolecules, 2004, 37, 651–661 CrossRef CAS.
- J. Tang, N. Du and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16153–16158 CrossRef CAS PubMed.
- B. Kundukad, J. Yan and P. S. Doyle, Soft Matter, 2014, 10, 9721–9728 RSC.
- J. Tang, S. Levy, D. Trahan, J. Jones, H. Craighead and P. Doyle, Macromolecules, 2010, 39, 7368–7737 CrossRef.
- J. Tang, D. Trahan and P. Doyle, Macromolecules, 2010, 43, 3081–3089 CrossRef CAS PubMed.
- C. Hsieh, A. Balducci and P. Doyle, Macromolecules, 2007, 40, 5196–5205 CrossRef CAS.
- C. E. Sing and A. Alexander-Katz, Macromolecules, 2010, 43, 3532–3541 CrossRef CAS.
- C. E. Sing and A. Alexander-Katz, J. Chem. Phys., 2011, 135, 014902 CrossRef PubMed.
- J. G. H. Cifre and J. G. de la Torre, J. Chem. Phys., 2001, 115, 9578–9584 CrossRef PubMed.
- P. Pierański, S. Przybył and A. Stasiak, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 123–128 CrossRef.
- X. Bao, H. Lee and S. Quake, Phys. Rev. Lett., 2003, 91, 265506 CrossRef.
- C. Schroeder, E. Shaqfeh and S. Chu, Macromolecules, 2004, 37, 9242–9256 CrossRef CAS.
- M. Di Stefano, L. Tubiana, M. Di Ventra and C. Micheletti, Soft Matter, 2014, 10, 6491–6498 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Channel schematic, DNA relaxation time, strain rate calibration, upper and lower extension threshold effects, and movies. See DOI: 10.1039/c4sm02738h |
| This journal is © The Royal Society of Chemistry 2015 |