Atomic-scale observation of rotational misorientation in suspended few-layer graphene sheets

Abstract

Single or few-layer graphene (FLG) sheets offer extraordinary electronic, thermal and mechanical properties and are expected to find a variety of applications. Fully exploiting the properties of graphene will require a method for the production of high-quality graphene sheets (almost pristine graphene) in large quantities. In this regard, we report a two-step method for obtaining a homogenous colloidal suspension of single or FLG sheets up to 0.15 mg ml⁻¹ in N,N-dimethylformamide solution. The graphene nanostructures are directly imaged using a high-resolution transmission electron microscope (HRTEM) operated at 200 kV with a point resolution of 0.16 nm. We observed rotational misorientation within the flake in the HRTEM images of 2, 4 and 6 layers of graphene sheets, giving rise to Moiré patterns. By filtering in the frequency domain using a Fourier transform, we reconstruct the graphene lattice of each sheet and determine the relative rotation between consecutive graphene layers up, to six separate sheets. Direct evidence is obtained for FLG sheets with packing that is different to the standard AB Bernal packing of bulk graphite. Furthermore, we observed periodic ripples in suspended graphene sheets in our TEM measurements. Electrostatic force microscopy was used to characterize the electric potential distribution on the surface of FLG sheets on SiO₂/Si substrates in ambient conditions. The FLG sheets were found to exhibit a conducting nature with small potential variations on the surface.

---

Introduction

Graphene, a two-dimensional carbon material, which takes the form of a planar honeycomb lattice of sp²-bonded carbon atoms has stimulated a vast amount of research interest in recent years.^1–7 Single or few-layer graphene (FLG) sheets have attracted an enormous amount of interest in the last five years because of their excellent mechanical, thermal and electronic properties.^8–12 However, the electrical properties of graphene vary between single and FLG sheets.^13–16 Therefore the method of preparation of graphene is highly crucial to control the graphene layers. In addition, the in-depth structural analysis of graphene sheets is highly desirable in order to exploit this material for future development of graphene-based nanoelectronic devices.^17–19

Single-layer graphene was first isolated using the scotch-tape method in 2004.²⁰ This method also produces samples composed of two or more atomic layers of graphene. However, this process has significant disadvantages in terms of yield and throughput. Fully exploiting the properties of graphene will require a method for the production of high-quality graphene sheets (almost pristine graphene) in large quantities. Two main routes are possible: (i) large-scale growth, and (ii) large-scale exfoliation. In the continuation of second approach, we are presenting a two-step method for a homogenous colloidal suspension of single or FLG sheets up to 0.15 mg ml⁻¹ in N,N-dimethylformamide (DMF) solution.

The two-step approach includes; (i) high temperature (∼2000 °C) heat treatment of commercially available pyrolytic graphite powders in a vacuum (<1 × 10⁻⁵ Torr) for 3 h (this heat treatment may reduce contamination) followed by (ii) sonication for 2 h by dissolving the heat-treated graphite in DMF using a probe-tip sonicator. Furthermore, the pyrolytic graphite is composed of a periodical stack of two-dimensional (2D) graphene sheets (layers) along the c-axis. Each of these layers is weakly bonded to its neighbouring layers by interlayer interaction forces; the graphene layers can easily slide against each other and peel off easily. As a result of the heat treatment of pyrolytic graphite at high temperature under vacuum, the interactions between graphene layers may soften, thus making their liquid-phase exfoliation with DMF easier.²¹

Our approach provides single or FLG sheets (2–6 layers) dispersed in DMF solution. The percentage of single-layer graphene is low in comparison to FLG sheets (2–6 layers). Moreover, DMF is well documented for its high synthetic value, high polarity and wide solubility range for both organic and inorganic compounds, including single and multi-walled carbon nanotubes.^22,23 Very recently, Liao et al.²⁴ also proved that probe-tip sonication is more powerful for the dispersion of carbon nanotubes in epoxy resin nanocomposites than bath sonication. This might be the reason for achieving a relatively higher graphene concentration in DMF solution compared to other reported results.^25–27 The homogenous colloidal suspension of graphene in DMF could be a promising candidate for potential applications such as energy-storage materials, polymer composites, liquid crystal devices and photovoltaic applications.^19,28–32

In our exfoliated samples, we observed a significant number of rotational stacking faults with various rotation angles in two-layer, four-layer and six-layer graphene sheets. The introduction of rotational stacking faults in AB Bernal stacked graphene bilayers changes the dispersion relationship close to the k-point from parabolic (AB) to linear band behaviour (rotation disorder) and leads to some monolayer graphene properties being observed in two-layer and FLG films.^13–16 Generally, atomic force microscopy (AFM), optical imaging and Raman spectroscopy are regularly used to determine the number of graphene layers within graphene sheets.^20,33,34 However, these techniques provide only indirect proof of single or FLG sheets and also they cannot determine the presence of rotational stacking faults within these FLG structures. In addition, scanning tunnelling microscopy (STM) is effective to produce atomically detailed images of surfaces of graphite and graphene, along with rotational stacking faults that give rise to superstructure in the STM images.³⁵ The superstructure attributed to Moiré patterns^35–37 is derived from complex three-dimensional tunnelling.³⁷ However, STM measurements are experimentally challenging under ultrahigh vacuum (UHV) conditions making the turnaround time for characterization relatively long.^38–41 On the other hand, transmission electron microscopy (TEM) offers a faster approach for direct imaging the atomic structure of rotational misorientation in FLG sheets, which gives rise to Moiré patterns.⁴² Here in our experiment, we used a conventional high-resolution TEM (JEOL 2200F TEM/STEM) operated at 200 kV with a point resolution of 0.16 nm, equipped with a GIF-2000 spectrometer. The electron beam was focused onto a monoatomic layer of graphene to observe the ball-and-stick model of an atomic lattice structure. In the structure, the bright contrast corresponds to atoms and dark contrast to the gaps between them.⁴³ In addition, we used electrostatic force microscopy (EFM)⁴⁴ to characterize the electrical potential distribution on the surface of FLG sheets on SiO₂/Si substrates and proved that FLG sheets on SiO₂/Si substrates exhibit a conducting nature with small potential variations on the surface.

Experimental section

Synthesis of high-quality single or few layer graphene sheets

Commercial available pyrolytic graphite powders (carbon content >99 wt%, Sigma-Aldrich, 2 g) were heated to ∼2000 °C for 3 h in a vacuum (<1 × 10⁻⁵ Torr) after being ground by a pestle in a mortar. After heat treatment the graphite powders were ground again and then dispersed in DMF (99.9 vol%, 500 ml) by using a probe-tip sonicator (Sonics Model VC 130, 20 kHz, probe tip (6 mm diameter), amplitude 80%, 2.2 kW) for 2 h. The resulting (4 mg ml⁻¹, 100 ml) solution was treated in an ultrasonic cleaner (KQ-100, frequency 40 kHz, output power 100 W) for 10 min, followed by high-speed centrifugation (5000 rpm, 30 min) to remove big particles. The resultant supernatant solution (gray colour) consisted of a homogenous colloidal solution of graphene (0.15 mg ml⁻¹) in DMF solution (see Scheme 1).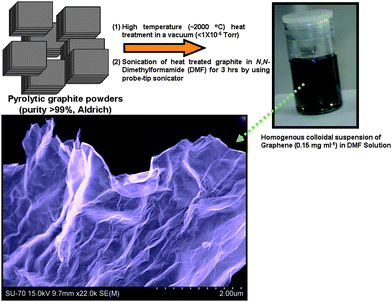

Scheme 1 Overview of the steps for the preparation of exfoliated single or few-layer graphene sheets in N,N-dimethylformamide (DMF) solution. The procedure started with pyrolytic graphite and was followed by heat treatment at a very high temperature in vacuum, and probe-tip sonication.

Surface characterization

The surface morphology of exfoliated graphene samples was examined by field-emission scanning electron microscopy (Hitachi S-800, and SU-70, 30 keV) and optical microscopy (Nikon Eclipse LV150 microscope), respectively. Moreover, the sample topography and thickness measurement of exfoliated graphene samples were performed by a commercial setup Multimode, NanoScope IIIA, DI atomic force microscope (AFM) in tapping mode. Micro-Raman spectra of the graphene samples were obtained at room temperature using a Renishaw spectrometer at 514 nm, with a notch filter cutting at ∼100 cm⁻¹. A 100× objective was used. Extreme care was taken to avoid sample damage or laser-induced heating. The incident power during the measurements was ∼0.04 mW.

Transmission electron microscopy and electron energy-loss spectroscopy

A conventional high-resolution (HR) TEM (JEOL 2200F TEM/STEM) was operated at 200 kV with a point resolution of 0.16 nm, equipped with a GIF-2000 spectrometer. Electron energy-loss spectroscopy (EELS) experiments were carried out in diffraction mode using a convergence semi-angle of 0.9 mrad, a collection semi-angle of 1.8 mrad, a nominal spot size of 0.5 nm, an energy dispersion of 0.3 eV per pixel and an energy resolution of approximately 1.2 eV.

Electrostatic force microscopy (EFM) measurements

A commercial setup Multimode, NanoScope IIIA, DI AFM with a conductive tip was used to record the sample topography and EFM phase. We used silicon cantilevers (NSG11) with a Pt conductive coating. The tip was set to vibrate with a piezo having a resonant frequency of 150.09 kHz and an amplitude of 30 nm.

Results and discussion

The single or FLG sheets were synthesized by the procedure outlined in Scheme 1. The procedure started with pyrolytic graphite powder followed by heat treatment at very high temperature in vacuum, and probe-tip sonication. The as-synthesized products were initially observed with SEM, optical microscopy, AFM and micro-Raman spectroscopy. Fig. 1(a) shows an SEM image of an as-produced folded graphene sheet (a paper-like structure) on a Si substrate. Furthermore, we performed systematic optical microscopy imaging of single or FLG samples on 300 nm SiO₂/Si substrates [see Fig. 1(b)–(d)]. These layers have a slightly different colour in the optical microscope [Fig. 1(b)–(d), and Fig. 2(a)]. It appears that the darker colour corresponds to thicker layers. A quick and accurate method for determining the number of layers of graphene sheets is required to accelerate research and exploitation of graphene. In this direction, AFM measurement is the most direct way to identify the number of layers of graphene sheets. Figs. 1(e)–(g) reveals AFM images of our exfoliated graphene sheets in tapping mode. Figs. 1(f) and (g) show 2–3 layer and 4-layer graphene sheets, respectively. The insets shows the height profiles. We also clearly observed the overlapping of graphene sheets in the AFM images [indicated by a black dotted arrow in Fig. 1(g)]. However, this technique has a very slow throughput, and also an instrumental offset of ∼0.5 nm (caused by different interaction forces) always exists, which is even larger than the thickness of a graphene monolayer and data fitting is required to extract the true thickness of the graphene sheets.^45,46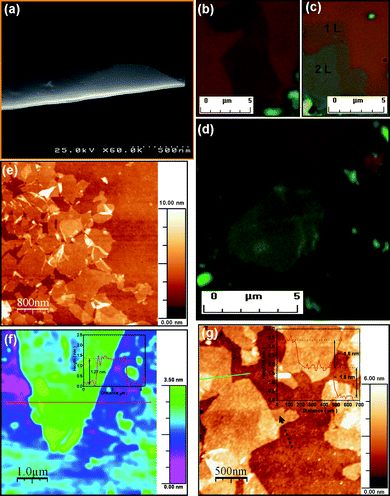

Fig. 1 Microstructural analyses of graphene sheet. (a) SEM image of exfoliated graphene sheet (with a paper-like morphology). (b)–(d) Optical microscopy images of single or FLG sheet samples on 300 nm SiO₂/Si substrates which clearly show the single-layer, two-layer, and more than four-layer graphene sheets, respectively. These layers have a slightly different colour in the optical microscope. It appears that the darker colour corresponds to thicker layers. (e)–(g) AFM images of graphene sheets in tapping mode. (f) and (g) show 2–3 layer and four-layer graphene sheets, respectively. The insets show the corresponding height profiles. The overlapping of misoriented graphene sheets is clearly indicated by a black dotted arrow in (g).

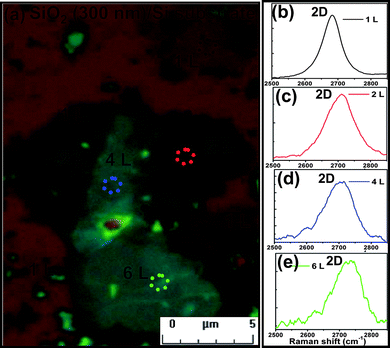Fig. 2 (a) Optical microscopy images of single-layer, two-layer, four-layer and six-layer graphene sheets on 300 nm SiO₂/Si substrates. (b)–(e) shows corresponding Raman spectra recorded from single-layer (black dotted circle), two-layer (red dotted circle), four-layer (blue dotted circle), and six-layer (green dotted circle), sheets respectively.

Recently, Raman spectroscopy has been shown to be a potential candidate for the non-destructive and quick characterization of the number of layers of graphene. The shape of the second-order band 2D is a characteristic that can be used to distinguish the number of layers of AB-stacked graphene.^47,48 We performed Raman spectroscopy on single-layer (black dotted circle), two-layer (red dotted circle), four-layer (blue dotted circle), and six-layer (green dotted circle) graphene sample on 300 nm SiO₂/Si substrates [see Fig. 2(a)]. Fig. 2(b)–(e), shows the 2D-band spectra of a single-layer (∼2670 cm⁻¹), and few-layer (2, 4 and 6 layers) graphene samples, respectively. It can be seen in Fig. 2(b)–(e), that the 2D-band becomes broader and blue-shifted when the graphene thickness increases from single-layer to FLG sheets. The Raman spectra of single or FLG sheets have been well documented and discussed by many authors.^49–52 Recently, Poncharal et al.⁵³ compared Raman scattering spectra from single-layer graphene with a bilayer in which the two layers are arbitrarily misoriented. Ni et al.⁵⁴ also discussed the electronic structures of 1 + 1 layer folded graphene sheets, which are different from AB (Bernal) stacking. However, this technique cannot determine the presence of rotational stacking faults or rotation angles with in the FLG sheets or more complex structures. Therefore, we relied on atomically resolved high-resolution TEM for in-depth study.^55,56

Detailed high-resolution TEM studies were performed on individual or few-layer freely suspended graphene sheets. For this experiment, the TEM samples were prepared by dipping a carbon-coated TEM grid into the (graphene/DMF) solution and allowing it to dry. Fig. 3(a) shows a bright-field TEM image of graphene crystallites attached to a TEM grid. The suspended graphene membranes consist of single-layer or FLG sheets. The two-layered graphene is clearly visible and it is marked by red square in Fig. 3(a). We also observed folded regions in the FLG sheets, which give rise to Moiré patterns from rotational stacking faults [see the blue box in Fig. 3(b)]. Fig. 3(b) depicts a highly magnified image of the green-square region of the Fig. 3(a). Fig. 3(b) describes single-layer, two-layer and four-layer graphene sheets, respectively. A 2D fast Fourier transform (FFT) was performed in the region indicated by a white box in Fig. 3(b). The FFT of a single hexagonal graphene network produces six spots of 0.21 ± 0.05 nm spacing which corresponds to a single layer. Fig. 3(c) exhibits an HRTEM image of single-layer graphene, which was acquired from the region indicated with red dotted arrow. Fig. 3(d) shows the image reconstructed by filtering in the frequency domain to remove unwanted noise. The hexagonal graphene network is clearly resolved in the inset of Fig. 3(d), showing the magnification of the small region indicated with a green box. The C–C bond length is measured to be 1.4 Å ± 0.2 Å and the measured lattice constant is 2.5 Å ± 0.2 Å, confirming that this is a single layer. However, in our graphene sample we did not observed single or di-vacancy defects as reported by previous methods.^43,57 In addition, it is also quite interesting to observe four graphene layers which are lying one on top of another in the same TEM image, indicated by a red box [Fig. 3(b)]. This is also further confirmed by FFT performed in the region indicated with a red box in Fig. 4(a). This allows a set of spots to be associated with each different orientation of the graphene sheets within the layer. The FFT shows 24 spots which resemble four different graphene layers. The HRTEM image of the red box region shows Moiré patterns [see Fig. 4(b)].

Fig. 3 HRTEM images of a freely suspended graphene membrane. (a) Bright-field TEM image of a suspended graphene membrane. (b) Magnified view of the region denoted by a green box in (a); the inset shows 2D FFT performed in the region indicated with a white box. (c) HRTEM image of single-layer graphene acquired from the region indicated with a red dotted arrow in (b). (d) Reconstructed image after filtering in the frequency domain to remove unwanted noise, for clarity. The inset shows the hexagonal graphene network.

Fig. 4 (a) Bright-field TEM image taken from a set of four graphene layers [indicated by a red box in Fig. 3(b)]; the inset shows FFT taken from the region indicated by a red box in (a). (b) HRTEM image of (a) (indicated by red box region) showing a Moiré pattern.

We found approximately 40–50% of the FLG sheets contain regions with observable Moiré patterns in the HRTEM images arising from rotational stacking faults. These rotational faults are most likely related to the back-folding of top graphene layers during the exfoliation (as we observed in Fig. 3(b) indicated by white dotted arrow). Intrinsic rotational stacking faults within the graphite structure may also contribute to the number of stacking disorders. In this work, we discuss in detail the simplest Moiré pattern (generated by only one rotational stacking fault) and a complex Moiré pattern (which consists of at least six graphene layers), respectively.

A two-layer graphene sheet (two graphene layers separated by 0.40 ± 0.02 nm) is clearly observed in Fig. 5(a) (indicated by a blue box), which shows a TEM image of a FLG sheet containing a top layer that has folded back and it is indicated by a white dotted arrow in Fig. 3(b). Fig. 5(b) is a bright-field TEM image of the region indicated with a red box in Fig. 5(a). A FFT of Fig. 5(a) is included in the inset and shows two sets of hexagons with a 7° rotation between them. Fig. 5(c) shows the image reconstructed by filtering in the frequency domain to remove unwanted noise. Fig. 5(d) clearly shows an HRTEM image of the Moiré pattern for the 7° rotational stacking fault presented in Fig. 5(c). Figs. 5(e) and 5(f) show the reconstructed image of the front and back graphene layers after filtering in the frequency domain to remove unwanted noise.

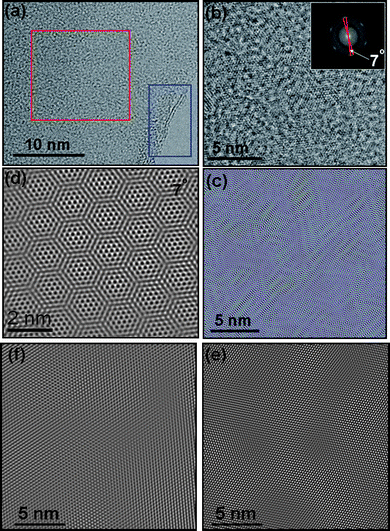Fig. 5 HRTEM images of a two-layer graphene sheet. (a) Bright-field TEM image of a two-layer graphene sheet. Two graphene layers separated by 0.34 ± 0.02 nm are clearly observed in the blue box. (b) TEM image of the region indicated with a red box in (a). The inset shows the FFT of the region indicated with a red box in (a), which shows two sets of hexagons with a 7° rotation between them. (c) FFT image corresponds to (b), for clarity. (d) HRTEM image of the Moiré pattern for the 7° rotational stacking fault presented in (c). (e)–(f) are the reconstructed images of the front and back graphene layers after filtering in the frequency domain to remove unwanted noise.

We have also used electron energy-loss spectroscopy (EELS) to analyse our FLG exfoliated sample. The single-layer or FLG sheets exhibit unique behaviour in their EELS spectra.⁵⁸ The low-loss EELS spectrum of graphitic structures is dominated by plasmon excitations consisting of π- and π + σ-plasmons, both exhibiting bulk and surface modes. The shape of the low-loss EELS spectrum for graphitic structures is highly dependent on the angle at which the incident beam hits the structure. Carbon nanotubes are an excellent example of this, as demonstrated both theoretically and experimentally.^59,60 Interestingly, we have also observed EELS spectra [taken in the region indicated with a black box in Fig. 6(a)] from a freely suspended graphene sheet, which is shown in the inset. Fig. 6(a) is more magnified view of the region indicated by white box in Fig. 3(a). The plasmon spectra shows that the π-mode, at 7 eV in graphite, has shifted to 4.98 eV. Furthermore, the spectrum also exhibits a π + σ-surface mode at 23 eV, which is very near to the 26 eV seen in graphite.⁶¹ We expect that there are at least six layers of graphene in that area. However, we further confirm this by HRTEM imaging [the Moiré pattern shown in Fig. 6(b) and (c)] taken from the same area. Fig. 6(b) depicts a bright-field TEM image of the black box region indicated in Fig. 6(a). Fig. 6(c) shows an HRTEM image of the region [indicated by a blue box in Fig. 6(b)] containing Moiré patterns. The plateau between 15 and 30 eV starts to appear, which becomes more pronounced as the number of sheets increases. The plasmon maximum keeps moving to higher energies, accompanied by further broadening. The plasmon structure for more than 10 sheets strongly resembles that of graphite.⁶² However, we could not perform EELS spectra on a single-layer graphene sheet using our HRTEM system. The theoretical predictions for π and π + σ-surface plasmon modes in free-standing single graphene sheets give ∼4.5 eV and ∼14.5 eV, which are substantially different from the six-layer graphene sheet.⁵⁸

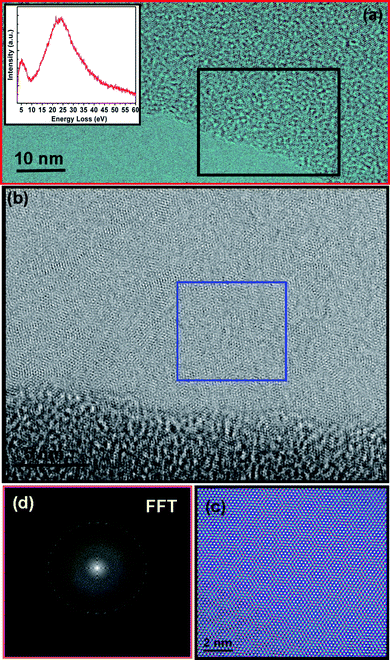Fig. 6 (a) HRTEM image of the edge of a FLG sheet with at least six layers. The inset shows the EELS spectra acquired from the black-box region. (b) High-magnification bright-field TEM image of the black-box region (c) HRTEM image of the blue-box region, showing a clear Moiré pattern. (d) FFT of panel (b) (blue-box region) showing six sets of hexagonal spots corresponding to six different graphene layer orientations.

The Moiré pattern was observed to be more complex in six-layered graphene sheets [Fig. 6(a)]. A FFT was also taken from this region, Fig. 6(d), and shows 36 spots. One set of six spots corresponds to each graphene layer. So, this indicates that at least six layers in this region have an average 10° rotation with respect to each other. The rotation angle and d-spacing between two consecutive spots is clearly indicated in a more detailed way in Fig. 7. The formation of this type of complex Moiré pattern is relatively different from the result described by Warner et al.⁶²Fig. 8(a)–(f) shows the reconstructed images for each graphene layer produced by filtering in the frequency domain.

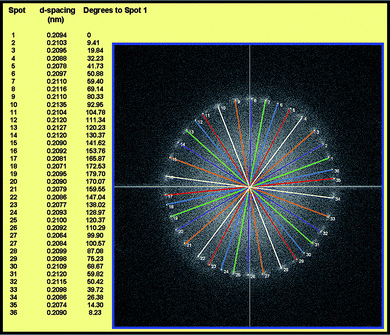Fig. 7 The relative rotation angle and d-spacing between two consecutive spots in more detail.

Fig. 8 (a)–(f) Reconstructed images showing the graphene layer associated with the relative set of spots indicated in Fig. 7.

These isolated graphene membranes could offer a unique platform for understanding the formation of ripples in suspended graphene.⁶³ Here in our TEM observation we directly observe corrugations and periodic ripples [indicated by the green and white dotted arrows, respectively in Fig. 9(a)] in suspended FLG sheets. The inset shows a schematic of a rippled graphene sheet. In a recent experimental observation Meyer et al.⁶⁴ also found ripples in suspended graphene sheets. To better understand the unusual behaviour of graphene, the researchers from Radboud University [Fasolino et al.⁶⁵] undertook atomistic Monte Carlo simulations at room (300 K) and high (1000, 2000, and 3500 K) temperatures. The researchers believe that the origin of the ripples is to be found in the carbon–carbon bonding in graphene. Fig. 9(b) shows a TEM image of a magnified view of area denoted by a white dotted arrow in Fig. 9(a). Fig. 9(c) shows a reconstructed image of Fig. 9(b) after filtering in the frequency domain to remove unwanted noise for clarity. The ripples are clearly observed in the red box of Fig. 9(c). We can also clearly observe the ripples in more than one layer of graphene taken from the area denoted by a green dotted arrow in Fig. 9(a). Figs. 9(d) and (e) show a bright-field TEM image and the corresponding FFT image, respectively. The inset shows a high-magnification image taken from the red dotted area. A recent article by Guinea et al.,⁶⁶ successfully discussed the effect of ripples in graphene on the density of states (DOS). They show that at strong ripple disorder, a divergence in the DOS can lead to an ordered ground state. They also discussed the formation of dislocations in corrugated systems, buckling effects in suspended samples, and the changes in the Landau levels due to the interplay between a real magnetic field and the gauge potential induced by ripples. Furthermore, Bao et al.⁶⁷ reported the direct observation and controlled creation of periodic ripples in suspended graphene sheets and also investigated the effect of rippling on the electrical properties of graphene-based nanoelectronic devices. A significant advantage of graphene is its two-dimensionality, making it compatible with existing planar device architectures. Moreover, recent theoretical work emphasizes the influence of edge states,⁶⁸ curved surfaces and rotational disorder within FLG sheets and pentagonal or heptagonal defects⁶⁹ on the electronic states of graphene sheets. Also, electric screening is expected to be poor in ideal graphene sheets⁷⁰ even if these are “good conductors” at room temperature.

Fig. 9 (a) Bright-field TEM image of single or FLG membrane across a TEM grid. The corrugations and ripples are directly imaged by TEM, and are indicated by green and white dotted arrows, respectively. The inset shows a schematic of a rippled graphene sheet. (b) TEM image of magnified view of area denoted by the white dotted arrow in (a). (c) Reconstructed image of (b) after filtering in the frequency domain to remove unwanted noise for clarity. The ripples are clearly observed in the red box of (c). (d) Ripples in more than one-layer graphene taken from the area denoted by the green dotted arrow in (a). (d) and (e) show a bright-field TEM image and the corresponding FFT image, respectively.

In this work, we used electrostatic force microscopy (EFM) to characterize the electric potential distribution on the surface of FLG sheets on SiO₂ ((300 nm)/Si substrates. We transferred our exfoliated samples by a drop-casting method onto SiO₂/Si under ambient conditions. A commercial setup Multimode, NanoScope IIIA, DI AFM with a conductive tip was used to record the sample topography and EFM phase in a two-pass mode (Scheme 2). In the first pass, the AFM tip traces the sample topography [Fig. 1(e)–(g) and 10(a)]. In the second pass the tip follows the track derived in the first pass with a fixed lift-up distance and measures the frequency shift caused by the electrostatic force while the tip is biased by a voltage of a few volts. We used silicon cantilevers (NSG11) with a Pt conductive coating. The tip is set to vibrate with a piezo having a resonant frequency of 150.09 kHz and amplitude of 30 nm. The interaction force between the scanning tip and a conducting material due to the applied bias voltage on the tip (responsible for the frequency shift) can be understood with a capacitor model.^71,72 EFM is an established technique for mapping the surface potential of planar samples, including semiconductor nanocrystals, thin films of polymers, polymer blends, and self-assembled monolayers.^44,73 Before performing experiments on our exfoliated graphene sample, first we measured the EFM signal on a conducting sample, which in principal should be constant. Fig. 10(b) shows an EFM image of a graphene flake on SiO₂/Si substrates with a tip voltage (V_tip) of +3 V. To be more specific, the EFM measurement was repeated several times on the same area with V_tip of +3 V and 100 nm lift-up distance. Figs. 10(c) and (d) shows height profiles and the corresponding surface potential, respectively. The bright area corresponds to the thin SiO₂ layer and the dark area corresponds to a thin layer of the graphene sheets, respectively. The above measurement shows small surface potential variations on the surface of the graphene flake.

Scheme 2 Overview of the experiment. FLG sheets are deposited on a SiO₂ substrate on a highly-doped Si ground plane. Sample topography and EFM phase are imaged simultaneously.

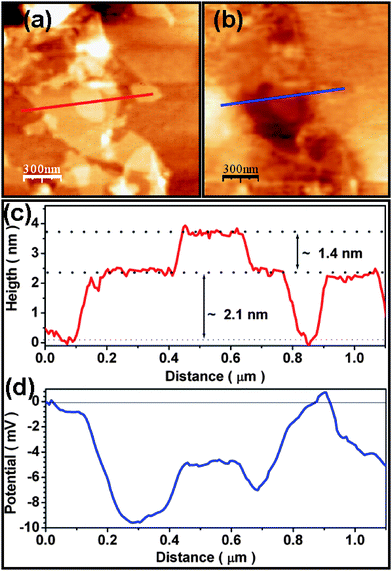Fig. 10 AFM and EFM images of a graphene flake. (a) AFM image of a graphene flake on a SiO₂/Si substrate. (b) Corresponding EFM phase image with tip voltage (V_tip) of +3 V. (c) and (d) show the height profile and corresponding surface potential, respectively.

Conclusions

We report a facile two-step method for the preparation of homogenous colloidal suspensions of single or FLG sheets up to 0.15 mg ml⁻¹ in DMF solution. The two-step approach includes; (i) High temperature (∼2000 °C) heat treatment of pyrolytic graphite powders in a vacuum (<1 × 10⁻⁵ Torr) for 3 h followed by (ii) sonication for 2 h by dissolving the heat-treated graphite in DMF using a probe-tip sonicator. Our approach provides single or FLG (2–6 layers) graphene sheets. However, in our experiment the percentage of single-layer graphene is low in comparison to FLG sheets. Taking into account the experimental evidence discussed above, a conventional HRTEM (JEOL 2200F TEM/STEM) operated at 200 kV is an effective tool for the direct imaging of the graphene sheets at the atomic level. The interpretation of HRTEM images is relatively simple and allows rotational misorientation to be easily characterized by analyzing in the frequency domain. These results show that the stacking in FLG sheets is not always the assumed AB Bernal stacking associated with bulk graphite. Here, we resolve the rotational misorientation for up to six individual layers within the graphene flake, and we show that the rotation angle between two consecutive layer is ∼10°. The complete atomic structural characterization of graphene flakes using HRTEM is necessary for its future applications in graphene-based nanoelectronic devices.^{19,28–32,74,75} Furthermore, the direct observation of periodic ripples in suspended graphene sheets is also presented. EFM was used to characterize the electric potential distribution on the surface of FLG sheets on SiO₂/Si substrates in ambient conditions which exhibit small potential variations on their surface. Systematic investigations are underway to further clarify the formation of the rippling in graphene sheets and also how it effects the electrical properties of single- or few-layer graphene sheets.

Acknowledgements

The authors M. K. Singh, E. Titus, P. A. A. P. Marques, and G. Gonçalves would like to thank the Ciência 2007 Program, Foundation of Science and Technology (FCT – Portugal), and INL (International Iberian Nanotechnology Laboratory) for the financial support of this work.

References

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
2. K. V. Emtsev, A. Bostwick, K. Horn, J. Jobst, G. L. Kellogg, L. Ley, J. L. McChesney, T. Ohta, S. A. Reshanov, J. Röhrl, E. Rotenberg, A. K. Schmid, D. Waldmann, H. B. Weber and T. Seyller, Nat. Mater., 2009, 8, 203.
3. S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217.
4. Ç. Ö. Girit, J. C. Meyer, R. Erni, M. D. Rossell, C. Kisielowski, L. Yang, C. Park, M. F. Crommie, M. L. Cohen, S. G. Louie and A. Zettl, Science, 2009, 323, 1705.
5. L. Jiao, L. Zhang, X. Wang, G. Diankov and H. Dai, Nature, 2009, 458, 877.
6. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706.
7. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312.
8. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
9. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
10. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902.
11. K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351.
12. I. W. Frank, D. M. Tanenbauma, A. M. van der Zande and P. L. McEuen, J. Vac. Sci. Technol., B, 2007, 25(6), 2558.
13. S. Latil, V. Meunier and L. Henrard, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 201402.
14. J. Hass, F. Varchon, J. E. Millan-Otoya, M. Spinkle, W. A. de Heer, C. Berger, P. N. First, L. Magaud and E. H. Conrad, Phys. Rev. Lett., 2008, 100, 125504.
15. F. Varchon, P. Mallet, L. Magaud and J.-Y. Veuillen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165415.
16. M. F. Craciun, S. Russo, M. Yamamoto, J. B. Oostinga, A. F. Morpurgo and S. Tarucha, Nat. Nanotechnol., 2009, 4, 383.
17. Y.-M. Lin, K. A. Jenkins, A. Valdes-Garcia, J. P. Small, D. B. Farmer and P. Avouris, Nano Lett., 2009, 9(1), 422.
18. X. Wang, Y. Ouyang, X. Li, H. Wang, J. Guo and H. Dai, Phys. Rev. Lett., 2008, 100, 206803.
19. P. Blake, P. D. Brimicombe, R. R. Nair, T. J. Booth, D. Jiang, F. Schedin, L. A. Ponomarenko, S. V. Morozov, H. F. Gleeson, E. W. Hill, A. K. Geim and K. S. Novoselov, Nano Lett., 2008, 8(6), 1704.
20. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
21. A. B. Bourlinos, V. Georgakilas, R. Zboril, T. A. Steriotis and A. K. Stub, Small, 2009, 5, 1841.
22. H. Zhao, W. Z. Yuan, L. Tang, J. Z. Sun, H. Xu, A. Qin, Y. Mao, J. K. Jin and B. Z. Tang, Macromolecules, 2008, 41, 8566.
23. I. Pastoriza-Santos and L. M. Liz-Marzán, Adv. Funct. Mater., 2009, 19, 679.
24. Y.-H. Liao, O. Marietta-Tondin, Z. Liang, C. Zhang and B. Wang, Mater. Sci. Eng., A, 2004, 385, 175.
25. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'Ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563.
26. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229.
27. X. Li, G. Zhang, X. Bai, X. Sun, X. Wang, E. Wang and H. Dai, Nat. Nanotechnol., 2008, 3, 538.
28. S. Patchkovskii, J. S. Tse, S. N. Yurchenko, L. Zhechkov, T. Heine and G. Seifert, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10439.
29. M. D. Stoller, S. Park, Y. Zhu, J. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498.
30. S.-M. Paek, E. Yoo and I. Honma, Nano Lett., 2009, 9(1), 72.
31. S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282.
32. T. Ramanathan, A. A. Abdala, S. Stankovich, D. A. Dikin, M. Herrera-Alonso, R. D. Piner, D. H. Adamson, H. C. Schniepp, X. Chen, R. S. Ruoff, S. T. Nguyen, I. A. Aksay, R. K. Prud'Homme and L. C. Brinson, Nat. Nanotechnol., 2008, 3, 327.
33. I. Jung, M. Pelton, R. Piner, D. A. Dikin, S. Stankovich, S. Watcharotone, M. Hausner and R. S. Ruoff, Nano Lett., 2007, 7, 3569.
34. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
35. G. M. Rutter, N. P. Guisinger, J. N. Crain, E. A. A. Jarvis, M. D. Stiles, T. Li, P. N. First and J. A. Stroscio, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235416.
36. D. Martoccia, P. R. Willmott, T. Brugger, M. Björck, S. Günther, C. M. Schlepütz, A. Cervellino, S. A. Pauli, B. D. Patterson, S. Marchini, J. Wintterlin, W. Moritz and T. Greber, Phys. Rev. Lett., 2008, 101, 126102.
37. J. M. Campanera, G. Savini, I. Suarez-Martinez and M. I. Heggie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235449.
38. E. Stolyarova, K. T. Rim, S. Ryu, J. Maultzsch, P. Kim, L. E. Brus, T. F. Heinz, M. S. Hybertsen and G. W. Flynn, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9209.
39. G. M. Rutter, J. N. Crain, N. P. Guisinger, T. Li, P. N. First and J. A. Stroscio, Science, 2007, 317, 219.
40. K. A. Ritter and J. W. Lyding, Nat. Mater., 2009, 8, 235.
41. J. W. G. Wildöer, L. C. Venema, A. G. Rinzler, R. E. Smalley and C. Dekker, Nature, 1998, 391, 59.
42. H. Fujimoto, A. Mabuchi, K. Tokumitsu and T. Kasuh, Carbon, 1996, 34, 1115.
43. J. C. Meyer, C. Kisielowski, R. Erni, M. D. Rossell, M. F. Crommie and A. Zettl, Nano Lett., 2008, 8(11), 3582.
44. D. C. Coffey and D. S. Ginger, Nat. Mater., 2006, 5, 735.
45. A. Gupta, G. Chen, P. Joshi, S. Tadigadapa and P. C. Eklund, Nano Lett., 2006, 6, 2667.
46. P. Nemes-Incze, Z. Osvath, K. Kamarás and L. P. Biró, Carbon, 2008, 46, 1435.
47. D. Graf, F. Molitor, K. Ensslin, C. Stampfer, A. Jungen, C. Hierold and L. Wirtz, Nano Lett., 2007, 7, 238.
48. L. M. Malard, M. A. Pimenta, G. Dresselhaus and M. S. Dresselhaus, Phys. Rep., 2009, 473, 51.
49. R. P. Vidano, D. B. Fischbach, L. J. Willis and T. M. Loehr, Solid State Commun., 1981, 39, 341.
50. R. J. Nemanich and S. A. Solin, Phys. Rev. B: Condens. Matter, 1979, 20, 392.
51. M. J. Matthews, M. A. Pimenta, G. Dresselhaus, M. S. Dresselhaus and M. Endo, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, R6585.
52. F. Tuinstra and J. L. Koenic, J. Chem. Phys., 1970, 53, 1126.
53. P. Poncharal, A. Ayari, T. Michel and J.-L. Sauvajol, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 113407.
54. Z. Ni, Y. Wang, T. Yu, Y. You and Z. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235403.
55. Z. Liu, K. Suenaga, P. J. F. Harris and S. Iijima, Phys. Rev. Lett., 2009, 102, 015501.
56. C. Jin, H. Lan, L. Peng, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 205501.
57. M. H. Gass, U. Bangert, A. L. Bleloch, P. Wang, R. R. Nair and A. K. Geim, Nat. Nanotechnol., 2008, 3, 676.
58. U. Bangert, T. Eberlein, R. R. Nair, R. Jones, M. Gass, A. L. Bleloch, K. S. Novoselov, A. K. Geim and P. R. Briddon, Phys. Status Solidi A, 2008, 205(9), 2265.
59. O. Stéphan, D. Taverna, M. Kociak, K. Suenaga, L. Henrard and C. Colliex, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155422.
60. M. Kociak, L. Henrard, O. Stephan, K. Suenaga and C. Colliex, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 13936.
61. M. Filippi and L. Calliari, Surf. Interface Anal., 2006, 38, 595.
62. J. H. Warner, M. H. Rummeli, T. Gemming, B. Buchner and G. A. D. Briggs, Nano Lett., 2009, 9(1), 102.
63. R. C. Thompson-Flagg, M. J. B. Moura and M. Marder, Europhys. Lett., 2009, 85, 46002.
64. J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60.
65. A. Fasolino, J. H. Los and M. I. Katsnelson, Nat. Mater., 2007, 6, 858.
66. F. Guinea, B. Horovitz and P. L. Doussal, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 205421.
67. W. Bao, F. Miao, Z. Chen, H. Zhang, W. Jang, C. Dames and C. N. Lau, Nat. Nanotechnol., 2009, 562.
68. M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920.
69. N. M. R. Peres, F. Guinea and A. H. C. Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125411.
70. J. González, F. Guinea and M. A. H. Vozmediano, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 134421.
71. C. Staii, A. T. Johnson and N. J. Pinto, Nano Lett., 2004, 4, 859.
72. M. Bockrath, N. Markovic, A. Shepard, M. Tinkham, L. Gurevich, L. P. Kouwenhoven, M. W. Wu and L. L. Sohn, Nano Lett., 2002, 2(3), 187.
73. H. Takano, S.-S. Wong, J. A. Harnisch and M. D. Porter, Langmuir, 2000, 16, 5231.
74. P. Avouris, Z. Chen and V. Perebeinos, Nat. Nanotechnol., 2007, 2, 605.
75. J. C. Meyer, C. O. Girit, M. F. Crommie and A. Zettl, Nature, 2008, 454, 319.

---