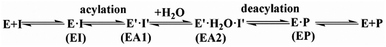Open Access Article
Open Access ArticleLinking inhibitor motions to proteolytic stability of sunflower trypsin inhibitor-1†
Wanqing Wei,
Jing Ma ,
Daiqian Xie
,
Daiqian Xie and
Yanzi Zhou
and
Yanzi Zhou *
*
Institute of Theoretical and Computational Chemistry, Laboratory of Mesoscopic Chemistry, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210023, China. E-mail: zhouyz@nju.edu.cn
First published on 3rd May 2019
Abstract
The remarkable capability of an enzyme isn't only determined by its active site but also controlled by the environment. To unravel the environment role in catalysis, the dynamic motions as well as the static mechanism need to be studied. In this work, QM/MM MD simulations were employed to study the proteolysis process of SFTI-1 and BiKF, which revealed that a combination of static non-bonded interactions and dynamic motions along the reaction coordinate can account for the different hydrolysis rates between them. A comparison among SFTI-1 and three analogs with similar non-bonded interactions further revealed a positive correlation between the mobility of inhibitors and the hydrolysis rates. Apart from the cyclic backbone and disulfide bond, intramolecular hydrogen bonds also increase the rigidity of the backbone of inhibitors, and therefore hinder inhibitor motions to resist proteolysis. These new detailed mechanistic insights suggest the need to consider inhibitor motions in the rational design of peptide inhibitors.
1. Introduction
Native peptides are often not directly suitable for use as convenient therapeutics due to their high susceptibility to proteases and other intrinsic weaknesses.1,2 So various peptide modification strategies have been developed to address this limitation, among which macrocyclization (such as a disulfide bridge or head-to-tail cyclization) is one of the most prominent methods.3–5 The smallest cyclic peptide among the Bowman–Birk inhibitor (BBI) family is sunflower trypsin inhibitor-1 (SFTI-1), which only has 14 amino acids but adopts a rigid and well-defined bicyclic structure6,7 containing a head-to-tail cyclization and a disulfide bridge. The potent activity of SFTI-1 against trypsin suggests it is an ideal framework for tuning selectivity towards clinically relevant proteases.8–11 Moreover, the very small size, strong inhibitory and high hydrolysis stability12,13 of SFTI-1 have made it an excellent scaffold14 for protein engineering.15–20 Sequences with completely novel function can be grafted into the SFTI-1 framework, for engineering of radiopharmaceuticals, antimicrobials, proangiogenic compounds, and rheumatoid arthritis and autoimmune disease peptides.21–28SFTI-1 binds to trypsin in a substrate manner but can resist proteolysis for a quite long time. The hydrolysis rates of SFTI-1 and its analogs have been studied extensively. Several studies have examined the contributions made by the cyclic backbone and a disulfide bond to the proteolytic stability of SFTI-1. Lack of either a disulfide bond or cyclic backbone showed decreased proteinase resistance to trypsin and inhibitory activity.6,13,20,29–32 The studies on two monocyclic analogs of SFTI-1 showed that the one keeping head-to-tail cycle was remarkably faster hydrolyzed than the with a disulfide bridge.13 On top of it, the hydrogen-bond network also appears to be a crucial determinant of the function of SFTI-1.29,33–35 However, the dynamic aspect, e.g. how the hydrolysis actually proceeds, haven't gained enough attention. Recently, conformational dynamics have been realized to be also important in enzyme reactions.36–39 Yet, the role of conformational changes in enzyme catalysis remains unclear. These studies on SFTI-1 and its analogs offer us a good opportunity to uncover the effects of conformational motions as well as structural factors on hydrolysis stability of SFTI-1.
In this work, we first studied the hydrolysis mechanism of SFTI-1, next compared the hydrolysis properties of SFTI-1 and BiKF. We uncovered the main structural and dynamic factors to control the hydrolysis rate and then successfully applied them to explain the hydrolysis rate for two monocyclic and one acyclic analogs of SFTI-1. Those findings would provide useful information for designing therapeutic and diagnostic agents with high proteolytic stability from peptide templates.
2. Results and discussion
2.1 The reaction mechanism for proteolysis of SFTI-1
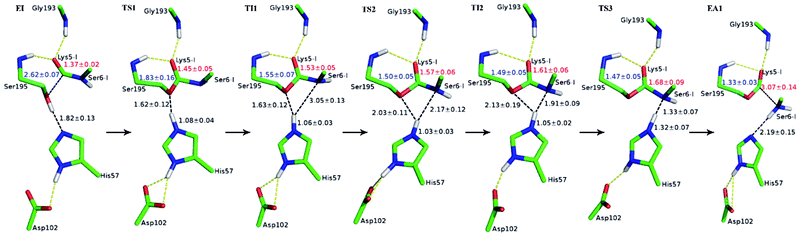
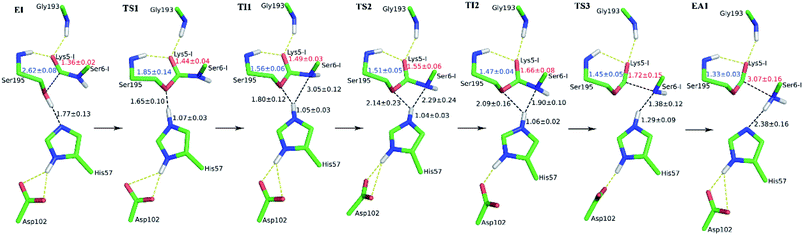
The first task of theoretical study is to computationally characterize the whole proteolysis process of SFTI-1. The scissile bond of SFTI-1 lies between Lys5-I and Ser6-I (“-I” refers to residues of inhibitor SFTI-1), and trypsin employs a catalytic triad Ser195/His57/Asp102. The process of SFTI-1 hydrolyzed by trypsin40 is outlined in Scheme 1 and Fig. S3:† the reaction proceeds in two chemical stages, acylation and deacylation; after acylation reaction, the hydrolytic water enters the active site, which is required in deacylation. The free energy curve for the whole proteolysis process is illustrated in Fig. 1, S5 and S7.† While the change of the reaction coordinates during the reaction was presented in Fig. S6 and S8.†Initially, trypsin and SFTI-1 form a tight binding enzyme–inhibitor complex (EI) with a dissociation constant of 3.0 × 10−10 M.12 The acylation reaction then proceeds in two chemical steps interspersed with one subtle His-ring re-orientation step between two distinct TI configurations, as shown in Fig. 2. First, the OG atom of Ser195 nucleophilic attacks the carbonyl carbon atom of Lys5-I to form a C–O bond. Meanwhile the proton transfers to the NE atom of His57, and then the first tetrahedral intermediate TI1 is formed. Asp102 serves to orient His57 and to neutralize the charge developed on it at transition states and intermediates. To check whether it adopts a stepwise or concerted mechanism, a two-dimensional free energy surface was constructed for the first step of acylation reaction as shown in Fig. S4,† in which one dimension represents the proton transfer process from Ser195 to His57 and the other represents the nucleophilic attack by Ser195 to the C atom of the scissile bond. Clearly, the two processes occur simultaneously. At the TI1, we can see that the protonated His57 is indeed still close to the OG atom of Ser195 and forms a stable hydrogen bond with a O⋯H distance at 1.63 ± 0.12 Å, while the proton is far from the leaving N of the scissile bond with an N⋯H distance at 3.05 ± 0.13 Å. In order to favor the forward progress of the reaction, our simulations indicate that the enzyme only needs a subtle re-orientation of the His57 ring to yield a second meta-stable tetrahedral intermediate TI2, in which the proton of His57 is well positioned to protonate the nitrogen of the leaving group, with an N⋯H distance at 1.91 ± 0.09 Å and a donor-hydrogen–acceptor angle at 146.9 ± 5.3°. Meanwhile, the subtle movement of His ring is accompanied with a slight change in the newly formed C–O bond and the C–N scissile bond. Next the proton transfers from His57 to the N atom of scissile bond and the C–N bond of SFTI-1 breaks leading to a stable product acyl-enzyme intermediate state (EA1). At the EA1 state, Lys5-I has been acylated meanwhile the proton of hydroxyl group of Ser195 has transferred to the N atom of Ser6-I. During the reaction, accumulated negative charge on the carbonyl oxygen atom of the scissile bond is stabilized by the oxyanion hole formed by the main chain NH group of Gly193 and Ser195. The calculated free energy barrier of 30.0 kcal mol−1 suggests that the acylation reaction takes place very slowly, and the free energy of EA1 is 2.5 kcal mol−1 lower than that of EI state, indicating the acylation process is exothermic. The intermediate TI1 and TI2 are in a shallow well as shown in Fig. S5.† To check whether they are real intermediates or just appearance of a mere computational shortcoming, we carried out unrestrained ab initio QM/MM MD simulations for 10 randomly chosen snapshots at TI1 and TI2 states respectively. The averaged lifetime of TI1 is about 2.5 ps showing that TI1 state can be meta-stable. While the lifetime of TI2 is only 300 fs which is on the order of a vibration period (∼100 fs),41,42 so the His-ring re-orientation stage and the second proton transfer stage might be considered as uncoupled concerted.
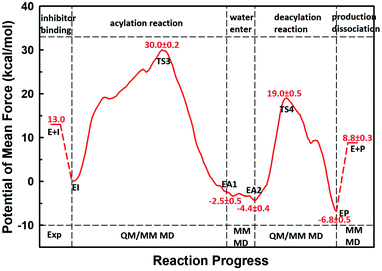 | ||
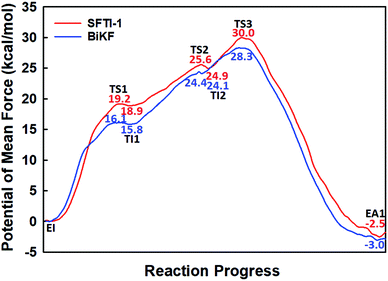
| Fig. 1 The free energy profile for trypsin-catalyzed SFTI-1 hydrolysis. The energy for E + I was derived from the experimental dissociation constant,12 while others were calculated from MD simulations with umbrella sampling. TS3 and TS4 are transition states of acylation and deacylation respectively. | ||
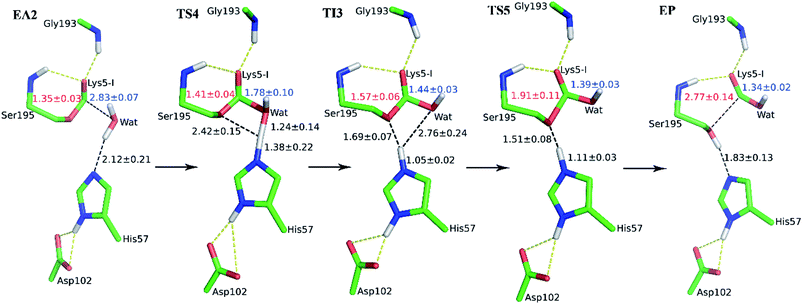
The second stage is the access of hydrolytic water to form another acyl-enzyme EA2. The C–N distance is 3.07 ± 0.14 Å at EA1 state from QM/MM-MD simulation. While during a 250 ns classical MD simulation at EA1 state, the C–N distance of the scissile bond fluctuated between 3 and 10 Å, with the most probable distance around 5.0 Å as illustrated in Fig. 3(a). After 50 ns MD simulations, water molecules can enter the active site automatically and be ideally positioned to nucleophilic attack the newly formed C–O bond when the C–N distance is larger than 4.4 Å, but will drift out when the C–N distance goes down. Then we chose the distance of the C–N bond as reaction coordinate to calculate the potential of mean force by employing 200 ns classical MD simulations with umbrella sampling, which is illustrated in Fig. 3(b). There is a shallow well around 3.1 Å and represents EA1 state. Then one water molecule forms a hydrogen bond with the N atom of Ser6-I at the C–N distance around 3.8 Å, accompanied by a slight decrease in energy. Water molecules can enter the active site when the distance is larger 4.5 Å and form an additional hydrogen bond with the NH2 group of Ser6-I at near 5.8 Å, which can help to further stabilize the structure and explain the energy well around 5.8 Å on the PMF. Therefore we located EA2 state here. From the MD simulations, clearly, the access of water can happen spontaneously after acylation, and no additional energy is required in this stage.
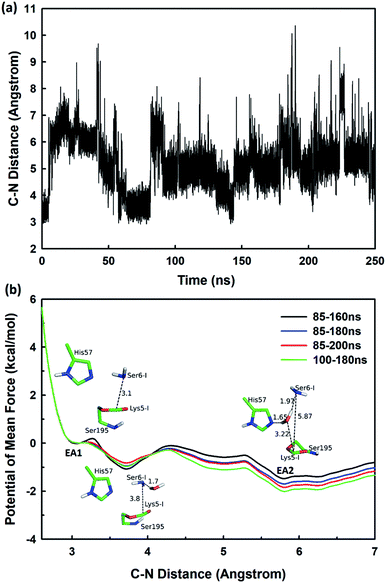 | ||
| Fig. 3 (a) The C–N distance of the scissile bond of SFTI-1 at EA1 state from 250 ns classical MD simulations; (b) the potential of mean force for the elongation of the scissile bond C–N distance. | ||
When it is right oriented in the active site, the water will serve as the nucleophile to attack the carbon atom of the newly formed C–O bond. The reaction mechanism of the deacylation is similar to that of acylation with a much lower energy barrier as illustrated in Fig. 1 and 4. Finally, the cleaved SFTI-1 (labeled as P in Scheme 1) will drift out of the enzyme to recover the free enzyme. From the whole free energy curve in Fig. 1, the acylation reaction is the rate-limiting step of proteolysis progress, and the total free energy barrier is 30.0 kcal mol−1 at pH = 7. Classical molecular dynamics simulations normally don't consider the quantum effects on the vibrations, which might cause significant errors in the potential of mean force. To achieve the quantum mechanical vibrational correction, we calculated the frequencies at EI and TS3 states for QM region at the same level of theory with projecting the reaction coordinate out of the Hessian43–45 by Gaussian16.46 Considering of quantum-mechanical correction to the classical vibrational free energy reduces the free energy barrier to 27.7 kcal mol−1. The experimental active energy barrier is 25.5 kcal mol−1 with transition state theory at pH = 8.3,13 while the estimated energy barrier is 23.7 kcal mol−1 derived from half-life of 435 ± 20 min at pH = 3.5.12 It is worth mentioning that the pH dependence of the overall hydrolysis rates for BBI family contrasts to the behavior of ordinary protein substrates displaying an optimum at physiological pH. Their rate constants are increased rather abruptly under acidic conditions.12,47 For example, when pH value increased from 3.5 to 7.0, the hydrolysis rate constant of the soybean Bowman–Birk inhibitor decreased by 2–3 orders of magnitude,47 corresponding to 2.7–4.1 kcal mol−1 increment in free energy. Considering the influence of pH on hydrolysis rates, our total free energy barrier is in agreement with the experimental value.
2.2 The environment role in acylation of SFTI-1 and BiKF
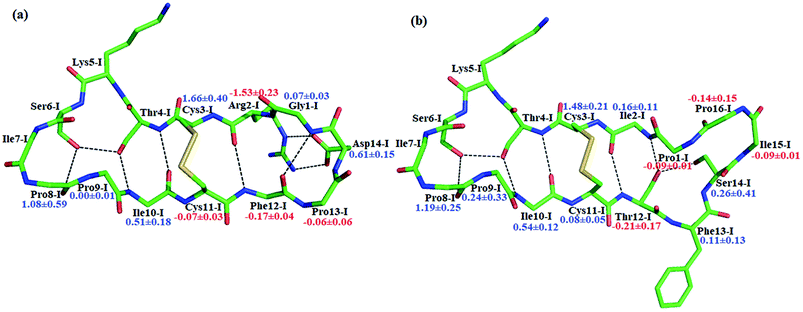
BiKF is a bicyclic mutant of SFTI-1, in which the non-reactive, 5-mer turn of SFTI-1 is replaced by a second, reactive 9-mer loop.12 Though the bicyclic structure is retained in BiKF, its hydrolysis half-life reduces 15 times compared to SFTI-1.12 Therefore it offers us a good opportunity to study the effect of other factors on hydrolysis resistance other than a disulfide bond or cyclic backbone. Since the acylation reaction is rate-limiting, we only studied this stage for BiKF on QM/MM level. The hydrolysis rate of BiKF is about 18 times faster than that of SFTI-1 according to the calculated acylation free energy barrier from Fig. 5, which is in reasonable agreement with the experimental ratio of 15.12 Our computation results indicate that the acylation reaction of BiKF shares the same reaction mechanism as SFTI-1 as illustrated in Fig. 6. The free energy curve and change of reaction coordinate were also presented in Fig. S9 and S10† for acylation reaction of BiKF. Clearly, both the energy curves and changes of bond lengths are similar for SFTI-1 and BiKF in acylation reaction. One should notice that the quantum dynamics effects have a significant effect on rate constants.44,48 The quantum effect of vibration decreases the free energy barrier by 2.3 and 2.2 kcal mol−1 for SFTI-1 and BiKF respectively. We also estimated the tunneling effect by fitting our PMFs to unsymmetrical Eckart function.49 For SFTI-1, the tunneling correction factor is 1.40 ± 0.04, while for BiKF, it's 1.36 ± 0.05. Although this model is inexpensive and very easy to use, it's not accurate. A more reliable way is to employ variational transition state theory,45,50 which requires the second derivative along the reaction path and is difficult to be applied to the high-level ab initio QM. Nevertheless, because the two systems have the same QM regions with similar energy curves, the tunneling contributions in calibrating energy surfaces between them might cancel out just as the estimated tunneling effect by the Eckart tunneling model indicates. The recrossing transmission coefficient was estimated by using Bennett-Chandler method.51,52 It's 0.53 and 0.46 for SFTI-1 and BiKF respectively. Though it's important to consider the recrossing effect in determining the absolute reaction rate, the contribution of recrossing is similar for the two inhibitors just as the tunneling effect does. Therefore, the relative reaction rate constants are still reliable.The reaction rate of enzyme catalysis isn't only determined by the active site but also controlled by its environment. To investigate the effect of environment on the free energy barrier, we first examined the contribution from non-bonded interactions between MM atoms and QM region to the energy barrier. Because of various inherent approximations employed in the energy decomposition calculations, the calculated values can only be employed as qualitative indicators. In order to further elucidate how the transition states are stabilized, we calculated the individual residue contribution to the TS3 stabilization from non-bonded interactions between MM atoms and QM region. For each state, 1000 structures were chosen and averaged interactions between individual residue and QM region were calculated using Amber99SB force field. The point charges of QM atoms were taken from the previous QM/MM calculation for individual structure. The contribution of one residue to the energy barrier was estimated as the interaction at the TS3 state minus that at the EI state. The negative value indicates that residue decreases the energy barrier therefore to stabilize the TS3 state, while the positive one is unfavorable. The total contribution from the enzyme and inhibitor environment to the acylation energy barrier of SFTI-1 is 4.91 ± 0.60 and 2.10 ± 0.79 kcal mol−1 respectively, while it is 5.31 ± 0.31 and 3.53 ± 0.69 kcal mol−1 to that of BiKF. The most difference originates from the residues in the secondary loop of the two inhibitors as listed in Fig. 7. Especially, the electrostatic interaction between the positively charged guanidinium group of Arg2-I and the accumulated negative charge on the oxygen atom of the carbonyl group of Lys5-I would favor the acylation reaction of SFTI-1, while the effect of Ile2-I in BiKF is minor. To our surprise, the total non-bonded interactions between the inhibitor and the active site increase the energy barrier of BiKF more than SFTI-1, which is opposite to the order of energy barrier heights.
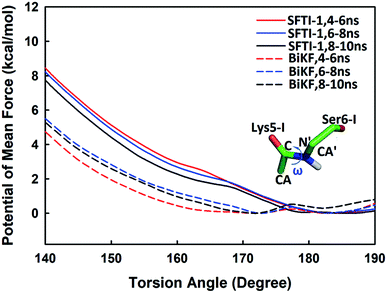
Beyond static views, conformational dynamics have been suggested to play an important role in enzyme reactions.36–39 In this work, we tried to distinguish out the motions representing conformational changes along the reaction coordinate and to estimate their effects on the hydrolysis rate. The superposition of EI (enzyme–inhibitor complex), TI1 (tetrahedral intermediate 1), TI2 (tetrahedral intermediate 2) and TS3 states in Fig. S5† shows that the acylation proceeds with a remarkable economy of motion.53–55 Once the motions required to form the tetrahedral transition state TS3 are retarded, the hydrolysis of serine proteases inhibitors will slow down. From EI state to TS3 state, the oxygen atom of the hydroxyl group of Ser195 will nucleophilic attack the C atom of scissile bond while the hydrogen atom will transfer to the N atom of Ser6-I, thus to cause the C–N bond between Lys5-I and Ser6-I to break down as shown in Fig. 2 and 6. Apart from the translation of atoms in the active site, a rotation of the scissile bond is also required since the hybrid state of the carbonyl carbon of scissile bond changes from sp2 at EI state to sp3 at the tetrahedral intermediates. Here, we employed the torsion angle ω defined in Fig. 8 to monitor this rotation, which is varying from near-planar structure to tetrahedral at TS3 state from our QM/MM MD simulations. Comparison of the structures among different states in Tables S1 and S2† shows that the conformational changes along the reaction path are subtle and similar for both SFTI-1 and BiKF. The small difference between the non-bonded contribution of protein to EI and TS3 state also indicated the reorganization of the protein is similar for the two inhibitors. However, the rotation of the amide bond might be affected by the inhibitor backbone rigidity. Therefore, we mainly focused on the motions of inhibitors. Hydrogen bonds might play an important role responsible for the different hydrolysis rates. Though the bicyclic structure is kept in BiKF, the inter- and intra- molecular hydrogen bonds are less extensive than SFTI-1 as listed in Tables S3 and S4,† which might make the rotation of BiKF easier. We calculated the free energy needed for ω angle rotating from planar to tetrahedral structure at EI state from 10 ns classical MD simulations with umbrella sampling, and found it required about 7.9 ± 0.3 kcal mol−1 for SFTI-1, which was 3.2 kcal mol−1 higher than for BiKF as illustrated in Fig. 8. Previous studies show that non-bonded interactions can stabilize the transition state for SFTI-1 1.8 kcal mol−1 more than BiKF, while the free energy barrier of SFTI-1 is 1.7 kcal mol−1 higher than BIKF. Obviously, the combination of inhibitor motions and non-bonded interactions together can account for different hydrolysis rates between SFTI-1 and BiKF.
2.3 The role of inhibitor motions in the hydrolysis rate
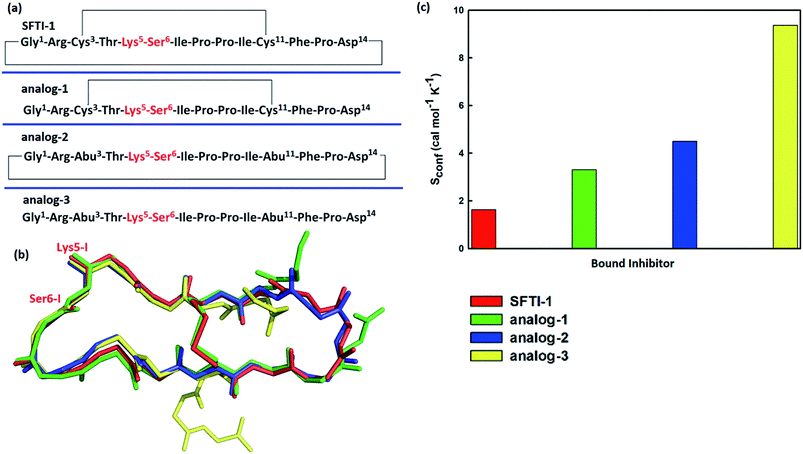
To further verify the effect of conformational motion of inhibitors on proteolysis, we studied two monocyclic analogs with either a disulfide-bridged loop or a head-to-tail cyclization, and one acyclic analog of SFTI-1. The change in the electrostatic environment of the enzyme or inhibitor will result in both the electronic cloud and the motions of enzyme or inhibitor. The former can be approximately measured by the non-bonded contribution of individual residue to the transition state stabilization. Because residues of these peptides are almost the same as SFTI-1 in Fig. 9(a) indicating non-bonded interactions within them are similar, we only focused on the effect of inhibitor motions on hydrolysis rates. First, a 100 ns NTP MD simulation was performed for each mutant at EI state. We aligned backbone structures of three bounded variants with SFTI-1 in Fig. 9(b). These analogs display similar backbone conformations in the binding loop to SFTI-1, but increased flexibility as the conformational entropy (Sconf)56 shown in Fig. 9(c), which heights are in the order of the hydrolysis rates. We then calculated the free energy required for the rotation of torsion angle ω at EI state for these mutants by 10 ns classical MD simulations with umbrella sampling. Table 1 illustrates that for SFTI-1 and the analogs, there is a positive correlation between the rotation energy barrier and the hydrolysis resistance. The introduction of one cyclic element (a disulfide bridge or head-to-tail cyclization) to the acyclic analog-3 increases its proteinase resistance. While the effect of both cycles is little larger than the sum of effects of the single cycle. The rotation free energy of analog-1 is about 1.5 kcal mol−1 higher than analog-2, which demonstrates the effect of the disulfide bond is more significant in resisting hydrolysis than the head-to-tail cyclization in this case.13 We summarized hydrogen bonds within these peptides at EI state in Tables S3 and S5† and found that hydrogen bonds are significantly weaker in these analogs than SFTI-1. Moreover, the number of hydrogen bonds in analog-1 is more than in analog-2, which may explain the higher efficiency of the disulfide bond. Obviously, hydrogen bonds also play an important role in peptide motions and therefore influence the hydrolytic stability.| Inhibitors | Rotation free energy | Hydrolysis ratea/s−1 | |
|---|---|---|---|
| ΔG (kcal mol−1) | exp (−ΔG/RT) | ||
| a The hydrolysis rates were estimated from experimental values.13 | |||
| SFTI-1 | 7.9 ± 0.3 | (1.0–2.7) × 10−6 | 1.2 × 10−6 |
| Analog-1 | 7.2 ± 0.1 | (4.4–6.2) × 10−6 | 4.1 × 10−6 |
| Analog-2 | 5.7 ± 0.2 | (0.5–0.9) × 10−4 | 1.1 × 10−4 |
| Analog-3 | 4.4 ± 0.1 | (5.0–7.0) × 10−4 | — |
3. Conclusion
In summary, we studied the whole proteolysis progress of SFTI-1 catalyzed by trypsin. The acylation reaction is the rate-determining step. Compared to BiKF, the non-bonded interaction would favor the nucleophilic attack of the OG atom of Ser195 to the scissile bond and thus could speed up the acylation reaction for SFTI-1. On the contrary, hindered inhibitor motions, to be specific, the increased rotation energy barrier of the peptide bond would slow down the acylation reaction more significant for SFTI-1 than for BiKF. Therefore, proteolytic stability of SFTI-1 is mainly caused by its retarded motions along the reaction coordinate.For the analogs lacking bicyclic structure, there is a negative correlation between the rotation energy of the scissile peptide bond and the hydrolysis rate, which illustrates the determinant role of the hindered inhibitor motions in the resistance to hydrolysis. Our studies showed that very small chemical changes can lead to a substantial decrease in proteolytic stability. The formation of a macrocycle greatly improves the rigidity of the backbone and therefore retards inhibitor motions. However, it alone appears insufficient to account for the rigidity. Particularly in SFTI-1, the increased rigidity can also be achieved by intramolecular interaction, especially the hydrogen bonds.
These days, particular attention has been paid to the impact of molecular motions within the protein or substrate on the enzyme's catalytic properties.36–39 Our results throw novel insights into the effect of inhibitor motions, which would not only be instructive for the rational design of peptides drugs, but also help to figure out how the enzyme works. However, there is still a long way to go to characterize the essential motions of substrate or enzyme, and to estimate their effect. Monitoring conformational changes along the reaction path introduces massive challenges for achieving sufficient spatial and temporal resolution of functionally linked motions. A combination of experiment and theory is necessary for the elucidation of a complete picture of enzyme catalysis.
4. Computational details
4.1 Preparation of initial reactant systems and classical MD simulations
The initial structure for the enzyme–inhibitor complex (EI) was based on the X-ray crystal structure (Protein Data Bank identification code: 1SFI)7 of the complex formed between bovine trypsin and SFTI-1. Besides the wild type, its variant BiKF was also studied in this paper, in which the non-reactive, 5-mer turn of SFTI-1 is replaced by a second, reactive 9-mer loop.12 The protonation states of charged residues were determined at constant pH 7 based on pKa calculations via the PROPKA57 program and the consideration of the local hydrogen bonding network. All His residues were identified as HIE except His57 as HID. Asp and Glu residues were deprotonated, while Lys and Arg were protonated. Next, the system was neutralized, solved, and equilibrated with a series of minimizations interspersed by short molecular dynamics simulations with periodic boundary condition. The system was initially placed in a rectangular water box with the dimension of 70 × 72 × 66 Å3 containing 10351 TIP3P water molecules. Finally, an extensive molecular dynamics simulation of 100 ns at constant temperature and pressure was carried out. The pressure was maintained at 1 atm and coupled with isotropic position scaling. The temperature was controlled at 298 K with Berendsen thermostat method.58 All the simulations were performed using Amber16 molecular dynamic package59 with Amber99SB60,61 force fields. The overall structure of the system is quite stable in the trajectories with backbone root-mean-squared deviation (RMSD) around 1.0 Å as shown in Fig. S1.†The inhibitor BiKF was first minimized by Amber 16 and then aligned with SFTI-1 in the pre-equilibrated SFTI-1-trypsin complex to get the initial structure of BiKF-trypsin complex. Then we relaxed the side chains of BiKF, all atoms of BiKF and the whole system step by step. Finally, an extensive molecular dynamics simulation of 100 ns at constant temperature and pressure was carried out.
A snapshot was randomly chosen for the subsequent QM/MM simulations. After acylation reaction, the partial charges of acyl-enzyme were fitted with HF/6-31G(d)62 calculations and the restrained electrostatic potential (RESP) module63 in the Amber package. Next, an MD simulation of 250 ns for an NTP ensemble was carried out for acyl-enzyme. Then steered molecular dynamics (SMD)64 pulling the scissile bond C–N distance to 7 Å were performed to identify the initial structures for leaving of the C–N terminal of inhibitors. Next, umbrella sampling was employed to calculate the potential of mean force, which are widely used in featuring the dynamical behaviors of biological macromolecules at the atomic level.65–67 For each window, 200 ns MD simulation was performed.
4.2 Setup for QM/MM MD simulations
Born−Oppenheimer MD simulations68,69 with ab initio QM/MM potential and the umbrella sampling method70–72 have been successfully applied to study several enzymes in our group.66,73,74 All ab initio QM/MM calculations were performed with modified Q-Chem75 and Amber12 programs.76 The scissile bond of the inhibitor lies between Lys5 and Ser6. The QM sub-system, including the side chains of the catalytic triad (Ser195, His57, and Asp102) of target enzyme and the scissile peptide portion of the inhibitor, was described at the B3LYP/6-31+G* level for acylation as shown in Fig. S2(a).† While for deacylation, the QM region was chosen as the catalytic triad, the water molecule in the active site, and Lys5 part as shown in Fig. S2(b).†The prepared QM/MM system was first minimized and then employed to map out a reaction path with B3LYP/6-31+G* QM/MM minimizations. Fig. S3† illustrates the reaction mechanism and reaction coordinates employed for each chemical reaction step. With a chosen reaction coordinate, first, a minimum energy path was mapped out with ab initio QM/MM restrained minimizations using the reaction coordinate driving (RCD) method.77 For each determined structure along the path, a 500 ps classical MD simulation was performed to equilibrate the MM subsystem, with the QM subsystem being frozen. Since the length of ab initio QM/MM MD simulations is quite short, this step is important that the MM sub-system can be relaxed given the change of QM sub-system. The final snapshot from the MM sub-system equilibration was used as the starting structure for Born-Oppenheimer B3LYP/6-31+G* QM/MM MD simulations with umbrella sampling for that window. For each window, at least 30 ps simulations have been carried out, and a harmonic potential force constant of 50 kcal mol−1 Å−2 was employed. The last twenty ps QM/MM MD simulations were used to calculate the free energy profile with the weighted histogram analysis method (WHAM).72,78,79 The statistical error was estimated by averaging the free energy difference between 10–20 ps and 20–30 ps.80,81
The QM/MM boundary was treated by the pseudo-bond approach77,82,83 with the improved parameters.84 All other atoms were described by the same molecular mechanical force field used in classical MD simulations. For all QM/MM calculations, a dual-focal ab initio QM/MM-PME potential with the periodic boundary condition85 was employed. The window size was chosen as 0.2 Å along the reaction path, and 0.1 Å around the transition state. The transition states were recognized as the highest points on the free energy profiles.86 If we do optimization starting from points very close to the transition states, the structures will go towards the minima connected by the transition states. The structures randomly chosen at TS3 have the highest negative frequencies around 1100 cm−1. Because they are not the saddle points on the potential energy surface, there are several other small negative frequencies (less than 200 cm−1), corresponding to small conformational fluctuations of the system. These calculations can confirm that those structures are close to saddle points on the PES.
In all above classical MD simulations and QM/MM MD simulations, long-range electrostatic interactions were treated with particle mash Ewald (PME) method87,88 and 12 Å cutoff was used for both PME and van der Waals (vdW) interactions. Time step of 1 fs was employed. And the frequencies for QM region were calculated at the same level of theory by the Gaussian 09 program.89
4.3 The estimation of transmission coefficient
Transition state theory (TST) was employed to describe the reaction rate in this work. However, it doesn't take the quantum effects into account. So we evaluated the nuclear tunneling and recrossing effects in addition.The asymmetric Eckart function90 was employed to obtain the tunneling transmission coefficient. The asymmetric Eckart tunneling correction can give reliable results at low temperatures. Since the two intermediates are both meta-stable with very shallow wells, we can employ only one asymmetric Eckart function to describe the whole reaction progress. The one-dimensional potential energy function is:
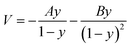 | (1) |
| y = −exp(2πx/L) | (2) |
| A = ΔV1 − ΔV2 | (3) |
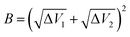 | (4) |
| ΔV1 = ETS − ERC | (5) |
| ΔV2 = ETS − EPC | (6) |
The recrossing transmission coefficient was then evaluated by employing Bennett–Chandler method.51,52 First, 100 snapshots were chosen from an equilibrated restrained QM/MM MD simulation at TS3. Then the restraint was removed and an unrestrained QM/MM MD simulation was conducted for snapshot with positive initial velocity along reaction coordinate. Finally the recrossing transmission coefficient can be calculated by the following formula:
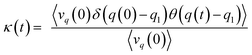 | (7) |
Conflicts of interest
The authors declare no competing financial interests.Abbreviations
| QM | Quantum mechanics |
| MM | Molecular mechanics |
| MD | Molecular dynamics |
| EI | Enzyme–inhibitor complex |
| EA1 | Acyl-enzyme after acylation |
| EA2 | Acyl-enzyme with a water molecule in the active site |
| EP | Enzyme binding with the cleaved inhibitor |
| TS1, TS2, TS3, TS4 and TS5 | Transition state 1, 2, 3, 4, 5 respectively |
| TI1, TI2 and TI3 | Tetrahedral intermediate 1, 2, 3 respectively |
Acknowledgements
This work was supported by the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20171333), the National Natural Science Foundation of China (Grant No. 21203090, 21590802, and 21733006), and the Fundamental Research Funds for the Central Universities (Grant No. 020514380119), the National Key Research and Development Program of China (2017YFB0702601). We thank the High Performance Computing Center of Nanjing University for providing computational resources.References
- C. K. Wang, S. E. Northfield, B. Colless, S. Chaousis, I. Hamernig, R.-J. Lohman, D. S. Nielsen, C. I. Schroeder, S. Liras, D. A. Price, D. P. Fairlie and D. J. Craik, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17504–17509 CrossRef CAS PubMed.
- M. Gongora-Benitez, J. Tulla-Puche and F. Albericio, Chem. Rev., 2014, 114, 901–926 CrossRef CAS PubMed.
- C. J. White and A. K. Yudin, Nat. Chem., 2011, 3, 509–524 CrossRef CAS PubMed.
- Y. H. Lau, P. De Andrade, Y. Wu and D. R. Spring, Chem. Soc. Rev., 2015, 44, 91–102 RSC.
- J. Wu, J. Tang, H. Chen, Y. He, H. Wang and H. Yao, Tetrahedron Lett., 2018, 59, 325–333 CrossRef CAS.
- M. L. J. Korsinczky, H. J. Schirra, K. J. Rosengren, J. West, B. A. Condie, L. Otvos, M. A. Anderson and D. J. Craik, J. Mol. Biol., 2001, 311, 579–591 CrossRef CAS PubMed.
- S. Luckett, R. S. Garcia, J. J. Barker, A. V. Konarev, P. R. Shewry, A. R. Clarke and R. L. Brady, J. Mol. Biol., 1999, 290, 525–533 CrossRef CAS PubMed.
- H. Fittler, O. Avrutina, B. Glotzbach, M. Empting and H. Kolmar, Org. Biomol. Chem., 2013, 11, 1848–1857 RSC.
- S. Jiang, P. Li, S.-L. Lee, C. Y. Lin, Y.-Q. Long, M. D. Johnson, R. B. Dickson and P. P. Roller, Org. Lett., 2007, 9, 9–12 CrossRef CAS PubMed.
- P. Li, S. Jiang, S.-L. Lee, C. Y. Lin, M. D. Johnson, R. B. Dickson, C. J. Michejda and P. P. Roller, J. Med. Chem., 2007, 50, 5976–5983 CrossRef CAS PubMed.
- Y. Q. Long, S. L. Lee, C. Y. Lin, I. J. Enyedy, S. M. Wang, P. Li, R. B. Dickson and P. P. Roller, Bioorg. Med. Chem. Lett., 2001, 11, 2515–2519 CrossRef CAS PubMed.
- A. M. Jaulent and R. J. Leatherbarrow, Protein Eng., Des. Sel., 2004, 17, 681–687 CrossRef CAS PubMed.
- E. Zablotna, K. Kazmierczak, A. Jaskiewicz, M. Stawikowski, G. Kupryszewski and K. Rolka, Biochem. Biophys. Res. Commun., 2002, 292, 855–859 CrossRef CAS PubMed.
- B. Franke, J. S. Mylne and K. J. Rosengren, Nat. Prod. Rep., 2018, 35, 137–146 RSC.
- J. E. Swedberg, C. Y. Li, S. J. de Veer, C. K. Wang and D. J. Craik, J. Med. Chem., 2017, 60, 658–667 CrossRef CAS PubMed.
- S. J. de Veer, C. K. Wang, J. M. Harris, D. J. Craik and J. E. Swedberg, J. Med. Chem., 2015, 58, 8257–8268 CrossRef CAS PubMed.
- D. Debowski, M. Pikula, M. Lubos, P. Langa, P. Trzonkowski, A. Lesner, A. Legowska and K. Rolka, PLoS One, 2014, 9, e89465 CrossRef PubMed.
- E. Zablotna, A. Jaskiewicz, A. Legowska, H. Miecznikowska, A. Lesner and K. Rolka, J. Pept. Sci., 2007, 13, 749–755 CrossRef CAS PubMed.
- K. Hilpert, G. Hansen, H. Wessner, R. Volkmer-Engert and W. Hohne, J. Biochem., 2005, 138, 383–390 CrossRef CAS PubMed.
- N. Karna, A. Legowska, S. Malicki, D. Debowski, P. Golik, A. Gitlin, P. Grudnik, B. Wladyka, K. Brzozowski, G. Dubin and K. Rolka, ChemBioChem, 2015, 16, 2036–2045 CrossRef CAS PubMed.
- S. Gunasekera, C. Fernandes-Cerqueira, S. Wennmalm, H. Wahamaa, Y. Sommarin, A. I. Catrina, P.-J. Jakobsson and U. Goransson, ACS Chem. Biol., 2018, 13, 1525–1535 CrossRef CAS PubMed.
- T. Durek, P. M. Cromm, A. M. White, C. I. Schroeder, Q. Kaas, J. Weidmann, A. A. Fuaad, O. Cheneval, P. J. Harvey, N. L. Daly, Y. Zhou, A. Dellsen, T. Osterlund, N. Larsson, L. Knerr, U. Bauer, H. Kessler, M. Cai, V. J. Hruby, A. T. Plowright and D. J. Craik, J. Med. Chem., 2018, 61, 3674–3684 CrossRef CAS PubMed.
- Y. B. Qiu, M. Taichi, N. Wei, H. Yang, K. Q. Luo and J. P. Tam, J. Med. Chem., 2017, 60, 504–510 CrossRef CAS PubMed.
- R. Sable, T. Durek, V. Taneja, D. J. Craik, S. Pallerla, T. Gauthier and S. Jois, ACS Chem. Biol., 2016, 11, 2366–2374 CrossRef CAS PubMed.
- T. Liu, G. Fu, X. Luo, Y. Liu, Y. Wang, R. E. Wang, P. G. Schultz and F. Wang, J. Am. Chem. Soc., 2015, 137, 4042–4045 CrossRef CAS PubMed.
- U. Malik, O. N. Silva, I. C. M. Fensterseifer, L. Y. Chan, R. J. Clark, O. L. Franco, N. L. Daly and D. J. Craik, Antimicrob. Agents Chemother., 2015, 59, 2113–2121 CrossRef CAS PubMed.
- L. Y. Chan, S. Gunasekera, S. T. Henriques, N. F. Worth, S.-J. Le, R. J. Clark, J. H. Campbell, D. J. Craik and N. L. Daly, Blood, 2011, 118, 6709–6717 CrossRef CAS PubMed.
- R. G. Boy, W. Mier, E. M. Nothelfer, A. Altmann, M. Eisenhut, H. Kolmar, M. Tomaszowski, S. Kraemer and U. Haberkorn, Mol. Imaging Biol., 2010, 12, 377–385 CrossRef PubMed.
- M. L. J. Korsinczky, R. J. Clark and D. J. Craik, Biochemistry, 2005, 44, 1145–1153 CrossRef CAS PubMed.
- K. Brzozowski, R. Majewski, A. Jaskiewicz, A. Legowska, L. Klaudel, S. Rodziewicz-Motowidto and K. Rolka, J. Pept. Sci., 2008, 14, 911–916 CrossRef CAS PubMed.
- A. Legowska, E. Bulak, M. Wysocka, A. Jaskiewicz, A. Lesner, D. Debowski and K. Rolka, Bioorg. Med. Chem., 2008, 16, 5644–5652 CrossRef CAS PubMed.
- A. Legowska, D. Debowski, R. Lukajtis, M. Wysocka, C. Czaplewski, A. Lesner and K. Rolka, Bioorg. Med. Chem., 2010, 18, 8188–8193 CrossRef CAS PubMed.
- N. L. Daly, Y.-K. Chen, F. M. Foley, P. S. Bansal, R. Bharathi, R. J. Clark, C. P. Sommerhoff and D. J. Craik, J. Biol. Chem., 2006, 281, 23668–23675 CrossRef CAS PubMed.
- X. Chen, B. T. Riley, S. J. de Veer, D. E. Hoke, J. Van Haeften, D. Leahy, J. E. Swedberg, M. Brattsand, P. J. Hartfield, A. M. Buckle and J. M. Harris, PLoS One, 2019, 14, e0210842 CrossRef CAS PubMed.
- S. J. de Veer, J. E. Swedberg, M. Akcan, K. J. Rosengren, M. Brattsand, D. J. Craik and J. M. Harris, Biochem. J., 2015, 469, 243–253 CrossRef CAS PubMed.
- P. Hanoian, C. T. Liu, S. Hammes-Schiffer and S. Benkovic, Acc. Chem. Res., 2015, 48, 482–489 CrossRef CAS PubMed.
- C. T. Liu, J. P. Layfield, R. J. Stewart III, J. B. French, P. Hanoian, J. B. Asbury, S. Hammes-Schiffer and S. J. Benkovic, J. Am. Chem. Soc., 2014, 136, 10349–10360 CrossRef CAS PubMed.
- S. J. Benkovic and S. Hammes-Schiffer, Science, 2003, 301, 1196–1202 CrossRef CAS PubMed.
- M. Delgado, S. Gorlich, J. E. Longbotham, N. S. Scrutton, S. Hay, V. Moliner and I. Tunon, ACS Catal., 2017, 7, 3190–3198 CrossRef CAS.
- R. L. Stein, in Kinetics of Enzyme Action, John Wiley & Sons, Inc., 2011, ch. 7, pp. 141–168 Search PubMed.
- J. Angel Martinez-Gonzalez, M. Gonzalez, L. Masgrau and R. Martinez, ACS Catal., 2015, 5, 246–255 CrossRef.
- W. P. Jencks, Chem. Soc. Rev., 1981, 10, 345–375 RSC.
- M. Garcia-Viloca, C. Alhambra, D. G. Truhlar and J. Gao, J. Chem. Phys., 2001, 114, 9953–9958 CrossRef CAS.
- C. Alhambra, J. Corchado, M. L. Sanchez, M. Garcia-Viloca, J. Gao and D. G. Truhlar, J. Phys. Chem. B, 2001, 105, 11326–11340 CrossRef CAS.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
- A. G. Baboul and H. B. Schlegel, J. Chem. Phys., 1997, 107, 9413–9417 CrossRef CAS.
- B. Jensen, K. K. Unger, J. Uebe, M. Gey, Y. M. Kim and P. Flecker, J. Biochem. Biophys. Methods, 1996, 33, 171–185 CrossRef CAS PubMed.
- L. Masgrau and D. G. Truhlar, Acc. Chem. Res., 2015, 48, 431–438 CrossRef CAS PubMed.
- H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
- J. Pu, J. Gao and D. G. Truhlar, Chem. Rev., 2006, 106, 3140–3169 CrossRef CAS PubMed.
- D. Chandler, J. Chem. Phys., 1978, 68, 2959–2970 CrossRef CAS.
- C. H. Bennett, in Algorithms for Chemical Computation, ed. R. E. Christofferson, 1977, ch. 4, pp. 63–97 Search PubMed.
- E. S. Radisky, J. M. Lee, C. J. K. Lu and D. E. Koshland, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6835–6840 CrossRef CAS PubMed.
- E. Zakharova, M. P. Horvath and D. P. Goldenberg, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11034–11039 CrossRef CAS PubMed.
- T. Ishida and S. Kato, J. Am. Chem. Soc., 2003, 125, 12035–12048 CrossRef CAS PubMed.
- A. S. Yang and B. Honig, J. Mol. Biol., 1995, 252, 351–365 CrossRef CAS PubMed.
- M. Rostkowski, M. H. M. Olsson, C. R. Sondergaard and J. H. Jensen, BMC Struct. Biol., 2011, 11 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. A. Case, R. M. Betz, W. Botello-Smith, D. S. Cerutti, T. E. Cheatham, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, et al., Amber16, University of California, San Francisco, CA, 2016 Search PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- W. Hehre, L. Radom, P. Schleyer and J. Pople, Ab Initio Molecular Orbital Theory, John Wiley & Sons, New York, 1986 Search PubMed.
- J. M. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- S. Park, F. Khalili-Araghi, E. Tajkhorshid and K. Schulten, J. Chem. Phys., 2003, 119, 3559–3566 CrossRef CAS.
- Y. Zhao, N. Chen, Y. Mo and Z. Cao, Phys. Chem. Chem. Phys., 2014, 16, 26864–26875 RSC.
- N. Chen, Y. Zhao, J. Lu, R. Wu and Z. Cao, J. Chem. Theory Comput., 2015, 11, 3180–3188 CrossRef CAS PubMed.
- Y. Zhao, N. Chen, C. Wang and Z. Cao, ACS Catal., 2016, 6, 2145–2157 CrossRef CAS.
- K. Meier, A. Choutko, J. Dolenc, A. P. Eichenberger, S. Riniker and W. F. van Gunsteren, Angew. Chem., Int. Ed., 2013, 52, 2820–2834 CrossRef CAS PubMed.
- R. Zhang, B. Lev, J. E. Cuervo, S. Y. Noskov and D. R. Salahub, in Advances in Quantum Chemistry, Vol 59: Combining Quantum Mechanics and Molecular Mechanics - Some Recent Progresses in QM/MM Methods, ed. J. R. Sabin, E. Brandas and S. Canuto, Elsevier, 2010, vol. 59, pp. 353–400 Search PubMed.
- G. N. Patey and J. P. Valleau, J. Chem. Phys., 1975, 63, 2334–2339 CrossRef CAS.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- E. M. Boczko and C. L. Brooks, J. Phys. Chem., 1993, 97, 4509–4513 CrossRef CAS.
- D. W. Rooklin, M. Lu and Y. Zhang, J. Am. Chem. Soc., 2012, 134, 15595–15603 CrossRef CAS PubMed.
- J. Lei, Y. Zhou, D. Xie and Y. Zhang, J. Am. Chem. Soc., 2015, 137, 70–73 CrossRef CAS PubMed.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. A. DiStasio Jr, R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer III, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC.
- D. A. Case, T. A. Darden, I. T. E. Cheatham, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. W. Götz, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, R. M. Wolf, J. Liu, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M.-J. Hsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollman, Amber16, University of California, San Francisco, CA, 2012 Search PubMed.
- Y. K. Zhang, H. Y. Liu and W. T. Yang, J. Chem. Phys., 2000, 112, 3483–3492 CrossRef CAS.
- M. Souaille and B. Roux, Comput. Phys. Commun., 2001, 135, 40–57 CrossRef CAS.
- A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1988, 61, 2635–2638 CrossRef CAS PubMed.
- D. Callegari, K. E. Ranaghan, C. J. Woods, R. Minari, M. Tiseo, M. Mor, A. J. Mulholland and A. Lodola, Chem. Sci., 2018, 9, 2740–2749 RSC.
- S. Y. Chen, D. Bertoldo, A. Angelini, F. Pojer and C. Heinis, Angew. Chem., Int. Ed., 2014, 53, 1602–1606 CrossRef CAS PubMed.
- X. Guo, J. Shi, Z. Tang, D. Cui and Y. Zhang, Chem. Biol. Drug Des., 2006, 68, 341–344 CrossRef CAS PubMed.
- Y. K. Zhang, T. S. Lee and W. T. Yang, J. Chem. Phys., 1999, 110, 46–54 CrossRef CAS.
- Y. K. Zhang, J. Chem. Phys., 2005, 122, 024114 CrossRef PubMed.
- Y. Zhou, S. Wang, Y. Li and Y. Zhang, in Computational Approaches for Studying Enzyme Mechanism, Pt A, ed. G. A. Voth, 2016, vol. 577, pp. 105–118 Search PubMed.
- H. Hu and W. Yang, Annu. Rev. Phys. Chem., 2008, 59, 573–601 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Revision B.01, Gaussian, Inc, Wallingford, CT, 2009 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- R. L. Brown, J. Res. Natl. Bur. Stand., 1981, 86, 357–359 CrossRef CAS.
- E. Dzib, J. Luis Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1 to S11 and Tables S1 to S5. See DOI: 10.1039/c9ra02114k |
| This journal is © The Royal Society of Chemistry 2019 |