Open Access Article
Open Access ArticleBenzobisthiadiazole-based high-spin donor–acceptor conjugated polymers with localized spin distribution†
Md Abdus
Sabuj
 ,
Md Masrul
Huda‡
,
Chandra Shekar
Sarap‡
and
Neeraj
Rai
,
Md Masrul
Huda‡
,
Chandra Shekar
Sarap‡
and
Neeraj
Rai
 *
*
Dave C. Swalm School of Chemical Engineering, and Center for Advanced Vehicular Systems, Mississippi State University, Mississippi State MS 39762, USA. E-mail: neerajrai@che.msstate.edu; Fax: +1-662-325-2482; Tel: +1-662-325-0790
First published on 10th March 2021
Abstract
Stable organic semiconductors (OSCs) with a high-spin ground-state can profoundly impact emerging technologies such as organic magnetism, spintronics, and medical imaging. Over the last decade, there has been a significant effort to design π-conjugated materials with unpaired spin centers. Here, we report new donor–acceptor (D–A) conjugated polymers comprising cyclopentadithiophene and cyclopentadiselenophene donors with benzobisthiadiazole (BBT) and iso-BBT acceptors. Density functional theory calculations show that the BBT-based polymers display a decreasing singlet–triplet energy gap with increasing oligomer chain length, with degenerate singlet and triplet states for a N = 8 repeat unit. Furthermore, a considerable distance between the unpaired electrons with a pure diradical character disrupts the π-bond covalency and localizes the unpaired spins at the polymer ends. However, replacing the BBT acceptor with iso-BBT leads to a closed-shell configuration with a low-spin ground-state and a localized spin density on the polymer cores. This study shows the significance of the judicious choice of π-conjugated scaffolds in generating low- (S = 0) and high-spin (S = 1) ground-states in the neutral form, by modulation of spin topology in extended π-conjugated D–A polymers for emergent optoelectronic applications.
Introduction
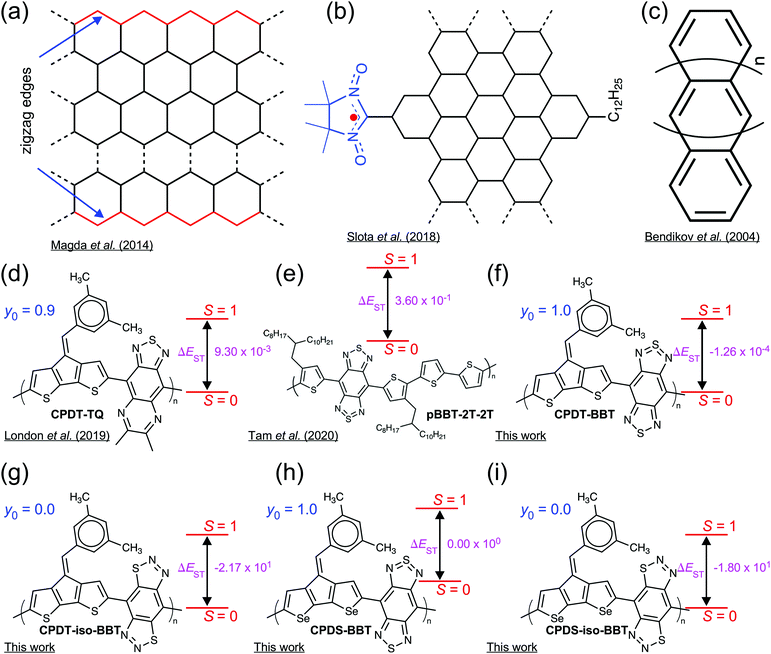
High-spin (S ≥ 1) organic molecules with a pure diradical character possess a wide variety of intriguing molecular and electronic properties and have potential applications for numerous advanced optoelectronic devices. The unpaired electrons in the high-spin molecules may impart strong ferromagnetic interactions, making them useful as a building block for the all-organic magnets,1–4 molecular spintronics,5–8 magnetic sensors,9 charge-storage,10 and rewritable memory devices.11 Although a large number of works have been conducted in designing and synthesizing high-spin organic molecules,12–15 only a handful of polymeric systems are reported, which invert the spin pairing in the singlet state (S = 0) and stabilize a high-spin (S = 1) ground-state in the neutral form.16–20Organic semiconductors (OSCs) with two unpaired electrons residing in two degenerate or nearly degenerate non-bonding frontier molecular orbitals (FMOs) possess a reduced antiferromagnetic (AFM) coupling between the unpaired electrons than the closed-shell molecules. These molecules show the small highest occupied MO (HOMO)-lowest unoccupied MO (LUMO) energy gap, and significantly reduce the energy difference between the low-to-high spin states (ΔE).10,16,21–27 The unpaired electrons in the open-shell OSCs impart exotic spin-correlated functionalities. The spin distribution along the polymer chain modulates ground-state spin multiplicity and magnetic properties of the materials.16,18,28,29 Although the presence of unpaired electrons is a requisite for the open-shell diradicals,30 localization of unpaired electrons on different sites in the π-conjugated scaffold has been rather difficult.18,31 Localized spin distribution has been achieved in radical-functionalized graphene nanoribbons (GNRs) or zigzag GNRs (ZGNRs) with crystallographic edge orientations, where the radical sites act as spin-bearing units, generating magnetic edge states (Fig. 1a and b).32–35 However, in the case of modified (Z)GNRs, the spin in these systems is a result of spin-bearing side-chain functionalization rather than an intrinsic property of these materials.36 Polyacenes (Fig. 1c), on the other hand, show disjointed non-bonding molecular orbitals leading to spin distribution localized at the core.32,37 The previous studies on high-spin state materials indicates a complete delocalization of the unpaired electrons on the π-conjugated backbone, providing thermodynamic stabilization of the molecules (Fig. 1d and e).16,17 Therefore, the development of new materials with intrinsic localized electron densities in the pristine form will not only allow us to understand the interplay between the electronic and spin-induced properties but also may lead to advanced optoelectronic and spin-controlled multifunctional technologies with both semiconducting and magnetic properties.5,38
Here, we present new donor–acceptor (D–A) conjugated polymers based on alternating cyclopentadithiophene (CPDT) and cyclopentadiselenophene (CPDS) donors, which are π-conjugated with benzobis[1,2-c;4,5-c′]bis[1,2,5]thiadiazole (BBT) and benzo[1,2-d:4,5-d′]bis([1,2,3]thiadiazole) (iso-BBT)39 acceptors, respectively (Fig. 1f–i), where the BBT-based polymers show a high-spin (S = 1) ground-state with a pure diradical character (y0 = 1); however, the iso-BBT-based polymers have a closed-shell (y0 = 0) configuration with a low-spin (S = 0) ground-state. These types of D–A topologies offer opportunity to tailor molecular structures to tune electronic properties, while having solution processability and backbone flexibility, making D–A polymers a suitable building block for numerous optoelectronic technologies.40–48
We employed the structurally symmetric BBT and iso-BBT acceptors to manipulate the spin density distribution to have open-shell and closed-shell configurations, respectively.22 The diradical nature of the BBT acceptor is well known along with its high electron affinity due to the hypervalent sulfur and strong pro-quinoid character, leading to the quinoidal molecular backbone and a small singlet–triplet gap (ΔEST).39,49–54 The lower LUMO energy level inherent to the BBT unit decreases the HOMO–LUMO energy gap, which facilitates admixing of HOMO and LUMO to the ground electronic state.55 Also, the thiadiazole units of the BBT recover aromatic stabilization energy in the open-shell ground-state, a driving force facilitating double-bond breaking.22,53,56 As a result, the CPDT-BBT and CPDS-BBT polymers show a pure diradical character and a degenerate ΔEST at the neutral state, which would facilitate magnetic switching from the low-spin to the high-spin ground-states.18,54 However, a large HOMO–LUMO energy gap in the iso-BBT-based polymers and lack of thiadiazole units create a highly aromatic backbone, leading to a closed-shell configuration with localized spin density in the polymer cores.
Computational details
Selection of appropriate functional
Geometry optimization is performed with the Gaussian 16 software package57 without any symmetry constraints. Molecular geometries for the electronic singlet (S = 0) and the triplet (S = 1) states of the model oligomers (N = 1 to 8) are optimized using hybrid density functional, B3LYP.58,59 For the Se and Si atoms, LANL2DZdp basis set is used along with associated effective core potentials60,61 and 6-31G(d,p)62 basis set is used for other atoms. All parameters for geometry optimization are set to default. For larger oligomers, geometries are considered optimized once the forces on all atoms converged to zero.63We have performed benchmark calculations on a dimer (N = 2) of CPDT-BBT polymer using different functionals with variable amount of Hartree–Fock (HF) exchange at the 6-31G(d,p) basis set (see Table S1, ESI†). Calculations are performed with pure functional, BLYP (HF exchange = 0.0%),58,64 hybrid functionals with low HF exchange, B3LYP (HF exchange = 20.0%),58 and PBE1PBE (HF exchange = 25.0%);65 hybrid functionals with intermediate HF exchange, BHandHLYP (HF exchange = 50.0%),58 and M062X (HF exchange = 54.0%);66 and long-range corrected hybrid functionals, CAM-B3LYP (HF exchange = 19.0% short-range and 65% long-range),67 and ωB97X-D (HF exchange = 22.0% short-range and 100% long-range).68 The B3LYP functional has the lowest spin-contamination among all the hybrid density functionals considered. Other functionals give a large spin-contamination that leads to an increase in the diradical character or even unphysical polyradical character, not observed in BBT-based materials.53 Also, both the y0 and spin contamination increased as HF exchange is increased in the hybrid functionals.69 The pure functional BLYP predicts that the dimer (N = 2) of CPDT-BBT polymer has a closed-shell configuration, indicating that a large repeat unit is necessary to display considerable open-shell character.32 Interestingly, both the BLYP and ωB97X-D predict the same ΔEST energy gap; however, due to a large spin-contamination, the diradical index is large with ωB97X-D functional. A similar trend in ΔEST and y0 is observed with B3LYP and M062X; however, a large spin-contamination increased the y0 for the latter one. In addition, our study on large polymeric systems indicates that the (U)B3LYP functional combined with 6-31G(d,p) basis set accurately predicted the experimental electrochemical bandgap.16
To see the effect of density functionals on these systems, we have also performed calculations with optimally tuned range-separated hybrid functional (OT-RSH) for the smaller oligomers of these conjugated polymers. The tuned parameter, ω, is determined based on the LC-ωHPBE functional.70 As representative molecules, we have considered the dimer and tetramer of CPDS-BBT (open-shell) and CPDS-iso-BBT (closed-shell) and computed the ΔEST values, diradical indexes, and spin densities. We have also investigated the performance using the screened version of RSH (OT-SRSH) at ε = 3.071 (typical dielectric constant for organic materials) to account for the electronic polarization. The range-separated parameter (ω) using LC-ωHPBE is determined by the ionization potential (IP)-scheme.72 In the case of OT-SRSH, the tunable parameter, α is set to 0.2071 and β is evaluated by 1/ε − α. The electronic properties calculated with (U)B3LYP, OT-RSH, and OT-SRSH methods are included in the ESI† (see Table S2). The results obtained with OT-(S)RSH methods are in agreement with the (U)B3LYP functional. Therefore, we have performed all the calculations and analysis with the (U)B3LYP functional and 6-31G(d,p) basis set.
Broken-symmetry (BS) calculation
The geometry optimization is initialized with a restricted wave function, and a broken-symmetry (BS)73 wave function is used to characterize the open-shell singlet state. A stability test on the wave function showed restricted-to-unrestricted instability for oligomers from monomers (N = 1) of the BBT-based polymers. However, no such instability is found in the case of the iso-BBT-based polymers. The triplet state is optimized with an unrestricted wave function. Also, the expectation value 〈S2〉 can be used as an indication of spin-contamination in the ground-state, where values of 1 and 2 indicate no spin-contamination in the pure singlet and triplet states using the BS method, respectively.30 After spin annihilation, triplet states indicate a 〈S2〉 value close to 2; however, in the case of singlet state, the 〈S2〉 value is found to be higher than 1, indicating spin-contamination of triplet spin multiplicities in the singlet ground-state. No spin-projection method74 is used to remove spin-contamination in this work.Diradical and tetraradical characters
The presence of unpaired electrons in an open-shell molecule is quantitatively defined by the multi-radical indexes (yi), where the indexes range from 0 ≤ yi ≤ 1 (i = 0–1), defining a pure open-shell molecule at yi = 1 and a closed-shell at yi = 0.21 The upper end value of the yi dictates a bond dissociation limit with a high degree of localization of the unpaired electrons, whereas, the lower end defines a higher electron–electron coupling and Coulomb repulsion.30,75 The diradical (y0) and tetraradical (y1) indexes are obtained from population analysis of natural orbitals as the occupation numbers of the lowest unoccupied natural orbitals (LUNOs).Prediction of the unpaired spin locations and orbital overlap (Sαβ)
The NBO6 program package76 is used to predict the unpaired spin locations from the natural spin densities of the Kohn–Sham molecular orbital (MO). The overlap between different spin orbitals (Sαβ) is computed with the Multiwfn program package,77 where Sαβ = 1.0 indicates a complete overlap between two spin orbitals.Prediction of aromatic character
To predict the aromatic/quinoidal nature of the individual rings on each polymer, isotropic nucleus-independent chemical shift (NICSiso(1))78 is computed using the gauge-independent atomic orbital (GIAO)79 method wherein a single point energy calculation is carried out with a ghost atom placed at 1 Å perpendicularly above the plane of the ring to account for only the π-electron contribution. A large negative NICSiso(1) value indicates that the corresponding ring is aromatic. Ring currents are analyzed with anisotropy of the induced current density (ACID) method80 at the CSGT-UB3LYP/6-31G(d,p) level of theory,81 and rendering is performed with a locally developed code. The 2D-ICSS (2D-iso-chemical shielding surface) maps are generated by the method developed by Klod et al.82 The harmonic oscillator model of aromaticity (HOMA)83 is calculated with the following equation: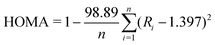 | (1) |
Results and discussion
Selection of the donor and acceptor units
We chose the donors and acceptors with extensive screening of different electron-rich and electron-deficient units based on the diradical character and ΔEST (see Fig. S1 and S2, ESI†).85 We have selected C-bridged CPDT and CPDS donors as they promote a planar molecular backbone and offer flexibility in using molecular topology to modulate electronic properties. They also have an elevated HOMO leading to a smaller band gap and a substantial π-conjugation along the molecular backbone.10,16,20,56,86 The substitution of S in CPDT with Se can increase the quinoidal character,46,86 leading to a higher diradical character. The BBT acceptor, when conjugated with CPDT donor, develops an open-shell diradical character and displays a smaller ΔEST than the other acceptors for the monomer unit (see Fig. S1, ESI†). The hypervalent sulfur in the BBT unit can transform from a high energy –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– structure to a lower energy –N–S–N– stable configuration in the open-shell resonance form, recovering aromatic stabilization energy in the ground-state; therefore, increasing diradical character.22,49,53,56 However, the iso-BBT acceptor has a higher LUMO level than the BBT unit, which increases the HOMO–LUMO energy gap, leading to a closed-shell configuration.22,39 Therefore, the selection of these two acceptors along with CPDT and CPDS donors can display two different regimes in the diradical character scale, which can provide insights into different spin distribution along the backbone of the polymer. Furthermore, an important observation from various acceptors with thiadiazole end-cap units (P8–P12, Fig. S1, ESI†) is that the head-to-head fusion of the thiadiazole unit with the six-member ring reduces the ΔEST and develop a small open-shell character (y0 = 0.040) (Fig. S1, ESI†). Therefore, designing new acceptors with head-to-head conjugation of thiadiazole units in a six-member core is an efficient technique to achieve diradical character in smaller oligomers.
N– structure to a lower energy –N–S–N– stable configuration in the open-shell resonance form, recovering aromatic stabilization energy in the ground-state; therefore, increasing diradical character.22,49,53,56 However, the iso-BBT acceptor has a higher LUMO level than the BBT unit, which increases the HOMO–LUMO energy gap, leading to a closed-shell configuration.22,39 Therefore, the selection of these two acceptors along with CPDT and CPDS donors can display two different regimes in the diradical character scale, which can provide insights into different spin distribution along the backbone of the polymer. Furthermore, an important observation from various acceptors with thiadiazole end-cap units (P8–P12, Fig. S1, ESI†) is that the head-to-head fusion of the thiadiazole unit with the six-member ring reduces the ΔEST and develop a small open-shell character (y0 = 0.040) (Fig. S1, ESI†). Therefore, designing new acceptors with head-to-head conjugation of thiadiazole units in a six-member core is an efficient technique to achieve diradical character in smaller oligomers.
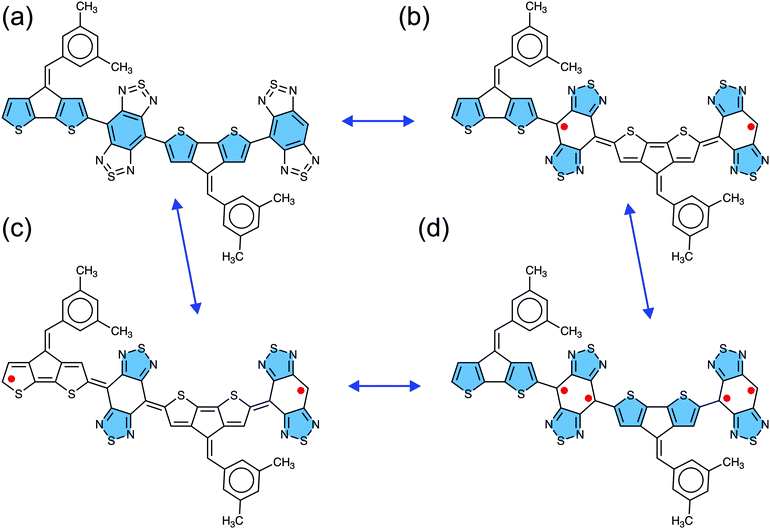
Closed-shell and open-shell resonance structures
The four canonical forms of the CPDT-BBT dimer (N = 2) representing closed-shell, open-shell diradical, and open-shell tetraradical character are given in Fig. 2, which describes the role of the thiadiazole and benzenoid units of the BBT acceptor, and the CPDT donor in obtaining open-shell configuration. In moving from high energy closed-shell (Fig. 2a) to stable open-shell diradical configurations (Fig. 2b and c), the four thiadiazole rings recover aromatic stabilization energy at the expense of the aromatic character of the two/four thiophene units of the CPDT donor and two benzenoid rings of the BBT acceptor, leading to a quinoidal character in the CPDT donor. However, in the tetraradical canonical form (Fig. 2d), although the same four thiadiazole rings get an aromatic character, only two benzenoid rings loose aromaticity in the BBT unit, while keeping the thiophene units of the CPDT donor aromatic as in the closed-shell form (Fig. 2a). Therefore, the tetraradical canonical form is not favored in the BBT-based polymers, indicating that the open-shell diradical form is the predominant configuration in the BBT-based materials.22,52,53 Also, the conjugation between the CPDT donor and BBT acceptor favors the formation of quinoidal character in the CPDT donor, which facilitates the separation of the unpaired spins towards the polymer ends, increasing the open-shell diradical character and reducing singlet–triplet energy gap. However, non-aromatic donors (such as, pentadiene and [10]annulene) (Fig. S3, ESI†) greatly reduce the quinoidal character in the polymer backbone, significantly reducing the open-shell character and increasing the singlet–triplet energy gap.Evolution of open-shell character and high-spin ground-state
The open-shell character and energy difference between the lowest singlet and the triplet state (ΔEST) correlate with one another.1,30 The key electronic properties of the polymers considered in this study are presented in Table 1 (see also Tables S3 and S4, ESI†). We have also included the data for the CPDT-TQ polymer, which has a high-spin ground-state as quantified through experimental characterization and validated with theoretical calculation at the (U)B3LYP functional and 6-31G(d,p) basis set.16 The increase in oligomer length is associated with a gradual decrease in ΔEST for BBT- and iso-BBT-based polymers (Table 1 and Table S4, ESI†). However, the rate of decrease is faster for the BBT-based polymers than that for the iso-BBT-based polymers. At N = 5, the ΔEST plateaus for the iso-BBT-based polymers (Table S4, ESI†); however, an opposite trend is observed for the BBT-based polymers, where addition of repeat units reduces the ΔEST, while increasing diradical character (y0) (Table 1 and Table S4, ESI†).| Polymer | N | ΔEST | P T | HOMO | LUMO | E g | y 0 |
|---|---|---|---|---|---|---|---|
| CPDT-TQ | 4 | −1.02 × 10−1 | 6.45 | −4.17 | −3.26 | 0.91 | 0.422 |
| 8 | −2.30 × 10−2 | 56.65 | −4.07 | −3.30 | 0.77 | 0.913 | |
| CPDT-BBT | 2 | −7.85 × 10−2 | 14.37 | −4.61 | −3.43 | 1.18 | 0.604 |
| 4 | −3.37 × 10−3 | 72.61 | −4.44 | −3.50 | 0.95 | 0.966 | |
| 6 | −1.44 × 10−4 | 74.90 | −4.40 | −3.51 | 0.89 | 0.997 | |
| 8 | −5.44 × 10−6 | 74.99 | −4.39 | −3.52 | 0.88 | 1.000 | |
| CPDT-iso-BBT | 2 | −10.50 × 10−1 | 0.00 | −5.08 | −3.07 | 2.01 | 0.000 |
| 4 | −9.50 × 10−1 | 0.00 | −4.93 | −3.24 | 1.69 | 0.000 | |
| 6 | −9.40 × 10−1 | 0.00 | −4.89 | −3.29 | 1.60 | 0.000 | |
| 8 | −9.40 × 10−1 | 0.00 | −4.88 | −3.31 | 1.57 | 0.000 | |
| CPDS-BBT | 2 | −4.88 × 10−2 | 33.26 | −4.61 | −3.46 | 1.16 | 0.700 |
| 4 | −7.51 × 10−4 | 74.48 | −4.47 | −3.51 | 0.96 | 0.984 | |
| 6 | −1.09 × 10−5 | 74.99 | −4.44 | −3.52 | 0.91 | 0.999 | |
| 8 | −0.00 × 100 | 75.00 | −4.43 | −3.53 | 0.89 | 1.000 | |
| CPDS-iso-BBT | 2 | −9.20 × 10−1 | 0.00 | −5.00 | −3.17 | 1.83 | 0.000 |
| 4 | −7.90 × 10−1 | 0.00 | −4.84 | −3.36 | 1.48 | 0.000 | |
| 6 | −7.80 × 10−1 | 0.00 | −4.79 | −3.41 | 1.38 | 0.000 | |
| 8 | −7.80 × 10−1 | 0.00 | −4.77 | −3.44 | 1.33 | 0.000 |
The narrowing of the ΔEST indicates more stabilization of the open-shell form than the closed-shell configuration (Fig. S4, ESI†). For instance, in tetramer (N = 4), the energy of the closed-shell is significantly increased (10.56 kcal mol−1 and 12.37 kcal mol−1 for CPDT-BBT and CPDS-BBT, respectively) compared to that of the open-shell state, and the triplet state lies only 0.08 kcal mol−1 in CPDT-BBT (0.02 kcal mol−1 in CPDS-BBT) above the singlet (Fig. S4, ESI†). Also, the ΔEST of the CPDT-BBT octamer reaches well below the thermal energy (kT) at room temperature, indicating a very high population (74.99%) of the triplet state at the ambient conditions, whereas singlet and triplet states of the CPDS-BBT (N = 7–8) are degenerate, showing 75.0% population of triplet state under room conditions (Table 1 and Table S4, ESI†). The diradical character also reaches the limit (y0 = 1.0), signifying the lack of covalency between the unpaired electrons. To examine the effect of non-aromatic donors, we replaced the CPDT with pentadiene and [10]annulene (Fig. S3, ESI†). The diradical character reduces significantly (y0 = 0.105 and 0.00 at N = 4, for pentadiene and [10]annulene, respectively) and a large increase in the ΔEST is observed (0.41 eV and 0.46 eV at N = 4, for pentadiene and [10]annulene, respectively), which indicates the important role of CPDT donor in realizing high-spin polymers than other non-aromatic donors.
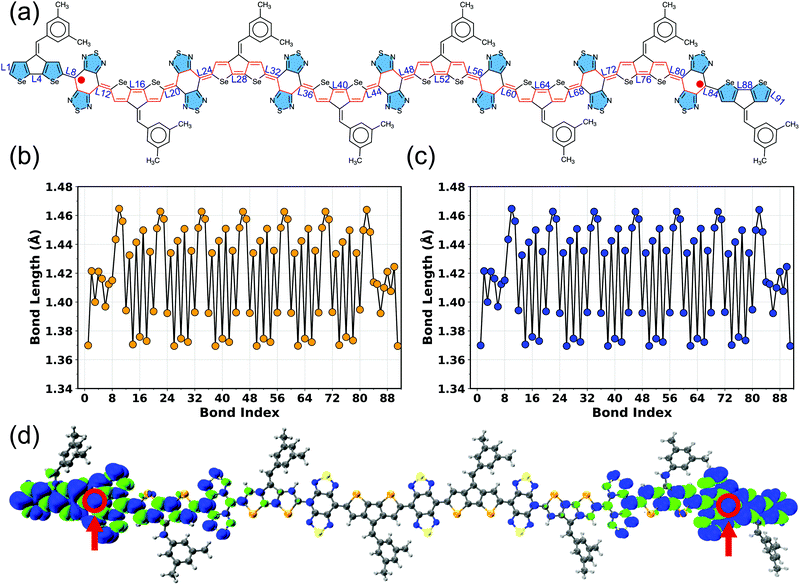
The connecting bonds between the donor and adjacent acceptor units vary within 1.392–1.420 Å in BBT-based polymers and 1.447–1.455 Å in iso-BBT-based polymers (Fig. S5–S19 and Tables S5, S6, ESI†), indicating a highly π-conjugated backbone in the case of the open-shell polymers, which can increase the electronic coherence and charge-transfer along the π-conjugated backbone. On the other hand, the non-aromatic donors reduce the π-conjugation, as observed from large connecting bonds (1.45 Å, and 1.47 Å) between the pentadiene and [10]annulene donors and BBT acceptor, respectively (Fig. S20 and S21, ESI†). A coplanar geometry (ϕ ≈ 180°) observed in the BBT-based polymers increases the diradical character and reduces ΔEST and HOMO–LUMO gaps (Fig. S22 and S23, ESI†). Also, a coplanar geometry facilitates π-stacking and induces strong intermolecular interactions between the unpaired electrons as well.17,28 However, the iso-BBT-based polymers are less planar (Fig. S24, ESI†) due to the steric repulsion between the sulfur in iso-BBT acceptor and hydrogen atom in the donor unit, reducing the π-conjugation, which is readily visible from the large connecting bonds. Moreover, the singlet and triplet electronic states display equal bond lengths (Tables S5 and S6, ESI†) for the larger repeat units (N = 7–8), signifying a (near-)degeneracy between these two electronic states, as evident from ΔEST of the BBT-based polymers (Table 1, Table S4 and Fig. S4, ESI†).
A very small ΔEST indicates a significant electronic correlation between these two states, therefore, increasing the exchange interaction in the triplet state.1,16 The MO diagrams (Fig. S25–S28 and S33–S36, ESI†) of the BBT-based molecules indicate that with the increase in oligomer length, the α-singly occupied MO (SOMO) and β-SOMOs progressively localize at the opposite ends of the polymer chain. Consequently, the unpaired electrons with antiparallel spins are permitted to correlate in separate spaces, reducing the bond covalency and increasing y0.16 These types of disjoint MOs are reported for longer acenes (Fig. 1c)32 or other long π-conjugated open-shell molecules,18,31,55 which has also recently been demonstrated in an alternating D–A scaffold.16 However, in the case of the iso-BBT-based polymers, the HOMO and LUMO are delocalized (Fig. S29–S32 and S37–S40, ESI†), increasing the overlap between two FMOs, which increases the ΔEST. Further increase in chain length expands the distance between the unpaired electrons (Fig. S41–S45, ESI†), thereby reducing the Coulomb repulsion in the triplet state and favoring the S = 1 ground-state in the long-chain limit.16,17,87 This is clearly evident from the extrapolation of the calculated ΔEST as a function of N, where an inflection point is achieved at N = 9 (Fig. S46, ESI†), and the intramolecular spin-coupling constant (ΔEST = 2J) is predicted to be ferromagnetic (J > 0).1,30 The previous CPDT-TQ high-spin polymer shows an inflection point at N = 13 (Fig. S46, ESI†) with DFT predicted ΔEST = −14.43 kcal mol−1 (at N = 8), whereas, the experimental EPR measured data when fitted to Bleaney–Bowers equation provide ΔEST = 9.30 × 10−3 kcal mol−1 (J = 1.62 cm−1), with the triplet being lower in energy.16 Therefore, the BBT-based polymers are anticipated to have a triplet ground-state at a smaller chain length than the CPDT-TQ polymer.
Spin density distribution of the D–A polymers
Control and modulation of localized spins (radical centers) are necessary to realize organic magnetic and spin manipulation devices.33,88 The spin density distribution along the polymer backbone is shown in Fig. 3 and Fig. S47–S50 in the ESI.† Increasing the oligomer length localizes the unpaired electrons at the polymer ends of the BBT-based polymers, indicating a complete polarization of the unpaired spins. We observe a greater localization in the CPDS-BBT polymer than in the CPDT-BBT polymer (see Fig. 3). For the iso-BBT-based polymers, upon increasing the chain length, the spin density distribution for the S = 1 state is localized at the polymer core instead of at the ends as observed in the BBT-based polymers (Fig. 3 and Fig. S47–S50, ESI†), which indicates that the choice of the acceptors manipulates the spin localization in these polymers.89 A large and diluted aromaticity in the pentadiene-based polymer delocalizes the spin density along the polymer backbone (Fig. S51, ESI†). We have also analyzed the spin density distribution of the triplet state (S = 1) for CPDT-BBT and CPDS-BBT octamers (N = 8) with a range-separated functional, ωB97X.68 We selected the ωB97X functional as it provided the smallest mean absolute deviation for selected polycyclic aromatic hydrocarbons when compared to that of QCISD spin densities.90 The spin density distribution predicted with ωB97X is consistent with the density distribution obtained with the UB3LYP functional (Fig. 3 and Fig. S54, ESI†), which indicates that the localized spin topology is an intrinsic property of the BBT-based polymers.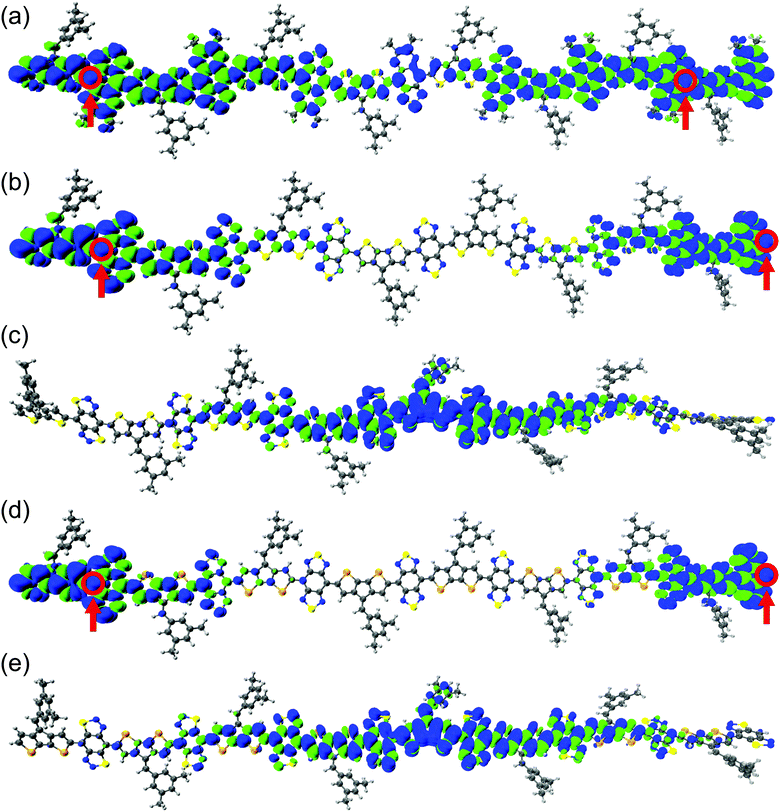 | ||
| Fig. 3 The ground-state geometry and pictorial representations of spin density distribution for the (a) CPDT-TQ16, (b) CPDT-BBT, (c) CPDT-iso-BBT, (d) CPDS-BBT, and (e) CPDS-iso-BBT (N = 8) polymers in their S = 1 states. The blue and green surfaces represent positive and negative contributions of the spin density at an isovalue = 0.0002 a.u. The most probable locations for the unpaired electrons with largest atomic spin density are highlighted in open circles. | ||
Generally, for an open-shell system, it is observed that unpaired electrons occupy the frontier molecular orbitals (i.e., highest energy singly occupied molecular orbitals). To see if this is the case for extended (polymeric) systems, we analyze the α- and β-SOMOs for CPDT-BBT and CPDS-BBT at N = 8. We find that the α-SOMO is delocalized along the polymer backbone, while the spin density plots show localized spin density at the polymer ends. The β-SOMO (Fig. S52, ESI†), however, is localized at the chain end. Upon further examination of SOMOs of CPDT-BBT (N = 8) with energies lower than the frontier SOMOs (Fig. S52 and S53, ESI†), we notice a significant overlap (Sαβ = 0.903) between the α-SOMO (E = −4.547 eV) and β-SOMO−1 (E = −4.579 eV), potentially cancelling the contribution to the total spin density of these orbitals. It turns out that the α-SOMO−1 (E = −4.631 eV) and β-SOMO (E = −4.388 eV) (Sαβ = 0.234) contribute to the total spin density (Fig. S52 and Table S7, ESI†), which is consistent with the inferences drawn from the spin density plots (Fig. 3). Furthermore, the atomic spin density calculated for the S = 0 and S = 1 states have the same positive values (0.26 and 0.38 in CPDT-BBT; 0.25 and 0.40 in CPDS-BBT, respectively) at the terminal C atoms (Fig. S44, ESI†), which increase from the cores to the ends of the BBT-based polymers, hence reducing the overlap between the unpaired electrons.31,91 Moreover, a large positive density is observed at the terminal nitrogen (N) atoms in the BBT acceptor, which can facilitate short intermolecular [S⋯N] contacts and spin–spin interactions, as reported in the case of BBT-based materials.53
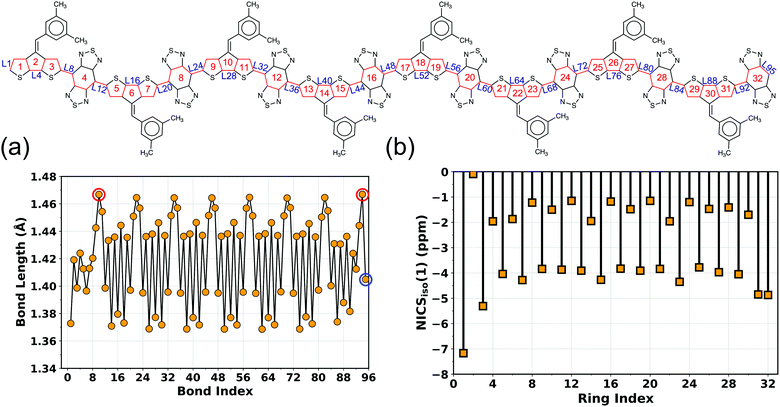
To better understand different spin topologies in the BBT and iso-BBT-based polymers and to gain insights into the aromatic/quinoidal nature of the π-conjugated backbones, we analyze the bond length alternation (BLA), HOMA, and NICSiso(1). The C–C bond lengths of the BBT core vary between 1.405 and 1.467 Å, indicating quinoidal character. Upon increasing the chain length, the BLA is increased in the core of the BBT-based polymers indicating transition towards a high energy quinoidal structure. In contrast, the opposite ends of the polymers show a reduced BLA (Fig. 4a, Fig. S5–S7 and S12–S15, ESI†), indicating energetically favorable aromatic structure (Fig. 2b).37,84,92,93 In the case of the CPDT-BBT octamer, the NICSiso(1) value of ring 1A is −7.20 ppm, whereas the NICSiso(1) value of the benzenoid ring of the BBT acceptor is −1.20 ppm (HOMA: 0.634) at the oligomer center (4E) and −4.90 ppm (HOMA: 0.738) (8E) at the end (Fig. 4b and Table S11, ESI†). Consequently, the charge densities are pushed from the higher energy quinoidal core to the lower energy aromatic ends to reduce Coulomb repulsion, ultimately localizing the unpaired spins at the ends of the BBT-based polymers (Fig. 2b). The NICSiso(1) is higher (less negative) in the CPDS-BBT octamer, where rings 1A, 4E, and 8E show NICSiso(1) values of −7.15, −1.13 (HOMA: 0.640), and −4.43 (HOMA: 0.739) ppm, respectively (Table S19, ESI†), which indicates a larger quinoidal contribution than that of the CPDT-BBT polymer. On the other hand, the iso-BBT-based polymers (N = 8) have large negative NICSiso(1) values (Tables S15 and S23, ESI†) along the backbone (−8.28, −8.72, and −10.51 ppm in CPDT-iso-BBT; −7.59, −8.71, and −10.23 ppm in CPDS-iso-BBT in the 1A, 4E, and 8E rings, respectively), with HOMA values >0.940 in the benzenoid rings, indicating a more aromatic backbone, which agrees with the reduced BLA parameter as well (Fig. S8–S11 and S16–S19, ESI†). However, the S = 1 state of the iso-BBT-based polymers have increased NICSiso(1) along the backbone (Tables S15 and S23, ESI†); the largest value is observed at the polymer core where the unpaired electrons are localized.
Effect of D and A units on the diradical character (y0)
To explore the effect of different acceptors and substituents on the donor unit, and to quantify the localization of the unpaired electrons, we have assessed the open-shell character with the quantitative descriptor diradical index (y0), where the index ranges from 0 ≤ y0 ≤ 1, defining a pure open-shell molecule at y0 = 1 and a closed-shell at y0 = 0. The y0 values depend on the acceptors used to π-conjugate with the donor units (see Table 1 and Table S4, ESI†). The hypervalent sulfur in the BBT unit imparts strong electron-accepting ability, as evident from the development of open-shell character even at the monomer unit, indicating that the open-shell diradical form is lower in energy than the closed-shell form (Table 1, Table S4 and Fig. S4, ESI†). The BBT acceptor has a deeper LUMO energy level than that of the iso-BBT, which reduces the HOMO–LUMO energy gap (Eg). Adding more repeat units in the polymer chain increases the HOMO and decreases LUMO energy levels; therefore, fine-tuning in the corresponding energy levels occurs, resulting in a gradual decrease in the Eg gap. A linear extrapolation of the Eg as a function of the inverse number of the repeating units (1/N) to the polymer chain limit (N → ∞) provides the electrochemical band gap. The band gaps obtained for the CPDT-BBT, CPDS-BBT, CPDT-iso-BBT, and CPDS-iso-BBT are 0.74, 0.76, 1.41, and 1.17 eV, respectively (Fig. S55, ESI†). A similar extrapolation for the CPDT-TQ polymer gives a band gap of 0.58 eV, which is in excellent agreement with the experimental electrochemical band gap.16 Clearly, the BBT-based polymers have a significantly narrower band gap than the iso-BBT based polymers, which facilitates admixing of the FMOs in the ground-state, leading to a significant population in the LUNOs; therefore, developing open-shell diradical character in the CPDT-BBT and CPDS-BBT polymers.16,21,22,55 A small band gap can enhance the ambipolar charge-transfer characteristics of these polymers as well.22,47The calculated y0 values correspond well to those obtained in previous oligomer studies of BBT-based diradicaloids.53 The tetraradical (y1) character for the octamer (N = 8) is found to be negligible (y1 = 0.05, as observed from the LUNO+1 occupancy) in both CPDT-BBT and CPDS-BBT polymers, indicating that the diradical character is predominant in the CPDT-BBT and CPDS-BBT polymers (Fig. 2b and d). The non-aromatic donors pentadiene and [10]annulene induce a large aromatic character in the polymer backbone, which can be realized by a small BLA in the BBT core (Fig. S20 and S21, ESI†). In the case of the pentadiene donor, a large negative NICSiso(1) value (≈−8.91 ppm) is observed in the benzenoid ring compared with that of the CPDT-BBT tetramer (≈−2.04 ppm) (see Tables S9 and S24, ESI†), reducing the diradical character in the former polymer (0.105 vs. 0.966 at N = 4). With the increase of the oligomer chain length in the CPDT-BBT and CPDS-BBT polymers, y0 increases rapidly and reaches to the diradical saturation limit at a larger chain length (Fig. S56, ESI†); therefore, diminishes the bonding covalency between the unpaired electrons and reaches the bond dissociation limit at N = 8, with a vanishing effective bond order (1 − y0).18,69,75,94 As a result, the unpaired electrons are completely decoupled and localized at individual sites with a higher degree of electronic coherence, where parallel alignment (either both spin-up or spin-down) is possible to reduce the electron–electron repulsion, resulting in S = 1 as a ground-state.16,17
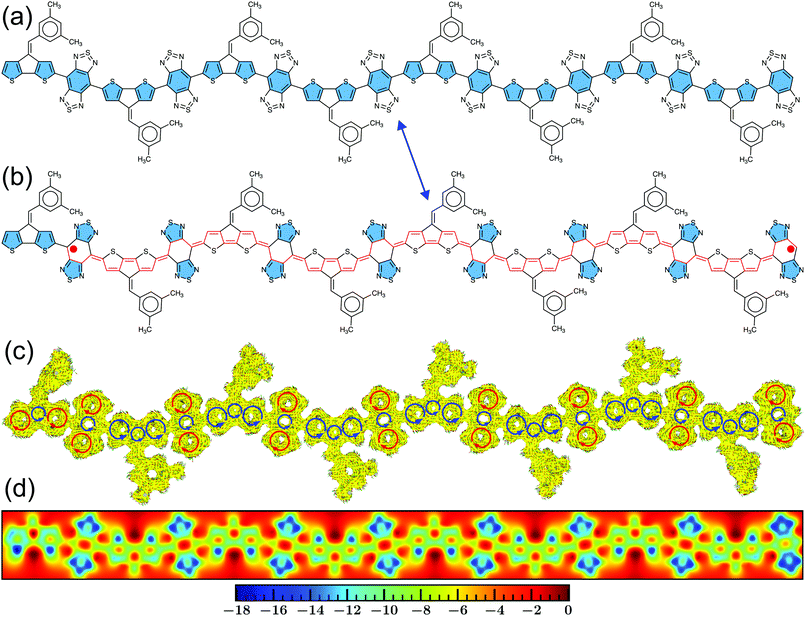
Looking at the resonance structures of the CPDT-BBT polymer, two thiadiazole units recover aromatic stabilization energy in the open-shell form from the closed-shell configuration (Fig. 5a and b).53 Upon increasing the polymer chain length, the number of aromatic thiadiazole units that recover stabilization energy increases (Fig. S57–S59, ESI†), adding to the driving force for π bond-breaking, therefore, increasing the y0, a manifestation of Clar's aromatic sextet rule.21,56,95 The NICSiso(1) values (Tables S8–S11 and S16–S19) obtained on the thiadiazole units of the BBT-based polymers show a considerable decrease (more negative) in the calculated value (−9.50 to −11.50 ppm), which indicates an aromatic character of the thiadiazole units, facilitating double-bond breaking. The ACID plots show two clockwise (diatropic) ring current circuits in the top and bottom of the BBT units, indicating a local aromatic character and recovery of aromatic stabilizing energy in the thiadiazole units (Fig. 5c and Fig. S57–S59, ESI†). The cyclopentane rings in the CPDT donor indicate counterclockwise ring currents, while the sulfur-containing five-member rings have clear clockwise ring currents at the end and diminished clockwise and counterclockwise ring current contributions at the core of the polymer chain. A significant decrease in the diatropic ring current contribution in moving from the terminal thiophene to the oligomer center coincides with the accumulation of charge density at the chain ends; therefore, increases the distance between the unpaired spins and reduces bond covalency, concomitantly, increasing y0 (Fig. 5c and Fig. S41–S45, S47–S49, ESI†). Furthermore, the 2D-ICSS plots indicate that the thiadiazole units of the BBT acceptor is magnetically shielded (negative 2D-ICSS). In contrast, the benzenoid units of the BBT acceptor and five-member rings in the donor are magnetically de-shielded (Fig. 5d and Fig. S57–S59, ESI†), which is further supported by the large negative NICSiso(1) values in the auxiliary rings (Tables S8–S11 and S16–S19, ESI†) and less negative NICSiso(1) values in the donor and acceptor cores (Fig. 4b). Therefore, the one-to-one correspondence between the calculated SOMOs, values of spin density, NICSiso(1), HOMA, and ACID, and 2D-ICSS plots unambiguously confirms that the BBT-based polymers develop a pure diradical character due to an increased number of aromatic thiadiazole units, and a small band gap, which admixes the HOMO and LUMO in the ground-state, and a significant quinoidal core with aromatic ends.
Effect of different end terminations
Besides the symmetric (–D–A–)N arrangement, we have also assessed the electronic properties with different end groups, such as placing D and A at both ends of the CPDS-BBT heptamer (N = 7) backbone, respectively. From the BLA, it is evident that when the polymers end with D units, both ends of the oligomer has increased aromaticity because the five-member rings with sulfur hetero-atom recovers aromaticity in the open-shell state, indicated by a reduced BLA in the donor units (Fig. 6b and c). Therefore, the unpaired electrons are localized at the two ends (Fig. 6d), which is in agreement with the α- and β-SOMO distribution on the oligomer backbone (Fig. S60, ESI†). However, when both ends contain BBT acceptor units, a significant quinoidal character is observed in the backbone with less localization in the α- and β-SOMOs (Fig. S61 and S62, ESI†), although the spin densities are localized at the ends due to a larger contribution of the α- and β-SOMO in the oligomer ends (Fig. S62, ESI†). The substitution of the D units does not change the HOMO energy level from the unsubstituted heptamer (Table 1 and Tables S3, S4, ESI†); however, the LUMO energy increased by 0.21 eV, increasing the HOMO–LUMO energy gap by the same amount. We observe the opposite phenomenon when both ends contain a BBT acceptor; now, the LUMO energy is unperturbed, down-shifting the HOMO by 0.19 eV, increasing the HOMO–LUMO energy gap. Interestingly, although a large shift in the calculated HOMO–LUMO energy gap is observed in the substituted analogs, the diradical character is unaffected from the unsubstituted heptamer (y0 = 1 in all cases), which is because the number of aromatic sextet rings are almost similar (Fig. 6a and Fig. S61, ESI†). The unpaired electrons are completely localized at the terminals, reducing the bond covalency between the unpaired electrons. Therefore, y0 depends on the spin localization and the number of aromatic sextet units than on the energy gap between the FMOs in this case. Therefore, if a larger separation between the unpaired electrons is ensured, the diradical character will be unaffected by the change in the HOMO–LUMO energy gap. Due to a large y0, a very small ΔEST gap is observed for both derivatives with significant thermal population (>74.99%) of the S = 1 state (Table 1 and Tables S3, S4, ESI†), although a small increase in the ΔEST gap is observed from the unsubstituted heptamer (N = 7). Therefore, structural symmetry in an alternating D–A polymer is important to have a small FMO energy gap, which is necessary for a broader absorption spectrum.Conclusions
We report donor–acceptor conjugated polymers wherein spin manipulation is achieved through careful selection of molecular scaffolds to have a closed-shell low-spin ground-state to an open-shell high-spin ground-state in the pristine form. The monomer units of the BBT-based polymers develop an open-shell character and achieve a pure open-shell character at N = 8. The essential design criteria involve utilizing a BBT acceptor in the polymer backbone to down-shift the LUMO energy level, where the CPDT/CPDS donors up-shift the HOMO level, reducing the HOMO–LUMO energy gap. A small electronic gap admixes the FMOs in the ground-state inducing an open-shell diradical character, whereas the aromatic stabilization energy of the thiadiazole units rapidly increases the diradical character as the number of repeat units is increased. This phenomenon, combined with the large spatial separation between the unpaired electrons, pushes the diradical character to the bond dissociation limit. Consequently, the Coulomb repulsion in the triplet state is decreased, reducing the energy gap between the singlet and triplet states, forming a degenerate state in the large chain-limit. This degeneracy will facilitate magnetic switching from a low-spin ground-state to high-spin ground-state, favoring the triplet multiplicity in the long polymer chain-limit, leading to an intramolecular ferromagnetic exchange coupling between the unpaired spins. However, the iso-BBT-based polymers have a significantly increased ΔEST and HOMO–LUMO energy gap, leading to a closed-shell configuration. This study paves the way towards molecular magnetism based on conjugated polymers without utilizing heavy inorganic elements.Author contributions
NR and MAS conceived and designed the study. MAS performed DFT calculations and analysis. MAS wrote the first draft of the manuscript and made subsequent revisions. MMH developed codes for generating AICD and 2D-ICSS diagrams and generated all the ACID and 2D-ICSS maps and contributed to the development of the first draft. CSS performed all the OT-(S)RSH and orbital overlap calculations and contributed to the development of the first draft. NR supervised the project and revised the manuscript. All the authors approved submission of the manuscript.Conflicts of interest
There is no conflict of interest to declare.Acknowledgements
This work is supported by the National Science Foundation (NSF) under grant no. OIA-1757220. The DFT calculations were performed at the high-performance computing center at Mississippi State University. Also, the Extreme Science and Engineering Discovery Environment (XSEDE) was used, which is supported by NSF grant number ACI-1548562. We acknowledge the Texas Advanced Computing Center (TACC) at the University of Texas at Austin for providing (HPC, Stampede 2 (through XSEDE allocation, TG-CHE140141)) resources that have contributed to the research results reported within this paper. CSS thanks Ryohei Kishi for the helpful discussions.Notes and references
- A. Rajca, Chem. Rev., 1994, 94, 871–893 CrossRef CAS.
- A. Rajca, J. Wongsriratanakul and S. Rajca, Science, 2001, 294, 1503–1505 CrossRef CAS PubMed.
- M. Abe, J. Ye and M. Mishima, Chem. Soc. Rev., 2012, 41, 3808–3820 RSC.
- M. Baumgarten, EPR of Free Radicals in Solids II, Springer, 2012, pp. 205–244 Search PubMed.
- S. Wolf, D. Awschalom, R. Buhrman, J. Daughton, V. S. von Molnár, M. Roukes, A. Y. Chtchelkanova and D. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nanoscience and Technology: A Collection of Reviews from Nature Journals, World Scientific, 2010, pp. 194–201 Search PubMed.
- A. R. Rocha, V. M. Garcia-Suarez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335 CrossRef CAS PubMed.
- S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- R. Gaudenzi, E. Burzuri, D. Reta, I. D. P. Moreira, S. T. Bromley, C. Rovira, J. Veciana and H. S. van der Zant, Nano Lett., 2016, 16, 2066–2071 CrossRef CAS PubMed.
- K. Wang, L. Huang, N. Eedugurala, S. Zhang, M. A. Sabuj, N. Rai, X. Gu, J. D. Azoulay and T. N. Ng, Adv. Energy Mater., 2019, 9, 1902806 CrossRef CAS.
- Y. Yonekuta, K. Susuki, K. Oyaizu, K. Honda and H. Nishide, J. Am. Chem. Soc., 2007, 129, 14128–14129 CrossRef CAS PubMed.
- N. M. Gallagher, A. Olankitwanit and A. Rajca, J. Org. Chem., 2015, 80, 1291–1298 CrossRef CAS PubMed.
- S. Kumar, Y. Kumar, S. K. Keshri and P. Mukhopadhyay, Magnetochemistry, 2016, 2, 42 CrossRef.
- N. M. Gallagher, J. J. Bauer, M. Pink, S. Rajca and A. Rajca, J. Am. Chem. Soc., 2016, 138, 9377–9380 CrossRef CAS PubMed.
- N. Gallagher, H. Zhang, T. Junghoefer, E. Giangrisostomi, R. Ovsyannikov, M. Pink, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2019, 141, 4764–4774 CrossRef CAS PubMed.
- A. E. London, H. Chen, M. Sabuj, J. Tropp, M. Saghayezhian, N. Eedugurala, B. Zhang, Y. Liu, X. Gu, B. Wong, N. Rai and J. Azoulay, Sci. Adv., 2019, 5, eaav2336 CrossRef CAS PubMed.
- T. L. D. Tam, G. Wu, S. W. Chien, S. F. V. Lim, S.-W. Yang and J. Xu, ACS Mater. Lett., 2020, 2, 147–152 CrossRef CAS.
- Z. Zeng, M. Ishida, J. L. Zafra, X. Zhu, Y. M. Sung, N. Bao, R. D. Webster, B. S. Lee, R.-W. Li and W. Zeng, J. Am. Chem. Soc., 2013, 135, 6363–6371 CrossRef CAS PubMed.
- P. Karafiloglou, J. Chem. Educ., 1989, 66, 816 CrossRef CAS.
- L. Huang, N. Eedugurala, A. Benasco, S. Zhang, K. S. Mayer, D. J. Adams, B. Fowler, M. M. Lockart, M. Saghayezhian and H. Tahir, Adv. Funct. Mater., 2020, 30, 1909805 CrossRef CAS.
- T. Y. Gopalakrishna, W. Zeng, X. Lu and J. Wu, Chem. Commun., 2018, 54, 2186–2199 RSC.
- M. A. Sabuj and N. Rai, Mol. Syst. Des. Eng., 2020, 5, 1477–1490 RSC.
- T. Kubo, A. Shimizu, M. Sakamoto, M. Uruichi, K. Yakushi, M. Nakano, D. Shiomi, K. Sato, T. Takui and Y. Morita, Angew. Chem., Int. Ed., 2005, 44, 6564–6568 CrossRef CAS PubMed.
- G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. P. Ortiz, C. J. Gómez-Garca and L. N. Zakharov, Nat. Chem., 2016, 8, 753–759 CrossRef CAS PubMed.
- Z. Sun, Q. Ye, C. Chi and J. Wu, Chem. Soc. Rev., 2012, 41, 7857–7889 RSC.
- J. J. Dressler, M. Teraoka, G. L. Espejo, R. Kishi, S. Takamuku, C. J. Gómez-Garca, L. N. Zakharov, M. Nakano, J. Casado and M. M. Haley, Nat. Chem., 2018, 10, 1134–1140 CrossRef CAS PubMed.
- M. A. Sabuj, PhD thesis, Dave C. Swalm School of Chemical Engineering, 2020.
- Y. Huang and E. Egap, Polym. J., 2018, 50, 603–614 CrossRef CAS.
- J. Su, W. Fan, P. Mutombo, X. Peng, S. Song, M. Ondracek, P. Golub, J. Brabec, L. Veis, M. Telychko and J. Wu, Nano Lett., 2020, 21, 861–867 CrossRef PubMed.
- M. Abe, Chem. Rev., 2013, 113, 7011–7088 CrossRef CAS PubMed.
- R. Ponce Ortiz, J. Casado, V. Hernández, J. T. López Navarrete, P. M. Viruela, E. Ort, K. Takimiya and T. Otsubo, Angew. Chem., Int. Ed., 2007, 46, 9057–9061 CrossRef PubMed.
- M. Bendikov, H. M. Duong, K. Starkey, K. Houk, E. A. Carter and F. Wudl, J. Am. Chem. Soc., 2004, 126, 7416–7417 CrossRef CAS PubMed.
- M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita and K. Müllen, Nature, 2018, 557, 691–695 CrossRef CAS PubMed.
- V. Morozov and E. Tretyakov, J. Mol. Model., 2019, 25, 58 CrossRef PubMed.
- G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Hwang, L. P. Biro and L. Tapaszto, Nature, 2014, 514, 608–611 CrossRef CAS PubMed.
- F. Luis and E. Coronado, Nature, 2018, 557, 645–647 CrossRef CAS PubMed.
- J. Poater, J. M. Bofill, P. Alemany and M. Sola, J. Phys. Chem. A, 2005, 109, 10629–10632 CrossRef CAS PubMed.
- K. Itoh and T. Takui, Proc. Jpn. Acad., Ser. B, 2004, 80, 29–40 CrossRef CAS.
- L. Bianchi, X. Zhang, Z. Chen, P. Chen, X. Zhou, Y. Tang, B. Liu, X. Guo and A. Facchetti, Chem. Mater., 2019, 31, 6519–6529 CrossRef CAS.
- Y. Cui, H. Yao, B. Gao, Y. Qin, S. Zhang, B. Yang, C. He, B. Xu and J. Hou, J. Am. Chem. Soc., 2017, 139, 7302–7309 CrossRef CAS PubMed.
- D. Dang, D. Yu and E. Wang, Adv. Mater., 2019, 1807019 CrossRef PubMed.
- C. Kanimozhi, N. Yaacobi-Gross, K. W. Chou, A. Amassian, T. D. Anthopoulos and S. Patil, J. Am. Chem. Soc., 2012, 134, 16532–16535 CrossRef CAS PubMed.
- Y. Yang, R. T. Farley, T. T. Steckler, S.-H. Eom, J. R. Reynolds, K. S. Schanze and J. Xue, Appl. Phys. Lett., 2008, 93, 388 Search PubMed.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CrossRef CAS.
- H. Bronstein, Z. Chen, R. S. Ashraf, W. Zhang, J. Du, J. R. Durrant, P. Shakya Tuladhar, K. Song, S. E. Watkins and Y. Geerts, J. Am. Chem. Soc., 2011, 133, 3272–3275 CrossRef CAS PubMed.
- R. S. Ashraf, I. Meager, M. Nikolka, M. Kirkus, M. Planells, B. C. Schroeder, S. Holliday, M. Hurhangee, C. B. Nielsen and H. Sirringhaus, J. Am. Chem. Soc., 2015, 137, 1314–1321 CrossRef CAS PubMed.
- T. T. Steckler, X. Zhang, J. Hwang, R. Honeyager, S. Ohira, X.-H. Zhang, A. Grant, S. Ellinger, S. A. Odom and D. Sweat, J. Am. Chem. Soc., 2009, 131, 2824–2826 CrossRef CAS PubMed.
- N. Stutzmann, R. H. Friend and H. Sirringhaus, Science, 2003, 299, 1881–1884 CrossRef CAS PubMed.
- J. D. Yuen, M. Wang, J. Fan, D. Sheberla, M. Kemei, N. Banerji, M. Scarongella, S. Valouch, T. Pho and R. Kumar, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 287–293 CrossRef CAS.
- K. Ono, S. Tanaka and Y. Yamashita, Angew. Chem., Int. Ed. Engl., 1994, 33, 1977–1979 CrossRef.
- T. L. D. Tam, T. Salim, H. Li, F. Zhou, S. G. Mhaisalkar, H. Su, Y. M. Lam and A. C. Grimsdale, J. Mater. Chem., 2012, 22, 18528–18534 RSC.
- A. Thomas, K. Bhanuprakash and K. K. Prasad, J. Phys. Org. Chem., 2011, 24, 821–832 CrossRef CAS.
- Y. Liu, H. Phan, T. S. Herng, T. Y. Gopalakrishna, J. Ding and J. Wu, Chem. – Asian J., 2017, 12, 2177–2182 CrossRef CAS PubMed.
- Z. Zeng, X. Shi, C. Chi, J. T. L. Navarrete, J. Casado and J. Wu, Chem. Soc. Rev., 2015, 44, 6578–6596 RSC.
- W. Zeng, H. Phan, T. S. Herng, T. Y. Gopalakrishna, N. Aratani, Z. Zeng, H. Yamada, J. Ding and J. Wu, Chem, 2017, 2, 81–92 CrossRef CAS PubMed.
- M. A. Sabuj, M. M. Huda and N. Rai, Iscience, 2020, 23, 101675 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision B.01, Gaussian Inc.Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- J. B. Foresman and Æ. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian, Gaussian Inc. Wallingford CT, 3rd edn, 2015 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. N. Intorp, M. Hodecker, M. Müller, O. Tverskoy, M. Rosenkranz, E. Dmitrieva, A. A. Popov, F. Rominger, J. Freudenberg and A. Dreuw, Angew. Chem., Int. Ed., 2020, 132, 12496–12501 CrossRef.
- T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, J. Chem. Phys., 2009, 131, 044108 CrossRef PubMed.
- E. Cho, V. Coropceanu and J.-L. Bredas, J. Chem. Theory Comput., 2020, 16, 3712–3719 CrossRef CAS PubMed.
- T. Stein, H. Eisenberg, L. Kronik and R. Baer, Phys. Rev. Lett., 2010, 105, 266802 CrossRef PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- K. Yamaguchi, Y. Yoshioka and T. Fueno, Chem. Phys. Lett., 1977, 46, 360–365 CrossRef CAS.
- M. Nakano, Chem. Rec., 2017, 17, 27–62 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. v. R. Schleyer, M. Manoharan, Z.-X. Wang, B. Kiran, H. Jiao, R. Puchta and N. J. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468 CrossRef CAS PubMed.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- R. Herges and D. Geuenich, J. Phys. Chem. A, 2001, 105, 3214–3220 CrossRef CAS.
- T. A. Keith and R. F. Bader, Chem. Phys. Lett., 1993, 210, 223–231 CrossRef CAS.
- S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2001, 1893–1898 CAS.
- J. Kruszewski and T. Krygowski, Tetrahedron Lett., 1972, 13, 3839–3842 CrossRef.
- T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420 CrossRef CAS PubMed.
- Z.-G. Zhang and J. Wang, J. Mater. Chem., 2012, 22, 4178–4187 RSC.
- Z. Fei, Y. Han, E. Gann, T. Hodsden, A. S. Chesman, C. R. McNeill, T. D. Anthopoulos and M. Heeney, J. Am. Chem. Soc., 2017, 139, 8552–8561 CrossRef CAS PubMed.
- G. J. Snyder, J. Phys. Chem. A, 2012, 116, 5272–5291 CrossRef CAS.
- X. Su, Z. Xue, G. Li and P. Yu, Nano Lett., 2018, 18, 5744–5751 CrossRef CAS PubMed.
- I. H. Nayyar, E. R. Batista, S. Tretiak, A. Saxena, D. Smith and R. L. Martin, J. Phys. Chem. Lett., 2011, 2, 566–571 CrossRef CAS.
- M. Savarese, E. Bremond, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2020, 16, 3567–3577 CrossRef CAS PubMed.
- Y. Zhang, R. Steyrleuthner and J.-L. Bredas, J. Phys. Chem. C, 2016, 120, 9671–9677 CrossRef CAS.
- J. Kürti and P. Surján, J. Chem. Phys., 1990, 92, 3247–3248 CrossRef.
- T. Ishida and J.-i. Aihara, Phys. Chem. Chem. Phys., 2009, 11, 7197–7201 RSC.
- M. Nakano, Excitation energies and properties of open-shell singlet molecules: applications to a new class of molecules for nonlinear optics and singlet fission, Springer, 2014 Search PubMed.
- E. Clar, The Aromatic Sextet, Wiley, London, 1972 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The electronic properties, MO and spin density plots, bond lengths, NICSiso(1) values, ACID plots, and 2D-ICSS maps are provided. See DOI: 10.1039/d1ma00144b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |