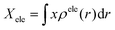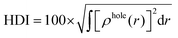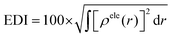Toward the search for new photosensitizers for DSSCs: theoretical study of both substituted Zn(II) and Si(IV) phthalocyanines

Abstract

We report a density functional theory (DFT) study performed for a set of 66 compounds based on zinc(II) and silicon(IV) phthalocyanines (Pcs) with potential applications in dye-sensitized solar cells (DSSCs). The effect of the metal center (Zn, Si), periplanar and axial substituents, and anchor groups like anhydrous, carboxyl, and catechol on the electronic, optical, photovoltaics, and adsorption properties is investigated. Using the TD-DFT methodology and M06 and CAM-B3LYP functionals, we calculated the absorption spectra on optimized structures and in the solution phase but not on structures relaxed in the solvent. We obtained a strong Q band and a weak Soret band in the UV-Vis region, which are attributed to the transitions of type π–π* as described by the Gouterman orbitals. Q bands calculated show absorption up to 667 nm for ZnPcs and up to 769 nm for SiPcs, suggesting an essential role of the metal atom. The systems have a bathochromic effect in the order of secondary amine > primary amine > hydroxyl > amide > ester. We also found that the anhydrous and carboxyl groups favor absorption at longer wavelengths than the catechol group. The ZnPc systems show a slightly larger electron injection ΔG_inj (∼1.1 eV) than SiPcs (∼0.9 eV), with similar values for the three anchor groups. The interaction energies (E_int) between ZnPcs/SiPcs and TiO₂ in molecular and periodic configuration and corrected by the counterpoise method indicate that SiPcs predict more negative values than ZnPcs. The anchor group effect is relevant; the carboxyl moiety leads to stronger interactions than the anhydrous moiety. The strategies used could help to identify new photosensitizers for DSSCs.

---

1. Introduction

In recent years, the world's energy demand has increased due to population growth. Additionally, there has been a rising use of fossil fuels, which generate numerous polluting compounds responsible for the greenhouse effect in the processes of extraction and refining, and especially in their use.^1,2 Because of this, the search for new sources of clean and renewable energy is necessary. One of the most important sources of clean energy is solar energy. In this field, during the last 50 years, different types of photovoltaic devices have been developed to convert solar energy into electrical energy, obtaining different efficiency percentages, 40.8% being the highest so far.^3,4 Different types of cells have been studied, where the first devices were developed based on inorganic compounds such as gallium arsenide,⁵ cadmium sulfide,⁶ cadmium tellurium,⁷ and silicon,^8,9 the latter being the most commercialized. However, producing these cells requires precursors with a high degree of purity, raising their final cost and generating highly polluting waste for the environment. A solution to the problem is the replacement of inorganic with organic precursors, which allows them to be deposited on substrates at lower temperatures, reducing production costs.¹⁰ Some organic molecules, like porphyrins, polymers, and phthalocyanines, possess specific electronic and optical properties that make them especially interesting for photovoltaic devices.^11–13 Additionally, the mixture of these properties with synthesis and favorable working conditions has aroused the scientific community's interest in recent years. These properties are mainly due to their chemical structure, where the alternation of single and double bonds occurs mainly between carbon atoms, which generates high electronic delocalization, leading to greater absorption in the visible region of the electromagnetic spectrum.¹⁴

Recently some organic molecules have been investigated for their potential use in different fields, such as organic light-emitting diodes (OLEDs),¹⁵ dye-sensitized solar cells (DSSCs),¹⁶ electrochromic systems,¹⁷ nonlinear optical materials,^18,19 and photodynamic cancer therapy,²⁰ among many other fields. Due to the environmental problems presented by inorganic analogs, dye-sensitized cells are one of the most interesting applications. These devices were first developed in 1991 by Grätzel and O’Regan.²¹ DSSCs have four main components: a semiconductor, an electrolyte, a counter electrode, and a photoactive dye. The latter is the part that most affects the conversion efficiency; it is here where organic-type dyes are used.²²

Being directly responsible for the conversion efficiency, the dyes must meet specific characteristics for possible use in DSSCs. They must be photostable, have high thermal stability, capture light efficiently, and show strong absorption in the visible region of the electromagnetic spectrum, in addition to optimal synthesis.²³ One organic molecule that fulfills these characteristics is phthalocyanine, a compound with four isoindoline fragments bonded by aza bridges, generating a macrocycle of 16 members with a system of 18π electrons.²⁴ Its main characteristic is the absorption in the visible region, exhibiting two absorptions, a very intense one close to the infrared region called the Q band (600–800 nm) and another one close to the ultraviolet known as the B band or Soret band (300–400 nm).²⁵

Phthalocyanines have electronic transfer ability, high molar absorption coefficients, light absorption in the visible region, and high thermal and chemical stability, among other properties that make them ideal candidates for use in these devices.²⁶ Additionally, these characteristics can be modified by the addition of substituents or introduction of metal ions, either divalent (Zn, Cu, etc.)^27–29 or tetravalent (Si, Ge, etc.).^30–32 However, due to their molecular structure, these compounds have low solubility and a high tendency to form especially H-type aggregates.³³ Fortunately, both of these problems can be solved by adding bulky substituent groups, increasing the solubility and decreasing their aggregation tendency.

To date, numerous studies have been carried out with different metals, with Zn being the most commonly used and giving the best results, mainly due to its longer half-life in the excited state.³⁴ Some of the substituents that have been used are ferulic acid,^26,35 3-pyridin 3-yl proxy,³⁶ diphenyl phenoxy,³⁷ and 2-mercaptoacetic acid.²⁸ Likewise, several studies have been carried out with silicon as the central atom in which different types of alkyl chains have mainly been used as axial-type substituents.^31,38,39 However, the loss of conjugation in the compounds and the use of other anchor groups result in a low percentage of conversion from solar to electrical energy.

Considering the above, the analysis of the electronic, optical, and photovoltaic properties of systems based on divalent and tetravalent phthalocyanines is proposed. Divalent phthalocyanines have zinc as the central atom. They will be asymmetrically tetrasubstituted in a periplanar position, where three of these positions (R₁) are replaced by phenoxy derivatives with electron donor groups such as hydroxyls, primary amines, secondary amines, amides, and esters and the fourth position (R₂) is occupied by an anchor group (anhydrous, carboxyl or catechol). In the case of tetravalent phthalocyanines, silicon is used as the central atom, and due to its tetravalence, the substitutions can occur in the axial position, where one of them is occupied by the phenoxy derivatives, and the remaining position is occupied by the anchor group. The analysis of the effect of substitutions in the axial position with groups that expand the conjugation of the systems is proposed to achieve absorption at a longer wavelength, a charge separation, and an improvement in the photovoltaic properties, all the above looking for better performance in the field of solar cells sensitized by dyes. The proposed systems are presented in Scheme 1.

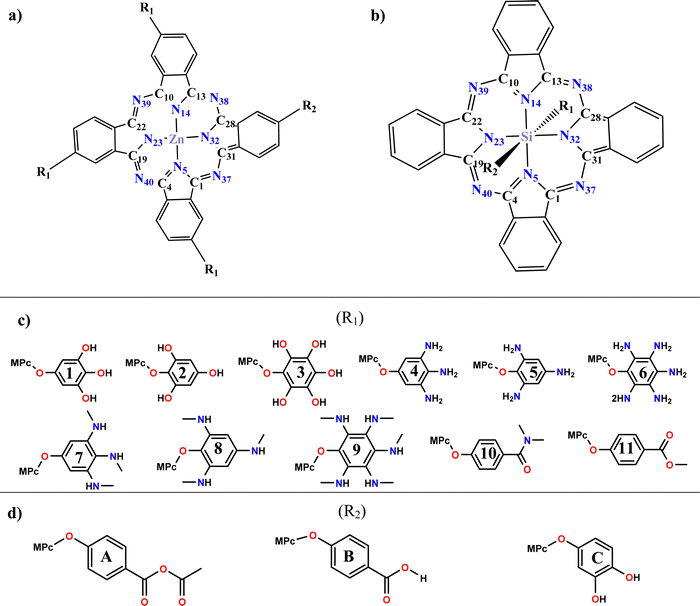Scheme 1 General view of proposed systems: (a) zinc phthalocyanine (ZnPc) (b) silicon phthalocyanine (SiPc) (c) substituents groups (R₁) (d) anchoring groups (R₂).

2. Computational methodology

The molecular structures of both substituted phthalocyanines ZnPc and SiPc (Scheme 1) were fully optimized in the gas phase at the level of density functional theory (DFT). For comparison, we included the unsubstituted ZnPc and SiPc. A hybrid-type functional such as B3LYP^40–42 and a set of Pople basis were used, specifically a double zeta base with p-type polarization orbitals for hydrogen atoms and d-type polarization orbitals for all the other atoms; the previous basis set has the form 6-31G(d,p). Additionally, the dispersion term D3 correction was added.⁴³ This level of theory was chosen since it has been widely used in similar systems, obtaining a good correlation between the experimental and the theoretical studies.^27,44,45 Once the structures were optimized, the vibrational frequencies were calculated to verify whether the system found corresponds to a global minimum of energy, finding positive values at all frequencies. The optimization and vibrational frequency calculations were carried out in the gas phase. The molecular structures of metal phthalocyanines obtained are discussed in Section 1 (S1) in the ESI.†

Once the minimum energy structures were obtained, the analysis of the electronic properties was carried out at the same level as used in the geometry optimization and was calculated in both the gas phase and the solvent phase. To simulate the solvent, a conductor-like polarizable continuum model (CPCM)^46,47 was used, and the solvent tetrahydrofuran (dielectric constant 7.58) was chosen, considering that it is the solvent used in the experimental measurements of the UV-Vis spectra reported. The effect of substituents and the change of the central metal atom (Zn, Si) was analyzed using the energy of the frontier molecular orbitals (HOMO: highest occupied and LUMO: lowest unoccupied molecular orbitals), which give information about the reactivity of the system. Additionally, the charge distribution was revised by the electrostatic potential calculated and the natural population analysis (NPA).⁴⁸ The analysis of the atomic charges of metal phthalocyanines is presented in Section 2 (S2) in the ESI.†

To determine the optical properties of the studied systems, the time-dependent density functional theory (TD-DFT) methodology was used. As TD-DFT is very dependent on the functional used, a benchmark was performed. In this case, the UV-Vis spectra were calculated using functionals that differ in their definition; GGA functionals (PBE^49,50), metaGGA functionals (TPSSh,^51,52 M06,⁵³ M06-2X⁵³), hybrid functionals (B3LYP,^40–42 PBE0⁵⁴) and long-range functionals (CAM-B3LYP) and the basis set 6-31G(d,p). The calculations are performed in the solvent phase under the aforementioned conditions. The analysis of the calculated spectra includes the identification of each excited state (absorption band) in terms of the electronic transitions between molecular orbitals. The excitation wavelength and intensity of each absorption band, as well as the metal and substituent effect on the bands, are studied. We calculated a number of 50 excited states for both substituted phthalocyanines.

On the other hand, to explore the ability of these phthalocyanines to be used in DSSCs, we determine the efficiency of the electron injection from the dye into a semiconductor by calculating the Gibbs free energy (ΔG_inj) by using eqn (1):

ΔG_inj = E_CB − ESOP (1)

where ESOP is the excited state oxidation potential and E_CB is the energy of the conduction band (CB) of the semiconductor in the vacuum. We will use titanium dioxide (TiO₂) as the semiconductor and the −4.2 eV value as the energy of the CB.⁵⁵ The ESOP value is the excited state oxidation potential and is calculated by:

ESOP = (G⁰ − G⁺)_ES ≈ GSOP − E_0–0 = (G⁰ − G⁺)_GS − E_0–0 (2)

In eqn (2), GSOP is the ground state oxidation potential and is obtained through G⁰ and G⁺, which are the total energies of the ground state and the cationic state of the dye, respectively. E_0–0 is the lower singlet–singlet vertical excitation energy corresponding to the lower excited singlet state obtained from the TD-DFT calculations. G⁺ is calculated using the Koopmans approximation, i.e., the cationic state is obtained using the optimized geometry of the ground state.^56,57 Furthermore, ΔG_reg was calculated by eqn (3), where E_redox corresponds to the energy of the redox potential of the electrolyte; in this case, we use I⁻/I₃⁻ (4.8 eV). All the above calculations were carried out using the Gaussian 09 software.⁵⁸

ΔG_reg = GSOP − E_redox (3)

Finally, the adsorption energy (E_ad) of substituted ZnPc and SiPc on TiO₂ was calculated in two ways. The first one was in a molecular configuration; in this case, we use a cluster model of semiconductors, for which the energy of the complex and each of the fragments will be obtained separately, with the Perdew–Burke–Ernzerhof exchange–correlation functional (GGA-PBE),⁴⁹ double ζ polarized basis set, and non-conserving pseudopotentials (PseudoDojo)⁵⁹ (H = 1s¹, C = 2s²p², N = 2s²2p³, O = 2s²2p⁴ Si = 3s²3p² Zn = 3s²3p⁶4s²3d¹⁰ Ti = 3s²3p⁶4s²3d²). Subsequently, in the second one, we use a periodic configuration, where the systems were adsorbed on a surface of titanium dioxide (101) in its anatase form; for this configuration, we use the PBESol functional used for the solid state (GGA-PBESol),⁶⁰ the double ζ polarized basis set, and non-conserving pseudopotentials (PseudoDojo). The geometry used for the fragments is that obtained in the optimization of the complex. The adsorption energy, in both cases, is determined according to eqn (4):

E_int = E_MPc–TiO2 − (E_MPc + E_TiO2) (4)

where E_MPc–TiO2 is the energy of the complex formed by the substituted metal phthalocyanine (ZnPc, SiPc) and the semiconductor and E_MPc and E_TiO2 are the respective fragments. To evaluate the energy cost due to the change in the geometry of both the surface and the system and to evidence the bond between phthalocyanines and the semiconductor, the adsorption energy, or also known as binding energy, was calculated for the systems at the molecular level. This was done through eqn (4) where the energy of the complex is the energy of the adsorbed system on the surface and the energy of its fragments is the energy of the separately optimized systems. In both cases, a single-layer surface of TiO₂ was used, which was made up of the crystallographic structure of anatase (101). In this case, the anatase phase was chosen because it has greater photocatalytic activity than the rutile and brookite phases. This is because it has a larger adsorption surface area and a lower rate of recombination of charge carriers, and the lifetime of the photogenerated electrons is also larger in the anatase phase.⁶¹ On the other hand, the most stable and most exposed phase in the crystal structure of anatase is 101 and represents more than 94% of the surface.⁶²

In the case of the extended configuration, the surface area was made large enough in directions a, b, and c to ensure an empty space of at least 12 Å thus avoiding interaction between continuous cells. For molecular configuration, we employ a cluster of a titanium dioxide surface. We have taken one layer of this structure and considered a size that contains 16 titanium atoms and 34 oxygen atoms, in addition to four hydrogen atoms to saturate oxygen atoms at the edges to preserve the anatase structure (101).⁶³ The cluster being of a single layer has only 5-fold coordinated titanium to oxygen atoms; there are also two types of oxygen atoms, 3-fold-coordinated and 2-fold-coordinated. The calculations of adsorption energies are performed by using the Quantum ATK package.^64,65

Finally, we carried out the electron–hole analysis^66,67 through Multiwfn 3.8 program,⁶⁸ where we obtained different parameters about the hole–electron distribution in the systems. The distance between the centroid of the hole and the electron gives us the charge transfer (CT) length in X/Y/Z. D_index is the total magnitude of CT length.

Dx = |X_ele − X_hole| Dy = |Y_ele − Y_hole| Dz = |Z_ele − Z_hole|

This parameter is calculated through the centroid which can be calculated to reveal the most representative position of the hole and electron distributions. For example, the X-coordinate of the electron's centroid is written as:

The parameter calculated, known as “t_index”, quantifies the degree of separation between the hole and the electron. Here, H_CT represents the average spread of holes and electrons in the direction of charge transfer (CT). A negative t_index value means an absence of substantial separation, while a positive value, with a larger magnitude (>2 Å), indicates the separation between the hole and the electron.

t_index = D_index − H_CT

The overlap between the hole and the electron, denoted as the S_r index, varies from 0 to 1. A value of 1 denotes complete overlap, while 0 indicates no overlap. The functions ρ_hole and ρ_ele, which correspond to the density of holes and electrons, respectively, describe the spatial distribution of holes and electrons across the entire space, where r is a vector of coordinates.

The exciton binding energy (E_Exc) between the hole and the electron can be calculated from the above equation.

The integral value of holes and electrons across the entire space is normalized to 1. The range of values for the hole delocalization index (HDI) and the electron delocalization index (EDI) is between 0 and 100. A lower HDI or EDI value indicates a higher degree of delocalization for the hole or the electron.

3. Results and discussions

3.1 Frontier molecular orbitals

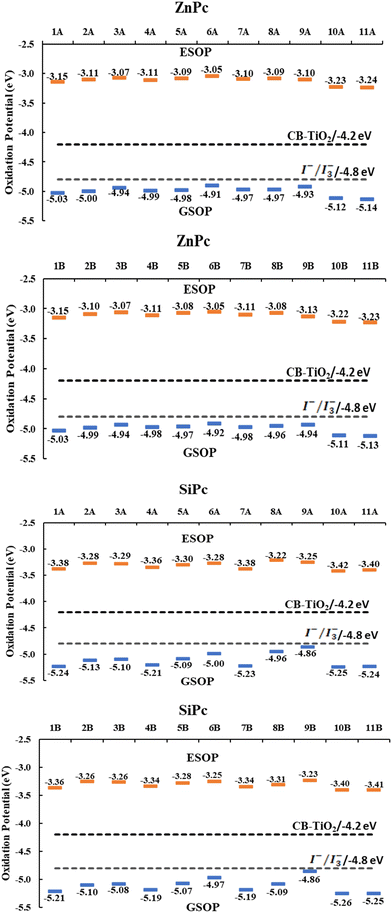
Subsequently, the energy of the frontier molecular orbitals (HOMO, LUMO) and the energy gap were analyzed in both the gas phase and the solution phase. The results for the systems with an anhydrous group (A) for both Pc's in the solution phase are shown in Fig. 1, while the other anchoring groups (B and C) are presented in Fig. S1 (ESI†). For all the structures analyzed (in the gas and solution phases), it was found that the energy values of the LUMOs are higher than that of the conduction band of titanium dioxide (−4.2 eV).^69,70 This means that optimal electron injection from the dye (metal phthalocyanine) into the semiconductor could occur. Additionally, the conduction band (CB) is higher than the energy values of the HOMOs, which ensures injection of the dye into the semiconductor and not the regeneration of the dye by this medium. Finally, in both cases, there is a stabilization of both orbitals in the solution phase compared with the gas phase. However, in general, we found that SiPc presents the lowest LUMO values and, in some cases, the lowest HOMO values than ZnPcs, which in this case generates a smaller difference between H–L in the SiPc.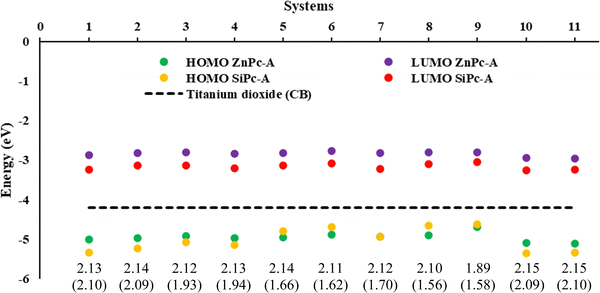

Fig. 1 Energies (eV) of the frontier molecular orbitals HOMO and LUMO, and gap H–L of ZnPc and SiPc in parenthesis, at the B3LYP/6-31G (d,p)/D3 level of theory in the solution phase (THF).

We evaluate first the Zn-based systems, where the values obtained for the H–L gaps go from 1.87 to 2.15 eV. It was found that system ZnPc-9, i.e., secondary amine, regardless of the anchor group, is the one with the lowest H–L gap. This decrease in the HOMO–LUMO gap, in this specific system, may be mainly due to the presence of the free electron pair in the nitrogen atom, as well as to conjugation effects with the system. On the other hand, ZnPcs systems 10A, 10B, 11A, 11B, 2C, and 5C, i.e. amide, ester, hydroxy and primary amine respectively, were the ones with the highest H–L gap with values of 2.15 eV.

On the other hand, the H–L gap of SiPcs is in the range of 1.56 to 2.10 eV. In this case, the greatest variations in the energies of the HOMO–LUMO gap are due to the presence of the substituents in the axial position. These modify the electron density of the system and therefore its properties, evidencing these notorious changes compared to zinc systems that have their substitutions in periplanar position. In these systems, the SiPc-8A (anhydrous anchoring group), which also corresponds to the secondary amine, was the one with the lowest gap; however, for the carboxyl (B) and catechol (C) anchor groups, it is the SiPc-9 secondary amine which presents the smallest gap. Likewise, systems SiPc-10 (amide) and SiPc-11 (ester) are the ones with the greatest H–L gap regardless of the anchor group. As can be seen in the results obtained, the lowest H–L gaps were found for systems with secondary amines as substituent groups, followed by primary amines. On the other hand, substituents such as amides and esters exhibit the greatest H–L gap. In all the cases evaluated (Fig. S2, ESI†), the trend obtained was similar.

Another important part of analyzing molecular orbitals is their distribution in the molecule, specifically those closest to the frontier orbitals (HOMO−1, LUMO+1, and LUMO+2). Therefore, Fig. 2 shows the distribution of molecular orbitals for system 9 (secondary amines) with both metal atoms and anhydrous as anchor groups.

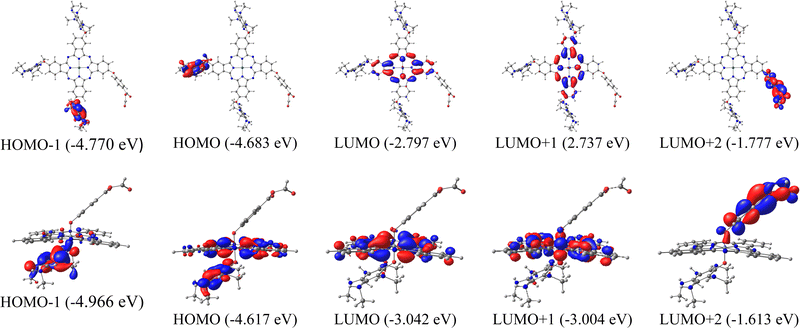Fig. 2 Surfaces of frontier molecular orbitals for 9A (anhydrous anchor group) calculated in the solution phase. Up: Zinc phthalocyanine. Down: Silicon phthalocyanine.

In the systems of ZnPc presented in Fig. 2, the HOMO−1 and HOMO are located in one of the substituents of the system, while the LUMO is located in the phthalocyanine core, this indicates that the HOMO LUMO-type excitations present in the Q bands are mainly due to intramolecular charge transfer. For silicon systems, HOMO−1 is completely located in the substituent, while HOMOs and LUMOs have a high participation of the phthalocyanine macrocycle, which indicates π–π transitions in the Q bands. It is also important to know the orbital where the anchor group is located, which in this case is in the LUMO+2, for both metal atoms, this trend was similar in the systems 9B and 9C (Fig. S2, ESI†). This is important in the field of solar cells since it is necessary that the systems to be used as sensitizers present states of charge separation throughout the system, as is the case of the molecules evaluated. In the other systems analyzed with the three anchor groups, the same trend occurs in the LUMO+2 and LUMO. However, the orbital HOMO appears on the macrocycle.

3.2 Molecular electrostatic potential

Molecular electrostatic potential (MEP) is calculated to provide information on the distribution of charges in the phthalocyanines studied. To facilitate the analysis, MEP is drawn in different colors along the molecule, going from blue, which indicates a positive charge region (electron-poor side), to red, which shows a negative charge region (electron-rich side). Regions with intermediate charge values are represented with green, yellow, and orange. Fig. 3 displays the MEP values for both metal phthalocyanines with an anhydrous anchoring group (A), and Fig. S3 (ESI†) includes the remaining systems with carboxyl (B) and catechol (C).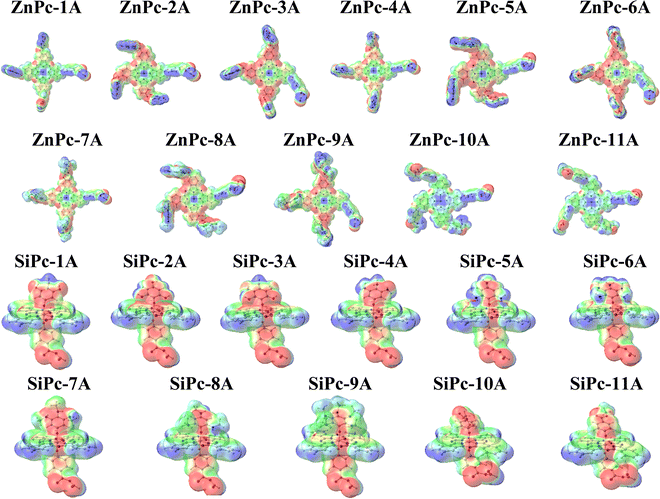

Fig. 3 Surfaces of molecular electrostatic potential mapped into the charge density isosurface of 0.002 electrons per Bohr³ for both MPcs with anhydrous as the anchoring group.

As can be seen in Fig. 3, for ZnPc, there is an electrophilic region in the metal center (blue) as expected and nucleophilic regions (red) in the zones of indole nitrogen atoms, aza bridges, and oxo bridges as expected for the presence of lone pairs in these atoms. This effect is greater for the systems with hydroxy groups (2, 3), primary amines (5, 6), and secondary amines (8, 9) for both systems (Zn, Si) and regardless of the anchor group. Meanwhile, for SiPc, a charge accumulation is observed along the axial substituents.

In addition, a strong nucleophilic region located in the anchor group is observed in the case of the anhydrous group (Fig. 3), which then interacts with the semiconductor; this is necessary as it will be shown in Section 3.5, these systems will be adsorbed on a surface of the semiconductor (TiO₂). Likewise, the results that reflect a concentration of charge in the substituents and in the anchor group demonstrate the high chemical reactivity necessary in the field of solar cells. Although the results shown are for the anhydrous anchoring group, this trend is observed in the same way for the carboxyl and catechol anchoring groups (Fig. S3, ESI†).

For systems without any substitution (Fig. S3, ESI†), charge accumulation can be observed in aza-type nitrogen atoms and a slight accumulation towards the rings of the isoindolic groups, in contrast to systems with substitutions which can be observed a greater accumulation in that area. On the other hand, in silicon systems, a large accumulation of charge can be observed in the chlorine in the axial position, these substitutions extract electron density from the macrocycle increasing its polarizability.

3.3 Electronic absorption spectrum

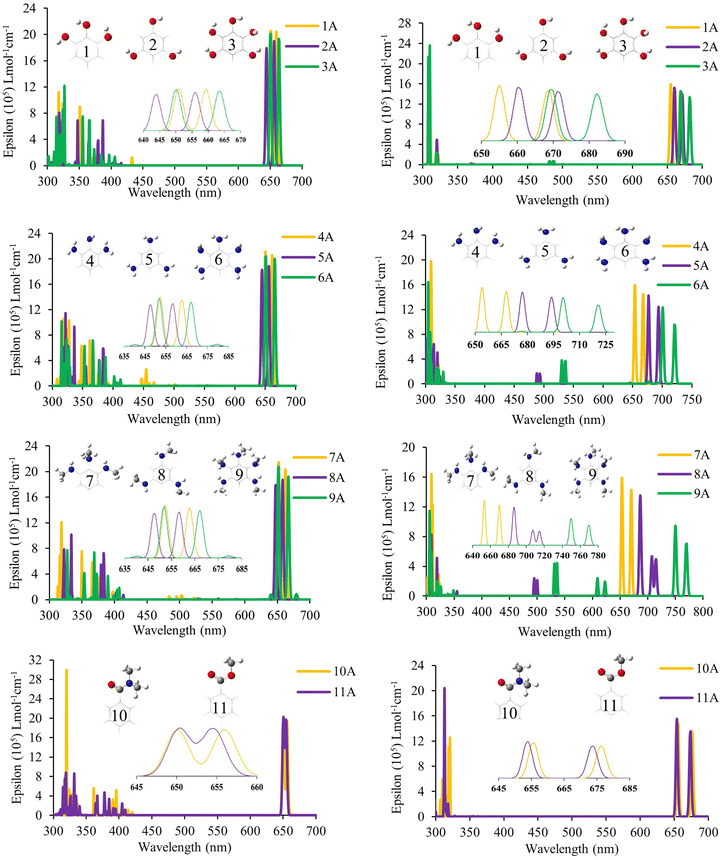
The optical properties were calculated for all systems evaluated through the calculation of the UV-Vis electronic absorption spectra using TD-DFT. Table 1 shows the most important absorptions, and Fig. 4 shows the spectra obtained for systems with anhydrous anchor group (A); the other systems are presented in Fig. S4 (ESI†) for the carboxyl anchor group (B) and Fig. S5 (ESI†) for the catechol anchor group (C). First, it was necessary to perform a search for the optimal function for these spectra, and seven density functionals were evaluated (B3LYP, CAM-B3LYP, M06, TPSSh, M06-2X, PBE, and PBE0). This evaluation was performed on molecules of ZnPc⁷⁰ and SiPc,⁷¹ like those used in this work, and was carried out in order to establish the best functional to describe the optical properties. The evaluation showed that the functional M06 achieves more similar spectra for zinc phthalocyanines with an error of 2.65% (0.05 eV) concerning the experimental spectrum. In contrast, the best functional for silicon phthalocyanines was CAM-B3LYP, with an error of 1.38% (0.02 eV). These deviations are considered very small for TD-DFT calculations, where the accepted error in the literature is 0.2–0.7 eV.^44,57,71,72 Once the functional was selected, the spectra were obtained for each molecule, which showed the typical spectrum of phthalocyanines with a strong band (Q band) in the visible region and a weak band close to the UV region (B band).

Table 1 Main parameters for the absorption of Q bands of ZnPc and SiPc: excitation wavelength (λ) and energy E, oscillator strength (f), and transition between molecular orbitals

Zn-Anh1						Si-Anh1
State	Band	λ/nm	E/eV	f	Transition	State	Band	λ/nm	E/eV	f	Transition
S1	Qx	659.3	1.88	0.761	H → L	S1	Qx	668.6	1.85	0.546	H → L
S2	Qy	650.9	1.9	0.788	H → L+1	S2	Qy	654.9	1.89	0.590	H → L+1
Zn-Anh2						Si-Anh2
S1	Qx	655.9	1.89	0.704	H → L	S1	Qx	671.4	1.85	0.536	H → L
S2	Qy	643.9	1.92	0.674	H → L+1	S2	Qy	660.4	1.88	0.584	H → L+1
Zn-Anh3						Si-Anh3
S1	Qx	663.5	1.87	0.74	H → L	S1	Qx	682.2	1.82	0.501	H → L
S2	Qy	650.1	1.91	0.768	H → L+1	S2	Qy	669.4	1.85	0.562	H → L+1
Zn-Anh4						Si-Anh4
S1	Qx	661.3	1.87	0.763	H → L	S1	Qx	667.8	1.86	0.539	H → L
S2	Qy	650.3	1.91	0.792	H → L+1	S2	Qy	653.9	1.9	0.591	H → L+1
Zn-Anh5						Si-Anh5
S1	Qx	655.9	1.89	0.699	H → L	S1	Qx	693.9	1.79	0.462	H → L
S2	Qy	644.6	1.92	0.684	H → L+1	S2	Qy	677.1	1.83	0.529	H → L+1
Zn-Anh6						Si-Anh6
S1	Qx	665.7	1.86	0.743	H → L	S1	Qx	720.8	1.72	0.367	H → L
S2	Qy	650.8	1.9	0.777	H → L+1	S2	Qy	700.6	1.77	0.457	H → L+1
Zn-Anh7						Si-Anh7
S1	Qx	662.6	1.87	0.763	H → L	S1	Qx	669.9	1.85	0.531	H → L
S2	Qy	652.2	1.9	0.807	H → L+1	S2	Qy	653.1	1.9	0.59	H → L+1
Zn-Anh8						Si-Anh8
S1	Qx	658.2	1.88	0.700	H → L	S1	Qx	714.4	1.73	0.187	H → L
S2	Qy	647.6	1.91	0.686	H → L+1	S2	Qy	707.1	1.75	0.198	H → L+1
Zn-Anh9						Si-Anh9
S2	Qy	667.1	1.86	0.788	H−1 → L	S1	Qx	769.5	1.61	0.268	H → L
S3	Qx	651.8	1.90	0.779	H−1 → L+1	S2	Qy	749.8	1.65	0.352	H→ L+1
Zn-Anh10						Si-Anh10
S1	Qx	655.9	1.89	0.724	H → L	S1	Qx	676.2	1.83	0.509	H → L
S2	Qy	650.1	1.91	0.724	H → L+1	S2	Qy	655.5	1.89	0.573	H → L+1
Zn-Anh11						Si-Anh11
S1	Qx	654.6	1.89	0.740	H → L	S1	Qx	673.6	1.84	0.515	H → L
S2	Qy	650.3	1.91	0.742	H → L+1	S2	Qy	653.8	1.89	0.58	H → L+1

---

Fig. 4 UV-Vis spectra calculated with TD-DFT both with the anhydrous group as the anchoring group. An enlargement of the Q-band region is included in the center of the figure. Left: ZnPc. Right: SiPc.

In all cases, the phthalocyanines have two separate absorption peaks in the visible region (Q and Soret). For this analysis, we focus on the absorption of the lowest energy, which is denominated Q bands, as can be seen in Table 1. These bands are attributed to the transitions of type π–π* and are described by the Gouterman orbitals, HOMO, LUMO, HOMO−1 and LUMO+1,^73–76 which, as previously observed in Fig. 2, are found mainly in the phthalocyanine nucleus, as expected in this type of compounds. In the case of Soret bands, because they present contributions from different molecular orbitals, it is necessary to evaluate them through the natural transition orbital (NTO) calculations to better describe the transitions involved. In the case of ZnPc, the Q band appears between 654 nm and 684 nm; the highest values of absorption of all series correspond to 9A, 9B, and 9C, which correspond to the systems with a secondary amine in all positions, with values of 667, 684, and 665 nm, respectively. Analyzing each of the series, it was found that 3A, 6A and, 9A (663, 665 and 667 nm, respectively) and 3B, 6B, and 9B (663, 664, and 684 nm, respectively) are the ones with the highest bathochromic displacement within each of their families. These systems have a complete substitution pattern (ortho, meta, and para) generating a greater presence of electrons and therefore exhibiting a red shift. In the case of ZnPc without substituents, the maximum absorption was 641 nm, which was lower than that of any system evaluated, which shows the role of substituents in bathochromic displacement.

Meanwhile, for SiPc, there is a shifting of up to 102 nm compared to their zinc analogs. This great bathochromic effect present in silicon systems is due to the greater dipole moment present in these systems due to the axial position of their substituents, as well as steric effects can cause a greater number of intramolecular interactions that affect both their electronic and optical properties. Likewise, systems 6 (primary amine) and, 9 (secondary amine) have the highest red shift in all three anchor groups. However, there is a decrease in the oscillator strength for these systems, which would affect their light harvesting efficiency (LHE). Since it is defined approximately as LHE = 1 − 10^−f, where f is the strength of the oscillator,^77,78 this parameter is important when evaluating the potential use of a dye in the field of solar cells. The greatest bathochromic effect was for 9 with both central atoms (Zn and Si) and all anchor groups; in the case of zinc, it reached 667 (9A) 684 nm (9B) and 665 (9C) nm, while in the silicon-based system, the greatest absorption was found at 769 (9A), 760 (9B) and 756 (9C) nm. These systems correspond to the secondary amine substituent, which has a strong resonant effect on donating electrons to the macrocycle. The unsubstituted SiPcCl₂ that corresponds to the commercial compound has a value of 675 nm for the Q band, which in general has a lower wavelength than substituted ones, showing the substituent effect on the red-shift.

Overall, with the results obtained, it can be concluded that the systems have a bathochromic effect in the order secondary amine > primary amine > hydroxyl > amide > ester; likewise, systems with central silicon atoms have a greater bathochromic effect than those based on zinc. Finally, the anhydrous and carboxyl groups as the anchoring groups favor the bathochromic effect on the catechol group.

3.4 Photovoltaics properties

Because the results found for the systems with the catechol anchoring group, which are lower than those obtained with the other anchor groups, the results presented from now on were only calculated for the carboxyl and anhydrous groups. The driving forces for the electron injection (ΔG_inj) and regeneration (ΔG_reg) were other properties evaluated in the systems. This property (ΔG_inj) is a good descriptor to measure the efficiency of the electron injection process from the dye (phthalocyanine) to the semiconductor (TiO₂). In the literature, there are different criteria for this descriptor. Some authors suggest that the value of ΔG_inj must be lower by −0.5 eV⁷⁹ related to the energy of the conduction band of TiO₂ to consider the electron injection as an efficient process, while other authors even suggest a value of −0.2 eV.⁸⁰

For the calculation of the mentioned properties, it was necessary to calculate the value of the ground state oxidation potential (GSOP) and the excited state oxidation potential (ESOP) obtained from eqn (2) described before in the Computational Methodology Section. The singlet–singlet vertical excitation energy corresponding to the Q band (E_Q) obtained from the TD-DFT computations was also required. As seen in Tables 2, 3 and Fig. 5, all systems have a ΔG_inj lower than −0.2 eV and −0.5 eV, which suggests an efficient electron injection, and therefore, a conversion of solar energy to electrical energy. These results are very close to each other and show that for zinc phthalocyanines (Tables 2), 3 (hydroxyl) and 6 (primary amine) have higher ΔG_inj values. In addition, no large differences are observed for the two anchoring groups evaluated, carboxyl and anhydrous. Likewise, SiPcs (Table 3) have a lower ΔG_inj than ZnPc, which is mainly due to their lower ESOP values. However, all systems evaluated achieve the values for optimal performance in solar cells (−0.2 or −0.5 eV).

Table 2 Photovoltaics properties (eV) of substituted ZnPc. All values were calculated at the M06/6-31G(d,p) theory level using the CPCM solvent model (THF)

ZnPc	1A	2A	3A	4A	5A	6A	7A	8A	9A	10A	11A
E Q	1.88	1.89	1.87	1.87	1.89	1.86	1.87	1.88	1.82	1.89	1.89
GSOP	−5.03	−5.00	−4.94	−4.99	−4.98	−4.91	−4.97	−4.97	−4.93	−5.12	−5.14
ESOP	−3.15	−3.11	−3.07	−3.11	−3.09	−3.05	−3.10	−3.09	−3.10	−3.23	−3.24
ΔGinj	−1.05	−1.09	−1.13	−1.09	−1.11	−1.15	−1.10	−1.11	−1.10	−0.97	−0.96
ΔGreg	−0.23	−0.20	−0.14	−0.19	−0.18	−0.11	−0.17	−0.17	−0.13	−0.32	−0.34

---

ZnPc	1B	2B	3B	4B	5B	6B	7B	8B	9B	10B	11B
E Q	1.88	1.89	1.87	1.87	1.89	1.87	1.87	1.88	1.81	1.89	1.89
GSOP	−5.03	−4.99	−4.94	−4.98	−4.97	−4.92	−4.98	−4.96	−4.94	−5.11	−5.13
ESOP	−3.15	−3.10	−3.07	−3.11	−3.08	−3.05	−3.11	−3.08	−3.13	−3.22	−3.23
ΔGinj	−1.05	−1.10	−1.13	−1.09	−1.12	−1.15	−1.09	−1.12	−1.07	−0.98	−0.97
ΔGreg	−0.23	−0.19	−0.14	−0.18	−0.17	−0.12	−0.18	−0.16	−0.14	−0.31	−0.33

---

Table 3 Photovoltaic properties (eV) of SiPc. All values were calculated at the CAM-B3LYP/6-31G(d,p) theory level using the CPCM solvent model (solvent THF)

SiPc	1A	2A	3A	4A	5A	6A	7A	8A	9A	10A	11A
E Q	1.85	1.85	1.82	1.86	1.79	1.72	1.85	1.74	1.61	1.83	1.84
GSOP	−5.24	−5.13	−5.10	−5.21	−5.09	−5.00	−5.23	−4.96	−4.86	−5.25	−5.24
ESOP	−3.38	−3.28	−3.29	−3.36	−3.30	−3.28	−3.38	−3.22	−3.25	−3.42	−3.40
ΔGinj	−0.82	−0.92	−0.91	−0.84	−0.90	−0.92	−0.82	−0.98	−0.95	−0.78	−0.80
ΔGreg	−0.44	−0.33	−0.30	−0.41	−0.29	−0.20	−0.43	−0.16	−0.06	−0.45	−0.44

---

SiPc	1B	2B	3B	4B	5B	6B	7B	8B	9B	10B	11B
E Q	1.85	1.85	1.82	1.85	1.79	1.72	1.84	1.78	1.63	1.85	1.85
GSOP	−5.21	−5.10	−5.08	−5.19	−5.07	−4.97	−5.19	−5.09	−4.86	−5.26	−5.25
ESOP	−3.36	−3.26	−3.26	−3.34	−3.28	−3.25	−3.34	−3.31	−3.23	−3.40	−3.41
ΔGinj	−0.84	−0.94	−0.94	−0.86	−0.92	−0.95	−0.86	−0.89	−0.97	−0.80	−0.79
ΔGreg	−0.41	−0.30	−0.28	−0.39	−0.27	−0.17	−0.39	−0.29	−0.06	−0.46	−0.45

---

Fig. 5 GSOP and ESOP values of the systems compared with the conduction band of TiO₂ and the oxidation potential of the I⁻/I₃⁻ redox mediator.

Additionally, all systems have an ESOP higher than the conduction band of the semiconductor and a GSOP lower than the oxidation potential of the I⁻/I₃⁻ redox mediator, which points to optimal electron injection and regeneration of the ground state of phthalocyanine, respectively. Large differences between anchor groups were not found for this property. Finally, it is interesting to highlight the values found for systems with substituents amide (10) and ester (11) since both metal atoms have higher values of ΔG_reg. This is mainly due to their low values of ESOP and GSOP compared to the other systems evaluated; however, for this same reason, these systems are those with a lower ΔG_inj.

3.5 Interaction of metal phthalocyanine on TiO₂

The present work also proposes the study of the interaction of metal phthalocyanines on a semiconductor. Different semiconductors have been studied in the field of dye-sensitized solar cells. The most used is the titanium dioxide (TiO₂). This semiconductor is found in nature in three different forms (anatase, rutile, and brookite), with the anatase type being the most widely used in this field.^44,81–83 We analyze the interaction energy of phthalocyanines on the semiconductor in two ways, and in both, we use the same crystallographic structure of anatase (101). The first corresponds to an extended configuration (bulk) and the second to a molecular configuration; both were performed considering the basis set superposition error (BBSE) through the counterpoise method. The latter was done to compare the behavior in the different configurations. During the bulk simulation, we experimented with different k-points, such as 2 × 2 × 2 and 3 × 3 × 3. However, the results obtained in terms of total energy remained constant. Therefore, we decided to use the lowest k-points to perform a quicker and more cost-effective calculation, considering the size of the surface and the adsorbed systems. All calculations performed in this section, whether with extended and molecular configuration, do not include solvent corrections.

We also tested the slab thickness of TiO₂ and its effect on properties such as energy band gap, density of states and interaction energies. The discussion of the results obtained is presented in the ESI† and Table S2. We investigated one, two and three layers of TiO₂ for a bulk configuration. We found that the changes in the mentioned properties are negligible. Based on that, we evaluated the computational cost and chose the surface with a single layer to decrease the number of atoms. For molecular configuration, we employ a cluster of a titanium dioxide surface (Fig. 6), which is made up of the crystallographic structure of anatase (101). We have taken one layer of this structure and considered a size that contains 16 titanium atoms and 34 oxygen atoms, in addition to four hydrogen atoms, to saturate oxygens at the edges to preserve the anatase structure (101).⁶³ Likewise, this cluster has a HOMO–LUMO gap of 3.3 eV calculated at the TB09LDA/PseudoDojo/double-ζ-polarized theory level close to the 3.2 eV obtained experimentally.⁸⁴ We have used the previously optimized structure for TiO₂ calculated with PBEsol. This result confirms that the cluster used is a good model for simulating the semiconductor TiO₂.

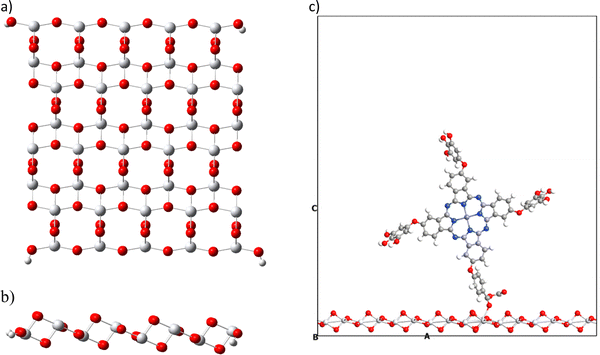Fig. 6 Molecular structure of titanium dioxide in the anatase form (101): (a) molecular top view, (b) molecular side view and (c) extended system with the vacuum space used.

The values for the adsorption and interaction energy (E_int) are calculated by eqn (4) and shown in Table 4 and Table S1 (ESI†). For the interaction energy, the energy of the fragments MPc and TiO₂ is calculated with the optimized geometry obtained in the complex MPc-TiO₂. The adsorption energy was calculated to ensure the junction between the system and the surface and serves to take into account the change in the geometry of the systems after adsorption, for which the energy of the fragments was the energy for the isolated optimized molecules. The results of the adsorption energy are shown in Table S1 (ESI†) and the trend was similar to that of the interaction energy, where negative adsorption energies were found indicating favorable adsorption processes on the surface. The interaction energy was corrected by the basis set superposition error (BSSE) through the counterpoise method.⁸⁵ Thus, E_CP is the corrected interaction energy. As seen in both phthalocyanines, there is a lower interaction energy for the systems evaluated with carboxyl (B) as the anchoring group than in the anhydrous moiety. This can be explained in general due to the distances up to 0.16 Å shorter in the case of carboxyl groups than the anhydrous group (A). Additionally, in the case of systems with anhydrous groups, values of similar energies were found in both metal atoms.

Table 4 Interaction energies (E_ad/eV) and corrected interaction energies (E_CP/eV) by the counterpoise method for ZnPc and SiPc with anhydrous (A) and carboxyl (B) anchor groups adsorbed on TiO₂ calculated for a periodic configuration. Values in parenthesis are calculated for a molecular configuration. Distances of oxygen–titanium (r_O–Ti/Å) are also included

ZnPc	1A	2A	3A	4A	5A	6A	7A	8A	9A	10A	11A
r O–Ti; distance between the oxygen atom from the anchor group and the titanium atom from the surface.
E int	−1.116 (−1.482)	−1.606 (−1.367)	−1.310 (−1.440)	−1.577 (−1.447)	−1.253 (−1.524)	−1.450 (−1.729)	−1.279 (−1.595)	−1.380 (−1.639)	−1.660 (−1.891)	−1.513 (−1.616)	−1.324 (−1.339)
E CP	−0.947 (−1.265)	−1.377 (−1.169)	−1.135 (−1.243)	−1.376 (−1.258)	−1.088 (−1.326)	−1.263 (−1.512)	−1.125 (−1.383)	−1.216 (−1.442)	−1.483 (−1.669)	−1.283 (−1.392)	−1.100 (−1.158)
r O–Ti	2.17 (2.25)	2.24 (2.21)	2.15 (2.21)	2.23 (2.23)	2.15 (2.22)	2.14 (2.23)	2.19 (2.21)	2.18 (2.22)	2.19 (2.22)	2.22 (2.18)	2.18 (2.24)

---

ZnPc	1B	2B	3B	4B	5B	6B	7B	8B	9B	10B	11B
E int	−7.156 (−4.522)	−6.433 (−3.940)	−10.117 (−3.890)	−7.337 (−3.813)	−7.648 (−3.813)	−7.796 (−3.992)	−7.567 (−4.381)	−7.839 (−3.891)	−7.535 (−3.994)	−7.615 (−3.973)	−7.500 (−3.979)
E CP	−6.958 (−4.348)	−6.253 (−3.763)	−9.853 (−3.714)	−7.007 (3.661)	−7.451 (−3.659)	−7.597 (−3.838)	−7.372 (−4.207)	−7.641 (−3.738)	−7.338 (−3.823)	−7.412 (−3.814)	−7.302 (−3.819)
r O–Ti	2.06 (2.03)	2.09 (1.86)	2.08 (1.87)	2.07 (1.96)	2.06 (1.86)	2.09 (1.89)	2.05 (2.03)	2.04 (1.87)	2.08 (1.88)	2.07 (1.86)	2.07 (1.86)

---

SiPc	1A	2A	3A	4A	5A	6A	7A	8A	9A	10A	11A
E int	−1.291 (−2.102)	−1.203 (−2.264)	−1.255 (−2.128)	−1.289 (−2.078)	−1.312 (−2.444)	−1.397 (−2.502)	−1.206 (−2.065)	−1.250 (−2.161)	−1.377 (−1.907)	−1.222 (−2.206)	−1.207 (−2.046)
E CP	−1.113 (−1.795)	−1.050 (−1.946)	−1.109 (−1.824)	−1.141 (−1.790)	−1.142 (−2.122)	−1.245 (−2.195)	−1.059 (−1.777)	−1.103 (−1.878)	−1.226 (−1.676)	−1.035 (−1.904)	−1.010 (−1.794)
r O–Ti	2.15 (2.18)	2.16 (2.19)	2.20 (2.21)	2.20 (2.22)	2.23 (2.21)	2.20 (2.23)	2.21 (2.19)	2.21 (2.21)	2.16 (2.20)	2.14 (2.18)	2.15 (2.23)

---

SiPc	1B	2B	3B	4B	5B	6B	7B	8B	9B	10B	11B
E int	−8.581 (−4.911)	−8.287 (−4.681)	−8.501 (−4.633)	−8.406 (−4.518)	−8.381 (−4.836)	−9.243 (−4.555)	−8.347 (−4.576)	−8.447 (−4.641)	−8.425 (−4.590)	−8.663 (−4.765)	−8.584 (−4.610)
E CP	−8.330 (−4.631)	−8.033 (−4.432)	−8.248 (−4.391)	−8.151 (−4.301)	−8.129 (−4.573)	−8.715 (−4.325)	−8.094 (−4.339)	−8.195 (−4.415)	−8.166 (−4.394)	−4.427 (−4.509)	−8.327 (−4.887)
r O–Ti	2.19 (1.86)	2.02 (1.83)	2.16 (1.84)	2.20 (1.86)	2.20 (1.87)	2.20 (1.85)	2.18 (1.84)	2.19 (1.85)	2.18 (1.98)	2.19 (1.85)	2.19 (1.83)

---

However, in the case of the carboxyl group, lower interaction energies were found for SiPcs obtaining values up to 1.78 eV lower than for ZnPcs, as it is the case of 2, mainly because this system is the one with the lowest interaction distance with the surface (2.02 Å). Table 4 shows that slightly shorter interaction distances were found for systems with carboxyl groups and more negative interaction energies. Therefore, the results suggest that the carboxyl group will interact more with the semiconductor than the anhydrous group. However, the negative values obtained for the anhydrous group also show that the interaction between the systems and the semiconductor is possible.

In general, lower interaction energies were found in the molecular configuration for systems with an anhydrous anchor group, with both silicon and zinc atoms. Additionally, interaction distances smaller than those corresponding at the molecular level were found in the bulk configuration. Likewise, the basis set superposition error, corrected by the counterpoise method, is around 0.2 eV.

On the other hand, the systems with the carboxyl group as the anchor group have interaction energies much lower than those of their anhydrous analogs. A large difference is observed between the molecular and bulk configurations in these systems. However, the trend was the same, where systems with amino groups (6–9) generally have lower interaction energies than the other groups evaluated. Regarding the effect of the substituent groups, no major differences were found. However, it can be established that the hydroxyl groups (1–3) generate lower interaction energies than the primary and secondary amine groups (secondary amine > primary amine > hydroxyl). Likewise, the interaction energies found for the hydroxyl groups are very similar to those reported for amides (10) and esters (11).

The above analysis shows that carboxyl as anchor groups generate more negative interaction energies independent of the method used (bulk, molecular) and the central atom (Zn, Si). It can also be inferred that amino groups help to further decrease the interaction energies between phthalocyanines and the surface of the semiconductor.

Fig. 7 shows the frontier molecular orbitals for system 9 for both metal atoms and for the anhydrous and carboxyl anchoring groups. As can be seen, in the silicon system the HOMO is strongly delocalized between the substituents and the phthalocyanine core, this trend was the same independently of the substituent evaluated and the anchoring group used (Fig. S6, ESI†). On the other hand, in the zinc phthalocyanines, the HOMO is strongly localized in the substituents; however, in the system with hydroxyl as a substituent, the HOMO is located on the phthalocyanine core. This can be explained by the strong donor character of the amine substituent. Finally, we found that in both cases, the LUMOs are delocalized on the TiO₂ surface. This trend suggests a strong interaction between the two phthalocyanines and the surface of the semiconductor with both anchoring groups, indicating that both carboxyl and anhydrous generate a strong interaction with the semiconductor.

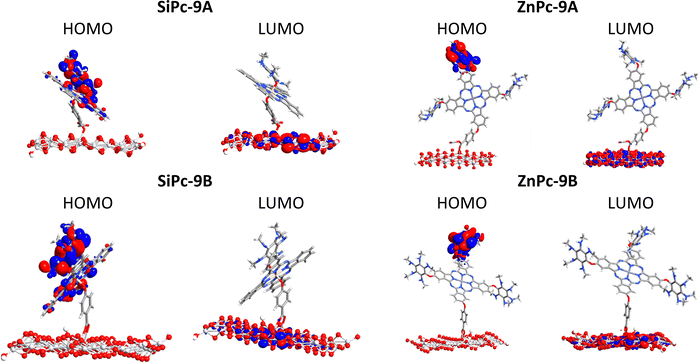Fig. 7 Surfaces of the frontier molecular orbitals calculated for the interaction dye-TiO₂ with an anhydrous group (top) and a carboxyl group (bottom).

3.6 Electron–hole analysis

The analysis of the distribution of holes and electrons in each system can be characterized quantitatively in different ways. This analysis is quite useful when it comes to identifying the type of electron excitations present in the systems evaluated. Tables 5 and 6 present some of the most well-known and commonly used parameters to carry out this type of analysis. First, the hole delocalization index (HDI) and electron delocalization index (EDI) were calculated. In terms of values, it is known that the lower the value, the greater the degree of delocalization throughout the system. As can be seen in all the systems evaluated, similar values were found, ranging from 4.80 to 9.82, which indicates a high delocalization throughout the systems. Likewise, the S_r index allows us to know the overlapping extent of the hole and the electron. This parameter (S_r) reports values in the range between 0 and 1, where 1 indicates complete overlap and 0 indicates no overlap. Regarding the values found for the systems, it can be observed that zinc systems have low values of the S_r index, which indicates a very low overlap and even close to non-existent overlap, the opposite is the case in silicon systems that have values ranging from 0.06 to 0.785.

Table 5 Hole–electron excitation analysis for the first five excited states of ZnPc's absorbed into the TiO₂ surface in the THF solvent calculated at M06/6-31G(d,p)

ZnPc-3A							ZnPc-6A
Excited state	D (Å)	S r (a.u.)	t (Å)	E exc (eV)	HDI	EDI	Excited state	D (Å)	S r (a.u.)	t (Å)	E exc (eV)	HDI	EDI
ES1	14.65	0.012	12.33	0.925	5.02	6.05	ES1	14.82	0.007	12.33	0.887	4.98	5.42
ES2	15.19	0.009	12.65	0.885	5.00	5.81	ES2	11.80	0.001	9.88	1.139	9.64	6.01
ES3	14.85	0.005	12.47	0.859	4.97	4.84	ES3	11.74	0.002	9.76	1.162	9.65	6.05
ES4	14.76	0.009	12.39	0.906	4.96	7.29	ES4	15.28	0.005	12.44	0.853	4.96	5.37
ES5	16.11	0.006	13.88	0.856	4.93	8.87	ES5	21.77	0.0004	19.87	0.644	9.82	5.52

---

ZnPc-9A
Excited state	D (Å)	S r (a.u.)	t (Å)	E exc (eV)	HDI	EDI
ES1	12.87	0.0012	10.83	1.093	9.13	6.29
ES2	24.18	0.0005	22.70	0.572	8.08	6.02
ES3	14.77	0.0009	12.26	0.930	8.92	5.90
ES4	24.35	0.0004	22.85	0.562	8.07	5.65
ES5	13.31	0.0009	10.95	0.986	8.88	5.51

---

Table 6 Hole–electron excitation analysis for the first five excited states of SiPc's absorbed into TiO₂ surface in the THF solvent calculated at Cam-B3LYP/6-31G(d,p)

SiPc-3A							SiPc-6A
Excited state	D (Å)	S r (a.u.)	t (Å)	E exc (eV)	HDI	EDI	Excited state	D (Å)	S r (a.u.)	t (Å)	E exc (eV)	HDI	EDI
ES1	0.46	0.719	−1.80	3.090	4.81	5.48	ES1	2.68	0.481	0.37	3.129	6.17	5.54
ES2	0.30	0.785	−1.89	3.297	4.84	5.39	ES2	2.28	0.607	−0.02	3.257	6.12	5.44
ES3	3.87	0.279	1.90	2.765	7.95	5.49	ES3	3.55	0.252	1.67	3.044	8.12	5.42
ES4	3.64	0.327	1.71	3.000	8.13	5.45	ES4	4.01	0.272	2.11	2.810	7.92	5.33
ES5	8.54	0.061	6.17	1.434	4.80	6.30	ES5	1.19	0.668	−1.16	2.972	4.12	5.32

---

SiPc-9A
Excited state	D (Å)	S r (a.u.)	t (Å)	E exc (eV)	HDI	EDI
ES1	2.28	0.547	0.06	3.149	5.78	5.57
ES2	2.35	0.565	0.24	3.195	6.45	5.30
ES3	2.68	0.431	0.71	3.094	7.41	5.04
ES4	3.01	0.433	0.95	3.061	7.18	5.36
ES5	2.13	0.575	−0.22	2.962	5.20	5.38

---

This trend can be corroborated through t_index and D_index. First, D_index gives the total magnitude of the charge transfer (CT) length, while t_index is a measure of the degree of separation of the hole and the electron in the CT direction. These two parameters, unlike the S_r index, give us information about the separation between the hole and the electron. As can be seen, zinc-based systems have higher values in both indices compared to silicon systems. In all cases, zinc systems had values higher than 2 Å in t_index, which indicates a unidirectional charge transfer excitation, while in the case of silicon, most of the states evaluated had values lower than 2 Å or even negative values, indicating that the hole and the electron are not substantially separated. i.e. the hole and electron occupy similar spatial regions. Finally, about the substituents evaluated, it can be observed that, in the case of zinc systems, system 9 corresponding to secondary amines presents a higher t_index value, specifically in states 2 and 4. This is mainly due to the greater donor capacity of these substituents compared to those present in systems 3 (hydroxyl) and 6 (primary amine).

On the other hand, the exciton energy (E_exc) was calculated, which is the binding energy of the exciton reflecting the energy needed to dissociate the pair of coulombically bonded electron holes into two free charge carriers. In the case of exciton energy, low values are sought since it induces a greater separation of charges and prevents the recombination of the charges generated; likewise, it generates a high mobility of charges which is quite useful, particularly in the field of solar cells. In the same sense, low exciton energy values lead to states of charge transfer, so it can be observed that zinc-based systems have low energies ranging from 0.562 eV to 1.162 eV and that, as mentioned above, they have a notable separation between the hole and the electron. In the case of silicon, they have higher exciton energies of up to 3297 eV, which leads to low charge separation and generates local excitations.

4. Conclusions

A theoretical study using density functional theory (DFT) was performed to investigate the electronic, optical, photovoltaics, and adsorption properties of a set of zinc(II) and silicon(IV) phthalocyanines (Pcs) (66 compounds). We aim to analyze different compounds that could be applied in dye-sensitized solar cells (DSSCs). Three types of effects were studied: the effect of the metal center (Zn, Si), both periplanar and axial substituents, and anchor groups like anhydrous (A), carboxyl (B), and catechol (C).

UV-Vis spectra show a greater red shift of the silicon phthalocyanine compounds than the zinc phthalocyanines. The longer wavelength corresponding to the Q band was obtained with secondary amine as a substituent and anhydrous anchor group (769 nm, SiPc-9,A). In contrast, in their zinc analogs, a longer wavelength was obtained for secondary amines and carboxyl groups (684 nm, ZnPc-9B). Compounds with catechol as an anchor group predict slightly lower values (756 nm, SiPc-9C, and 665 nm, ZnPc-9C). The results obtained could be explained by the fact that the secondary amine has a strong resonant effect on the donation of electrons to the macrocycle, favoring the red shift of Q bands of the type π → π*.

ΔG_inj values show that all compounds could present an efficient electron injection and, therefore, a possible conversion of solar energy into electrical energy because the value of this parameter is higher than 0.2 eV concerning the conduction band of the semiconductor TiO₂. Additionally, all systems have a GSOP lower than the oxidation potential of the I⁻/I₃⁻ redox mediator, which indicates an optimal regeneration of the ground state of metal phthalocyanine. Large differences between anchor groups were not found for this property.

For all compounds studied, the interaction energies between metal phthalocyanine and the semiconductor TiO₂ show a favorable interaction reflected in the negative values for this energy, which suggests that the adsorption of these systems on the semiconductor would be possible. This interaction is favored in the case of systems with amino groups and carboxyl anchor groups.

Zinc-based systems exhibit higher charge separation states compared to silicon systems, mainly due to their low exciton energy values, which generate high charge mobility in these systems.

It can be concluded that systems with amino substituent groups, both primary and secondary have better electronic and optical properties than systems with hydroxyl, amide, and ester groups. Likewise, it is possible to establish that the carboxyl group interacts better with titanium dioxide than the other anchor groups. This is important because it is the main semiconductor for dye-sensitized solar cells. However, all the systems evaluated have the necessary characteristics and properties to be implemented in the field of solar cells.

Author contributions

Michael Zambrano-Angulo: design, writing initial draft, and theoretical calculations. Gloria Cárdenas-Jirón: design, project administration, writing the initial draft, revision of final version, and submission.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We thank the financial support of ANID/Chile under the Project FONDECYT 1221072 (G. C.-J.) and the Program/Doctorado Becas Nacionales 2021/21210406 (M. Z.-A). Powered@NLHPC: This research was partially supported by the NLHPC (ECM-02) supercomputing infrastructure of the Universidad de Chile.

References

1. R. K. Pachauri, M. R. Allen, V. R. Barros, J. Broome, W. Cramer, R. Christ, J. A. Church, L. Clarke, Q. Dahe and P. Dasgupta, Climate change 2014: synthesis report. Contribution of Working Groups I, II and III to the fifth assessment report of the Intergovernmental Panel on Climate Change, Ipcc, 2014.
2. U. Berardi, Resour., Conserv. Recycl., 2017, 123, 230–241.
3. M. Hosenuzzaman, N. A. Rahim, J. Selvaraj, M. Hasanuzzaman, A. B. M. A. Malek and A. Nahar, Renewable Sustainable Energy Rev., 2015, 41, 284–297.
4. M. Tao, J. Electrochem. Soc., 2008, 17, 30.
5. J. A. Luceño-Sánchez, A. M. Díez-Pascual and R. Peña Capilla, Int. J. Mol. Sci., 2019, 20, 976.
6. M. Marandi and N. Torabi, Opt. Mater., 2020, 105, 109918.
7. A. Hu, J. Zhou, P. Zhou, X. Wu and D. Yang, Sol. Energy Mater., 2020, 214, 110595.
8. R. Cariou, J. Benick, F. Feldmann, O. Höhn, H. Hauser, P. Beutel, N. Razek, M. Wimplinger, B. Bläsi, D. Lackner, M. Hermle, G. Siefer, S. W. Glunz, A. W. Bett and F. Dimroth, Nat. Energy, 2018, 3, 326–333.
9. L. C. Andreani, A. Bozzola, P. Kowalczewski, M. Liscidini and L. Redorici, Adv. Phys.: X, 2019, 4, 1548305.
10. Y. Li, G. Xu, C. Cui and Y. Li, Adv. Energy Mater., 2018, 8, 1701791.
11. J. Miao, B. Meng, J. Liu and L. Wang, Chem. Commun., 2018, 54, 303–306.
12. Y. Wang, J. Lee, X. Hou, C. Labanti, J. Yan, E. Mazzolini, A. Parhar, J. Nelson, J. S. Kim and Z. Li, Adv. Energy Mater., 2021, 11, 2003002.
13. R. Zhou, Z. Jiang, C. Yang, J. Yu, J. Feng, M. A. Adil, D. Deng, W. Zou, J. Zhang, K. Lu, W. Ma, F. Gao and Z. Wei, Nat. Commun., 2019, 10, 5393.
14. P. P. Manousiadis, K. Yoshida, G. A. Turnbull and I. D. Samuel, Philos. Trans. R. Soc., A, 2020, 378, 20190186.
15. X. Zhang, H. Dong and W. Hu, J. Adv. Mater., 2018, 30, 1801048.
16. M. G. Walter, A. B. Rudine and C. C. Wamser, J. Porphyrins Phthalocyanines, 2010, 14, 759–792.
17. Y. Shirota, J. Mater. Chem., 2000, 10, 1–25.
18. T. Wang, X. Wang, J. Zhang, C. Wang, J. Shao, Z. Jiang and Y. Zhang, Dyes Pigm., 2018, 154, 75–81.
19. X. Chen, J. Zhang, W. Wei, Z. Jiang and Y. Zhang, Eur. Polym. J., 2014, 53, 58–64.
20. M. Lan, S. Zhao, W. Liu, C. S. Lee, W. Zhang and P. Wang, Adv. Healthcare Mater., 2019, 8, 1900132.
21. B. O’regan and M. Grätzel, Nature, 1991, 353, 737–740.
22. S. Dayan, N. Kayaci and N. Kalaycioğlu Özpozan, J. Mol. Struct., 2020, 1209, 127920.
23. M. M. Al Mogren, N. M. Ahmed and A. A. Hasanein, J. Saudi Chem. Soc., 2020, 24, 303–320.
24. M. Urbani, G. de la Torre, M. K. Nazeeruddin and T. Torres, Chem. Soc. Rev., 2019, 48, 2738–2766.
25. R. Seoudi, G. El-Bahy and Z. El Sayed, Opt. Mater., 2006, 29, 304–312.
26. S. Gorduk and A. Altindal, J. Mol. Struct., 2019, 1196, 747–753.
27. K. Harmandar, K. Granados-Tavera, M. Gezgin, M. Nebioğlu, İ. Şişman, G. Cárdenas-Jirón, D. Atilla and A. G. Gürek, New J. Chem., 2022, 46, 714–725.
28. C. Ilgün, A. M. Sevim, S. Çakar, M. Özacar and A. Gül, Sol. Energy, 2021, 218, 169–179.
29. S. Şenoğlu, M. Özer, F. Dumludağ, N. Acar, B. Salih and Ö. Bekaroğlu, Sens. Actuators, B, 2020, 310, 127860.
30. N. J. Yutronkie, B. King, O. A. Melville, B. H. Lessard and J. L. Brusso, J. Mater. Chem. C, 2021, 9, 10119–10126.
31. E. Güzel, H. Baş, Z. Biyiklioglu and İ. Şişman, Appl. Organomet. Chem., 2021, 35, e6214.
32. A. Suzuki, H. Okumura, Y. Yamasaki and T. Oku, Appl. Surf. Sci., 2019, 488, 586–592.
33. A. W. Snow, Porphyrin Handbook: Phthalocyanines: Properties and Materials, 2003, vol. 17, p. 129.
34. R. Milan, G. Singh Selopal, M. Cavazzini, S. Orlandi, R. Boaretto, S. Caramori, I. Concina and G. Pozzi, Sci. Rep., 2020, 10, 1176.
35. S. Gorduk and A. Altindal, J. Mol. Struct., 2020, 1204, 127636.
36. T. Keleş, Z. Biyiklioglu, E. Güzel, M. Nebioğlu and İ. Şişman, Appl. Organomet. Chem., 2021, 35, e6076.
37. B. Yıldız, B. S. Arslan, E. Güzel, M. Nebioğlu, N. Menges, İ. Şişman and M. Kasım Şener, Sol. Energy, 2021, 226, 173–179.
38. R. R. Cranston, M. C. Vebber, N. A. Rice, C. Tonnelé, F. Castet, L. Muccioli, J. L. Brusso and B. H. Lessard, ACS Appl. Electron. Mater., 2021, 3, 1873–1885.
39. M. C. Vebber, T. M. Grant, J. L. Brusso and B. H. Lessard, Langmuir, 2020, 36, 2612–2621.
40. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
41. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
42. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
43. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
44. G. Tunç, M. Zambrano-Angulo, B. S. Arslan, E. Güzel, M. Nebioğlu, V. Ahsen, İ. Şişman, G. Cárdenas-Jirón and A. G. Gürek, Dalton Trans., 2021, 50, 2981–2996.
45. G. Cárdenas-Jirón, M. Borges-Martínez, E. Sikorski and T. Baruah, J. Phys. Chem. C, 2017, 121, 4859–4872.
46. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
47. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
48. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Gaussian Inc., Pittsburgh, 2003.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
51. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
52. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
53. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
54. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
55. W. Zhang and Y. Chen, J. Nanopart. Res., 2012, 15, 1334.
56. R. Dutta, S. Ahmed and D. J. Kalita, Mater. Today Commun., 2020, 22, 100731.
57. M. Borges-Martínez, N. Montenegro-Pohlhammer, X. Zhang, D. E. Galvez-Aranda, V. Ponce, J. M. Seminario and G. Cárdenas-Jirón, Spectrochim. Acta, Part A, 2022, 269, 120740.
58. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009.
59. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G. M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
60. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
61. J. Zhang, P. Zhou, J. Liu and J. Yu, Phys. Chem. Chem. Phys., 2014, 16, 20382–20386.
62. M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409.
63. R. Urzúa-Leiva, R. Pino-Rios and G. Cárdenas-Jirón, Phys. Chem. Chem. Phys., 2019, 21, 4339–4348.
64. S. Q. QuantumATK version Q-2021.06. Synopsys QuantumATK (https://www.synopsys.com/silicon/quantumatk.html).
65. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2019, 32, 015901.
66. Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467.
67. W. Liu, Q. Liu, C. Xiang, H. Zhou, L. Jiang and Y. Zou, Surf. Interfaces, 2021, 26, 101385.
68. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
69. Y. Xu and M. A. Schoonen, Am. Mineral., 2000, 85, 543–556.
70. W. Zhang and Y. Chen, J. Nanopart. Res., 2013, 15, 1–7.
71. A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
72. K. Granados-Tavera, M. Zambrano-Angulo, N. Montenegro-Pohlhammer, G. Yaşa Atmaca, L. Sobotta, E. Güzel, G. Cárdenas-Jirón, A. Erdoğmuş and A. G. Gürek, Dyes Pigm., 2023, 210, 110986.
73. M. Gouterman, D. Holten and E. Lieberman, Chem. Phys., 1977, 25, 139–153.
74. M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163.
75. M. Gouterman, J. Chem. Phys., 1959, 30, 1139–1161.
76. M. Kato, H. Yoshizawa, M. Nakaya, Y. Kitagawa, K. Okamoto, T. Yamada, M. Yoshino, K. Tanaka and J. Onoe, Sci. Rep., 2022, 12, 8810.
77. M. R. S. A. Janjua, M. U. Khan, M. Khalid, N. Ullah, R. Kalgaonkar, K. Alnoaimi, N. Baqader and S. Jamil, J. Cluster Sci., 2021, 32, 243–253.
78. V. S. Kumar, Y. S. Mary, K. Pradhan, D. Brahman, Y. S. Mary, R. Thomas, M. S. Roxy and C. V. Alsenoy, J. Mol. Struct., 2020, 1199, 127035.
79. M. Grätzel, Acc. Chem. Res., 2009, 42, 1788–1798.
80. M. Pastore, S. Fantacci and F. De Angelis, J. Phys. Chem. C, 2013, 117, 3685–3700.
81. M. Shakeel Ahmad, A. K. Pandey and N. Abd Rahim, Renewable Sustainable Energy Rev., 2017, 77, 89–108.
82. E. German, R. Faccio and A. W. Mombrú, Appl. Surf. Sci., 2018, 428, 118–123.
83. H. Etabti, A. Fitri, A. T. Benjelloun, M. Hachi, M. Benzakour and M. McHarfi, Res. Chem. Intermed., 2021, 47, 4257–4280.
84. L. Kavan, M. Grätzel, S. E. Gilbert, C. Klemenz and H. J. Scheel, J. Am. Chem. Soc., 1996, 118, 6716–6723.
85. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.

---

Footnote

† Electronic supplementary information (ESI) available: The optimized structural parameters, atomic charges, energy of the frontier molecular orbitals, molecular electrostatic potential, and UV-Vis spectra. See DOI: https://doi.org/10.1039/d3cp04417c

---