 Open Access Article
Open Access ArticleIdentification of the interchromophore interaction in the electronic absorption and circular dichroism spectra of bis-phenanthrenes†
Yuchuan
Xu
,
Xunkun
Huang
,
Yu-Chen
Wang
,
Yi
Zhao
 and
WanZhen
Liang
and
WanZhen
Liang
 *
*
State Key Laboratory of Physical Chemistry of Solid Surfaces, Collaborative Innovation Center of Chemistry for Energy Materials, Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry, and Department of Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, P. R. China. E-mail: liangwz@xmu.edu.cn
First published on 20th January 2024
Abstract
We characterize the low-lying excited electronic states of a series of bis-phenanthrenes using our newly developed diabatic scheme called the fragment particle–hole density (FPHD) method and calculate both the electronic absorption and circular dichroism (ECD) spectra using the time-dependent density functional theory (TDDFT) and the FPHD-based exciton model which couples intrachromophore local excitations (LEs) and the interchromophore charge–transfer excitations (CTEs). TDDFT treats each bis-phenanthrene as a single molecule while the mixed LE–CTE exciton model partitions the molecule into two phenanthrene-based aromatic moieties, and then applies the electronic coupling between the various quasi-diabatic states to cover the interactions. It is found that TDDFT and the mixed LE–CTE model reproduce all experimentally observed trends in the spectral profiles, and the hybridization between LE and CTE states is displayed differently in absorption and ECD spectral intensities, as it usually decreases the absorption maxima and affects the positive/negative extrema of the ECD irregularly. By comparing the results yielded by the LE–CTE model with and without the LE–CTE coupling, we identify the contribution of CTE on the main dipole-allowed transitions.
1 Introduction
The ECD spectrum is defined as the difference in absorption between the left-circularly polarized and right-circularly polarized light associated with the electronic transitions of chromophores presented in a molecule.1,2 ECD is strictly allied with molecular chirality and is sensitive to its absolute configuration as well as to its features of conformation. Molecular ECD spectra can be experimentally measured and theoretically calculated. By following the corresponding changes in the experimentally measured ECD spectrum, one can monitor the molecular structural changes.3 The ECD spectra of small to medium-sized molecules can be calculated by many high-level quantum chemistry (QC) methods,4–9 which allows the close comparison between experimental and calculated spectra for assigning the absolute configuration of chiral molecules.10For the chiral compounds containing two or more chromophores with electric dipole allowed transitions, the interaction between the chromophores gives an effect known as exciton coupling. The well-established ECD exciton chirality method (ECM)11–13 has usually been adopted to interpret the ECD spectra without the requirement of QC calculations. The exciton chirality rule correlates the sign of an exciton couplet (two ECD bands with opposite sign and similar intensity) with the overall molecular stereochemistry, including the absolute configuration.14 The ECM applies the concepts of exciton coupling15–17 and assumes that the coupling is dominated by the Coulomb coupling and the exciton coupling mechanism is the major source of the observed ECD signals.
For closely-stacked or bond-linked chromophores, the interchromophore interactions may give rise to significant overlap between the frontier molecular orbitals on adjacent chromophores, leading to through-space18/bond19 charge delocalization along the stacking/bond direction. Consequently, the photo-induced interchromophore electronic exchange or charge-transfer excitations (CTEs) take place easily, in which electron and hole are located on adjacent chromophores. CTEs play an important role in both the spectra and the exciton dynamics of these compounds.20–25 For example, for a system with two chromophores AB, optical excitation may generate four types of states of a single electron–hole pair:  . The first two pairs correspond to an electron and a hole located on the same chromophore A (or B), which are called LE states. The last two pairs correspond to indirect electron–hole pairs, e.g., electron on A (or B), and hole on B (or A), which are created optically only when molecular orbitals (MOs) on two chromophores couple. With the representation of above quasi-diabatic states, the Hamiltonian Hdia can be constructed, whose diagonal and non-diagonal elements correspond to the excitation energies of diabatic states and electronic couplings between the diabatic states, respectively. The dimeric exciton states (or the adiabatic states of the compound) |Φ〉, which are linear combinations of quasi-diabatic states, are obtained by solving the eigenvalue equation
. The first two pairs correspond to an electron and a hole located on the same chromophore A (or B), which are called LE states. The last two pairs correspond to indirect electron–hole pairs, e.g., electron on A (or B), and hole on B (or A), which are created optically only when molecular orbitals (MOs) on two chromophores couple. With the representation of above quasi-diabatic states, the Hamiltonian Hdia can be constructed, whose diagonal and non-diagonal elements correspond to the excitation energies of diabatic states and electronic couplings between the diabatic states, respectively. The dimeric exciton states (or the adiabatic states of the compound) |Φ〉, which are linear combinations of quasi-diabatic states, are obtained by solving the eigenvalue equation 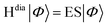 . Therefore, when the LEs and CTEs are coupled, the two types of exciton states mix sufficiently to form hybrid excited electronic states of systems, which possess the characters of both LEs and CTEs. The mixing degree between LEs and CTEs, the energy spacing and the order of dark/bright exciton of dimeric excitonic states are determined by the energies of LEs and CTEs, and the couplings between all the LEs and CTEs.26 Therefore, there are complex photophysical processes in adiabatic states of (AB)* because of the mixing between various kinds of LE and CTE states.21,27 Essentially, the LE–CT mixed states can remarkably affect the electronic absorption spectra.21 In our previous work,28–30 we have demonstrated that the mixing between a bright LE state and a dark CT state can lead to the two absorption peaks, and the relative peak intensities are closely associated with the intermolecular distances, aggregation lengths, and long-range excitation energy transfer.
. Therefore, when the LEs and CTEs are coupled, the two types of exciton states mix sufficiently to form hybrid excited electronic states of systems, which possess the characters of both LEs and CTEs. The mixing degree between LEs and CTEs, the energy spacing and the order of dark/bright exciton of dimeric excitonic states are determined by the energies of LEs and CTEs, and the couplings between all the LEs and CTEs.26 Therefore, there are complex photophysical processes in adiabatic states of (AB)* because of the mixing between various kinds of LE and CTE states.21,27 Essentially, the LE–CT mixed states can remarkably affect the electronic absorption spectra.21 In our previous work,28–30 we have demonstrated that the mixing between a bright LE state and a dark CT state can lead to the two absorption peaks, and the relative peak intensities are closely associated with the intermolecular distances, aggregation lengths, and long-range excitation energy transfer.
Numerous phenanthrenes and their derivatives have been found, mainly in higher plants. Two or three monophenanthrenes can be linked together at many different positions to form the natural compounds,32 which are a promising and expanding group of biologically active natural compounds and have the potential to be exploited by the pharmaceutical industry and optoelectronic devices. Bis-phenanthrenes, i.e. chiral compounds like 1–3, are shown in Fig. 1, in which two phenanthrenes are directly attached to each other via C–C bonding. Here 4-4′, 1-1′, and 3-3′ linkages are involved in the connection, and their ECD spectra have been extensively investigated in many experimental works.31,33–35
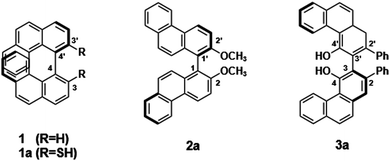 | ||
| Fig. 1 Compounds containing bis-phenanthrenes with different connections.31 | ||
Because of their relatively small molecular size and the reduced flexibility, bis-phenanthrenes have been the subject of many theoretical works aimed at reproducing and interpreting experimental ECD spectra.33–37 In the previous calculations, single molecules or the exciton coupling modes have been adopted. For example, Harada et al. have investigated biphenanthryl compounds and suggested that the exciton model may yield ambiguous conclusions in certain chiral biphenanthryl systems, and simple qualitative predictions based on the exciton method may not be suitable for 1,1′-biphenanthryl compounds.34 Jurinovich et al. conducted simulations of exciton CD spectra for biphenanthryl derivatives, using a gauge-independent formulation to explore the impact of the coupling between combined electric and magnetic transition moments (μm terms) and electric/electric coupling (μμ terms) on the spectra.31 Although the μm + μμ terms were included in the exciton model, their results significantly deviated from those obtained by time-dependent density functional theory (TDDFT) calculations, potentially due to an oversight regarding the consideration of CTE states.
Here we perform theoretical investigation on biphenanthryl derivatives and aim to quantitatively identify the enhanced exciton interactions in bis-phenanthrenes. Both the TDDFT with long-range-corrected (LRC) DFT exchange–correlation (XC) functional and the mixed LE–CT exciton model will be used to calculate the electronic absorption and ECD spectra. TDDFT treats each bis-phenanthrene as a single molecule and computes the vertical excitation energies, oscillator and rotatory strengths of the corresponding electronic transitions while the exciton model partitions the molecule into two aromatic moieties, then applies the exciton couplings between the various quasi-diabatic states to cover the interactions. By comparing the results yielded by the mixed LE–CT exciton model with and without decoupling the interaction between LE and CTE states, we give a qualitative description of the contribution of different types of excitons to the electronic spectra of those bis-phenanthrenes, and the deviation arisen by the Frenkel exciton model or ECD ECM. Each low-lying excited electronic state is also characterized.
2 Theoretical method and computational details
2.1 Absorption and ECD spectra
The ECD and absorption spectral cross sections can be calculated as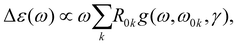 | (1) |
 | (2) |
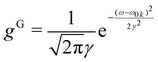 or
or 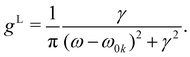 γ denotes one-half of the width of the function at half-maximum (HWHM) intensity. In the atomic unit, the electric transition dipole can be defined as μ0kl = −〈k|
γ denotes one-half of the width of the function at half-maximum (HWHM) intensity. In the atomic unit, the electric transition dipole can be defined as μ0kl = −〈k|![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) |0〉 in the length gauge and
|0〉 in the length gauge and  in the velocity gauge, respectively, for the transition from the ground state
in the velocity gauge, respectively, for the transition from the ground state  to excited state
to excited state  with transition energy ω0k.
with transition energy ω0k. ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) and
and ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) are the position operator and the momentum operator. R0k, the optical rotatory strength, can be expressed as the imaginary part of the dot product of the electric transition dipole and the magnetic transition dipole moments,
are the position operator and the momentum operator. R0k, the optical rotatory strength, can be expressed as the imaginary part of the dot product of the electric transition dipole and the magnetic transition dipole moments,R0k = Im{〈0|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |k〉·〈k| |k〉·〈k|![[m with combining circumflex]](https://www.rsc.org/images/entities/b_char_006d_0302.gif) |0〉}, |0〉}, | (3) |
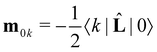 . Here
. Here ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) is the angular momentum operator. However, it should be noted that the magnetic transition dipole moment varies with changes in the gauge origin R,
is the angular momentum operator. However, it should be noted that the magnetic transition dipole moment varies with changes in the gauge origin R, | (4) |
Using this formula, two magnetic moment sources emerge: the first term constitutes the molecule's intrinsic magnetic moment, while the second term hinges on the molecule's positioning within the reference frame. Fortunately, the rotatory strengths can be origin-independent if the electric transition dipole in the velocity gauge is adopted because μ0kv is always perpendicular to the second term of the magnetic transition dipole (μ0kv·R × μ0kv = 0). The rotatory strength in velocity gauge is
 | (5) |
In this work, R0kv will be adopted.
2.2 LE–CTE model
With the mixed LE–CTE model, the electronic Hamiltonian of multi-chromophore system in the representation of quasi-diabatic electronic states can be expressed as | (6) |
In the matrix representation,
 | (7) |
To parameterize the electronic Hamiltonian of eqn (7), the diabatization schemes were usually applied, where the diabatic electronic states are expressed as a linear combination of the adiabatic states which are obtained from ab initio calculations such as time-dependent density functional theory.24,38–41 Within the framework of diabatization schemes, finding the diabatic states is equivalent to constructing an optimal adiabatic-to-diabatic (ATD) transformation matrix. Here we adopt our newly developed diabatization scheme called the fragment particle-hole density (FPHD) method42,43 to obtain the corresponding state energies and couplings. The central idea of FPHD is to search for orthonormal electronic states that maximally localize electron and hole densities in terms of predefined molecular fragments.
In the following we give a brief introduction to the implementation of FPHD method. Firstly, the TDDFT calculation is performed for the compound to obtain the corresponding vertical excitation energies, transition electric/magnetic dipole moments and transition density matrices of the first N transitions. The compound is then partitioned into fragments based on the chromophores. The transition density matrices are used to calculate electron and hole number matrices of predefined fragments. Then, the unitary ATD transformation matrix is obtained by simultaneously diagonalizing the number matrices using the Jacobi sweep algorithm. Finally, the corresponding parameters in the quasi-diabatic representation such as site energies and couplings are obtained by the ATD transformation based on the obtained unitary transformation matrix U as
| Hedia = UTHeadiaU. | (8) |
H e adia represents a diagonal matrix with the vertical excitation energies as diagonal elements, which can be calculated by QC methods such as TDDFT. The electric/magnetic dipole moments of the diabatic states can also be obtained through the linear transformation of those moments associated with the corresponding adiabatic states based on the ATD transformation matrix.
| ∇dia = UT∇adiaU | (9) |
| mdia = UTmadiaU | (10) |
After finishing the construction of Hdia with the matrix dimension N, we take Mdia lowest-lying quasi-diabatic states (Mdia ≤ N) to construct the truncated matrix of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) dia because usually we are interested in the lowest-lying electronic states. Then
dia because usually we are interested in the lowest-lying electronic states. Then ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) dia is diagonalized to obtain the energies and wavefunctions of aggregate excitonic states. The percentage contributions of different kinds of quasi-diabatic states (LE or CTE) to each dimeric excitonic state
dia is diagonalized to obtain the energies and wavefunctions of aggregate excitonic states. The percentage contributions of different kinds of quasi-diabatic states (LE or CTE) to each dimeric excitonic state  are obtained by
are obtained by  (m ∈ MdiaLE and m ∈ MdiaCTE for the contributions of LE and CTE states, respectively). Here MdiaLE and MdiaCTE denote the number of LE and CTE states with MdiaLE + MdiaCTE = Mdia. C is the corresponding eigenfunction of
(m ∈ MdiaLE and m ∈ MdiaCTE for the contributions of LE and CTE states, respectively). Here MdiaLE and MdiaCTE denote the number of LE and CTE states with MdiaLE + MdiaCTE = Mdia. C is the corresponding eigenfunction of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) dia. The general flowchart is shown in Fig. 2.
dia. The general flowchart is shown in Fig. 2.
The electric and magnetic transition dipole moments for the  transition can be represented as a linear combination of the transition dipole moments associated with the individual diabatic states. This representation allows for the use of electric transition dipole in either the length or velocity gauge:
transition can be represented as a linear combination of the transition dipole moments associated with the individual diabatic states. This representation allows for the use of electric transition dipole in either the length or velocity gauge:
 | (11) |
 | (12) |
By substituting eqn (11) and (12) into eqn (5), we finally obtain
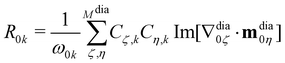 | (13) |
If the LE and CTE states are assumed to be not coupled, the couplings between LEs and CTEs in ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) dia are set to be zero. In this case, the dimeric excitonic states will have a pure LE or CTE character.
dia are set to be zero. In this case, the dimeric excitonic states will have a pure LE or CTE character.
It is noted that the mixed LE–CTE model has been adopted to calculate ECD of guanine quadruplexes.24 Green et al. also adopted a diabatization scheme to find the diabatic states, which starts with the TDDFT calculation to the adiabatic electronic states and construction of the ATD transformation matrix through calculation of the overlapping of the reference states of the fragments with the adiabatic states.38 Our FPHD schemes42,43 maximally localize the particles and holes in terms of predefined molecular fragments, in the end the quasi-diabatic states with well-defined characters can be automatically constructed and the couplings between the diabatic states can be directly obtained. They don't require the reference states of the fragments. Our earlier FPHD scheme is based on the transition density.42 In the present version we have extended to construct the ATD matrix from the difference density which can be calculated by using both multi-reference ab initio methods and the single-reference TDDFT approach. Therefore, the FPHD scheme is very general in that it applies to electronic states with various spin multiplicities and can be combined with various kinds of preliminary electronic structure calculations. As shown later, the FPHD-based LE–CTE model is accurate because we can fully recover the spectra yielded by the TDDFT calculations.
2.3 Computational details
The geometry optimizations of compound 1 are finished at the theoretical level of B3LYP/6-311G(d,p), while those of compound 1a, 2a, and 3a are performed at the ωB97X-D/6-311G(d,p) level. The the vertical excitation energies, transition electric/magnetic dipole moments, transition electronic density matrices, etc. of adiabatic excited states are calculated by TDDFT with the long-range-corrected (LRC) DFT XC functional ωB97X-D.44 The solvent effect is covered by the polarizable continuum model with the integral equation formalism variant45,46 to mimic the experimental environment. All the calculations are performed within the Gaussian 16 software package.47 The diabatization scheme FPHD is adopted to perform ATD transformation. The optical spectra are calculated by the home-made software. The Gaussian broadening lineshape function is applied.3 Results
3.1 Compound 1
We first check how the different orientation of two aromatic moieties affects the ECD spectra, and aim to elucidate the interplay between configurational and conformational factors. The ECD spectra of the model system, 4,4′-bis-phenanthrenes (compound 1) with the different dihedral angles of 3-4-4′-3′ (denoted by θ), are computed by full TDDFT and the mixed LE–CTE exciton model with and without LE–CTE coupling (JLE–CTE). Here we construct different arrangements of two aromatic moieties by setting θ to different values. The constrained geometry optimizations are subsequently performed. With the optimized geometries, TD-ωB97XD/6-311G(d,p) calculations are finished to yield the lowest 50 adiabatic excited states. After that, the FPHD approach is used to obtain the energies and couplings among 50 quasi-diabatic states. The Hamiltonian in the representation of 50 diabatic states is diagonalized to obtain the information of dimeric excitonic states. In the process of FPHD, the compound 1 is partitioned into two fragments by separating the 4-4′ C–C bridged bond. The lowest-lying 16 exciton states are utilized to generate the ECD spectra. Fig. 3 shows the calculated results. The full TDDFT and the mixed LE–CTE model with the coupled LE and CTE states reproduce the same results. The energy level of diabatic states and the hybridization degree between LE and CTE states, which are controlled by θ, affect ECD profiles significantly.The TDDFT calculation shows that the phenanthrene monomer in compound 1 (the 4-4′ broken bond is saturated by hydrogen atom) possesses three low-lying dipole-allowed exited singlet states with excitation energies (oscillator strengths) 5.32 (0.2121), 5.38 (0.6306), and 5.48 (0.5236) eV (see Table S2 in the ESI†), whose transitions are polarized along the long axis of the phenanthrene plane (see Fig. S1 in the ESI†). The lowest two excited states with energies of 4.26 and 4.56 eV are nearly dark states. The ECD spectra of compound 1 with the optimal geometry (θ = −97°) mainly lies in the energy range of around 5 eV, shows a negative exciton couplet with positive extrema in the short-wavelength range and negative extrema in the long wavelength range. The exciton model with and without the LE–CTE couplings produces similar exciton couplets. However, the relative peak intensities and locations are quite different, indicating that the contribution of CTEs cannot be ignored.
At θ = −90°, regardless of whether JLE–CTE are set to be zero or not, the peak positions and relative intensities are nearly identical, indicating that the interchromophore electronic exchange in this conformation is the smallest, and the overall contribution from CTEs to ECD spectra in this energy range is negligible. As θ increases, the spectral lineshapes produced by the exciton model with or without JLE–CTE are consistent (a transformation from negative to positive extrema). However, the differences between peak positions and relative intensities are remarkable. The larger the θ value, the larger is the deviation from the full TDDFT computational results. For θ < −97°, when JLE–CTE are set to be zero, the exciton model produces fully different spectral lineshapes, significantly deviating from those involving the LE–CTE couplings. In this scenario, the exciton charity rule which only considers LE–LE couplings fails completely, indicating that there is a strong wavefunction overlap between two aromatic moieties, and the influence of CTE states to the optical physical processes must be taken into account.
3.2 Compounds 1a, 2a, and 3a
To gain deep insights into the structure–property relationship and interpret the experimental spectra, we conducted investigation into three organic compounds, 3,3′-dithio-4,4′-bis-phenanthrene (1a), 1,1′-diphenanthrene-2,2′-dithiol (2a), and 2,2′-diphenyl-[3,3′-biphenanthrene]-4,4′-diol (3a), whose absorption and ECD spectra have been experimentally measured. To facilitate comparison with the experimental spectra, solvent effects were considered in the calculations. Specifically, for the compounds 1a, 2a, and 3a, we selected cyclohexane,33 ethanol,34 and dichloromethane35 as solvents.At first, we characterize the adiabatic excited states of 1a, 2a, 3a. The computed vertical excitation energies, oscillator strengths (defined as  ) and rotatory strengths of lowest-lying 20 excited states at the theoretical level of TD-ωB97X-D/cc-pVTZ are listed in Tables 1, 2 and 4, respectively. Most of the adiabatic states have hybridized LE and CTE characters. The lowest-lying 4 excited states with relative weak oscillator strengths mainly possess LE characters. These states which contribute to the spectral range with maximum absorption/CD intensities even have the large CT components.
) and rotatory strengths of lowest-lying 20 excited states at the theoretical level of TD-ωB97X-D/cc-pVTZ are listed in Tables 1, 2 and 4, respectively. Most of the adiabatic states have hybridized LE and CTE characters. The lowest-lying 4 excited states with relative weak oscillator strengths mainly possess LE characters. These states which contribute to the spectral range with maximum absorption/CD intensities even have the large CT components.
| No. | Adiabatic states | Diabatic states | ||||
|---|---|---|---|---|---|---|
| Energy | f | R v | CT% | Energy | Character | |
| S1 | 4.07 | 0.02 | 86.24 | 4.29 | 4.11 | LE |
| S2 | 4.09 | 0.05 | −31.23 | 0.50 | 4.11 | LE |
| S3 | 4.34 | 0.32 | −672.99 | 2.58 | 4.37 | LE |
| S4 | 4.34 | 0.26 | 753.04 | 1.26 | 4.37 | LE |
| S5 | 4.75 | 0.18 | −265.17 | 69.31 | 4.93 | CT |
| S6 | 4.79 | 0.04 | 157.49 | 73.82 | 4.93 | CT |
| S7 | 4.97 | 0.51 | −261.78 | 30.56 | 5.04 | LE |
| S8 | 4.99 | 0.21 | 729.99 | 49.87 | 5.04 | LE |
| S9 | 5.03 | 0.56 | −1359.48 | 6.00 | 5.10 | LE |
| S10 | 5.05 | 0.25 | −637.55 | 67.75 | 5.10 | LE |
| S11 | 5.10 | 0.22 | 503.00 | 51.02 | 5.14 | CT |
| S12 | 5.17 | 0.48 | 990.47 | 1.59 | 5.14 | CT |
| S13 | 5.28 | 0.00 | 17.86 | 7.81 | 5.28 | LE |
| S14 | 5.28 | 0.21 | −194.54 | 17.31 | 5.28 | LE |
| S15 | 5.49 | 0.06 | 266.80 | 9.16 | 5.51 | LE |
| S16 | 5.51 | 0.20 | 183.72 | 10.97 | 5.51 | LE |
| S17 | 5.54 | 0.32 | −271.84 | 10.19 | 5.55 | LE |
| S18 | 5.54 | 0.03 | 93.89 | 13.64 | 5.55 | LE |
| S19 | 5.66 | 0.00 | 15.33 | 84.53 | 5.75 | CT |
| S20 | 5.68 | 0.05 | −98.01 | 67.98 | 5.75 | CT |
| No. | Adiabatic states | Diabatic states | ||||
|---|---|---|---|---|---|---|
| Energy | f | R v | CT% | Energy | Character | |
| S1 | 4.14 | 0.11 | 9.72 | 1.20 | 4.17 | LE |
| S2 | 4.17 | 0.01 | 29.99 | 0.98 | 4.17 | LE |
| S3 | 4.44 | 0.22 | 40.04 | 0.38 | 4.48 | LE |
| S4 | 4.50 | 0.01 | −20.49 | 0.57 | 4.48 | LE |
| S5 | 4.93 | 1.54 | −282.80 | 9.89 | 4.97 | LE |
| S6 | 4.97 | 0.80 | 498.71 | 3.83 | 4.97 | LE |
| S7 | 5.03 | 0.33 | −93.02 | 14.31 | 5.11 | CT |
| S8 | 5.06 | 0.01 | −28.08 | 73.80 | 5.11 | CT |
| S9 | 5.12 | 0.35 | 113.84 | 73.57 | 5.11 | LE |
| S10 | 5.18 | 0.09 | −242.69 | 19.81 | 5.11 | LE |
| S11 | 5.32 | 0.24 | −464.25 | 2.19 | 5.33 | LE |
| S12 | 5.33 | 0.28 | 407.01 | 4.05 | 5.33 | LE |
| S13 | 5.75 | 0.01 | −45.89 | 84.56 | 5.76 | CT |
| S14 | 5.75 | 0.01 | 20.07 | 85.65 | 5.76 | CT |
| S15 | 5.78 | 0.00 | −5.11 | 88.95 | 5.79 | CT |
| S16 | 5.78 | 0.04 | 5.73 | 91.98 | 5.79 | CT |
| S17 | 5.87 | 0.12 | −258.28 | 18.39 | 5.86 | LE |
| S18 | 5.89 | 0.04 | 165.90 | 19.06 | 5.86 | LE |
| S19 | 5.98 | 0.04 | −156.48 | 1.59 | 6.02 | LE |
| S20 | 6.03 | 0.04 | 134.59 | 2.06 | 6.02 | LE |
Here we computed 70 adiabatic states and employed the FPHD method to construct 70 diabatic states, which encompass both LE states and CTE states. Then the Hamiltonian matrices in the presentation of diabatic states are diagonalized to construct dimeric excitonic states. Tables S6, S10 and S14 in the ESI† show the low-lying diabatic states. The corresponding ECD and absorption spectra are shown in Fig. 4–6, contributed by the lowest 26 excitonic states for 1a and 3a, and 20 for 2a. Compared with the experimentally measured energy spacings and oscillator strengths of bis-phenanthrenes, TD-ωB97X-D yields the consistent results with the experimental measurements, however, it overestimates the excitation energies.
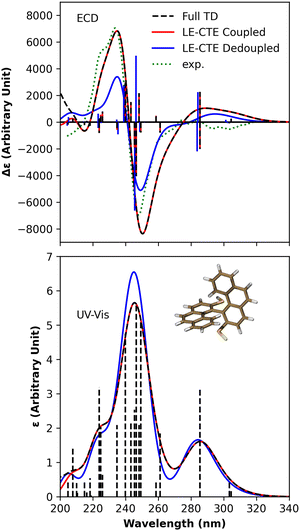 | ||
| Fig. 4 The theoretical and experimental ECD and electronic absorption spectra of compound 1a. The black dashed line represents the full TDDFT computational results, and the blue and red lines denote the results produced by the exciton models with and without LE–CTE interactions, respectively. The experimental ECD spectrum33 in cyclohexane solution is blue-shifted by 0.45 eV for close comparison. The vertical lines represent the rotatory strength in ECD and the oscillator strength in absorption which come from the full TDDFT calculation. The Gaussian lineshape with γ = 0.175 eV was employed. | ||
 | ||
| Fig. 5 The theoretical and experimental ECD and electronic absorption spectra of compound 2a. The experimental spectra in ethanol solution were blue-shifted by 0.45 eV. | ||
 | ||
| Fig. 6 The theoretical and experimental ECD and electronic absorption spectra of 3a. The experimental spectra in dichloromethane solution were blue-shifted by 0.12 eV. | ||
As Fig. 4 shows, the ECD spectrum of compound 1a in 240 nm region shows a negative couplet (λ ∼ 250 nm, Δε ∼ −8000, λ ∼ 235 nm, Δε ∼ 7000), in very good agreement with the experimental data. The CT states have a significant impact on the ECD spectra in the range of 200–260 nm, where the strongest absorption band is observed. CTE states affect the absorption and CD intensities quite differently. This can be explained by the hybridization character of adiabatic states. Diabatic CTE states are nearly dark states so that the hybridization of LEs and CTEs decreases the oscillator strengths of dimeric excitonic states which contribute to the strongest absorption band. By decoupling the LE–CTE interaction, all the dipole-allowed dimeric excitonic states are constructed by the LEs. As a result, the absorption intensity is slightly enhanced in the absence of the LE–CTE hybridization.
Table S6 in the ESI† for compound 1a shows that two pairs of CT states appear in the energy range of 5 eV, one with the energy of 4.93 eV and the other with the energy of 5.14 eV. Those CT states are close in energy to the strongest dipole-allowed LE states, making the adiabatic states around 5 eV possess the mixed LE–CTE character. Table 3 lists the main states which contribute to the strongest CT bands. The negative extreme in CT spectra appears in the 250 nm region, mainly contributed by the 9th and 10th dimeric excitonic states, in which the former has pure LE character and the latter has hybridized LE–CTE character with a CT component of more than 67%. Even though the 8th excitonic state exhibits significant positive rotatory strength, its energy is close to that of the 9th excitonic state, and the absolute value of the 9th exciton state's rotatory strength is much larger than that of the 8th exciton state. Thus, the spectra exhibit a negative extreme. The 10th exciton state with CT component of 68% is a hybridized LE–CTE state. In the absence of LE–CTE couplings, the rotatory strength of this exciton state is close to zero. The positive extrema at ∼250 nm are mainly contributed by the 11th and 12th excitonic states. The 11th exciton state has a CT component of about 51%, and in the absence of CT states, its rotatory strength approaches zero.
| Adia. states (eV) | Dia. states (eV) | Character | Components (%) | |μl| | |μv| | |m| | θ (m,μv) |
|---|---|---|---|---|---|---|---|
| 9(5.03) | 7(5.04) | LE | 44.8 | 1.9955 | 1.9901 | 0.0103 | 90.68 |
| 8(5.04) | LE | 44.8 | 1.9956 | 1.9902 | 0.0103 | 90.68 | |
| 10(5.05) | 11(5.14) | CT | 32.5 | 0.1215 | 0.1222 | 0.0004 | 129.06 |
| 12(5.14) | CT | 32.5 | 0.1216 | 0.1223 | 0.0004 | 129.07 | |
| 13(5.28) | LE | 5.9 | 1.1875 | 1.1862 | 0.0055 | 92.05 | |
| 14(5.28) | LE | 5.9 | 1.1872 | 1.1862 | 0.0055 | 92.05 | |
| 11(5.10) | 7(5.04) | LE | 20.6 | 1.9955 | 1.9901 | 0.0103 | 90.68 |
| 8(5.04) | LE | 20.6 | 1.9956 | 1.9902 | 0.0103 | 90.68 | |
| 11(5.14) | CT | 21.2 | 0.1215 | 0.1222 | 0.0004 | 129.06 | |
| 12(5.14) | CT | 21.2 | 0.1216 | 0.1223 | 0.0004 | 129.07 | |
| 12(5.17) | 9(5.10) | LE | 45.0 | 2.5232 | 2.5089 | 0.0089 | 89.49 |
| 10(5.10) | LE | 45.0 | 2.5230 | 2.5088 | 0.0089 | 89.49 |
| No. | Adiabatic states | Diabatic states | ||||
|---|---|---|---|---|---|---|
| Energy | f | R v | CT% | Energy | Character | |
| S1 | 4.10 | 0.31 | 259.49 | 1.45 | 4.14 | LE |
| S2 | 4.12 | 0.06 | −146.53 | 1.83 | 4.14 | LE |
| S3 | 4.38 | 0.11 | 180.72 | 4.49 | 4.45 | LE |
| S4 | 4.43 | 0.03 | −122.50 | 1.19 | 4.45 | LE |
| S5 | 4.77 | 2.01 | 1113.64 | 4.31 | 4.89 | LE |
| S6 | 4.92 | 1.43 | −2814.78 | 3.42 | 4.89 | LE |
| S7 | 5.01 | 0.03 | −138.99 | 14.94 | 5.07 | LE |
| S8 | 5.02 | 0.35 | 1111.51 | 3.03 | 5.07 | LE |
| S9 | 5.23 | 0.14 | −203.73 | 12.62 | 5.32 | LE |
| S10 | 5.24 | 0.02 | 54.49 | 6.37 | 5.32 | LE |
| S11 | 5.28 | 0.17 | 542.87 | 45.84 | 5.37 | LE |
| S12 | 5.32 | 0.03 | −73.00 | 14.17 | 5.37 | LE |
| S13 | 5.39 | 0.17 | 133.20 | 23.35 | 5.43 | CT |
| S14 | 5.42 | 0.02 | −67.18 | 68.09 | 5.44 | CT |
| S15 | 5.58 | 0.06 | 193.53 | 79.41 | 5.65 | CT |
| S16 | 5.63 | 0.01 | −41.29 | 44.50 | 5.65 | CT |
| S17 | 5.64 | 0.00 | −16.10 | 81.40 | 5.76 | LE |
| S18 | 5.75 | 0.20 | −445.38 | 17.86 | 5.76 | LE |
| S19 | 5.83 | 0.00 | −22.47 | 6.87 | 5.86 | LE |
| S20 | 5.86 | 0.00 | 7.19 | 53.40 | 5.86 | LE |
The two naphthalene rings in 2a are nearly oriented perpendicularly with 2-1-1′-2′ dihedral angle of −90.67°. It can be anticipated that CT states have a minimal impact on the spectra. From Fig. 5, it is evident that in the range of 200–260 nm, the ECD spectrum exhibits two distinct negative peaks and one positive peak. In this scenario, whether or not the contribution of CT states is considered, the shape and intensity of the spectral lines closely resemble those of the full TDDFT results. Regarding the positive peaks in the 240–260 nm range, they are primarily contributed by the 5th and 6th exciton states. The 6th exciton state has a low CT component, so whether or not LE–CTE couplings are considered, the value of rotatory strength remains around 496. As for the negative peaks in the 220–240 nm range, they are mainly attributed to the contributions of the 10th and 11th exciton states, and the negative peaks in the 200–220 nm range are attributed to the contributions of the 17th and 19th exciton states. For these exciton states with significant contributions, the CT component is relatively low, and whether or not LE–CTE coupling states are considered, the impact on the rotatory strength is slight.
In 3a, the two phenanthrene rings are oriented in different spatial directions with a 2-3-3′-2′ dihedral angle of −102.71°; there is some spatial overlap between a benzene ring on one fragment and the phenanthrene ring on the other fragment. It can be inferred that CT states may have a significant impact on the ECD spectrum. In the range of 220–280 nm, the theoretically calculated spectra exhibit two distinct positive peaks and one negative peak. When including LE–CTE couplings, the results are almost identical to full TDDFT. However, if the contribution of CT states is not considered, the shape of the spectral lines deviates completely from the full TDDFT results. Additionally, in the 220–240 nm region, there is a positive peak in both experimental measurements and theoretical calculations. When LE and CTE states are coupled, the positive peak near 260 nm originates from the 5th dimeric exciton state, and the negative peak near 250 nm is contributed by the 6th exciton state. Since the CT components in both excitonic states are small, the 5th and 6th excitonic states still exhibit significant rotatory strengths after excluding LE–CTE coupling. The positive peak in the 230–240 nm region comes from the 11th exciton state. However, when LE–CTE states are decoupled, even though the 11th exciton state also has a significant positive rotatory strength, the nearby exciton states (especially the 12th exciton state, which is degenerated with the 11th exciton state) have a significant negative rotatory strength, leading to the disappearance of the positive peak in the 230–240 nm range when LE–CTE states are decoupled.
4 Conclusions
By using TDDFT and the mixed LE–CTE exciton model with the LE–CTE coupled or decoupled, we have calculated the electronic absorption and ECD spectra of a family of bis-phenanthrenes. Overall, the calculated spectral lineshapes by TDDFT and the exciton model with the LE–CTE coupling are in excellent agreement with the experimental measurement. The analysis of the excited states underlying the main absorption peaks reveals the hybridized LE–CTE characters of these states and gives direct visualization of interchromophore interactions. The mixed LE–CTE model, which contains the contributions from an electrostatic Coulombic interaction for singlet–singlet exciton couplings as well as interchromophore orbital overlap-dependent terms resulted from the charge-separated configurations, is appropriate for the interpretation of the spectra of the series.We also check how the different orientation of two aromatic moieties affects the ECD spectra since it controls the energy level of diabatic states and the hybridization degree between LE and CTE states. It is found that ECD spectra vary significantly with the orientation of two phenanthrenes and whether the LE and CTE states are coupled or decoupled. As the spatial overlap of two phenanthrene derivatives is small, both the electrostatic Coulombic coupling and interchromophore orbital overlap-dependent terms become weak, in this case the Frenkel exciton model which only accounts for LE–LE couplings can be appropriate while it fully breaks down for compound 1 with θ < 97°, which shows a strong electronic coherence between two chromophores.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 22173074, 22033006 and 92372105). Y.C. Wang acknowledges support from the Chinese Postdoctoral Science Foundation (Grant No. 2021M702734).Notes and references
- J. A. Schellman, Chem. Rev., 1975, 75, 323–331 CrossRef CAS.
- N. Berova, K. Nakanishi and R. W. Woody, Circular dichroism: principles and applications, John Wiley & Sons, 2000 Search PubMed.
- N. Berova, L. D. Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914–931 RSC.
- J. Autschbach, T. Ziegler, S. J. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 116, 6930–6940 CrossRef CAS.
- A. E. Hansen and K. Bak, Enantiomer, 1999, 4, 455 CAS.
- K. L. Bak, A. E. Hansen, K. Ruud, T. Helgaker, J. Olsen and P. Jørgensen, Theor. Chem. Acc., 1995, 90, 441–458 Search PubMed.
- J. H. Andersen, K. D. Nanda, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2022, 18, 1748–1764 CrossRef CAS PubMed.
- M. Krykunov, M. D. Kundrat and J. Autschbach, J. Chem. Phys., 2006, 125, 194110 CrossRef PubMed.
- M. Scott, D. R. Rehn, S. Coriani, P. Norman and A. Dreuw, J. Chem. Phys., 2021, 154, 064107 CrossRef CAS PubMed.
- I. Warnke and F. Furche, WIREs Comput. Mol. Sci., 2012, 2, 150–166 CrossRef CAS.
- N. Harada and K. Nakanishi, Acc. Chem. Res., 1972, 5, 257–263 CrossRef CAS.
- N. Harada and K. Nakanishi, Circular dichroic spectroscopy: exciton coupling in organic stereochemistry, University Science Books, Mill Valley, CA, 1983 Search PubMed.
- N. Harada, Chirality, 2020, 32, 535–546 CrossRef CAS PubMed.
- G. Pescitelli, Chirality, 2022, 34, 333–363 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1937, 5, 479–491 CrossRef CAS.
- W. Kuhn, Trans. Faraday Soc., 1930, 26, 293–308 RSC.
- F. Bertocchi, C. Sissa and A. Painelli, Chirality, 2023, 35, 681–691 CrossRef CAS PubMed.
- H. Tsujimoto, D.-G. Ha, G. Markopoulos, H. S. Chae, M. A. Baldo and T. M. Swager, J. Am. Chem. Soc., 2017, 139, 4894–4900 CrossRef CAS PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- F. Gao, Y. Zhao and W. Liang, J. Phys. Chem. B, 2011, 115, 2699–2708 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- F. J. Hernández and R. Crespo-Otero, Annu. Rev. Phys. Chem., 2023, 74, 547–571 CrossRef PubMed.
- W. Liang and W. Wu, Sci. China: Chem., 2013, 56, 1267–1270 CrossRef CAS.
- J. A. Green, H. Asha, F. Santoro and R. Improta, J. Chem. Theory Comput., 2021, 17, 405–415 CrossRef CAS PubMed.
- Z.-Q. You and C.-P. Hsu, Int. J. Quantum Chem., 2014, 114, 102–115 CrossRef CAS.
- F. Pan, F. Gao, W. Liang and Y. Zhao, J. Phys. Chem. B, 2009, 113, 14581–14587 CrossRef CAS PubMed.
- C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148 CrossRef CAS PubMed.
- S. Feng, Y.-C. Wang, Y. Ke, W. Liang and Y. Zhao, J. Chem. Phys., 2020, 153, 034116 CrossRef CAS PubMed.
- S. Feng, Y.-C. Wang, W. Liang and Y. Zhao, J. Phys. Chem. A, 2021, 125, 2932–2943 CrossRef CAS PubMed.
- S. Feng, Y.-C. Wang, W. Liang and Y. Zhao, Phys. Chem. Chem. Phys., 2022, 24, 2974–2987 RSC.
- S. Jurinovich, C. A. Guido, T. Bruhn, G. Pescitelli and B. Mennucci, Chem. Commun., 2015, 51, 10498–10501 RSC.
- A. Kovács, A. Vasas and J. Hohmann, Phytochemistry, 2008, 69, 1084–1110 CrossRef PubMed.
- G. Gottarelli, G. Proni, G. P. Spada, D. Fabbri, S. Gladiali and C. Rosini, J. Org. Chem., 1996, 61, 2013–2019 CrossRef CAS.
- T. Hattori, K. Sakurai, N. Koike, S. Miyano, H. Goto, F. Ishiya and N. Harada, J. Am. Chem. Soc., 1998, 120, 9086–9087 CrossRef CAS.
- A. G. Petrovic, S. E. Vick and P. L. Polavarapu, Chirality, 2008, 20, 501–510 CrossRef CAS PubMed.
- N. Harada, T. Hattori, T. Suzuki, A. Okamura, H. Ono, S. Miyano and H. Uda, Tetrahedron: Asymmetry, 1993, 4, 1789–1792 CrossRef CAS.
- A. Solladié-Cavallo, C. Marsol, G. Pescitelli, L. D. Bari, P. Salvadori, X. Huang, N. Fujioka, N. Berova, X. Cao and T. B. Freedman, et al. , Eur. J. Org. Chem., 2002, 1788–1796 CrossRef.
- M. Yaghoubi Jouybari, Y. Liu, R. Improta and F. Santoro, J. Chem. Theory Comput., 2020, 16, 5792–5808 CrossRef CAS PubMed.
- A. A. Voityuk, J. Phys. Chem. A, 2017, 121, 5414–5419 CrossRef CAS PubMed.
- H. Tamura, J. Phys. Chem. A, 2016, 120, 9341–9347 CrossRef CAS PubMed.
- Q. Ou and J. E. Subotnik, J. Phys. Chem. C, 2013, 117, 19839–19849 CrossRef CAS.
- Y.-C. Wang, S. Feng, W. Liang and Y. Zhao, J. Phys. Chem. Lett., 2021, 12, 1032–1039 CrossRef CAS PubMed.
- Y.-C. Wang, S. Feng, Y. Kong, X. Huang, W. Liang and Y. Zhao, J. Chem. Theory Comput., 2023, 19, 3900–3914 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- E. Cancés, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef.
- B. Mennucci, E. Cancés and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506–10517 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian-16 Revision A.03, 2016, Gaussian Inc., Wallingford CT Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Main geometric parameters, the TDDFT excited states for four monomers, ECD spectra of compound 1 varied with the number of CT states, and the adiabatic and diabatic states for compounds 1a, 2a, and 3a. The impacts of the basis set and the DFT XC functional on the spectra. See DOI: https://doi.org/10.1039/d3cp05684h |
| This journal is © the Owner Societies 2024 |


