Rate-dependent stress-order coupling in main-chain liquid crystal elastomers
Chen
Wei
a,
Scott
Cao
a,
Yu
Zhou
a,
Dehao
Lin†
ab and
Lihua
Jin
 *a
*a
aMechanical & Aerospace Engineering Department, University of California, Los Angeles, Los Angeles, CA 90095, USA. E-mail: lihuajin@seas.ucla.edu
bEngineering Department, El Camino College, Torrance, CA 90506, USA
First published on 3rd October 2023
Abstract
Liquid crystal elastomers (LCEs) exhibit significant viscoelasticity. Although the rate-dependent stress–strain relation of LCEs has already been widely observed, the effect of the intricate interplay of director rotation and network extension on the viscoelastic behavior of main-chain LCEs remains inadequately understood. In this study, we report real-time measurements of the stress, director rotation, and all strain components in main-chain nematic LCEs subjected to uniaxial tension both parallel and tilted to the initial directors at different loading rates and relaxation tests. We find that both network extension and director rotation play roles in viscoelasticity, and the characteristic relaxation time of the network extension is much larger than that of the director rotation. Interestingly, the gradual change of the director in a long-time relaxation indicates the director reorientation delay is not solely due to the viscous rotation of liquid crystals but also arises from its coupling with the highly viscous network. Additionally, significant rate-dependent shear strain occurs in LCEs under uniaxial tension, showing non-monotonic changes when the angle between the stretching and the initial director is large enough. Finally, a viscoelastic constitutive model, only considering the viscosity of the network by introducing multiplicative decomposition of the deformation gradient, is utilized to manifest the relation between rate-dependent macroscopic deformation and microscopic director rotation in LCEs.
1. Introduction
Liquid Crystal Elastomers (LCEs) are special polymers combining crosslinked elastomers with rod-like liquid crystal (LC) mesogens.1 Nematic LC mesogens tend to align in a specific orientation, with the average direction called the director, d,2–4 which can be identified by their uniaxial optical axis. LCEs have unique mechanical behavior attributed to the strong coupling effect between their macroscopic stress and microscopic director order. When LC mesogens are heated above a transition temperature Tni, they undergo a phase transition from the aligned nematic phase to randomly oriented isotropic phase, inducing macroscopic contraction of LCEs.1 Moreover, external stimuli, such as light irradiation,5–7 magnetic fields,8–10 and electrical fields11–14 can trigger the phase transition or reorient the director of LCEs, which can lead to spontaneous strain approaching 400%15,16 or stress if constrained. On the other hand, mechanical deformation not parallel to the director can reorient the director to the stretching direction,1,17–22 inducing a stress plateau in the stress–strain relation.1,23 The unique mechanical behaviors endow LCEs with many potential applications, including soft robots,5,24–26 thermomechanical actuators,27,28 artificial muscles,15,29 and so on.Significantly rate-dependent stress–strain relations and extremely slow shape recovery during relaxation have been reported in LCEs.17,18,30–42 A large number of previous studies about side-chain LCEs show mesogen rotation and network extension have different characteristic times.12,32,34,36 Fukunaga et al.12 studied the deformation of side-chain LCEs under an electro-optical effect and found the director rotates about 1 order of magnitude faster than the mechanical deformation. Clarke et al.32 studied stress relaxation during the polydomain-monodomain transition with stress fitting by a power law in a short time and a logarithmic scale in a long time, which they explained by a proposed theoretical model considering a cooperative mechanical barrier for each domain rotation. Hotta and Terentjev34 systematically investigated the rate-dependent and relaxation responses of side-chain LCEs, and also reported two distinct relaxation regions for long-time stress relaxation. Although fitting both regions by power laws, they found the short-time region shows a power exponent of 0.67, representing the stress relaxation is facilitated by the director rotation due to the polydomain-to-monodomain transformation, while the long-time region shows a power exponent of 0.15, where the director relaxation is almost finished and the LCEs behave like isotropic rubber. Schonstein et al.43 reported a broad distribution of director relaxation times but with a small mean relaxation time on the order of 0.01 s via light scattering. Previous studies showed that shape recovery of LCEs takes a very long time and requires a very slow loading rate of around  to reach quasi-equilibrium mainly due to the slow relaxation of the network.17,34,37,42 These findings suggest that the director rotates slightly faster than the network deforms. Researchers have also shown that the crosslinker forming conditions, director fields, LC phases, chemical components, and many other parameters could profoundly influence the viscoelasticity of LCEs.33,36–41 However, the viscoelasticity of main-chain LCEs was not studied intensively until very recently. The comprehensive understanding of viscoelasticity in main-chain LCEs remains challenging due to the complicated synergy of the network extension and mesogen rotation to give rise to high viscosity. Azoug et al.31 and Martin Linares et al.35 studied the main-chain polydomain LCEs under uniaxial tension, reporting rate-dependent anisotropic stress responses. Moreover, Luo et al.20 evaluated the director alignment of main-chain monodomain LCEs by optical measurements, finding the director almost reaches equilibrium rotation at the loading rate of 450% per min. However, it is not clear what the relaxation time scales of the network extension and director rotation are for main-chain LCEs, and how they influence the macroscopic stress–strain behavior and microscopic director rotation.
to reach quasi-equilibrium mainly due to the slow relaxation of the network.17,34,37,42 These findings suggest that the director rotates slightly faster than the network deforms. Researchers have also shown that the crosslinker forming conditions, director fields, LC phases, chemical components, and many other parameters could profoundly influence the viscoelasticity of LCEs.33,36–41 However, the viscoelasticity of main-chain LCEs was not studied intensively until very recently. The comprehensive understanding of viscoelasticity in main-chain LCEs remains challenging due to the complicated synergy of the network extension and mesogen rotation to give rise to high viscosity. Azoug et al.31 and Martin Linares et al.35 studied the main-chain polydomain LCEs under uniaxial tension, reporting rate-dependent anisotropic stress responses. Moreover, Luo et al.20 evaluated the director alignment of main-chain monodomain LCEs by optical measurements, finding the director almost reaches equilibrium rotation at the loading rate of 450% per min. However, it is not clear what the relaxation time scales of the network extension and director rotation are for main-chain LCEs, and how they influence the macroscopic stress–strain behavior and microscopic director rotation.
To better understand how viscoelastic LC reorientation affects the mechanical responses of LCEs, we need to capture the real-time director rotation at different loading rates. Wide-angle X-ray scattering17,44–46 (WAXS) and polarized Fourier transform infrared spectroscopy22,23,47,48 (FTIR) have been used to measure the mesogen reorientation. However, WAXS can only obtain diffraction patterns at quasi-static loading, while FTIR has a strict requirement of specific functional groups on the chain backbone, giving an angular-dependent absorbance spectrum. Both of them have the restriction that they cannot measure universal main-chain LCEs orientation dynamically. Conversely, polarized optical microscopy is an alternative method to capture mesogen reorientation under fast loading.19,20,46,49 Recently, Luo et al.20 used crossed-polarized optical measurements to evaluate the director rotation in monodomain LCEs at different loading rates. Mistry et al.19 used polarized optical microscopy to measure the director distribution in LCEs subjected to step stretching almost perpendicular to the initial director. Here, we will use crossed-polarized optical measurement to characterize the director rotation of LCEs under oblique stretching at different rates. The optical data will be recorded at different angles of the crossed polarizer and analyzer with respect to the stretching direction at different strains to probe the director. More details can be found in Section 2.
Some viscoelastic models are developed to better understand the viscoelasticity mechanism of LCEs. Zhang et al.50 and Zhou and Bhattacharya51 proposed a viscoelastic model considering both viscous network and director via applying a simple Rayleigh dissipation energy. It shows the semi-soft elasticity effect, rate-dependent stress, and director rotation. However, as the stress is the summation of the elastic and viscoelastic contributions, which is equivalent to a simple Kelvin-Voigt model, it cannot accurately capture the stress response under high loading rates due to an impractical instantaneous non-zero stress, and neither can it capture relaxation tests due to an unrealistic constant stress. Later, Wang et al.52 proposed a nonlinear viscoelastic model by multiplicative decomposition of the deformation gradient to elastic and viscous parts. The predicted stress–strain behavior of LCEs under loading perpendicular to the initial director agrees well with the experimental results.31 Here, following the work of Wang et al.,52 we establish a viscoelastic LCE model by considering more realistic viscosity of the network and low viscosity of the director based on our experimental measurements. Furthermore, the semi-soft elasticity is introduced in the elastic free energy.
This work aims to bridge the existing knowledge gap in understanding the effect of the intricate interplay of director rotation and network extension on the viscoelastic behavior of LCEs. In particular, we systematically characterize the real-time director–stress–stretch relations for main-chain monodomain LCEs with different initial directors under different loading rates, showing not only rate-dependent stress-stretch behavior, but also rate-dependent director–stretch relation. Since director rotation also induces shear strain, we apply digital image correlation (DIC) to quantitatively measure the fields of all the rate-dependent strain components relative to the mesogen rotation. Moreover, we conduct relaxation tests, and record the time evolution of the stress and director under fixed stretch. By comparing the the results from the rate-dependent director–stress–stretch measurements and relaxation tests, we further distinguish the relaxation times of the network and director. To better understand how the two viscoelastic dissipation processes govern the microscopic director rotation and macroscopic deformation, we develop a viscoelastic model via the multiplicative decomposition-based method, which implements more realistic viscosity and elastic energy compared to existing literature. This paper is organized as follows. In Section 2, we introduce the experimental methodology. In Section 3, we report the experimental results, including rate-dependent stress–strain and director-strain relations, and stress and director relaxation results. The theoretical model and the predicted viscoelastic behavior compared with the experimental results are presented in Section 4. Section 5 concludes the paper.
2. Experimental methods
2.1 Sample preparation
In this study, the main-chain monodomain LCEs are synthesized via a two-stage thiol-acrylate Michael addition-photopolymerization (TAMAP) reaction.53 The crosslinker, pentaerythritol tetrakis(3-mercaptopropionate) (PETMP, 95%), and chain extender, 2,2-(ethylenedioxy)diethanethiol (EDDET, 95%), were obtained from Sigma-Aldrich and used as received. The diacrylate mesogen, 1,4-bis-[4-(3-arcyloyoxypropyloxy)benzoyloxy]-2-methylbenzene (RM257, 95%), was purchased from Wilshire company. Dipropylamine (DPA, 98%) and (2-hydroxyethoxy)-2-methylpropiophenone (HHMP, 98%) were selected as the catalyst and photoinitiator to enable the second-stage photopolymerization reaction, respectively. Toluene (98%) was used as the solvent for RM257. To prepare a sample, firstly, RM257 was fully dissolved in a vial with 60 wt% of toluene at 80 °C. Then, PETMP, EDDET, HHMP, and DPA solution (DPA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene = 1
toluene = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) were poured into the solution and mixed using a vortex mixer for 60 s to obtain a uniform solution. The molar ratio of thiol functional groups between PETMP and EDDET was 15
50) were poured into the solution and mixed using a vortex mixer for 60 s to obtain a uniform solution. The molar ratio of thiol functional groups between PETMP and EDDET was 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85, corresponding to a ratio of 15 mol% PETMP. The molar ratio of DPA with respect to the thiol functional group was 1 mol%, while the molar ratio of HHMP was 1 mol%. The solution was degassed for about 2 min to remove all bubbles and then poured into a mold. Then the samples were cured at room temperature for 24 hours and put into an oven at 80 °C for another 24 hours to remove the toluene from the LCE sample. At this stage, thiol-acrylate formed a loose network and the sample showed an opaque appearance at room temperature. There would be an excess of 15 mol% acrylate groups for a second-stage photo-crosslinking reaction. In the second stage, the LCE sample was stretched uniaxially to 90% strain by a mechanical stretcher. The pre-stretch forced mesogens to reorientate to the tension direction, and the sample became transparent, indicating a monodomain LCE. The pre-stretched sample was exposed to UV light for 1 hour to photopolymerize the excessive acrylate groups, forming a denser network. After releasing the samples from the stretcher, a thin film of monodomain LCE sheet remains.
85, corresponding to a ratio of 15 mol% PETMP. The molar ratio of DPA with respect to the thiol functional group was 1 mol%, while the molar ratio of HHMP was 1 mol%. The solution was degassed for about 2 min to remove all bubbles and then poured into a mold. Then the samples were cured at room temperature for 24 hours and put into an oven at 80 °C for another 24 hours to remove the toluene from the LCE sample. At this stage, thiol-acrylate formed a loose network and the sample showed an opaque appearance at room temperature. There would be an excess of 15 mol% acrylate groups for a second-stage photo-crosslinking reaction. In the second stage, the LCE sample was stretched uniaxially to 90% strain by a mechanical stretcher. The pre-stretch forced mesogens to reorientate to the tension direction, and the sample became transparent, indicating a monodomain LCE. The pre-stretched sample was exposed to UV light for 1 hour to photopolymerize the excessive acrylate groups, forming a denser network. After releasing the samples from the stretcher, a thin film of monodomain LCE sheet remains.
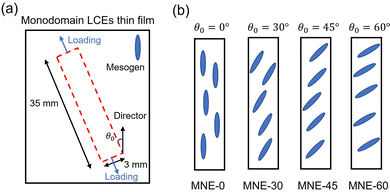
Rectangular strips with a width of 3 mm and length of 35 mm were cut out of the LCE sheet with angles 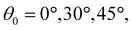 and
and  between the director and the longitudinal direction, shown in Fig. 1. The angles between the longitudinal direction and the director were measured by a protractor and further verified by the optical polariscopy method, which will be discussed in Section 2.3. The samples are designated as monodomain nematic elastomers-θ0 (MNE-θ0), i.e. MNE-0, MNE-30, MNE-45 and MNE-60.
between the director and the longitudinal direction, shown in Fig. 1. The angles between the longitudinal direction and the director were measured by a protractor and further verified by the optical polariscopy method, which will be discussed in Section 2.3. The samples are designated as monodomain nematic elastomers-θ0 (MNE-θ0), i.e. MNE-0, MNE-30, MNE-45 and MNE-60.
2.2 Uniaxial stretch
Uniaxial tension measurement was performed in the longitudinal direction of a LCE specimen at different loading rates using an Instron universal testing machine (Model 5944) with a 50 N load cell to record the LCE rate-dependent stress–strain relationship. A specimen was mounted in a pair of tensile grips, leaving a gauge length of 15 mm. The ratio of the length to width (= 5) is high enough to ensure that the majority of the specimen undergoes uniaxial tension, with negligible edge effects. The thickness was measured at three locations by an electronic caliper, giving the average thickness over all specimens to be 0.11 ± 0.01 mm. The specimens MNE-0, MNE-30, MNE-45, and MNE-60 were uniaxially stretched up to 40%, 100%, 150%, and 200% strain, respectively, with loading rates of 10%/s, 1%/s, and 0.1%/s, and unloaded at the same rates until stress reached zero. The maximum stretches were set as high as possible, but below the fracture points of specimens with different directors to ensure completion of the tests. Although the specimens show complete recovery at room temperature after unloading, to accelerate the recovery process, after each loading and unloading, a specimen was put on a hotplate at 30 °C for 5 min and then at room temperature for another 10 min to release any residual stress. The next test would be run once the specimen was fully recovered. From these tests, we were able to plot the nominal stress as a function of stretch. Here the stretch is defined as λ = L/L0, where L0 is the unstretched gauge length (15 mm) and L is the extended length.2.3 Crossed-polarized optical measurement
Director rotation driven by stretching at different loading rates was dynamically characterized by the crossed-polarized optical measurement. A light source, a polarizer, a specimen stretched by the Instron universal testing machine, an analyzer with the polarization perpendicular to the polarizer, and a camera were set up in the order as shown in Fig. 2a. The appearance change of the specimen under uniaxial tension was recorded by a Canon EOS 6D DSLR camera per 1% strain simultaneously with the measured stress–strain relation. The recorded images were used to measure the transmitted light intensity by ImageJ. Because the dramatic change of specimen thickness under large stretching can alter the measurement of brightness, we recorded the transmitted light intensity for different orientations of the crossed-polarizers by rotating them every 10° to determine the director as a function of stretch. Since the director d is symmetric (d = −d) and the initial director is known, the light intensity is cycled every 90°. Therefore, we can calculate director rotation by only measuring the transmitted light at different angles between the polarizer and the tension direction, φ, from 0° to 90°. The measured transmitted intensity I for different φ (Fig. 2a), can be fitted by the following equation to determine the director,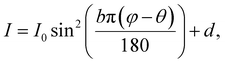 | (1) |
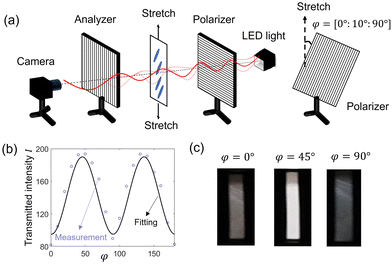 | ||
| Fig. 2 (a) Schematics of the setup of the crossed-polarized optical measurement for directors. (b) The transmitted intensity I was measured as a function of the angle between the polarizer and the tension direction, φ, and fitted by eqn (1) to determine the director θ. (c) The appearance of an MNE-0 specimen showing different brightness was captured by a camera with different angles φ = 0°, 45°, and 90°. | ||
2.4 Digital image correlation (DIC)
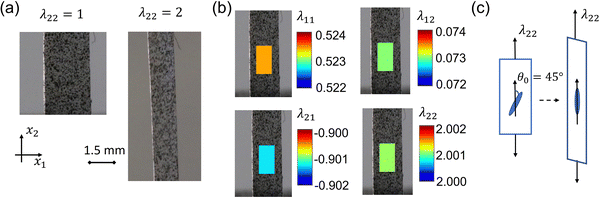
Attributed to director reorientation, LCEs can experience shear strain even under uniaxial external tension. Here we use the 2D digital image correlation (DIC) method to measure all the strain components in the middle region of specimens at different loading rates. To generate a high-quality pattern, Koh-I-Noor Rapidraw ink, which dries fast and has a dark color, was sprayed using a Gocheer airbrush, which generates small droplets, at 30 psi with a 0.3 mm nozzle. The changes of the speckle patterns under deformation were recorded as videos by a Canon EOS 6D DSLR camera along with a Canon 100 mm F/2.8 L macro lens. The videos were set at 30 frames per second (fps). To enhance the optical contrast, a whiteboard was used as a background, and a white LED light was shot on the sample. Fig. 3a presents an example of an MNE-45 specimen with speckle patterns in the undeformed (left) and stretched (right) states.After testing, videos were converted to images by the open-source software FFmpeg, with an imaging rate of 2 fps, 0.5 fps, and 0.2 fps for loading rates of 10%/s, 1%/s, and 0.1%/s, respectively. The images were then read by an open-source 2D DIC Matlab software, Ncorr,54 to calculate the deformation gradient F. We selected the middle part of a specimen as the region of interest (ROI) and set the image of the undeformed sample as the reference image. Here, we set the three critical parameters which can affect the results as the following: subset radius as 25, subset spacing as 3, and strain radius as 20. More details are available in the instruction manual (https://www.ncorr.com/). Fig. 3b shows the distributions of the components of the deformation gradient calculated by Ncorr for the MNE-45 specimen at 100% external strain in the x2 direction at the loading rate of 1%/s. The deformation gradient F under uniaxial tension could be written as:
 | (2) |
2.5 Relaxation tests
To characterize the reduction of stress and evolution of directors of LCEs during relaxation, specimens were subjected to uniaxial stretch performed in the same apparatus as described in Sections 2.2 and 2.3. Specimens MNE-0, MNE-30, MNE-45, and MNE-60 were stretched to a fixed strain, ε0 = 30%, 50%, 70%, and 100%, respectively, at a very high loading rate of 267%/s. The specimens were then held for 3600 seconds, and the stress and director rotation were recorded as functions of time by an Instron universal testing machine and the crossed-polarized optical measurement, respectively. The applied strains are different for different specimens to observe significant director rotation and ensure that specimens would not break during the tests. As the loading rate is very fast, the stress oscillates at the very beginning. We counted the time t0 as the end of loading when the oscillation dies out. t0 is 0.40 s, 0.47 s, 0.56 s, and 0.74 s for specimens MNE-0, MNE-30, MNE-45, and MNE-60, respectively. The stress relaxation curves were fitted with a power law:| σ(t) = m1 + m2(t − t0)−β, | (3) |
3. Experimental results
3.1 Rate-dependent director–stress–strain relationship
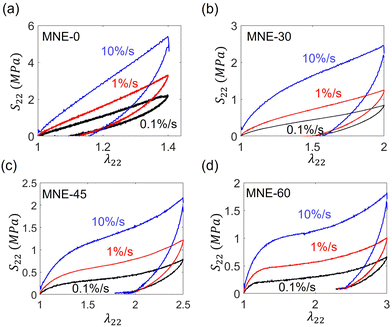
The uniaxial loading-unloading nominal stress–strain curves for LCE specimens with different initial directors under different loading rates, 10%/s, 1%/s, and 0.1%/s, are shown in Fig. 4. The corresponding director–strain relations during loading are shown in Fig. 5. In general, the prepared samples show birefringence, indicating they are monodomain, and the measured initial director is close to the design. For MNE-0, the director does not rotate with strain independent of the loading rates (Fig. 5a). Consequently, the stress–strain loading curves are similar to that of classical neo-Hookean materials. When the initial director is oblique to the elongation direction, as in MNE-30, MNE-45, and MNE-60, the director gradually rotates as the strain increases, and eventually approaches the elongation direction when the strain is high enough (Fig. 5b–d). As a result, the director rotation produces high spontaneous strain and stress plateau in the stress-stretch relation, where the stress increases a little while the strain increases a lot (Fig. 4b–d). For a LCE with a higher initial director angle θ0, the nominal stress is lower at a given level of strain, and the specimen can survive a higher stretch due to the spontaneous strain.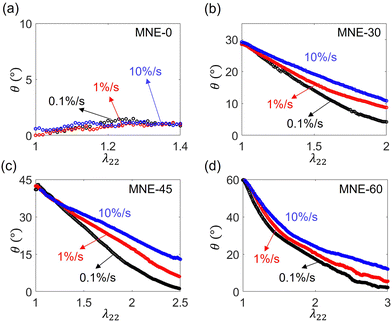 | ||
| Fig. 5 Director reorientation as a function of the applied external stretch λ22 at loading rates 10%/s, 1%/s, and 0.1%/s for (a) MNE-0, (b) MNE-30, (c) MNE-45, and (d) MNE-60, respectively. | ||
All the specimens exhibit rate-dependent stress and director responses. Since the area between a loading and an unloading stress–strain curve represents dissipation energy, our results show that the specimens do not reach equilibrium even at 0.1%/s (Fig. 4). A higher loading rate leads to higher nominal stress and higher dissipation. For MNE-0, where no director rotation occurs, the stress–strain curve is highly rate-dependent and hysteretic, suggesting a highly viscous network extension. For LCEs with initial directors oblique to stretching (MNE-30, MNE-45, MNE-60), directors show rate-dependent rotation from the initial angles to the elongation direction (θ = 0°). At a higher loading rate, the directors rotate less at a given strain, showing delayed behavior due to a shorter response time.
From Fig. 4 and 5, it is obvious that there is a strong relationship between director rotation and stress responses. From MNE-45 and MNE-60, we could observe the stress–strain curves show three regimes: (1) when the stretch λ22 is small, the stress is neo-Hookean-like; (2) as the sample is stretched more, the director rotates more, and a stress plateau occurs; (3) when the director approaches the elongation direction, the stress–strain curve becomes stiffened again. The stress plateau is caused by the spontaneous deformation due to director rotation elaborated by previous studies.1,17,19 As we have shown the rate-dependent director in Fig. 5, it is expected to observe a rate-dependent stress plateau. When a fast loading at 10%/s is applied, the director rotation is delayed, so the sample's deformation is mainly accommodated by network extension. When a slow loading at 0.1%/s is applied, the director rotates more, so the stress plateau is wider and occurs at a lower strain level. In Section 3.3, we will further distinguish the contributions of the director and the network viscosity by stress relaxation tests.
3.2 DIC measurement
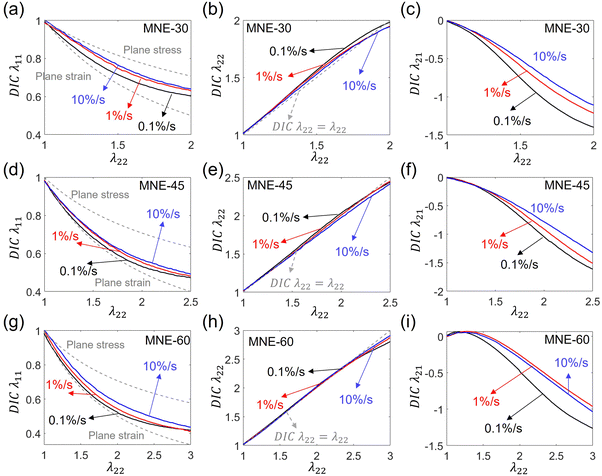
The rate-dependent strain fields of LCEs were measured by DIC. The median value of the strain components λ11, λ21 and λ22 were calculated by Ncorr. Fig. 6 shows λ11, λ22, and λ21 of MNE-30, MNE-45, and MNE-60 measured from DIC at loading rates of 10%/s, 1%/s, and 0.1%/s. Fig. 6b, e and h plot the axial stretch λ22 measured by DIC versus λ22 prescribed by the Instron. Their values are very close (grey dashed curve) for all different loading rates and initial directors, verifying the accuracy of the DIC method.The transverse stretch λ11 measured for MNE-30, MNE-45, and MNE-60 is rate-dependent (Fig. 6a, d and g). When the loading rate is higher, as mentioned in Section 3.1, the director rotates less, leading to lower spontaneous deformation. As a result, LCEs behave more like traditional incompressible elastomers. The stress state is closer to the uniaxial state, which satisfies  (grey soild lines in Fig. 6a, d and g). We could see that the measured λ11 under fast loadings (blue curves) is closer to that of the uniaxial (plaine stress) condition. When the loading rate is low, the spontaneous strain caused by director rotation dominates the deformation. As the director rotation mainly occurs in the x1–x2 plane of the specimens,17 the deformation is close to a plane strain condition (λ11 = 1/λ22, λ33 = 1, grey dashed lines in Fig. 6a, d and g). Our results indeed show that the measured λ11 under slow loadings (black curves) is closer to that of the plane strain case. Moreover, since a lower initial director angle θ0 corresponds to less director rotation, λ11 of MNE-30 is closest to that of the uniaxial condition among the three cases under the same loading condition, while MNE-60 is closest to that of the plane strain condition.
(grey soild lines in Fig. 6a, d and g). We could see that the measured λ11 under fast loadings (blue curves) is closer to that of the uniaxial (plaine stress) condition. When the loading rate is low, the spontaneous strain caused by director rotation dominates the deformation. As the director rotation mainly occurs in the x1–x2 plane of the specimens,17 the deformation is close to a plane strain condition (λ11 = 1/λ22, λ33 = 1, grey dashed lines in Fig. 6a, d and g). Our results indeed show that the measured λ11 under slow loadings (black curves) is closer to that of the plane strain case. Moreover, since a lower initial director angle θ0 corresponds to less director rotation, λ11 of MNE-30 is closest to that of the uniaxial condition among the three cases under the same loading condition, while MNE-60 is closest to that of the plane strain condition.
Fig. 6c, f and i show the measured shear deformation λ21 as a function of the external stretch λ22. Different from traditional elastomers, LCEs exhibit considerable shear strain under uniaxial tension due to the director rotation. As the director is rate-dependent, it is not surprising to see the rate-dependent shear strain. For MNE-30 and MNE-45, the absolute value of λ21 monotonically increases with λ22, exhibiting large shear strain (∼−1.4 for MNE-30 and ∼−1.6 for MNE-45) when the director rotates almost parallel to the stretching direction (λ22 = 2 for MNE-30 and λ22 = 2.5 for MNE-45) at the loading rate of 0.1%/s. For MNE-60, it is interesting to observe that λ21 non-monotonically changes with λ22, i.e. at a small stretch, the shear strain first rises to be positive and then decreases with the stretch to a negative value. When the director rotates almost parallel to the stretching direction (λ22 = 3 at the loading rate of 0.1%/s), the shear strain is around −1.26. Such non-monotonic shearing has been predicted by theoretical modeling before.50,55 When the external stretch λ22 is high, faster loading rates lead to lower shear strain for all different directors due to a delay in director rotation.
3.3 Relaxation test
The stress relaxation of viscoelastic LCEs has been documented for many years.32,34,36 Compared to traditional elastomers, LCEs show more complex relaxation behavior due to the relaxation of both the director and the network, and their coupling effort. Here by applying a nearly instantaneous stretch, we characterize both the stress relaxation and director reorientation over time to distinguish the different characteristic time scales of the network extension and director rotation.Fig. 7 shows the stress relaxation of MNE-0, where the director hardly rotates. The specimen was stretched to 30% strain nearly instantaneously in a short time period t0 and held for 3600 s. The stress was measured as a function of the total experimental time t. The relaxation of stress shows two distinct relaxation regimes and can be fitted by two different power laws as shown in eqn (3). At the early stage (t < 1.5 s), the power law with an exponent around 0.14 fits the experimental data well, while at the long term (t > 1.5 s), relaxation follows a power law with an exponent around 0.40. The long-term exponent is similar to the one previously reported for main-chain smectic polydomain LCEs.36 At a short time, the stress does not match the long-time fitting curve, which may be caused by slight director rotation since mesogens may not align perfectly with the stretching direction.
Fig. 8 shows the relaxation of stress (Fig. 8a–c) and directors (Fig. 8d–i) for MNE-30, MNE-45, and MNE-60. The specimens were stretched to different fixed strains, 50%, 70%, and 100%, respectively, to ensure significant director rotation but no fracture during a test. Then the specimens were held for 3600 s, and the stress and directors were recorded over time. Stress relaxation could be divided into two parts. Compared to MNE-0, the stress relaxation in LCEs with a titled director with respect to the stretching is more complicated at the early stage (t < 1.5 s), as stress relaxation is a synergy of the director reorientation, the backbone orientation, and the polymer chain sliding. As Fig. 8g–i show, the director has already rotated a lot by the time the loading is completed (t = t0). At the stage t0 < t < 1.5 s, MNE-30, MNE-45 and MNE-60, particularly MNE-60, show a the sharp drop in stress (Fig. 8a–c), caused by the spontaneous strain due to director rotation. When t > 1.5 s, the director rotates smoothly, and the stress relaxation can be fitted by a power law well with a power exponent around 0.4 for all the samples, which behaves similarly to MNE-0. This suggests that after t > 1.5 s, stress relaxation is dominated by the network viscosity. The further relaxation of the director after t > 1.5 s may be due to the further extension of the network. As mesogens locate on the backbone, the network slow extension can drag the mesogens to further realign to the stretching direction. Furthermore, it is coincident that the director relaxation could be fitted well with the same power law formula θ = m1 + 20(t − t0)−β of stress relaxation (eqn (3)), but with a much smaller power exponent around 0.04 (Fig. 8d–f).
To probe the characteristic times of the network relaxation and director rotation, we compare the director and stress values from the uniaxial tension tests at different rates and the relaxation tests. We choose some representative cases in Tables 1 and 2.
| Uniaxial tests at 10%/s under 50%, 70% and 100% | Relaxation tests at 5 s, 7 s and 10 s | Uniaxial tests at 1%/s under 50%, 70% and 100% | Relaxation tests at 50 s, 70 s and 100 s | Uniaxial tests at 0.1%/s under 50%, 70% and 100% | Relaxation tests at 500 s, 700 s and 1000 s | |
|---|---|---|---|---|---|---|
| MNE-30 | 19.1 | 16.8 | 16.3 | 15.3 | 14.1 | 13.9 |
| MNE-45 | 26.4 | 23.8 | 24.2 | 22 | 19.1 | 20.9 |
| MNE-60 | 24.2 | 21.1 | 20.7 | 19.0 | 17.4 | 17.3 |
| Uniaxial tests at 100%/s under 30%, 50%, 70% and 100% | Relaxation tests at 3 s, 5 s, 7 s and 10 s | Uniaxial tests at 1%/s under 30%, 50%, 70% and 100% | Relaxation tests at 30 s, 50 s, 70 s and 100 s | Uniaxial tests at 0.1%/s under 30%, 50%, 70% and 100% | Relaxation tests at 300 s, 500 s, 700 s and 1000 s | |
|---|---|---|---|---|---|---|
| MNE-0 | 4.11 | 2.20 | 2.41 | 1.44 | 1.66 | 1.10 |
| MNE-30 | 1.63 | 1.07 | 0.77 | 0.57 | 0.45 | 0.38 |
| MNE-45 | 1.29 | 0.66 | 0.65 | 0.40 | 0.36 | 0.28 |
| MNE-60 | 1.13 | 0.58 | 0.57 | 0.35 | 0.30 | 0.24 |
In Table 1, we listed the directors measured for MNE-30 at 50% uniaxial strain, for MNE-45 at 70% strain, and for MNE-60 at 100% strain at the loading rates of 10%/s (1st column), 1%/s (3rd column), and 0.1%/s (5th column). In 2nd, 4th, and 6th columns, we compared them with the directors measured from the relaxation tests for MNE-30, MNE-45, and MNE-60 at the relaxation time equal to the time needed to load the specimens to the corresponding strain in the uniaxial tests. If the directors from the uniaxial tension tests equal or approach those from the relaxation, this means the director rotation reaches equilibrium at that loading rate. We find that the directors measured from the uniaxial tension tests at 1%/s are close to those from the relaxation tests, and the directors measured from the uniaxial tension tests at 0.1%/s are almost the same as those from the relaxation tests (Table 1). To be more specific, taking MNE-30 as an example, the director is about 19.1° under 50% strain at the rate of 10%/s, while the director reaches around 16.8° when relaxing for 5 s in the relaxation test; the director is about 16.3° under 50% strain at the rate of 1%/s, while the director reaches around 15.3° when relaxing for 50 s in the relaxation test; the director is about 14.1° under 50% strain at the rate of 0.1%/s, while the director reaches around 13.9° when relaxing for 500 s. Allowing ±1° natural error, the results suggest mesogen reorientation approaches equilibrium at 1%/s and has already reached equilibrium at 0.1%/s.
In Table 2, we listed the stress measured for MNE-0 at 30% uniaxial strain, for MNE-30 at 50% strain, for MNE-45 at 70% strain, and for MNE-60 at 100% strain at the loading rates of 10%/s (1st column), 1%/s (3rd column), and 0.1%/s (5th column). Similarly, in the 2nd, 4th, and 6th columns, we compared them with the stress measured from the relaxation tests at the corresponding relaxation time. As a result, the stress values measured from the uniaxial tension tests are much higher than those in the corresponding relaxation tests for all specimens at all rates, which means the material is far away from the equilibrium state. Taking MNE-30 as an example, the stress is about 1.63 MPa under 30% strain at the rate of 10%/s, 0.77 MPa at the rate of 1%/s, and 0.45 MPa at the rate of 0.1%/s, while the stress is around 1.07, 0.57 MPa and 0.38 when the specimens are relaxed for 3 s, 30 s and 300 s, respectively, in the relaxation tests. As we have discussed that the director almost reaches equilibrium at 0.1%/s, we could conclude that the viscosity at slow loading is due to the reorganization of the viscoelastic network. And the director relaxes at least two orders of magnitude faster than the network.
In general, based on the relaxation of the director and stress, we can see that the relaxation time of the network is much larger than that of directors, and the long-time stress relaxation (t > 1.5 s) is mainly attributed to the reorganization of the viscoelastic network. However, since the mesogens are on the main chains of the polymer network, the relaxation is the synergy of the director and network. On one hand, the fast-responsive director rotation causes fast macroscopic deformation, leading to a sharp stress drop at the early stage of stress relaxation. On the other hand, the slowly relaxed network extension further facilitates the director alignment at a long relaxation time.
4. Theoretical model
LCEs show unique stress behavior distinct from traditional elastomers mainly due to mesogen alignment and director rotation. Recently, some viscoelastic models have been developed to describe the rate-dependent stress and director of LCEs subjected to external stretching.50,52 Here, following the work of Wang et al.,52 we will establish a viscoelastic model for LCEs based on multiplicative decomposition, which is widely used for modeling viscoelastic elastomers.52,56 The viscoelastic constitutive model assumes the elastic energy as the sum of the neo-classical free energy and the semi-soft energy,1,57–59 but only considers the viscosity of the network. After fitting to our experimental results, the model will be used to manifest the relation between rate-dependent macroscopic deformation and microscopic director rotation.4.1 A general continuum viscoelastic model for LCEs
Consider a material particle in a body in the reference configuration labeled by its position vector X. It moves to position x at time t in the current configuration. The deformation gradient is defined as FiK = ∂xi(X,t)/∂XK. The rheological model is composed in parallel of an equilibrium spring, representing the elasticity after viscoelastic relaxation, and a Maxwell unit with a non-equilibrium spring and a dashpot connected in series, describing non-equilibrium behavior (Fig. 9). In the Maxwell unit, we assume the total deformation gradient F can be decomposed into an elastic part Fe and a viscoelastic part Fv, F = FeFv. Based on the experiments in Sections 2 and 3, we know that the viscosity of the director rotation is much smaller than that of the network, so we could assume the viscosity is mainly from the network. Thus, the dashpot in the rheological model in Fig. 9 represents the viscous behavior of the network. Here we assume the free energy density in the reference state fr is a function of the deformation gradient F, the elastic part Fe, and director d, fr = fr(F,Fe,d). According to the free energy imbalance for the isothermal condition, we can write the nonequilibrium thermodynamics requirement as | (4) |
 in ḟr,
in ḟr, ![[u with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0075_0307.gif) and ḋ represents a small variation over a small time increment,
and ḋ represents a small variation over a small time increment,  the volume element dV and area element dA are both defined in the reference configuration; the body force and traction do work at the rate
the volume element dV and area element dA are both defined in the reference configuration; the body force and traction do work at the rate  ; γd is a Lagrange multiplier to enforce the unit vector constraint of d, d·d ≡ 1. Using the relation
; γd is a Lagrange multiplier to enforce the unit vector constraint of d, d·d ≡ 1. Using the relation  , we could further expand the inequality (4) in the following manner
, we could further expand the inequality (4) in the following manner | (5) |
 is the first Piola–Kirchhoff stress. The inequality should always be satisfied, requiring each of the above terms to be positive or equal to zero due to the independency of
is the first Piola–Kirchhoff stress. The inequality should always be satisfied, requiring each of the above terms to be positive or equal to zero due to the independency of ![[u with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0075_0307.gif) , ḋ and Ḟe (and therefore Ḟv).
, ḋ and Ḟe (and therefore Ḟv).
Then we can get the force balance equation and traction relation from the first two terms:
| B + divX(S) = 0, | (6) |
| −S·N + T = 0. | (7) |
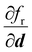 should be in the same direction as d, requiring that
should be in the same direction as d, requiring that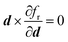 | (8) |
 | (9) |
Next, we assume the free energy of LCEs includes the synergetic work of the director rotation and network extension. We employed the free energy as the summation of the equilibrium and nonequilibrium parts based on the neo-classical theory including the semi-soft elasticity,1,61,62fr = feqr + fneqr, with
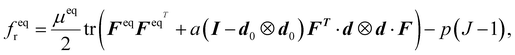 | (10) |
 | (11) |
 and
and  . The effective lengths along or perpendicular to the director (l‖ and l⊥) are assumed to remain constant during deformation, and we can denote their ratio as
. The effective lengths along or perpendicular to the director (l‖ and l⊥) are assumed to remain constant during deformation, and we can denote their ratio as | (12) |
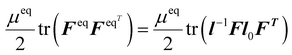 . The energy term could also be interpreted as the classical neo-Hookean elastic energy incorporating a deformation gradient Feq = l−1/2Fl01/2 from the isotropic phase of the reference configuration to the isotropic phase of the current configuration.55 The energy term
. The energy term could also be interpreted as the classical neo-Hookean elastic energy incorporating a deformation gradient Feq = l−1/2Fl01/2 from the isotropic phase of the reference configuration to the isotropic phase of the current configuration.55 The energy term 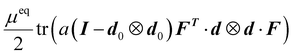 represents the semi-soft elasticity, describing fluctuation of chains with various anisotropy r. When a = 0, it implies the director can rotate with negligible stress; when a > 0, a stress threshold is required to initiate the rotation of the director. We can also rewrite the term as
represents the semi-soft elasticity, describing fluctuation of chains with various anisotropy r. When a = 0, it implies the director can rotate with negligible stress; when a > 0, a stress threshold is required to initiate the rotation of the director. We can also rewrite the term as  indicating that the energy vanishes when FTd is parallel to d0.
indicating that the energy vanishes when FTd is parallel to d0.
Consider the homogeneous deformation of a thin LCE sample with a tilted director subjected to uniaxial stress in the x2 direction, and we assume the director only rotates in the x1–x2 plane, i.e. d = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,0)T. We can rewrite the first Piola-Kirchhoff stress, evolution equation for Lveqn (9), and the constitutive equation for the director eqn (8) as
θ,0)T. We can rewrite the first Piola-Kirchhoff stress, evolution equation for Lveqn (9), and the constitutive equation for the director eqn (8) as
 | (13) |
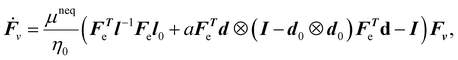 | (14) |
| seqd × d + sneqd × d = 0. | (15) |
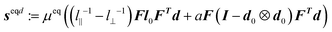 and
and  . Since the deformation is homogeneous, the force balance equation eqn (6) is satisfied automatically. As discussed in Section 2.4, the deformation gradient under uniaxial tension could be written as
. Since the deformation is homogeneous, the force balance equation eqn (6) is satisfied automatically. As discussed in Section 2.4, the deformation gradient under uniaxial tension could be written as | (16) |
 | (17) |
4.2 Analysis of uniaxial tension
Here we study the director θ, shear strain λ21 and engineering stress S22 as functions of the normal stretch λ22 at different loading rates![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) 22. The viscoelastic model proposed in Section 4.1 has five material parameters. As the viscoelastic relaxation is significant, we estimate μneq/μeq = 9 based on the stress relaxation test on MNE-0. The network viscosity η0/(μneq + μeq) = 1 s and the semi-soft parameter a = 0.08 are selected to fit the director reorientation and stress response from the uniaxial tension tests. The parameter r = 5.5 is calculated based on the following thermomechanical deformation test. We recorded the length of a monodomain LCE sample in the nematic configuration at room temperature as lnem. Then we heated the specimen up to 130 °C, which is above the phase transition temperature Tni, using a hotplate, and recorded the length in the isotropic configuration as liso. The macroscopic length change in response to the temperature change is purely due to the phase transition of LCs, correlating to the magnitude of the anisotropic backbone,1,17 and relates to r via:
22. The viscoelastic model proposed in Section 4.1 has five material parameters. As the viscoelastic relaxation is significant, we estimate μneq/μeq = 9 based on the stress relaxation test on MNE-0. The network viscosity η0/(μneq + μeq) = 1 s and the semi-soft parameter a = 0.08 are selected to fit the director reorientation and stress response from the uniaxial tension tests. The parameter r = 5.5 is calculated based on the following thermomechanical deformation test. We recorded the length of a monodomain LCE sample in the nematic configuration at room temperature as lnem. Then we heated the specimen up to 130 °C, which is above the phase transition temperature Tni, using a hotplate, and recorded the length in the isotropic configuration as liso. The macroscopic length change in response to the temperature change is purely due to the phase transition of LCs, correlating to the magnitude of the anisotropic backbone,1,17 and relates to r via: | (18) |
Analytical solutions of the uniaxial engineering stress S22 (Fig. 10a–c), the director angle θ (Fig. 10d–f), and shear strain λ21 (Fig. 10g–i) at different loading rates ![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) 22 = 0.1%/s, 1%/s and 10%/s for different initial directors are plotted as functions of the normal stretch λ22. Obvious rate-dependent stress, director rotation, and shear deformation are observed. At a low loading rate, the director rotates more, providing more spontaneous strain, and the stress caused by the viscosity of the network (the dashpot in Fig. 9) is smaller. As a result, the stress is lower at a lower loading rate. Generally, the stress–strain behavior predicted by the model exhibits a consistent agreement with the experimental observations.
22 = 0.1%/s, 1%/s and 10%/s for different initial directors are plotted as functions of the normal stretch λ22. Obvious rate-dependent stress, director rotation, and shear deformation are observed. At a low loading rate, the director rotates more, providing more spontaneous strain, and the stress caused by the viscosity of the network (the dashpot in Fig. 9) is smaller. As a result, the stress is lower at a lower loading rate. Generally, the stress–strain behavior predicted by the model exhibits a consistent agreement with the experimental observations.
For all applied rates, the director approaches the stretching direction (θ = 0°) as the normal stretch λ22 increases (Fig. 10d–f). However, it is evident that the director rotation is slower at higher loading rates, exhibiting a noticeable delay. Although we only consider the network viscosity in the model, we still observe time-dependent director rotation due to the strong influence of the network on the director in main-chain LCEs. When a uniaxial stress oblique to the initial director is applied, the director tends to rotate instantaneously, but the slow extension of the network can impede the director rotation. As a result, at a high loading rate, the network deforms less under a given normal stretch, constricting the director rotation, and causing a pronounced delay in director rotation. Conversely, at a low rate, as the network deforms more, the director also rotates more.
Fig. 10g–i show the shear strain λ21 as a function of the normal stretch λ22 at different loading rates. The occurrence of shear strain is a consequence of director rotation. In general, it is observed that an increase in λ22 leads to greater rotation of the director, and an increase in the magnitude of λ21 in MNE-30 and MNE-45. Particularly in the case of loading rates at 1%/s and 0.1%/s, the modeling results exhibit a high level of agreement with the experimental findings. However, the shear strain at 10%/s presents inconsistencies with the experimental observation, as it shows a lower value at a lower normal stretch compared to the 1%/s loading rate, which can be attributed to the omission of the viscosity of director rotation in the model. Experimental evidence has indicated that the director does not reach the equilibrium at 10%/s loading rate, and both the viscosity of the director rotation and network extension contribute to the delayed direction rotation.
Moreover, we observe non-monotonic shear strain λ21 with respect to the normal stretch λ22 in MNE-60. The shear strain initially grows to a positive value and then drops to a negative value with the increased normal stretch. Warner and Terentjev et al.1,63,64 have discussed non-monotonic shear strain when the initial director is perpendicular to the stretching direction (θ = 0°). Without the viscous effect, the director and shear strain can be expressed as
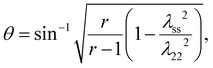 | (19) |
 | (20) |
 related to semi-soft elasticity. When a = 0, λss = 1, and the above equations reflect the case of soft elasticity.
related to semi-soft elasticity. When a = 0, λss = 1, and the above equations reflect the case of soft elasticity.
Fig. 11a and b illustrate the behavior of the director and shear strain based on eqn (19) and (20) for a = 0.1. The director and shear strain start with θ = 90° and λ21 = 0 when λ22 = 1. As the director angle decreases, the shear strain non-monotonically increases and then decreases. Then the director and shear strain end with θ = 0° and λ21 = 0 when  . After the director becomes parallel to the stretching direction, the network further extends with an elastic energy cost without director rotation, behaving the same as traditional neo-Hookean materials.
. After the director becomes parallel to the stretching direction, the network further extends with an elastic energy cost without director rotation, behaving the same as traditional neo-Hookean materials.
The experimental measurement of shear strain for MNE-60 is presented in Fig. 11d as a function of the director. The macroscopic deformation under stretching is depicted in Fig. 11c, illustrating the transition of shear strain from a positive value to a negative value induced by the director rotation. Based on the perpendicular loading discussed earlier, considering the shear strain at the initial director θ0 = 60° as zero in Fig. 11b, the shear strain exhibits non-monotonic behavior as the stretch increases and as the director θ changes from 60° to 0°. Consequently, the non-monotonic shear strain is expected when the initial director deviates much from the stretching direction.
5. Conclusion
To summarize, this paper presents controlled experiments to manifest the relation among mechanical stress, director, and stretch for LCEs with different initial directors at different loading rates. Examined by dynamically uniaxial tension and relaxation tests, we find that the viscoelasticity of LCEs is a synergy of rate-dependent network deformation and mesogen rotation, giving rise to the unique mechanical responses of LCEs, which is further verified by a general continuum viscoelastic model.We successfully measure the rate-dependent stress and director rotation in dynamic tension and relaxation tests. In the uniaxial tension tests, the loading rates range from 0.1%/s to 10%/s and the initial director ranges from 0° to 60° oblique to the stretching direction. We observe realignment of oblique directors to the stretching direction, and reorientation delay when the loading rate is high. A larger director rotation produces a higher spontaneous strain, which leads to a higher stretchability and a more obvious stress plateau. By comparing the stress and director values in uniaxial tension and relaxation tests, we find the viscosity of director rotation is much smaller than that of the network extension. For all specimens, stress does not reach equilibrium even at the slow loading rate of 0.1%/s, while the director almost reaches equilibrium at around 1%/s. Moreover, the stress relaxation in a short time reflects the complicated synergy of quick director rotation and network extension, while in a long time, the stress relaxation can be fitted by a power law which is similar to traditional rubbers, suggesting that the relaxation is dominated by the network extension. Although the viscosity of director rotation is considerably small, in a long-term relaxation, the director continues to rotate as the viscous network extension further realigns the director, and the director relaxation could also be fitted by a power law.
We quantitatively measure the rate-dependent strain components via DIC for LCEs with different initial directors. Our DIC results under uniaxial tension tests reveal homogenous deformation in the middle parts of the LCE samples. At a lower rate, the macroscopic deformation is primarily originated from spontaneous deformation arising from director rotation, exhibiting the stress–strain relation closer to the plane strain case; conversely, at a higher rate, the macroscopic deformation is more attributed to network extension, leading the stress–strain relation closer to the plane stress case. DIC measurements present notable rate-dependent shear strain, where faster loading leads to smaller shear strain, and vice versa. Non-monotonic shear strain is observed when the angle between the initial director and the stretching is large.
We further use a general continuum viscoelastic model to explain the rate-dependent stress, director, and strain. The model incorporates the effect of the viscous network deformation via applying multiplicative decomposition of the deformation gradient to elastic and viscous parts. No director viscosity is considered in this analysis. The analytical solution elucidates the strong coupling between the macroscopic deformation and microscopic director rotation – on one hand, the director rotation provides additional spontaneous deformation, reducing the network extension and corresponding stress levels; on the other hand, the observation of the director reorientation delay indicates that the rate-dependent network deformation influences the rate-dependent director rotation. Furthermore, the analytical results indicate the possibility of non-monotonic shear strain when the angle between the initial director and the stretching direction is large enough.
This work provides a comprehensive investigation into and mechanistic understanding of the rate-dependent behavior of LCEs. The utilization of crossed-polarized optical measurement and DIC allows us to dynamically probe the director and deformation fields for LCEs of different directors under different loading conditions. We conduct experiments to characterize the distinct relaxation time scales of the director rotation and network extension and explain the rate-dependent results using a general viscoelastic continuum model, which enhances our understanding of the director–stress coupling effect. However, it is important to note that a much lower loading rate needs to be applied in order to reach the full equilibrium stress–strain behavior of LCEs.17 Moreover, the efficacy of the model diminishes at high loading rates, where the viscosity of both the director and network needs to be accurately accounted for.50,52
Author contributions
Conceptualization, C. W. and L. J.; methodology – experiment, C. W., S. C. and D. L.; methodology – theory, C. W. and Y. Z.; validation, L. J.; writing – original draft preparation, C. W.; writing – review and editing, S. C., D. L., Y. Z. and L. J.; supervision, L. J.; funding acquisition, L. J. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Science Foundation (NSF) through Grant No. CMMI-1925790. S. C. is supported by a NSF Research Experiences for Undergraduates (REU) supplement through Grant No. CMMI-2131479, and D. L. acknowledges the MESA program at the El Camino Community college for leveraging the financial support, and the Samueli Engineering Transfer Student Summer Research Program (TSSRP) and Summer Undergraduate Research Program (SURP) at the University of California, Los Angeles (UCLA).References
- M. Warner and E. M. Terentjev, Liquid Crystal Elastomers, OUP Oxford, 2007 Search PubMed.
- J. L. Ericksen, Arch. Ration. Mech. Anal., 1991, 113, 97–120 CrossRef.
- F. M. Leslie, Contin. Mech. Thermodyn., 1992, 4, 167–175 CrossRef.
- M. J. Stephen and J. P. Straley, Rev. Mod. Phys., 1974, 46, 617–704 CrossRef CAS.
- M. Rogóż, H. Zeng, C. Xuan, D. S. Wiersma and P. Wasylczyk, Adv. Opt. Mater., 2016, 4, 1689–1694 CrossRef.
- H. Finkelmann, E. Nishikawa, G. G. Pereira and M. Warner, Phys. Rev. Lett., 2001, 87, 015501 CrossRef CAS PubMed.
- Y. Yu, M. Nakano and T. Ikeda, Nature, 2003, 425, 145 CrossRef CAS PubMed.
- M. Winkler, A. Kaiser, S. Krause, H. Finkelmann and A. M. Schmidt, Macromol. Symp., 2010, 291–292, 186–192 CrossRef CAS.
- S. Schuhladen, F. Preller, R. Rix, S. Petsch, R. Zentel and H. Zappe, Adv. Mater., 2014, 26, 7247–7251 CrossRef CAS PubMed.
- A. Kaiser, M. Winkler, S. Krause, H. Finkelmann and A. M. Schmidt, J. Mater. Chem., 2009, 19, 538–543 RSC.
- S. Courty, J. Miné, A. Tajbakhsh and E. Terentjev, Europhys. Lett., 2003, 64(5), 654 CrossRef CAS.
- A. Fukunaga, K. Urayama, T. Takigawa, A. DeSimone and L. Teresi, Macromolecules, 2008, 41, 9389–9396 CrossRef CAS.
- W. Lehmann, H. Skupin, C. Tolksdorf, E. Gebhard, R. Zentel, P. Krüger, M. Lösche and F. Kremer, Nature, 2001, 410, 447–450 CrossRef CAS PubMed.
- E. M. Terentjev, M. Warner and P. Bladon, J. Phys. II, 1994, 4, 667–676 CrossRef CAS.
- H. Wermter and H. Finkelmann, e-Polym., 2001, 1, 013 Search PubMed.
- A. R. Tajbakhsh and E. M. Terentjev, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 181–188 CrossRef CAS.
- S. Okamoto, S. Sakurai and K. Urayama, Soft Matter, 2021, 17, 3128–3136 RSC.
- X. He, Y. Zheng, Q. He and S. Cai, Extreme Mech. Lett., 2020, 40, 100936 CrossRef.
- D. Mistry, P. B. Morgan, J. H. Clamp and H. F. Gleeson, Soft Matter, 2018, 14, 1301–1310 RSC.
- C. Luo, C. Chung, C. M. Yakacki, K. Long and K. Yu, ACS Appl. Mater. Interfaces, 2022, 14, 1961–1972 CrossRef CAS PubMed.
- J. Küupfer and H. Finkelmann, Macromol. Chem. Phys., 1994, 195, 1353–1367 CrossRef.
- H. Higaki, T. Takigawa and K. Urayama, Macromolecules, 2013, 46, 5223–5231 CrossRef CAS.
- K. Urayama, R. Mashita, I. Kobayashi and T. Takigawa, Macromolecules, 2007, 40, 7665–7670 CrossRef CAS.
- C. Ahn, X. Liang and S. Cai, Adv. Mater. Technol., 2019, 4, 1900185 CrossRef CAS.
- S. Wu, Y. Hong, Y. Zhao, J. Yin and Y. Zhu, Sci. Adv., 2023, 9, eadf8014 CrossRef CAS PubMed.
- C. Wang, K. Sim, J. Chen, H. Kim, Z. Rao, Y. Li, W. Chen, J. Song, R. Verduzco and C. Yu, Adv. Mater., 2018, 30, 1706695 CrossRef PubMed.
- K. M. Lee, M. L. Smith, H. Koerner, N. Tabiryan, R. A. Vaia, T. J. Bunning and T. J. White, Adv. Funct. Mater., 2011, 21, 2913–2918 CrossRef CAS.
- C. Ohm, M. Brehmer and R. Zentel, Adv. Mater., 2010, 22, 3366–3387 CrossRef CAS PubMed.
- H. Tian, Z. Wang, Y. Chen, J. Shao, T. Gao and S. Cai, ACS Appl. Mater. Interfaces, 2018, 10, 8307–8316 CrossRef CAS PubMed.
- D. Mistry, N. A. Traugutt, B. Sanborn, R. H. Volpe, L. S. Chatham, R. Zhou, B. Song, K. Yu, K. N. Long and C. M. Yakacki, Nat. Commun., 2021, 12, 6677 CrossRef CAS PubMed.
- A. Azoug, V. Vasconcellos, J. Dooling, M. Saed, C. M. Yakacki and T. D. Nguyen, Polymer, 2016, 98, 165–171 CrossRef CAS.
- S. M. Clarke and E. M. Terentjev, Phys. Rev. Lett., 1998, 81, 4436–4439 CrossRef CAS.
- M. Giamberini, V. Ambrogi, P. Cerruti and C. Carfagna, Polymer, 2006, 47, 4490–4496 CrossRef CAS.
- A. Hotta and E. Terentjev, J. Phys.: Condens. Matter, 2001, 13, 11453–11464 CrossRef CAS.
- C. P. Martin Linares, N. A. Traugutt, M. O. Saed, A. Martin Linares, C. M. Yakacki and T. D. Nguyen, Soft Matter, 2020, 16, 8782–8798 RSC.
- C. Ortiz, C. K. Ober and E. J. Kramer, Polymer, 1998, 39, 3713–3718 CrossRef CAS.
- K. Urayama, S. Honda and T. Takigawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041709 CrossRef PubMed.
- K. Urayama, H. Kondo, Y. O. Arai and T. Takigawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051713 CrossRef PubMed.
- K. Urayama, S. Honda and T. Takigawa, Macromolecules, 2006, 39, 1943–1949 CrossRef CAS.
- S. M. Clarke, A. Hotta, A. R. Tajbakhsh and E. M. Terentjev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 021804 CrossRef CAS PubMed.
- S. Clarke, A. Tajbakhsh, E. Terentjev, C. Remillat, G. Tomlinson and J. House, J. Appl. Phys., 2001, 89, 6530–6535 CrossRef CAS.
- S. M. Clarke and E. M. Terentjev, Faraday Discuss., 1999, 112, 325–333 RSC.
- M. Schönstein, W. Stille and G. Strobl, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 511–517 CrossRef.
- N. A. Traugutt, R. H. Volpe, M. S. Bollinger, M. O. Saed, A. H. Torbati, K. Yu, N. Dadivanyan and C. M. Yakacki, Soft Matter, 2017, 13, 7013–7025 RSC.
- N. S. Murthy and H. Minor, Polymer, 1990, 31, 996–1002 CrossRef CAS.
- C. Ortiz, M. Wagner, N. Bhargava, C. K. Ober and E. J. Kramer, Macromolecules, 1998, 31, 8531–8539 CrossRef CAS.
- J. Li, M. Tammer, F. Kremer, A. Komp and H. Finkelmann, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 17, 423–428 CrossRef CAS PubMed.
- M. Tammer, J. Li, A. Komp, H. Finkelmann and F. Kremer, Macromol. Chem. Phys., 2005, 206, 709–714 CrossRef CAS.
- C. Ortiz, R. Kim, E. Rodighiero, C. K. Ober and E. J. Kramer, Macromolecules, 1998, 31, 4074–4088 CrossRef CAS.
- Y. Zhang, C. Xuan, Y. Jiang and Y. Huo, J. Mech. Phys. Solids, 2019, 126, 285–303 CrossRef CAS.
- H. Zhou and K. Bhattacharya, J. Mech. Phys. Solids, 2021, 153, 104470 CrossRef CAS.
- Z. Wang, A. El Hajj Chehade, S. Govindjee and T. D. Nguyen, J. Mech. Phys. Solids, 2022, 163, 104829 CrossRef CAS.
- M. O. Saed, A. H. Torbati, D. P. Nair and C. M. Yakacki, JoVE J. Vis. Exp., 2016, e53546 Search PubMed.
- J. Blaber, B. Adair and A. Antoniou, Exp. Mech., 2015, 55, 1105–1122 CrossRef.
- L. Jin, Z. Zeng and Y. Huo, J. Mech. Phys. Solids, 2010, 58, 1907–1927 CrossRef CAS.
- S. Reese and S. Govindjee, Int. J. Solids Struct., 1998, 35, 3455–3482 CrossRef.
- G. C. Verwey and M. Warner, Macromolecules, 1995, 28, 4303–4306 CrossRef CAS.
- M. Warner, P. Bladon and E. M. Terentjev, J. Phys. II, 1994, 4, 93–102 CrossRef CAS.
- P. Bladon, E. M. Terentjev and M. Warner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 47, R3838–R3840 CrossRef CAS PubMed.
- A. M. Sonnet and E. G. Virga, Dissipative Ordered Fluids: Theories for Liquid Crystals, Springer Science & Business Media, 2012 Search PubMed.
- J. S. Biggins, E. M. Terentjev and M. Warner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041704 CrossRef CAS PubMed.
- Y. Jiang, L. Jin and Y. Huo, J. Mech. Phys. Solids, 2021, 156, 104615 CrossRef CAS.
- G. C. Verwey, M. Warner and E. M. Terentjev, J. Phys. II, 1996, 6, 1273–1290 CrossRef CAS.
- H. Finkelmann, I. Kundler, E. M. Terentjev and M. Warner, J. Phys. II, 1997, 7, 1059–1069 CrossRef CAS.
Footnote |
| † Current address: Mechanical & Aerospace Engineering Department, University of California, San Diego, La Jolla, CA, 92093, USA. |
| This journal is © The Royal Society of Chemistry 2023 |