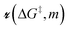Grafting metal complexes onto amorphous supports: from elementary steps to catalyst site populations via kernel regression†
Salman A.
Khan‡
 a,
Craig A.
Vandervelden‡
a,
Craig A.
Vandervelden‡
 a,
Susannah L.
Scott
a,
Susannah L.
Scott
 ab and
Baron
Peters
*cd
ab and
Baron
Peters
*cd
aDepartment of Chemical Engineering, University of California, Santa Barbara, California 93106-5080, USA
bDepartment of Chemistry & Biochemistry, University of California, Santa Barbara, California 93106-5080, USA
cDepartment of Chemical & Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA. E-mail: baronp@illinois.edu
dDepartment of Chemistry, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA
First published on 31st October 2019
Abstract
Ab initio computational studies have made tremendous progress in describing the behavior of molecular (homogeneous) catalysts and crystalline versions of heterogeneous catalysts, but not for amorphous heterogeneous catalysts. Even widely used industrial amorphous catalysts like atomically dispersed Cr on silica remain poorly understood and largely intractable to computational investigation. The central problems are that (i) the amorphous support presents an unknown quenched disordered structure, (ii) metal atoms attach to various surface grafting sites with different rates, and (iii) the resulting grafted sites have different activation and catalytic reaction kinetics. This study combines kernel regression and importance sampling techniques to efficiently model grafting of metal ions onto a non-uniform ensemble of support environments. Our analysis uses a simple model of the quenched disordered support environment, grafting chemistry, and catalytic activity of the resulting grafted sites.
1. Introduction
Most ab initio computational catalysis studies focus on homogeneous catalysts,1–3 enzymes,4–6 or heterogeneous catalysts with ordered structures such as metals,7–11 zeolites,12–14 and crystalline metal oxides.15–17 All of these materials have in common the advantage that many features of the catalyst structure are known. Even for molecular catalysts and enzymes, where the active site resides within a fluctuating environment, there are systematic computational frameworks for averaging over the fluctuations.18–20 In contrast, amorphous catalysts cannot be modelled with small, periodically repeating solid structures, nor by sampling a well-defined ensemble for liquid phase disorder. Instead, the quenched disorder in an amorphous heterogeneous catalyst21,22 is a permanent signature of its non-equilibrium preparation history. Examples within this family include the Phillips catalyst (Cr/SiO2) for ethylene polymerization,23 molybdenum (Mo/SiO2) and tungsten (W/SiO2) catalysts for olefin metathesis,24 and titanium catalysts (Ti/SiO2) for alkene epoxidation.25Because of these difficulties, amorphous catalysts have mostly been avoided in ab initio computational studies. Those exceptions in which calculations on amorphous catalysts were attempted were forced to rely on questionable assumptions.22,26–34 For example, are the model sites representative of the real material? Do the models accurately represent the most active sites? Can reliable conclusions about the reaction kinetics be drawn from a single-site computational model? At present, none of these questions can be satisfactorily answered with ab initio calculations.
These questions are addressed in two papers, this one and a companion. They provide a computational framework that combines machine learning, statistical importance sampling, and population balance modeling techniques. To illustrate the concepts and methods, we begin with a model for an atomically-dispersed catalyst on an amorphous support. The essential features of the model are a quenched disordered support scaffold (to represent an amorphous silica matrix), surface silanol sites where precursors can be attached (to represent surface hydroxyl groups), and a microkinetic model for grafting at each silanol site. These microkinetic models have rate parameters that depend on the individual grafting site characteristics. The rate parameters at each grafting site will be determined, much like in a real ab initio calculation, by structural optimization of the intermediates using a simple force field.
This first paper deals with how the active sites are generated during catalyst preparation. In particular, we show how the populations of both grafted sites and the unreacted grafting sites evolve during an idealized grafting process. If the surface reactions are irreversible, the final metal site distribution will be determined by those surface grafting sites with the fastest grafting kinetics. However, if the surface reactions are reversible, the final grafted site distribution will favor grafted sites that lead to the most stable grafted species. To enable ab initio studies in the future, the algorithm must efficiently predict the characteristics of the most reactive grafting sites and their abundances, without performing exhaustive ab initio calculations for many thousands of grafting sites. We demonstrate how kernel regression can learn to anticipate the outcomes of these optimizations. Then, by applying the kernel regression model to thousands of grafting sites, we can construct a population balance model for the grafting process. The simplicity of our model system allows us to test the accelerated predictions against an exhaustive parameterization from structure optimizations at thousands of grafting sites.
The companion paper uses a grafted site population that reflects both the disordered support and the superimposed grafting kinetics to predict site-averaged kinetics. Because turnover frequencies at individual grafting sites depend exponentially on their activation energies, site-averaged kinetics are difficult to converge without rare events sampling methods. The second paper deals with averaging over the non-uniform distribution of grafted sites to predict the overall kinetics.
The remainder of this paper is as follows. First, we introduce simple models for the amorphous support and grafting kinetics. Next, we use kernel regression tools to predict the grafting thermodynamics and kinetics based on a concise list of grafting site characteristics. Finally, we use the kernel regression results and kinetic models to parameterize the population balance model for grafting.
2. Amorphous silica
Amorphous silica is a commonly used catalyst support because of its thermal and mechanical stability, large surface area, and its chemical inertness. The surface of silica is terminated by silanol groups which may be categorized as isolated, geminal, vicinal etc. Real amorphous silicas are created via sol–gel synthesis, spray drying, pyrolysis, or precipitation methods. Silica can be calcined to increase its mechanical strength and to remove adsorbed water.35–40 The calcination temperature also determines the residual surface silanol density, which in turn influences the activity of the supported catalyst.23,41,42Many studies have used spectroscopic techniques like IR, NMR, and EPR to investigate the populations of different silanol types.43,44 However, in contrast to crystalline materials, the absence of long-range order results in broad peaks that complicate the precise characterization of silica.
Silicas of different types exhibit different ring size distributions,45–47 and silanols of the same type can have different bond angles and different dihedral angles.35,44 These subtle structural differences between silanols and their environments are likely to influence their reactivity. Many investigators have grafted metal atoms to silica via reactions between silanols and molecular complexes like AlCl3,48 GaR3,49,50 TiCl4,51–53 and VOCl3.54,55 These grafting reactions are useful both as probes of local structure and as routes to supported organometallic catalysts.
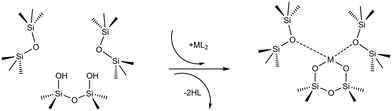
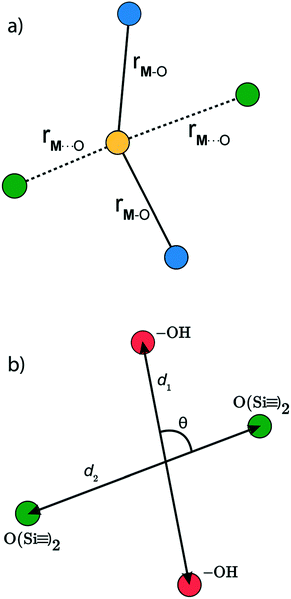
In a typical grafting experiment, a fluid phase molecular precursor reacts with amorphous silica.49,55,56 A protonolysis reaction between the precursor and surface silanols results in a metal atom grafted to the silica surface with one, two, or three M–O–Si linkages, sometimes called monopodal, bipodal, or tripodal species, Fig. 1.24,57–60
Computational studies of atomically-dispersed metals on silica often use cluster models terminated by hydroxyl groups or hydrogen atoms. These models generally range in sizes from a few to tens of silicon atoms.28,30,34,61–67 The cluster models are often carved from crystalline materials like zeolites68 or β-cristobalite.66,69 In such clusters, the peripheral atoms are fixed at positions characteristic of the crystalline material. The de facto assumption is that larger cluster models are more representative of the real amorphous catalyst. Indeed large cluster models more accurately account for elasticity of the silica matrix and for dispersion interactions between adsorbates and the support.33,70 However, each layer of silica requires additional and unjustified assumptions about the environment. In this sense, large cluster models are overly specific, while small cluster models are amenable to systematic investigation of the effects of local grafting site geometry.22
In the past decade, some computational studies generated amorphous silica surfaces that attempt to reproduce experimental observables like surface silanol density and the IR spectrum.71–74 Typically, such surfaces are prepared by molecular dynamics simulations, in which crystalline models are heated to high temperatures followed by rapid quenching to generate disordered structures. Then the bulk amorphous structure is cleaved to create the surface. Unsaturated oxygens are capped with hydrogen atoms, and unsaturated silicons are capped with hydroxyl groups. Finally, pairs of proximal silanols are condensed to achieve the correct surface silanol density. These methods generate atomistic amorphous models of silica with a non-uniform structural distribution of surface silanols. However, such in silico preparation routes for amorphous silica do not correspond to experimental synthesis procedures. In particular, the high surface area of a real silica does not result from cleavage and subsequent functionalization. In addition, the system sizes modelled are typically quite small (100–200 silanols). For comparison, a 10 mg sample of silica with area 350 m2 g−1 and 1.0 silanols per nm2 contains about 1018 silanols.
2.1. A simple model for amorphous silica
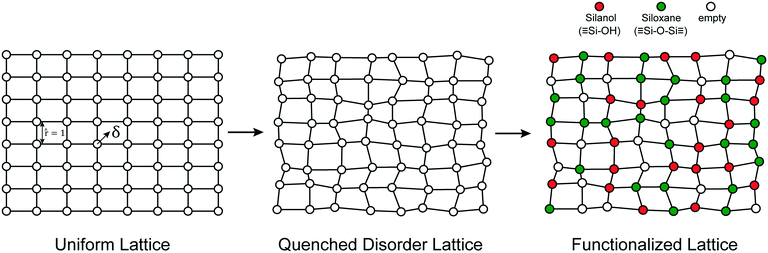
The mechanisms of grafting, activation, and catalytic reactions are still debated for many amorphous catalysts.26,30,50,58,69,75–77 To resolve the outstanding questions, we need methods that can predict the kinetics at each grafting site and estimate proper site-averaged kinetic properties. Then a given support model (if large enough) and proposed mechanism will yield well-defined, site-averaged predictions to be tested against experiments. To develop such methods, we selected a simple example system for which benchmark calculations can be performed exhaustively, for the full ensemble of non-uniform sites. In this section, we propose a simple abstract model of the amorphous support.We model the amorphous support as a 2D lattice with quenched disorder, Fig. 2. Note the loose similarity to the qualitative model of Peri and Hensley.48 First, a uniform lattice is created in which nearest neighbours are separated by a unit (dimensionless) distance. Each site is randomly displaced (δ) from the uniform lattice by random displacements along the x and y directions to create a disordered lattice. Displacements are drawn from an isotropic 2-D Gaussian distribution (described in the ESI†). The lattice is then “functionalized” with hydroxyl (–OH), siloxane (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiOSi
SiOSi![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ), and empty sites with probabilities pOH,psiloxane, and pempty.
), and empty sites with probabilities pOH,psiloxane, and pempty.
2.2. Grafting molecular metal complexes: a simple model
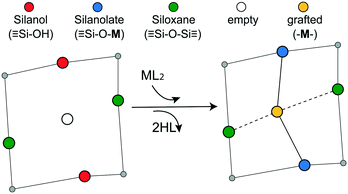
Grafting sites in our model are empty sites surrounded by a pair of vicinal hydroxyls on one axis and a pair of siloxanes on the other axis. Fig. 3 shows a grafting site located between vicinal silanols (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiOH)2 and two siloxanes (
SiOH)2 and two siloxanes (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiOSi
SiOSi![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ). The precursor ML2, a molecular complex, in our model has two displaceable ligands. A real catalyst precursor may have additional ligands like chloride, oxo, or methyl groups that remain bonded to the metal M after grafting. The metal is grafted as a bipodal species (
). The precursor ML2, a molecular complex, in our model has two displaceable ligands. A real catalyst precursor may have additional ligands like chloride, oxo, or methyl groups that remain bonded to the metal M after grafting. The metal is grafted as a bipodal species (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiOMOSi
SiOMOSi![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ) upon reaction of ML2 with the vicinal hydroxyls to eliminate two HL molecules. The metal may also interact with neighbouring siloxanes to form M⋯O(Si
) upon reaction of ML2 with the vicinal hydroxyls to eliminate two HL molecules. The metal may also interact with neighbouring siloxanes to form M⋯O(Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) )2 bonds. The strengths of the
)2 bonds. The strengths of the ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO–M and M⋯O(Si
SiO–M and M⋯O(Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) )2 bonds depend on the local geometry near the grafting site.
)2 bonds depend on the local geometry near the grafting site.
2.3. Computing grafting rates on the amorphous silica model
To model grafting kinetics of vicinal silanol sites on the amorphous 2D lattice, we consider the grafting mechanism outlined in sec. 2.2. The grafting process at each vicinal silanol site is assumed to be irreversible with the following rate law:| r(x) = k(x)[ML2]. | (1) |
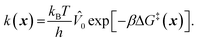 | (2) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 0) per particle.
0) per particle.
Next, we use a linear free energy relationship (LFER) to model the grafting free energy barrier. Specifically, we assume that the free energy of grafting is linearly related to the activation barrier for grafting:78
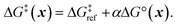 | (3) |
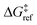 is the grafting barrier for a reference grafting site with a thermoneutral grafting free energy (ΔG° = 0). The value of α indicates the position of the transition state between the reactant and product states. Small values of α (near 0) indicate an early transition state that resembles the reactants. Large values of α (near 1) indicate a transition state that resembles the products. In practice, intermediate values of α are common, so we have chosen α = 1/2.85 The value of
is the grafting barrier for a reference grafting site with a thermoneutral grafting free energy (ΔG° = 0). The value of α indicates the position of the transition state between the reactant and product states. Small values of α (near 0) indicate an early transition state that resembles the reactants. Large values of α (near 1) indicate a transition state that resembles the products. In practice, intermediate values of α are common, so we have chosen α = 1/2.85 The value of 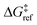 determines the time scale for grafting, but it will have no bearing on results after non-dimensionalization. Thus, to complete the kinetic model, including the effects of non-uniform grafting sites, we only need a model for ΔG°(x). The energy to graft the precursor at an empty site is
determines the time scale for grafting, but it will have no bearing on results after non-dimensionalization. Thus, to complete the kinetic model, including the effects of non-uniform grafting sites, we only need a model for ΔG°(x). The energy to graft the precursor at an empty site is| ΔE(x) = 2εHL + VM*(x) − V* − 2εML. | (4) |
| V* = 2εOH. | (5) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) bond energy and M⋯O(Si
bond energy and M⋯O(Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) )2 bond energy are modelled as Morse potentials:
)2 bond energy are modelled as Morse potentials:| εi(r) = Di(1 − exp[−ai(r − ri,eq)])2 − Di. | (6) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) or M⋯O(Si
or M⋯O(Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) )2), Di is the equilibrium energy of the interaction, ai is related to the width of the potential well, ri,eq is the equilibrium distance, and r is the metal–oxygen bond length. All constants defined in this section are shown in Table 1. VM*(x) is computed by optimizing the position of the metal with surrounding hydroxyl and siloxane positions fixed:
)2), Di is the equilibrium energy of the interaction, ai is related to the width of the potential well, ri,eq is the equilibrium distance, and r is the metal–oxygen bond length. All constants defined in this section are shown in Table 1. VM*(x) is computed by optimizing the position of the metal with surrounding hydroxyl and siloxane positions fixed: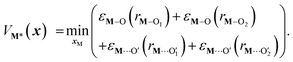 | (7) |
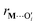 is a metal–siloxane coordination distance, as shown in Fig. 4a. The bond lengths are functions of the (variable) metal atom position xM and the (quenched/fixed) peripheral siloxane and silanol locations in x. The optimization indicated in eqn (7) therefore involves optimization of the metal atom position within the fixed peripheral environment.
is a metal–siloxane coordination distance, as shown in Fig. 4a. The bond lengths are functions of the (variable) metal atom position xM and the (quenched/fixed) peripheral siloxane and silanol locations in x. The optimization indicated in eqn (7) therefore involves optimization of the metal atom position within the fixed peripheral environment.
Finally, the free energy of grafting is computed using
| ΔG°(x) = ΔE(x) + ΔPV − TΔS°. | (8) |
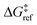 , the site-independent terms in eqn (8) have no bearing on the results after non-dimensionalization.
, the site-independent terms in eqn (8) have no bearing on the results after non-dimensionalization.
3. Kernel regression model for grafting barriers
Because ab initio calculations are costly, computational studies of catalyst grafting have been based on single sites, or at most a few sites. Ultimately, one hopes to make predictions about grafting across the entire distribution of non-uniform sites. In this section, we propose a machine learning method (kernel regression) to learn structure–property relations from a modest number of training calculations.86–88 Kernel regression was chosen because it is a non-parametric method; hence it does not need a predefined form for the fitting function. Specifically, we will use calculations at a small collection of grafting sites to predict barriers and kinetics for all grafting sites.The training data includes a collection of computed barriers, ΔG‡(x1), ΔG‡(x2), ΔG‡(x3), etc. The estimated barrier for a new peripheral environment x is a kernel-weighted average of the training data:
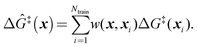 | (9) |
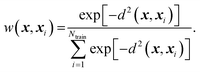 | (10) |
| d2(x, x′) = (x − x′)TS(x − x′). | (11) |
| S = AAT. | (12) |
The training data from optimization of a small collection of grafting sites is used in a leave-one-out objective function
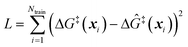 | (13) |
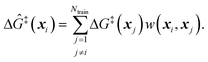 | (14) |
4. Local coordinates
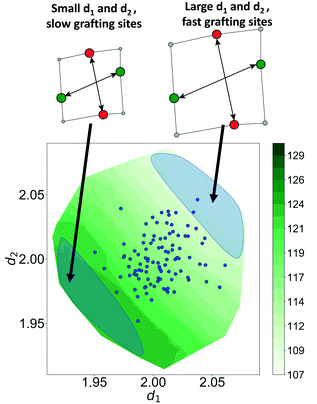
The Gaussian kernel function in eqn (9) can be constructed from the complete set of internal coordinates for the local environment. However, a subset of the internal coordinates will usually be sufficient to predict the activation barriers. We do not know a priori which coordinates are most important, but these can be identified as illustrated below.The local environment of silanol and siloxane groups in our model is specified by five coordinates (2 dimensions × 4 “atoms” – 1 rotation – 2 centre-of-mass translations). We use three of the five coordinates to construct the kernel regression model: (1) distance between OH groups (d1), (2) distance between siloxane groups (d2), and (3) angle between the OH-siloxane groups (θ), Fig. 4.
5. Sites with non-uniform grafting barriers: a population balance perspective
As described in sec. 2., an amorphous support will have a distribution of grafting sites with different grafting rates. As time progresses, the most reactive grafting sites will be consumed, while grafting sites with higher reaction barriers remain unreacted and reduce the rate of further grafting. This situation can be modelled using the following population balance scheme: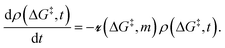 | (15) |
is the rate at which the sites react (eqn (1)), and m = [ML2]/
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 0−1 is the ratio of the concentration of the precursor ML2 in the gas phase to the reference concentration (
0−1 is the ratio of the concentration of the precursor ML2 in the gas phase to the reference concentration (![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 0−1) at which ΔG‡ is computed. The rate of change of m is
0−1) at which ΔG‡ is computed. The rate of change of m is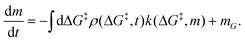 | (16) |
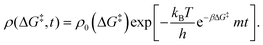 | (17) |
Defining non-dimensional time as:
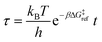 | (18) |
| ρ(ΔG‡, τ) = ρ0(ΔG‡)exp[−e−βαΔG°mτ]. | (19) |
6. Results and discussion
6.1. Evolution of grafting site population
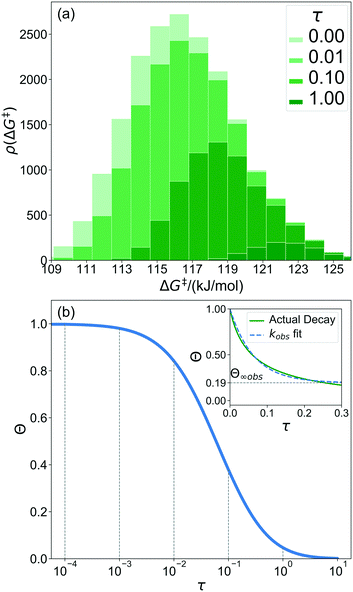
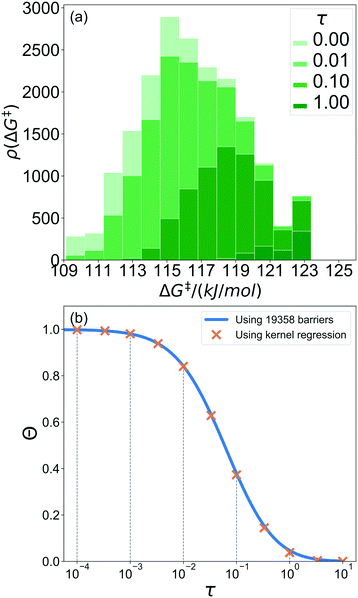
A 1500 × 1500 lattice was randomly perturbed using the procedure outlined in sec. 2.1. A total of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 grafting sites were identified. A metal atom was placed in each grafting site, and its position was optimized. The grafting free energy barrier was computed for each grafting site. A histogram of the results was constructed to approximate the initial distribution ρ0(ΔG‡). Note that the horizontal axis depends on the choice of
368 grafting sites were identified. A metal atom was placed in each grafting site, and its position was optimized. The grafting free energy barrier was computed for each grafting site. A histogram of the results was constructed to approximate the initial distribution ρ0(ΔG‡). Note that the horizontal axis depends on the choice of 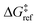 and ΔS°/kB, i.e., different values of these parameters will shift the distribution left and right along the ΔG‡ axis. In a real system, ab initio calculations yield ΔG‡ and ΔS° values for all grafting sites with no adjustable parameters, so there would be no arbitrary shift. Following this, eqn (19) was used to compute the evolution of the unreacted grafting site population, Fig. 5a.
and ΔS°/kB, i.e., different values of these parameters will shift the distribution left and right along the ΔG‡ axis. In a real system, ab initio calculations yield ΔG‡ and ΔS° values for all grafting sites with no adjustable parameters, so there would be no arbitrary shift. Following this, eqn (19) was used to compute the evolution of the unreacted grafting site population, Fig. 5a.
The initial range of grafting barriers spans 23 kJ mol−1. Grafting sites with the lowest barriers react first, so the distribution shifts to the right as grafting proceeds. The 23 kJ mol−1 width of the distribution causes the grafting sites to react at markedly different rates. The fastest grafting sites react in about 10−4τ. Grafting is complete in about 10 τ.
During a grafting experiment, the total number of grafted sites at any time can be measured, e.g., by monitoring the amount of HL released. The fraction of unreacted vicinal silanol sites (relative to the total number of vicinal silanol sites) is:
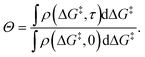 | (20) |
Fig. 5b shows the evolution of the fraction of unreacted vicinal silanols (note the log scale). Grafting progress slows dramatically as the most reactive grafting sites vanish from the distribution. In an experiment, the reaction might seem complete when all the vicinal silanols with low barriers have reacted. The inset of Fig. 5b shows how the data would appear if the fraction of unreacted silanols were monitored only for time 0 < τ < 0.3. The inset also shows a fit to the common pseudo-first-order kinetic model Θ = Θ∞ (1 − Θ∞)exp(−kobsτ). Here Θ∞ is a “final” fraction of unreacted vicinal silanol sites and kobs is an “apparent” grafting rate constant. Over the range 0 < τ < 0.3, the data appears to be approximately an exponential decay, thus one might infer that all silanols react with the same rate constant (kobs), and that 19% (from Θ∞obs = 0.19) of the vicinal silanol sites are unreactive. However, all of the silanols (in this model) do react at exponentially longer time intervals. The final silanol sites react last because they are different. Therefore, they change the distribution of grafted sites, and may also change the catalytic activity. Hence, it is important to analyse grafting kinetics on a logarithmic time scale.
Predictions about catalytic activity require information about the abundance of grafted sites and their characteristics. Both the grafting kinetics and the catalytic turnover frequency at a particular grafted site depend on the local grafted site environment. However, the most readily grafted sites may not correspond to the most catalytically active sites. Therefore, predictions of the overall catalyst activity require predictions about grafting propensity and characteristics of the grafted sites. The companion paper develops tools for computing site-averaged kinetics starting from the grafted distribution.93
6.2. Applying kernel regression to predict grafting barriers
The kernel regression model was trained on grafting barriers for 100 vicinal silanol sites randomly sampled from the set of all 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 grafting sites using local coordinates described in sec. 4. Justification for choosing a training set size of 100 is provided in section S2 of the ESI.† A parity plot of the true ΔG‡ values and kernel regression ΔG‡ predictions is shown in Fig. 6.
368 grafting sites using local coordinates described in sec. 4. Justification for choosing a training set size of 100 is provided in section S2 of the ESI.† A parity plot of the true ΔG‡ values and kernel regression ΔG‡ predictions is shown in Fig. 6.
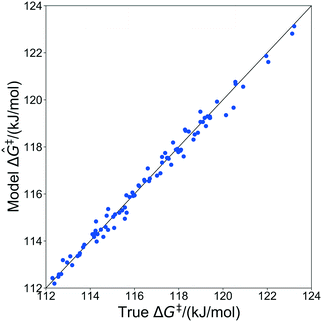 | ||
| Fig. 6 Parity plot showing predictions of grafting activation barriers by the kernel regression model trained on 100 grafting sites. | ||
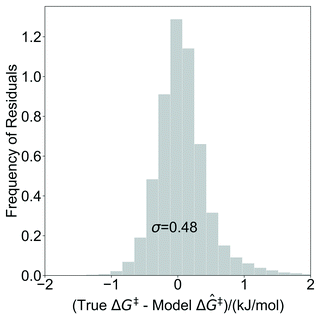
The model trained with 100 ΔG‡ calculations was used to predict grafting barriers for all 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 grafting sites. After training, the only input information for each grafting site are its values of d1, d2, and θ. The residuals of the predictions are plotted as a distribution in Fig. 7. Nearly all residuals are within ±1 kJ mol−1, and the standard deviation of the residual distribution is 0.48 kJ mol−1.
368 grafting sites. After training, the only input information for each grafting site are its values of d1, d2, and θ. The residuals of the predictions are plotted as a distribution in Fig. 7. Nearly all residuals are within ±1 kJ mol−1, and the standard deviation of the residual distribution is 0.48 kJ mol−1.
6.3. Identifying important local coordinates
The results in sec. 6.2. used three of five coordinates to construct the kernel regression model. Three is already a relatively compact structural parameter set, but for this model it can be reduced further. To evaluate the importance of different combinations of local coordinates, the model was retrained by systematically excluding some coordinates. Table 2 shows R2 values for fits with different coordinates. Fig. 8 shows parity plots like the one in Fig. 6, but for a model based only on d1, and for a model based on d1 and d2 (i.e., without θ).| Coordinates | R 2 |
|---|---|
| θ | −0.02 |
| d 2 | 0.52 |
| d 1 | 0.60 |
| d 2, θ | 0.52 |
| d 1, θ | 0.60 |
| d 1, d2 | 0.99 |
| d 1, d2, θ | 0.99 |
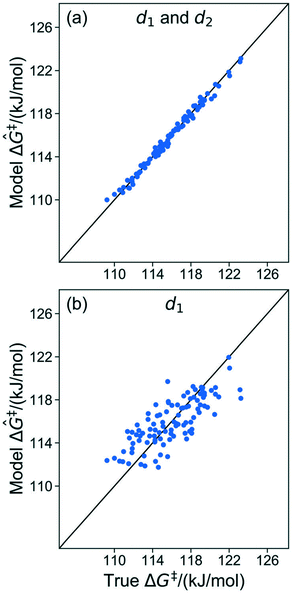 | ||
| Fig. 8 (a) Parity plot of the model trained with d1 and d2. (b) Parity plot of the model trained with d1 only. | ||
The model trained using d1 and d2 (R2 = 0.99) is comparable in accuracy to the model trained using all coordinates (R2 = 0.99). Clearly, d1 and d2 are both important for describing barriers, but θ is inconsequential as its omission does not diminish the accuracy of the kernel regression model. We can also see that the model cannot be further simplified from d1 and d2 dependence. The models trained on only d1 (R2 = 0.60) and d2 (R2 = 0.52) have severely diminished accuracy.
Now, using just two coordinates, we can project the grafting free energy barriers onto a 2D plot, Fig. 9. The barrier decreases monotonically with increasing d1 or d2. Therefore, grafting sites with large values of d1 and d2 react first, while grafting sites with small values of d1 and d2 react more slowly. We emphasize that, even with this simple model, it was not obvious a priori how structural characteristics would influence the grafting kinetics. The procedures in this paper should help to identify features of the most reactive silanol sites.
6.4. Predicting the time evolving population of grafting sites
In this section, we recompute results from section 6.1., now using the kernel regression model. We use the model based only on d1 and d2 and trained on just 100 randomly sampled grafting sites to predict the evolving population of unreacted silanols. The results are shown in Fig. 10a.The training set of 100 grafting sites does not include examples of grafting sites at the extreme fast and slow grafting limits. Accordingly, the trained model does not accurately predict grafting kinetics at the extreme fast and slow limits. Fortunately, the extreme tails account for only a small portion of the total grafting sites, so important properties like the overall grafting progress are still accurately predicted by the model, Fig. 10b.
7. Conclusions
Several factors make ab initio rate calculations prohibitively difficult for single-atom catalysts grafted to amorphous supports such as silica. First, the quenched disorder of the support presents an unknown distribution of local environments. Second, grafted site abundances depend on differences in grafting kinetics at different grafting sites. Third, differences between the grafted sites can cause differences in their catalytic activity. Several investigators are working to overcome the first challenge.71–74 This paper addresses the second challenge by combining transition state theory, kernel regression, and population balance models. A companion paper to this one addresses the third challenge.93To illustrate and test the new methodology, we introduce a simple 2D disordered lattice model of amorphous silica. The model allows us to compute the grafting rate at nearly 20 thousand grafting sites to obtain essentially exact solutions for the evolving grafting/grafted site population during grafting. Then, we trained a kernel regression model to predict grafting rates from a training set of rate calculations at just 100 grafting sites. The regression model predicted barriers with ca. ±0.5 kJ mol−1 accuracy on the test set of about 20 thousand grafting sites. We also showed how the kernel regression results can identify those grafting site characteristics that most strongly influence the grafting kinetics. Finally, the trained kernel regression model was used to predict the evolving population of unreacted silanols.
In future work, we will use this framework with ab initio calculations and more realistic silica models to predict grafting rates and active site abundances during the preparation of real single-site catalysts on amorphous silica. Given a model of amorphous silica, the new algorithm should enable quantitative predictions about the grafting process and the grafted site distribution without assuming the characteristics of the most active or most abundant sites.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Bryan Goldsmith, Marco Caricato, Ward Thompson, Brian Laird and Frederick Tielens for helpful discussions. Department of Energy Basic Energy Sciences Catalysis Award DE-FG02-03ER15467 supported the kernel regression model development. National Science Foundation CBET Award 1605867 supported the population balance model. Department of Energy Computational Chemical Sciences Award DE-SC0019488 supported development of quench-disordered lattice model system. Use was made of computational facilities purchased with funds from the National Science Foundation (CNS-1725797) and administered by the Center for Scientific Computing (CSC). The CSC is supported by the California NanoSystems Institute and the Materials Research Science and Engineering Center (MRSEC; NSF DMR 1720256) at UC Santa Barbara.References
- K. Morokuma and D. G. Musaev, Computational Modeling for Homogeneous and Enzymatic Catalysis: A Knowledge-Base for Designing Efficient Catalysis, John Wiley & Sons, 2008 Search PubMed.
- T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef CAS PubMed.
- B. R. Goldsmith, T. Hwang, S. Seritan, B. Peters and S. L. Scott, J. Am. Chem. Soc., 2015, 137, 9604–9616 CrossRef CAS.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186 CrossRef CAS.
- G. Voth, Computational approaches for studying enzyme mechanism, Academic Press, 2016 Search PubMed.
- I. Tuñón and V. Moliner, Simulating enzyme reactivity: computational methods in enzyme catalysis, Royal Society of Chemistry, 2016 Search PubMed.
- B. Hammer and J. K. Nørskov, in Advances in Catalysis, Academic Press, 2000, vol. 45, pp. 71–129 Search PubMed.
- R. B. Getman, W. F. Schneider, A. D. Smeltz, W. N. Delgass and F. H. Ribeiro, Phys. Rev. Lett., 2009, 102, 076101 CrossRef CAS.
- J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef.
- M. Saleheen and A. Heyden, ACS Catal., 2018, 8, 2188–2194 CrossRef CAS.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef CAS.
- S. R. Blaszkowski and R. A. van Santen, J. Phys. Chem. B, 1997, 101, 2292–2305 CrossRef CAS.
- Y.-P. Li, M. Head-Gordon and A. T. Bell, ACS Catal., 2014, 4, 1537–1545 CrossRef CAS.
- D. Newsome and M.-O. Coppens, Chem. Eng. Sci., 2015, 121, 300–312 CrossRef CAS.
- E. W. McFarland and H. Metiu, Chem. Rev., 2013, 113, 4391–4427 CrossRef CAS.
- T. Le Bahers, M. Rérat and P. Sautet, J. Phys. Chem. C, 2014, 118, 5997–6008 CrossRef.
- F. Li, S. Luo, Z. Sun, X. Bao and L.-S. Fan, Energy Environ. Sci., 2011, 4, 3661–3667 RSC.
- B. C. Knott, M. Haddad Momeni, M. F. Crowley, L. F. Mackenzie, A. W. Götz, M. Sandgren, S. G. Withers, J. Ståhlberg and G. T. Beckham, J. Am. Chem. Soc., 2014, 136, 321–329 CrossRef CAS.
- L. Masgrau and D. G. Truhlar, Acc. Chem. Res., 2015, 48, 431–438 CrossRef CAS.
- E. Brunk, J. S. Arey and U. Rothlisberger, J. Am. Chem. Soc., 2012, 134, 8608–8616 CrossRef CAS.
- B. Peters and S. L. Scott, J. Chem. Phys., 2015, 142, 104708 CrossRef.
- B. R. Goldsmith, E. D. Sanderson, D. Bean and B. Peters, J. Chem. Phys., 2013, 138, 204105 CrossRef.
- M. P. McDaniel, in Advances in Catalysis, ed. B. C. Gates and H. Knözinger, Academic Press, 2010, vol. 53, pp. 123–606 Search PubMed.
- C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323–421 CrossRef PubMed.
- J. K. F. Buijink, J. J. M. van Vlaanderen, M. Crocker and F. G. M. Niele, Catal. Today, 2004, 93–95, 199–204 CrossRef CAS.
- M. F. Delley, F. Núñez-Zarur, M. P. Conley, A. Comas-Vives, G. Siddiqi, S. Norsic, V. Monteil, O. V. Safonova and C. Copéret, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11624 CrossRef CAS.
- L. Floryan, A. P. Borosy, F. Núñez-Zarur, A. Comas-Vives and C. Copéret, J. Catal., 2017, 346, 50–56 CrossRef CAS.
- Ø. Espelid and K. J. Børve, J. Catal., 2002, 206, 331–338 CrossRef.
- A. Fong, C. Vandervelden, S. L. Scott and B. Peters, ACS Catal., 2018, 8, 1728–1733 CrossRef CAS.
- A. Fong, Y. Yuan, S. L. Ivry, S. L. Scott and B. Peters, ACS Catal., 2015, 5, 3360–3374 CrossRef CAS.
- M. Gierada and J. Handzlik, J. Catal., 2018, 359, 261–271 CrossRef CAS.
- H. Guesmi and F. Tielens, J. Phys. Chem. C, 2012, 116, 994–1001 CrossRef CAS.
- C. S. Ewing, A. Bagusetty, E. G. Patriarca, D. S. Lambrecht, G. Veser and J. K. Johnson, Ind. Eng. Chem. Res., 2016, 55, 12350–12357 CrossRef CAS.
- A. M. Jystad, A. Biancardi and M. Caricato, J. Phys. Chem. C, 2017, 121, 22258–22267 CrossRef CAS.
- E. F. Vansant, P. Van Der Voort and K. C. Vrancken, Characterization and chemical modification of the silica surface, Elsevier, 1995 Search PubMed.
- C. J. Brinker and G. W. Scherer, Sol-gel science: the physics and chemistry of sol-gel processing, Academic press, 1990 Search PubMed.
- H. E. Bergna and W. O. Roberts, Colloidal silica: fundamentals and applications, CRC Press, 2005 Search PubMed.
- R. Brückner, J. Non-Cryst. Solids, 1970, 5, 123–175 CrossRef.
- R. Brückner, J. Non-Cryst. Solids, 1971, 5, 177–216 CrossRef.
- O. W. Flörke, H. A. Graetsch, F. Brunk, L. Benda, S. Paschen, H. E. Bergna, W. O. Roberts, W. A. Welsh, C. Libanati and M. Ettlinger, in Ullmann's Encyclopedia of Industrial Chemistry, John Wiley & Sons, 2000 Search PubMed.
- M. Atiqullah, M. N. Akhtar, A. A. Moman, A. H. Abu-Raqabah, S. J. Palackal, H. A. Al-Muallem and O. M. Hamed, Appl. Catal., A, 2007, 320, 134–143 CrossRef CAS.
- M. Oschatz, T. W. van Deelen, J. L. Weber, W. S. Lamme, G. Wang, B. Goderis, O. Verkinderen, A. I. Dugulan and K. P. de Jong, Catal. Sci. Technol., 2016, 6, 8464–8473 RSC.
- A. Rimola, D. Costa, M. Sodupe, J.-F. Lambert and P. Ugliengo, Chem. Rev., 2013, 113, 4216–4313 CrossRef CAS PubMed.
- L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- S. K. Sharma, J. F. Mammone and M. F. Nicol, Nature, 1981, 292, 140–141 CrossRef CAS.
- C. J. Brinker, R. K. Brow, D. R. Tallant and R. J. Kirkpatrick, J. Non-Cryst. Solids, 1990, 120, 26–33 CrossRef CAS.
- B. Humbert, A. Burneau, J. P. Gallas and J. C. Lavalley, J. Non-Cryst. Solids, 1992, 143, 75–83 CrossRef CAS.
- J. B. Peri and A. L. Hensley, J. Phys. Chem., 1968, 72, 2926–2933 CrossRef CAS.
- Z. A. Taha, E. W. Deguns, S. Chattopadhyay and S. L. Scott, Organometallics, 2006, 25, 1891–1899 CrossRef CAS.
- S. D. Fleischman and S. L. Scott, J. Am. Chem. Soc., 2011, 133, 4847–4855 CrossRef CAS.
- A. O. Bouh, G. L. Rice and S. L. Scott, J. Am. Chem. Soc., 1999, 121, 7201–7210 CrossRef CAS.
- X. Gao, S. R. Bare, J. L. G. Fierro, M. A. Banares and I. E. Wachs, J. Phys. Chem. B, 1998, 102, 5653–5666 CrossRef CAS.
- A. Kytökivi and S. Haukka, J. Phys. Chem. B, 1997, 101, 10365–10372 CrossRef.
- E. W. Deguns, Z. Taha, G. D. Meitzner and S. L. Scott, J. Phys. Chem. B, 2005, 109, 5005–5011 CrossRef CAS PubMed.
- H. Zhu, S. Ould-Chikh, H. Dong, I. Llorens, Y. Saih, D. H. Anjum, J.-L. Hazemann and J.-M. Basset, ChemCatChem, 2015, 7, 3332–3339 CrossRef CAS.
- J. Jarupatrakorn and T. D. Tilley, J. Am. Chem. Soc., 2002, 124, 8380–8388 CrossRef CAS.
- J. M. Fraile, J. I. García, J. A. Mayoral and E. Vispe, J. Catal., 2005, 233, 90–99 CrossRef CAS.
- L. Zhong, M.-Y. Lee, Z. Liu, Y.-J. Wanglee, B. Liu and S. L. Scott, J. Catal., 2012, 293, 1–12 CrossRef CAS.
- K. Fukudome, N.-o. Ikenaga, T. Miyake and T. Suzuki, Catal. Sci. Technol., 2011, 1, 987–998 RSC.
- M. K. Samantaray, E. Pump, A. Bendjeriou-Sedjerari, V. D'Elia, J. D. A. Pelletier, M. Guidotti, R. Psaro and J.-M. Basset, Chem. Soc. Rev., 2018, 47, 8403–8437 RSC.
- J. Handzlik, R. Grybos and F. Tielens, J. Phys. Chem. C, 2013, 117, 8138–8149 CrossRef CAS.
- M. Cavalleri, K. Hermann, A. Knop-Gericke, M. Hävecker, R. Herbert, C. Hess, A. Oestereich, J. Döbler and R. Schlögl, J. Catal., 2009, 262, 215–223 CrossRef CAS.
- R. Z. Khaliullin and A. T. Bell, J. Phys. Chem. B, 2002, 106, 7832–7838 CrossRef CAS.
- T.-H. Wang, J. L. Gole, M. G. White, C. Watkins, S. C. Street, Z. Fang and D. A. Dixon, Chem. Phys. Lett., 2011, 501, 159–165 CrossRef CAS.
- N. R. Jaegers, C. Wan, M. Y. Hu, M. Vasiliu, D. A. Dixon, E. Walter, I. E. Wachs, Y. Wang and J. Z. Hu, J. Phys. Chem. C, 2017, 121, 6246–6254 CrossRef CAS.
- J. Handzlik, Int. J. Quantum Chem., 2007, 107, 2111–2119 CrossRef CAS.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS.
- T. P. M. Goumans, C. R. A. Catlow and W. A. Brown, J. Chem. Phys., 2008, 128, 134709 CrossRef CAS PubMed.
- J. Handzlik and J. Ogonowski, J. Phys. Chem. C, 2012, 116, 5571–5584 CrossRef CAS.
- J. Gomes, P. M. Zimmerman, M. Head-Gordon and A. T. Bell, J. Phys. Chem. C, 2012, 116, 15406–15414 CrossRef CAS.
- C. S. Ewing, S. Bhavsar, G. Veser, J. J. McCarthy and J. K. Johnson, Langmuir, 2014, 30, 5133–5141 CrossRef CAS PubMed.
- P. Ugliengo, M. Sodupe, F. Musso, I. J. Bush, R. Orlando and R. Dovesi, Adv. Mater., 2008, 20, 4579–4583 CrossRef CAS.
- A. Comas-Vives, Phys. Chem. Chem. Phys., 2016, 18, 7475–7482 RSC.
- F. Tielens, C. Gervais, J. F. Lambert, F. Mauri and D. Costa, Chem. Mater., 2008, 20, 3336–3344 CrossRef CAS.
- B. Peters, S. L. Scott, A. Fong, Y. Wang and A. E. Stiegman, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E4160 CrossRef CAS PubMed.
- N. M. Peek, D. B. Jeffcoat, C. Moisii, L. van de Burgt, S. Profeta, S. L. Scott and A. E. Stiegman, J. Phys. Chem. C, 2018, 122, 4349–4358 CrossRef CAS.
- S. Lwin, Y. Li, A. I. Frenkel and I. E. Wachs, ACS Catal., 2016, 6, 3061–3071 CrossRef CAS.
- B. Peters, Reaction rate theory and rare events, Elsevier, 2017 Search PubMed.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, Wiley, 2014 Search PubMed.
- B. Peters, J. Phys. Chem. B, 2015, 119, 6349–6356 CrossRef CAS PubMed.
- I. Chorkendorff and J. W. Niemantsverdriet, Concepts of modern catalysis and kinetics, John Wiley & Sons, 2017 Search PubMed.
- M. Boudart and G. Djéga-Mariadassou, Kinetics of heterogeneous catalytic reactions, Princeton University Press, 2014 Search PubMed.
- R. A. Van Santen and M. Neurock, Molecular heterogeneous catalysis: a conceptual and computational approach, John Wiley & Sons, 2009 Search PubMed.
- F. Jensen, Introduction to computational chemistry, John wiley & sons, 2017 Search PubMed.
- J. E. Leffler, Science, 1953, 117, 340–341 CrossRef CAS PubMed.
- P. C. Mahalanobis, Proc. Natl. Inst. Sci. India, 1936, 2, 49–55 Search PubMed.
- T. Hofmann, B. Schölkopf and A. J. Smola, Ann. Stat., 2008, 36, 1171–1220 CrossRef.
- M. Mohri, A. Rostamizadeh and A. Talwalkar, Foundations of machine learning, MIT press, 2018 Search PubMed.
- K. Q. Weinberger and G. Tesauro, Metric learning for kernel regression, International Conference on Artificial Intelligence and Statistics, 2007 Search PubMed.
- G. Strang and S. Strang, Linear Algebra and Its Applications, Thomson, Brooks/Cole, 2006 Search PubMed.
- J. Nocedal and S. Wright, Numerical optimization, Springer Science & Business Media, 2006 Search PubMed.
- C. J. Carey and Y. Tang, metric-learn, 2015 Search PubMed.
- C. Vandervelden, S. A. Khan, S. L. Scott and B. Peters, React. Chem. Eng., 2019 10.1039/C9RE00356H.
Footnotes |
| † Electronic supplementary information (ESI) available: Setting parameters in model chemistry and testing set error for the kernel regression model. See DOI: 10.1039/c9re00357f |
| ‡ Authors with equal contribution. |
| This journal is © The Royal Society of Chemistry 2020 |