Adapted MLP-Mixer network based on crossbar arrays of fast and multilevel switching (Co–Fe–B)x(LiNbO3)100−x nanocomposite memristors†
Aleksandr I.
Iliasov‡
 ab,
Anna N.
Matsukatova‡
ab,
Anna N.
Matsukatova‡
 ab,
Andrey V.
Emelyanov‡
ab,
Andrey V.
Emelyanov‡
 *ac,
Pavel S.
Slepov
d,
Kristina E.
Nikiruy§
a and
Vladimir V.
Rylkov
*ac,
Pavel S.
Slepov
d,
Kristina E.
Nikiruy§
a and
Vladimir V.
Rylkov
 ae
ae
aNational Research Centre Kurchatov Institute, 123182 Moscow, Russia. E-mail: emelyanov_av@nrcki.ru
bFaculty of Physics, Lomonosov Moscow State University, 119991 Moscow, Russia
cMoscow Institute of Physics and Technology (State University), 141700 Dolgoprudny, Moscow Region, Russia
dSteklov Mathematical Institute RAS, 119991 Moscow, Russia
eKotelnikov Institute of Radio Engineering and Electronics RAS, 141190 Fryazino, Moscow Region, Russia
First published on 14th December 2023
Abstract
MLP-Mixer based on multilayer perceptrons (MLPs) is a novel architecture of a neuromorphic computing system (NCS) introduced for image classification tasks without convolutional layers. Its software realization demonstrates high classification accuracy, although the number of trainable weights is relatively low. One more promising way of improving the NCS performance, especially in terms of power consumption, is its hardware realization using memristors. Therefore, in this work, we proposed an NCS with an adapted MLP-Mixer architecture and memristive weights. For this purpose, we used a passive crossbar array of (Co–Fe–B)x(LiNbO3)100−x memristors. Firstly, we studied the characteristics of such memristors, including their minimal resistive switching time, which was extrapolated to be in the picosecond range. Secondly, we created a fully hardware NCS with memristive weights that are capable of classification of simple 4-bit vectors. The system was shown to be robust to noise introduction in the input patterns. Finally, we used experimental memristive characteristics to simulate an adapted MLP-Mixer architecture that demonstrated a classification accuracy of (94.7 ± 0.3)% on the Modified National Institute of Standards and Technology (MNIST) dataset. The obtained results are the first steps toward the realization of memristive NCS with a promising MLP-Mixer architecture.
New conceptsMost existing studies on memristors incorporate them in some typical software network architectures, observing the importance of the memristive structure and characteristics but not that of the network architecture itself. In this work, we highlight the importance of adaptation of software architectures for their subsequent hardware memristive implementation. For this purpose, we use a crossbar array of promising (Co–Fe–B)x(LiNbO3)100−x nanocomposite memristors, which demonstrate some superior characteristics. The eligibility of these memristors for neuromorphic applications is confirmed via hardware perceptron implementation. The presented adapted MLP-Mixer architecture model with incorporated memristive characteristics demonstrates higher classification accuracy on the MNIST dataset and, more importantly, higher robustness to memristive variations and stuck devices in comparison with standard fully connected networks. The obtained results could motivate the development of many more adapted network architectures, paving the way for the realization of efficient and reliable neuromorphic systems based on partially unreliable analog elements. |
Introduction
Brain-inspired neuromorphic computing systems (NCSs) based on neural networks generally have high interconnectivity through synapses, allowing for massively parallel computation and high defect tolerance. They are not confined by time and energy demanding data transfer between storage and computing blocks, which is required for conventional von Neumann systems. These features allow NCSs to efficiently solve cognitive tasks (pattern and speech recognition, big data processing, prediction, etc.).1–4 The last few years have been dedicated to a persistent search for new solutions and architectures for software NCSs, resulting in numerous contributions to the ongoing accuracy race of such systems. The breakthrough 8-layer AlexNet demonstrated the superiority of the convolutional architecture over fully connected architectures in the ImageNet challenge.5 This led to the explosive development and progressive deepening of convolutional architectures, e.g., the ResNet had up to 152 layers and tens of millions of trainable parameters.6 Nowadays, researchers strive to create architectures with reduced dimensions and preserved accuracies, e.g., MobileNet V.2 had about 4 million parameters,7 ENet had about 0.4 million parameters.8 The reduction of the architecture dimensions is favorable for the software implementation of NCSs because large architectures are slow during inference, and the training process of such systems may be complicated.The reduction of the architecture complexity becomes even more crucial for the hardware implementation of NCSs based on memristors. Memristors, devices capable of reversible dynamical resistive switching,9,10 may be based on various materials (e.g., inorganic, organic, nanocomposite, ferroelectric, two-dimensional)11–14 and may emulate synapses15 or neurons16,17 in NCSs. Memristors have been used for NCS realizations, and schemes such as multilayer perceptrons (MLPs),18–20 convolutional,21 long short-term memory22 and others,23,24 including macro25 and neuromorphic vision26 networks, have been successfully demonstrated. Memristors can be organized in passive or active (1T1M) crossbar arrays (with half-pitch size down to 6 nm27) to perform multiply–accumulate operations in a simple one-step way by the electrical current summation, weighted by the conductance state (according to the Kirchhoff's and Ohm's laws).28 Memristor-based formal NCSs are extremely sensitive to undesirable parameter variations inherent in memristive devices (e.g., variation of only 5% can destroy the convergence).29 Therefore, some extreme reductions of the NCS architecture dimensions have been used in this case, e.g., reservoir computing,30 sparse coding,31 or most valuable parameter selection32 schemes. However, these solutions usually lead to a considerable accuracy decrease.33 Another way to mitigate the problem of memristive variations is to realize spiking NCSs with bio-inspired algorithms.34–38 Although there is certain progress in the training of spiking NCSs, such as deep learning-inspired approaches,39 surrogate gradient learning40 and Python packages for spiking NCSs modelling like SpikingJelly41 and SNNTorch,39 efficient training algorithms for spiking NCSs are still underdeveloped, which complicates the transfer of memristor-based spiking NCSs from the current device level to a large system level.42 Consequently, the search for new efficient memristor-based NCS architectures and training algorithms is of high interest.
Recently, Google Research introduced MLP-Mixer, a novel architecture with no convolutional layers and high classification accuracy.43 The MLP-Mixer architecture is especially suitable for the classification of large images. The image is split into several patches, and then two types of fully connected layers are applied: to each image patch independently (channel-mixing) and across patches (token-mixing).43 This research led to a large-scale ongoing discussion about the cause of MLP-Mixer's success and effective reduction of the parameter number, e.g., MLP-Mixer uses the same channel-mixing (token-mixing) MLP for each image patch (across patches), preventing architecture growth. Nevertheless, this architecture still has numerous parameters for a hardware NCS. In this regard, it is particularly interesting to determine whether its strengths may be transferred to a similar architecture with a lower dimensionality for the implementation of a memristor-based NCS with high classification accuracy.
Hence, several points are addressed in the scope of this paper. First of all, we provide a thorough study of passive crossbar arrays of (Co–Fe–B)x(LiNbO3)100−x nanocomposite (CFB-LNO NC) memristors, including a study of the resistive switching (RS) time of such memristors. LiNbO3-based memristors have recently become of high interest,44–46 particularly CFB-LNO NC ones.47 CFB-LNO NC memristors operate through a multifilamentary RS mechanism,48 demonstrate high endurance and long retention, and possess multilevel RS (or very high level of plasticity).49 Secondly, we demonstrate the possibility of perceptron NCS hardware realization with crossbar arrays. Finally, we simulate a formal NCS, which is based on the measured memristive characteristics and possesses the strength of the MLP-Mixer. We emphasize that this is one of the first important steps toward the development of the memristive MLP-Mixer.
Results and discussion
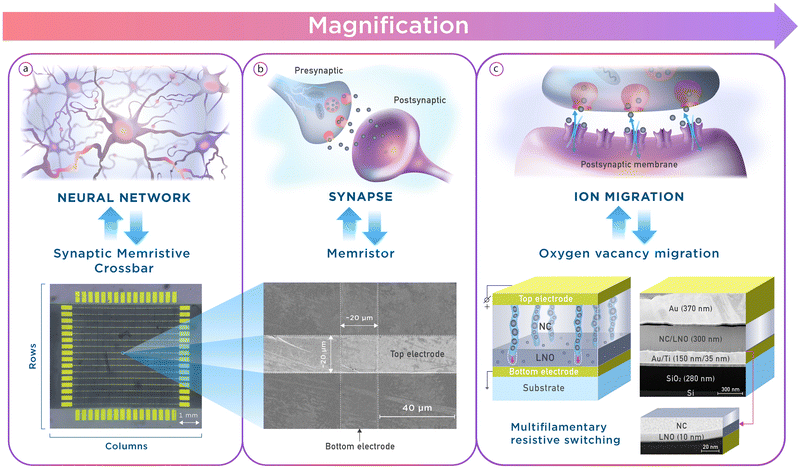
Since the fundamental principles of NCSs are bioinspired, numerous analogies at different scales can be drawn between them and biological neural networks (Fig. 1). Looking at the general picture (Fig. 1a), the latter consist of neurons connected via synapses, and the strength of each connection is determined by the weight, adjustable in the learning process, of the corresponding synapse. Similarly, the conductivity of memristors in the crossbar array can be modified to obtain the required weights of connections between the neurons of NCS. Thus, the crossbar array of memristors is an analog of a net of synapses (Fig. 1a). An optical image of the 16 × 16 memristor crossbar under study is shown in Fig. 1a. The wide dark stripe represents the active memristive material, CFB-LNO NC, and the gold pads are contacts for Au row (horizontal, top) and column (vertical, bottom) electrode buses, made with an additional Ti layer for better adhesion to the wafer.Diving deeper into the details, a single synaptic connection is equivalent to a single memristor at the intersection of the horizontal and vertical electrode buses of the crossbar (Fig. 1b). As a synapse connects an axon of a presynaptic neuron and a dendrite of a postsynaptic one, a single memristor transfers an electric signal from one electrode bus to another, i.e., between artificial neurons connected to these buses. The image of the intersection of the two buses obtained by scanning electron microscopy (SEM) is presented in Fig. 1b. The widths of the electrode buses are 20 μm for both rows and columns. All 256 (16 × 16) of such intersections are separate memristors of the array with the corresponding row bus and column one.
Finally, zooming into the physics and biochemistry of a synapse, the mechanism of synaptic transmission – release of neurotransmitters due to the migration of Ca2+ ions – can be compared to the RS mechanism of CFB-LNO NC memristors (Fig. 1c). The RS mechanism relies on the formation/disruption of a large number of conductive nanochannels (filaments) in the NC and LNO layers due to the nucleation of Co and Fe atoms in the NC and electromigration of oxygen vacancies in the LNO layer.47 Percolation chains of metallic nanoparticles in the former layer act as electrodes with a complex morphology for the latter, the presence of which prevents short-circuiting of the memristor via these chains. The resistive switching process is schematically depicted in Fig. 1c along with a dark-field transmission electron microscopy (TEM) image of a single memristor cross-section and a high-resolution bright-field TEM image of the interface region near the bottom electrode. The latter showed that the thickness of the amorphous LNO layer near the bottom electrode was approximately 10 nm and along with energy dispersive X-ray (EDX) analysis (Fig. S1, ESI†) revealed that the NC layer consists of CoFe nanogranules with an average diameter of 2.4 nm distributed in the LNO matrix (Fig. S2, ESI†).
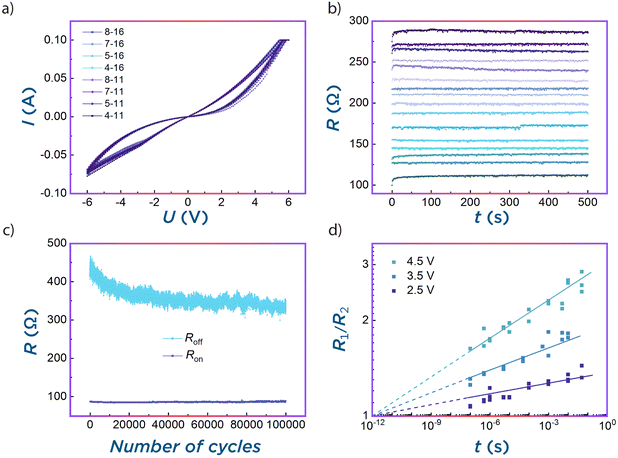
First, the memristive characteristics of the crossbar elements were thoroughly studied. For the following one-layer perceptron architecture realization in hardware, eight memristive weights were needed (the perceptron and its architecture will be discussed further in the manuscript). After measuring and analyzing the characteristics of each memristor in the crossbar array, we chose rows 4, 5, 7, and 8 in columns 11 and 16. This choice was justified by the small device-to-device and cycle-to-cycle variations in the current–voltage characteristics of these memristors (I–V curves in Fig. 2a and Fig. S3, ESI†). It is clear from the figure that the chosen memristors have close low and high resistance states (LRS and HRS, respectively) and RS voltage values. Another subject worth mentioning is the memristors’ working current and, consequently, power consumption. Although the working current is high for the presented memristors, there are several ways to improve it: by decreasing the area of a memristor or altering materials and/or thicknesses of the active layers. The first approach can reduce the current flowing through the device by decreasing the number of conductive filaments in it. Fig. S4 (ESI†) demonstrates RHRS and RLRS for cross-point devices with different areas, while their active layers are the same for each of them and for crossbar memristors. It can be seen that the working current decreases and the resistance increases with a decrease in area. Fig. S5 (ESI†) demonstrates the I–V characteristics of a single memristor made of the same active materials with different thicknesses: ∼230 nm of NC and ∼20 nm of LiNbO3 in contrast to 290 nm of NC and 10 nm of LiNbO3 layers in the crossbar. The working currents are decreased by an order of magnitude in this case. Another important characteristic is plasticity (multilevel RS), which was studied for one typical memristor (Fig. 2b). This memristor demonstrated 16 different resistance states that are stable for at least 500 s (and more than 104 s retention of low and high resistance states, see Fig. S6, ESI†). The stability of each state can be evaluated by calculating the difference between the maximum and minimum resistance (resistance range) of the memristor at this state during the 500 s measuring period. The maximum resistance range was less than 13 Ω for the lowest resistive state and less than 16 Ω for the highest resistive state, whereas the ranges for other states did not exceed 9 Ω (4.5 Ω on average). This value can be considered the minimal step between two consecutive resistive states, which means that ideally, at least 17 states may be possible between the highest and the lowest state (i.e., 19 states in total). It is worth mentioning that all 16 resistive states were obtained using a previously developed write-and-verify algorithm50 with a 5% error tolerance. A decrease in this tolerance or utilization of a recently proposed method of state denoising51 may greatly increase the number of obtainable resistive states. Memristors with stable multilevel resistive switching can be used in further studies with more complex NCSs capable of learning, such as convolutional networks and others.25,52,53 During training and inference processes, memristors are switched between different resistive states multiple times, so their immunity to such consecutive switches (endurance) is crucial for NCS operation. Fig. 2c shows the lack of significant changes in Roff and Ron (the utmost HRS and LRS states, respectively) and the overall operability of the memristor after 105 cycles, which is sufficient for most tasks. It should be noted that the resistance values of the obtained memristors are low (≤1 kΩ), which may cause undesirable sneak current effects in a crossbar array,54,55 which could exceed 40% in our case (Supplementary Note 1 and Fig. S7, ESI†). Special write/read schemes (such as “0”, “V/2” or “V/3”)56 could be accounted for in crossbar measurements to address this issue. In this work, memristors from close rows and columns of the crossbar were used for realization of hardware perceptron to decrease the inequality of sneak currents and electrode buses’ resistance between synapses associated with each output neuron and to minimize the overall power consumption.
Although there are many works regarding LNO-based memristors, their RS kinetics have not been studied in depth yet. Meanwhile, this information may be very helpful for understanding processes that occur during resistive switching of memristors and for the estimation of the RS energy, which may lead to more conscious engineering of such devices. Also, in hardware realization of memristive NCSs (e.g., MLP-Mixer) with in situ learning, a schematically simple yet effective way of synaptic conductivity tuning is by applying voltage pulses to the device. Thus, it is crucial to know the reaction of the memristors to pulses with different amplitudes and durations to achieve the most energy-efficient switching procedure. Therefore, one of the important subjects is the RS kinetics of the separate CFB-LNO NC memristor from the array. A common approach to study the RS kinetics between extreme resistive states Roff and Ron is to apply a switching voltage pulse to the memristor and simultaneously measure its current output57 (see also Methods and Fig. S9, ESI†). In our case, the switching time from HRS to LRS is determined by the time of the voltage pulse setting process, i.e., by the process of charging the memristor capacity (RC-process), which is approximately 50 ns (see Fig. S10, ESI†). Under these conditions, it is clearly impossible to directly study the RS time (tRS) between different resistive states, which can be significantly less than 50 ns. There are some approaches to circumvent this obstacle and measure switching in the picosecond range (almost) directly;58 however, this requires a special design and geometry of the memristor, applicable only for RS kinetics measurement. Meanwhile, in this study, the main goal was to investigate switching time in a real device. Therefore, we developed another approach to estimate the tRS, which includes 3 pulses. The first and last pulses, with amplitude U1 = U3 = 1 V, were used to determine the initial (R1) and final (R2) resistances of the memristor. The middle pulse with varying durations switched the memristor. The switching behavior was studied for the set process with 3 different switching pulse amplitudes: +4.5 V, +3.5 V, and +2.5 V. Pulse durations varied from 100 ns to 50 ms. Further investigation with a higher voltage amplitude and/or shorter pulse time was impossible in our case due to the limitations of the used equipment. The resistance ratios R1/R2 for utilized switching pulse amplitudes and durations are plotted in Fig. 2d (Fig. S11 for the reset process, using pulses with an amplitude of –5 V, ESI†), as well as a linear approximation of the results on a double logarithmic scale. All three approximation lines cross at point (tRS ∼ 10−12; R1/R2 = 1); it means that the minimal internal time of RS in CFB-LNO NC memristors lies in the picosecond range. From this, we estimate the minimal switching energy in the pJ range. It is to note that such a switching time even surpasses that of the figure of merits for memristors.59 Due to the clear dependence of the R1/R2 ratio on the duration of the voltage pulse, the possibility of resistance fine-tuning by altering not only the amplitude but also the duration of the switching pulse can be expected for such memristors (Fig. 2d). Another possibility of the RS to the required state may be by varying the number of short consecutive voltage pulses with the same parameters. The latter approach can be useful in the fully hardware implementation of the memristive NCSs because of the schematic simplicity of such switching circuits. This approach is demonstrated for CFB-LNO NC memristors further in this paper.
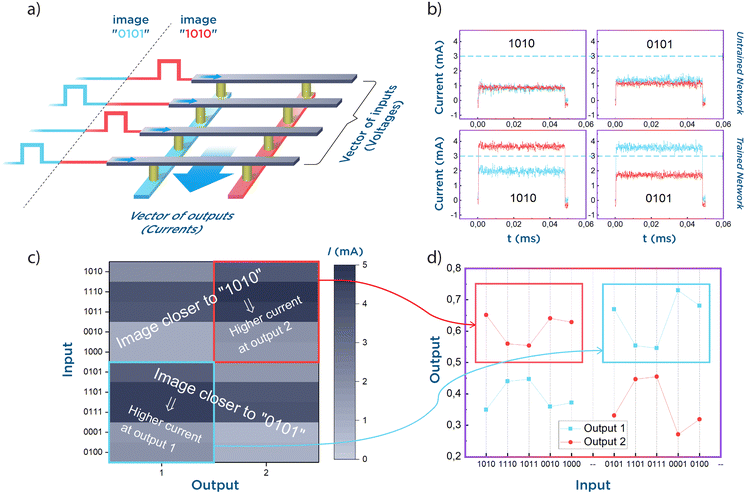
The second part of the manuscript is dedicated to fully connected perceptron realization, a simple yet demonstrative example of memristive NCSs. Fig. 3a shows a scheme of the created hardware perceptron with 4 inputs (rows) and 2 outputs (columns). The goal of this NCS is to perform the classification of two vectors: “0101” and “1010”. A logical one (“1” bit) is fed to the system as a voltage pulse at the corresponding row. The lack of such a pulse at the current iteration (classification of the current vector) means that a logical zero (“0” bit) is fed to the system. Two output currents are measured while the NCS is exposed to the input voltages. A higher current represents the vector being fed to the system. So, the index of the output with a higher current unequivocally states the result of the classification performed by our NCS.
In order to facilitate the training process of the perceptron, it was done ex situ (see Supplementary Note 2 for training process clarification, ESI†). Initially, all 8 utilized memristors were in the Roff state. Then, the obtained weight map in binarized form was transferred to the crossbar array: memristors corresponding to positive weights were switched to Ron, while memristors corresponding to negative weights remained in Roff. Due to the relatively long retention time of our memristors (Fig. 2b and Fig. S4, ESI†), the resulting distribution of the resistances is stable during further operation (inference) of the NCS. After tuning the resistances, the memristors in the crossbar array are able to weight the input voltages with their conductances as weight coefficients in terms of Kirchhoff's and Ohm's laws, thus creating output currents. Fig. 3b shows these currents from the NCS output before (two top plots) and after training (two bottom plots; see Fig. S13 (ESI†) for the weight map of trained NCS) for both possible vectors fed to the system: “1010” (two left plots) and “0101” (two right plots). They can be distinguished only in the case of a trained network – current at the output corresponding to the presented vector is higher than the demarcation line, while the current at another output is lower; the minimal difference between them is more than 16%. The color maps of the outputs are presented in Fig. S14 (ESI†).
The important case of the perceptron's operation, worth paying closer attention to, is noise in the input data. The behavior of the created system under such circumstances was studied by presenting vectors with one flipped bit: logical 1 was changed to logical 0 and vice versa. Output signals of the NCS for every possible noisy input (2 ideal vectors and 4 variants of noise in each of the two vectors; 10 vectors in total) are shown in Fig. 3c. Evidently, the ranges of the output currents vary significantly depending on the total number of logical ones in the presented noisy vector, and the same approach of comparing current to some fixed value is unsuitable. However, after the normalization of the output signals I1,2: Inormalizedk = Ik/(I1 + I2), k = {1, 2}, I1 and I2 are the currents measured in the experiment from the first and second outputs, respectively. The resulting currents can be easily distinguished by comparison with the same value for each noisy input vector. Fig. 3d demonstrates that the created NCS with the normalized current approach is robust to the noise (up to 1 inversed bit in a 4-bit vector) in the input data.
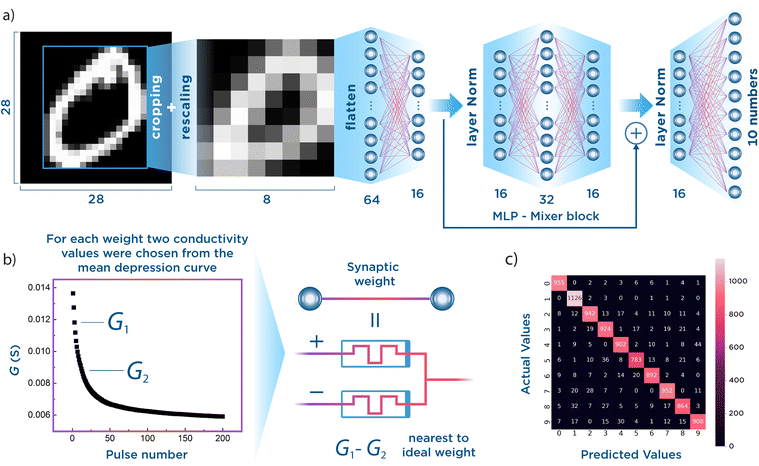
The last part of this manuscript is dedicated to the simulation of more complex NCS architectures based on the memristive characteristics demonstrated above. The Modified National Institute of Standards and Technology (MNIST) dataset classification problem was chosen to facilitate the comparison with other research works. Two architectures were chosen for this problem: a fully connected 2-layer 64 × 54 × 10 NCS and an adapted MLP-Mixer. The fully connected 2-layer NCS and dataset preparation were implemented in accordance with the reference research work.60 The original MLP-Mixer architecture had to be adapted to the chosen problem and reduced to minimize the number of trainable parameters (i.e., weights) without a considerable accuracy decrease. The reduction of architecture dimensions is a crucial step to partially mitigate the influence of memristive variability on network operation. It is also necessary to adjust it to the rescaled MNIST dataset (e.g., splitting images into patches is unnecessary in this case). The proposed adapted architecture is presented in Fig. 4a, and the MLP-Mixer has only channel-mixing layers (details are given in the Experimental section). For simplicity, we refer to this adapted MLP-Mixer architecture as the MLP-Mixer in the following text. Fig. 4b explains the algorithm of the memristor introduction to the neural network, i.e., two conductance values are chosen from the experimental memristive depression curve, so that their difference is the closest to the calculated ideal synaptic weight. More details on this algorithm, including consideration of memristive variability and stuck devices, can be found in the Experimental section.
In this way, two simulations of the memristive NCSs were implemented. The averaged experimental coefficient of variation (CV) for the depression curve equaled ∼1%. A critical problem of the memristive NCSs is the emergence of stuck devices during the training process,61 so 10% of the memristors in the simulation were stuck in Ron state and were untrainable (in accordance with the reference research work).60 The memristive 2-layer NCS demonstrated (91.4 ± 1.1) % accuracy on the test dataset classification, while the memristive MLP-Mixer demonstrated (92.5 ± 0.3) % accuracy (Fig. 4c depicts the confusion matrix for the trained memristive MLP-Mixer, Fig. S15 depicts the training curves for both simulations, ESI†). Note that the number of trainable parameters is almost two times less in the case of the MLP-Mixer architecture. The results of the training process were averaged over 10 consecutive runs. The obtained accuracy of the memristive 2-layer NCS is in good agreement with the reference research work (91.7%).60
Although the depression curve in Fig. 4b considers cycle-to-cycle variations for one device, numerous devices would constitute the future hardware implementation of the network. Therefore, it is necessary to address device-to-device variations. The depression curves obtained from the two memristive devices are shown in Fig. S16 (ESI†). The CV in the case of two memristors (∼3%) is already increased (the CV is ∼1% for one device in Fig. 4b). It is assumed that 10% CV may be considered an approximation of device-to-device variations for many devices. The difference between the two neural network models in this case is more significant: (79.1 ± 3.1) % accuracy for the 2-layer NCS and (82.0 ± 1.3) % accuracy for the MLP-Mixer (Fig. S17 demonstrates the training curves for the both simulations, ESI†). The MLP-Mixer model is more robust to memristive variations due to the reduced number of memristive weights. Table S1 (ESI†) summarizes all obtained results.
Finally, the MLP-Mixer architecture was tested on the full-sized MNIST dataset. In this case, it was sensible to split the images into patches, so 28 × 28 images were split into 4 patches, also the number of neurons increased to process larger images (all layers with 16 neurons were replaced with 64 neurons, while layers with 32 neurons – with 128 neurons). The test accuracy equaled (94.7 ± 0.3)%. Here, the main objective was to demonstrate that the MLP-Mixer architecture is flexible and can be successfully adjusted to the input images of any size while retaining a relatively small number of parameters. Considering the above, MLP-Mixer may be regarded as an optimal architecture. However, the search for other adapted architectures is important in order to create a software basis for the hardware implementation of efficient and reliable memristor-based NCSs.
Conclusions
Thus, we fabricated a 16 × 16 crossbar array of nanocomposite (Co–Fe–B)x(LiNbO3)100−x memristors. We demonstrated their current–voltage characteristics that showed small cycle-to-cycle and device-to-device variations, plasticity with 16 different resistive states, and endurance of more than 105 cycles. We have developed a method for estimating the RS time between the intermediate states of the nanocomposite memristor and have shown that this time can reach the picosecond range. After typical characterization of the memristive devices under study, eight crossbar memristors were implemented in a simple hardware NCS capable of classification of two vectors: “0101” and “1010”. Successful operation of this NCS after setting synaptic weights was shown for both ideal and “noisy” inputs, for which one bit of the image was inverted. Finally, more sophisticated NCSs based on the memristive characteristics were simulated. The simulation demonstrated that the usage of the memristors under study in the accurately adapted MLP-Mixer architecture results in high classification accuracy that is resilient to memristive variations and stuck devices.Experimental
Device fabrication
The M/NC/LNO/M-based crossbar array of memristors was fabricated using laser photolithography on the Heidelberg 66 fs lithograph (patterning electrode buses); ion-beam sputtering on the original system: first, target LiNbO3 (resulting in an ≈10 nm thick layer) and then composite target (Co40Fe40B20)x(LiNbO3)100−x with x ≈10–25 at% and a layer thickness of ≈290 nm; plasma chemical deposition via Trion Oracle III for deposition of an isolating Si3N4 layer (≈40 nm) designated to liquidate edge effects in memristors that may cause electrical breakdown (see details in ref. 62).Electrical measurements
The electrophysical characterization of memristors was performed with the source measurement unit (National Instruments PXIe-4140). Electrical signals, fed to the perceptron, were created via a signal generator (National Instruments PXIe-5413). Output currents (results of perceptron operations) were measured with a 2-channel digital oscilloscope (National Instruments PXIe-5110) as voltages on two resistors (47 Ω), in series to the corresponding outputs of the perceptron. The same scheme and equipment were used in the switching kinetic experiments (see Fig. S9 for the electric scheme, ESI†). For I–V measurements, the compliance current was set to 100 mA for both voltage polarities, with the rate of voltage scan equals 2 V s−1. Depression pulse measurements were performed using square pulses with an amplitude of −3.5 V and a duration of 50 ms, with 200 pulses for each depression curve. It is also worth noting that while switching with shorter than 50 ms pulses as well as obtaining a larger resistance range (like one shown in Fig. 2) with higher voltage pulse amplitudes is possible, we tried to find a compromise between the curve linearity and the resistance ratio.TEM
The structural investigations were carried out using a scanning/transmission electron microscope (S/TEM) Osiris (Thermo Fisher Scientific, USA), equipped with a high angle annular dark field (HAADF) detector (Fischione, USA).NCS simulation
Table 1 summarizes the details on the MLP-Mixer, 2-layer NCS, and reference 2-layer NCS architectures along with the dataset preparation details.| Parameter name | 2-layer NCS (ref. 44) | 2-layer NCS (this work) | MLP-Mixer (this work) |
| Images | Gray + central crop + resized 8 × 8 | Gray + central crop + resized 8 × 8 | Gray + central crop + resized 8 × 8 |
| Mini-batch size | 50 | 100 | 100 |
| Overall images in the training dataset | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Validation dataset | − | + | + |
| Test dataset | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Training cycles (after each the weights were tuned) | 1600 | 800 | 800 |
| Activation function | Rectified linear unit (ReLU) | Gaussian error linear unit (GELU) | (GELU) |
| Architecture | 64 × 54 × 10 | 64 × 54 × 10 | see Fig. 4a |
| Number of weights | 3996 | 3996 | 2208 |
In order to simulate the introduction of the experimental memristive characteristics to the NCS (i.e., on-chip training), the following procedure was conducted for each weight of the network. For each mini-batch, the theoretically required weight update was calculated, using the back-propagation algorithm. Then, the nearest to theoretical experimental weight update was found, calculated as the difference between two mean conduction states of the memristor (both states were chosen from the averaged and normalized depression curve in Fig. 4b). As long as the depression curve had some cycle-to-cycle variation, the chosen states were replaced with corresponding normally distributed random values (experimental standard deviation and mean value were used). Finally, the actual NCS weight was equaled to the difference between these two resulting states. To simulate stuck devices, a random Boolean matrix was created with a fixed ratio of the true/false values and of the same dimensions as the NCS weight matrix. After each mini-batch, all the values of the final NCS weight matrix for which the corresponding Boolean matrix value was true equaled 1, which simulated the memristor stuck in the Ron state. This model is convenient for practical applications and offers a compromise between the over-simplified ideal models and accurate structure-specific models.63
Data availability statement
The data that support the findings of this study is available from the corresponding author upon reasonable request.Author contributions
Aleksandr I. Iliasov, Anna N. Matsukatova and Andrey V. Emelyanov designed and conducted the experiments, and wrote the main manuscript text. Pavel S. Slepov provided the simulations of the sneak current estimations. Kristina E. Nikiruy realized the methodology for crossbar array electrical measurements. Vladimir V. Rylkov provided the funding support and conceptualized the work. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Science Foundation (project no. 22-19-00171) in part of the memristive characteristics investigation and by the NRC Kurchatov Institute (no. 86) in part of the structural investigation. A.N. Matsukatova acknowledges financial support from the Non-commercial Foundation for the Advancement of Science and Education INTELLECT in the neural network simulation part. Measurements were carried out with the equipment of the Resource Centres (NRC Kurchatov Institute). The authors are thankful to N.Yu. Lukashina (illustrator) for the high-quality illustrations, and Yu.V. Grishchenko, K.Yu. Chernoglazov and Prof. A.V. Sitnikov for the sample fabrication.References
- Y. Zhang, Z. Wang, J. Zhu, Y. Yang, M. Rao, W. Song, Y. Zhuo, X. Zhang, M. Cui, L. Shen, R. Huang and J. Joshua Yang, Appl. Phys. Rev., 2020, 7, 011308 CAS.
- K. Berggren, Q. Xia, K. K. Likharev, D. B. Strukov, H. Jiang, T. Mikolajick, D. Querlioz, M. Salinga, J. R. Erickson, S. Pi, F. Xiong, P. Lin, C. Li, Y. Chen, S. Xiong, B. D. Hoskins, M. W. Daniels, A. Madhavan, J. A. Liddle, J. J. McClelland, Y. Yang, J. Rupp, S. S. Nonnenmann, K.-T. Cheng, N. Gong, M. A. Lastras-Montaño, A. A. Talin, A. Salleo, B. J. Shastri, T. F. de Lima, P. Prucnal, A. N. Tait, Y. Shen, H. Meng, C. Roques-Carmes, Z. Cheng, H. Bhaskaran, D. Jariwala, H. Wang, J. M. Shainline, K. Segall, J. J. Yang, K. Roy, S. Datta and A. Raychowdhury, Nanotechnology, 2021, 32, 012002 CrossRef CAS PubMed.
- G. Zhou, Z. Wang, B. Sun, F. Zhou, L. Sun, H. Zhao, X. Hu, X. Peng, J. Yan, H. Wang, W. Wang, J. Li, B. Yan, D. Kuang, Y. Wang, L. Wang and S. Duan, Adv. Electron. Mater., 2022, 8, 2101127 CrossRef CAS.
- X. Niu, B. Tian, Q. Zhu, B. Dkhil and C. Duan, Appl. Phys. Rev., 2022, 9, 021309 CAS.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, Adv. Neural Inf. Process. Syst., 2012, 25, 1097–1105 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770–778 Search PubMed.
- M. Sandler, A. Howard, M. Zhu and A. Zhmoginov, 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 4510–4520 Search PubMed.
- A. Paszke, A. Chaurasia, S. Kim and E. Culurciello, ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation, 2016 DOI:10.48550/arXiv.1606.02147.
- Y. Zhuo, R. Midya, W. Song, Z. Wang, S. Asapu, M. Rao, P. Lin, H. Jiang, Q. Xia, R. S. Williams and J. J. Yang, Adv. Electron. Mater., 2022, 8, 2100696 CrossRef CAS.
- R. Chaurasiya, L.-C. Shih, K.-T. Chen and J.-S. Chen, Mater. Today, 2023, 68, 356 CrossRef CAS.
- Q. Zhao, Z. Xie, Y.-P. Peng, K. Wang, H. Wang, X. Li, H. Wang, J. Chen, H. Zhang and X. Yan, Mater. Horiz., 2020, 7, 1495 RSC.
- R. Guo, W. Lin, X. Yan, T. Venkatesan and J. Chen, Appl. Phys. Rev., 2020, 7, 011304 CAS.
- J.-E. Kim, B. Kim, H. T. Kwon, J. Kim, K. Kim, D.-W. Park and Y. Kim, IEEE Access, 2022, 10, 109760 Search PubMed.
- J. H. Yoon, Y.-W. Song, W. Ham, J.-M. Park and J.-Y. Kwon, APL Mater., 2023, 11, 090701 CrossRef CAS.
- W. Wang, L. Danial, Y. Li, E. Herbelin, E. Pikhay, Y. Roizin, B. Hoffer, Z. Wang and S. Kvatinsky, Nat. Electron., 2022, 5, 870 CrossRef.
- T. Fu, X. Liu, H. Gao, J. E. Ward, X. Liu, B. Yin, Z. Wang, Y. Zhuo, D. J. F. Walker, J. Joshua Yang, J. Chen, D. R. Lovley and J. Yao, Nat. Commun., 2020, 11, 1861 CrossRef CAS PubMed.
- J. Bian, Z. Liu, Y. Tao, Z. Wang, X. Zhao, Y. Lin, H. Xu and Y. Liu, Int. J. Extreme Manuf., 2024, 6, 012002 CrossRef.
- M. Prezioso, F. Merrikh-Bayat, B. D. Hoskins, G. C. Adam, K. K. Likharev and D. B. Strukov, Nature, 2015, 521, 61 CrossRef CAS PubMed.
- A. V. Emelyanov, D. A. Lapkin, V. A. Demin, V. V. Erokhin, S. Battistoni, G. Baldi, A. Dimonte, A. N. Korovin, S. Iannotta, P. K. Kashkarov and M. V. Kovalchuk, AIP Adv., 2016, 6, 111301 CrossRef.
- S. Shchanikov, A. Zuev, I. Bordanov, S. Danilin, V. Lukoyanov, D. Korolev, A. Belov, Y. Pigareva, A. Gladkov, A. Pimashkin, A. Mikhaylov, V. Kazantsev and A. Serb, Chaos, Solitons Fractals, 2021, 142, 110504 CrossRef.
- P. Yao, H. Wu, B. Gao, J. Tang, Q. Zhang, W. Zhang, J. J. Yang and H. Qian, Nature, 2020, 577, 641 CrossRef CAS PubMed.
- C. Li, Z. Wang, M. Rao, D. Belkin, W. Song, H. Jiang, P. Yan, Y. Li, P. Lin, M. Hu, N. Ge, J. P. Strachan, M. Barnell, Q. Wu, R. S. Williams, J. J. Yang and Q. Xia, Nat. Mach. Intell., 2019, 1, 49 CrossRef.
- M. Park, J. Park and S. Kim, J. Alloys Compd., 2022, 903, 163870 CrossRef CAS.
- X. Shan, C. Zhao, X. Wang, Z. Wang, S. Fu, Y. Lin, T. Zeng, X. Zhao, H. Xu, X. Zhang and Y. Liu, Adv. Sci., 2022, 9, 2104632 CrossRef CAS PubMed.
- W. Wan, R. Kubendran, C. Schaefer, S. B. Eryilmaz, W. Zhang, D. Wu, S. Deiss, P. Raina, H. Qian, B. Gao, S. Joshi, H. Wu, H.-S. P. Wong and G. Cauwenberghs, Nature, 2022, 608, 504 CrossRef CAS PubMed.
- X. Wang, C. Chen, L. Zhu, K. Shi, B. Peng, Y. Zhu, H. Mao, H. Long, S. Ke, C. Fu, Y. Zhu, C. Wan and Q. Wan, Nat. Commun., 2023, 14, 3444 CrossRef CAS PubMed.
- S. Pi, C. Li, H. Jiang, W. Xia, H. Xin, J. J. Yang and Q. Xia, Nat. Nanotechnol., 2019, 14, 35 CrossRef CAS PubMed.
- Q. Xia and J. J. Yang, Nat. Mater., 2019, 18, 309 CrossRef CAS PubMed.
- Z. Wang, C. Li, W. Song, M. Rao, D. Belkin, Y. Li, P. Yan, H. Jiang, P. Lin, M. Hu, J. P. Strachan, N. Ge, M. Barnell, Q. Wu, A. G. Barto, Q. Qiu, R. S. Williams, Q. Xia and J. J. Yang, Nat. Electron., 2019, 2, 115 CrossRef.
- G. Milano, G. Pedretti, K. Montano, S. Ricci, S. Hashemkhani, L. Boarino, D. Ielmini and C. Ricciardi, Nat. Mater., 2022, 21, 195 CrossRef CAS PubMed.
- P. M. Sheridan, F. Cai, C. Du, W. Ma, Z. Zhang and W. D. Lu, Nat. Nanotechnol., 2017, 12, 784 CrossRef CAS PubMed.
- A. N. Matsukatova, A. Y. Vdovichenko, T. D. Patsaev, P. A. Forsh, P. K. Kashkarov, V. A. Demin and A. V. Emelyanov, Nano Res., 2023, 16, 3207 CrossRef CAS.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef.
- M. Prezioso, M. R. Mahmoodi, F. M. Bayat, H. Nili, H. Kim, A. Vincent and D. B. Strukov, Nat. Commun., 2018, 9, 5311 CrossRef CAS.
- A. N. Matsukatova, A. V. Emelyanov, V. A. Kulagin, A. Y. Vdovichenko, A. A. Minnekhanov and V. A. Demin, Org. Electron., 2022, 102, 106455 CrossRef CAS.
- V. A. Makarov, S. A. Lobov, S. Shchanikov, A. Mikhaylov and V. B. Kazantsev, Front. Comput. Neurosci., 2022, 16, 859874 CrossRef PubMed.
- A. Sboev, D. Vlasov, R. Rybka, Y. Davydov, A. Serenko and V. Demin, Mathematics, 2021, 9, 3237 CrossRef.
- A. N. Matsukatova, N. V. Prudnikov, V. A. Kulagin, S. Battistoni, A. A. Minnekhanov, A. D. Trofimov, A. A. Nesmelov, S. A. Zavyalov, Y. N. Malakhova, M. Parmeggiani, A. Ballesio, S. L. Marasso, S. N. Chvalun, V. A. Demin, A. V. Emelyanov and V. Erokhin, Adv. Intell. Syst., 2023, 5, 2200407 CrossRef.
- J. K. Eshraghian, M. Ward, E. O. Neftci, X. Wang, G. Lenz, G. Dwivedi, M. Bennamoun, D. S. Jeong and W. D. Lu, Proc. IEEE, 2023, 111, 1016 Search PubMed.
- E. O. Neftci, H. Mostafa and F. Zenke, IEEE Signal Process. Mag., 2019, 36(6), 51–63 Search PubMed.
- W. Fang, Y. Chen, J. Ding, Z. Yu, L. Huang, H. Zhou, G. Li and Y. Tian, Sci. Adv., 2023, 9, 1480 CrossRef PubMed.
- F. Liu, W. Zhao, Y. Chen, Z. Wang, T. Yang and L. Jiang, Front. Neurosci., 2021, 15 CAS.
- I. Tolstikhin, N. Houlsby, A. Kolesnikov, L. Beyer, X. Zhai, T. Unterthiner, J. Yung, A. Steiner, D. Keysers, J. Uszkoreit, M. Lucic and A. Dosovitskiy, Adv. Neural Inf. Process. Syst., 2021, 24261–24272 Search PubMed.
- C. Yakopcic, S. Wang, W. Wang, E. Shin, J. Boeckl, G. Subramanyam and T. M. Taha, Neural Comput. Appl., 2018, 30, 3773 CrossRef.
- S. Huang, W. Luo, X. Pan, J. Zhao, S. Qiao, Y. Shuai, K. Zhang, X. Bai, G. Niu, C. Wu and W. Zhang, Adv. Electron. Mater., 2021, 7, 2100301 CrossRef CAS.
- J. Wang, X. Pan, Q. Wang, W. Luo, Y. Shuai, Q. Xie, H. Zeng, G. Niu, C. Wu and W. Zhang, Appl. Surf. Sci., 2022, 596, 153653 CrossRef CAS.
- V. V. Rylkov, A. V. Emelyanov, S. N. Nikolaev, K. E. Nikiruy, A. V. Sitnikov, E. A. Fadeev, V. A. Demin and A. B. Granovsky, J. Exp. Theor. Phys., 2020, 131, 160 CrossRef.
- M. N. Martyshov, A. V. Emelyanov, V. A. Demin, K. E. Nikiruy, A. A. Minnekhanov, S. N. Nikolaev, A. N. Taldenkov, A. V. Ovcharov, M. Y. Presnyakov, A. V. Sitnikov, A. L. Vasiliev, P. A. Forsh, A. B. Granovsky, P. K. Kashkarov, M. V. Kovalchuk and V. V. Rylkov, Phys. Rev. Appl., 2020, 14, 034016 CrossRef CAS.
- A. V. Emelyanov, K. E. Nikiruy, A. V. Serenko, A. V. Sitnikov, M. Y. Presnyakov, R. B. Rybka, A. G. Sboev, V. V. Rylkov, P. K. Kashkarov, M. V. Kovalchuk and V. A. Demin, Nanotechnology, 2020, 31, 045201 CrossRef CAS.
- K. E. Nikiruy, A. V. Emelyanov, V. A. Demin, V. V. Rylkov, A. V. Sitnikov and P. K. Kashkarov, Tech. Phys. Lett., 2018, 44, 416 CrossRef CAS.
- M. Rao, H. Tang, J. Wu, W. Song, M. Zhang, W. Yin, Y. Zhuo, F. Kiani, B. Chen, X. Jiang, H. Liu, H. Y. Chen, R. Midya, F. Ye, H. Jiang, Z. Wang, M. Wu, M. Hu, H. Wang, Q. Xia, N. Ge, J. Li and J. J. Yang, Nature, 2023, 615, 823 CrossRef CAS PubMed.
- A. N. Matsukatova, A. I. Iliasov, K. E. Nikiruy, E. V. Kukueva, A. L. Vasiliev, B. V. Goncharov, A. V. Sitnikov, M. L. Zanaveskin, A. S. Bugaev, V. A. Demin, V. V. Rylkov and A. V. Emelyanov, Nanomaterials, 2022, 12, 3455 CrossRef CAS PubMed.
- Z. Wang, C. Li, P. Lin, M. Rao, Y. Nie, W. Song, Q. Qiu, Y. Li, P. Yan, J. P. Strachan, N. Ge, N. McDonald, Q. Wu, M. Hu, H. Wu, R. S. Williams, Q. Xia and J. J. Yang, Nat. Mach. Intell., 2019, 1, 434 CrossRef.
- C.-L. Lo, T.-H. Hou, M.-C. Chen and J.-J. Huang, IEEE Trans. Electron Devices, 2013, 60, 420 CAS.
- Z. Tang, Y. Wang, Y. Chi and L. Fang, Electronics, 2018, 7, 224 CrossRef CAS.
- L. Shi, G. Zheng, B. Tian, B. Dkhil and C. Duan, Nanoscale Adv., 2020, 2, 1811 RSC.
- Y. Nishi, S. Menzel, K. Fleck, U. Bottger and R. Waser, IEEE Electron Device Lett., 2014, 35, 259 CAS.
- M. Csontos, Y. Horst, N. J. Olalla, U. Koch, I. Shorubalko, A. Halbritter and J. Leuthold, Adv. Electron. Mater., 2023, 9, 2201104 CrossRef CAS.
- Z. Wang, H. Wu, G. W. Burr, C. S. Hwang, K. L. Wang, Q. Xia and J. J. Yang, Nat. Rev. Mater., 2020, 5, 173 CrossRef CAS.
- C. Li, D. Belkin, Y. Li, P. Yan, M. Hu, N. Ge, H. Jiang, E. Montgomery, P. Lin, Z. Wang, W. Song, J. P. Strachan, M. Barnell, Q. Wu, R. S. Williams, J. J. Yang and Q. Xia, Nat. Commun., 2018, 9, 2385 CrossRef PubMed.
- F. M. Bayat, M. Prezioso, B. Chakrabarti, H. Nili, I. Kataeva and D. Strukov, Nat. Commun., 2018, 9, 2331 CrossRef PubMed.
- A. I. Ilyasov, K. E. Nikiruy, A. V. Emelyanov, K. Y. Chernoglazov, A. V. Sitnikov, V. V. Rylkov and V. A. Demin, Nanobiotechnol. Rep., 2022, 17, 118 CrossRef.
- Y. V. Pershin and M. Di Ventra, Neural Networks, 2020, 121, 52 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00421j |
| ‡ These authors contributed equally. |
| § Present address: Technische Universtität Ilmenau, Ehrenbergstrasse 29, 98693 Ilmenau, Germany. |
| This journal is © The Royal Society of Chemistry 2024 |