Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single-particle measurements and estimations of activity coefficients for semi-volatile organic compounds in organic aerosol of known chemical speciation†
Thomas G.
Hilditch
a,
Daniel A.
Hardy
 a,
Natasha J.
Stevens
b,
Peter B.
Glover
b and
Jonathan P.
Reid
a,
Natasha J.
Stevens
b,
Peter B.
Glover
b and
Jonathan P.
Reid
 *a
*a
aSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK. E-mail: j.p.reid@bristol.ac.uk
bDefence Science and Technology Laboratory, Porton Down, Salisbury, SP4 0JQ, UK
First published on 3rd April 2023
Abstract
Organic aerosol is a highly complex mixture of ∼104 to 105 unique compounds all possessing their own set of physico-chemical properties such as saturation vapour pressure and hygroscopicity. Most of these properties have not been experimentally measured and so must be estimated, resulting in large uncertainties in their predicted gas-particle partitioning and subsequent effect on human health and the climate. Dicarboxylic acids (DCAs) have been used extensively to represent oxidised organic aerosol due to their ubiquity in the atmosphere and commercial availability. Pure component saturation vapour pressures have been obtained by different techniques to enable accurate treatment of their partitioning in atmospheric models. However, an understanding of the synergistic interactions between molecules in multi-component droplets containing DCAs under atmospherically relevant conditions remains limited, relying on group contribution models to estimate physicochemical properties such as activity coefficients in complex organic multicomponent matrices. In this work, a method for extracting activity coefficients of organic species in binary organic component droplets has been developed for investigating the effect of matrix character (such as functionality and molecular weight) on component volatility. Droplets containing a compound of interest and a low-volatility organic liquid are suspended in an electro-dynamic balance for hours to days and the evaporation rate is estimated as the droplet evolves in composition. Comparison with a liquid-like evaporation model allows for the extraction of experimental activity coefficients for a range of mole fractions. Activity coefficients extracted from simple binary organic systems have been compared to and have shown good agreement with an activity coefficient estimator, Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC). The activity coefficients of a range of DCAs dissolved in a mixed-component organic droplet have also been measured and compared to AIOMFAC. The changes in DCA activity coefficient with evolving composition from experiments mostly show reasonable agreement with AIOMFAC for all systems investigated. This showcases the ability of AIOMFAC to predict activities for multi-organic systems containing no water.
Environmental significanceAtmospheric aerosol is a complex mixture of inorganic and organic components with each unique compound having a unique set of physicochemical properties such as saturation vapour pressure and hygroscopicity. Laboratory studies provide a route to quantifying these properties for individual compounds and mixtures of compounds, supporting models of atmospheric aerosol and interpretation of field data. The partitioning of organic compounds between the gaseous and condensed phases, governed by component vapour pressures, impacts on particulate mass concentrations, air quality, atmospheric optics, for example. However, there are very few studies of the dependence of component vapour pressures of organic compounds on the complexity of the condensed phase organic matrix in which they are found. We present a single particle study that reports the vapour pressures of dicarboxylic acids in an organic matrix, providing insight into the current accuracy of predictions used in quantifying organic aerosol mass in the atmosphere. |
I Introduction
Organic aerosol (OA) is ubiquitous in the atmosphere and is estimated to contribute a major fraction in mass to the total sub-micrometre sized aerosol in the Northern Hemisphere.1 It is comprised of a vast number of species in the order 104 to 105, all of which possess unique physicochemical properties, including pure component vapour pressures, refractive indices, and solubilities in water.2 These properties combine, often synergistically, to determine the hygroscopicity, optical scattering and gas-particle partitioning of semi-volatile components in aerosols of complex chemical composition, impacting on the climate, weather systems, visibility and health.3 For most atmospheric organic components, very few of the physicochemical properties have been experimentally determined for individual components. For a comprehensive exploration of the role of organic components in the atmosphere, they must instead be estimated, which can impart large uncertainties into their atmospheric impacts.The effective saturation mass concentration of an organic species “i”, 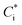 , can be represented by an expression derived by Pankow and rewritten by Donahue et al., relating saturation vapour pressure (pi,sat), activity coefficient (γi), molecular weight (Mi) and temperature (T), where R is the molar gas constant.3–5
, can be represented by an expression derived by Pankow and rewritten by Donahue et al., relating saturation vapour pressure (pi,sat), activity coefficient (γi), molecular weight (Mi) and temperature (T), where R is the molar gas constant.3–5
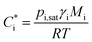 | (1) |
Equilibrium partitioning in ambient OA can be modelled in two ways, a top-down or bottom-up approach. Top-down approaches separate compositionally complex OA into volatility bins to generate volatility basis sets which can then be readily manipulated in models.6 Conversely, bottom-up models input concentrations of individual organic species and then estimate their partitioning based on their physicochemical properties, such as saturation vapour pressure, psat. Bottom-up models assume that OA is comprised of homogeneous liquid droplets where the timescale for internal mixing is instantaneous relative to mass flux to and from the droplet. This means that, from eqn (1), the partitioning of organics is dependent on pi,sat and γi. It is therefore imperative to use accurate values of these properties, especially for compounds whose partitioning has the highest sensitivity to organic mass loading, specifically compounds with similar 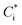 to COA, i.e. semi-volatile organic compounds (SVOCs). Consequently, measuring psat of atmospherically relevant organic species with sensitive partitioning has become a focus in the literature.7–10
to COA, i.e. semi-volatile organic compounds (SVOCs). Consequently, measuring psat of atmospherically relevant organic species with sensitive partitioning has become a focus in the literature.7–10
Several group contribution models (GCM) have been developed to estimate the physico-chemical and transport properties of organic species, with varying degrees of accuracy.11–14 These models are fitted from literature data which are most abundant for small molecules with simple functionality and little atmospheric relevance. For compounds with increasing molecular weight and complexity of functionality, data are often highly extrapolated or missing, resulting in poorer estimation of their psat.
Increasing the complexity from single-to multi-component systems introduces the need for an additional term, the activity coefficient (γ), which describes the heteromolecular interactivity. This term quantitatively describes the deviation from Raoult's law, as expressed in expression 2, where, for a compound “i”, pi is the vapour pressure at the surface of a solution and xi is the mole fraction.
| pi = pi,satxiγi | (2) |
Many studies have measured the activity coefficient of water (γw) for a range of different organics of varying functionalities and structures due to the importance of quantifying water uptake on to organic aerosol.15,16 In binary aqueous systems, organic activity coefficients can be calculated via the Gibbs–Duhem relationship, provided the water activity is correctly measured. Activity coefficients of solution species can be predicted using group contribution method-based models. One such model is the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC), which has parameterised the interactivity of different functional groups based on a large body of experimental data.17 It is also consistent with the Gibbs–Duhem relationship, meaning accurate predictions of water activity give accurate predictions of organic γ.18 Most of the organic species in the fitting set of AIOMFAC are small with simple functionality, meaning some interactivity may not be well understood for species with more complex functionality, leading to higher uncertainty in the predicted activity coefficient. Additionally, organics in multi-organic systems in lower RH environments may exhibit strong interactions with one another. The effects of these organic–organic interactions for atmospherically relevant organic species must be explored experimentally for future inclusion in group contribution models.
Only a handful of studies, to the authors' knowledge, have directly measured γ of the organic components in aerosol droplets, despite the importance of knowing departures from ideality when determining the equilibrium partitioning. In particular, there are even fewer studies that have systematically explored the dependence of the volatility of a single component on the character of the solubilizing organic matrix (e.g. chemical functionality, O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
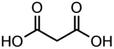
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio, molecular mass). Instead, most atmospheric models use estimated activity coefficients such as those generated by online group contribution estimators, e.g. AIOMFAC, for inclusion in box models, or simply assume γorg values are unity.17,19 One such experimental study of γorg was conducted by Saleh and Khlystov whereby an integrated volume method was used to determine the effect of polarity on the volatility of adipic acid in binary droplets.20 The particle phase was not measured and the internal mixing was inferred from the partitioning. Cappa et al. measured γorg values of dicarboxylic acids (DCAs) in a multi-component solid-state sample using thermal-desorption mass spectrometry (TD-MS).21 The temperature was ramped resulting in DCAs evaporating in order of decreasing volatility. This technique quantified bulk volatility; however, the changing composition of the sample with successive component desorption means all DCA activity coefficients are retrieved from the experimental data at different compositions. As component activity coefficients can be strongly dependent on composition, they cannot be directly compared with one another in these experiments and instead must be quoted for their own individual matrix compositions. This same reasoning challenges assumptions made when estimating the volatility of organic components in FIGAERO-CIMS measurements, especially for compounds likely to have activity coefficients significantly different to unity.22 Most recently, Liu et al. used isothermal evaporation experiments to identify the change in partitioning of multi-component organic aerosol.23 Secondary organic aerosol (SOA) was generated in a chamber from common atmospheric precursors and introduced to a range of atmospherically relevant seed particles. Bulk SOA “activity coefficients” were then inferred through comparison of experiment with a box model. The benefit of this method is that it examines the partitioning of realistic samples on realistic seeds. However, it is not possible to draw conclusions on a molecular level about the factors affecting γorg. Only bulk values for activities are calculated which are not applicable if the composition were to be adapted.
C ratio, molecular mass). Instead, most atmospheric models use estimated activity coefficients such as those generated by online group contribution estimators, e.g. AIOMFAC, for inclusion in box models, or simply assume γorg values are unity.17,19 One such experimental study of γorg was conducted by Saleh and Khlystov whereby an integrated volume method was used to determine the effect of polarity on the volatility of adipic acid in binary droplets.20 The particle phase was not measured and the internal mixing was inferred from the partitioning. Cappa et al. measured γorg values of dicarboxylic acids (DCAs) in a multi-component solid-state sample using thermal-desorption mass spectrometry (TD-MS).21 The temperature was ramped resulting in DCAs evaporating in order of decreasing volatility. This technique quantified bulk volatility; however, the changing composition of the sample with successive component desorption means all DCA activity coefficients are retrieved from the experimental data at different compositions. As component activity coefficients can be strongly dependent on composition, they cannot be directly compared with one another in these experiments and instead must be quoted for their own individual matrix compositions. This same reasoning challenges assumptions made when estimating the volatility of organic components in FIGAERO-CIMS measurements, especially for compounds likely to have activity coefficients significantly different to unity.22 Most recently, Liu et al. used isothermal evaporation experiments to identify the change in partitioning of multi-component organic aerosol.23 Secondary organic aerosol (SOA) was generated in a chamber from common atmospheric precursors and introduced to a range of atmospherically relevant seed particles. Bulk SOA “activity coefficients” were then inferred through comparison of experiment with a box model. The benefit of this method is that it examines the partitioning of realistic samples on realistic seeds. However, it is not possible to draw conclusions on a molecular level about the factors affecting γorg. Only bulk values for activities are calculated which are not applicable if the composition were to be adapted.
An improved understanding of the interactivity of a wide range of different species in well-described mixed-component organic systems at a molecular level is essential, such that results can be integrated directly into bottom-up box models more accurately. These experimental values can then be directly compared with estimations from tools such as AIOMFAC. In this work, a method has been developed for estimating γorg for species dissolved in a low-volatility organic matrix in a spherical, homogeneous droplet. The evaporation rate of a binary organic droplet is measured in an electrodynamic balance (EDB) and compared to an ideal continuum flux model to yield organic activity coefficient (γorg) estimates. Using this method, the effect of functionality and isomerism on the interactivity of the matrix can be probed. Section II details the methodology to obtain γorg from experimental data and model simulations. Section III then describes the sensitivities of the results to a range of experimental and model uncertainties. For the purposes of demonstrating the methodology and the uncertainties in Sections II and III, a binary organic droplet containing Tween 20 (T20) and diethylene glycol (DEG) has been used as a model system, where DEG is the volatile evaporating from the droplet. Section III also contains data from 4 different simple binary organic droplets used to validate the new method by comparison with AIOMFAC. The approach is then applied to mixtures of DCAs with T20 in Section IV, to explore synergistic interactions between typical atmospheric SVOCs and a complex organic matrix.
II Method for estimating γorg in binary organic droplets
II.a Electrodynamic balance (EDB) measurements
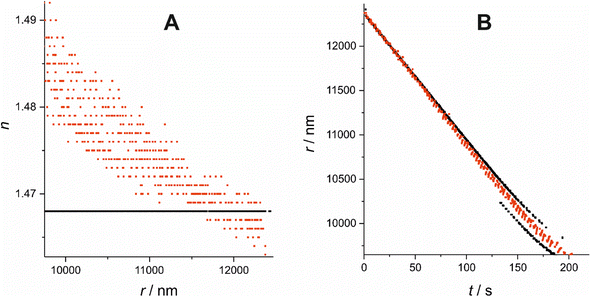
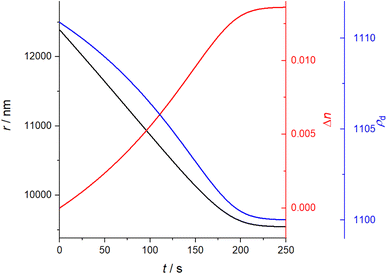
A solution containing 2 organic components, one of which is significantly more volatile than the other, and an appropriate solvent, such as ethanol or water, is made. The solution is dispensed using a MicroFab piezo-actuated micro-dispenser and suspended electrodynamically in an EDB in a dry nitrogen gas flow of controlled temperature. The solvent completely evaporates from the droplet in 1–2 seconds, leaving a binary organic droplet suspended in the EDB. The droplet is illuminated by a 532 nm laser and resultant elastically scattered light centred around 45° from the forwards direction is collected with a CCD camera and recorded for analysis of the radius. The light scattering pattern is referred to as the phase function. This methodology has been described in detail in previous work and will not be described in detail here.24 The EDB setup described has been used in previous studies to measure the vapour pressure of organics of a range of volatilities.25The method used to estimate the radius, herein referred to as the “Mie peak fitting method”, compares the angular positions of the interference fringes in the phase function against a library of simulated fringe positions for a given refractive index or refractive index range, a method described by Davies et al.26 For an evaporating droplet of changing n (i.e. a mixed-component droplet), the fringes are compared to a library of angles spanning a range of r and n at once, rather than assuming a fixed n and correcting at a later stage as is done, for example, using the geometric optics approximation method in previous studies.24,27 Often, several refractive index and radius combinations will provide sufficiently low error to be identified giving seemingly offset trends in evolving radius with time. In this case, the fitted data can be constrained offline to report a single trend which most closely matches the expected evolving n. To demonstrate the importance of using a varied n approach, a comparison has been made between the fixed and varied n Mie peak fitting methods for an example binary droplet of T20 and DEG (outlined in Section I), with initial xDEG = 0.93, shown in Fig. 1. Compound structures are shown in Table 1.
Fig. 1(A) shows the fixed n treatment in black and the varied n treatment in red. Using a fixed n treatment to estimate r of a droplet of changing n will give an incorrect evaporation gradient, but with a reduced scatter in the evolution of radius with time. If Δn is sufficiently large, however, the radius can sometimes switch to an alternative trend line which has a better fit for the fixed value of n chosen. Fig. 1(B) shows the radius switching between 2 parallel offset radius tracks when using the fixed n approach, illustrating the problem of using this approach to estimate the evolving radius of a droplet of changing n. By contrast, the varied n approach smoothly traverses between these 2 parallel tracks, giving a different, more reliable evaporation rate to that calculated from either of the 2 parallel tracks of the fixed n approach.
II.b Simulating ideal evaporation in binary droplets
Simulations of evolving radius as a function of time have been performed using a numerical model based on the Maxwell equation for evaporative flux. Maxwell's equation is valid for spherical homogeneous droplets in the continuum regime, where evaporative cooling is negligible, meaning the temperature of the droplet surface is equal to the temperature of the surrounding gas. Eqn (3) combines the Maxwell equation with Raoult's law (eqn (2)) to give the mass flux of a component “i”, dmi/dt, where r is the droplet radius, Mi is the component molecular weight, Di is the component diffusion coefficient, T is the droplet and gas flow temperature, and pi,∞ is the partial pressure of “i” at an infinite distance from the surface: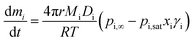 | (3) |
Modified versions of this equation have been used to generate models in earlier studies.28,29Eqn (3) can also be expressed in terms of the change in radius squared with time, dr2/dt, as shown in eqn (4).
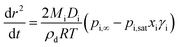 | (4) |
The model requires an initial radius and composition, given in terms of component mole fractions, xi, along with component physicochemical properties required in eqn (3). The evaporative mass loss is then calculated and summed for all components in a designated timestep, and the droplet mass, density, radius and component mole fractions are updated. This process is then repeated for a given number of timesteps to generate an evolving mass, which can be converted to radius with the droplet density, ρd. In this first step in the analysis methodology, the interactivity is assumed to be ideal, meaning γ is set to 1. For the same T20/DEG droplet measurement reported in Fig. 1, evolving r, n and ρdvs. t have been simulated in Fig. 2.
It is it assumed that the rate of mass transport is slow compared to the rate of heat transport to the droplet surface and, thus, the droplet experiences negligible evaporative cooling. For evaporating “semi-volatile” species at room temperature and pressure, this is the case. It is assumed that there are no kinetic limitations to mass transport such as can be imposed by surface films or viscosity, and there is no reactivity. Binary gas diffusion coefficients in nitrogen gas, Di,N2, are estimated using the Chapman–Enskog method described in Bilde et al. (2003) and the Neufeld parameterisation for estimating the collisional cross section.30–32ρd is calculated assuming volume additivity in using the mass fraction mixing rule for density, given in eqn (6), where MFi and ρi,melt are the mass fraction and melt density of component “i” respectively. This means that any deviation in mixed-component density from ideality has been omitted. This is unlikely to be a significant factor for liquid droplets comprised of organics in which the strongest interactions are hydrogen bonds and would more likely be significant for solid mixtures of salts.
Lastly, the droplet refractive index, nd, has been calculated using the molar refraction mixing rule, given in eqn (8). This requires the calculation of several pure and mixed-component properties, using mixing rules given in eqn (5)–(8). Eqn (5) is used to calculate the molar refraction of each component, Ri, which can be calculated from the pure component properties n, Mi and ρi,melt. Eqn (7) and (8) are used to calculate the average molecular weight, Md, and molar refraction of the droplet, Rd. Eqn (9) is simply a rearranged form of eqn (5), using droplet properties rather than pure component properties. While this mixing rule has been found to be the most appropriate in work by Cai et al., it requires ρd which assumes volume additivity, as mentioned above.33
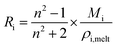 | (5) |
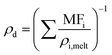 | (6) |
| Md = ∑xiMi | (7) |
| Rd = ∑xiRi | (8) |
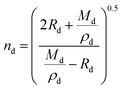 | (9) |
II.c Estimation of γorg
Following the first coarse step in the analysis method described in II.b, estimation of γ is performed using a bespoke Python script. The gradient of radius squared with time, dr2/dt, is calculated for the experimental and model data as a function of time. Using the simulated x vs. t from the model, dr2/dt is then converted to a function of x. A polynomial is then used to fit the experimental dr2/dt vs. x to remove the impact of optical radius fluctuations. A polynomial order of 2 or 3 is sufficient to capture the shape of the data without inadvertently fitting the optical radius fluctuations. Using eqn (4), for a small change in x, δx, γ can be estimated from the difference between experimental and ideally modelled dr2/dt at equivalent x, and, thus, compositions, as given in the expression below: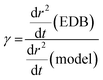 | (10) |
The dependence of γ on x can then be estimated for the whole compositional range accessed in the experiment by iterating forwards in time. γ is estimated at a minimum of 100 nm radius intervals, double the Δr that the Mie peak fitting technique (described in Section IIa) can resolve.26 This is demonstrated in Fig. 3 for the example T20/DEG droplet used throughout this section.
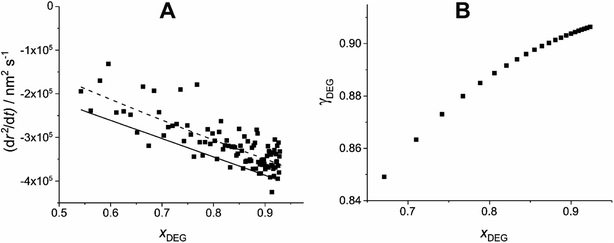 | ||
| Fig. 3 Demonstration of the estimation of γ through comparison of experimental and simulated evaporation of a T20/DEG droplet at 298.15 K and 0% RH. (A) Experimental (scatter), polynomial fitted experimental (dashed line) and modelled (solid line) evaporation, dr2/dt, as a function of xDEG. (B) The resulting estimated relationship of γ vs. x for DEG, using eqn (9), using the fitted experimental data (dashed line). | ||
As the DEG evaporates from the droplet, the Δr required per Δx decreases (i.e. less DEG needs to evaporate to change its mole fraction). This results in adjacent γ values being increasingly spaced in x at smaller xDEG.
III Sensitivity of estimated γorg to uncertainties and validation of method with AIOMFAC
The uncertainty in the retrieval of activity coefficients and the corresponding mole fractions can be attributed to a combination of experimental and model uncertainties. We consider these individually using the T20/DEG droplet as a test system, before discussing the overall uncertainty.III.a Experimental uncertainties
Firstly, there is a radius uncertainty of ±100 nm in the fitting of the phase function with the Mie peak fitting method.26 For the test system, this imparts an uncertainty in x which increases with decreasing x to >±9% for x < 0.5. This is shown for the T20/DEG droplet in Fig. S1 in the ESI.† The larger the molecular weight of the evaporating compound compared to the matrix compound, and the larger the starting radius of the droplet, the lower the sensitivity of x to r. The uncertainty imparted on γ from the uncertainty in optical r is only minor due to the 2nd order polynomial fit, which removes the fluctuations in dr2/dt from optical radius fluctuations. Secondly, there is an uncertainty in experimental temperature of ±1 K from the thermocouple measurement which imparts an uncertainty on the psat of the evaporating organic used in the model through the Clausius–Clayperon relationship. Using an average literature ΔHvap for DEG of 63.3 kJ mol−1, a ±1 K uncertainty in T corresponds to a 9% average uncertainty in psat.34 This impacts the simulated evaporation rates of droplets (as per eqn (3)) which, in turn, impact estimations of γ. The % uncertainty imparted on γ by a constant uncertainty in T scales proportionally with ΔHvap, as shown in Fig, S2 in the ESI.†III.b Model uncertainties
There are uncertainties in the properties used in the evaporation model which also impact the estimated value of γ, including the component melt densities, calculated droplet density from volume additivity and estimated diffusion coefficients. To quantify the effects of these uncertainties on the uncertainty in γ, sensitivity analyses have been conducted using reasonable expected uncertainties in the properties. Simulated evaporation curves for T20/DEG droplets, such as shown in Fig. 2, were generated using the evaporation model and the input properties were modified to assess their impact on γ. An uncertainty in liquid/melt density will impart an uncertainty on the estimated γ, through altering the modelled dr2/dt, and the simulated mole fraction for which the estimated γ is assigned. To quantify this, a ±5% uncertainty in DEG liquid density, ρDEG, was imposed, and the resulting uncertainty in both γ and x were identified as a function of x. The results are shown in Fig. S3 in the ESI.†The resulting uncertainty in x increases as x decreases, in a similar way to the impact of optical radius uncertainty. For xDEG < 0.5, where very small changes in radius correspond to large changes in xDEG, large decreases in calculated γDEG could instead be explained by an incorrect melt ρDEG resulting in a lower modelled radius corresponding to complete DEG loss. As no composition information is retrieved, such as would be from Raman spectroscopy, the amount of DEG remaining in the droplet is not known. Thus, it is best to avoid estimating γDEG at radii that could feasibly correspond to near or complete loss of DEG (and low mole fractions). A ±5% uncertainty in liquid/melt ρ imparts a 5–7% uncertainty in γ with a minor dependence on x.
The uncertainty arising from deviation from ideality in the estimate of the mixed-component density has been investigated. For compounds that have similar molecular weights (Mi), the maximum deviation in density from ideality would be expected when there are equal amounts of both compounds.33 However, some systems will have components with a significantly different Mi to one another, meaning that there is a significant difference in mass fraction (MFS)-dependent or x-dependent non-ideality. Additionally, binary systems comprised of significantly different sized molecules are likely to exhibit higher density than predicted by assuming volume additivity. To investigate this, x and MFS-dependent non-ideality were investigated separately. In both systems, a maximum of 5% higher density than volume additivity was considered, which is close to the maximum departure from volume additivity of aqueous sodium chloride (∼6%). The maximum resulting uncertainties in γ and x from both experiments were ±5% and 0.4% respectively, which are significantly lower than the experimental uncertainties, and so can be ignored.
An uncertainty of ±6% in gas diffusion coefficient, Di, typical of the error from the Chapman–Enskog method, imparts an almost equivalent uncertainty on γ (±6%) but imparts no uncertainty in x. In the same way, γ depends upon the psat value used in the model, which is not always possible to measure directly with this methodology. In the case where it is not possible to measure the pure component psat values with this technique, values must be taken from the literature, which have quoted associated uncertainties. These uncertainties can be quite large, especially for semi-volatile species that are solid at room temperature which, in the example of DCAs, can range from ±20% for glutaric acid to ±75% for some functionalised DCAs. In this case, the uncertainty in literature psat dominates the resulting uncertainty in γ.
III.c Total uncertainty
The uncertainty in x is dominated by the uncertainties in optical radius and liquid/melt densities of the components, with increase as x decreases in both cases. Liquid/melt densities of species that have been parameterised from aqueous solutions typically have an uncertainty of <1%, which would result in a much lower uncertainty in x than calculated in this study. The uncertainty in γ is derived from uncertainties in T (through its impact on psat), Di, ρd and optical r. The optical r and ρd have the smallest impact on the uncertainty of γ. If the uncertainty in pure component vapour pressure is also small, the uncertainties in Di and T determine the overall uncertainty in γ at ∼6–15% each. However, psat values of atmospherically relevant semi-volatile at 298 K are rarely quoted to within ±15% uncertainty in the literature, as mentioned in the previous sub-section. This means that in most cases, the uncertainty in γ will be dominated by the uncertainty in pure component psat.III.d Validation of method by comparison with AIOMFAC
To show that this method can be used to accurately retrieve activity coefficients of organics, four binary organic systems of different functionality and O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
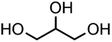
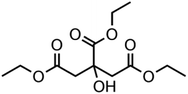
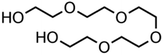
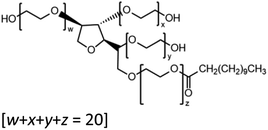
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio were tested and the results were compared with AIOMFAC. Systems were chosen that are likely to be well characterised by AIOMFAC, such that AIOMFAC could be assumed to give correct values. The volatile compound was the same for all binary droplets and the matrix compound was changed (see Table 1). Although DEG has been used as the volatile compound for the previous analyses, its psat is within an order of magnitude to some of the proposed matrix compounds, meaning the assumption of negligible matrix compound evaporation would be invalid. A volatile organic such as ethanol is volatile enough to lead to significant evaporative cooling at 298 K, and uncertainties in evaporative cooling would lead to greater uncertainties in the simulated evaporation rate and subsequent estimation of γ, thus ethanol was not chosen either. Instead, carbitol was selected to be the volatile for these experiments. With a psat over an order of magnitude larger than all matrix compounds, carbitol can be assumed to be responsible for all mass loss in a carbitol/matrix droplet, without causing noticeable evaporative cooling, meaning it was a perfect candidate for the volatile compound. All matrix compounds are either in the drop-down menu of AIOMFAC or are chemically similar to compounds that are. All matrix compounds are liquids at room temperature with known pure refractive indices and densities, removing the uncertainties associated with these properties. To avoid an uncertainty in carbitol vapour pressure from temperature fluctuations, a droplet of pure carbitol was injected prior to every droplet of carbitol/matrix solution. The vapour pressure of the pure carbitol was then calculated using the Maxwell equation in terms of radius squared, given in eqn (4), where dr2/dt is constant for a pure component droplet. A similar comparative kinetics approach is commonly used in EDB-based hygroscopicity experiments, where the evaporation kinetics of a water droplet is used to infer the relative humidity of the gas flow prior to the injection of a solute of unknown hygroscopicity.35 In the case of all experimental droplets in this study, pi,∞ was assumed to be 0 due to the dry N2 gas flow removing organics from the surface of the droplet. Additionally, the uncertainty in carbitol diffusion coefficient is also removed by this comparative kinetics approach, as it is kept constant for both pure and mixed-component calculations in eqn (3) and (4). During the series of experiments, the extracted psat for the pure carbitol varied from 16–18 Pa, which agrees very well with the literature value of 17 Pa.36Table 1 contains the structure of the volatile, carbitol, and the different matrix compounds used in this set of experiments, glycerol, triethyl citrate, pentaethylene glycol and Tween 20.
C ratio were tested and the results were compared with AIOMFAC. Systems were chosen that are likely to be well characterised by AIOMFAC, such that AIOMFAC could be assumed to give correct values. The volatile compound was the same for all binary droplets and the matrix compound was changed (see Table 1). Although DEG has been used as the volatile compound for the previous analyses, its psat is within an order of magnitude to some of the proposed matrix compounds, meaning the assumption of negligible matrix compound evaporation would be invalid. A volatile organic such as ethanol is volatile enough to lead to significant evaporative cooling at 298 K, and uncertainties in evaporative cooling would lead to greater uncertainties in the simulated evaporation rate and subsequent estimation of γ, thus ethanol was not chosen either. Instead, carbitol was selected to be the volatile for these experiments. With a psat over an order of magnitude larger than all matrix compounds, carbitol can be assumed to be responsible for all mass loss in a carbitol/matrix droplet, without causing noticeable evaporative cooling, meaning it was a perfect candidate for the volatile compound. All matrix compounds are either in the drop-down menu of AIOMFAC or are chemically similar to compounds that are. All matrix compounds are liquids at room temperature with known pure refractive indices and densities, removing the uncertainties associated with these properties. To avoid an uncertainty in carbitol vapour pressure from temperature fluctuations, a droplet of pure carbitol was injected prior to every droplet of carbitol/matrix solution. The vapour pressure of the pure carbitol was then calculated using the Maxwell equation in terms of radius squared, given in eqn (4), where dr2/dt is constant for a pure component droplet. A similar comparative kinetics approach is commonly used in EDB-based hygroscopicity experiments, where the evaporation kinetics of a water droplet is used to infer the relative humidity of the gas flow prior to the injection of a solute of unknown hygroscopicity.35 In the case of all experimental droplets in this study, pi,∞ was assumed to be 0 due to the dry N2 gas flow removing organics from the surface of the droplet. Additionally, the uncertainty in carbitol diffusion coefficient is also removed by this comparative kinetics approach, as it is kept constant for both pure and mixed-component calculations in eqn (3) and (4). During the series of experiments, the extracted psat for the pure carbitol varied from 16–18 Pa, which agrees very well with the literature value of 17 Pa.36Table 1 contains the structure of the volatile, carbitol, and the different matrix compounds used in this set of experiments, glycerol, triethyl citrate, pentaethylene glycol and Tween 20.
Fig. 4 shows the experimental estimations of γ vs. x for carbitol in carbitol/matrix droplets, compared to AIOMFAC predictions. For clarity, data points have been selected every 500 nm rather than every 100 nm. The experimental estimations of γ vs. x show good agreement with AIOMFAC for all systems tested, within the combined experimental and model error. Perhaps surprisingly, the experimental γ vs. x of carbitol in T20 (Fig. 4(D)) also shows good agreement with AIOMFAC, despite the high molecular weight and complex functionality of T20. This supports the use of AIOMFAC to predict the interactivity of complex molecules in the atmosphere. Overall, these data validate the method for estimation of organic activity coefficients in binary organic droplets.
IV Activity coefficients of dicarboxylic acids (γDCA) dissolved in a Tween 20 matrix
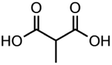
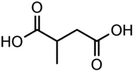
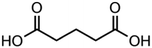
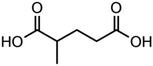
To demonstrate the use of this technique for atmospherically relevant species, a selection of binary organic droplets containing Tween 20 and a dicarboxylic acid, herein referred to as “T20/DCA droplets”, have been investigated and γorg has been estimated for a range of mole fractions. The range of DCAs investigated is shown in Table 2, along with the properties used in the model simulations. Estimations of γorg were also compared to AIOMFAC. Tween 20 was selected due to its liquid phase state at room temperature and pressure, its low viscosity of ∼400 mPa s−1 and its low volatility of <10−6 Pa (from pure component EDB measurements). Thus, its contribution to droplet evaporation is negligible and it does not kinetically inhibit the evaporation of the DCA. As it is non-volatile, its values for diffusion coefficient and vapour pressure were not included in Table 2. T20 is also soluble in solvents with a range of polarities, meaning a large range of organic compounds with varying polarity can be dissolved in this matrix and studied using this technique. T20 also contains atmospherically relevant functional groups such as esters, hydrocarbon chains and hydroxyl groups, as seen in Table 1. This justifies its use as an atmospheric analogue despite not being naturally present in the atmosphere. DCAs were chosen due to their atmospheric abundance, commercial availability and known physico-chemical properties such as psat.The gas flow was dry nitrogen at 298.15 ± 1 K. The RH was assumed to be 0% but was not measured directly due to the inaccuracy of humidity probes and the lack of a suitable probe droplet composition, often used in our EDB studies, which can be adopted under these conditions.37 It was not possible to measure the psat values of the pure DCAs in the same way as was described in the section IIId, as pure DCA particles are solid at 298.15 K, and thus do not produce the regular interference fringes needed for radius estimation. Instead, melt psat values were taken from Bilde et al. (2015) and pure component melt ρ and n values were extrapolated from bulk solution data as described in Cai et al. (2016).8,33
Total uncertainty was calculated using the sensitivity analysis described in Section III, using compound-specific uncertainties.33 The resulting uncertainty in AIOMFAC predictions from the uncertainty in temperature of ±1 K is <1% at its maximum.
The maximum xDCA studied in these experiments for each DCA corresponds to the maximum amount of DCA while keeping the droplet homogeneous, i.e. the experimentally determined solubility limit. Measurements for succinic acid were also attempted but droplets of homogeneous morphology were not formed at any composition, preventing inference of activity coefficients by this approach. This may be due to its high lattice enthalpy which aids its efflorescence.
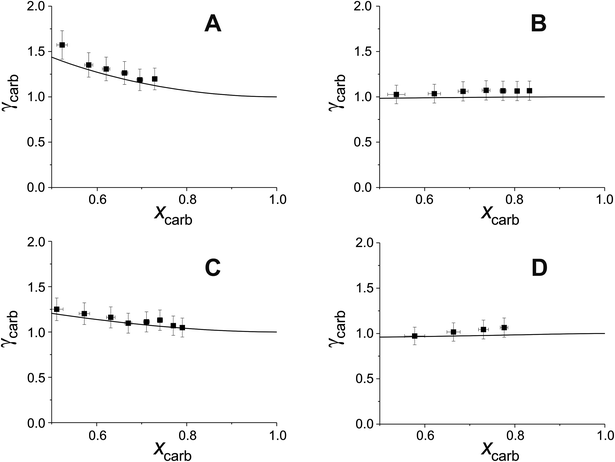
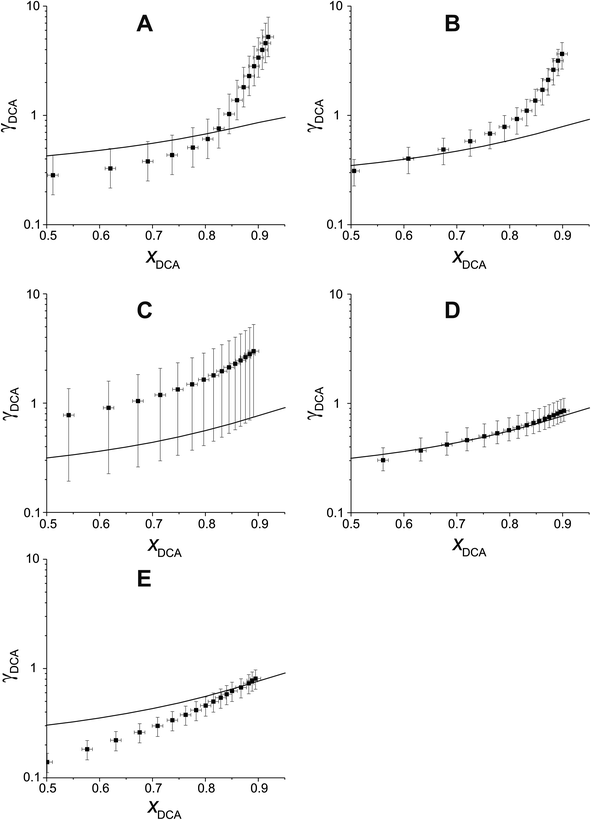
Fig. 5 compares experimental estimations and AIOMFAC predictions of γ vs. x for 5 different DCAs in T20/DCA droplets. The directional trends of decreasing γ with decreasing x match AIOMFAC predictions, however, the magnitude of this decrease is larger than predicted by AIOMFAC for the malonic acids at high mole fractions of DCA. Experimental estimations of glutaric acid show highest agreement with AIOMFAC, which is unsurprising considering its extensive coverage in the literature.
As xDCA approaches 1, i.e. the droplet tends towards pure dicarboxylic acid, γ should also tend towards 1. For glutaric and methylglutaric acid, this is the case, indicating good agreement of these experiments with the literature psat values used. However, for malonic, methylmalonic and methylsuccinic acid, γ tends towards a value greater than 1, which may indicate a higher pure component psat than agreed upon in the literature. Extrapolating γ to x = 1 for the malonic acids gives a value of ∼10, which would correspond to an order of magnitude higher psat than the literature. Although the psat values have not been directly measured in this experiment, they have been agreed upon by several different studies at 298 K with a quoted uncertainty much lower than an order of magnitude. Disagreement between psat values inferred from this study and the literature at the same temperature are unlikely to amount to an order of magnitude, meaning the disagreement between the results in this study and AIOMFAC at higher x cannot be fully accounted for by psat. Another possibility is that the interactivity of T20 and the malonic acids are not well understood by AIOMFAC at high xDCA for these species. For the malonic acids, experimentally estimated DCA activities become greater than 1, indicating that phase separation would be thermodynamically favourable, however, phase separation is not predicted by AIOMFAC at any x.
Overall, DCAs show reasonable agreement with AIOMFAC at lower xDCA, but show deviations both in absolute values of γ and changes in γ with x at high x for malonic acids. The reasons for this need to be investigated further in future work.
V Conclusions and future work
This work provides a methodology for measuring γorg for an organic species dissolved in a homogeneous mixed-component organic droplet. Binary organic droplets are suspended in an electrodynamic balance and their evolving radius is measured as the droplet evaporates. The activity coefficient can then be calculated as the composition of the droplet changes through comparison with an ideal liquid-like evaporation model. Several simple binary organic systems, deemed as well understood by AIOMFAC, were tested with this method and showed good agreement with AIOMFAC predictions of activity coefficient. To demonstrate this method for atmospherically relevant OA species, γDCA was estimated for dicarboxylic acids dissolved in Tween 20 and estimations were compared to AIOMFAC predictions. In general, AIOMFAC correctly predicted the direction and magnitude of the change in activity coefficient with evolving composition, particularly at lower x, however deviations in the experimental values from AIOMFAC were observed at higher x for malonic acids. Further investigation is needed to understand the reason for these observations. Future work will expand the coverage of different functionalities and isomers to investigate the complex relationship between γorg and the chemical character of the matrix in different atmospherically relevant conditions, and investigate the potential for this methodology to be used for >2 organics per droplet.Conflicts of interest
There are no conflicts to declare.References
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- A. H. Goldstein and I. E. Galbally, Environ. Sci. Technol., 2007, 41, 1514–1521 CrossRef CAS PubMed.
- N. M. Donahue, A. L. Robinson, C. O. Stanier and S. N. Pandis, Environ. Sci. Technol., 2006, 40, 2635–2643 CrossRef CAS PubMed.
- J. F. Pankow, Atmos. Environ., 1994, 28, 189–193 CrossRef CAS.
- J. H. Seinfeld and J. F. Pankow, Annu. Rev. Phys. Chem., 2003, 54, 121–140 CrossRef CAS PubMed.
- T. E. Lane, N. M. Donahue and S. N. Pandis, Atmos. Environ., 2008, 42, 7439–7451 CrossRef CAS.
- A. M. Booth, M. H. Barley, D. O. Topping, G. McFiggans, A. Garforth and C. J. Percival, Atmos. Chem. Phys., 2010, 10, 4879–4892 CrossRef CAS.
- M. Bilde, K. Barsanti, M. Booth, C. D. Cappa, N. M. Donahue, E. U. Emanuelsson, G. McFiggans, U. K. Krieger, C. Marcolli, D. Topping, P. Ziemann, M. Barley, S. Clegg, B. Dennis-Smither, M. Hallquist, Å. M. Hallquist, A. Khlystov, M. Kulmala, D. Mogensen, C. J. Percival, F. Pope, J. P. Reid, M. A. V. Ribeiro da Silva, T. Rosenoern, K. Salo, V. P. Soonsin, T. Yli-Juuti, N. L. Prisle, J. Pagels, J. Rarey, A. A. Zardini and I. Riipinen, Chem. Rev., 2015, 115, 4115–4156 CrossRef CAS PubMed.
- V. Soonsin, A. A. Zardini, C. Marcolli, A. Zuend and U. K. Krieger, Atmos. Chem. Phys., 2010, 10, 11753–11767 CrossRef CAS.
- A. A. Zardini, U. K. Krieger and C. Marcolli, Opt. Express, 2006, 14, 6951–6962 CrossRef CAS PubMed.
- S. Compernolle, K. Ceulemans and J. F. Muller, Atmos. Chem. Phys., 2011, 11, 9431–9450 CrossRef CAS.
- Y. Nannoolal, J. Rarey and D. Ramjugernath, Fluid Phase Equilib., 2008, 269, 117–133 CrossRef CAS.
- M. H. Barley and G. McFiggans, Atmos. Chem. Phys., 2010, 10, 749–767 CrossRef CAS.
- M. Capouet and J. F. Muller, Atmos. Chem. Phys., 2006, 6, 1455–1467 CrossRef CAS.
- M. N. Chan, S. M. Kreidenweis and C. K. Chan, Environ. Sci. Technol., 2008, 42, 3602–3608 CrossRef CAS PubMed.
- A. Marsh, R. E. H. Miles, G. Rovelli, A. G. Cowling, L. Nandy, C. S. Dutcher and J. P. Reid, Atmos. Chem. Phys., 2017, 17, 5583–5599 CrossRef CAS.
- A. Zuend, C. Marcolli, A. M. Booth, D. M. Lienhard, V. Soonsin, U. K. Krieger, D. O. Topping, G. McFiggans, T. Peter and J. H. Seinfeld, Atmos. Chem. Phys., 2011, 11, 9155–9206 CrossRef CAS.
- A. Zuend, C. Marcolli, B. P. Luo and T. Peter, Atmos. Chem. Phys., 2008, 8, 4559–4593 CrossRef CAS.
- G. Ganbavale, A. Zuend, C. Marcolli and T. Peter, Atmos. Chem. Phys., 2015, 15, 447–493 CrossRef.
- R. Saleh and A. Khlystov, Aerosol Sci. Technol., 2009, 43, 838–846 CrossRef CAS.
- D. Cappa Christopher, R. Lovejoy Edward and A. R. Ravishankara, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18687–18691 CrossRef CAS PubMed.
- T. J. Bannan, M. Le Breton, M. Priestley, S. D. Worrall, A. Bacak, N. A. Marsden, A. Mehra, J. Hammes, M. Hallquist, M. R. Alfarra, U. K. Krieger, J. P. Reid, J. Jayne, W. Robinson, G. McFiggans, H. Coe, C. J. Percival and D. Topping, Atmos. Meas. Tech., 2019, 12, 1429–1439 CrossRef CAS.
- X. Liu, D. A. Day, J. E. Krechmer, P. J. Ziemann and J. L. Jimenez, Environ. Sci. Technol. Lett., 2021, 8, 212–217 CrossRef CAS.
- J. F. Davies, A. E. Haddrell and J. P. Reid, Aerosol Sci. Technol., 2012, 46, 666–677 CrossRef CAS.
- U. K. Krieger, F. Siegrist, C. Marcolli, E. U. Emanuelsson, F. M. Gobel, M. Bilde, A. Marsh, J. P. Reid, A. J. Huisman, I. Riipinen, N. Hyttinen, N. Myllys, T. Kurten, T. Bannan, C. J. Percival and D. Topping, Atmos. Meas. Tech., 2018, 11, 49–63 CrossRef.
- J. F. Davies, Aerosol Sci. Technol., 2019, 53, 309–320 CrossRef CAS.
- W. J. Glantschnig and S.-H. Chen, Appl. Opt., 1981, 20, 2499–2509 CrossRef CAS PubMed.
- E. Periasamy Ravindran and J. Davis, J. Colloid Interface Sci., 1982, 85, 278–288 CrossRef.
- J. F. Widmann and E. J. Davis, Aerosol Sci. Technol., 1997, 27, 243–254 CrossRef CAS.
- S. Chapman and T. G. Cowling, The Mathematical Theory of Non-Uniform Gases, Cambridge University Press, Cambridge, 1970 Search PubMed.
- M. Bilde, B. Svenningsson, J. Mønster and T. Rosenørn, Environ. Sci. Technol., 2003, 37, 1371–1378 CrossRef CAS.
- P. D. Neufeld, A. R. Janzen and R. A. Aziz, J. Chem. Phys., 1972, 57, 1100–1102 CrossRef CAS.
- C. Cai, R. E. H. Miles, M. I. Cotterell, A. Marsh, G. Rovelli, A. M. J. Rickards, Y. H. Zhang and J. P. Reid, J. Phys. Chem. A, 2016, 120, 6604–6617 CrossRef CAS PubMed.
- J. S. Chickos and W. E. Acree, J. Phys. Chem. Ref. Data, 2003, 32, 519–878 CrossRef CAS.
- A. M. J. Rickards, R. E. H. Miles, J. F. Davies, F. H. Marshall and J. P. Reid, J. Phys. Chem. A, 2013, 117, 14120–14131 CrossRef CAS PubMed.
- CAMEO Chemicals, https://cameochemicals.noaa.gov/chemical/8539, accessed March 2023 Search PubMed.
- J. F. Davies, A. E. Haddrell, R. E. H. Miles, C. R. Bull and J. P. Reid, J. Phys. Chem. A, 2012, 116, 10987–10998 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00180b |
| This journal is © The Royal Society of Chemistry 2023 |