Open Access Article
Open Access ArticleAn open source computational workflow for the discovery of autocatalytic networks in abiotic reactions†
Aayush
Arya
 ab,
Jessica
Ray
b,
Siddhant
Sharma
ab,
Jessica
Ray
b,
Siddhant
Sharma
 bc,
Romulo
Cruz Simbron
bc,
Romulo
Cruz Simbron
 bdj,
Alejandro
Lozano
be,
Harrison B.
Smith
bdj,
Alejandro
Lozano
be,
Harrison B.
Smith
 f,
Jakob Lykke
Andersen
g,
Huan
Chen
f,
Jakob Lykke
Andersen
g,
Huan
Chen
 h,
Markus
Meringer
h,
Markus
Meringer
 i and
Henderson James
Cleaves
II
i and
Henderson James
Cleaves
II
 *bf
*bf
aDepartment of Physics, Lovely Professional University, Jalandhar Delhi-GT Road, Phagwara, Punjab 144411, India
bBlue Marble Space Institute of Science, Seattle, Washington 98104, USA
cDepartment of Biochemistry, Deshbandhu College, University of Delhi, New Delhi 110019, India
dLaboratorio de Investigación Fisicoquímica (LABINFIS), Universidad Nacional de Ingeniería, Av. Túpac Amaru 210, Lima, Peru
eUnidad Profesional Interdisciplinaria de Biotecnología – Instituto Politécnico Nacional, 550 Av. Acueducto, 07340 Mexico City, Mexico
fEarth-Life Science Institute, Tokyo Institute of Technology, Tokyo, Japan. E-mail: hcleaves@elsi.jp
gDepartment of Mathematics and Computer Science, University of Southern Denmark, Campusvej 55, 5230 Odense M, Denmark
hNational High Magnetic Field Laboratory, Tallahassee, Florida 32310, USA
iGerman Aerospace Center (DLR), 82234 Oberpfaffenhofen, Wessling, Germany
jCentro de Tecnologías de la Información y Comunicaciones (CTIC UNI), Universidad Nacional de Ingenieria, Av. Túpac Amaru 210, Lima, Peru
First published on 23rd March 2022
Abstract
A central question in origins of life research is how non-entailed chemical processes, which simply dissipate chemical energy because they can do so due to immediate reaction kinetics and thermodynamics, enabled the origin of highly-entailed ones, in which concatenated kinetically and thermodynamically favorable processes enhanced some processes over others. Some degree of molecular complexity likely had to be supplied by environmental processes to produce entailed self-replicating processes. The origin of entailment, therefore, must connect to fundamental chemistry that builds molecular complexity. We present here an open-source chemoinformatic workflow to model abiological chemistry to discover such entailment. This pipeline automates generation of chemical reaction networks and their analysis to discover novel compounds and autocatalytic processes. We demonstrate this pipeline's capabilities against a well-studied model system by vetting it against experimental data. This workflow can enable rapid identification of products of complex chemistries and their underlying synthetic relationships to help identify autocatalysis, and potentially self-organization, in such systems. The algorithms used in this study are open-source and reconfigurable by other user-developed workflows.
Introduction
Organic chemistry has evolved as a science by the development of methods allowing for predictive application of high-yielding bond-transformation techniques to produce desired products,1 generally focusing less on the side-products of such transformations. Low-yield, diversity-generating, multi-step, single-pot reactions have thus received less scrutiny, though these may include reactions of interest to fields including green,2 organic geo-,3 food,4 and prebiotic chemistry.5Provided there are propagable reaction centers, relatively simple organic compounds can seed complex one-pot reaction networks to give rise to complex product mixtures, sometimes producing thousands or millions of unique isomeric products. Examples include Maillard chemistry (important in taste and flavor development in cooking, e.g., ref. 4), and the chemical complexity observed in carbonaceous meteorites6 and other chemistries which may have been important for the origins of life (e.g., ref. 7).
The chemical diversity of the products of such complex chemical reaction networks (CRNs) can contribute to their emergent bulk properties. Due to the complexity of their chemistry, reaction circuits (that is to say concatenated reactions that lead to some defined outcome) that are not immediately obvious may have an outsized impact on the overall evolution and emergent properties of CRNs.8 For example, the flavor and aroma of cooked foods may derive from robust underlying diversity-generating reactions among relatively simple ingredients,4 the chemical complexity of source petroleum may affect the cost of its purification9 and the decomposition of pharmaceuticals during storage may affect their efficacy.10
It is unknown which compounds were important for the origins of life, and it can be difficult for chemists to analyze the underlying chemistry of CRNs and their resulting products.11 Chemists are thus often left with using the presence or absence of specific compounds in prebiotic samples and simulants to evaluate the importance of both the compounds themselves and the processes which produce them.12,13
Computational modeling of CRNs gives rise to chemical reaction network representations (CRNRs), which may allow accurate prediction of which compounds are most likely produced in CRNs, as well as minor and perhaps transient products which heavily affect their course. CRNRs are a framework for interpreting CRNs via their likely underlying chemistry, and can shed light on which compounds and processes are crucial for CRN evolution.
Chemists typically learn generic “named” reaction mechanisms that become their conceptual “toolkit” for predicting reaction outcomes and planning syntheses.14 Over the last few decades, computational methods have been developed to heuristically predict reaction outcomes of CRNs, which has made retrosynthetic analysis and reaction outcome prediction increasingly amenable to computational automation.15,16
CRNs may efficiently produce one or a few major products, with a variably complex coterie of side-products, or distribute products among a complex mixture without there being an easily identifiable major product set. In many cases, a few common heuristic reaction mechanisms may be able to explain the majority of CRN observed chemical diversity. On another axis, specific products, whether singular or multitudinous, may dominate the overall properties of the product mixture, or be involved in dynamical processes which are not detectable in simple end-point product analyses. Some examples of these possible outcomes include the phenomenon of “boar taint,” in which highly sensorially detectable contaminants can ruin flavor perception at low detection thresholds,17 or the detection of specific compounds such as adenine in HCN polymerizations,18 in low yield has perhaps pushed the perceived importance of HCN chemistry for the origins of life.19
Conversely, the synthesis of a key compound in low abundance, if generated in the context of an amplifying or selective reaction mechanism, may lead to the formation of large amounts of non-obvious products that may be important for the overall progression of complex reactions. An example of this is Robinson's tropinone synthesis.20 Such phenomena in which transient unstable compounds help establish and propagate networks of rare, but self-amplifying reactions, may be crucial for understanding the chemical origins of life.
Carbonaceous chondrite (CC) meteorites have been heavily studied as examples abiological organic chemistry,21,22 and contain both small, soluble, and easily identifiable molecular products as well as higher molecular weight products. Various laboratory models have been proposed as approximations of the processes which produced CC organics,22–26 but none of these models are completely able to explain all of the measured features of CC organics.
High resolution Fourier Transform Ion Cyclotron Resonance (FT-ICR) mass spectra offer snapshots of the molecular diversity produced by CRNs (see Fig. 1D and ESI Fig. 1†), and provide benchmarks for CRNRs. The products of CRNs are often extremely heterogeneous, and untargeted product identification is challenging given organic structural isomerism.27In silico computed CRNRs generate analyzable approximations of CRN mixtures and offer a way to collapse the possible isomer space for product identification and reaction exploration in CRNs.
It is difficult to understand the relational aspects of the underlying chemistry in CRNs, for example to detect the phenomenon of autocatalysis. Autocatalysis has attracted considerable attention in the context of the origins of life.28 In large CRNs, autocatalysis may be common but hard to detect even using high-resolution MS due to isobaric product degeneracy.29 Autocatalysis can be engendered in various ways.30–32 In the formose reaction,33,34 in which formaldehyde (HCHO), reacted in the presence of glycolaldehyde (HOCH2CHO) under basic conditions to form complex products, autocatalysis arises because reaction products serve as reaction catalysts.34 Many other examples of simple, generic autocatalytic reaction sequences may exist, and in silico reaction modeling may be able to help find them.
We present here an open-source computational workflow to help identify CRN products and processes, including autocatalysis, and the prediction of their properties. To demonstrate the potential power of this approach, we explore a well-studied simple CRN, the aqueous alkaline degradation of glucose (ADG). Glucose is among the most abundant biological monomers, and is especially abundant in the biosphere in the form of cellulose which is a major component of plant mass (wood, leaves, etc.) and is continuously introduced into the environment in copious amounts by processes such as the seasonal dropping of deciduous leaf litter and microbial biomass turnover. The large variety of glucose aging products which may contribute to seawater dissolved organic matter (DOM) which ultimately become incorporated in ubiquitous kerogen is thus of fundamental interest.
Glucose is relatively stable at room temperature and low humidity,35 but decomposes into a complex caramel mixture rapidly when heated, or under basic conditions.36 Caramel can be derived from various sugars (most typically from sucrose), and has complex taste classifications which underscore how its properties depend on subtleties of reaction conditions.37 While ADG is a simple test-bed for the development of this workflow, this workflow can easily be adapted to other reaction chemistries including those relevant for understanding geochemical transformations of organic materials, the origins of complex organics in astrochemical settings, and the origins of life.
Results and discussion
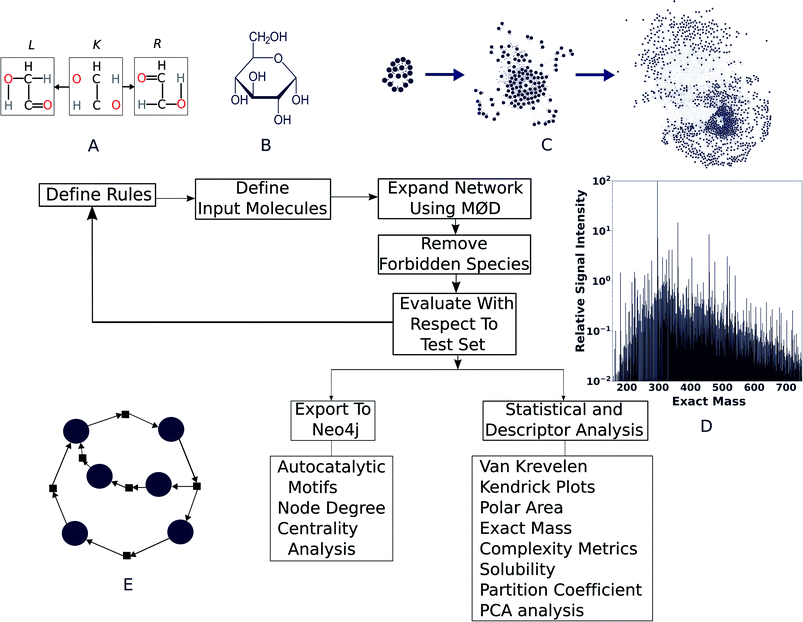
We modelled the degradation of glucose in silico using purely open-source tools. To asses whether our simulation is capable of explaining real world chemistry, we tested if it could explain the species reported in a comprehensive study on the same by ref. 36 and our own high-resolution mass spectra collected for the purpose of this study. We found good agreement with observations, which are described below. For modeling purposes, the workflow presented here uses MØD,38 which is a graph theory-based chemical reaction modeling software package. In MØD, graphs provide a framework for representing chemical reactions where molecules can be treated as nodes in a graph, while the edges connecting them symbolise reactions.39 In the workflow presented here, molecules are also given another graph representation in which individual atoms are abstracted as nodes and labelled edges indicate chemical bonds between them. A detailed discussion of the methods can be found in ESI Section 3,† but an overview of the pipeline is presented here (see Fig. 1).A set of reaction mechanisms was first compiled, with each mechanism written in GML format.40 Removal and addition of edges within a graph (here, a molecule), mimics the effect of breaking and creating chemical bonds—essentially creating a new molecule. In the example shown in Fig. 1A, we show a motif (or “reaction rule”) which dictates that the bonds in the R graph are to be created and those in L are to be destroyed, given that a common context K can be found in both species. During the course of the reaction, K is the part of the molecule that remains unaltered (see ESI Fig. 2, and ESI Section 3.1†). The molecule(s) resulting from the graph transformation are the product(s) of the reaction. A complete library of reaction rules is applied to a set of initial reactants, giving rise to an initial set of products, which became input as reactants for the next generation of reactions. As the process is iterative, we shall call this initial set of products “Generation 1”. This process can be continued for any number of iterations (or generations) decided by the user, which causes the network grow at each step. After completion of all reaction iterations, the entire network can be dumped into a format that can be processed using other tools and further analysis such as comparison with experimental data, computing molecular descriptors, and searching for autocatalytic cycles within it (Fig. 1E). This pipeline is open-source, written mostly in Python, and can be easily accessed along with relevant documentation at https://github.com/Reaction-Space-Explorer/reac-space-exp. Further, extensive examples of loading chemicals and reaction rules among other procedures can be found on the MØD documentation pages at https://jakobandersen.github.io/mod/ which also have an interactive playground for testing scripts without requiring local installation.
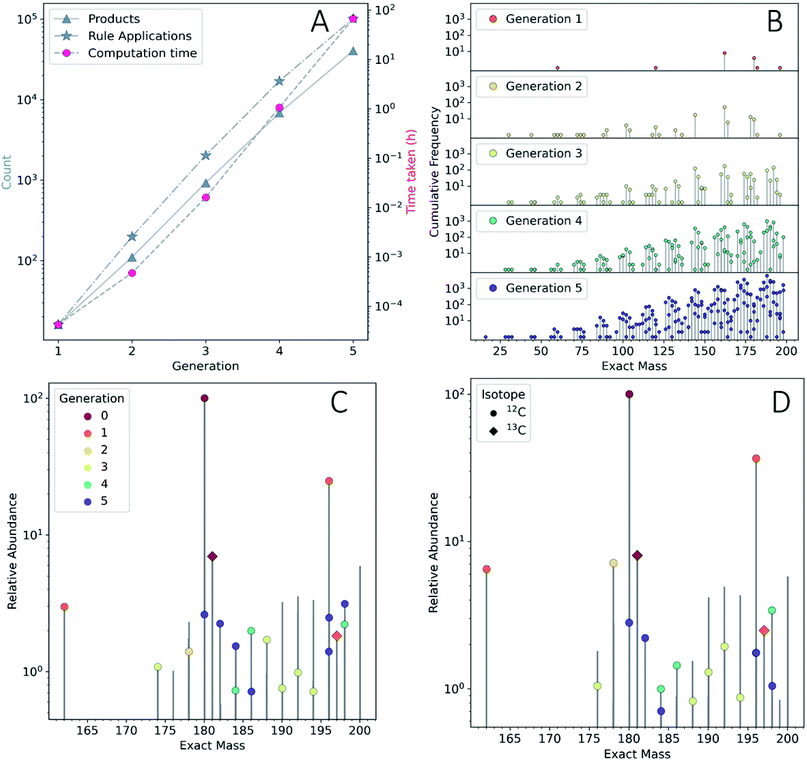
To show the application of this workflow, we examined the reaction of water and glucose as initial reactants and allowed all mechanisms defined in our reaction rule set to operate. This rule set was selected based on our chemical intuition and literature precedent (see ESI Section 3.2† for details). We iterated the reaction for a total of five generations. As this process was elaborated, the rules for reaction network expansion allowed any potential reaction to occur as soon as potential substrates were produced. Fig. 2A shows the numbers of products, rule applications and computation times as a function of generation (see also ESI Table 1†).
We quickly found that some rules in our set caused a sharp growth in computing time. The computing resources required can quickly become a bottleneck, even after imposing a cutoff of 200 amu on the maximum allowed product mass, it was possible to expand the network practically to only five generations using desktop computational resources (see Methods†). The fifth generation produced 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 products—with a cumulative total of 48
512 products—with a cumulative total of 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 unique products across all generations. Since this computed model is only an approximation of real chemistry, following41 we refer to this network as a CRNR. Fig. 2B shows the mass distribution and frequency of isobaric isomers generated in this CRNR.
401 unique products across all generations. Since this computed model is only an approximation of real chemistry, following41 we refer to this network as a CRNR. Fig. 2B shows the mass distribution and frequency of isobaric isomers generated in this CRNR.
It is clear from Fig. 2A that computation time increases roughly exponentially for each generation, though this only became ponderous in generation five. Extrapolating these values using least squares fits suggests 6th and 7th generations would take months to years using our employed computational resources, and would produce ∼3.2 × 105 and ∼2.3 × 106 structures, respectively. These values are expected to change with the upper mass limit described previously, an effect we illustrate in ESI Fig. 4† by varying the maximum mass limit from 200 to 300 amu. Certainly, at some point all possible structures ≤200 amu reachable using these rules would be computed, and correspondingly the differential number of output products and computation time would decrease to zero. Graphical representations of the overall ADG CRNR output, including its connectivity after five generations is shown in Fig. 3.
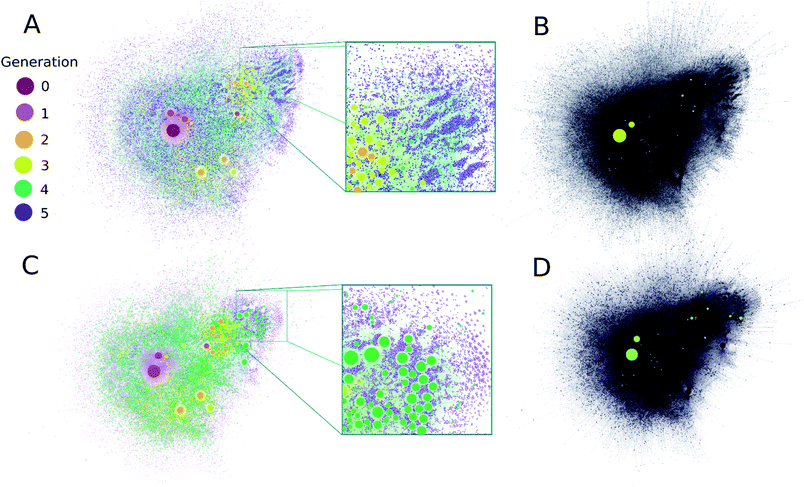 | ||
| Fig. 3 (A) A comprehensive representation of the ADG CRNR after five generations with compounds colored by their first generation of appearance. Node size is proportional to the in-degree of compounds. (B) Compounds detected in ref. 36 produced in this CRNR are shown in light-green. (C) A comprehensive visualization of the computed network after five generations colored by the out-degree of each compound. (D) Representation of plot (C) for the compounds detected in ref. 36. Experimentally verified compounds are a small subset of those predicted by the CRN, but there is also some clustering of the identified compounds in regions of the CRN where high in- and out-degree compounds from the CRN also cluster. Zoomed insets in (A and C) show the fine scale structure of the ADG CRNR, demonstrating the large number of potential CRN by-products which may contribute to the CRN's overall compositional diversity. | ||
A metric that quantifies the connectivity of a node in a graph is its node degree. Compounds generated earlier in networks generally have both higher in- and out-node degrees (see ESI Fig. 4A and B†). This is mainly due to their early formation during CRNR synthesis. Novel fifth generation compounds can't have out-degrees in this computation, and often have low in-degree scores. Related to this point, the majority of compounds in the CRNR, including most produced in early generations, have low in- or out-degree (see ESI Fig. 4A and B†). In other words, relatively few reactions have produced or consumed them. Reaction efficiency distributed over so many compounds may generate only extremely trace yields of output species in real world chemistry after a lengthy series of reactions. Indeed, this underscores the point that many analyses of complex diversity generating reactions are likely myopic due to analytical limitations.
It can be seen in Fig. 3 that highly connected compounds generally cluster together. Some of these highly connected compounds correspond to the compounds identified in ref. 36. One might expect that compounds which are produced in early generations with high in-degree and low out-degree would be abundant products but in practice, kinetics and thermodynamics undoubtedly combine to sculpt observed product abundances over time. However, there is no significant difference in the average in- and out-degrees of molecules that have been identified analytically (discussed later) and the rest of the network (see ESI Fig. 5†). Although part of the point of this work is to help identify minor species in complex reactions, the first-order CRNR only identifies plausible network products. This methodology makes no claim as to the relative product abundances at any point in the course of reactions. ESI Fig. 6† shows the prominence of each codified reaction distributed across the network; it can readily be appreciated that kinetic weighting of the rules would affect the ultimate abundance of network products.
Experimental validation
Given the centrality of glucose in biochemistry, its abundance in biomass in the form of compounds such as starch and cellulose (e.g., ref. 42), and the economic importance of using such abundant by-products of agriculture (e.g., corn-stover43), there is considerable interest in understanding how to convert glucose to other economically useful compounds (e.g., lactic acid44). We tested the validity of our ADG CRNR simulation by matching our model's output against the compounds identified in a previous comprehensive GC-MS analysis of this reaction36 (see ESI Section 3.5† for details). In addition, using our own ESI-FT-ICR measurements of the laboratory degradation of glucose done for this study, we sought to explain peaks in the mass spectrometry with our CRNR. Electrospray ionization (ESI) is not necessarily superior to GC-MS, but it may allow the detection of higher MW underivatized polar compounds, as it is not affected by chromatographic effects. To this end, we reacted two samples of D(+)-glucose (≥99.5%, Aldrich), under either drying or aqueous solution conditions. Details of sample preparation, mass calibration and data processing methods are provided in ESI Section 3.7.†Matching with literature data
In just five generations, 73% of the entire suite of compounds with reported molecular structure by ref. 36 could be matched. We used an approach similar in nature to retrosynthetic analysis to demonstrate that 47 of 49 (∼96%) of the test set targets are accounted for within nine generations (see ESI Section 3.6† for details). We present the complete list of matched compounds annotated by their generation of appearance in ESI Fig. 8†. This correspondence between our model and observations illustrates that these simulation methods can predict detected compounds.However, this analysis does not explain the abundance of the matched compounds, or the non-detection of CRNR compounds. The CRNR produces many more compounds than have been detected analytically. There are two main explanations for this. First, using GC-MS analysis, some compounds cannot be identified due to the lack of reference standards or mass spectral library matches. Some compounds perhaps do not derivatize well, some may bind irreversibly to chromatographic columns or chromatograph poorly, and many minor compounds could be present in abundances below analytical detection limits. Indeed, several unknown compound peaks were noted in ref. 36, and summation of the product yields provided in Tables 1 and 2† of reference36 gives a carbon recovery of ∼60% in the form of identified compounds, including scores of compounds identified in ≤1% yield. The four most abundant compounds identified, accounting for ∼25% of the recovered yield, include lactic acid, 2,4-dihydroxy butanoic acid, 2-C-methyl-glyceric acid and formic acid. The first three are produced here in generation 3, the fourth in generation 4.
Second, the CRNR allows for reactions which may be kinetically or thermodynamically inhibited, and thus may over-represent their importance. In the ADG reaction, and likely in various similar reactions, some subset of the analytes can be easily assigned to structures, though mass balance calculations suggest these analyses miss a large number of products (e.g., ref. 36).
Overlap with mass spectrometry
Even though GC-MS analysis can be extremely informative for analyzing low-MW fractions of complex organic mixtures, higher MW fractions may require additional analysis. High-resolution MS coupled with ESI offers an orthogonal way to characterize ADG reaction products. The FT-ICR-MS methods used here have a low-end MW cutoff of ∼150 amu, and our computational methods imposed an upper MW limit of 200 amu for their practical exploration due to computational resource limitations. Given these limitations, it was of interest to examine the general concordancy of the ADG CRNR output by comparing it to FT-ICR-MS data.For a more informative representation, we created Kendrick mass defect (KMD) and van Krevelen diagrams to see if the model's products have a similar elemental composition as that measured using mass spectrometry. Kendrick plots are used for the identification of chemically related compounds in high resolution MS, and produce easily visualizable graphical representations of complex organic mixtures45 by placing the one-dimensional MS peaks in a two-dimensional display. Each mass peak having a unique composition has its own Kendrick mass defect, which allows peaks to be resolved separately (see ref. 46 for a discussion, and see ref. 47 for an application of these techniques to prebiotic chemistry).
Fig. 4A shows an overlay of the ADG CRNR with experimental negative ionization mode FT-ICR-MS data adjusted to correspond to M–H educt masses.‡ The CRNR data have no kinetic or thermodynamic weighting, but the general trends of the modeled and measured data show good correspondence. The CRNR output widens to include compounds either not measured or not measurable in the experimental data. This may partly be due to their low molecular weight and potentially low abundance. There is considerable overlap of the modeled and measured data in the ∼175–200 amu regime where the two datasets are directly comparable (Fig. 4B).
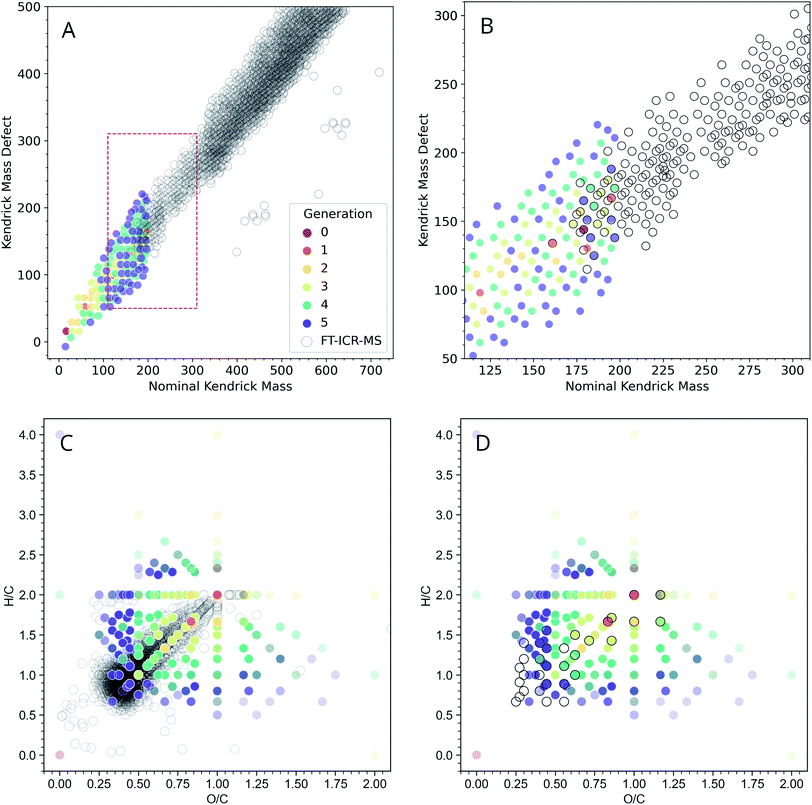 | ||
| Fig. 4 Modeled negative ionization mode Kendrick plot of the ADG CRNR (open gray circles) overlaid on measured “wet” ADG products as measured using negative mode ESI-FT-ICR-MS (dots colored by first generation of appearance in the CRNR). (A) The ADG CRNR extends from m/z 14 to 200 while the FT-ICR-MS data extends from m/z ∼150 to 750. (B) A zoomed view of the area in the red box in (A) in which the overlap of the CRNR and measured data is more clearly evident (where colored dots fall inside gray circles). (C) A van Krevelen diagram of the computed ADG products overlaid with data from the “wet” ADG experiment; (D) as in C but after truncating the dataset with the upper mass limit imposed in the simulation (200 amu), which makes the correspondence between computer and laboratory experiments more apparent. Experimental details can be found in ESI Section 3.7.† | ||
The extent of overlap can be quantified by counting the number of overlapping data points. For simplicity, we have excluded the consideration of 13C isotopologues in this plot. Thus, in the narrow regime depicted in Fig. 4B, 19 out of 30 points (63.3%) from the MS data are reproduced by the model. This strongly suggests that the CRNR accurately reflects the mass transformations of real ADG chemistry. There are two primary reasons the model may not be able to recover all compounds observed by MS analysis. First, the simulation may not been able to explore the chemical space exhaustively in just five generations. Second, the selected set of reaction rules was based on our own chemical intuition and may not be complete. That is to say, some of the chemical space may not be reachable using these rules. One benefit of these methods, however, is that the user can readily add and select their own reaction rules. Another way of characterizing bulk composition is the use of van Krevelen diagrams, in which atomic ratios resolve species. In Fig. 4C, it can be seen that as the CRNR evolves, an overdensity of products tends to shift near the origin of the H/C–O/C plane. This likely indicates the effect of sequential H2O loss.48 The experimental data closest to the origin with H/C < 0.7, and O/C < 0.3 likely represent polycyclic aromatic hydrocarbons (PAHs) and other condensed aromatics, which the ADG CRNR does not produce over the number of reaction generations modeled here.
Molecules produced in the ADG CRNR closest to this group of aromatics are shown in ESI Fig. 10.† This group includes o- and p-benzoquinone, which are known to easily engage in both one and two electron redox reactions. The dense experimental cluster centered around H/C ∼ 1.2 and O/C ∼ 0.3 likely correspond to so-called CRAM (Carboxyl-Rich Alicyclic Molecules),49 which are produced in the later generations of the ADG CRNR. The effect of experimental conditions on the ADG reaction product suite can be seen in ESI Fig. 9,† in which van Krevelen diagrams of the wet and dry samples are compared.
It is apparent there are numerous CRNR values which do not match the measured data, and the network attributes which differentiate the corresponding and non-corresponding values are places where more refined analysis (for example by automated evaluation of which reactions or reaction sequences produce non-matching data points) could be of predictive value. Further measurements using MS techniques sensitive to lower mass ranges would provide constraints for CRNR development.
The trajectory of the ADG CRNR as analyzed using Kendrick plots thus matches laboratory measurements well where good data exists, and tracks the general trend of mass measurements of higher MW products, especially for the earlier generation products, though it also overpredicts in some respects, which are good places for future refinement of the techniques described here. As for the Kendrick plot, for the van Krevelen diagram (Fig. 4C), there is a significant amount of real data from masses outside the simulation range, but the matched data makes predictions about the nature of these compounds. For example, the branch in the data extending horizontally from (H/C = 2, O/C = 1) is mainly matched by polyhydroxy acids in the CRNR.
Chemical descriptor evaluation of ADG CRNR
It is useful to be able to quantitatively estimate the physical and chemical properties of the large number of molecules generated in large network such as the one considered here. Molecular descriptors provide such quantitative metrics, and can help explore how certain phenomena emerge with the growth of the network. Descriptors and their calculation methods are provided in ESI Section 3.8.† These methods also allow rapid computation of chemical descriptors for compounds that have not yet been identified in experimental CRNs, potentially leading to the a priori identification of emergent chemical behaviors which can be connected to autocatalysis.
Fig. 5 shows the computed evolution of cLog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P properties in the CRNR, which may predict how the products could be expected to behave in terms of their solubility. It is evident that the CRNR produces increasingly hydrophobic compounds which may eventually lead to phase separation.
P properties in the CRNR, which may predict how the products could be expected to behave in terms of their solubility. It is evident that the CRNR produces increasingly hydrophobic compounds which may eventually lead to phase separation.
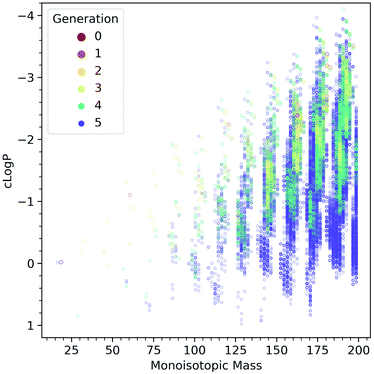 | ||
Fig. 5 Computed cLog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values as a function of molecular mass, colored by the generation in which the species are first produced. The network produces more and more hydrophobic species as it evolves. P values as a function of molecular mass, colored by the generation in which the species are first produced. The network produces more and more hydrophobic species as it evolves. | ||
Fig. 4C shows that the atomic ratios of elements in the ADG CRNR products change markedly during the reaction, causing their cLog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PFig. 5 properties to evolve to be both higher and lower than that of glucose, though the products generally tend to be predicted to be more hydrophobic, as glucose is already at a very high O/C ratio and very water-soluble. This maturation effect has been shown to produce interesting self-organizational properties in glucose-ammonia reactions,50 and has been noted recently in experimental molecular cloud analog maturation experiments.51
PFig. 5 properties to evolve to be both higher and lower than that of glucose, though the products generally tend to be predicted to be more hydrophobic, as glucose is already at a very high O/C ratio and very water-soluble. This maturation effect has been shown to produce interesting self-organizational properties in glucose-ammonia reactions,50 and has been noted recently in experimental molecular cloud analog maturation experiments.51
This suggests that the production of new phase-forming materials is a common property of CRNs simply due to the ways CRNs enable changes in the overall properties of product molecules. Such descriptors can be combined with other user-defined ones to identify autocatalytic reaction motifs which can give rise to connected emergent properties besides novel phase generation.
Consideration of enantiomers
All contemporary biology is highly chiral, as biology almost exclusively constructs itself using L-amino acids and D-sugars. The vast majority of possible organic compounds are themselves chiral,52,53 which is a simple attribute of the coordination number of organic compounds. It has been proposed that large chemical networks are likely to undergo spontaneous symmetry breaking toward homochiral states.54 The computed ADG network starts from a single organic compound with four chiral centers, which are known to interconvert during the transformations modeled here. This network does not track or favor one stereoisomer over another. Most measurements, to the extent they exist, suggest racemization is rapid in these kinds of transformations. The extent to which a few catalysts might control and favor the development of homochirality in networks becomes a tangible question using these methods. For example, though it might be moderately computationally challenging, it would be possible to explore at which points in these networks enantioselective catalysts would flip nodes to cohesive chiralities.The methods used here do not explicitly take stereochemistry into account; stereoisomers are flattened into constitutional isomers in this workflow. Most of the reactions modeled here would generate a mix of stereoisomer products. Fig. 6 shows the reaction connectivity of the 333![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 computed stereoisomers generated from the 48
501 computed stereoisomers generated from the 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 unique flattened initial ADG CRNR product structures after five reaction generations (see ESI Section 3.8† for details).
403 unique flattened initial ADG CRNR product structures after five reaction generations (see ESI Section 3.8† for details).
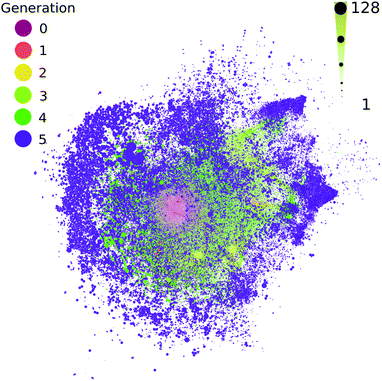 | ||
| Fig. 6 The number of potential stereoisomers as a function of reaction generation (left color scale) for the computed ADG network. Node size is linearly proportional to stereoisomer number (bottom size scale). A circle pack layout in Gephi55 with generational hierarchy as an attribute has been made. | ||
Fig. 6 suggests that most chirally redundant compounds appear in the periphery of the network, chirality likely scales with MW (see ESI Fig. 11†), and there is likely considerable correlation between the number of stereoisomers across generations.
This model ignores two important points, first that kinetic effects may favor one enantiomer over another, and second that there may be stereochemical feedback in reaction networks which are not explicit in the rules used to generate the modeled network. If such effects are common, it should be a common phenomenon that CRNs should be capable of amplifying enantiomeric excesses, albeit perhaps randomly according to stochastic seeding and as determined by kinetic and network effects, which are not necessarily as yet computationally predictable (e.g., ref. 54), similar to spin-glass models.56 Given the importance placed on understanding the onset of homochirality in the origins of life community, such potential effects should be a prime target for refining this kind of modeling.
It has been suggested that modern metabolism, which is mainly mediated by enzymatic catalysis, has its roots in non- or semi-enzymatic processes.57 The ADG CRNR reveals a myriad of flux possibilities for organic compounds starting with a relatively simple input compound. Glucose is not formally determined with respect to its stereochemistry in this model, but one could expect that starting with the L-enantiomer of glucose, or any one of the 16 stereoisomers of hexose, essentially the same stereochemically flattened network would be obtained.
Various organic compounds in carbonaceous meteorites have been shown to display enantiomeric excesses, including amino acids,58–61 and hydroxy acids.62–64 The enantiomeric excesses of sugar-derived compounds in the Murchison meteorite have also been found to have a systematic enantiomeric excess which appears to propagate across these species with increasing MW.65 Mechanisms have been suggested for how such enantio enrichments can be achieved (e.g., ref. 66), but the methods presented here may offer novel ways of identifying amplifying mechanisms of observed enantio enrichments, which may have implications for biases which become “locked in” during the origins of life.
Detection of autocatalytic motifs
There are two fundamentally different types of catalytic reaction networks. In the first type, there are no formal catalysts, and the closure of the reaction cycle is the catalyst.67 The analysis here easily finds such cycles. The second type of catalytic reaction network involves compounds which are best thought of as non-covalent shape-recognizing catalysts, models considering such networks have considerable history (e.g., ref. 68). In principle such feedback mechanisms could be measured and formalized, this is a “holy grail” in this research domain (e.g., ref. 69), the methods presented here are a step in this direction as they present a prescreened set of compounds connected by plausible reactions.We explored two methods to detect autocatalytic reaction motifs. The first used an “imperative” approach (see below), the second used a “declarative” approach, in which the pattern to be searched for was defined beforehand, and then a query engine produced its own solution to find the pattern (see ESI Section 3.10†).
A benefit of the imperative approach is that since it can be programmed in Python, it helps the pipeline fit together, since the declarative approach relies on the user having Neo4j (a graph query database) implemented, though Neo4j is also open-source. The declarative approach has the benefit that the network can be cached in the Neo4j database so that the network can be built up over time, and the whole database does not necessarily need to be read into RAM for calculations. This method may be preferable where scale/computation time is an issue, or where researchers build up reaction network databases that need to be kept on hand for reference, or the search pattern to be matched becomes very complex. Within a declarative pattern match query one can also define the catalytic molecule, e.g. by adding a clause in the pattern to filter by SMILES representation. The benefit of this graph query language is that it is not necessary to dig into graph algorithm code to modify the patterns returned: the user needs only modify the query, and Neo4j finds a solution to match the pattern the query describes.
The imperative approach uses the Ford–Fulkerson algorithm,71 performing a similar task as the declarative approach. The user can here choose which node is the catalytic node (e.g., the node from which one edge leaves and two edges arrive). The program then returns all defined autocatalytic motifs in which this node is catalytic. This program took about 4 hours using our computational resources to search for all such cycles among the computed ADG CRNR and consumed ∼8 GB of RAM in each task. ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 autocatalytic reaction cycles were found in the generation 5 ADG network looking for autocatalytic cycles using glucose as a starting or catalytic molecule. Many cycles of different lengths were returned and the distribution of returned cycle sizes had a maximum around a certain cycle size, although this may have been affected by the fact that only 5 generations of reaction expansion were generated and explored.
000 autocatalytic reaction cycles were found in the generation 5 ADG network looking for autocatalytic cycles using glucose as a starting or catalytic molecule. Many cycles of different lengths were returned and the distribution of returned cycle sizes had a maximum around a certain cycle size, although this may have been affected by the fact that only 5 generations of reaction expansion were generated and explored.
The Neo4J defined search pattern doesn't guarantee a pathway identified as topologically autocatalytic is energetically favorable, since the reactions derived from reaction expansion do not specifically encode energetic information. To address this problem, we merged computed thermochemical information derived from the eQuilibrator API70 (see ESI Section 3.9† for details) onto the CRNR nodes so that network queries could constrain energetic favorability. For example, sorting the pattern match results by the minimum aggregated energy across the reactions in the ring path and returning the lowest energy paths should yield the most energetically favorable reaction motifs.
Using the imperative approach possible autocatalytic cycles in which all reactions were spontaneous according to thermochemical calculations carried out under basic conditions (e.g., for which the free energy for each reaction, ΔrG′, is negative at pH 10, Fig. 7) were extracted from the ADG CRNR. By restricting the search for spontaneous cycles, there is a considerable reduction in the number of cycles. The percentage of cycles with spontaneous reactions with respect to the total number of cycles found by the algorithm are: hexonic acid (16.6% of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902), 2,3,4-trihydroxybutanoic (0.6% of 16
902), 2,3,4-trihydroxybutanoic (0.6% of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900), tetrose (0.3% of 16
900), tetrose (0.3% of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900) and pyruvic acid (0.1% of 16
900) and pyruvic acid (0.1% of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902). The similarity in the number of total reactions in each case is coincidental.
902). The similarity in the number of total reactions in each case is coincidental.
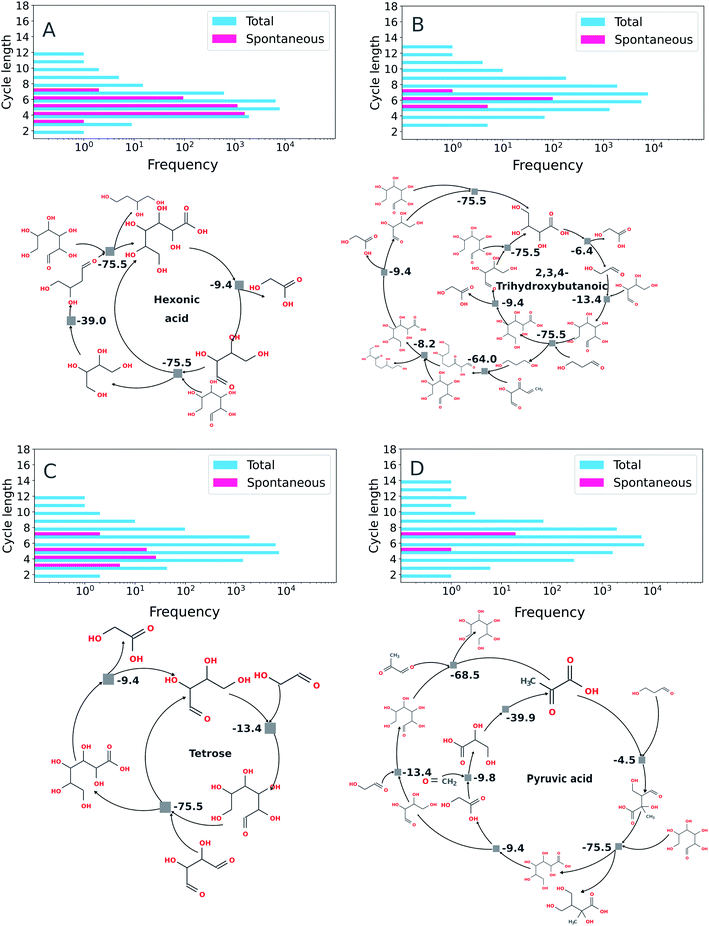 | ||
| Fig. 7 Exemplary autocatalytic motifs found in the ADG CRNR identified as autocatalytic and thermodynamically favorable. Panels (A) through (D) show the frequency distributions of topologically identified autocatalytic cycles as a function of cycle length (top left in each panel), as defined in the methods section by implementation of the imperative search strategy. In the upper right of each panel, the distributions of thermodynamically favorable autocatalytic cycles among the topologically identified sets as determined using eQuilibrator70 as a function of cycle length are shown, and exemplary cycles are shown below. (A) Two identified autocatalytic motifs using hexonic acid (produced in generation 1 from the ADG of glucose) as the “catalytic molecule.” The cycle on the left only requires glucose as a feedstock once hexonic acid is produced. (B) An identified autocatalytic motif using 2,3,4-trihydroxybutanoic acid as the “catalytic molecule.” This cycle is fed by glucose (provided in G0), tetrose (produced in G1) and 2-hydroxy-3-oxo-4-pentenal (produced in G4). (C) Autocatalytic motifs found which use tetrose as catalyst. The motif on the left requires glycolaldehyde (produced in G1 from glucose) and 2,3-dihydroxybutanedial (produced in G2 from glucose) as feedstocks; the motif on the right is fed by glycolaldehyde and glyoxal (produced in G2). (D) An autocatalytic motif using pyruvic acid (produced in G3) as the catalytic molecule. This cycle is fed by 3-hydroxypropanal (produced in G3), glucose (initial feedstock), glycolaldehyde, methylglyoxal (produced in G2) and formaldehyde (produced in G2). | ||
Some recently discovered reaction sequences of prebiotic interest, e.g. the rTCA analogue studied in Stubbs et al.,72 could not be discovered in this network, since they contain components with masses >200 amu (namely citroylformate, isocitroyl formate and aconitoylformate). This is notable as the apparent abundance of autocatalytic cycles containing only molecules of MW < 200 in the ADG CRNR which may be able to accomplish similar chemistries as other cycles which have been studied in vitro points to there being many other interesting cycles left to investigate, and also because there may be many nascent cycles whose roots are discovered by this analysis but which would require further iterations for full elucidation using these methods.
Various studies suggesting methods for exploring chemical space, and more particularly in prebiotic chemistry,41 using CRNRs have been published (e.g., ref. 73), including a recent report using methods based on scraping chemical databases for reactions known to occur under what the authors considered plausible prebiotic conditions.16 There is a wide variety of reaction conditions to explore, and thus the chemical space of simple reactions may be complex and require deeper automated exploration and analysis.74 Orgel75 pointed out that the kinetics which allow chemists to explore prebiotic chemistry are possibly skewed more by the lengths of graduate and post-doctoral fellowships than anything inherent to chemistry, a notion reiterated and explored more deeply in ref. 76. Thus, scraping the “prebiotic chemistry literature” likely over-explores a small area of chemical reaction space, which is itself overly focused on producing species present in modern biological chemical space due to biases researchers introduce into how they conceive life may have started.
The reaction mechanisms applied here were hand-selected, but they are extremely general, and were applied liberally with a single filter: are such reactions known to occur under basic conditions? If so, they were incorporated in the network, even though their kinetics are not parameterized explicitly. According to this logic, this creates a reaction landscape that can be bootstrapped and explored according to criteria outlined for example in ref. 16 and 76.
This workflow may be considered overly permissive, but it allows for reaction mechanisms to produce compounds which have not been identified or looked for because they are easily related to modern biochemistry, which side-steps an important criticism (e.g., ref. 27, 77 and 78) of such methods and enables exploration of chemical landscapes which lead in less obvious ways to modern reaction cycles involving known compounds, and allows for discovery of novel compounds and reaction motifs and ways to generate phase separation, the development of information transfer systems, and autocatalysis in ways consistent with Ganti's chemoton model,69,79e.g., in which the development of chemical properties is related to the development of systemic chemical network properties.
Emergent catalysis could become a mechanism for reinforcing chemical transformation pathways as permitted by chemical kinetics and thermodynamics. We explored here the possibility that the ADG CRNR offers a simple way to explore how CRNs may switch between major modes of flow, which can be expanded to other CRNs such as those including other heavy atoms such as N and S, as well as environmental influences including transition metals and photochemistry. Discovering structurally-based catalysis is presently complicated, as it depends on knowing how compounds interact and stabilize transition states. This is undoubtedly a key aspect of how autocatalytic reactions may have led to the origins of life. In contrast, it may be relatively simple to find network autocatalytic reactions, as defined in for example (ref. 31, 67 and 80) and these may already imbue CRNs with emergent properties, for example by generating compounds capable of forming new phases (e.g., ref. 50 and 81), which may further help organize CRNs.
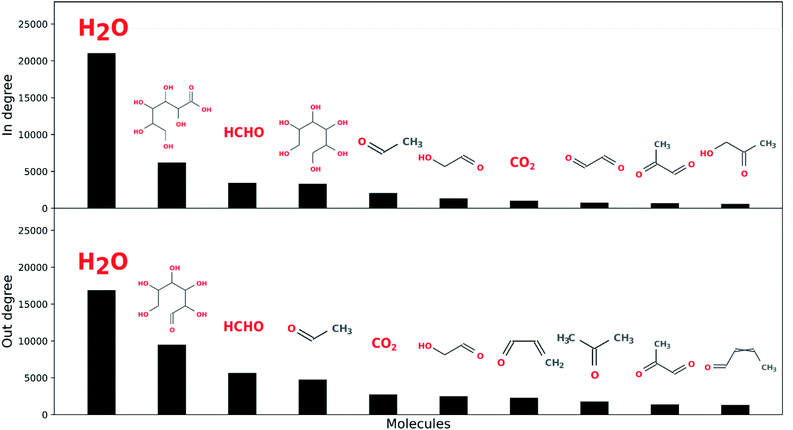
Water is the most connected component over the five reaction network generations explored here, followed by input open-chain glucose, formaldehyde, acetaldehyde, hexanoic acid, hexitol, acrolein, crotonaldehyde and CO2 (see Fig. 8). This suggests, as might be expected, there is considerable overlap between sugar degradation and formose chemistry, and also among both of these chemistries and fermentative metabolism, although the latter is considerably more cannelized.82 Furthermore, water is also the most connected component in terrestrial biological metabolism.83 We do not necessarily ascribe a great deal of meaning to this, though it may be unlikely that there exist any other solvents (HCONH2, N2, H2, CO2, CH4, etc.) which can exist under any planetary combinations of pressure and temperature which so easily exchange mass with the reaction networks they solubilize. This may be a unique aspect of aqueous chemistry with respect to enabling living systems.
Comparison with biological databases
The ADG CRNR contains tens of thousands of compounds produced after only a few generations. To assess the extent to which ADG CRNR products exist in biology, we compared the ADG CRNR with two well-known databases of biological molecules: the Human Metabolites Database (HMDB84), the Kyoto Encyclopedia of Genes and Genomes (KEGG85), and the E. coli Metabolome Database (ECMDB86). Since SMILES representations of molecules can be written in several ways, to make direct comparison between the CRNR output and the databases, both sets were converted to canonical SMILES representations. To make accurate dataset-to-dataset comparisons, the HMDB, KEGG and ECMDB matches were limited to compounds of ≤200 amu containing only CHO.The overlap of this network with biological metabolic transformations is small (see ESI Fig. 13†), thus although arguments have been made that ADG may mirror the ontogeny of aspects of glycolysis, the same could be said of many sugars, thus this sort of retrograde inspection may be suspect, except with regard to considerations such as the relatively low reactivity barriers of sugars87 in general, or glucose's tendency to form a cyclic hemiacetal.88
Reduction of isobaric isomer search space
This analysis can assist in the identification of compounds in complex mixtures. Identifying compounds in complex mixtures solely using 1D MS data can be complicated by the large number of potential isobaric isomers for any given m/z value. Reaction network modeling allows for an extreme reduction in the unknown product search space. Our model's agreement with the FT-ICR-MS data presented here does not guarantee the unequivocal identification of unique species, but it reduces the chemical search space by several orders of magnitude.Fig. 9 shows the number of unique molecular graphs per nominal mass produced by this ADG CRNR compared to those present in repositories, including the Beilstein and NIST MS databases,89 as well as the number expected to be theoretically possible. For consistent comparison, numbers were limited to CHO-containing molecules, based on Appendix D of ref. 90. Fig. 9 highlights the utility of the methods presented here to MS analysis of complex mixtures. Although the reference data presented in Fig. 9 is now ∼16 years old, it is apparent that not all of the compounds that could exist, whose numerosity grows exponentially with increasing MW, have been synthesized in laboratories or detected in nature. Second, MS databases generally contain fewer compounds than are known to exist (see the cross and diamond data points in Fig. 9A). Importantly, the number of unique molecular graphs generated by the ADG network is much smaller compared to that computed to possibly exist by several orders of magnitude for a given nominal mass over the mass range of 16–150 amu, but also fewer in number compared to known compounds in databases by more than an order of magnitude over this mass range, then exceeding this above ∼128 amu. This suggests present MS libraries are ill-equipped for the characterization of novel compounds beyond 128 amu. The trends in these data suggest that these discrepancies grow with increasing mass, and thus compound identification incorporating reaction network generators could both increase the accuracy of compound identification in complex mixtures and speed the search time by many orders of magnitude. A major contribution of this work to understanding the composition of complex mixtures is thus the extreme compression of the search space which needs to be explored to understand the generative relationships of compounds and mass features in complex mixtures.
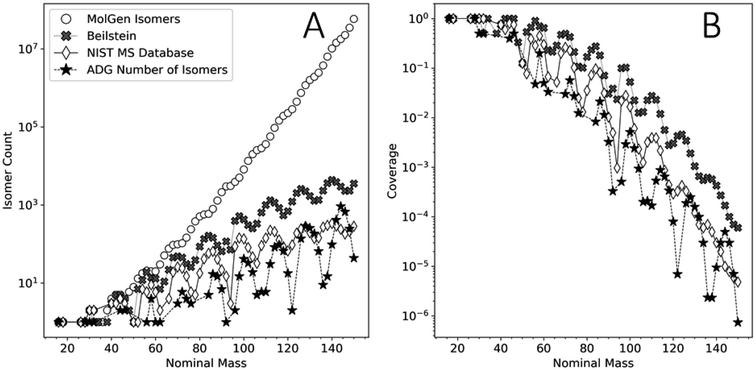 | ||
| Fig. 9 (A) Comparison of the number of unique molecular graphs as a function of nominal mass obtained by MolGen, the Beilstein database, the NIST MS database (data adapted from ref. 90) and the computed ADG CRNR from this study. (B) Coverage of the molecular graph space by the ADG network (filled asterisks), the Beilstein database (filled crosses) and the NIST MS database (open diamonds) relative to the cumulative isomer spaces computed by MolGen. | ||
Dissipative structures and reaction networks
The ADG CRNR explored here allows exploration of the potential frequency of autocatalytic cycles within CRNs. Autocatalytic reaction motifs and nonlinear chemical dynamics are essential for the appearance of processes far from thermodynamic equilibrium and the dissipation of entropy in chemical systems.91 It should be possible to use numerical methods to predict which autocatalytic motifs most deterministically steer CRNs to produce specific outcomes. These motifs could indicate oscillatory chemical processes or the formation of dissipative reaction pathways. Such dissipative pathways could have played an important role in the evolution of life and its ability to complexify and self-organize.92 The irreversibility highlighted by a considerable number of rules in our MØD-derived model (e.g., reactions with high free energy changes, elimination, elimination + enol_keto, Cannizaro, unsaturated acid decarboxylation), and the nonlinearity of most reactions suggest there may be directionality in the progression of the ADG reaction. Irreversibility, combined with fluctuations, are what Prigogine and collaborators have shown are the main characteristics of the evolution and self-organization of dynamic chemical systems.93,94Conclusions
We present here an open-access user-modifiable workflow for exploring the chemistry of CRNs to identify real reaction products and processes. The presented methods can be used to identify formally autocatalytic cycles, flows which are thermodynamically favorable,95 as well as products with novel properties, including those enabling phase separation.There is room for algorithm improvement and refinement in this pipeline. As this workflow is open source, this process is modifiable. Improvements could involve including new reaction rules,96 or the use of machine learning to generate reaction rules,97 and filtering generated CRNs for tautomers.
Regardless of which processes explain the origins of the organics observed in CRNs, it is not clear which organics they contain were important for the origins of life.13 There are also likely nuanced differences in the course and outcome of CRNs that depend on kinetics dependent on reaction conditions.98 Nevertheless, most origins of life models focus on autocatalytic reactions, regardless of whether these depend on specific ribozymes99,100 or collections of small molecules.77 Such models diverge in their assumptions of the required complexity of the molecules assumed to have been involved versus the complexity of the processes involved.101 This workflow offers a simple way to parse complex data collected in this context. We are presently using this workflow to explore other CRNs which are more easily relatable to the origins of life.
Data availability
The data underlying this study are available in the published article and its ESI† or are publicly available through the Open Science Framework at https://osf.io/jrhvs/?view_only=b383facf13f44cac915f1d97ebb80dcc. This model's code is available open-source on GitHub, along with supporting documentation at https://github.com/Reaction-Space-Explorer/reac-space-exp.Author contributions
AA conducted the majority of the MØD simulations and coded most of the reaction mechanisms, JR designed and wrote the Neo4J queries, SS conducted the descriptor computations and visualizations, RC performed the searches for spontaneous autocatalytic cycles, and created the Gephi visualizations, EALG conducted the database comparison studies, HBS conducted the thermodynamic computations, JLA developed MØD and helped implement its use in this study, HC conducted the FT-ICR-MS analysis, MM provided assistance with database overlap analysis, HJC designed and oversaw this study, and conducted the laboratory experiments. All authors contributed to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AA, JR, SS, RC, EALG, and HJC would like to thank the Blue Marble Space Institute of Science (BMSIS) for organizational support. JA and HJC would like to thank the Earth-Life Science Institute (ELSI) and the ELSI Origins Network (EON) for financial support during the early development of this work. EON was supported by a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. SS would like to acknowledge the SETI Forward Award from the SETI Institute. RC wishes to acknowledge FONDECYT (Convenio 208-2015-FONDECYT) for his Master scholarship. He would also like to thank Miguel Miní for his suggestion and support in the imperative search code for autocatalytic cycles. JA is also supported by the Novo Nordisk Foundation grant NNF19OC0057834 and by the Independent Research Fund Denmark, Natural Sciences, grant DFF-0135-00420B. A portion of this work was funded by the National Science Foundation Division of Chemistry and Division of Materials Research through NSF DMR-1644779, and the state of Florida. We would like to thank the anonymous referees for their constructive feedback that led to improvements in the manuscript. We would also like to express our sincere regards to Rana Dogan for her assistance in the early phases of this work.Notes and references
- K. C. Nicolaou and T. Montagnon, Molecules That Changed the World, Wiley, Weinheim, Germany, 2008 Search PubMed.
- P. Anastas and N. Eghbali, Chem. Soc. Rev., 2009, 39, 301–312 RSC.
- S. D. Killops and V. J. Killops, Introduction to Organic Geochemistry, Wiley, Hoboken, NJ, USA, 2nd edn, 2013 Search PubMed.
- V. A. Vaclavik and E. W. Christian, Essentials of Food Science, Springer, New York, NY, USA, 2008 Search PubMed.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285–366 CrossRef CAS PubMed.
- P. Schmitt-Kopplin, Z. Gabelica, R. D. Gougeon, A. Fekete, B. Kanawati, M. Harir, I. Gebefuegi, G. Eckel and N. Hertkorn, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2763–2768 CrossRef CAS PubMed.
- N. Guttenberg, H. Chen, T. Mochizuki and H. J. Cleaves, Life, 2021, 11, 234 CrossRef CAS PubMed.
- H. J. Cleaves, Life, 2013, 3, 331–345 CrossRef CAS PubMed.
- S. Zhang, J. Huo, X. Sun, F. Yang, P. Wang, J. Wu, Y. Zhang and Q. Shi, Energy Fuels, 2021, 35, 473–478 CrossRef CAS.
- K. C. Waterman, Handbook of Stability Testing in Pharmaceutical Development: Regulations, Methodologies, and Best Practices, Springer, New York, NY, USA, 2009, pp. 115–135 Search PubMed.
- A. J. Surman, M. Rodriguez-Garcia, Y. M. Abul-Haija, G. J. T. Cooper, P. S. Gromski, R. Turk-MacLeod, M. Mullin, C. Mathis, S. I. Walker and L. Cronin, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5387–5392 CrossRef CAS PubMed.
- R. Shapiro, Origins Life, 1984, 14, 565–570 CrossRef CAS PubMed.
- H. J. Cleaves, Evolution: Education and Outreach, 2012, 5, 342–360 Search PubMed.
- J. J. Li and E. J. Corey, Name Reactions of Functional Group Transformations, Wiley, Hoboken, NJ, USA, 2007 Search PubMed.
- A. Cook, A. P. Johnson, J. Law, M. Mirzazadeh, O. Ravitz and A. Simon, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 79–107 CAS.
- A. Wołos, R. Roszak, A. Ż
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) dło Dobrowolska, W. Beker, B. Mikulak-Klucznik, G. Spólnik, M. Dygas, S. Szymkuć and B. A. Grzybowski, Science, 2020, 369, eaaw1955 CrossRef PubMed.
dło Dobrowolska, W. Beker, B. Mikulak-Klucznik, G. Spólnik, M. Dygas, S. Szymkuć and B. A. Grzybowski, Science, 2020, 369, eaaw1955 CrossRef PubMed. - M. Bonneau, Livest. Prod. Sci., 1982, 9(6), 687–705 CrossRef CAS.
- J. Oro and A. P. Kimball, Arch. Biochem. Biophys., 1961, 94, 217–227 CrossRef CAS PubMed.
- A. Eschenmoser and E. Loewenthal, Chem. Soc. Rev., 1992, 21, 1–16 RSC.
- R. Robinson, J. Chem. Soc., Trans., 1917, 111, 762–768 RSC.
- S. Pizzarello and E. Shock, Cold Spring Harbor Perspect. Biol., 2010, 2, a002105 Search PubMed.
- Y. Kebukawa, A. L. D. Kilcoyne and G. D. Cody, Astrophys. J., 2013, 771, 19 CrossRef.
- Y. Wolman, W. J. Haverland and S. L. Miller, Proc. Natl. Acad. Sci. U. S. A., 1972, 69, 809–811 CrossRef CAS PubMed.
- E. Anders, R. Hayatsu and M. H. Studier, Science, 1973, 182, 781–790 CrossRef CAS PubMed.
- M. Ruiz-Bermejo, J. L. de la Fuente, C. Pérez-Fernández and E. Mateo-Martí, Processes, 2021, 9, 597 CrossRef CAS.
- C. N. Matthews, Origins Life Evol. Biospheres, 1991, 21, 421–434 CrossRef CAS.
- M. Meringer and H. J. Cleaves, Philos. Trans. R. Soc., A, 2017, 375, 20160344 CrossRef PubMed.
- S. Ameta, Y. J. Matsubara, N. Chakraborty, S. Krishna and S. Thutupalli, Life, 2021, 11, 308 CrossRef CAS PubMed.
- T. Kind and O. Fiehn, BMC Bioinf., 2007, 8, 1–20 CrossRef PubMed.
- A. J. Bissette and S. P. Fletcher, Angew. Chem., Int. Ed., 2013, 52, 12800–12826 CrossRef CAS PubMed.
- A. Blokhuis, D. Lacoste and P. Nghe, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 25230–25236 CrossRef CAS PubMed.
- A. I. Hanopolskyi, V. A. Smaliak, A. I. Novichkov and S. N. Semenov, ChemSystemsChem, 2021, 3, e2000026 CrossRef CAS.
- A. F. Boutlerow, Comptes rendus de l'Académie des Sciences, 1861, 53, 145–147 Search PubMed.
- R. Breslow, Tetrahedron Lett., 1959, 1, 22–26 CrossRef.
- B. Makower and W. B. Dye, J. Agric. Food Chem., 1956, 4, 72–77 CrossRef CAS.
- B. Y. Yang and R. Montgomery, Carbohydr. Res., 1996, 280, 27–45 CrossRef CAS.
- G. Sengar and H. K. Sharma, J. Food Sci. Technol., 2014, 51, 1686–1696 CrossRef CAS PubMed.
- J. L. Andersen, C. Flamm, D. Merkle and P. F. Stadler, Graph Transformation, Springer, Cham, Switzerland, 2016, pp. 73–88 Search PubMed.
- J. L. Andersen, C. Flamm, D. Merkle and P. F. Stadler, J. Syst. Chem., 2013, 4, 1–14 CrossRef.
- M. Himsolt, GML: A portable graph file format, Technical report, universitat passau technical report, 1997 Search PubMed.
- S. Sharma, A. Arya, R. Cruz and H. J. Cleaves II, Life, 2021, 11, 1140 CrossRef PubMed.
- S. Kumar, U. Kothari, L. Kong, Y. Y. Lee and R. B. Gupta, Biomass Bioenergy, 2011, 35, 956–968 CrossRef CAS.
- D. Aboagye, N. Banadda, R. Kambugu, J. Seay, N. Kiggundu, A. Zziwa and I. Kabenge, Journal of Ecology and Environment, 2017, 41, 1–11 CrossRef.
- X. Liu, Q. Zhang, R. Wang and H. Li, Curr. Green Chem., 2020, 7, 282–289 CrossRef CAS.
- Z. Wu, R. P. Rodgers and A. G. Marshall, Anal. Chem., 2004, 76, 2511–2516 CrossRef CAS PubMed.
- C. A. Hughey, C. L. Hendrickson, R. P. Rodgers, A. G. Marshall and K. Qian, Anal. Chem., 2001, 73, 4676–4681 CrossRef CAS PubMed.
- E. Wollrab, S. Scherer, F. Aubriet, V. Carré, T. Carlomagno, L. Codutti and A. Ott, Origins Life Evol. Biospheres, 2016, 46, 149–169 CrossRef CAS PubMed.
- A. Golon and N. Kuhnert, J. Agric. Food Chem., 2012, 60, 3266–3274 CrossRef CAS PubMed.
- N. Hertkorn, M. Frommberger, M. Witt, B. P. Koch, Ph. Schmitt-Kopplin and E. M. Perdue, Anal. Chem., 2008, 80, 8908–8919 CrossRef CAS PubMed.
- A. L. Weber, Origins Life Evol. Biospheres, 2005, 35, 523–536 CrossRef PubMed.
- G. Danger, V. Vinogradoff, M. Matzka, J.-C. Viennet, L. Remusat, S. Bernard, A. Ruf, L. Le Sergeant d'Hendecourt and P. Schmitt-Kopplin, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed.
- W. A. Bonner, Origins Life Evol. Biospheres, 1991, 21, 59–111 CrossRef CAS PubMed.
- J. L. Bada, Nature, 1995, 374, 594–595 CrossRef CAS PubMed.
- G. Laurent, D. Lacoste and P. Gaspard, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2012741118 CrossRef CAS PubMed.
- M. Bastian, S. Heymann and M. Jacomy, Third international AAAI conference on weblogs and social media, 2009 Search PubMed.
- D. J. Amit, H. Gutfreund and H. Sompolinsky, Phys. Rev. Lett., 1985, 55, 1530–1533 CrossRef PubMed.
- A. Becerra, J. Mol. Evol., 2021, 89, 183–188 CrossRef CAS PubMed.
- M. H. Engel, S. A. Macko and J. A. Silfer, Nature, 1990, 348, 47–49 CrossRef CAS PubMed.
- J. R. Cronin and S. Pizzarello, Adv. Space Res., 1999, 23, 293–299 CrossRef CAS.
- M. H. Engel and S. A. Macko, Precambrian Res., 2001, 106, 35–45 CrossRef CAS.
- S. Pizzarello and C. T. Yarnes, Earth Planet. Sci. Lett., 2016, 443, 176–184 CrossRef CAS.
- E. T. Peltzer and J. L. Bada, Nature, 1978, 272, 443–444 CrossRef CAS.
- S. Pizzarello and E. Shock, Origins Life Evol. Biospheres, 2017, 47, 249–260 CrossRef CAS PubMed.
- J. C. Aponte, J. E. Elsila, J. E. Hein, J. P. Dworkin, D. P. Glavin, H. L. McLain, E. T. Parker, T. Cao, E. L. Berger and A. S. Burton, Meteorit. Planet. Sci., 2020, 55, 2422–2439 CrossRef CAS PubMed.
- G. Cooper and A. C. Rios, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E3322–E3331 CrossRef CAS PubMed.
- R. Egel, D.-H. Lankenau and A. Y. Mulkidjanian, Origins of Life: The Primal Self-Organization, Springer, Berlin, Germany, 2011 Search PubMed.
- A. Eschenmoser, Chem. Biodiversity, 2007, 4, 554–573 CrossRef CAS PubMed.
- S. A. Kauffman, J. Theor. Biol., 1986, 119, 1–24 CrossRef CAS PubMed.
- C. J. Butch, M. Meringer, J.-S. Gagnon and H. J. Cleaves, Commun. Chem., 2021, 4, 1–4 CrossRef.
- M. E. Beber, M. G. Gollub, D. Mozaffari, K. M. Shebek, A. I. Flamholz, R. Milo and E. Noor, Nucleic Acids Res., 2022, 50, D603–D609 CrossRef CAS PubMed.
- L. R. Ford and D. R. Fulkerson, Can. J. Math., 1956, 8, 399–404 CrossRef.
- R. T. Stubbs, M. Yadav, R. Krishnamurthy and G. Springsteen, Nat. Chem., 2020, 12, 1016–1022 CrossRef CAS PubMed.
- J. L. Andersen, C. Flamm, D. Merkle and P. F. Stadler, Graph Transformation, Springer, Cham, Switzerland, 2017, pp. 54–69 Search PubMed.
- H. J. Cleaves, C. Butch, P. B. Burger, J. Goodwin and M. Meringer, J. Chem. Inf. Model., 2019, 59, 4266–4277 CrossRef CAS PubMed.
- L. E. Orgel, Origins Life Evol. Biospheres, 1998, 28, 91–96 CrossRef CAS PubMed.
- C. Richert, Nat. Commun., 2018, 9, 1–3 CrossRef PubMed.
- R. Shapiro, Sci. Am., 2007, 296, 46–53 CrossRef PubMed.
- H. H. Smith, A. S. Hyde, D. N. Simkus, E. Libby, S. E. Maurer, H. V. Graham, C. P. Kempes, B. Sherwood Lollar, L. Chou, A. D. Ellington, G. M. Fricke, P. R. Girguis, N. M. Grefenstette, C. I. Pozarycki, C. H. House and S. S. Johnson, Life, 2021, 11, 498 CrossRef CAS PubMed.
- T. Gánti, Biosystems, 1975, 7, 15–21 CrossRef.
- D. G. Blackmond, Angew. Chem., 2009, 121, 392–396 CrossRef.
- T. Z. Jia, K. Chandru, Y. Hongo, R. Afrin, T. Usui, K. Myojo and H. J. Cleaves, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 15830–15835 CrossRef CAS PubMed.
- R. A. Kennedy, M. E. Rumpho and T. C. Fox, Plant Physiol., 1992, 100, 1–6 CrossRef CAS PubMed.
- M. Frenkel-Pinter, V. Rajaei, J. B. Glass, N. V. Hud and L. D. Williams, J. Mol. Evol., 2021, 89, 2–11 CrossRef CAS PubMed.
- D. S. Wishart, Y. D. Feunang, A. Marcu, A. C. Guo, K. Liang, R. Vázquez-Fresno, T. Sajed, D. Johnson, C. Li, N. Karu, Z. Sayeeda, E. Lo, N. Assempour, M. Berjanskii, S. Singhal, D. Arndt, Y. Liang, H. Badran, J. Grant, A. Serra-Cayuela, Y. Liu, R. Mandal, V. Neveu, A. Pon, C. Knox, M. Wilson, C. Manach and A. Scalbert, Nucleic Acids Res., 2018, 46, D608–D617 CrossRef CAS PubMed.
- M. Kanehisa and S. Goto, Nucleic Acids Res., 2000, 28, 27–30 CrossRef CAS PubMed.
- T. Sajed, A. Marcu, M. Ramirez, A. Pon, A. C. Guo, C. Knox, M. Wilson, J. R. Grant, Y. Djoumbou and D. S. Wishart, Nucleic Acids Res., 2016, 44, D495–D501 CrossRef CAS PubMed.
- A. L. Weber, Origins Life Evol. Biospheres, 2000, 30, 33–43 CrossRef CAS PubMed.
- J. P. Dworkin and S. L. Miller, Carbohydr. Res., 2000, 329, 359–365 CrossRef CAS PubMed.
- A. Kerber, R. Laue, M. Meringer and C. Rücker, MATCH Communications in Mathematical and in Computer Chemistry, 2005, 54, 301–312 CAS.
- A. Kerber, R. Laue, M. Meringer, C. Rücker and E. Schymanski, Mathematical Chemistry and Chemoinformatics, De Gruyter, Berlin, Germany, 2013 Search PubMed.
- I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics, Oxford University Press, Oxford, England, UK, 1998 Search PubMed.
- G. Nicolis, Aspects of Chemical Evolution: Proceedings of 17th Solvay Conference on Chemistry, Wiley, Hoboken, NJ, USA, 2009, vol. 55 Search PubMed.
- I. Prigogine, Introduction to Thermodynamics of Irreversible Processes, 1967 Search PubMed.
- D. K. Kondepudi, B. De Bari and J. A. Dixon, Entropy, 2020, 22, 1305 CrossRef CAS PubMed.
- I. Prigogine and R. Lefever, Synergetics, Vieweg+Teubner Verlag, Wiesbaden, Germany, 1973, pp. 124–135 Search PubMed.
- S. M. Kearnes, M. R. Maser, M. Wleklinski, A. Kast, A. G. Doyle, S. D. Dreher, J. M. Hawkins, K. F. Jensen and C. W. Coley, J. Am. Chem. Soc., 2021, 143, 18820–18826 CrossRef CAS PubMed.
- C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443 CrossRef CAS PubMed.
- H. J. Cleaves and J. H. Chalmers, Astrobiology, 2004, 4, 1–9 CrossRef CAS PubMed.
- J. Peretó, Chem. Soc. Rev., 2012, 41, 5394–5403 RSC.
- N. Vaidya, M. L. Manapat, I. A. Chen, R. Xulvi-Brunet, E. J. Hayden and N. Lehman, Nature, 2012, 491, 72–77 CrossRef CAS PubMed.
- Z. R. Adam, D. Zubarev, M. Aono and H. J. Cleaves, Philos. Trans. R. Soc., A, 2017, 375, 20160348 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2sc00256f |
| ‡ https://fiehnlab.ucdavis.edu/staff/kind/Metabolomics/. |
| This journal is © The Royal Society of Chemistry 2022 |