Electronic structure, cold ion–atom elastic collision properties and possibility of laser cooling of BeCs+ molecular ion†
Hela
Ladjimi
 *a,
Wissem
Zrafi
a,
Mohamed
Farjallah
a,
Mohamed
Bejaoui
a and
Hamid
Berriche
*a,
Wissem
Zrafi
a,
Mohamed
Farjallah
a,
Mohamed
Bejaoui
a and
Hamid
Berriche
 *ab
*ab
aLaboratory of Interfaces and Advanced Materials, Faculty of Science, University of Monastir, 5019 Monastir, Tunisia. E-mail: hamidberriche@yahoo.fr; helaladjimi91@gmail.com
bDepartment of Mathematics and Natural Sciences, School of Arts and Sciences, American University of Ras Al Khaimah, RAK, P.O. Box 10021, United Arab Emirates. E-mail: hamid.berriche@aurak.ac.ae
First published on 28th June 2022
Abstract
The BeCs+ system represents a possible future candidate for the realization of samples of cold or ultra-cold molecular ion species that have not yet been investigated experimentally or theoretically. With the aim of highlighting the spectroscopic and electronic structure of the cesium and beryllium cation BeCs+, we theoretically investigate ground and low lying excited states of 1,3Σ+, 1,3Π and 1,3Δ symmetries below the first nine asymptotic limits dissociating into Be+(2s) + Cs(6s, 6p, 5d) and Be(2s2, 2s2p, 2s3s, 2p2) + Cs+. We used a quantum chemistry approach based on a semi-empirical pseudo potential for Be2+ and Cs+ cores, core polarization potentials (CPP), large Gaussian basis sets and full configuration interaction (FCI) method for the valence electrons. Additional calculations have been performed for the ground state using CCSD(T)/CI methods with different basis sets. Adiabatic potential energy curves, spectroscopic constants, vibrational levels, and permanent and transition dipole moments are reported in this work. Furthermore, the elastic scattering properties at low energy for both ground 11Σ+ and second excited states 31Σ+, of BeCs+ are theoretically investigated, and isotopic effects on cold and ultra-cold energy collisions are also detected. Vibrational lifetimes of the ground state 11Σ+ are calculated taking into account both spontaneous and stimulated emissions and also the absorption induced by black body radiation at room temperature (T = 300 K). Vibrational radiative lifetimes for the first 21Σ+ and second 31Σ+ excited states are also calculated and extensively analyzed. We found that the radiative lifetimes of the lower vibrational levels of the 11Σ+ state have an order of magnitude of seconds (s), while those of 21Σ+ and 31Σ+ states have an order of nanoseconds (ns). The Franck–Condon factors are also calculated for transitions from the low lying excited 21Σ+, 31Σ+, 11Π states to the ground state 11Σ+. We found that the favourite vibrational transition to the 11Σ+(v = 0) ground state is obtained for 11Π (v′′′ = 0)–11Σ+(v = 0) with a diagonal structure and a large Franck–Condon factor value of 0.94. This Franck–Condon factor value is sufficiently large to make the BeCs+ system a favorable candidate for direct laser cooling.
1. Introduction
In recent years, a novel field of physics and chemistry has received considerable attention where cold trapped ions and ultra-cold atomic gases brought into contact with each other, especially the mixture of alkaline-earth metal ions and alkali metal atoms.1,2 Combining trapped ions with ultra-cold atoms has yielded a variety of new theoretical and experimental research and many perspectives for the study of ion-neutral interactions from cold collisions studies,3–5 quantum control of chemical reactions at ultralow energies4,6–9 to buffer gas cooling, hybrid traps10–13 and atom–ion sympathetic cooling in Paul traps.14 Likewise, it offers the opportunity to study collisional dynamics in the quantum s-wave scattering regime associated with special long-range interactions between an ion and atom.15–18 Also, the development in this field allows the formation of microscopic quantum systems consisting of a single ion weakly bound to an ensemble of ultra-cold atoms.19 This field covers research areas including atomic molecular and optical physics, chemistry, quantum information science, quantum stimulations and quantum simulators.20 Therefore, several experimentalists have carried out experiments with various cold combinations of alkali atoms and alkaline-earth atomic ions: Rb/Ca+,21 and Rb/Ba+.22 In addition, an optical dipole trap of Rb atoms has been merged in a Paul trap containing a few Ba+ atoms.23,24 The collisional cooling of laser precooled Ca+ ions by ultra-cold Na atoms is experimentally performed.25,26Despite beryllium being a rare and toxic element, singly-ionized beryllium is a particularly attractive metallic reactant to use for such studies because it is both theoretically tractable and experimentally highly controllable.27,28 The production of Be+ ions – using laser ablation of metallic Be trapped in a linear radio frequency Paul trap – can be experimentally achieved making them a good candidate choice. Moreover, the laser cooling technique28 can be used to cool the translational motion of the ions resulting in a coulomb crystal of Be+ ions. In addition, beryllium is of interest for astrophysics and astrochemistry,29 and despite its low abundance, Be+ ions are considered an important astrophysical tracer. The relatively simple electronic structure of this two-electron valence atom allows both highly accurate characterization of its electronic structure and laser cooling30 and the low mass of Be+ lends itself to high motional frequencies. This work was also encouraged by the experimental production of the Bose–Einstein condensate of Cs atoms.31 Despite this, no investigation has been presented for BeCs+ molecules to date, its spectroscopic study would provide important input for the current research in cold ions and ultra-cold atomic gas interactions. The special long-range interaction between a Be+ ion and a Cs atom offers the opportunity to study collisional dynamics in the quantum s-wave scattering regime, since the possible experimental situation can be imagined as a single Be+ ion immersed in a Bose–Einstein condensate of Cs atoms in a hybrid trap. Dimers consisting of an alkali bound to an alkaline-earth metal are of a great interest due to their bonding properties and their prospective formation by laser cooling at cold and ultra-cold temperatures. Alkali/alkaline-earth ionic molecules have closed shell state, 1Σ+ ground states. They could be trapped and handled by means of external electric and magnetic fields. A series of experiments have been planned in the group of Heaven et al. at Emory University to characterize alkali/alkaline-earth dimers using LIF, dispersed LIF (DLIF), RE2PI, photoionization efficiency (PIE) and PFI-ZEKE spectroscopy techniques.33 They have already started investigations of several alkali/alkaline-earth ionic and neutral dimers by laser ablation. This technique was used in their recent published work for MgLi/MgLi+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and BeLi/BeLi+
33 and BeLi/BeLi+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 (in preparation) dimers. They are also planning to study BeCs/BeCs+ dimers, where a beryllium rod surface will be coated with Cs using a standard evaporative coating technique.32 The Cs coating will be applied by rubbing samples of Cs metal against the surface of the Be rod.
32 (in preparation) dimers. They are also planning to study BeCs/BeCs+ dimers, where a beryllium rod surface will be coated with Cs using a standard evaporative coating technique.32 The Cs coating will be applied by rubbing samples of Cs metal against the surface of the Be rod.
Recently, ionic molecules forming compounds with alkali–alkaline-earth atoms Be/Li+,34 Mg/Li+,35 Sr/Alk+,36 Ca+, Sr+, Ba+, Yb+/Rb and Li/Yb+,37 Be/Na+, K+ and Rb+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 and Ca/Alk+,39 have been theoretically studied using the quantum chemistry approach based on effective core potential (ECP), core polarization potentials (CPP) methods and full configuration interaction (FCI) calculations using the CIPSI package. This approach demonstrates its accuracy compared with experimental and other theoretical approaches. Elastic scattering properties of BeAlk+ (Alk = Na, K and Rb) and the possibility of the formation of these molecular ions from an ion–atom mixture by stimulated Raman adiabatic process have also been theoretically studied.40 Similar theoretical quantum approaches are used here to calculate the electronic structure of BeCs+. The present study is devoted to characterize the ground state and 22 lowest excited states of 1,3Σ+, 1,3Π and 1,3Δ symmetries dissociating below the nine first ionic asymptotic limits: Be+(2s) + Cs(6s, 6p, 5d) and Be(2s2, 2s2p, 2s3s, 2p2) + Cs+ and the corresponding potential energy curves, spectroscopic parameters, vibrational energies and permanent and transition dipole moments are calculated. Next, we employ the electronic data to determine the cold and ultra-cold elastic collision properties. Finally, the lifetimes for the ground 11Σ+ vibrational states are calculated taking into account the spontaneous emission and stimulated emission and absorption induced by black body radiation. Furthermore, the lifetime of the first 21Σ+ and second 31Σ+ excited states are also calculated and extensively analyzed. Finally, we have calculated Franck–Condon factors between low-lying excited state of symmetries 21Σ+, 31Σ+ and 11Π and the ground state 11Σ+. The accurate calculation can help optimize their production by radiative processes in cold ion–atoms and can be very important for understanding, designing and simulating photoassociation experiments.
38 and Ca/Alk+,39 have been theoretically studied using the quantum chemistry approach based on effective core potential (ECP), core polarization potentials (CPP) methods and full configuration interaction (FCI) calculations using the CIPSI package. This approach demonstrates its accuracy compared with experimental and other theoretical approaches. Elastic scattering properties of BeAlk+ (Alk = Na, K and Rb) and the possibility of the formation of these molecular ions from an ion–atom mixture by stimulated Raman adiabatic process have also been theoretically studied.40 Similar theoretical quantum approaches are used here to calculate the electronic structure of BeCs+. The present study is devoted to characterize the ground state and 22 lowest excited states of 1,3Σ+, 1,3Π and 1,3Δ symmetries dissociating below the nine first ionic asymptotic limits: Be+(2s) + Cs(6s, 6p, 5d) and Be(2s2, 2s2p, 2s3s, 2p2) + Cs+ and the corresponding potential energy curves, spectroscopic parameters, vibrational energies and permanent and transition dipole moments are calculated. Next, we employ the electronic data to determine the cold and ultra-cold elastic collision properties. Finally, the lifetimes for the ground 11Σ+ vibrational states are calculated taking into account the spontaneous emission and stimulated emission and absorption induced by black body radiation. Furthermore, the lifetime of the first 21Σ+ and second 31Σ+ excited states are also calculated and extensively analyzed. Finally, we have calculated Franck–Condon factors between low-lying excited state of symmetries 21Σ+, 31Σ+ and 11Π and the ground state 11Σ+. The accurate calculation can help optimize their production by radiative processes in cold ion–atoms and can be very important for understanding, designing and simulating photoassociation experiments.
The plan of our paper is as follows: in Section 2, we briefly present the computational method and give numerical details. In Section 3, we represent and discuss results, including spectroscopic and electronic structure, vibrational levels, permanent and transition dipole moments. The long-range properties and elastic collision results of the ground 11Σ+ and the second excited 31Σ+ states of BeCs+ are also presented and discussed. Vibrational state lifetimes and Franck–Condon factors are reported in the last parts of Section 3. Finally, we summarize our conclusions in Section 4.
2. Ab initio method of calculation
The electronic calculations were determined starting with the self-consistent field (SCF) level of theory including the core valence electron correlation with effective core potential (ECP) and core polarization potential (CPP) methods, and then a full configuration interaction (FCI) calculation is performed. We used the CIPSI package (configuration interaction by perturbation of a multiconfiguration wave function selected iteratively)41 developed in the “Laboratoire de Physique et Chimie Quantique, Université Toulouse III-Paul Sabatier’ (France)”.42 This approach allows the use of large Gaussian basis sets to attain many excited molecular states. The molecular ionic system BeCs+ was carried out, here, using the semi-empirical pseudopotential method in their semi-local form proposed by Barthelat and Durand43,44 where each core Be2+ and Cs+ is replaced by an effective core potential. Subsequently, our ionic system is modeled as a molecule with two valence electrons moving in the field of the two Be2+ and Cs+ ions and the interaction between the polarizable Be2+ and Cs+ cores and the valence electrons are treated using the core polarization potential VCPP given by Müller et al.45 defined as: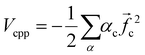 | (1) |
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) c represent the dipole polarizability of the core (c) and the electric field created by the valence electron and the other cores, respectively. The
c represent the dipole polarizability of the core (c) and the electric field created by the valence electron and the other cores, respectively. The ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) c expression is defined as:
c expression is defined as: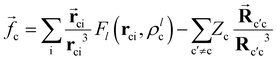 | (2) |
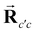 is the core–core vector,
is the core–core vector, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0072_20d1.gif) ci is the core–electron vector, and Fl(rci, ρlc) represents the l-dependent cut-off function explored by Foucrault et al.,46 which is written as follows:
ci is the core–electron vector, and Fl(rci, ρlc) represents the l-dependent cut-off function explored by Foucrault et al.,46 which is written as follows: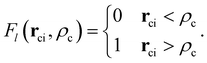 | (3) |
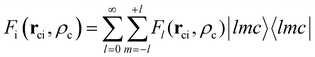 | (4) |
where |lmc lmc| is a spherical harmonic in the center of the c core.
The CIPSI approach approximates the FCI energy through an adaptively refined selected CI procedure, corrected for discarded determinants through second-order multireference perturbation theory. The CIPSI class of method builds upon selected CI ideas and has been successfully used to converge to FCI correlation energies, one-body properties and potential surfaces. The CIPSI algorithm used in this work uses iteratively enlarged selected CI and Møller–Plesset multireference perturbation theory.
The CIPSI energy is given by:
| ECIPSI = Ev + E(e) | (5) |
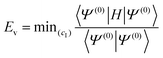 | (6) |
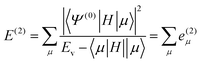 | (7) |
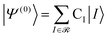 | (8) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) and μ is a determinant outside this space. The CIPSI energy is systematically refined by doubling the size of the CI reference space at each iteration, selecting the determinants μ with the largest |e(2)μ|, and the energy defined as a function of the size of the reference space.
and μ is a determinant outside this space. The CIPSI energy is systematically refined by doubling the size of the CI reference space at each iteration, selecting the determinants μ with the largest |e(2)μ|, and the energy defined as a function of the size of the reference space.
In the present work, valence electrons are described with large Gaussian basis sets. To describe the Be atom and its Be+ ion, we used Gaussian-type basis set orbital functions (7s9p10d/7s9p9d). The use of this basis set allowed us to reproduce the atomic states 2s, 2p, 3s, 3p and 3d for Be+; and 2s2, 2s2p, 2s3s, 2p2, 2s3p and 2s3d for Be.47 For the Cs atom, we used the (7s4p5d/6s4p4d) Gaussian-type basis set, that makes it possible to represent the atomic spectrum of Cs up to the (8s) atomic level.48 We note that the orbital f is not considered in our calculation since we are interested only in the lowest excited states in this system. The parameters of both basis sets are reported in ESI† (Table S1). The core polarizabilities of Be2+ and Cs+ are respectively αBe2+ = 0.052ao3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38,47 and αCs+ = 15.117ao3.48
38,47 and αCs+ = 15.117ao3.48
The values of the cut-off radii of the Be atom are (ρs = 0.889, ρp = 0.882 and ρd = 1.14) and those of the Cs atom are (ρs = 2.690, ρp = 1.850 and ρd = 2.810). In order to verify the reliability of our CPP approach, we calculated and compared the molecular asymptotic energies of the BeCs+ with the experimental results as illustrated in Table 1. This table describes the binding energy of valence electrons, which is the difference between the energy of the (Be + Cs)+ atomic threshold with two valence electrons and the (Be + Cs)3+ triple ionized form without any valence electrons on Be or Cs. Experimental values are obtained from the first and second ionization energies of Be, and the first ionization energy of the Cs atom.49 From this table, we can conclude that the dissociation limits are in good agreement with the experimental results49 and the largest difference (ΔE/EExp) is about 0.23% for the asymptotic limit: Be(2s2) + Cs+. Description of the ground 1S and excited 1P electronic states of the Be atom is the most challenging with discrepancies of 517 cm−1 and 508 cm−1 for related atomic limits, respectively. The reason for such difference comes from the optimization of a basis set that describes at the same time Be+ and Be, which was a challenge in previous similar studies as mentioned above. In a separate way, we are able to produce atomic basis sets that produce exact atomic energy levels for Be+ or Be. However in practice, we have to optimize a common basis set that describes both species and is usable for one and two electron calculations equally. This task is one of the most time consuming as we have to ensure that all molecular states that involve Be+ and Be atomic limits, are well described by the basis set. Although a few hundreds of wavelength seems to be a big error, compared to the atomic energy it is less than 0.3%. This is acceptable not only in our calculation but also in similar calculations (see Aymar et al. Sr/alkali+ paper36). Nevertheless, the overall agreement is good, leading to the good accuracy of our molecular calculations.
| Asymptotic limit | E Th | E Exp 49 | |ΔE| = |ETh − EExp| | Molecular states |
|---|---|---|---|---|
| Be(1S(2s2)) + Cs+(1S) | −222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
−222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 073 073 |
517 | 11Σ+ |
| Be(3P(2s2p)) + Cs+(1S) | −200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 490 |
−200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 095 095 |
395 | 13Σ+, 13Π |
| Be(1P(2s2p)) + Cs+(1S) | −178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 998 |
−179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
508 | 21Σ+, 11Π |
| Be+(2S(2s)) + Cs(2S(6s)) | −178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 296 |
−178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 288 |
8 | 31Σ+, 23Σ+ |
| Be(3S(2s3s)) + Cs+(1S) | −169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 981 |
−169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 983 983 |
2 | 33Σ+ |
| Be(1S(2s3s)) + Cs+(1S) | −167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 471 |
−167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 398 398 |
73 | 41Σ+ |
| Be+(2S(2s))+ Cs(2P(6p)) | −166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 747 |
−166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
6 | 51Σ+, 43Σ+, 21,3Π |
| Be(1D(2p2)) + Cs+(1S) | −165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 146 |
−165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 193 193 |
47 | 61Σ+, 31Π, 11Δ |
| Be+(2S (2s)) + Cs(2D(5d)) | −163![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
−163![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
15 | 71Σ+, 53Σ+, 41Π, 33Π, 21Δ, 13Δ |
The radiative transition probabilities (Einstein A coefficients) and radiative lifetimes of alkaline–alkaline–earth systems have been calculated and detailed in several previous works.53,54 The lifetimes of the vibrational levels of the ground state 11Σ+ of BeCs+ are determined using the equation:
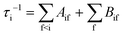 | (9) |
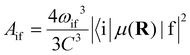 | (10) |
The second term in eqn (9), described by the Einstein coefficient Bif = AifN(ωif), is related to black body radiation (BBR) where the number of black body photons depends on the temperature T. BBR is due to the surrounding environment at T = 300 K. It induces stimulated absorption and emission processes as described by Bif = AifN(ωif), where N(ωif), is the number of black body photons of frequency ωif. Black body photons are stimulated emitted photons associated with black body radiation.
The number of black body photons is given by:
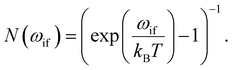 | (11) |
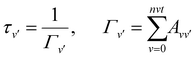 | (12) |
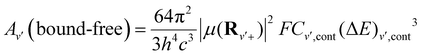 | (13) |
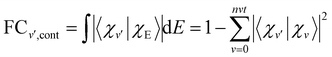 | (14) |
3. Results and discussion
3.1. Adiabatic potential energy curves and spectroscopic constants
Using the ab initio method reported in the previous section, a full and expanded calculation was undertaken for the (1–7)1Σ+, (1–5)3Σ+, (1–4)1Π, (1–3)3Π, (1–2)1Δ and (1)3Δ electronic states of BeCs+. They are dissociating into the first nine ionic limits (Be+(2s) + Cs(6s, 6p, 5d) and Be(2s2, 2s2p, 2s3s, 2p2) + Cs+) for an interval of intermolecular distances varying from 4.50 to 200.0 bohr. The potential energy curves of 1,3Σ+, 1,3Π and 1,3Δ are presented in Fig. 1. As can be seen in this figure, the ground state 11Σ+ of the BeCs+ system is well separated from the highest states of the same symmetry and it is found with a unique minimum. This state correlates at large distances to a ground-state neutral Be atom and a closed-shell alkali-metal Cs+ ion similarly to the (Be-Alk)+ ionic systems.38,40 Unlike the alkaline-earth ionic systems, the first excited state of symmetry 1Σ+, for the BeCs+ molecular ion, is correlated to a first excited-state neutral alkaline-earth atom (3P) and a closed-shell alkali-metal ion due to the properties of the Cs atom. This state is quite close to the next state, 31Σ+, and maintains an energy gap of about 321.75 cm−1 at the internuclear distance R = 200 bohr. It is found with a unique minimum at 9.70 bohr and a very large depth well of 4910 cm−1.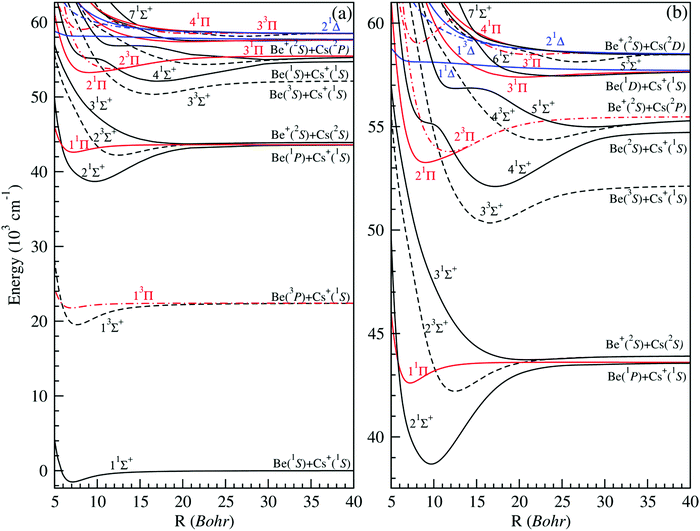 | ||
| Fig. 1 Potential energy curves of singlet and triplet electronic states in Σ+, Π and Δ symmetries of the BeCs+ molecular ion (panel (a)). Zoomed-in view of the higher excited states (panel (b)). | ||
The second excited state 31Σ+, dissociating into Be+(2S) and Cs(2S), where one valence electron is attached to each atomic partner, is presented with a very small and almost repulsive well with a depth value of 189 cm−1, due to the strong repulsion induced by the first excited state 21Σ+. An accurate analysis of these curves shows that the most strongly bound states are the first excited states of both singlet and triplet Σ+ states with well depths of 4910 and 2875 cm−1 located at 9.70 and 7.61 bohr, respectively. The 1,3Π states are weakly bound with small attractive wells and barriers, except the 21Π state which is provided with a deep well (De = 2210 cm−1) located at 9.03 bohr. As for the 1,3Δ symmetry, the first three potential energy curves dissociating into Be (2p2) + Cs+ and Be+ (2s) + Cs (5d) are also calculated. We found that all these states are repulsive. Therefore, this cationic molecular system is unstable in the states 1,3Δ.
We note that the density of electronic states increases with the higher excited states, where some of the excited atomic thresholds are close to each other and furthermore facilitates interactions between associated electronic states. As a result, several excited states have undulations leading to a potential shape with more than one minimum corresponding to the Rydberg character of these states.
The excited states become closer to each other and they are interacting as can be seen with the presence of several crossovers normally avoided (see Fig. 1(b)). The avoided crossing locations give fundamental information for the study of the charge transfer between states. This is due to the proximity of the Cs + Be+ and Cs+ + Be limits of the higher states and the ability to capture the electron between Be+ and Cs+. In addition, avoided (in the adiabatic representation) or real (in the diabatic representation) crossings allow for efficient non-radiative transitions in excited electronic states such as the predissociation.
The positions of such avoided crossings are gathered in Table S2 (ESI†). Such crossings or avoided crossings can dramatically alter the stability of molecules owing to the possibility of crossing from one state to another, and their presence can be important to study non-adiabatic transitions.55 Moreover, the inclusion of relativistic spin–orbit couplings between non-relativistic electronic states of the same symmetry, inducing avoided crossings, may severely perturb the observed progression of vibrational states and crossings between non-relativistic states of different symmetries.
Next, the spectroscopic constants of all these states were calculated using the interpolation of the vibrational levels by the least-squares approach. The equilibrium distance Re, well depth De, electronic excitation energy Te, frequency ωe, anharmonic constant ωeχe, and rotational constant Be of all symmetries using the CIPSI package are presented in Table 2 for the ground and the excited states. For all calculations, the reduced mass for the (9Be + 135Cs)+ is taken to be 8.43988 a.u. Since no experimental or theoretical results are presently available for BeCs+, and in order to confirm our CIPSI calculation, we performed several other ground state calculations via the MOLPRO package.56 The results of the ground state using different approaches are also reported in Table 2. The spectroscopic constants obtained using the CIPSI package (Re = 7.11 bohr, De = 1511 cm−1 and ωe = 108.85 cm−1) are in good agreement with CCSD(T) (Re = 7.52 bohr, De = 1558 cm−1 and ωe = 108.23 cm−1) and CI (Re = 7.48 bohr, De = 1578 cm−1 and ωe = 115.19 cm−1) calculations using ADZP basis sets. The well depths obtained with the three methods agree, with the mean absolute difference of 47 cm−1 for the CCSD(T) method and of 67 cm−1 for CI calculations. In addition, a very good agreement is observed for ωe between these three methods.
| States | R e (bohr) | D e (cm−1) | T e (cm−1) | ω e (cm−1) | ω e χ e (cm−1) | B e (cm−1) | Ref. |
|---|---|---|---|---|---|---|---|
| a Barrier. b CIPSI with optimized basis sets. c Molpro, CCSD(T)/ADZP. d Molpro, CI/ADZP. | |||||||
| 11Σ+ | 7.11 | 1511 | 0 | 108.85 | 1.96 | 0.141063 | This workb |
| 7.52 | 1558 | 0 | 108.23 | 1.87 | 0.126722 | This workc | |
| 7.48 | 1578 | 0 | 115.19 | 2.08 | 0.127367 | This workd | |
| 21Σ+ | 9.70 | 4910 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
79.10 | 0.48 | 0.075763 | This workb |
| 31Σ+ | 20.79 | 189 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242 242 |
16.95 | 0.27 | 0.016502 | This workb |
| 41Σ+ | 17.17 | 2681 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 615 615 |
39.23 | 0.12 | 0.024191 | This workb |
| 51Σ+ | 12.56a | 20 | This workb | ||||
| 28.98 | 479 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013 013 |
21.70 | 0.76 | 0.008491 | This workb | |
| 61Σ+ | 28.25 | 206 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 996 |
15.64 | 0.42 | 0.008937 | This workb |
| 71Σ+ | Repulsive | This workb | |||||
| 13Σ+ | 7.61 | 2875 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 036 036 |
113.68 | 1.74 | 0.123159 | This workb |
| 23Σ+ | 12.46 | 1710 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 722 |
59.88 | 0.30 | 0.045985 | This workb |
| 33Σ+ | 16.55 | 1831 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 845 |
42.19 | 0.13 | 0.026045 | This workb |
| 43Σ+ | 22.48 | 1119 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 861 |
26.18 | 0.35 | 0.014117 | This workb |
| 53Σ+ | 26.94 | 344 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
20.6 | 0.65 | 0.009829 | This workb |
| 11Π | 7.23 | 993 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118 118 |
85.67 | 1.27 | 0.136595 | This workb |
| 21Π | 9.03 | 2210 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 773 773 |
54.93 | 0.4 | 0.087476 | This workb |
| 31Π | 20.29 | 300 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
13.86 | 1.32 | 0.017369 | This workb |
| 13Π | 6.98 | 625 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 287 |
82.37 | 4.88 | 0.146135 | This workb |
| 23Π | 11.74 | 1680 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 302 302 |
46.19 | 0.34 | 0.051735 | This workb |
| 21.41a | 63 | This workb | |||||
| 33Π | 8.17a | 1149 | This workb | ||||
| 11Δ | Repulsive | This workb | |||||
| 21Δ | Repulsive | This workb | |||||
| 13Δ | Repulsive | This workb | |||||
Calculations with large core pseudopotentials with the CIPSI package give slightly smaller equilibrium distances with the mean difference of 0.41 bohr compared to that obtained with the CCSD(T) calculations, and 0.37 bohr compared to that obtained with the CI calculations. This small difference can be explained by the different methods of treatment of the correlation energy, and by the use of large core pseudopotentials for the CIPSI calculation.
In addition, we compare our results for the BeCs+ ground state with those of (Be-Alk)+ reported in previous work.34,38,40 Indeed, the well depth of the ground state decreases with the mass of the alkali atoms. Thus, the smallest De is for BeCs+ (1511 cm−1) and the largest one is for the BeLi+ (4862 cm−1),34 while the band lengths of the ground state systematically decrease with the increasing atomic number of the alkali-metal atoms from 4.94 bohr for BeLi+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 to 7.11 bohr for BeCs+. The overall good agreement between our previous calculations for the BeLi+ and BeNa+ molecular ions,34,38 using the pseudopotential approach and FCI method, with other diverse theoretical and experimental results, suggests that similar accuracy is expected for our results for the BeCs+ molecular ion, which has not yet been studied.
34 to 7.11 bohr for BeCs+. The overall good agreement between our previous calculations for the BeLi+ and BeNa+ molecular ions,34,38 using the pseudopotential approach and FCI method, with other diverse theoretical and experimental results, suggests that similar accuracy is expected for our results for the BeCs+ molecular ion, which has not yet been studied.
Obtained potential energy curves for the BeCs+ molecular ions may correspondingly find many applications in the context of experimental studies of a mixture of laser-cooled Be+ ions in a linear Paul trap overlapped with ultracold Cs atoms in a magneto-optical trap.
3.2 Permanent and transition dipole moments
Additionally to the potential energy curves, the practical implementation of cold molecule formation via photoassociation requires a much better knowledge of their electronic properties, such as the radial variation of permanent or transition dipole moments. In fact, the knowledge of the dipole function of molecular systems can be considered as a sensitive test for the accuracy of the calculated electronic wave functions and energies. Within such perspectives and in order to complete our study of the BeCs+ molecular ion, we have determined the permanent and transition dipole moments for the same large and dense grid of internuclear distances used for the potential energies. The permanent dipole moments as a function of the intermolecular distance R, of all states previously studied (1–7)1Σ+, (1–5)3Σ+, (1–4)1Π, (1–3)3Π, (1–2)1Δ and (1)3Δ are displayed in Fig. 2. Whereas, some transition dipole moments between electronic states of the same spin and spatial symmetries are presented in Fig. 3. Noting, the permanent dipole moments for charged molecules depend on the choice of the coordinate system origin. In this work, the permanent dipole moments were calculated with respects to the center of mass, which is a normal choice for investigating the rovibrational dynamics. As presented in Fig. 2, the absolute values of permanent dipole moment increase with increasing internuclear distance and asymptotically approach the two limit cases where the charge is completely localized at one of the atoms.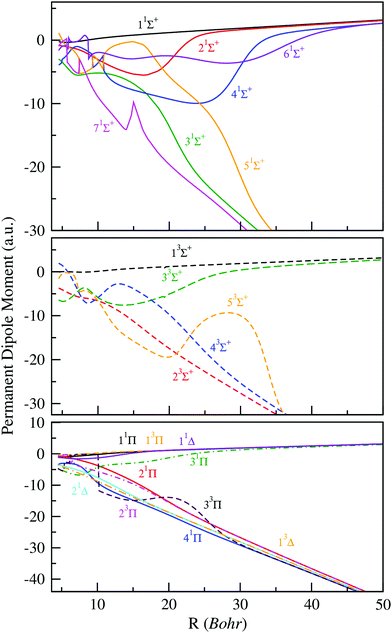 | ||
| Fig. 2 Permanent electric dipole moments of electronic states of 1,3Σ+, 1,3Π and 1,3Δ of the BeCs+ molecular ion. | ||
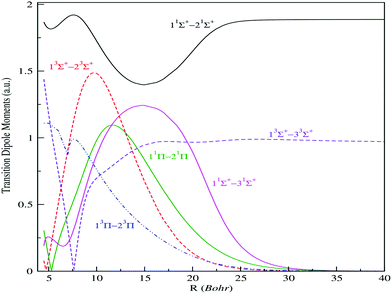 | ||
| Fig. 3 Transition electric dipole moments (n2s+1|Λ| → m2s+1|Λ|) between low-lying 1,3Σ+ and 1,3Π electronic states of the BeCs+ molecular ion. | ||
The change of the sign of the dipole moment, as compared to the limits, means that the center of charge moved to the other side of the center of mass. Therefore, at large internuclear distances, the magnitude of the permanent dipole moment of the 11Σ+, 21Σ+, 41Σ+ and 61Σ+ states, dissociating into Be + Cs+, are almost positive. For the remaining states 31Σ+, 51Σ+ and 71Σ+ dissociating into Be+ + Cs, we note significant negative permanent dipole moments in a particular region yield the same linear behavior at large distances, showing the increasing distance between the negative and positive center-of-charge. This behavior is typically observed for heteronuclear molecular ions,34–40 and implies that even molecular ions in very weakly bound states have effectively a significant permanent electric dipole moment. For the permanent dipole moments of the of 3Σ+, 1,3Π and 1,3Δ electronic states, we get the same observation as for the permanent dipole moments of the 1Σ+ states.
As reported in Fig. 3, the transition dipole moments shows, at small internuclear distances, a meaningful variation with numerous extrema, which are assigned to the avoided crossing positions. Also, the change of sign of the transition dipole moments corresponds to sudden changes of electronic wave-function usually related to the avoided crossings between the potential energy curves. We remark that the transition dipole moments between two distant states possess low variation compared to the transition between neighbor states. However, the adjacent states interact much more and possess an important transition.
They present maximums located at particular internuclear distances corresponding to an important overlap between the corresponding molecular wave functions. Also, a quick and sudden variation of the transition dipole moments is observed when the crossings between corresponding potential curves become weakly avoided. This can be explained by the quick change of the wave function content at the vicinity of this position. Thus, the avoided crossing, which appears between the potential curves, is already reflected. At larger internuclear distances, some transitions, such as 11Σ+–21Σ+, 13Σ+–23Σ+, asymptotically reach a constant corresponding to the atomic oscillator strength of the allowed atomic transitions. But for ionic-neutral type transitions, their moment tends to zero, as the wave functions through the dipole moment operator does not allow any cover at large internuclear distance.
3.3 Long range and elastic collision properties
Theoretical analysis of molecular ion collisions at low temperature has played an important role in the development of the research field of cold molecules. One of the effects of elastic collisions is the sympathetic cooling of an ion in an ultra-cold gas of atoms. Ion–atom collisions in the ultra-cold regime are determined primarily by long-range ion–atom interactions, described as: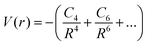 | (15) |
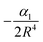 where α1 is the static polarizability of the Be atom. However, for the second excited state 31Σ+ dissociating into Be+(2S(2s)) + Cs(2S(6s)), the long range ion–atom interaction is determined by the Cs atom static polarizability. In order to check the accuracy of our calculated potential energy curves and to prove the behavior at long-range, we have interpolated the potential energy curve for both ground state and second excited state by analytically fitting the long range part of our curves with a single parameter using eqn (15). The rough fit of the long-range part of the potential energy curve of the ground state 11Σ+ yields α1(Be(2s2)) ∼ 36.45 a.u. The comparison of our polarizability of Be(2s2) with the available results of Porsev57 and Archibong58 show good agreement; their values are respectively, 36.7 and 37.76 ± 0.22 a.u. As the second excited state 31Σ+ dissociates at large distances to the ground state Cs atom and Be+ ion, its long-range interaction is determined by the Cs static polarizability. The long-range part of the potential energy curve of the second excited state 31Σ+ was also fitted and gave α1(Cs)∼407.02 a.u. As expected, our polarizability of Cs(6s) agrees well with the available theoretical and experimental results of Derevianko59 and Ekstrom,60 their values are respectively 399.9 ± (1.9) a.u. and 403.6 ± 8.1 a.u. This good agreement improves the reliably of our calculations and the level of the used theory.
where α1 is the static polarizability of the Be atom. However, for the second excited state 31Σ+ dissociating into Be+(2S(2s)) + Cs(2S(6s)), the long range ion–atom interaction is determined by the Cs atom static polarizability. In order to check the accuracy of our calculated potential energy curves and to prove the behavior at long-range, we have interpolated the potential energy curve for both ground state and second excited state by analytically fitting the long range part of our curves with a single parameter using eqn (15). The rough fit of the long-range part of the potential energy curve of the ground state 11Σ+ yields α1(Be(2s2)) ∼ 36.45 a.u. The comparison of our polarizability of Be(2s2) with the available results of Porsev57 and Archibong58 show good agreement; their values are respectively, 36.7 and 37.76 ± 0.22 a.u. As the second excited state 31Σ+ dissociates at large distances to the ground state Cs atom and Be+ ion, its long-range interaction is determined by the Cs static polarizability. The long-range part of the potential energy curve of the second excited state 31Σ+ was also fitted and gave α1(Cs)∼407.02 a.u. As expected, our polarizability of Cs(6s) agrees well with the available theoretical and experimental results of Derevianko59 and Ekstrom,60 their values are respectively 399.9 ± (1.9) a.u. and 403.6 ± 8.1 a.u. This good agreement improves the reliably of our calculations and the level of the used theory.
The interaction potential energies of the ground and second excited states calculated above were used here as input data for the short-range potential, and the long-range part is given by eqn (15). Thereafter, we have determined the properties of the low and ultra-low energy collision using the Numerov algorithm where the continuum scattering wave function of the lth partial wave for atom–ion cold collision is obtained by solving the partial wave of the radial Schrödinger equation:
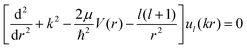 | (16) |
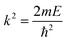 | (17) |
| ul(kr) = rRl(kr) | (18) |
R l (kr) is the radial wave function used in the expansion of the most general solution of the Schrödinger equation:
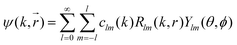 | (19) |
Due to the spherical symmetry the scattered wave function must not depend on the azimuthal angle ϕ and m = 0.
The wave function ul(kr) has the asymptotic form:
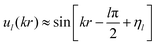 | (20) |
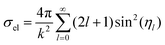 | (21) |
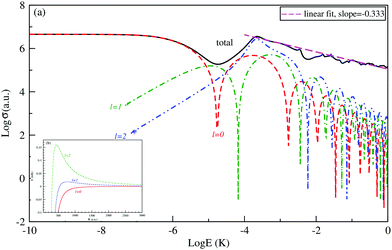
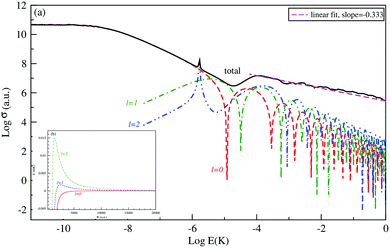
The logarithm of the total and the first three partial-waves s, p and d elastic cross sections are presented as a function of the logarithm of collision energies E (in Kelvin). Both collisions, between Be and Cs+ in the ground state 11Σ+ and that between the Cs atom and Be+ ion in the second excited state 31Σ+ in are presented, respectively, in Fig. 4 and 5.
For both collisions, we note that, the partial elastic cross sections satisfy the Wigner's threshold law. According to this law, for k → 0, the phase shift of the lth partial-wave behaves as nl∼ k2l+1 if l < (n − 3)/2, otherwise it varies as nl ∼ kn−2 for a long-range potential behaving as 1/Rn. For our case and for atom–ion collisions, the potential energy interaction is 1/R4 in the asymptotic limit, as k → 0, the s-wave scattering cross section becomes independent of energy, while all other higher partial wave cross sections are ∼k2 (see Fig. 4(a) and 5(a)).
We note that the Wigner’s threshold regime reached an energy of micro-Kelvin for the ground state 11Σ+ and of nano-Kelvin for the second excited state 31Σ+. In this regime and at energy sufficiently close to zero, only the s partial wave contributes to the total elastic cross sections.
The centrifugal barriers eliminate the higher partial wave potentials. This can be explained by the effect of the internal part of the long-range potential of the higher partial waves. The centrifugal energies for the first three partial waves s(l = 0), p(l =1) and d(l = 2) are represented against ion–atom separation for both ground (11Σ+) (see Fig. 4(b)) and second excited (31Σ+) states (see Fig. 5(b)) of the BeCs+ system. The values of the centrifugal barrier for the d-wave are about 0.158 and 0.0147 mK for the 11Σ+ and 31Σ+ states respectively. Unlike atom–atom systems, the values of the potential energy barriers for low-lying higher partial waves of atom–ion systems are very low allowing tunnelling of the wave function towards the inner region of the barriers.
Beyond the Wigner threshold regime, a number of partial waves can significantly contribute to the ion–atom scattering cross section. In addition, the partial wave cross section presents abrupt minimums: for the values where sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηl ∼ 0. These minimums correspond to the Ramsauer–Townsend effect.61–63 For higher energies, the total cross section starts to exhibit some structures related to shape resonances appearing due to the contribution of the higher partial wave. To calculate the total cross section with converging results of energies greater than milli-Kelvin, we require more than 55 partial waves for the ground state, 11Σ+, and about 70 partial waves for the 31Σ+ state. The elastic scattering results of the BeCs+ system are comparable to those of hetero-nuclear alkali-metal and alkaline-earth metal molecular ion systems.17,40,64 We observe a similar behavior at ultralow energies governed by the Wigner threshold law. At high collision energies, and for both cases, the total elastic cross sections decrease as E−1/3, is represented by this equation:
ηl ∼ 0. These minimums correspond to the Ramsauer–Townsend effect.61–63 For higher energies, the total cross section starts to exhibit some structures related to shape resonances appearing due to the contribution of the higher partial wave. To calculate the total cross section with converging results of energies greater than milli-Kelvin, we require more than 55 partial waves for the ground state, 11Σ+, and about 70 partial waves for the 31Σ+ state. The elastic scattering results of the BeCs+ system are comparable to those of hetero-nuclear alkali-metal and alkaline-earth metal molecular ion systems.17,40,64 We observe a similar behavior at ultralow energies governed by the Wigner threshold law. At high collision energies, and for both cases, the total elastic cross sections decrease as E−1/3, is represented by this equation:
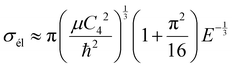 | (22) |
As presented in Fig. 4 and 5, the total scattering cross section exhibits asymptotic energy dependence and decreases as E−1/3. We have checked numerically that the slope of the linear fitting of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtotvs. log
σtotvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E is quite close to −1/3. The proportionality constant CE of the expression σtot(E → ∞) = CEE−1/3 is calculated using eqn (22) for the ground state 11Σ+ and second excited 31Σ+ state and is found to be equal to 3.14 and 3.86 a.u., respectively; while the linear fit to the curves σtot as a function of E gives CE = 3.51 a.u. and 4.11 a.u. respectively.
E is quite close to −1/3. The proportionality constant CE of the expression σtot(E → ∞) = CEE−1/3 is calculated using eqn (22) for the ground state 11Σ+ and second excited 31Σ+ state and is found to be equal to 3.14 and 3.86 a.u., respectively; while the linear fit to the curves σtot as a function of E gives CE = 3.51 a.u. and 4.11 a.u. respectively.
The isotopic effect on low and ultra-low energy collisions is also studied and presented. Firstly, we considered the collision of the 9Be atom with the three isotopes of the Cs+ ion: 133Cs+, 135Cs+ and 137Cs+. As presented in Fig. 6, at ultra-low energy the patterns are the same, but the magnitude quantitatively differs. At large energy, the total scattering cross section of different isotopes exhibits similar asymptotic energy dependence with almost the same magnitude. After that, we estimated that the isotopic effect collision of the 133Cs+ ion with the two isotopes of the Be atom – 8Be and 9Be – is considerable at ultra and low energy (see Fig. 6). Indeed, the cold collision of the ground state of BeCs+ depends on the reduced mass of the Be atom and the Cs ion. However, it is clear that the isotopic effect on the total elastic cross section due to Be is more significant than that due to Cs.
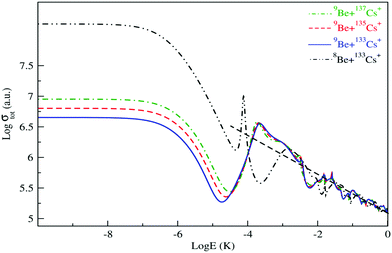 | ||
| Fig. 6 Total elastic collision cross section of 9Be atom with the three isotopes of 133Cs+, 135Cs+ and 137Cs+ ions and of 8Be with 133Cs+. | ||
3.4 Vibrational radiative lifetimes and Franck–Condon factors: the possibility of laser cooling
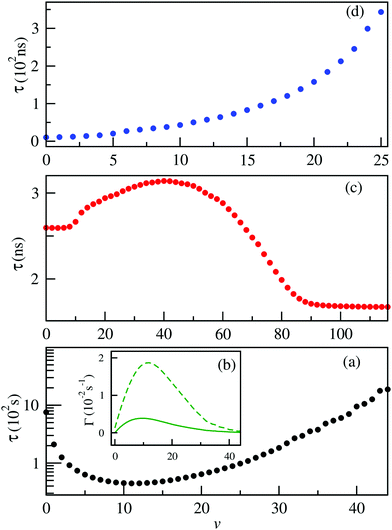
Measurements of the vibrational lifetimes of the ground and the lower excited states are crucial to assess prospects for the formation of alkali–alkaline-earth neutral and ionic systems as reported in several previous studies.38,39,50–52,54 The radiative transition probabilities (Einstein A coefficients) and radiative lifetimes have been calculated involving the vibrational levels of the ground state of BeCs+ using the ground potential energy and permanent dipole moment curves. These lifetimes are presented in Fig. 7(a). As can be seen (Fig. 7(a)), the lifetime of the vibrational levels of the ground state are second order of magnitude and we found that the ground vibrational state v = 0 lifetime is 758.62 s at temperature T = 300 K.Many diatomic heteronuclear systems like LiBe+, LiMg+, NaBe+, NaMg+ have been studied before by Fedorov et al.,52 who observed similar behaviors. We note that, after an initial decay, the lifetime reaches a minimum and then increases reaching the values closer, or even larger, than the lifetime of the ground vibrational state. For the highly excited vibrational states, the transition frequency becomes very small due to the large anharmonicity of the potential energy curve, which is influenced by the increases of the vibrational lifetime.
Besides, the interplay between the spontaneous and stimulated transitions are plotted in Fig. 7(b), where we compare the spontaneous and stimulated transition rates for the vibrational levels of the ground electronic state of the BeCs+ molecular ion, 11Σ+. We note that the shortest lifetime is found for v = 11, which corresponds to the peak in the stimulated transition rate and close to the maximum of the spontaneous transition rate. For higher v, both spontaneous and stimulated rates monotonically decrease because the transition frequencies ωif between the highly excited vibrational states become lower due to the highly excited states being energetically closer to each other than the lower-energy states. Also, the radiative vibrational state lifetimes of the first 21Σ+ (Fig. 7(c)) and second 31Σ+ (Fig. 7(d)) excited states were calculated taking into account the two possible transitions: bound–bound and bound–free (see eqn (12)–(14)). The approximations presented in our previous work,38,49,54 provide accurate radiative lifetimes especially for the higher excited vibrational states where the continuum is larger. The lifetimes of vibrational levels of the first excited electronic state (21Σ+) are presented in Fig. 7(c) and are governed by the transition electric dipole moment to the ground electronic state associated with emitting an optical photon. Note that the 21Σ+ → 11Σ+ transition moment is significant at short internuclear distances and tends to the constant at large distances corresponding to the atomic Be(1P) → Be(1S) transition (see Fig. 4). Therefore, the vibrational lifetime ascent reaches a maximum of 3.1 ns for v = 41; then, descends to attain a constant of about 1.67 ns for the higher vibrational levels near the dissociation limit. It corresponds to the pure atomic lifetime of the second exited state 1Po(2s2p) of the Be atom, determined previously by Fischer et al.65 and is about 1.78 ns. In addition, the magnitude of the vibrational lifetime of the second exited state has an order of nanoseconds and for v = 0 it is predicted to be 2.595 ns. Furthermore, the radiative lifetime of the second excited state 31Σ+, takes into account the 31Σ+ → 11Σ+ and 31Σ+ → 21Σ+ transitions, showing increasing variation in the vibrational levels. Their values are from tens to hundreds of nanoseconds. Note that for the lowest vibrational state v = 0 the radiative lifetime is equal to 10.3625 ns. These calculations are very useful to assess the prospect for the formation and spectroscopy of the BeCs+ molecular ion in modern experiments with cold ion–atom mixtures.
Franck–Condon factor coefficients play a key role in the selection of vibrational electronic states and analyzing possible single or two-photon optical pathways for formation of ground state molecular ions. Therefore, Franck–Condon factors are calculated between vibrational levels of the ground electronic state, 11Σ+, and that of the first low-lying three electronic states: 21Σ+, 31Σ+, and 11Π of the BeCs+ molecular ion. The Franck–Condon factors, presented as three dimensional intensity plots in Fig. 8, describe the overlap of the vibrational wave functions. It is clear that for vibrational transitions 21Σ+(v′) → 11Σ+(v) (see Fig. 8(a)) the values of the Franck–Condon factor is off diagonal with a maximum of about 0.312 corresponding to the highest overlap which is obtained for 21Σ+(v’ = 0) → 11Σ+(v = 9) vibrational transitions. For the 31Σ+(v′′) → 11Σ+(v) vibrational transition (see Fig. 8(b)), the significant Franck–Condon factors are obtained for the higher vibrational states of the ground electronic state (for v > 30), due to the large difference on the equilibrium distances between the 11Σ+ (Re = 7.11 bohr) and 31Σ+ (Re = 20.79 bohr).
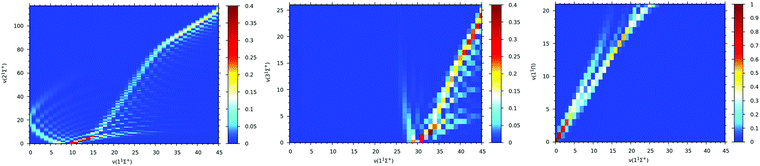 | ||
| Fig. 8 Franck–Condon factors between vibrational levels of the ground state 11Σ+ and 21Σ+(panel (a)), 31Σ+(panel (b)) and 11Π (panel (c)) excited sates of the BeCs+ molecular ion. | ||
The favorite Franck–Condon transition is obtained between 31Σ+(v” = 0) → 11Σ+(v = 30) with a Franck–Condon factor of 0.4. Whereas, the 11Π and the ground 11Σ+ electronic states have close equilibrium distances with (Re = 7.23 bohr) and (Re = 7.11 bohr) respectively (see Table 2). Therefore, the Franck–Condon factor graphics in Fig. 8(c) show a diagonal structure with the largest value of 0.94 corresponding to the 11Π(v′′′ = 0) → 11Σ+(v = 0) transition overlap. The values of the Franck–Condon factors are sufficiently large for laser cooling. As represented, the positions of the turning point, and consequently, the efficiency of the de-excitation, are strongly dependent on the equilibrium distances between two states.
4. Conclusions
The current work provides an extended study devoted to the BeCs+ molecular ion which is motivated by recent experimental and theoretical studies on ultra-cold mixtures of alkaline-earth ions immersed in alkali-metal atoms. The molecular calculations are performed using an ab initio approach based on semi-empirical pseudopotentials for Be2+ and Cs+ cores, parameterized l-dependent polarization potentials and FCI calculations through the CIPSI quantum chemistry package. We have calculated the adiabatic potential energy curves of 1,3Σ+, 1,3Π and 1,3Δ symmetry states dissociating below the first nine asymptotic limits, their spectroscopic constants, vibrational levels as well as the electric permanent and transition dipole moments. We have analyzed in detail the elastic processes of collisions that can occur in a system of Be+ ions interacting with cold Cs atoms, and between Be atom interactions with Cs+ ions. We determined theoretically ground and second excited state elastic scattering properties at low-energy. We found that the Wigner threshold regime reached an energy of micro-Kelvins for the ground state 11Σ+, and of nano-Kelvins for the second excited state 31Σ+. At a higher energy regime, the 1/3 law of scattering is obtained for both collisions. The isotopic effects of low and ultra-low energy collisions are also detected. The low-energy scattering results could be explored for photoassociative or radiative formation of cold diatomic BeCs+ molecular ions in the future. Afterwards, the calculation of vibrational state lifetimes of the ground 11Σ+, first 21Σ+ and second 31Σ+ states are presented. We found that the radiative lifetimes of the lower vibrational levels of the 11Σ+ state have an order of magnitude of second and that of 21Σ+ and 31Σ+ have an order of nanoseconds. Finally, we have calculated and analyzed the Franck–Condon factors between low-lying excited state of symmetry – 21Σ+, 31Σ+ and 11Π – and the ground state 11Σ+. We have shown that the favorite vibrational transition is obtained for 11Π (v′′′ = 0) →11Σ+(v = 0), which can be essential for the process of direct laser cooling. This work serves as an initial step for the formation of cold BeCs+ molecular ions. A possible extension of this study would require spin–orbit coupling calculations which could affect the spectroscopic results and consequently its dynamics. Such analysis would be ideally done in conjunction with high-precision spectroscopy experiments. Potential energy, permanent and transition electric dipole moments as a function of interatomic distance are available in the numerical form for BeCs+ systems in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. B. would like to acknowledge the financial support of the American University of Ras Al Khaimah under grant no. AAS/001/22.References
- M. Tomza, K. Jachymski, R. Gerritsma, A. Negretti, T. CalarcoZ, I. Dziaszek and P. S. Julienne, Rev. Mod. Phys., 2019, 91, 035001 CrossRef CAS.
- W. W. Smith, O. P. Makarov and J. Lin, J. Mod. Opt., 2005, 52, 2253–2260 CrossRef CAS.
- C. Zipkes, S. Palzer, C. Sias and M. Köhl, Nature, 2010, 464, 388–391 CrossRef CAS PubMed.
- K. Ravi, S. Lee, A. Sharma, G. Werth and S. A. Rangwala, Nat. Commun., 2012, 3, 1–7 Search PubMed.
- R. Côté and A. Dalgarno, Ultracold atom–ion collisions, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 012709 CrossRef.
- W. G. Rellergert, S. T. Sullivan, S. J. Schowalter, S. Kotochigova, K. Chen and E. R. Hudson, Nature, 2013, 495, 490–494 CrossRef CAS PubMed.
- L. Ratschbacher, C. Zipkes, C. Sias and M. Köhl, Nat. Phys., 2012, 8, 649–652 Search PubMed.
- S. Schmid, A. Härter and J. H. Denschlag, Phys. Rev. Lett., 2010, 105, 133202 CrossRef PubMed.
- F. H. Hall and S. Willitsch, Phys. Rev. Lett., 2012, 109, 233202 CrossRef PubMed.
- T. Feldker, H. Fürst, H. Hirzler, N. V. Ewald, M. Mazzanti, D. Wiater, M. Tomza and R. Gerritsma, Nat. Phys., 2020, 16, 413 Search PubMed.
- I. Sivarajah, D. S. Goodman, J. E. Wells, F. A. Narducci and W. W. Smith, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 063419 CrossRef.
- S. Haze, S. Hata, M. Fujinaga and T. Mekaiyama, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 052715 CrossRef.
- T. GrierA, M. Cetina, F. Oručević and V. Vuletić, Phys. Rev. Lett., 2009, 102, 223201 CrossRef PubMed.
- M. Cetina, A. T. Grier and V. Vuletić, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 109, 253201 Search PubMed.
- H. da Silva Jr, M. Raoult, M. Aymar and O. Dulieu, New J. Phys., 2015, 17, 045015 CrossRef.
- A. D. Dörfler, P. Eberle, D. Koner, M. Tomza, M. Meuwly and S. Willitsch, Nat. Commun., 2019, 10, 1–10 CrossRef PubMed.
- A. Rakshit and B. Deb, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 022703 CrossRef.
- J. Kaur, D. K. Nandy, B. Arora and B. K. Sahoo, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 012705 CrossRef.
- R. Côté, V. Kharchenko and M. D. Lukin, Phys. Rev. Lett., 2002, 89, 093001 CrossRef PubMed.
- L. D. Carr, D. DeMille, R. V. Kremsand and J. Ye, New J. Phys., 2009, 11, 055049 CrossRef.
- F. H. Hall, P. Eberle, G. Hegi, M. Raoult, M. Aymar, O. Dulieu and S. Willitsch, Mol. Phys., 2013, 111, 2020–2032 CrossRef CAS.
- F. H. Hall, M. Aymar, M. Raoult, O. Dulieu and S. Willitsch, Mol. Phys., 2013, 111, 1683–1690 CrossRef CAS.
- S. Schmid, A. Härter and J. H. Denschlag, Phys. Rev. Lett., 2010, 105, 133202 CrossRef PubMed.
- S. Schmid, A. Härter, A. Frisch, S. Hoinka and J. H. Denschlag, Rev. Sci. Instrum., 2012, 83, 053108 CrossRef PubMed.
- Z. Idziaszek, T. Calarco, P. S. Julienne and A. Simoni, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 010702 CrossRef.
- O. P. Makarov, R. Côté, H. Michels and W. W. Smith, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 042705 CrossRef.
- W. Paul, Rev. Mod. Phys., 1990, 62, 531 CrossRef CAS.
- D. J. Winel and W. M. Itano, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 1521 CrossRef.
- M. Pospelov and J. Pradler, Phys. Rev. Lett., 2011, 106, 121305 CrossRef PubMed.
- J. J. Bollinger, J. S. Wells, D. J. Wineland and W. M. Itano, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 2711 CrossRef CAS PubMed.
- A. D. Lercher, T. Takekoshi, M. Debatin, B. Schuster, R. Rameshan, F. Ferlaino and H. C. Nägerl, Eur. Phys. J. D, 2011, 65, 3–9 CrossRef CAS.
- Private communication: http://mheaven@emory.edu.
- T. D. Persinger, J. Han and M. C. Heaven, J. Phys. Chem. A, 2021, 125, 3653–3663 CrossRef CAS PubMed.
- C. Ghanmi, M. Farjallah and H. Berriche, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 055101 CrossRef.
- R. ElOualhazi and H. Berriche, J. Phys. Chem. A, 2016, 120, 452–465 CrossRef CAS PubMed.
- M. Aymar, R. Guérout and O. Dulieu, J. Chem. Phys., 2011, 135, 064305 CrossRef CAS PubMed.
- H. da Silva Jr, M. Raoult, M. Aymar and O. Dulieu, New J. Phys., 2015, 17, 045015 CrossRef.
- H. Ladjimi, M. Farjallah and H. Berriche, Phys. Scr., 2020, 95, 055404 CrossRef CAS.
- W. Zrafi, H. Ladjimi, H. Said, H. Berriche and M. Tomza, New J. Phys., 2020, 22, 073015 CrossRef CAS.
- H. Ladjimi, D. Sardar, M. Farjallah, N. Alharzali, S. Naskar, R. Mlika, H. Berriche and B. Deb, Mol. Phys., 2018, 116, 1812–1826 CrossRef CAS.
- B. Huron, J. P. Malrieu and P. Rancurel, J. Chem. Phys., 1973, 58, 5745–5759 CrossRef CAS.
- S. Evangelisti, J. P. Daudey and J. P. Malrieu, Chem. Phys., 1983, 75, 91–102 CrossRef CAS.
- P. Durand and J. C. Barthelat, Theor. Chem. Acc., 1975, 38, 283–302 Search PubMed.
- P. Durand and J. C. Barthelat, Chem. Phys. Lett., 1974, 27, 191–194 CrossRef CAS.
- W. Müller, J. Flesch and W. Meyer, J. Chem. Phys., 1984, 80, 3297–3310 CrossRef.
- M. Foucrault, P. Millié and J. P. Daudey, J. Chem. Phys., 1992, 96, 1257–1264 CrossRef CAS.
- P. Fuentealba, L. Von Szentpaly, H. Preuss and H. Stoll, J. Phys. B: At., Mol. Opt. Phys., 1985, 18, 1287 CrossRef CAS.
- D. Pavolini, T. Gustavsson, F. Spiegelmann and J. P. Daudey, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 1721 CrossRef CAS.
- A. E. Kramida, Y. Ralchenko and J. Reader, NIST ASD Team, NIST Atomic Spectra Database (ver. 5.5.6), National Institute of Standards and Technology, Gaithersburg, MD, 2018 Search PubMed.
- M. Gacesa, J. A. Montgomery Jr, H. H. Michels and R. Côté, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 94, 013407 CrossRef.
- G. Gopakumar, M. Abe, M. Kajita and M. Hada, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 062514 CrossRef.
- D. A. Fedorov, D. K. Barnes and S. A. Varganov, J. Chem. Phys., 2017, 147, 124304 CrossRef PubMed.
- W. T. Zemke, J. B. Crooks and W. C. Stwalley, J. Chem. Phys., 1978, 68, 4628–4630 CrossRef CAS.
- N. Mabrouk and H. Berriche, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 155101 CrossRef.
- I. Jendoubi, H. Berriche, H. Ben Ouada and F. X. Gadea, J. Phys. Chem. A, 2012, 116, 2945–2960 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schut, et al., MOLPRO, version 2010.1, a package of ab initio programs, 2010, see https://www.molpro.net Search PubMed.
- S. G. Porsev and A. Derevianko, J. Exp. Theor. Phys., 2006, 102, 195–205 CrossRef CAS.
- E. F. Archibong and A. J. Thakkar, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 5478 CrossRef CAS PubMed.
- A. Derevianko, W. R. Johnson, M. S. Safronova and J. F. Babb, Phys. Rev. Lett., 1999, 82, 3589 CrossRef CAS.
- C. R. Ekstrom, J. Schmiedmayer, M. S. Chapman, T. D. Hammond and D. E. Pritchard, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 3883 CrossRef CAS PubMed.
- L. Landau and E. Lifshitz, Course of theoretical Physics, 1977, 3 Search PubMed.
- N. F. Mott and H. S. W. Massey, Theory of atomic collisions, Tac., 1949 Search PubMed.
- J. Weiner, V. S. Bagnato, S. Zilio and P. S. Julienne, Rev. Mod. Phys., 1999, 71, 1 CrossRef CAS.
- A. Rakshit, C. Ghanmi, H. Berriche and B. Deb, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 105202 CrossRef.
- C. F. Fischer and G. Tachiev, At. Data Nucl. Data Tables, 2004, 87, 1–184 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00808d |
| This journal is © the Owner Societies 2022 |