Application of machine-learning-based global optimization: potential-dependent co-electrosorbed structure and activity on the Pd(110) surface†
Li-Yuan
Wang
and
Ya-Hui
Fang
 *
*
School of Chemical and Environmental Engineering, Shanghai Institute of Technology, Shanghai, 201418, China. E-mail: huihuifang@sit.edu.cn
First published on 13th July 2022
Abstract
Electrodes can adsorb different reaction intermediates under electrochemical conditions, which in turn significantly affect their electrochemical performance. This complex phenomenon attracts continuous interest in both science and industry for understanding the co-electrosorbed structure and activity under electrochemical conditions. Here, we report the first theoretical attempt by combining the machine-learning-based global optimization (SSW-NN method) and modified Poisson–Boltzmann continuum solvation (CM-MPB) based on first-principles calculations to elucidate the potential-dependent co-electrosorbed species on the Pd(110) surface. We reveal the potential-dependence adsorption/absorption hydrogen phases, the phase transition of α-Hri/Pd to β-Hri/Pd, and the co-electrosorbed Hri-NHy surface structures. In particular, we found that Hri-NH2 and Hri-NH3 are favorable intermediates for the N2 reduction reaction, and the subsurface H is the key species responsible for NH2 hydrogenation on the Pd(110) electrode.
1. Introduction
Potential-dependent co-electrosorbed reaction intermediates occur commonly in electrocatalytic reactions. The interaction and reaction of electrosorbates is of fundamental scientific and technological importance in electrochemistry.1,2 Palladium, as a unique material for the hydrogen storage,3–5 has long demonstrated that hydrogen can easily adsorb on the surface and then permeate into the metal sublayer.6–9 It is naturally expected that H and reactive species could occur on the surface simultaneously at the reduction potential, where the co-electrosorbed species further regulate the electrocatalytic reaction, such as the N2 reduction reaction (NRR).4,10,11 It was thus a long-standing challenge to probe the potential-dependent atomic structure at the co-electrosorbed species/electrode interface in order to shed light on the co-electrosorbed surface structures and their impact on the catalytic reactivity.Hydrogen adsorption/absorption on Pd metal has been intensely studied in history.8,12–14 It has been shown that two Hr/Pd phases are formed in gas and electrochemical experiments,15–18 namely α-Hr/Pd (r ∼ 0.03 (r = nH/nPd) and β-Hr/Pd (r ∼ 0.6). In electrochemistry, it is noted that hydrogen firstly adsorbed on the surface to form the α-Hr/Pd phase at low hydrogen concentration and high potential (>0.05 V). Then, there is a sharp increase in the H/Pd ratio in a narrow potential range (0.04 to −0.02 V) due to the α-β Hr/Pd phase transition.19–21 Palladium hydrides exhibit reversible hydrogen storage properties and could be envisioned as promising NRR electrocatalysts. It has been found that Pd hydride can advance the electrochemical NRR reaction and NH3 yield.1,10,22 To clarify the effect of the Hr/Pd system on the electrochemical reaction, atomic level knowledge of the electrode is required, which involves complex hydrogen adsorption/absorption phases and co-adsorbed Hr-NHy state at local atomic structures.
The reaction mechanism of NRR has been actively investigated for years.11,23 The dissociative and associative mechanisms have been generally accepted.24–26 In the dissociative pathway, the N2 triple bond is broken before the addition of H to the N atoms, forming the N, NH, NH2, and NH3 intermediates continuously. For the associative pathway, N2 is first hydrogenated and then further cleaved to NH, NH2, or NH3. Recently, Wang et al. found that surface hydrogenation can drive N2 reduction to N2H2 and N2H3, and then dissociation to NH2 and NH3.27 The studies showed that the H and NHy (N, NH, NH2 and NH3) intermediates are the basic species of the N2 reduction reaction. It is naturally expected that the Pd electrode could also contain adsorbed/absorbed hydrogen and co-adsorbed NHy species under electrochemical conditions. However, determining the co-adsorbed surface structures under electrocatalytic conditions remains a key problem in the field, which needs to be taken into account, at least the electrosorbed hydrogen phases, and the co-adsorbate surface structures at the solid/liquid interface.
Herein, we aim to understand the potential-dependent co-adsorbate structures and how they affect the reaction activity. Using machine-learning simulation, we have mapped out the low energy structures of Hri/Pd(110) under electrochemical conditions. Then, the co-adsorbed Hri-NHy surface structures have been extensively studied. In particular, stable Hri-NHy structures have been identified at different Hri/Pd ratios. We further calculated the reaction energy of the adsorbed NHy species at different potentials and the activity of NH2 hydrogenation with surface and subsurface hydrogen atoms. Our results reveal the effect of adsorption/absorption hydrogen on the adsorbed NHy activity.
2. Methods
The SSW-NN method28–32 is a fast global structure search by combining the global neural network (G-NN) potential with the stochastic surface walking (SSW) global optimization method. With SSW-NN simulation, one can routinely search for 107 structures on global PES for systems up to 200 atoms per cell and cover all likely ratio. The details of the method and the calculation setup have been described in a recent publication.32 The G-NN potential is generated by the iterative self-learning of the DFT global PES dataset generated from SSW exploration, which contains three steps: (i) global dataset generation based on DFT calculations using selected structures from SSW simulation, (ii) G-NN potential fitting, and (iii) SSW global optimization using G-NN potential. These three steps are iteratively performed until the G-NN potential is transferable and robust enough to describe the global PES. Then, the Bayesian optimization algorithm is utilized to guide the SSW-NN global PES search (Bayesian-SSW-NN) for selected Hr/Pd and Hr-NHy/Pd systems to guarantee the correct global minima (GM) configuration being obtained.For the Pd(110) surface, we utilized p(3 × 2) (12 atoms per layer) six-layer slabs with the top two layers being relaxed. The solid/liquid interface was described using the periodic continuum solvation model based on the modified Poisson–Boltzmann equation (CM-MPB), which can take into account the solvation and potential effect.33–35 It should be mentioned that DFT calculations have been utilized to validate the low energy structures and confirm the identified global minimum. All energetics reported in this work are from DFT without specifically mentioning. The other calculation details on SSW and DFT calculation setups can also be found in the ESI.†
3. Results and discussion
3.1 Hri/Pd(110) surface phases
To study the potential-dependent electrosorbed hydrogen phases and the related Hri/Pd(110) structures, it is essential to identify the low energy phases under electrochemical potentials, which is needed to determine the amount of electrosorbed hydrogen on/in the Pd(110) surface (expressed as electrosorbed hydrogen atoms to relaxed Pd atoms ratio) at different potentials. Our methodology for calculating the electrocatalytic phases and reactions has been described in recent publications.36–38 Here, we briefly overview the framework of the current approach, focusing on how to calculate the hydrogen adsorption/absorption phases and the related electrocatalytic properties. In this study, we consider the possibility of hydrogen adsorption/absorption surface structures with the help of machine-learning atomic simulation. We extensively explore the ratio (ri) of H at a series of adsorption/absorption H atoms, i.e., ri = nHi/nrelaxed−Pd with nHi = 1, 2, 3…, 15, 20, 24 hydrogen atoms on/in Pd(110) with different geometries by the SSW-NN global optimization. For each ratio (ri), defined by a certain adsorption/absorption H on/in Pd(110) with a particular surface geometry, its thermodynamic stability can be evaluated by computing the reaction free energy in eqn (1), where the adsorbed hydrogen is treated to be in equilibrium (H+ + e− ↔ H*|ri) with the solvated proton in solution from our previous studies and other works.34,39 | (1) |
 | (2) |
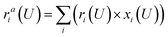 | (3) |
Eqn (1) shows that the reaction free energy of hydrogen at ratio ri is dependent on the potential (U), where G (ri) is the Gibbs free energy of the electrosorbed H surface at the ratio ri and Gsur is Gibbs free energy of clean surface. Further, the population of a ratio at U, is obtained from eqn (2) based on Boltzmann distribution. Finally, the average H ratio (rai (U)) at the potential U can be derived by summing up the contribution from all the possible ratios (eqn (3)). Using eqn (1)–(3), the hydrogen ratio versus potential diagram can be determined.
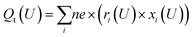 | (4) |
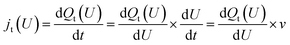 | (5) |
For the Hri/Pd(110) cyclic voltammetry (CV) curves, we have calculated the total passed charge (Qt (U)) using eqn (4) by summing the passed charge of all the phases due to discharging, where n refers to the discharge (e) number of protons to electrosorbed H atoms. The current (jt (U)/(μA cm−2)) in eqn (5) can then be computed by differentiating total passed charge vs. time,40 where the equation can equally rewrite the derivation with respect to potential and obtain eqn (5) by relating to the sweep rate v (set as 50 mV s−1), that is, dU/dt. It is thus possible to calculate the Hri/Pd(110) CV curves based on the calculated charge and related potential using eqn (5).36
Following the above procedure, we have identified the low energy Hri/Pd structures in the potential range of −0.05–0.3 V. The side and top view of these structures are shown in Fig. 1 (also see ESI† Fig. S1). The average ratio of Hri/Pd(110) and the related CV curve versus potential have been further plotted. In the following, we describe the potential-dependent electrochemical properties and the typical structures at the representative ratios (0, 0.25, 0.375, 0.5, 0.625, and 1) in detail.
For the Pd(110) surface, it is the surface commonly known as the missing-row reconstructed Pd(110)-(1 × 2) domain (Fig. 1(b)), where the ridge sites are separated by the wider (111) valleys. H atoms start to adsorb at the upper 3-fold terrace hollow sites at a high potential (>0.25 V) with low hydrogen ratio (ri < 0.25), as shown in Fig. 1(c). The H atoms will then occupy the vacancy valley sites at lower potential (∼0.05 V), as shown in Fig. 1(d). By lowering the electrochemical potential (<0.05 V), it is noted that the additional hydrogen atoms started to penetrate into the subsurface tetrahedral interstitial sites (Fig. 1(e and f)). The increased H atoms can further occupy the sublayer interstitial sites in succession and arrive at a high hydrogen ratio (ri = 1) under lower potential (∼−0.05 V), as shown in Fig. 1(g).
In our search for the best electrosorbed surface and subsurface hydrogen structures, we noticed that the adsorbed H atoms generally prefer to bond to the surface first. It is mainly due to the surface unsaturated Pd atoms, which are active for the adsorbates. Then, the additional hydrogen atoms tend to occupy the subsurface tetrahedral interstitial site when the surface is covered by a sufficient amount of hydrogen atoms (ri > 0.375). The subsurface hydrogen is essential in order to reduce the steric repulsion between the surface adsorbed atoms. It should be mentioned that the stable subsurface tetrahedral interstitial site is consistent with the recent experiment observation41 where the subsurface hydrogen at the near Pd surface is directly identified to occupy the tetrahedral interstices using differentiated and integrated differential phase contrast within an aberration-corrected scanning transmission electron microscope.
According to our results for the determined H adsorbed structures, we have further plotted the potential-dependent diagram of the average Hri/Pd ratio in Fig. 1(a) (cyan line in Fig. 1(a)). It was found that the electrosorbed H is highly dependent on the applied electrochemical potential. Generally, it is noted that the average Hri/Pd ratio rises slowly in the high potential range (0.5–0.3 V), which corresponds to the hydrogen adsorbed on the surface (refer to the α-Hri/Pd), as shown in Fig. 1(c and d). Then, a steep increase in the Hri/Pd ratio is observed at a narrow potential range (0.05 to −0.05 V), where the subsurface H is formed with decreasing potential (Fig. 1(e–g)). Looking closely at the Hri/Pd ratio curve, we observe roughly two plateaus at a high potential and a significant increase at a low potential. The surface is already covered by H atoms at relatively high potentials (>0.3 V). It is further occupied by ∼0.25 ratio of H in between 0.30 and 0.25 V, and grows to ∼0.35 hydrogen ratio at 0.15 V. It is then that the potential-dependent ratio increases greatly (0.38 to 1) from 0.05 V to −0.05 V, where the calculated ratio is similar to the experimental results on Pd surface, about ∼0.78 at 0 V.20
The CV curve is derived by differentiating the total passed charge with respect to potential; thus, each CV peak corresponds to a change in the potential ratio curve of Fig. 1(a). Fig. 1(a) shows that the calculated CV curve has two peaks for the Pd(110) surface centered at about 0.21 and 0 V in the electrosorbed hydrogen region from −0.05 to 0.3 V (dotted dark yellow line in Fig. 2(a)). These CV peaks correspond to the transition of different surface H phases. For example, the 0.21 V peak is associated with an average H ratio from 0.25 to 0.35. The peak at ∼0 V is of interest, which reflects the α to β transformation, where the average H ratio also sharply increases from 0.38 to 1. The ∼0.21 V and ∼0 V peaks from our calculation are in accordance with the experimental results, where the ∼0.26 V42 and ∼0 V43 peaks have been assigned to the underpotential deposited hydrogen (surface adsorbed H) and β-H phase, respectively.
From the above results, it can be noticed that the surface phases and CV curve are closely correlated. The ratio of H on/in Pd(110) would be increased to yield different plateaus with the decrease in the electrochemical potential. Moreover, the CV peaks can be utilized to distinguish the transition of different electrosorbed hydrogen phases. Interestingly, it can be utilized to identify the α-β Hri/Pd phase transformation. The peak at ∼0 V is the transition of surface adsorbed H to the sublayer H, where the hydrogen ratio increases evidently between 0.05 and −0.05 V. The calculated results are consistent with the experimental findings, where a sharp increase in the absorption capacity is observed at 0.04 to −0.02 V, reflecting the αβ phase transition.20
3.2 Hri-NHy/Pd co-adsorbed surface phases
It is generally believed that the electrosorbed H and NHy coexist for the NRR reaction at the low electrochemical potential conditions. Then, NHy can be activated and reduced into NHy+1 by the adsorbed H atom. We mainly focus on the Hri-NHy co-adsorbed surface phases calculation, where the key NHy intermediate structures at different Hri/Pd(110) ratios have been searched using SSW-NN, namely Hri-N, Hri-NH, Hri-NH2, and Hri-NH3 co-adsorbed surface structures. The side and top view of the co-adsorbed structures are shown in Fig. 2 (also see ESI† Fig. S2–S5). From SSW global optimization, it is clear that the more the termination of N has H atoms, the less the bonding of N with the surface Pd atoms. The results show that the unsaturated N always bonds with more Pd atoms, and the saturated NH3 is preferentially adsorbed on one surface Pd atom. It is also interesting noticed that subsurface hydrogen atoms are gradually declined with the hydrogenation of NHy at the concerned potential. In the following, we describe the optimized structures for the four co-adsorbed Hr–NHy phases in detail.Hri-N Surface The N atom firstly preferentially adsorbed on the valley bridge, forming four-coordinated N (N4c) sites with the neighboring Pd atoms at high potential (>0.25 V), as shown in Fig. 2(a). Then, it would move onto the valley top site and form five-coordinated N (N5c) with decreasing potentials (<0.2 V) to accommodate additional adsorbed H (Fig. 2(b–d)), which could decrease the steric effect of adsorbed N and H atoms. For the co-adsorbed H atoms, the adsorbed sites are similar to the Hri/Pd counterpart. The H atoms adsorbed on the upper terrace fcc sites near the ridge, the lower fcc sites near the valley, and the subsurface interstitial sites in succession with decreasing potential.
Hri-NH Surface The NH atom preferentially adsorbed on the terrace three-fold hollow site. Similarly, the co-adsorbed H atoms firstly adsorbed on the upper terrace three-fold hollow sites and next on the lower terrace three-fold hollow sites (Fig. 2(e and f)). When the adsorbed hydrogen ratio is higher than 0.375, the additional H is diffused to the sublayer interstitial sites (see Fig. 2(g and h)).
Hri-NH2 Surface It is observed that the NH2 firstly preferentially adsorbed on the ridge bridge site at high potential (>0.2 V) with low Hri/Pd ratio (ri ∼ 0.25) (see Fig. 2(i)). The adsorbed NH2 will further reposition to the valley bridge site by lowering the potential, as shown in Fig. 2(j–l). It is noted that the co-adsorbed H atoms would occupy the valley bridge site to form 4-coordinated hydrogen and then the subsurface interstitial sites at a lower potential (<0.05 V), namely the high hydrogen ratio (ri > 0.42).
Hri-NH3 Surface For NH3 species with saturated hydrogen atoms, it is noted that NH3 prefers to adsorb on the ridge top site. The co-adsorbed H firstly adsorbed on the upper terrace three-fold hollow sites and next on the lower terrace three-fold hollow sites (Fig. 2(o)). When the hydrogen ratio is higher than 0.5, the additional H would diffuse to the sublayer interstitial sites (see Fig. 2(p)).
On the basis of the phase diagram, we are now able to model the NHy reaction energy at the particular Hri/Pd(110) ratios (0.25, 0.375, 0.5, and 1), which refers to the typical electrochemical potentials at ∼0.25 V, ∼0.05 V, ∼0.03 V, and ∼−0.05 V, respectively. We initiated our investigation from the hydrogen terminated phase, which has a relatively simple surface structure and is also the most relevant to the NHy activity in the experiment.3 We have calculated the reaction energy of the four key intermediates, namely N, NH, NH2, and NH3, using eqn (6), where the reaction energy is calculated with respect to the gas-phase molecule of nitrogen and the corresponding Hri/Pd surface.
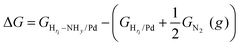 | (6) |
Starting with an H-covered surface, the reaction energies of adsorbed N, NH, NH2, and NH3 at different potentials, namely Hri/Pd ratios, have been calculated using eqn (6). As shown in Fig. 3(a), it is energetically unfavorable for the N and NH intermediates. For the N intermediate, it is endothermically increasingly (>1.32) with decreasing potential. It is also observed that the NH intermediate is thermodynamically unstable at the co-adsorbed surface (>1.24 eV). For the NH2 intermediate, the reaction energy is not higher than 0.70 eV at the concerned potential, suggesting that the reaction is able to occur thermodynamically at the ambient temperature. It is noted that the ΔG of adsorbed NH3 is 0.14 eV, −0.08 eV, −0.60 eV, and −0.52 eV at 0.25 V, 0.05 V, 0.03 V, and −0.05 V, respectively (Fig. 3(a)), where the reaction energy of NH3 would decrease with decreasing potential. Our results show that the reaction steps are strongly endothermic for the N and NH intermediates. It is thus reasonable to believe that the NH2 and NH3 pathway is preferred at the H-electrosorbed surface thermodynamically.
The barriers of HyN–NHy direct dissociation (e.g., N–N, N–NHy, and NHy–NHy) and H-associative HyN–NH2 dissociation (e.g., NHy–NH2 + H → NH3 + NH2) have been further calculated at 0.25 V, as shown in Fig. S6 (ESI†). We found that the N–N dissociation is kinetically inhibited (3.2 eV). For the NH pathway, the reaction barrier is still very high (∼1.7 eV). It is noticed that the reaction barrier of the NH2 pathway is kinetically favored (∼1.2 eV), where it is reasonable to believe that NH2 is the key intermediate in the NRR reaction.
We are now in a position to understand the combination of NH2–H and the transfer of the sublayer H to the surface adsorbed H. Using SSW-NN simulation, we have extensively explored the likely pathways from the hydrogenation of NH2 to NH3. The lowest energy pathway determined at 0.5 ratio is shown in Fig. 3(b), together with the structures along the whole pathway (also in Fig. S7, ESI†).
The reaction can be divided into four elementary steps with an overall barrier 0.76 eV at 0.5 H ratio, suggesting that the reaction is able to occur at the ambient temperature. The four steps of NH3 formation contain two H rearrangement steps, and one combination of H and NH2 and the rearrangement of NH3. The reaction starts from the subsurface H to the surface (the small red ball in state MS1, Fig. 3). The first transition state (TS1) occurs when the subsurface H migrates from the sublayer to the surface (see Fig. 3 TS1). The migrated H atoms then couple with the valley bridge NH2 to form NH3 (TS2, Fig. 3). In the step, the moving NH2 reacts with the bridge H and starts to be coordinated at the terrace top site (MS2, Fig. 3). Then, the other subsurface H move across from the subsurface to the surface with a low barrier (0.30 eV). In the final state, after NH3 is formed, NH3 at the terrace site tends to be adsorbed at the ridge top site to form the stable NH3 surface structure.
| ΔG = GniH/Pd − Gni−1H/Pd | (7) |
We have further calculated NH2 coupling with the surface H atoms (terrace fcc and valley bridged H atoms). However, the reaction barriers are higher, about 0.84 and 0.91 eV (ESI† Fig. S8). The difference in the barriers of NH2 coupling with different H atoms may be understood from the stability of adsorbed hydrogen, where the H differential adsorption energy (eqn (7)) of subsurface H, surface valley H, and surface fcc H are 0.008 eV, −0.12 eV, and −0.21 eV, respectively. Thus, the less stable subsurface hydrogen is active to react with the adsorbed NH2.
By focusing on the coupling step of NH2 and H, we have evaluated the reaction barriers at different Hri/Pd ratios. The reaction barriers obtained are 1.02, 0.88, 0.77, and 0.75 eV for 0.25, 0.375, 0.625, and 1 hydrogen ratio, respectively. The detailed TSs geometry are shown in ESI† Fig. S9. Indeed, we found that the coupling barrier (Ea) of NH2 and H decreases rapidly with the increase in the H ratio. At low H ratio (0.25), which corresponds to a voltage above 0.25 V (see Fig. 1), the reaction barrier is substantially high, above 1 eV. Above 0.375 H ratio (below 0.05 V), the barrier reaches to a rather constant value of ∼0.8 eV. In fact, this phenomenon can be explained from the TS geometry, where only above 0.375, the adsorbed NH2 reacts with subsurface H atom. Obviously, the additional absorbed subsurface H is the active species in NH2 coupling.
4. Conclusions
This work represents the first theoretical attempt to elucidate the in situ surface structures of the Pd(110) electrode under electrochemical conditions. We have calculated the Hri/Pd phases and Hri-NHy co-adsorbed surface structures using SSW-NN simulation and the CM-MPB method. The thermodynamic and kinetic results for the co-adsorbed Hri-NHy/Pd(110) phases show that NH2 and NH3 are the key intermediates of NRR. It is also noted that the subsurface hydrogen is active for the hydrogenation of NH2. The calculation provides atomic-level information on the co-adsorbed structures and the variation in the catalytic activity upon the change in the surface structure and the applied potential. This detailed knowledge may benefit the rational design of better electrode materials in the future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by National Science Foundation of China (21573149) and Shanghai “ChenGuang” project (13CG61).Notes and references
- W. Xu, G. Fan, J. Chen, J. Li, L. Zhang, S. Zhu, X. Su, F. Cheng and J. Chen, Angew. Chem., Int. Ed., 2020, 59, 3511–3516 CrossRef CAS PubMed.
- M. Lukaszewski, K. Hubkowska and A. Czerwinski, Phys. Chem. Chem. Phys., 2010, 12, 14567–14572 RSC.
- Z. Wang, Z. Dai, S. Wang, H. Zhang, W. Tian, Y. Xu, X. Li, L. Wang and H. Wang, Chem. Eng. J., 2021, 416, 129105 CrossRef CAS.
- M. J. W. Blom, W. P. M. van Swaaij, G. Mul and S. R. A. Kersten, ACS Catal., 2021, 11, 6883–6891 CrossRef CAS.
- A. Schneemann, J. L. White, S. Kang, S. Jeong, L. F. Wan, E. S. Cho, T. W. Heo, D. Prendergast, J. J. Urban, B. C. Wood, M. D. Allendorf and V. Stavila, Chem. Rev., 2018, 118, 10775–10839 CrossRef CAS PubMed.
- G. Li, H. Kobayashi, J. M. Taylor, R. Ikeda, Y. Kubota, K. Kato, M. Takata, T. Yamamoto, S. Toh, S. Matsumura and H. Kitagawa, Nat. Mater., 2014, 13, 802–806 CrossRef CAS PubMed.
- A. Baldi, T. C. Narayan, A. L. Koh and J. A. Dionne, Nat. Mater., 2014, 13, 1143–1148 CrossRef CAS PubMed.
- C. Gabrielli, P. P. Grand, A. Lasia and H. Perrot, J. Electrochem. Soc., 2004, 151, A1943–A1949 CrossRef CAS.
- J. D. Benck, Chem. Mater., 2019, 31, 4234–4245 CrossRef CAS.
- X. Zhao, G. Hu, G.-F. Chen, H. Zhang, S. Zhang and H. Wang, Adv. Mater., 2021, 33, 2007650 CrossRef CAS PubMed.
- X. Cui, C. Tang and Q. Zhang, Adv. Energy Mater., 2018, 8, 1800369 CrossRef.
- Z. Zhao, X. Huang, M. Li, G. Wang, C. Lee, E. Zhu, X. Duan and Y. Huang, J. Am. Chem. Soc., 2015, 137, 15672–15675 CrossRef CAS PubMed.
- S. Schuldiner, G. W. Castellan and J. P. Hoare, J. Chem. Phys., 1958, 28, 16–19 CrossRef CAS.
- M. Łukaszewski and A. Czerwiński, J. Solid State Electrochem., 2011, 15, 2489–2522 CrossRef.
- F. D. Manchester, A. San-Martin and J. M. Pitre, J. Phase Equilib., 1994, 15, 62–83 CrossRef CAS.
- R. B. Schwarz, A. K. Khachaturyan, A. Caro, M. I. Baskes and E. Martinez, J. Mater. Sci., 2020, 55, 4864–4882 CrossRef CAS.
- R. J. Wolf, M. W. Lee and J. R. Ray, Phys. Rev. Lett., 1994, 73, 557–560 CrossRef CAS PubMed.
- L. Jewell and B. Davis, Appl. Catal., A, 2006, 310, 1–15 CrossRef CAS.
- M. Łukaszewski, K. Klimek, A. Żurowski, T. Kędra and A. Czerwiński, Solid State Ionics, 2011, 190, 18–24 CrossRef.
- M. Łukaszewski, K. Hubkowska and A. Czerwiński, J. Electroanal. Chem., 2011, 651, 131–142 CrossRef.
- M. H. Martin and A. Lasia, Electrochim. Acta, 2008, 53, 6317–6322 CrossRef CAS.
- J. Wang, L. Yu, L. Hu, G. Chen, H. L. Xin and X. F. Feng, Nat. Commun., 2018, 9, 1795 CrossRef PubMed.
- A. R. Singh, B. A. Rohr, J. A. Schwalbe, M. Cargnello, K. Chan, T. F. Jaramillo, I. Chorkendorff and J. K. Nørskov, ACS Catal., 2017, 7, 706–709 CrossRef CAS.
- C. J. M. van der Ham, M. T. M. Koper and D. G. H. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191 RSC.
- J. G. Howalt, T. Bligaard, J. Rossmeisl and T. Vegge, Phys. Chem. Chem. Phys., 2013, 15, 7785–7795 RSC.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC.
- C. Ling, Y. Zhang, Q. Li, X. Bai, L. Shi and J. Wang, J. Am. Chem. Soc., 2019, 141, 18264–18270 CrossRef CAS PubMed.
- S. D. Huang, C. Shang, X. J. Zhang and Z.-P. Liu, Chem. Sci., 2017, 8, 6327–6337 RSC.
- S. Ma, S. D. Huang, Y. H. Fang and Z. P. Liu, ACS Catal., 2018, 8, 9711–9721 CrossRef CAS.
- C. Shang, S. D. Huang and Z. P. Liu, J. Comput. Chem., 2019, 40, 1091–1096 CrossRef CAS PubMed.
- L. Zhou, X. F. Zhou, X. D. Huang, Z. P. Liu, D. Y. Zhao, X. D. Yao and C. Z. Yu, J. Mater. Chem. A, 2013, 1, 837–842 RSC.
- Y. H. Fang, S. C. Ma and Z. P. Liu, J. Phys. Chem. C, 2019, 123, 19347–19353 CrossRef CAS.
- Y. H. Fang and Z. P. Liu, J. Am. Chem. Soc., 2010, 132, 18214–18222 CrossRef CAS PubMed.
- Y.-H. Fang, G.-F. Wei and Z.-P. Liu, J. Phys. Chem. C, 2013, 117, 7669–7680 CrossRef CAS.
- C. Shang and Z. P. Liu, J. Am. Chem. Soc., 2011, 133, 9938–9947 CrossRef CAS PubMed.
- Y. H. Fang, D. D. Song, H. X. Li and Z. P. Liu, J. Phys. Chem. C, 2021, 125, 10955–10963 CrossRef CAS.
- Y. H. Fang and Z. P. Liu, ACS Catal., 2014, 4, 4364–4376 CrossRef CAS.
- Y. H. Fang, G. F. Wei and Z. P. Liu, J. Phys. Chem. C, 2013, 117, 7669–7680 CrossRef CAS.
- J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Norskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- G. S. Karlberg, T. F. Jaramillo, E. Skúlason, J. Rossmeisl, T. Bligaard, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 126101 CrossRef CAS PubMed.
- B. Lin, X. Wu, L. Xie, Y. Kang, H. Du, F. Kang, J. Li and L. Gan, Angew. Chem., Int. Ed., 2020, 59, 20348–20352 CrossRef CAS PubMed.
- J. Zheng, S. Zhou, S. Gu, B. Xu and Y. Yan, J. Electrochem. Soc., 2016, 163, F499–F506 CrossRef CAS.
- M. Łukaszewski, A. Żurowski, M. Grdeń and A. Czerwiński, Electrochem. Commun., 2007, 9, 671–676 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Theoretical methods and calculation detail, the optimized stable structure of Hri/Pd(110) and Hri-NHy/Pd(110) and XYZ coordinates for the structures in Fig. 1 and Fig. 2. See DOI: https://doi.org/10.1039/d2cp01610a |
| This journal is © the Owner Societies 2022 |