Probing the electronic structure and spectroscopy of pyrrolyl and imidazolyl radicals using high-resolution photoelectron imaging of cryogenically cooled anions

Abstract

High-resolution photoelectron imaging and photodetachment spectroscopy of cryogenically cooled pyrrolide and imidazolide anions are used to probe the electronic structure and spectroscopy of pyrrolyl and imidazolyl radicals. The high-resolution data allow the ground state vibronic structures of the two radicals to be completely resolved, yielding accurate electron affinities of 2.1433 ± 0.0008 eV and 2.6046 ± 0.0006 eV for pyrrolyl and imidazolyl radicals, respectively. Fundamental frequencies for eight vibrational modes of pyrrolyl and ten vibrational modes of imidazolyl are measured, including several nonsymmetric Franck–Condon-forbidden modes. Two electronic excited states are also observed for the two radicals, displaying diffuse spectral features in both systems. The observations of nonsymmetric vibrational modes in the ground states and the diffuse excited state features provide strong evidence for vibronic couplings between the ground state and the two close-by excited states. The 2-pyrrolide isomer is also observed as a minor species from the electrospray ionization source and the electron affinity of 2-pyrrolyl is measured to be 1.6690 ± 0.0030 eV along with five vibrational frequencies. Even though the HOMOs of both pyrrolide and imidazolide anions are p orbitals, photodetachment spectroscopy reveals completely different threshold behaviors for the two anions: a d-wave-dominated spectrum for pyrrolide and an s-wave-dominated spectrum for imidazolide. The current study provides a wealth of electronic and spectroscopic information, which is ideal to compare with more accurate vibronic coupling calculations for these two important radicals, as well as interesting information about the photodetachment dynamics of the two anions.

---

1 Introduction

Nitrogen-containing polycyclic aromatic hydrocarbons (PANHs) have attracted continued research attention due to their importance in combustion chemistry, environmental science, astrochemistry, and planetary science. Thermal decomposition of PANH species is an important source of atmospheric NO_x, which are significant air pollutants.^1–4 PANHs have also been identified in meteorites with nonterrestrial isotopic abundance.⁵ Although no PANH molecules have been detected in space to date,^6–8 experimental studies on interstellar ice analogues under UV irradiation have produced these compounds.^9–12 Derivatives of PANHs are chromophores of nucleobases and aromatic amino acids, which are key building blocks of living organisms.^13–15 In particular, pyrrole (C₄H₅N), an important building block of PANHs, appears as a fundamental unit in many biological molecules. Substituted pyrroles are closely related to pyrimidine DNA bases and are also the constituents of porphyrin-based pigments and related compounds.^16–18 Thus, pyrrole and its derivatives have been investigated extensively both experimentally and theoretically.^19–29 Another five-membered-ring heterocycle, imidazole (C₃H₄N₂), which is similar to pyrrole but contains two separated nitrogen atoms, has been found in the side chain of the amino acid, histidine, and has been studied as an important PANH building block.^30–33

The radical intermediates of pyrrole (pyrrolyl, C₄H₄N) and imidazole (imidazolyl, C₃H₃N₂) by rupture of a C–H or N–H bond play key roles in atmospheric chemistry, combustion, biochemistry and many other chemical processes due to their high reactivity. Pyrrolyl has three isomeric forms: a 1-pyrrolyl radical (or simply pyrrolyl) that arises by N–H bond fission in pyrrole and 2- and 3-pyrrolyl radicals that come from C–H bond fission in the α and β sites, respectively. Photodissociation of pyrrole to produce pyrrolyl has been studied extensively both experimentally^34–40 and theoretically,^41–48 revealing complex dynamics. The electron affinity (EA) of the pyrrolyl radical was determined to be 2.145 ± 0.010 eV using photoelectron spectroscopy (PES) by Gianola et al. in 2004.⁴⁰ Limited vibrational features for the ground state (²A₂) of pyrrolyl were resolved in a previous PES study, whereas only a very weak diffuse continuum was observed for the first excited electronic state (²B₁). The PES study stimulated theoretical investigations about vibronic coupling between the ground state and the first excited state.^44,45 Nonsymmetric vibrational features of b₂ symmetry appeared in the simulated photoelectron (PE) spectra, but were not resolved in a previous PES study. More importantly, the extremely low intensity of the ²B₁ excited state was not predicted theoretically, even though its diffused nature was reproduced. Gianola et al. also conducted a PES study of imidazolide in 2005,⁴⁹ yielding the EA of the imidazolyl radical as 2.613 ± 0.006 eV and frequencies for three vibrational modes. There have been photodissociation and electron attachment experiments on imidazole and theoretical studies on imidazole and other five-membered ring heterocycles.^50–56 Although numerous photochemistry experiments have been carried out on pyrrolyl and imidazolyl radicals, there have been no direct spectroscopic measurements except the PES studies.^40,49

Here, we present a high-resolution PE imaging (PEI) study of cryogenically cooled pyrrolide and imidazolide anions produced from an electrospray ionization (ESI) source. The combination of high-resolution PEI^57,58 and cryogenically cooled ion trap, which operates at 4.6 K and can completely eliminate vibrational hot bands,^59–69 allow us to obtain accurate EAs and rich vibrational information for the pyrrolyl and imidazolyl radicals. The EAs of pyrrolyl and imidazolyl are measured accurately to be 2.1433 ± 0.0008 eV and 2.6046 ± 0.0006 eV, respectively. Frequencies of eight vibrational modes are obtained for the ground electronic state of pyrrolyl and ten vibrational modes for imidazolyl, including several Franck–Condon (FC) forbidden modes due to vibronic coupling. We have also observed 2-pyrrolide as a minor isomer and obtained an EA of 1.6990 eV for 2-pyrrolyl. In addition, two electronic excited states are observed for both pyrrolyl and imidazolyl. Photodetachment spectra are recorded for the two anions near the detachment thresholds and are fitted according to the Wigner threshold law.⁷⁰ Surprisingly, completely different threshold behaviors are observed for the two anions: a d-wave-dominated spectrum is observed for pyrrolide, but an s-wave-dominated spectrum is observed for imidazolide. The current results are compared with previous theoretical calculations and provide excellent data to test both vibronic coupling models and theoretical methods to predict the accurate spectroscopic information for the pyrrolyl and imidazolyl radicals.

2 Results

2.1 Photoelectron spectroscopy of pyrrolide and imidazolide at high photon energies

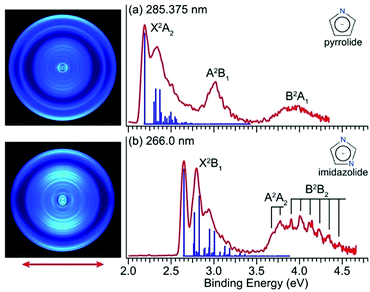
Fig. 1 shows the PE images and spectra of pyrrolide and imidazolide at 285.375 nm and 266.0 nm, respectively. The wavelength at 285.375 nm was generated by frequency doubling of the dye laser output at 570.75 nm, and the 266.0 nm light was the fourth harmonic of the Nd:YAG laser.

Fig. 1 PE images and spectra of (a) pyrrolide at 285.375 nm (4.3446 eV) and (b) imidazolide at 266.0 nm (4.6611 eV). The calculated FC factors for the ground electronic states are represented as blue sticks for comparison. The insets display the molecular structures of the two anions. The double arrow below the images indicates the polarization direction of the detachment laser.

2.1.1 Pyrrolide. The PE spectrum of pyrrolide (Fig. 1a) reveals detachment transitions to the ground electronic state (X²A₂) and two electronic excited states (A²B₁ and B²A₁) of pyrrolyl. Vibrational features are partially resolved for the X²A₂ band, whereas both the A²B₁ and B²A₁ bands are diffuse and featureless. The binding energy (BE) for the 0–0 transition of the X²A₂ band is measured to be about 2.14 eV, which gives a rough estimate of the EA of the pyrrolyl radical, and a much more accurate value is determined from the high-resolution spectra at lower photon energies (vide infra). The vertical detachment energies (VDEs) of the A²B₁ and B²A₁ excited states are measured to be 3.01 and 3.94 eV and the corresponding energy separations (vertical excitation energies) from the ground electronic state are 0.87 and 1.80 eV, respectively. The adiabatic excitation energies for the two excited states could not be determined with any reasonable accuracy because the A²B₁ and B²A₁ bands in the PE spectrum are broad without clearly defined thresholds. No fine features can be resolved for the A²B₁ state even when a near-threshold spectrum is recorded at 401.25 nm (3.0900 eV), as given in Fig. S1 (ESI†).

2.1.2 Imidazolide. The PE spectrum of imidazolide at 266.0 nm (Fig. 1b) displays detachment transitions to the X²B₁ ground state and a very broad band from 3.6 to 4.6 eV. Partial vibrational features are resolved in both bands. The EA of imidazolyl is estimated to be around 2.61 eV, according to the 0–0 transition in the X²B₁ band. A much more accurate EA is obtained from high-resolution PE spectra at lower photon energies (vide infra). The broad high BE band should correspond to excited state features, but its broad width is unusual. It seems to consist of a vibrational progression starting from ∼3.9 eV. We use lower photon energy spectra to try to resolve fine features of the broad band, as shown in Fig. S2 (ESI†). The vibrational progression is not better resolved: all spectral features remain diffuse, and no sharp vibrational peaks could be observed even for near-threshold features. These broad signals appear to contain two overlapping excited state bands, each with partially resolved vibrational features. The first excited state (A²A₂) from 3.6 eV to 3.9 eV consists of a vibrational progression with a spacing of 810 ± 60 cm⁻¹. The second excited state (B²B₂) starting from 3.90 eV consists of the broad vibrational progression with a spacing of 900 ± 80 cm⁻¹. The higher BE part of the A²A₂ band is likely to overlap with that of the B²B₂ band. The adiabatic detachment energy (ADE) of the A²A₂ band is estimated to be 3.68 eV and its VDE is about 3.78 eV. The first vibrational peak for the B²B₂ excited state yields an ADE of 3.90 eV and the second vibrational peak yields a VDE of 4.01 eV, resulting in excitation energies of 1.07 eV and 1.29 eV for the A²A₂ and B²B₂ excited states, respectively.

2.2 Near-threshold photoelectron imaging and accurate determination of the EAs of pyrrolyl and imidazolyl

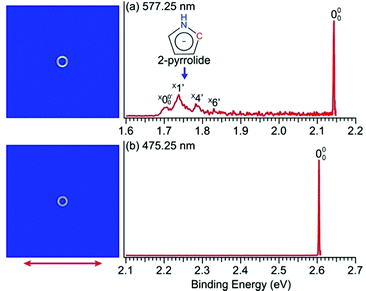
The PEI technique can achieve very high-resolution for low energy electrons.^71–73 To obtain accurate EAs for pyrrolyl and imidazolyl, we measured the high-resolution near-threshold PE images at 577.25 nm (2.1478 eV) and 475.25 nm (2.6088 eV) for pyrrolide and imidazolide, respectively, as shown in Fig. 2. Due to the high spectral resolution and the complete elimination of vibrational hot bands, the line width is mainly due to rotational broadening. The high-resolution data yielded accurate EAs of 2.1433 ± 0.0008 eV (17 287 ± 6 cm⁻¹) and 2.6046 ± 0.0006 eV (21 008 ± 5 cm⁻¹) for pyrrolide and imidazolide, respectively, compared to 2.145 ± 0.010 eV and 2.613 ± 0.006 eV reported previously.^40,49

Fig. 2 Near-threshold PE images and spectra of (a) pyrrolide at 577.25 nm (2.1478 eV) and (b) imidazolide at 475.25 nm (2.6088 eV). The double arrow indicates the polarization direction of the detachment laser.

2.3 Observation of the 2-pyrrolide isomer

In Fig. 2a, very weak signals with discernible vibrational fine structures were also observed at a lower BE side (<1.9 eV). Four peaks were resolved and labeled as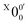 , ^X1′, ^X4′, and ^X6′. To better resolve these features, we used a higher resolution spectrum at 670.75 nm (1.8484 eV), as shown in Fig. 3, where additional weak transitions were resolved and labeled as 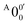, ^X2′, ^X3′, and ^X5′. The BEs of these peaks are given in Table S1 (ESI†). As will be discussed later, these weak features came from one of the isomers of pyrrolide, i.e. 2-pyrrolide, which is due to deprotonation from the α-carbon (see the inset in Fig. 2a). Very weak 2-pyrrolide signals were also observed in the 401.25 nm spectrum (Fig. S1, ESI†), which indicated that the 2-pyrrolide ion signal from the ESI† source was probably <1% of that of 1-pyrrolide (according to the estimated intensity ratio of 2-pyrrolide to pyrrolide, as shown in Fig. S1, ESI†).

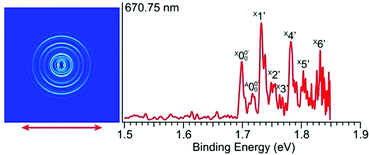Fig. 3 Photoelectron image and spectrum of 2-pyrrolide at 670.75 nm (1.8484 eV). The double arrow indicates the polarization direction of the detachment laser.

2.4 High-resolution photoelectron imaging for the ground state of pyrrolyl

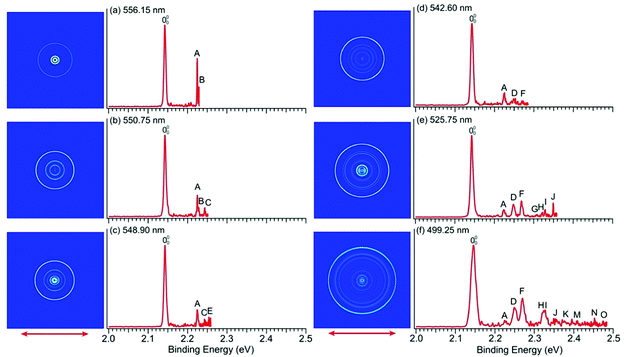
To resolve vibrational structures for the ground state of pyrrolyl, we obtained PE images at successively higher photon energies across the X²A₂ PES band of Fig. 1a. Eleven high-resolution PE images and spectra were recorded for the pyrrolide anion with wavelengths ranging from 556.15 nm (2.2293 eV) to 499.25 nm (2.4834 eV), revealing numerous vibronic features. Six of these images and spectra are shown in Fig. 4 and the remaining five are presented in Fig. S3 (ESI†). It should be noted that, except the spectrum in Fig. 4a, all the near-threshold vibronic transitions have much lower detachment cross-sections and they are clearly non-FC in comparison with the simulated FC profile of the X²A₂ band shown in Fig. 1a.

Fig. 4 PE images and spectra of pyrrolide at (a) 556.15 nm (2.2293 eV), (b) 550.75 nm (2.2512 eV), (c) 548.90 nm (2.2588 eV), (d) 542.60 nm (2.2850 eV), (e) 525.75 nm (2.3582 eV) and (f) 499.25 nm (2.4834 eV). The double arrows indicate the polarization direction of the detachment laser.

The high-resolution data allowed us to resolve fifteen vibrational peaks with BEs up to 2.49 eV, which are labeled from A to O. Because of the complete elimination of vibrational hot bands, all the observed peaks should be due to detachment transitions from the ground vibrational state of the pyrrolide anion to different vibrational levels of the pyrrolyl radical. The BEs of all the observed peaks are given in Table 1 and every BE is measured from the best resolved near-threshold spectra. The shifts of these peaks relative to the 0–0 transition, their assignments, and comparison with theoretical calculations are also given in Table 1. Except for peaks A and B in Fig. 4a, all other near-threshold peaks display extremely low detachment cross-sections. For example, while peak D has a significant intensity in the higher photon energy spectra, it completely disappeared in the near-threshold spectra in Fig. 4b and 4c. In fact, each spectrum shown in Fig. 4 and Fig. S3 (ESI†) was accumulated for more than 8 hours, in order to obtain reasonable counting statistics to resolve the weak near-threshold vibrational peaks.

Table 1 The observed vibrational peaks for pyrrolyl with their binding energies (BEs), shifts relative to the 0–0 transition, and their assignments. The theoretical frequencies (ω) are also given for comparison (see Table S4 and Fig. S7, ESI)

Observed peak	BE^a (eV)	BE^a (cm^−1)	Shift (cm^−1)	Assignment	ω (cm^−1)	ω (cm^−1)
a The numbers in parentheses indicate experimental uncertainties in the last digit. b The frequencies are calculated at the B3LYP/6-311++G** level of theory. c From ref. 46, calculated at the fc-CCSD(T)/ANO level of theory.
0^00	2.1433(8)	17 287(6)	0	Neutral ground state
A	2.2247(9)	17 943(7)	656	21^1	664	668.3
B	2.2286(9)	17 975(7)	688	13^1	710	700.9
C	2.2435(15)	18 095(12)	808	10^1	817	815.0
D	2.2480(19)	18 131(15)	844	8^1	882	869.5
E	2.2537(11)	18 177(8)	890	9^1	904	885.3
F	2.2695(19)	18 305(15)	1018	7^1	1043	1039.1
G	2.3087(15)	18 621(12)	1334	21^2	1328	1336.6
H	2.3226(18)	18 733(14)	1446	4^1	1433	1447.3
I	2.3290(11)	18 785(9)	1498	10^113^1	1527	1515.9
J	2.3492(10)	18 948(8)	1661	8^2	1764	1739.0
K	2.3839(18)	19 227(14)	1940	7^19^1	1947	1924.4
L	2.3994(14)	19 352(11)	2065	7^2	2086	2078.2
M	2.4100(18)	19 438(14)	2151	8^121^2	2210	2206.1
N	2.4528(13)	19 783(10)	2496	4^17^1	2476	2486.4
O	2.4744(15)	19 957(12)	2670	4^15^1	2635	2635.9

---

2.5 High-resolution photoelectron imaging for the ground state of imidazolyl

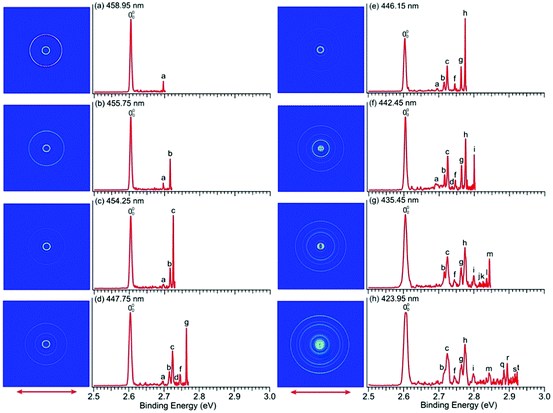
We conducted similar high-resolution studies to probe the vibrational structures of the ground state of imidazolyl. Thirteen high-resolution PE images and spectra were obtained for the imidazolide anion across the X²B₁ PES band and are shown in Fig. 1b with wavelengths ranging from 458.95 nm (2.7015 eV) to 423.95 nm (2.9245 eV). Eight of the high-resolution spectra are shown in Fig. 5 and the remaining five are shown in Fig. S4 (ESI†). In contrast to pyrrolide, the near-threshold vibrational peaks seem to be enhanced in all the spectra for imidazolide. Twenty distinct vibrational peaks up to 2.93 eV are clearly resolved and labeled with lower-case letters from a to t. Their BEs are accurately measured from the best resolved spectra, as shown in Table 2, where the shifts of these peaks relative to the 0–0 transition, their assignments, and comparison with theoretical calculations are also given.

Fig. 5 PE images and spectra of the imidazolide anion at (a) 458.95 nm (2.7015 eV), (b) 455.75 nm (2.7204 eV), (c) 454.25 nm (2.7294 eV), (d) 447.75 nm (2.7691 eV), (e) 446.15 nm (2.7790 eV), (f) 442.45 nm (2.8022 eV), (g) 435.45 nm (2.8473 eV) and (h) 423.95 nm (2.9245 eV). The double arrows indicate the polarization direction of the detachment laser.

Table 2 The observed vibrational peaks for imidazolyl with their binding energies (BE), shifts relative to the 0–0 transition, and their assignments. The theoretical frequencies (ω) are also given for comparison (see Table S5 and Fig. S8, ESI)

Observed peak	BE^a (eV)	BE^a (cm^−1)	Shift (cm^−1)	Assignment	ω (cm^−1)
a The numbers in parentheses indicate experimental uncertainties in the last digit. b The frequencies are calculated at the B3LYP/6-311++G** level of theory. These data are the same as those reported in ref. 49 computed at the same level of theory.
0^00	2.6046(6)	21 008(5)	0	Neutral ground state
a	2.6964(8)	21 748(6)	740	11^1	756
b	2.7160(8)	21 906(6)	898	7^1	919
c	2.7248(8)	21 977(6)	969	6^1	982
d	2.7315(7)	22 031(6)	1023	12^2	1022
e	2.7398(8)	22 098(6)	1090	9^2	1120
f	2.7459(8)	22 147(6)	1139	5^1	1166
g	2.7639(9)	22 292(7)	1284	4^1	1313
h	2.7755(7)	22 386(6)	1378	3^1	1436
i	2.7996(6)	22 580(5)	1572	18^2	1560
j	2.8158(8)	22 711(6)	1703	8^2	1748
k	2.8279(14)	22 809(11)	1801	7^2	1838
l	2.8368(12)	22 880(10)	1872	6^17^1	1901
m	2.8444(9)	22 942(7)	1934	6^2	1964
n	2.8664(14)	23 119(11)	2111	5^16^1	2148
o	2.8743(8)	23 183(6)	2175	4^17^1	2232
p	2.8840(10)	23 261(8)	2253	4^16^1	2295
q	2.8869(11)	23 284(9)	2276	3^17^1	2355
r	2.8948(9)	23 348(7)	2340	3^16^1	2418
s	2.9165(8)	23 523(6)	2515	3^15^1	2602
t	2.9225(7)	23 572(6)	2564	4^2	2626

---

2.6 Photodetachment spectroscopy for pyrrolide and imidazolide

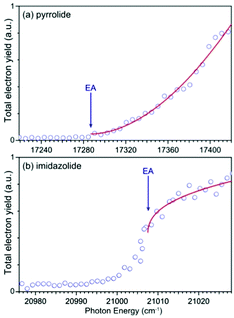
We carried out photodetachment spectroscopy experiments for pyrrolide and imidazolide by monitoring the total electron yields while scanning the photon energy across their respective detachment thresholds. These experiments were conducted for two purposes: (1) to study the different threshold photodetachment behaviors of the two anions as suggested in the photon energy dependent PEI experiments presented above and (2) to search for dipole-bound excited states, which manifest themselves as near-threshold resonances for anions with polar neutral cores.^63–69 The photodetachment spectra for the two anions are shown in Fig. 6, where the arrows indicate the positions of the EAs measured from the high-resolution PEI experiments (Fig. 2). The measured data points are shown as circles, and the solid curves are fit to the experimental data according to the Wigner threshold law, σ ∼ (hν − EA)^l+1/2, where σ is the detachment cross-section and hν is the photon energy.⁷⁰ The two photodetachment spectra are very different: the detachment cross-section of pyrrolide shows a smooth increase above the threshold, whereas that of imidazolide shows an abrupt increase at the threshold. The near-threshold detachment cross-section for pyrrolide is extremely low, as noted already in the photon energy dependent PEI data presented in Fig. 4 and Fig. S3 (ESI†). The signals below the detachment threshold for imidazolide (Fig. 6b) were due to rotational broadening. The rotational temperature of ions in our cryogenic ion trap was previously estimated to be ∼30 K when the ion trap was operated at 4.5 K.^74,75 It should be pointed out that no resonances were observed near the threshold in both systems, suggesting that dipole-bound states do not exist in these two anions. This observation was not surprising because the dipole moments of both pyrrolyl (μ = 2.18 D) and imidazolyl (μ = 1.75 D) are below the critical dipole moment (μ ∼ 2.5 D) to support excited dipole-bound states.⁷⁶

Fig. 6 Photodetachment spectra of (a) pyrrolide and (b) imidazolide. The EA of each anion is indicated by the arrow. The photodetachment spectra are fitted by the Wigner threshold law: σ = A × (hν − EA)^l+1/2, where A is the parameter related to the PE signal intensity, hν is the photon energy, and l is the angular momentum of the photoelectron. The l value is found to be 1.4 for (a) and −0.1 for (b).

3 Discussion

3.1 High photon energy spectra and the electronic structure of pyrrolide and imidazolide

3.1.1 Pyrrolide. Compared to the spectrum reported previously by Gianolo et al. at 363.8 nm,⁴⁰ the A²B₁ band in the current study at 285.375 nm is much better defined and its relative intensity is significantly higher. We also recorded the spectrum of pyrrolide at 401.25 nm (3.0900 eV) (Fig. S1, ESI†) and found that the relative intensity of the A²B₁ state was substantially reduced. Thus, the low detachment cross-section near the threshold and the low detection efficiency for low KE electrons in the PES experiment by Gianolo et al. were probably the causes for their inability to observe the A²B₁ band. In addition, the current higher photon energy spectrum also allowed the second excited state (B²A₁) to be observed. The measured VDEs for the two excited states (3.01 eV and 3.94 eV) are in good agreement with theoretical predictions reported previously using the electron propagator method (2.92 eV and 3.99 eV).⁵⁵ The relative intensities for the X²A₂ and A²B₁ bands agree well with the simulated spectra by Motzke et al.⁴⁵ and Zhu and Yarkony.⁴⁴ The featureless A²B₁ band, even at 401.25 nm (Fig. S1, ESI†), is consistent with the observation by Gianolo et al.⁴⁰ This is due to strong vibronic coupling with the ground state, as studied in detail by Motzke et al.⁴⁵ and Zhu and Yarkony.⁴⁴ The current study revealed that the B²A₁ state is also broad and featureless, which may suggest strong vibronic coupling with the A²B₁ state or even vibronic coupling involving the first three electronic states in pyrrolyl.

3.1.2 Imidazolide. A previous study by Gianolo et al. at 351.1 nm only reached the ground state detachment transition for the imidazolide anion.⁴⁹ The current study at 266.0 nm (Fig. 1b) revealed a broad band between 3.6 and 4.6 eV due to the electronic excited states of imidazolyl. The large width and the resolved vibrational features suggested that the broad band contained two overlapping excited states of imidazolyl. The vibrational progression starting from 3.90 eV with a spacing of 900 cm⁻¹ represent the B²B₂ state and the first two features with a spacing of 810 cm⁻¹ correspond to the A²A₂ state. The higher BE part of the A²A₂ state is likely to overlap with that of the B²B₂ state. These assignments resulted in VDEs of 3.78 and 4.01 eV for the A²A₂ and B²B₂ states, respectively. These results are in excellent agreement with previous theoretical predictions using the electron propagator method (3.85 and 4.07 eV, respectively)⁵⁵ and the CCSD(T) method.⁷⁷

We have also recorded the spectra at 302.375 nm and 285.375 nm for imidazolide (Fig. S2, ESI†), but were unable to resolve the two excited state features better; all vibrational peaks were still rather broad. This observation suggests that there may be strong vibronic coupling between the two excited states since they are very close in energy. Previous theoretical studies indicated that the vibronic coupling between the ground state and the first excited state is weak due to their large energy separation.⁷⁷

3.1.3 Franck–Condon factors, valence molecular orbitals, and angular distributions. The calculated FC factors from the ground state detachment transitions are represented as blue vertical lines in Fig. 1 for both anions. The low-resolution PE spectra at the high photon energies did not allow detailed vibronic peaks to be resolved and only afforded broad FC profiles for the ground state detachment transitions, which are generally in good agreement with the simulated FC profiles. The FC factors computed currently are identical to those reported previously by Gianolo et al.^40,49 The FC factor calculations only involve totally symmetric vibrational modes and cannot capture vibronic coupling effects, which result in the observation of FC-forbidden modes, as will be shown below in the high-resolution PE spectra.

The electronic structure and chemical bonding of pyrrolide and imidazolide are well known. Their valence molecular orbitals (MOs) that are relevant to the current experiments are shown in Fig. S5 and S6 (ESI†) for pyrrolide and imidazolide, respectively. The highest occupied MO (HOMO) (a₂) and HOMO−1 (b₁) of pyrrolide are π orbitals, whereas its HOMO−2 (a₁) is a σ orbital. Electron detachment from these three valence MOs gives rise to the three PES bands presented in Fig. 1a. The HOMO (b₁) and HOMO−1 (a₂) of imidazolide are also π orbitals, whereas its HOMO−2 (b₂) is a σ orbital, corresponding to the observed PES bands shown in Fig. 1b. It should be noted that the HOMOs of the two anions have different symmetries, which result in significantly different threshold photodetachment behaviors, as will be discussed later.

The X²A₂ state of pyrrolyl and the X²B₁ state of imidazolyl correspond to the outermost rings in the PE images of Fig. 1a and Fig. 1b, respectively. The s + d photoelectron angular distributions (PADs) with anisotropy parameter (β) values of −0.60 (pyrrolyl) and −0.75 (imidazolyl) are consistent with the π HOMOs of the two anions. Similarly, the s + d PADs for the A²B₁ state of pyrrolyl (β = −0.60) and the A²A₂ state of imidazolyl (β = −0.65) also agree well with the π HOMO−1 of the two anions. On the other hand, the B²A₁ state in the spectrum of pyrrolide and the B²B₂ state in the spectrum of imidazolide come from the σ HOMO−2 and their PADs are more isotropic.

3.2 The observed vibrational features in the ground electronic state of pyrrolyl

In a previous PES study of pyrrolide by Gianola et al.,⁴⁰ three vibrational frequencies were reported for pyrrolyl: 925 ± 65, 1012 ± 25, and 1464 ± 20 cm⁻¹ due to the ν₈, ν₇, and ν₄ modes, respectively, which are all FC-allowed totally symmetric modes of a₁ symmetry. The high-resolution data shown in Fig. 4 and Fig. S3 (ESI†) allowed us to resolve fifteen vibrational fine features for the ground electronic state of pyrrolyl (X²A₂). The binding energies of these features and their shifts relative to the 0–0 transition are given in Table 1. There have been several previous calculations of the vibrational frequencies for pyrrolyl,^44–47 including a very recent study at the CCSD(T) level.⁴⁶ To help with the spectral assignments, we have performed additional calculations at the DFT level (Table S4 and Fig. S7, ESI†). These values and the most recent CCSD(T) values are used for the spectral assignments, as shown in Table 1. The frequencies calculated using B3LYP and CCSD(T) methods agree well with each other. In general, the CCSD(T) frequencies are slightly better in comparison with the experimental data.

In addition to the three a₁ modes (ν₈, ν₇, and ν₄) observed previously (peaks D, F, and H, respectively), vibrational features involving FC-forbidden nonsymmetric modes are also resolved. In particular, the 556.15 nm spectrum (Fig. 4a) resolved two sharp near-threshold peaks, A and B, which are 656 and 688 cm⁻¹ above the 0–0 transition. These two peaks are assigned to the fundamental vibrations of ν₂₁ (b₂) (peak A) and ν₁₃ (b₁) (peak B), as shown in Table 1. The observed frequencies are in good agreement with the calculated values from B3LYP and CCSD(T). The 550.75 nm spectrum (Fig. 4b) resolved a new threshold peak C, which is assigned to the ν₁₀ (a₂) mode, whereas the 548.90 nm spectrum (Fig. 4c) resolved a new peak E, which is assigned to the ν₉ (a₂) mode. Indeed, the overtone transition of the ν₂₁ (b₂) mode was observed, peak G, which was resolved more clearly in the 535.75 nm spectrum (Fig. S3a, ESI†). High BE peaks above peak I involve overtone vibrational peaks or combinational levels. Some of the combinational levels are tentatively assigned because there may be more than one possibility. It is also interesting to note that all the FC-allowed vibrational peaks exhibit very low cross-sections near the threshold, while some of the FC-forbidden vibrational peaks exhibited enhanced cross-sections near the threshold, most prominently peak A (ν₂₁) and B (ν₁₃) in the 556.15 nm spectrum (Fig. 4a). Overall, the fundamental frequencies for eight vibrational modes are obtained in the current study. They are summarized in Table S2 (ESI†) and compared with the calculated values from B3LYP and CCSD(T).

The observations of the FC-forbidden transitions are due to vibronic coupling between the ground (X²A₂) and first excited (A²B₁) electronic states of pyrrolyl, as studied in detail by Motzke et al.⁴⁵ and Zhu and Yarkony.⁴⁴ Only the b₂ modes can couple the two electronic states in the first order. Specifically, both the previous vibronic coupling calculations predicted the excitation of the ν₂₁ (b₂) mode with calculated frequencies of 655.6 cm⁻¹ from ref. 45 and 656.4 cm⁻¹ from ref.44, in excellent agreement with the current experimental frequency measured for peak A (656 cm⁻¹) in Fig. 4a and Table 1. In fact, Zhu and Yarkony predicted spectral lines for the ν₂₁ mode and its overtones at 675.73 and 1374.40 cm⁻¹, respectively,⁴⁴ in good agreement with our observation for peak A at 656 cm⁻¹ and peak G at 1334 cm⁻¹ above the 0–0 transition (Table 1). Interestingly, we also observed nonsymmetric modes ν₁₃ (b₁) (peak B), ν₁₀ (a₂) (peak C), and ν₉ (a₂) (peak E), which can only arise from higher order vibronic couplings or possibly three-state vibronic couplings involving the B²A₁ excited state. The relatively small energy separation between the B²A₁ state and the first excited electronic state suggests that such three-state vibronic couplings may be viable. The broad and diffuse nature of the B²A₁ state observed in the 285.373 nm spectrum (Fig. 1a) provides strong evidence of vibronic couplings. Thus, the current experimental data are ideal to compare with more sophisticated vibronic coupling treatments of the pyrrolyl radical in future.

3.3 The observation of 2-pyrrolide as a minor isomer

The weak broad features observed in Fig. 2a between 1.7 and 1.9 eV, which are better resolved in the high-resolution spectrum in Fig. 3, come from one of the isomers of pyrrolide, produced from our ESI source. There are two other isomers derived from deprotonation from α-carbon (2-pyrrolide) and β-carbon (3-pyrrolide), which are much higher in energy than 1-pyrrolide.^47,56 A recent calculation showed that 2-pyrrolide and 3-pyrrolide are 36.50 and 47.28 kcal mol⁻¹ higher in energy than 1-pyrrolide in ref. 47 and 39.16 and 49.35 kcal mol⁻¹ higher in energy in ref. 56 In addition to the energetics, the 3-pyrrolide isomer can be excluded on the basis of the relatively low EA predicted for 3-pyrrolyl: 1.18 eV^47,53 or 1.35 eV.⁵⁶ The EA of the observed species is defined by the position of peak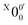 (Fig. 3) and is found to be 1.6990 ± 0.0030 eV (13 703 ± 24 cm⁻¹), which agrees well with the recently calculated EA for 2-pyrrolyl of 1.68 eV using CCSD(T)/CBS by Hendrix et al. in 2020⁴⁷ and an earlier calculated value of 1.66 eV using CBS-APNO by Silva et al. in 2006.⁵³ The BEs and energy shifts to peak 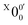of all the resolved peaks (Fig. 3) are summarized in Table S1 (ESI†). It was surprising that such a high energy isomer was observed in our ESI source. There must be a large energy barrier between the 2-pyrrolide isomer and the more stable 1-pyrrolide.

The vibrational frequencies for 2-pyrrolyl have been computed recently by Johansen et al. at the fc-CCST(T) level.⁴⁶ We also calculated the vibrational frequencies for 2-pyrrolyl at the B3LYP level, as shown in Fig. S9 and Table S6 (ESI†). According to the data in Table S1 (ESI†), the energy separation between peaks 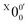and 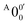is 146 cm⁻¹, which is much smaller than the lowest frequency (mode ν₂₁) of the ground state of 2-pyrrolyl (Table S6, ESI†). Therefore, peak 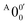is attributed to the detachment transition to the first electronic excited state of 2-pyrrolyl. In order to assign the features in the spectrum shown in Fig. 3, the angular anisotropy parameters (β values) of all the resolved peaks are obtained from the experimental image in Fig. 3, except for peak ^X3′ which is too weak to be accurately fitted. The obtained β values are also given in Table S1. Peak 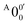has a slightly positive β value (0.1), which is opposite to all the other peaks which have negative β values ranging from −0.2 to −0.5. Thus, the PAD results also suggest that peak 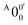belongs to a different electronic state of 2-pyrrolyl, consistent with the assumption based on the energy separation. The BE of peak 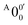is measured to be 1.7170 ± 0.0053 eV. The very small energy difference between the first two electronic states of 2-pyrrrolyl (146 cm⁻¹ or 18 meV) is consistent with the theoretical result calculated by Melin et al. in 2007.⁵⁶ On the basis of the calculated frequencies for 2-pyrrolyl (Table S6, ESI†), the peaks in Fig. 3 can all be assigned (Table S1, ESI†). For example, peaks ^X6′ and ^X3′ could be assigned to the fundamental mode ν₁₂ and the overtone of ν₂₁, respectively. Peak ^X5′ could be assigned to excitation of either the ν₁₅ or ν₁₆ mode, which has similar vibrational frequencies (Table S6, ESI†). The most prominent peak ^X1′ and peaks ^X2′ and ^X4′, assigned to the ν₂₁, ν₂₀ and ν₁₈ modes, respectively, are all out-of-plane bending modes with a′′ symmetry (Fig. S9 and Table S6, ESI†), suggesting that the 2-pyrrolyl ground state may experience slight out-of-plane distortions or strong vibronic coupling with the first excited state.

3.4 The observed vibrational features for the ground electronic state of imidazolyl

There is no other experimental spectroscopic information for imidazolyl, except the PES study by Gianola et al.,⁴⁹ who reported two FC-active modes, ν₃ and ν₆, with vibrational frequencies of 1365 ± 30 and 955 ± 15 cm⁻¹, respectively. The overtone of the nonsymmetric mode (ν₁₈) was also observed at 1575 ± 30 cm⁻¹ above the 0–0 transition, which was attributed to the Fermi resonance by Gianola et al. Several vibrational peaks due to the overtones of the ν₃ or ν₆ modes and their combinational levels were also partially resolved in a previous study.⁴⁹ The current high-resolution study using cryogenically cooled anions resolved twenty vibrational peaks for the ground state detachment transition of imidazolide (Table 2), which yielded fundamental frequencies for ten vibrational modes for the ground state of imidazolyl (X²B₁), as shown in Table S3 (ESI†). In contrast to pyrrolide, imidazolide displayed enhanced near-threshold detachment cross-sections, allowing us to measure the vibrational peaks more accurately. In addition to the ν₃ and ν₆ modes, we observed three more totally symmetric modes, ν₄, ν₅, and ν₇. The observed frequencies of these modes are in good agreement with harmonic frequencies calculated at the B3LYP level. More interestingly, besides the ν₁₈ (b₂) mode, we also observed several vibrational modes with b₁ symmetry (ν₁₁ and ν₁₂) and a₂ symmetry (ν₈ and ν₉). The observation of the ν₁₁ mode defined by peak a (Fig. 5 and Table 2) can be assigned with confidence. For modes ν₁₂, ν₉, and ν₈, only their overtone transitions were observed, similar to mode ν₁₈, but the corresponding PES peaks were extremely weak (peaks d, e, and j, respectively, Fig. 5 and Fig. S4, ESI†). Thus, their assignments should be considered to be tentative.

Compared to pyrrolyl, there have been relatively few theoretical studies about the imidazolyl radical. Ichino et al. simulated the PE spectrum of imidazolide as a reference system in their study of the vibronic coupling in pyrazolyl.⁷⁷ They found that the vibronic coupling in imidazolyl is weak because of the large energy separation between the first excited state and the ground state. An adiabatic simulation reproduced most of the PE spectral features reported by Gianolo et al.⁴⁹ When vibronic coupling with the first excited state (²A₂) was included, the 18² vibrational peak was reproduced. The current high-resolution data are consistent with the conclusion that vibronic coupling of the ground state with the first excited state is weak because only weak nonsymmetric vibrational modes were observed, in comparison with pyrrolyl. As pointed out by Ichino et al., the 18² Fermi resonance could be reproduced even in an adiabatic simulation if anharmonicity was included. Similarly, the observation of the weak 12², 9², and 8² vibrational peaks could probably also be reproduced with the inclusion of anharmonicity. However, the ν₁₁ (b₁) vibrational feature was not reproduced in the nonadiabatic simulation by Ichino et al. This peak may indicate vibronic coupling with the excited states, both of which are very close in energy. The current PE spectra (Fig. 1b and Fig. S2, ESI†) showed that the A²A₂ and B²B₂ excited states have broad spectral features even under high-resolution conditions, evident of strong vibronic couplings.

3.5 The different threshold detachment behaviors of pyrrolide and imidazolide

All the near-threshold vibrational peaks for pyrrolide shown in Fig. 4 and Fig. S3 (ESI†) exhibited very low detachment cross sections except the FC-forbidden transitions, 21¹ (peak A) and 13¹ (peak B), whereas the near-threshold vibrational peaks displayed enhanced detachment cross sections for imidazolide (Fig. 5 and Fig. S4, ESI†). The opposite threshold behaviors for the two anions were revealed more clearly in the photodetachment spectra shown in Fig. 6, which showed negligible near-threshold detachment cross sections for pyrrolide. Because of the low cross sections near the threshold, all the spectra shown in Fig. 4 and Fig. S3 (ESI†) for pyrrolide required extremely long data acquisition times. This was also the reason that an early photodetachment study severely overestimated the EA of pyrrolyl (2.39 ± 0.13 eV) even under room temperature conditions.⁷⁸ Electron detachment from the π HOMO of pyrrolide or imidazolide (Fig. S5 and S6, ESI†) should result in s + d partial waves for the outgoing electrons. Indeed, the PE images at high photon energies shown in Fig. 1 revealed s + d PADs for the ground state detachment bands for the two anions. The threshold behavior is governed by the Wigner threshold law,⁷⁰σ(hν − E_th)^l+1/2, where hν is the detachment photon energy and E_th is the detachment threshold, i.e., the EA of the neutral radicals, and l is the angular momentum of the outgoing photoelectron. Since both s and d partial waves are present for the outgoing electrons, the different threshold behaviors for pyrrolide and imidazolide suggested that different partial waves dominating for the two anions near the threshold. We fitted the photodetachment spectra in Fig. 6 using the Wigner threshold law, σ = A × (hν − EA)^l+1/2, where A is simply the parameter related to the total detachment cross sections, as shown by the solid curves.

The fit yielded l = 1.4 for pyrrolide and l = −0.1 for imidazolide, compared to l = 2 for an ideal d-wave and l = 0 for an ideal s-wave, respectively. These results clearly suggest that the d-wave dominates the detachment process of pyrrolide near the threshold, whereas the s-wave dominates in the case of imidazolide. The different threshold behaviors of the two anions are surprising because the low angular momentum partial wave is supposed to dominate in both cases. For complex molecular systems, many factors may influence the threshold detachment behaviors. Anions with polar neutral cores can lead to modifications of the Wigner threshold law.^79,80 However, this modification is minor and cannot explain the apparently different partial wave nature of the outgoing electrons. Furthermore, both pyrrolyl (μ = 2.18 D) and imidazolyl (μ = 1.75 D) are polar and their dipole moments are not dramatically different. The symmetry of the HOMO may hold the key. While both pyrrolide and imidazolide have C_2v symmetry, the symmetries of their HOMOs are different. The HOMO of pyrrolide has a₂ symmetry, which has no electron density along the C₂ axis. On the other hand, the HOMO of imidazolide has b₁ symmetry, which has a maximum electron density along the C₂ axis. More interestingly, the HOMO of pyrrolide resembles that of the π* HOMO of O₂⁻, which displays a similar threshold behavior with a slow increase of detachment cross-sections near the threshold.⁸¹ The opposite threshold detachment behaviors of pyrrolide and imidazolide are interesting and deserve further theoretical investigations.⁸²

4 Conclusion

In summary, we report high-resolution photoelectron imaging of cryogenically cooled pyrrolide and imidazolide, yielding accurate electron affinities for the pyrrolyl and imidazolyl radicals as 2.1433 ± 0.0008 eV and 2.6046 ± 0.0006 eV, respectively. Extensive vibrational structures were observed for the ground electronic states of pyrrolyl and imidazolyl. A total of fifteen vibrational peaks were observed in the high-resolution spectra of pyrrolide, resulting in the measurements of eight fundamental vibrational frequencies for pyrrolyl. Besides the Franck–Condon-allowed modes with a₁ symmetry, several Franck–Condon forbidden modes with b₂, a₂ or b₁ symmetries are also observed, suggesting strong vibronic coupling effects. The first and second electronic excited states of pyrrolyl were also observed, which were both broad and featureless, evident of strong vibronic couplings. Very weak 2-pyrrolide anion signals were also observed, leading to the determination of the electron affinity for 2-pyrrolyl (1.6990 ± 0.0030 eV) and the observation of several vibrational peaks. Twenty vibrational peaks were observed for imidazolyl, corresponding to ten vibrational modes of imidazolyl. The first and second electronic excited states of imidazolyl were also observed, which were shown to be close in energy. The observation of Franck–Condon-forbidden vibrational modes in the ground state of imidazolyl and broad features of the two electronic excited states also suggest strong vibronic coupling effects. The threshold detachment behaviors of pyrrolide and imidazolide were found to be totally different. Pyrrolide displayed a d-wave dominated behavior with very low detachment cross-sections near the threshold, whereas imidazolide showed an s-wave dominated behavior with an increase of detachment cross-sections near the threshold.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by the Department of Energy, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division under Grant DE-SC0018679 (to L. S. W.). The calculation was performed using computational resources and services provided by the CCV of Brown University.

References

1. D. W. Pershing and J. O. L. Wendt, Ind. Eng. Chem. Proc. Des. Dev., 1979, 18, 60–67.
2. L. Moller, I. Lax and L. C. Eriksson, Environ. Health Perspect., 1993, 101, 309–315.
3. J. Bünger, J. Krahl, O. Schröder, L. Schmidt and G. A. Westphal, Crit. Rev. Toxicol., 2012, 42, 732–750.
4. I. Oluwoye, M. Altarawneh, J. Gore and B. Z. Dlugogorski, Fuel, 2020, 274, 117805.
5. Z. Martins, Life, 2018, 8(3), 28.
6. M. L. Kutner, D. E. Machnik, K. D. Tucker and R. L. Dickman, Astrophys. J., 1980, 242, 541.
7. P. C. Myers, P. Thaddeus and R. A. Linke, Astrophys. J., 1980, 241, 155.
8. B. A. McGuire, Astrophys. J. Suppl. Ser., 2018, 239, 17.
9. C. K. Materese, M. Nuevo, P. P. Bera, T. J. Lee and S. A. Sandford, Astrobiology, 2013, 13, 948–962.
10. C. K. Materese, M. Nuevo and S. A. Sandford, Astrophys. J., 2015, 800, 116.
11. M. Nuevo, S. N. Milam and S. A. Sandford, Astrobiology, 2012, 12, 295–314.
12. K. I. Öberg, Chem. Rev., 2016, 116, 9631–9663.
13. P. R. Callis, Annu. Rev. Phys. Chem., 1983, 34, 329–357.
14. D. Creed, Photochem. Photobiol., 1984, 39, 537–562.
15. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2020.
16. A. L. Sobolewski and W. Domcke, Eur. Phys. J. D, 2002, 20(3), 369–374.
17. A. Kumar, M. Kołaski and K. S. Kim, J. Chem. Phys., 2008, 128, 034304.
18. L. D. Quin and J. A. Tyrell, Fundamentals of Heterocyclic Chemistry: Importance in Nature and in the Synthesis of Pharmaceuticals, Wiley, Hoboken, NJ, 2010.
19. D. Jadoun, M. Gudem and M. Kowalewski, Struct. Dyn., 2021, 8, 034101.
20. K. Saita, M. G. D. Nix and D. V. Shalashilin, Phys. Chem. Chem. Phys., 2013, 15, 16227.
21. B. Liu, Y. Wang and L. Wang, J. Phys. Chem. A, 2012, 116, 111–118.
22. R. Montero, Á. P. Conde, V. Ovejas, M. Fernández-Fernández, F. Castaño, J. R. Vázquez de Aldana and A. Longarte, J. Chem. Phys., 2012, 137, 064317.
23. M. Barbatti, J. Pittner, M. Pederzoli, U. Werner, R. Mitrić, V. Bonačić-Koutecký and H. Lischka, Chem. Phys., 2010, 375, 26–34.
24. B. Cronin, M. G. D. Nix, R. H. Qadiri and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2004, 6, 5031.
25. D. M. P. Holland and L. Karlsson, J. Electron Spectrosc. Relat. Phenom., 2001, 113, 221–239.
26. W. M. Flicker, O. A. Mosher and A. Kuppermann, J. Chem. Phys., 1976, 64, 1315–1321.
27. E. H. Vanveen, Chem. Phys. Lett., 1976, 41, 4.
28. J. A. Sell and A. Kuppermann, Chem. Phys. Lett., 1979, 61, 355–362.
29. A. J. van den Brom, M. Kapelios, T. N. Kitsopoulos, N. H. Nahler, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2005, 7, 892–899.
30. M. Mendes, G. García, M.-C. Bacchus-Montabonel and P. Limão-Vieira, Int. J. Mol. Sci., 2019, 20, 6170.
31. K. Huvaere and L. H. Skibsted, J. Am. Chem. Soc., 2009, 131, 8049–8060.
32. M. Kuhn, S. Raggl, P. Martini, N. Gitzl, M. M. Darian, M. Goulart, J. Postler, L. Feketeová and P. Scheier, Eur. Phys. J. D, 2018, 72, 38.
33. S. A. Pshenichnyuk, I. I. Fabrikant, A. Modelli, S. Ptasińska and A. S. Komolov, Phys. Rev. A, 2019, 100, 012708.
34. D. A. Blank, S. W. North and Y. T. Lee, Chem. Phys., 1994, 187, 35–47.
35. H. Lippert, H.-H. Ritze, I. V. Hertel and W. Radloff, ChemPhysChem, 2004, 5, 1423–1427.
36. G. M. Roberts, C. A. Williams, H. Yu, A. S. Chatterley, J. D. Young, S. Ullrich and V. G. Stavros, Faraday Discuss., 2013, 163, 95.
37. J. Wei, A. Kuczmann, J. Riedel, F. Renth and F. Temps, Phys. Chem. Chem. Phys., 2003, 5, 315–320.
38. L. Rubio-Lago, D. Zaouris, Y. Sakellariou, D. Sofikitis, T. N. Kitsopoulos, F. Wang, X. Yang, B. Cronin, A. L. Devine, G. A. King, M. G. D. Nix, M. N. R. Ashfold and S. S. Xantheas, J. Chem. Phys., 2007, 127, 064306.
39. F. Holzmeier, I. Wagner, I. Fischer, A. Bodi and P. Hemberger, J. Phys. Chem. A, 2016, 120, 4702–4710.
40. A. J. Gianola, T. Ichino, R. L. Hoenigman, S. Kato, V. M. Bierbaum and W. C. Lineberger, J. Phys. Chem. A, 2004, 108, 10326–10335.
41. S. Y. Grebenshchikov and D. Picconi, Phys. Chem. Chem. Phys., 2017, 19, 14902–14906.
42. D. Picconi and S. Y. Grebenshchikov, J. Chem. Phys., 2018, 148, 104103.
43. K. R. Nandipati, A. K. Kanakati, H. Singh, Z. Lan and S. Mahapatra, Eur. Phys. J. D, 2017, 71, 222.
44. X. Zhu and D. R. Yarkony, J. Phys. Chem. C, 2010, 114, 5312–5320.
45. A. Motzke, Z. Lan, C. Woywod and W. Domcke, Chem. Phys., 2006, 329, 50–64.
46. S. L. Johansen, Z. Xu, J. H. Westerfield, A. C. Wannenmacher and K. N. Crabtree, J. Phys. Chem. A, 2021, 125, 1257–1268.
47. J. Hendrix, P. P. Bera, T. J. Lee and M. Head-Gordon, J. Phys. Chem. A, 2020, 124, 2001–2013.
48. C. Sah, A. K. Yadav and S. Venkataramani, J. Phys. Chem. A, 2018, 122, 5464–5476.
49. A. J. Gianola, T. Ichino, R. L. Hoenigman, S. Kato, V. M. Bierbaum and W. C. Lineberger, J. Phys. Chem. A, 2005, 109, 11504–11514.
50. A. L. Devine, B. Cronin, M. G. D. Nix and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 184302.
51. A. Ribar, K. Fink, Z. Li, S. Ptasińska, I. Carmichael, L. Feketeová and S. Denifl, Phys. Chem. Chem. Phys., 2017, 19, 6406–6415.
52. M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640.
53. G. da Silva, E. E. Moore and J. W. Bozzelli, J. Phys. Chem. A, 2006, 110, 13979–13988.
54. G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, J. Chem. Phys., 2010, 132, 064305.
55. J. Melin, M. K. Mishra and J. V. Ortiz, J. Phys. Chem. A, 2006, 110, 12231–12235.
56. J. Melin, R. K. Singh, M. K. Mishra and J. V. Ortiz, J. Phys. Chem. A, 2007, 111, 13069–13074.
57. I. León, Z. Yang and L. S. Wang, J. Chem. Phys., 2013, 138, 184304.
58. Z. Yang, I. León and L. S. Wang, J. Chem. Phys., 2013, 139, 021106.
59. H. T. Liu, C. G. Ning, D. L. Huang, P. D. Dau and L. S. Wang, Angew. Chem., Int. Ed., 2013, 52, 8976–8979.
60. D. L. Huang, P. D. Dau, H. T. Liu and L. S. Wang, J. Chem. Phys., 2014, 140, 224315.
61. G. Z. Zhu, Y. Hashikawa, Y. Liu, Q. F. Zhang, L. F. Cheung, Y. Murata and L. S. Wang, J. Phys. Chem. Lett., 2017, 8, 6220–6225.
62. G. Z. Zhu, Y. Liu, Y. Hashikawa, Q. F. Zhang, Y. Murata and L. S. Wang, Chem. Sci., 2018, 9, 5666–5671.
63. G. Z. Zhu and L. S. Wang, Chem. Sci., 2019, 10, 9409–9423.
64. C. H. Qian, G. Z. Zhu, Y. R. Zhang and L. S. Wang, J. Chem. Phys., 2020, 152, 214307.
65. D. F. Yuan, Y. Liu, C. H. Qian, Y. R. Zhang, B. M. Rubenstein and L. S. Wang, Phys. Rev. Lett., 2020, 125, 073003.
66. D. F. Yuan, Y. Liu, C. H. Qian, G. S. Kocheril, Y. R. Zhang, B. M. Rubenstein and L. S. Wang, J. Phys. Chem. Lett., 2020, 11, 7914–7919.
67. C. H. Qian, Y. R. Zhang, D. F. Yuan and L. S. Wang, J. Chem. Phys., 2021, 154, 094308.
68. D. F. Yuan, Y. R. Zhang, C. H. Qian, Y. Liu and L. S. Wang, J. Phys. Chem. A, 2021, 125, 2967–2976.
69. Y. R. Zhang, D. F. Yuan, C. H. Qian and L. S. Wang, J. Chem. Phys., 2021, 155, 124305.
70. E. P. Wigner, Phys. Rev., 1948, 73, 1002–1009.
71. I. León, Z. Yang, H. T. Liu and L. S. Wang, Rev. Sci. Instrum., 2014, 85, 083106.
72. D. M. Neumark, J. Phys. Chem. A, 2008, 112, 13287–13301.
73. A. Osterwalder, M. J. Nee, J. Zhou and D. M. Neumark, J. Chem. Phys., 2004, 121, 6317–6322.
74. H. T. Liu, C. G. Ning, D. L. Huang and L. S. Wang, Angew. Chem., Int. Ed., 2014, 53, 2464–2468.
75. G. Z. Zhu, Y. Liu and L. S. Wang, Phys. Rev. Lett., 2017, 119, 023002.
76. C. H. Qian, G. Z. Zhu and L. S. Wang, J. Phys. Chem. Lett., 2019, 10, 6472–6477.
77. T. Ichino, A. J. Gianola, W. C. Lineberger and J. F. Stanton, J. Chem. Phys., 2006, 125, 084312.
78. J. H. Richardson, L. M. Stephenson and J. I. Brauman, J. Am. Chem. Soc., 1975, 97, 1160–1162.
79. S. Geltman, Phys. Rev., 1958, 112, 176–178.
80. T. F. O’Malley, Phys. Rev., 1965, 137, A1668–A1672.
81. D. S. Burch, S. J. Smith and L. M. Branscomb, Phys. Rev., 1958, 112, 171–175.
82. C. M. Oana and A. I. Krylov, J. Chem. Phys., 2009, 131, 124114.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of experimental procedures, related images and spectra, molecular orbitals, vibrational modes and corresponding assignments. See DOI: 10.1039/d2cp00189f

‡ Equal contribution.

---