Open Access Article
Open Access ArticleDestructive quantum interference in heterocyclic alkanes: the search for ultra-short molecular insulators†
Boyuan
Zhang‡
 a,
Marc H.
Garner‡
a,
Marc H.
Garner‡
 b,
Liang
Li
b,
Liang
Li
 c,
Luis M.
Campos
c,
Luis M.
Campos
 c,
Gemma C.
Solomon
c,
Gemma C.
Solomon
 *b and
Latha
Venkataraman
*b and
Latha
Venkataraman
 *ac
*ac
aDepartment of Applied Physics and Applied Mathematics, Columbia University, New York, New York 10027, USA. E-mail: lv2117@columbia.edu
bNano-Science Center and Department of Chemistry, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark. E-mail: gsolomon@chem.ku.dk
cDepartment of Chemistry, Columbia University, New York, New York 10027, USA
First published on 30th June 2021
Abstract
Designing highly insulating sub-nanometer molecules is difficult because tunneling conductance increases exponentially with decreasing molecular length. This challenge is further enhanced by the fact that most molecules cannot achieve full conductance suppression with destructive quantum interference. Here, we present results for a series of small saturated heterocyclic alkanes where we show that conductance is suppressed due to destructive interference. Using the STM-BJ technique and density functional theory calculations, we confirm that their single-molecule junction conductance is lower than analogous alkanes of similar length. We rationalize the suppression of conductance in the junctions through analysis of the computed ballistic current density. We find there are highly symmetric ring currents, which reverse direction at the antiresonance in the Landauer transmission near the Fermi energy. This pattern has not been seen in earlier studies of larger bicyclic systems exhibiting interference effects and constitutes clear-cut evidence of destructive σ-interference. The finding of heterocyclic alkanes with destructive quantum interference charts a pathway for chemical design of short molecular insulators using organic molecules.
Introduction
Designing and measuring sub-nanometer molecular insulators constitutes a fundamental challenge. Current mediated by coherent tunneling increases exponentially with decreasing molecular length.1,2 Consequently, even molecules with a large HOMO–LUMO gap will not be effective insulators if they are very short. A different route to creating highly insulating molecules is to use molecules with destructive quantum interference effects, which can effectively suppress the coherent single-molecule conductance in the low-bias regime.3 This effect has been demonstrated in a range of π-conjugated organic molecules4–8 and in saturated σ-conjugated silanes.9–12 Saturated molecules with destructive interference in the σ-system have particularly low conductance, as there is no π-channel and transmission through the σ-channel is suppressed.13–17 This opens a potential avenue for using molecules with destructive σ-interference as molecular insulators. However, the potential has been limited to date by the restrictive structural requirements for the molecules in which the effect appears.18–20Destructive σ-interference has been demonstrated experimentally in cyclic and bicyclic permethylated silanes,11,12 and computationally in permethylated alkanes.10 These molecules have a backbone that is constrained to a cisoid dihedral angle, i.e., one that is approaching 0°.9,11,21 Alkanes with gauche defects have been accessed experimentally and assessed computationally,22–27 but the suppression of the conductance is modest. This is presumably due of lack of methyl substituents in the systems that have been examined.10,28 However, permethylated cyclic and bicyclic alkanes are not synthetically accessible. If the destructive σ-interference effect is to benefit from the broad range of complex molecules available through modern organic synthesis, different classes of saturated systems with the effect need to be explored.
In this article, we examine the single-molecule junction properties of saturated heterocyclic cyclohexane derivates, 1,4-dithiane, 1,4-piperazine and 1,4-diazabicyclo[2.2.2]octane, C222-diaza, also known as DABCO, shown in Scheme 1. These molecules all have molecular length below 5 Å, and thus constitute some of the shortest that can be measured in Au–molecule–Au junctions. Unlike previously explored non-methylated alkanes and methylthiomethyl-functionalized cyclohexanes, we find that these heterocyclic alkanes show significant suppression of conductance due to destructive quantum interference in the σ-system.
Results
Piperazine, C222-diaza, and dithiane are structurally similar to previously explored silanes12 exhibiting destructive σ-interference, with the dihedral angles across the cyclic and bicyclic motifs inherently constrained. For piperazine and dithiane in their dominant chair conformations, these dihedral angles (N–C–C–N and S–C–C–S) are 52° and 67°, respectively. In C222-diaza the N–C–C–N dihedral angles are close to 0°. All three systems differ from previous σ-interference systems10 by the absence of methyl substituents. Furthermore, the molecules studied here are much shorter making them possible insulators over an ultra-short length scale.Piperazine and C222-diaza
We measure the single-molecule junction conductance of piperazine and C222-diaza using the scanning tunnelling microscope-based break-junction technique (STM-BJ). We show logarithmically binned two-dimensional (2D) conductance histograms generated from these measurements in Fig. 1a and b. In the STM-BJtechnique, single molecule measurements are done by trapping the target molecule between Au electrodes after forming and elongating a single Au atom contact. The conductance feature between 10−2 and 10−3G0 in the 2D histograms between 0 and 0.2 nm displacement correspond to the molecular junction and indicate that these junctions have plateau lengths that extend to about 0.2 nm. Consistent with previous studies, the molecular junction plateau lengths are systematically shorter than the molecular backbone length by roughly 5–8 Å.29 The tension that the Au-contact is under during the elongation process will cause the relaxation of the electrodes when the Au-contact ruptures, making it difficult to have every junction elongated by the backbone length. Additionally, we cannot assume that every junction forms with the molecule exactly parallel to the pulling direction. Taking such effects into account, both molecules form junctions at short electrode displacement in accordance with their short molecular length. The corresponding one-dimensional (1D) conductance histograms are shown in Fig. 1c, along with that of their linear alkane counterpart ethylenediamine (C2-NH2). We determine their junction conductance values by fitting Gaussian functions to these peaks. The conductance values are centered at 9.5 × 10−4G0 and 1.9 × 10−3G0 for C222-diaza and piperazine, respectively, lower than that of C2-NH2 (5.6 × 10−3G0). We note that these histograms represent both the spread in conductance and most frequently measured values.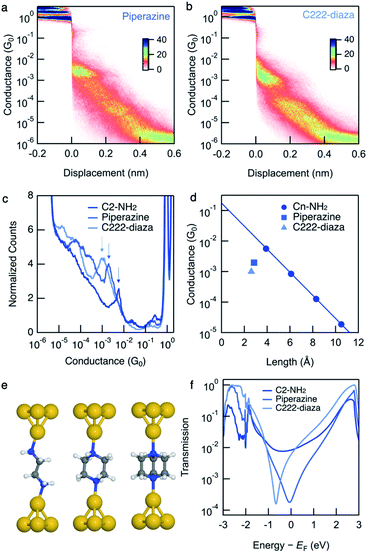 | ||
| Fig. 1 Logarithmically binned 2D histograms of conductance traces measured with (a) piperazine and (b) C222-diaza, compiled from 3000–5000 traces without any data selection. (c) Logarithmically binned 1D histograms of conductance traces measured with C2-NH2, piperazine and C222-diaza, compiled from 3000–5000 traces without any data selection. (d) Measured conductance values (histogram peaks) plotted against the molecular length (N–N and is obtained from DFT-optimized structure). Piperazine, C222-diaza and dithiane are below the respective fit conductance decay line for the alkane. See Fig. S1† for raw data. (e) Optimized Au–molecule–Au junction structures of C2-NH2, piperazine, and C222-diaza. (f) Calculated transmissions of Au–molecule–Au junctions plotted against energy relative to Fermi energy, showing anti-resonance around Fermi energy for piperazine and C222-diaza. | ||
We compare these experimental conductances with those of amine-terminated linear alkanes. Their experimental single-molecule conductance is plotted against N–N distances obtained from DFT calculations in Fig. 1d. The conductance of the alkane series decays exponentially with increasing length, thereby exhibiting linear decay on a semi-log plot as shown in Fig. 1d. Piperazine and C222-diaza are both shorter than C2-NH2 while having the same number of equivalent atoms. Their conductances are below the line of the alkane series, indicating that they are more insulating than an alkane of the same N–N length.
The amine-terminated alkanes we used to plot the conductance decay line in Fig. 1d are primary amines, while the linkers of piperazine are secondary amines and those of C222-diaza are tertiary amines. To further validate that the insulating trends of piperazine and C222-diaza are independent of binding groups, we measure the conductance of secondary and tertiary amine-terminated linear alkanes to understand if the different N linkers account for this reduced conductance. Fig. S2† shows the conductance histogram for a butane backbone with NH2, NH–CH3 and N–(CH3)2 linkers where we can see that there is almost no discernible difference among these three indicating that methyl groups on the terminal amine do not alter junction conductance. We can thus conclude that piperazine and C222-diaza are more insulating than their linear alkane counterparts of the same length, regardless of the structure of the terminal N. We therefore hypothesize that σ-interference in cyclic and bicyclic moiety of piperazine and C222-diaza can suppress their conductance compared with linear alkanes.
We compute the Landauer transmission of the fully extended Au–molecule–Au junctions visualised in Fig. 1e. Piperazine has conformational freedom, but only conformations where the nitrogen lone-pairs are in equatorial positions appear to be long enough to form junctions in room temperature experiments considering the gap that opens after the gold point-contact is ruptured.29 Transmission of the shorter junctions are discussed in ESI† part 3. Plotted in Fig. 1f, the transmission of piperazine and C222-diaza is significantly suppressed in an energy range close to the Fermi energy compared to C2-NH2. Piperazine and C222-diaza both have an antiresonance (dip) close to the Fermi energy in these calculations, which is a signature of destructive quantum interference. We note that the exact energetic position of the antiresonance cannot be exactly predicted due to the quantitative limitations of DFT.30 The antiresonance is in the vicinity of the Fermi energy in both cases and will affect the single-molecule conductance when a bias-window is opened.
Dithiane
Conductance data obtained from measurements of dithiane are shown in Fig. 2a and c. Dithiane has well-defined junction geometry that is very similar to –SMe binding motives.31,32Dithiane has two peaks in the 1D histogram which can be identified as junctions of two different lengths from the 2D histogram. Dithiane primarily adapts a chair conformation, which has sulfur lone-pairs available for bonding with the Au electrodes in equatorial and axial positions as illustrated in Fig. 2b. Based on the calculation results shown in Fig. S7,† we attribute the higher-conducting and shorter junction to molecular conformations where the Au is bound either in an axial–axial configuration or axial–equatorial configuration as both of these junctions have roughly the same length and calculated transmission. The shorter junction conformations of SMe-functionalized alkanes were measured in a previous study,31 where it was found that these also have higher conductance than the fully extended alkane junctions. We attribute the lower-conducting longer junctions to the equatorial–equatorial configuration and focus the rest of this discussion to this junction which has a conductance of 4.1 × 10−4G0.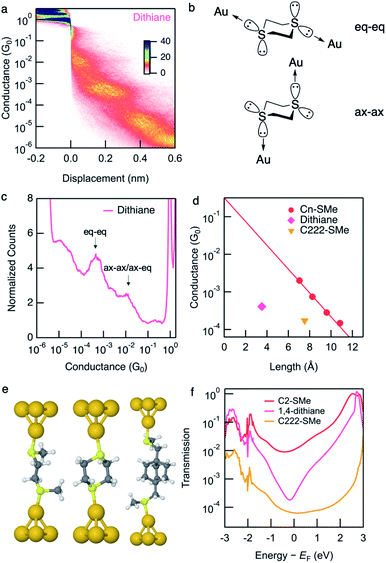 | ||
| Fig. 2 (a) Logarithmically binned 2D histograms of conductance traces measured with dithiane compiled from 3000 traces without any data selection. (b) Dithiane structure showing the two S-lone pairs with equatorial–equatorial and axial–axial configurations. (c) Logarithmically binned 1D histograms of conductance traces used to generate panel (a). (d) Measured conductance values (histogram peaks) plotted against the molecular length (S–S length obtained from DFT-optimized structure). Values for linear alkanes are also shown. Conductance values for Cn-SMe are reproduced from the previous work.12Dithiane and C222-SMe are below the fit conductance decay line for the alkane. (e) Optimized Au–molecule–Au junction structures of C2-SMe, dithiane, and C222-SMe. (f) Calculated transmissions of Au–molecule–Au junctions plotted against energy relative to Fermi energy, showing anti-resonance around Fermi energy for dithiane. | ||
We next compare the experimental conductances of C2-SMe, dithiane, and C222-SMe with those of a series of thiomethyl-terminated linear alkanes, plotted against calculated S–S distance in Fig. 2d. Synthesis and measurements of Cn-SMe was reported in ref. 12. The conductance of longest conformation of dithiane is significantly lower than that of linear thiomethyl-functionalized alkanes of the same length. By extrapolating the conductance decay trend of the alkanes we see that dithiane is more than an order of magnitude lower in conductance. Compared with the previously studied methylthiomethyl-functionalized bicyclo[2.2.2]octane (C222-SMe),10 the conductance is in the same low range as C222-SMe at 1.7 × 10−4G0. However, dithiane is much shorter molecular length as evident in Fig. 2d.
Calculation of the Landauer transmission of the Au–molecule–Au junction shown in Fig. 2e support the experimentally observed trend. Significant suppression is evident when we compare the transmission of dithiane with its alkane counterpart C2-SMe in Fig. 2f. Again, we see an antiresonance in the transmission of dithiane suggesting destructive quantum interference. This is also the case for some of the shorter junction conformations, although shorter junctions inevitably have somewhat higher transmission. The transmission for all junction conformations of dithiane are included in Fig. S7.†
While the transmission of previously studied C222-SMe is also very low, the transmission function is flat around EF and does not show a clear signature of interference.10 We note further that dithiane, piperazine, and C222-diaza do not have methyl substituents unlike C222-SMe, and we shall explore this difference in more detail below.
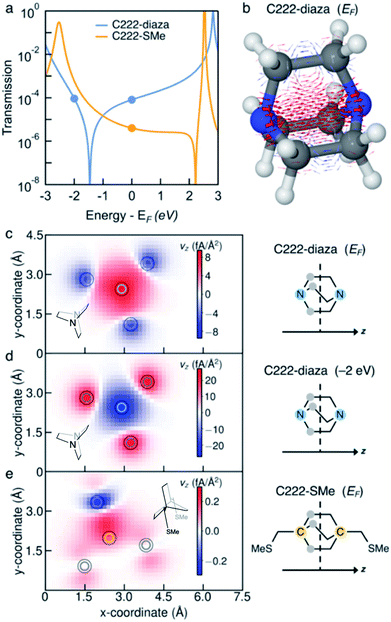
Ballistic current density
We investigate the transmission suppression in piperazine, C222-diaza, and dithiane by computing the ballistic current density through the molecules.33,34 The Landauer transmission and current density of C222-diaza and C222-SMe calculated in the wide-band limit are shown in Fig. 3; that of piperazine and dithiane are included in Fig. S3.† In good agreement with the transmission computed with explicit Au electrodes (Fig. 1f and 2f), C222-diaza has an antiresonance between the HOMO and LUMO resonances. C222-SMe has an antiresonance close to the LUMO resonance, which is not clear in the computations shown in Fig. 2f, where Au electrodes are explicitly included. We first examine the current density of C222-diaza at the Fermi energy. We plot it as three-dimensional vectors in Fig. 3b, where the arrow thickness is the vector-length, and in Fig. 3c as a heat map of current through the xy-plane in the middle of the bicyclic structure (z being the direction of the current). We see that the vector field is dominated by forward current (red) directly between the two nitrogen atoms, with a backwards ring current (blue) being formed by three contributions through the through-bond paths. In Fig. 3d, we plot the current density of C222-diaza at −2.0 eV, i.e., an energy at the other side of the antiresonance in the transmission. A clear signature of destructive quantum interference,28 the ring currents reverse their direction and the direct current between the nitrogen atoms is now in the backwards direction (blue).Turning to the question of why we see sharp interference features with the absence of methyl substituents, the current density indicates that despite the structural similarity C222-diaza differs significantly from C222-SMe. While the injection will be different into the bicyclic cage, the central parts are almost identical. We have not observed the threefold symmetry of the cage-structure retained in the current before. As can be seen in Fig. 3e, the current through C222-SMe is injected into the cage through the transoid path of the CH2SMe linker,35 and the current predominantly follows one through-bond path through the bicyclic cage. Direct current between the bridgehead carbon atoms (marked in orange) is fairly small. This analysis indicates that the strong suppression in the transmission of C222-diaza comes from a different balance between the through-bond and through-space paths through the molecule.36–40 The three-fold symmetry in the current density is an indication of this different behaviour.
Furthermore, we do not see the significant substituent dependence in C222-diaza (Fig. S4†) that was seen in C222-SMe;10 methylation in fact seems to give higher transmission in line with other saturated molecules.41 The injection from the electrode directly into the bridgehead nitrogen atoms of piperazine and C222-diaza, and sulfur atoms of dithiane, thus enables the suppression of conductance in the single-molecule junctions.
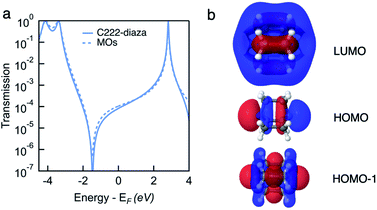
To understand the interference in C222-diaza from a molecular orbital perspective, we reconstruct the transmission of C222-diaza around EF calculated in the wide-band limit in Fig. 3 using three resonances, the LUMO, HOMO, and HOMO−1. Each resonance at an energy εj is coupled to the leads with a coupling γj. The phase factor, θj, describes the phase relation of the MO with respect to its overlap with either lead.42–44
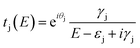 | (1) |
As an approximation, we use a phase factor of 0 or π depending on the symmetry of the orbital.45
In Fig. 4a, we see that the model transmission matches that obtained with DFT very well. The sharp antiresonance structure near EF originates primarily from a destructive interference between the HOMO and HOMO−1 which have opposite phases (θHOMO − θHOMO−1 = π). This can be further confirmed by looking at the calculated MOs shown in Fig. 4b. The HOMO and HOMO−1 have opposite parity at the nitrogens which couple to the leads. In the reconstructed transmission function, the HOMO and HOMO−1 are both nearly an order of magnitude better coupled to the leads than the LUMO. Therefore, the strong destructive quantum interference between HOMO and HOMO−1 can further suppress the constructive quantum interference between the HOMO and LUMO, resulting in low conductance for C222-diaza.42 Analogous analyses for the other two systems are presented in the ESI.†
Conclusions
In this article we have demonstrated that the single-molecule conductance of three heterocyclic alkanes, piperazine, C222-diaza and dithiane, are significantly suppressed in STM-BJ experiments. Through computational analysis of the Landauer transmission and ballistic current density, we reveal that the conductance suppression is due to destructive quantum interference in the σ-system. Conclusively, we find a sharp antiresonance in the transmission near the Fermi energy, and ring currents that reverse direction at the antiresonance energy.The measured conductance of the heterocyclic alkanes is compared to analogous linear alkanes of similar length. The conductance is suppressed in all three cases; in the case of dithiane the difference is over an order of magnitude. These levels of suppression have not previously been observed with any synthetically feasible carbon-based molecules. With molecular lengths around 3 Å, these heterocyclic alkanes are ultra-short molecular insulators. This finding allows us to move beyond earlier suggestions for the structural requirements for destructive σ-interference and charts a clear pathway for rational chemical design of short insulating organic molecules.
Methods
N,N′-Dimethyl-1,4-butanediamine was purchased from Ambeed. Ethylenediamine, 1,4-dithiane, 1,4-piperazine, 1,4-diazabicyclo[2.2.2]octane, N,N,N′,N′-tetramethyl-1,4-butanediamine and all of the solvent were purchased from Sigma Aldrich.The molecular junction conductance was measured via the scanning tunneling microscope-based break junction (STM-BJ) technique at room temperature.46,47 A sharp gold tip was driven in and out of contact with a gold substrate using 1,2,4-trichlorobenzene (TCB) as a solvent for the target molecules. One-dimensional (1D) conductance histograms are constructed using logarithmic bins (100/decade), and two-dimensional (2D) histograms use logarithmic bins along the conductance axis (100/decade) and linear bins (1000/nm) along the displacement axis, compiled from 3000–5000 traces measured at 100 mV. Junction conductance values are determined by fitting Gaussian functions without any data selection.
We analysed the experimental results by computing the Landauer transmission. All molecular geometries are optimized to local minima in vacuum to 0.01 eV Å−1 using density functional theory (DFT) with the PBE functional and DZP basis set as implemented in the Atomic Simulation Environment (ASE) and GPAW.48–50 A conformational analysis is also carried out for the molecules as discussed in part 3 of the ESI.† To form Au–molecule–Au junctions, the optimized structures were placed between two four-atom Au pyramids on Au(111) surfaces and the molecular geometries were relaxed to 0.05 eV Å−1. The transmission was computed at the same level of theory using the nonequilibrium Green's functions formalism as implemented in ASE.50
Calculation of ballistic current density was done using DFT at the same level of theory as was employed in the full transport calculations using GPAW and ASE.48,50 Due to computational constraints, we used s-band electrodes approximated to the wide-band limit to model these single-molecule junctions. That means the gold electrodes were not explicitly included in the computation but the transmission is qualitatively similar to computations where the Au electrodes are explicitly considered.19 The current density was calculated under an applied bias of 1 mV. More extensive computational details of this method are included in part 4 of the ESI† and in previous works.16,51
Data availability
The data that support the findings of this study not included in the ESI are available from the corresponding author upon reasonable request.Author contributions
B. Z. carried STM-BJ measurements, data analysis and molecular orbital analysis, M. H. G. carried out all the computation, L. L. measured the linear alkanes, and all authors co-wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Experimental work was supported primarily by the National Science Foundation (DMR-1807580). G. C. S. and M. H. G. received funding from the Danish Council for Independent Research|Natural Sciences.Notes and references
- A. Nitzan, Annu. Rev. Phys. Chem., 2001, 52(1), 681–750 CrossRef CAS.
- J. G. Simmons, J. Appl. Phys., 1963, 34(6), 1793–1803 CrossRef.
- P. Sautet and C. Joachim, Chem. Phys. Lett., 1988, 153(6), 511–516 CrossRef CAS.
- V. Rabache, J. Chaste, P. Petit, M. L. Della Rocca, P. Martin, J.-C. Lacroix, R. L. McCreery and P. Lafarge, J. Am. Chem. Soc., 2013, 135(28), 10218–10221 CrossRef CAS.
- X. Li, Z. Tan, X. Huang, J. Bai, J. Liu and W. Hong, J. Mater. Chem. C, 2019, 7(41), 12790–12808 RSC.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Angew. Chem., Int. Ed., 2013, 52(11), 3152–3155 CrossRef CAS PubMed.
- C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. van der Molen, Nat. Nanotechnol., 2012, 7(5), 305–309 CrossRef PubMed.
- M. Mayor, H. B. Weber, J. Reichert, M. Elbing, C. von Hänisch, D. Beckmann and M. Fischer, Angew. Chem., Int. Ed., 2003, 42(47), 5834–5838 CrossRef CAS PubMed.
- C. B. George, M. A. Ratner and J. B. Lambert, J. Phys. Chem. A, 2009, 113(16), 3876–3880 CrossRef CAS PubMed.
- M. H. Garner, H. Li, M. Neupane, Q. Zou, T. Liu, T. A. Su, Z. Shangguan, D. W. Paley, F. Ng, S. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, J. Am. Chem. Soc., 2019, 141(39), 15471–15476 CrossRef CAS PubMed.
- H. Li, M. H. Garner, Z. Shangguan, Y. Chen, Q. Zheng, T. A. Su, M. Neupane, T. Liu, M. L. Steigerwald, F. Ng, C. Nuckolls, S. Xiao, G. C. Solomon and L. Venkataraman, J. Am. Chem. Soc., 2018, 140(44), 15080–15088 CrossRef CAS PubMed.
- M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li, S. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558(7710), 415–419 CrossRef CAS PubMed.
- D. Q. Andrews, G. C. Solomon, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130(51), 17309–17319 CrossRef CAS PubMed.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1(3), 16002 CrossRef CAS.
- G. M. Locke, S. S. R. Bernhard and M. O. Senge, Chem.–Eur. J., 2019, 25(18), 4590–4647 CrossRef CAS.
- M. H. Garner and G. C. Solomon, J. Phys. Chem. Lett., 2020, 11(17), 7400–7406 CrossRef CAS PubMed.
- A. Borges, E. D. Fung, F. Ng, L. Venkataraman and G. C. Solomon, J. Phys. Chem. Lett., 2016, 7(23), 4825–4829 CrossRef CAS PubMed.
- H. Löfås, R. Emanuelsson, R. Ahuja, A. Grigoriev and H. Ottosson, J. Phys. Chem. C, 2013, 117(42), 21692–21699 CrossRef.
- M. H. Garner, M. Koerstz, J. H. Jensen and G. C. Solomon, J. Phys. Chem. Lett., 2018, 9(24), 6941–6947 CrossRef CAS.
- R. Emanuelsson, H. Löfås, A. Wallner, D. Nauroozi, J. Baumgartner, C. Marschner, R. Ahuja, S. Ott, A. Grigoriev and H. Ottosson, Chem.–Eur. J., 2014, 20(30), 9304–9311 CrossRef CAS PubMed.
- H. Li, M. H. Garner, Z. Shangguan, Q. Zheng, T. A. Su, M. Neupane, P. Li, A. Velian, M. L. Steigerwald, S. Xiao, C. Nuckolls, G. C. Solomon and L. Venkataraman, Chem. Sci., 2016, 7(9), 5657–5662 RSC.
- A. K. Ismael and C. J. Lambert, J. Mater. Chem. C, 2019, 7(22), 6578–6581 RSC.
- L. Mejía, N. Renaud and I. Franco, J. Phys. Chem. Lett., 2018, 9(4), 745–750 CrossRef PubMed.
- S. A. Paz, M. E. Zoloff Michoff, C. F. A. Negre, J. A. Olmos-Asar, M. M. Mariscal, C. G. Sánchez and E. P. M. Leiva, J. Chem. Theory Comput., 2012, 8(11), 4539–4545 CrossRef CAS PubMed.
- M. Paulsson, C. Krag, T. Frederiksen and M. Brandbyge, Nano Lett., 2009, 9(1), 117–121 CrossRef CAS PubMed.
- S. Martín, F. Giustiniano, W. Haiss, S. J. Higgins, R. J. Whitby and R. J. Nichols, J. Phys. Chem. C, 2009, 113(43), 18884–18890 CrossRef.
- C. Li, I. Pobelov, T. Wandlowski, A. Bagrets, A. Arnold and F. Evers, J. Am. Chem. Soc., 2008, 130(1), 318–326 CrossRef CAS PubMed.
- G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Nat. Chem., 2010, 2(3), 223–228 CrossRef CAS PubMed.
- M. Kamenetska, M. Koentopp, A. C. Whalley, Y. S. Park, M. L. Steigerwald, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Phys. Rev. Lett., 2009, 102(12), 126803 CrossRef CAS PubMed.
- I. Tamblyn, P. Darancet, S. Y. Quek, S. A. Bonev and J. B. Neaton, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(20), 201402 CrossRef.
- T. A. Su, H. Li, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Chem., 2015, 7(3), 215–220 CrossRef CAS PubMed.
- M. Wang, Y. Wang, S. Sanvito and S. Hou, J. Chem. Phys., 2017, 147(5), 054702 CrossRef PubMed.
- G. Cabra, A. Jensen and M. Galperin, J. Chem. Phys., 2018, 148(20), 204103 CrossRef PubMed.
- Y. Xue and M. A. Ratner, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(8), 081404 CrossRef.
- J. Michl and R. West, Acc. Chem. Res., 2000, 33(12), 821–823 CrossRef CAS PubMed.
- A. Borges, J. Xia, S. H. Liu, L. Venkataraman and G. C. Solomon, Nano Lett., 2017, 17(7), 4436–4442 CrossRef CAS PubMed.
- C. Jia, M. Famili, M. Carlotti, Y. Liu, P. Wang, I. M. Grace, Z. Feng, Y. Wang, Z. Zhao, M. Ding, X. Xu, C. Wang, S.-J. Lee, Y. Huang, R. C. Chiechi, C. J. Lambert and X. Duan, Sci. Adv., 2018, 4(10), eaat8237 CrossRef CAS PubMed.
- M. Carlotti, A. Kovalchuk, T. Wächter, X. Qiu, M. Zharnikov and R. C. Chiechi, Nat. Commun., 2016, 7(1), 13904 CrossRef CAS PubMed.
- D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. van der Zant, Nano Lett., 2018, 18(9), 5981–5988 CrossRef CAS PubMed.
- R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8(12), 1099–1104 CrossRef CAS PubMed.
- G. Gryn'ova and C. Corminboeuf, J. Phys. Chem. Lett., 2019, 10(4), 825–830 CrossRef PubMed.
- J. E. Greenwald, J. Cameron, N. J. Findlay, T. Fu, S. Gunasekaran, P. J. Skabara and L. Venkataraman, Nat. Nanotechnol., 2021, 16(3), 313–317 CrossRef CAS PubMed.
- R. Schuster, E. Buks, M. Heiblum, D. Mahalu, V. Umansky and H. Shtrikman, Nature, 1997, 385(6615), 417–420 CrossRef CAS.
- G. Breit and E. Wigner, Phys. Rev., 1936, 49(7), 519–531 CrossRef CAS.
- S. Gunasekaran, J. E. Greenwald and L. Venkataraman, Nano Lett., 2020, 20(4), 2843–2848 CrossRef CAS PubMed.
- B. Xu and N. Tao, Science, 2003, 301(5637), 1221–1223 CrossRef CAS.
- L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2006, 6(3), 458–462 CrossRef CAS.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22(25), 253202 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29(27), 273002 CrossRef PubMed.
- A. Jensen, M. H. Garner and G. C. Solomon, J. Phys. Chem. C, 2019, 123(19), 12042–12051 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: STM-break junction experiment details, conformational analysis, computational details and additional figures. See DOI: 10.1039/d1sc02287c |
| ‡ B. Z. and M. H. G. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |