Computational insight into effective decomposition of NO_X gas pollutants using N-vacancies in graphitic carbon nitride

Abstract

Nitrogen oxide (NO_X) gas pollutants pose severe threats to human health, the ozone layer, and the global climate, and thus finding suitable materials and methods to efficiently remove NO_X has been of great interest for years. By studying the related photocatalysis and surface reactions, we herein propose to use the graphitic carbon nitride (g-CN) film with N-vacancies (g-CN_NV) to decompose NO_X. Based on density functional theory (DFT) and time-dependent DFT calculations, we revealed the decomposition mechanism of NO/NO₂ gas on g-CN_NV. We found that the N–O bond cleavage of NO_X is usually accompanied by the N occupying the N-vacancy and oxygen formation, and subsequent light excitation promotes the oxygen desorption from the g-CN surface through photochemical processes of intersystem crossing and conical intersection. We demonstrated that the g-CN_NV film under illumination can effectively decompose NO_X into harmless oxygen. Therefore, coating the g-CN_NV film on the outer walls of buildings or chimneys may be a promising green and economical strategy for NO_X removal, given that the sunlight and surface defects can synergistically affect the electronic states of adsorbates and facilitate their favorable transformation by gas–solid interaction. This work offers a deep understanding of the fundamental process of surface photocatalytic reactions.

---

Introduction

Nitrogen oxides (NO_X, including about 95% NO and 5% NO₂),¹ as the unavoidable primary pollutants in exhaust gas, are harmful to the human respiratory tract, ozone layer, and atmospheric composition.² Owing to the positive standard Gibbs free energies of formation (Δ_fG^O) of 0.90 eV for NO and 0.53 eV for NO₂ at room temperature and one standard atmospheric pressure,³ their reverse processes (i.e. NO_X decomposition into non-toxic N₂ and O₂) are supposed to be thermodynamically favorable. However, the chemical reaction of NO_X → N₂ + O₂ is very hard to directly achieve experimentally, which may be due to the extremely high barrier that makes it kinetically hard to occur.⁴ Great efforts have been made for over 40 years to efficiently remove NO_X pollutants,^5–8 through selective catalytic reduction (SCR), selective non-catalytic reduction (SNCR), wet scrubbing, electron beam, adsorption method, electrochemical method, non-thermal plasma method (Table S1†), etc. As an SCR method, the NO_X decomposition on the material surface by photocatalytic assistance may be a green and economical strategy since cheap and efficient materials are expected to be screened from extensive and diverse candidates, such as noble metals,⁵ metal oxides,⁶ and carbon-based materials.^7–10

Owing to the advantages of low price, stability, and non-toxicity, carbon-based catalysts have attracted great attention in the field of NO_X removal. To suppress the NO_X emission from charcoal combustion, the solid char bound with nitrogen (char(N)) is often used as a NO-reducing agent.⁷ Many efforts in experiments and calculations have been made to study the possible reaction pathways between NO and char(N).^11–15 It was computationally demonstrated that the heteroatom N distributed on the edge of the char(N) is usually the active site to chemically anchor the NO and reduce the energy barrier of NO reduction to N₂.¹⁴ Since the graphitic carbon nitride (g-CN) material contains N, it was also adopted to study the NO_X removal.^4,16–21 However, direct NO decomposition into N₂ and O₂ on pure g-CN was not observed until the temperature was raised to 450 °C with a low conversion efficiency of 0.6% and 550 °C with a conversion efficiency of 8.9%.¹⁶ Higher temperatures of over 700 °C are expected to effectively decompose NO, but such temperatures are not suitable for the stable existence of g-CN. Computationally, the NO_X is demonstrated to be merely physisorbed on pristine g-CN and a large activation energy (3.62 eV) is required for NO decomposition into N and O radicals on g-CN.¹⁷ Therefore, the catalytic ability of pristine g-CN is not ideal for NO_X removal. The difference in the catalytic abilities between char(N) and pristine g-CN is attributed to their different N amounts. The few N heteroatoms in char(N) play the role of active sites in regulating the electron polarization and energy levels of frontier molecular orbitals, while the large amount of N in pristine g-CN makes the electron distribution so even that it is almost inert to NO_X.

To enhance the catalytic activity of g-CN for NO_X removal, experimental studies have attempted to dope Zn,⁴ Bi,¹⁸ the IIA group of elements (like Mg, Ca, Sr, and Ba),¹⁹ or N defects²⁰ into the pristine g-CN. In these works, the NO_X removal efficiencies have been substantially increased to ∼30–69%, especially for Zn- and Ba-doped g-CN with efficiencies as high as 69.4% and 62%. While the synthesis procedures of doping heteroatoms into g-CN are complicated, the g-CN with N vacancies (g-CN_NV) can be easily synthesized by controlling the annealing temperature and condensation time.^21–23 The N defects were identified as catalytic sites by the in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) technique, which demonstrated the photocatalytic activity of g-CN_NV with a NO removal efficiency of 43.6%, much higher than the 29.9% of pristine g-CN.²⁰ For practical applications, it is very cost-effective to develop such metal-free and easy-to-synthesize g-CN_NV films to be placed outdoors to remove NO_X pollutant gases in the ambient environment.

By far, there is still a lack of direct experimental evidence that NO is indeed decomposed into products of N₂ and O₂,¹⁶ which indicates that the mechanism of NO_X decomposition has not been sufficiently studied. Computational studies based on density functional theory (DFT) can be an ideal approach to provide a molecular-level understanding and demonstrate the chemical reaction mechanism according to experimental observation. For example, Cantatore et al. have used DFT to propose a novel strategy for the catalytic reduction of NO via oligomerization on B-doped graphene, where the energy landscapes showed the channels of NO decomposition into N₂, N₂O, NO₂, and O₂via N₂O₂⁻ and N₃O₃⁻ intermediates.²⁴ Few computational studies of the NO_X decomposition mechanism using g-CN as a catalyst are available, which triggers us to perform a DFT study on the gas–solid interaction between NO_X and g-CN_NV.

In this work, we computationally demonstrate whether the carbonaceous material of g-CN_NV can effectively remove NOx gas pollutants. The NO_X decomposition mechanism on g-CN_NV will be elucidated by carrying out a series of DFT and time-dependent DFT (TD-DFT) calculations. The role of g-CN_NV in the NO_X decomposition will be revealed by showing the energy profiles for the chemical reactions of NO_X with g-CN_NV in the ground and excited states. This work would be of great significance for understanding the strong attractions of N vacancies of g-CN film to NO_X molecules and their fundamental process of photo-assisted decompositions.

Computational methods and models

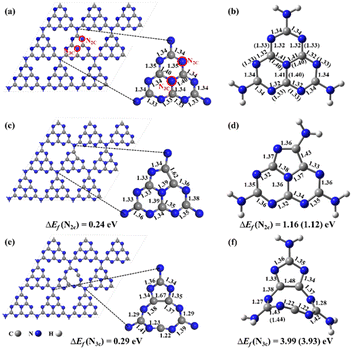
The previous experimental studies proved that g-CN was composed of numerous heptazines (also named tri-s-triazines) with a layered structure using X-ray diffraction patterns and X-ray photoelectron spectroscopy.^22,23 Accordingly, a buckled and single-layered g-CN surface in a supercell of 3 × 3 × 1 (Fig. 1a) was constructed for anchoring the NO_X species.²⁵ To well study the chemical reactions and photochemical properties of NO_X decomposition on the substrate, a cluster model was used, and the structure was cut out from the pristine g-CN and saturated by H atoms, named heptazine (stoichiometry: C₆N₁₀H₆) (Fig. 1b). The N vacancy (NV) can be a missing two-coordinated N atom (N_2C), named g-CN_NV (N_2C) (Fig. 1c) and heptazine_NV (N_2C) (Fig. 1d), and also be a missing three-coordinated N atom (N_3C), named g-CN_NV (N_3C) (Fig. 1e) and heptazine_NV (N_3C) (Fig. 1f).

Fig. 1 The optimized geometries of (a) pristine g-CN and (b) heptazine; (c) g-CN_NV (N_2C) and (d) heptazine_NV (N_2C); (e) g-CN_NV (N_3C) and (f) heptazine_NV (N_3C), with the key bond lengths (unit: Å) and NV formation energy ΔE_f marked. The supercells in a lattice of a = b = 21.03 Å, c = 16.00 Å, and α = β = 90°, γ = 120° were optimized at the level of GGA/PBE. The heptazine-based clusters were optimized by ωB97XD/6-31G(d,p) and ωB97XD/aug-cc-pVDZ. The data shown in brackets are the bond-length or ΔE_f results obtained by ωB97XD/aug-cc-pVDZ only when the results are different from those by ωB97XD/6-31G(d,p).

The simulations of periodic systems in this work were implemented using the Vienna Ab initio Simulation Package (VASP).^26,27 The vacuum layers were set as 15 Å to avoid the slab–image interaction. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional based on the generalized gradient approximation (GGA) is adopted with Grimme's D3 correction to well consider the van der Waals (vdW) interaction between the slab and adsorbents.^28,29 For the plane-wave basis set, the electron–ion interaction is described by the projector augmented wave (PAW) method with a cutoff energy of 450 eV.^30,31 The Monkhorst–Pack grids for k-space were set as 5 × 5 × 1. The forces for reaching equilibria of geometry optimizations were set as less than 0.01 eV Å⁻¹ and the energy convergence criterion was 1.0 × 10⁻⁶ eV per atom. The electron population for adsorbents attached to the surface was analyzed using the Bader charge code.³² To investigate the thermal stability of NV in g-CN_NV film, ab initio molecular dynamics (AIMD) simulation was performed in the NVT ensemble at temperatures of T = 500 K and 700 K for 10 ps with a time step of 2 fs.

All the cluster calculations were conducted on the Gaussian 09 program package.³³ The ωB97XD exchange–correlation functional was employed for geometry optimizations and frequency calculations with the basis set of 6-31G(d,p) or aug-cc-pVDZ. The ωB97XD functional has been frequently employed in many previous g-CN studies.^34–38 Local minima are confirmed without imaginary frequencies and transition states (TS) are confirmed with only one imaginary frequency, followed by the intrinsic reaction coordinate (IRC) calculations to verify that the TS is connected with the desired reactant and product. The charge transfer was analyzed by the natural population analysis (NPA) method.³⁹ TD-ωB97XD/6-31G(d,p) and TD-ωB97XD/aug-cc-pVDZ calculations were performed to study the photochemical properties involved in the NO_X decomposition in excited states. The spatial distributions of photogenerated holes and electrons were analyzed using the Multiwfn Code.⁴⁰

The geometries optimized from supercells and clusters (Fig. 1a–f) are almost the same except for the heavier deformation of heptazine_NV (N_3C) than g-CN_NV (N_3C) due to the nine-membered ring which is strongly buckled in the cluster model. For N_2C vacancy, the stable five-membered ring can be formed in both heptazine_NV (N_2C) and g-CN_NV (N_2C). The bond lengths of the heptazine backbone (Fig. 1b, d, and 1f) calculated with two basis sets of 6-31G(d,p) and aug-cc-pVDZ are very close, which indicates that the cluster structures predicted at the medium level of ωB97XD/6-31G(d,p) are comparable to the high level of ωB97XD/aug-cc-pVDZ.

To compare the thermal stability of the NV between N_2C and N_3C, the formation energy (ΔE_f) is calculated as:

ΔE_f = E_{g-CNNV/heptazineNV} + μ_N − E_{g-CN/heptazine},

where E_{g-CN/heptazine} and E_{g-CNNV/heptazineNV} are the total energies of pristine g-CN (or heptazine) and g-CN_NV (or heptazine_NV), and μ_N stands for the chemical potential of the N atom, i.e. one-half of the total energy of a free N₂ molecule.⁴¹ The ΔE_f of NV at the N_2C position are all smaller than those at N_3C calculated from the periodic supercells and isolated clusters (Fig. 1c–f), which indicates the more stable existence of NV at the N_2C position, consistent with our previous work.²² Hereafter, we only adopt the g-CN_NV(N_2C)/heptazine_NV(N_2C) (simply expressed as g-CN_NV/heptazine_NV) as the calculation model for interacting with NO_X species.

The adsorption energy (ΔE_ads) for NO_X on the substrate is calculated as:

ΔE_ads = E_tot(complex) − E_tot(NOX) − E_{tot(substrate)},

where E_tot(complex), E_tot(NOX), and E_{tot(substrate)} are the total energies of the complex between the substrate and adsorbate, the isolated adsorbate, and the substrate without adsorbate, respectively.^42–44 Negative ΔE_ads indicates that the adsorption structure is thermodynamically stable to form.

To consider the effects of temperature and entropy on the energy profiles of NOx decomposition on the substrate, Gibbs free energy is calculated as ΔG = ΔE + ΔZPE − TΔS.^44,45 ΔG stands for the Gibbs free energy difference, ΔE is the difference of the internal energy between the products and the reactants, and ΔZPE is the change in the zero-point energy and ΔS is the change in the entropy.

Results and discussion

Active N_2C vacancy for NO/NO₂ chemisorption

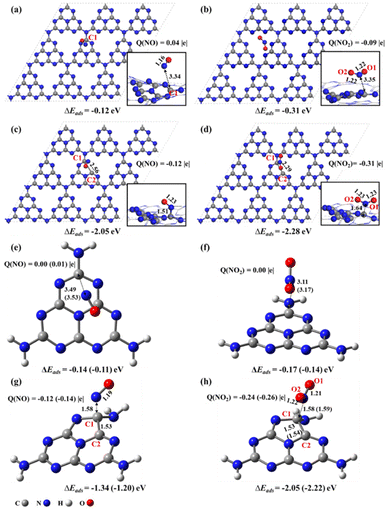
For pristine g-CN in the supercell (Fig. 2a and b), there only exists the physisorption with NO/NO₂, as demonstrated by the long-range distance of 3.43/3.35 Å, small adsorption energies of −0.12/−0.31 eV, and slight charge transfer of less than 0.10 |e| between NO/NO₂ and g-CN, in agreement with a previous study.¹⁷ These data well explain the low catalytic activity of pristine g-CN in the experimental work.¹⁶ By contrast, when there exists an N_2C vacancy in the substrate, chemical bonding between NO/NO₂ and g-CN_NV (Fig. 2c and d) can be formed, as supported by the shorter distance of 1.51/1.64 Å between the N of NO/NO₂ and the substrate C1 atom near the N_2C, stronger adsorption energies of −2.05/−2.28 eV, and significant electron transfer of −0.12/−0.31 |e| from g-CN_NV to NO/NO₂. This indicates that the N_2C vacancy is indeed an active site in the g-CN_NV film for attracting NO_X species, consistent with the previous experimental detection by situ-DRIFTS.²⁰

Fig. 2 Top views and side views (bottom right) of adsorption configurations of (a) NO@g-CN, (b) NO₂@g-CN, (c) NO@g-CN_NV, and (d) NO₂@g-CN_NV by GGA/PBE optimizations. Adsorption configurations of (e) NO@heptazine, (f) NO₂@heptazine, (g) NO@heptazine_NV, and (h) NO₂@heptazine_NV by ωB97XD/6-31G(d,p) and ωB97XD/aug-cc-pVDZ optimizations. The key interatomic distances (unit: Å), charges (Q) on NO/NO₂, and adsorption energies (ΔE_ads) are marked. The data obtained by ωB97XD/aug-cc-pVDZ are labeled in brackets only if the results differ from those by ωB97XD/6-31G(d,p).

The calculated band gap of pristine g-CN is predicted to be 2.82 eV (Fig. S1a†), close to the experimental value of 2.74 eV.²³ When the N_2C vacancy is formed, the valence bands and conduction bands of g-CN_NV (N_2C) both move to lower energy levels and the band gap decreases to 2.52 eV (Fig. S1b†). This indicates that the g-CN_NV with N_2C vacancy is more favourable for the visible-light absorption than pristine g-CN to help convert NO_X pollutants into harmless species.

With the cluster models, the NO/NO₂ attachments on the perfect heptazine (Fig. 2e and f) and heptazine_NV containing N_2C (Fig. 2g and h) are also physisorption and chemisorption between NO/NO₂ and heptazine/heptazine_NV, as confirmed by the N–C1 distances and the charge transfer between the NO/NO₂ and substrates. Consistent with the results based on supercell models, the NO/NO₂ molecule acts as an electron acceptor when reaching the N_2C vacancy. The C1–C2 bond of heptazine_NV is slightly elongated to 1.53/1.53 Å by ωB97XD/6-31G(d,p) and 1.53/1.54 Å by ωB97XD/aug-cc-pVDZ due to the chemical bonding with NO/NO₂. Similar results of cluster systems, compared to those of supercells, indicate that the cluster models instead of periodic ones can describe the NO_X decomposition reactions on g-CN_NV film.

The above results indicate that the g-CN_NV/heptazine_NV containing N_2C vacancy is sensitive to the effective capture of NO_X pollutant gas through gas–solid interaction. The NO_X always has the N atom preferentially pointing towards the substrate, i.e. the N-oriented configuration is energetically lower than the O-oriented one for chemical bonding. This is fundamentally attributed to the favorable orbital matching between the N of NO_X and the substrate. The frontier unoccupied molecular orbitals (MO) of NO/NO₂ (Fig. S2a and b†) show that due to the significant orbital distribution on N, which is more than that on O, N is the more active site to form covalent bonds with the substrate. In addition, the frontier occupied MO of heptazine_NV (Fig. S2c†) shows that the orbital is localized on the C1–C2 bond near the N_2C vacancy (i.e. α-state HOMO), but basically uniformly distributes on the C₃N₃-rings of heptazine (Fig. S2d†), reflecting that the pristine g-CN is inert while the g-CN_NV containing N_2C vacancy is active to adsorbents.

NO decomposition catalyzed by the N_2C vacancy

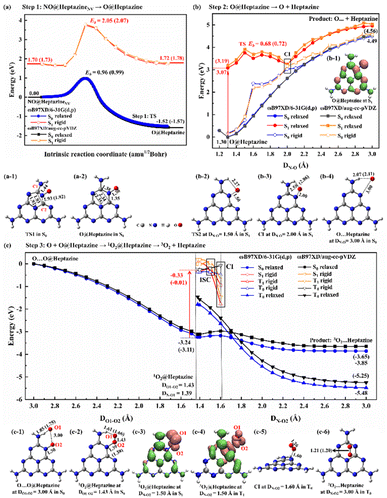
The NO decomposition catalyzed by N_2C vacancy undergoes three steps, starting from the NO@heptazine_NV configuration (Fig. 2g). Step 1 (Fig. 3a) is the N-intercalation into heptazine_NV to leave the O chemically attached to heptazine (i.e. O@heptazine) in the ground state (S₀). Step 2 (Fig. 3b) is the O-detachment from heptazine in the first singlet excited state (S₁) under illumination. And step 3 (Fig. 3c) is the combination of the detached O with the remaining O@heptazine to eventually form triplet O₂ (³O₂) by photo assistance. The following discussion focusing on the DFT-calculated energy profiles will demonstrate that the overall reaction NO + heptazine_NV → ³O₂ + heptazine is feasible.

Fig. 3 The DFT-calculated energy profiles of (a) step 1: N of NO intercalation into heptazineNV in S₀ and S₁ states with the (a-1) TS1 and (a-2) O@heptazine in S₀; (b) step 2: O-desorption from heptazine in S₀ and S₁, with the (b-1) spatial distribution of the photo-induced hole (pink) and electron (green) (isovalue = 0.002 a.u.) of O@heptazine in S1, (b-2) TS2 at the N–O distance of NO (D_N–O) = 1.50 Å in S₁, (b-3) approximate CI-point at D_N–O = 2.00 Å in S₁, and (b-4) O⋯heptazine at D_N–O = 3.00 Å in S₀; and (c) step 3: the combination of the hydrogen-bonding O with O@heptazine to release triplet ³O₂ under illumination, with the (c-1) O⋯O@heptazine at D_O1–O2 = 3.00 Å in S₀, (c-2) ¹O₂@heptazine at D_O1–O2 = 1.43 Å in S₀, spatial distribution of the photo-induced hole (pink) and electron (green) (isovalue = 0.002 a.u.) at D_N–O2 = 1.50 Å in (c-3) S₁ and (c-4) T₁, (c-5) approximate CI-point at D_N–O2 = 1.60 Å in T0, and (c-6) ³O₂⋯heptazine at D_N–O2 = 3.00 Å in T₀. The filled symbols refer to the relaxed scanning (i.e. constrained optimizations) by manually fixing the D_N–O as 1.20–3.00 Å, D_O1–O2 as 3.00–1.43 Å, or D_N–O2 as 1.38–3.00 Å, while hollow symbols refer to the rigid scanning (i.e. single-point energy calculations) based on the optimized geometries. The key energies E (unit: eV) and interatomic distances (unit: Å) are marked. The data obtained by ωB97XD/aug-cc-pVDZ are labeled in brackets only if the results differ from those by ωB97XD/6-31G(d,p).

For step 1, when the N of NO is chemically bound with the C1 atom of heptazine_NV, the C1–C2 bond will be stretched until broken, and meanwhile, the C2 atom will attract the N atom of NO to form a new bond, so that the N (of NO) can be inserted into the middle of C1 and C2 to form a new conjugated bond of C1=N–C2 and heptazine_NV becomes a perfect heptazine. In the TS1 structure (Fig. 3a-1), the distance of C1–C2 (D_C1–C2) is enlarged to 1.93/1.92 Å and that of C2–N (D_C2–N) is shortened to 1.93/1.92 Å, until the O of NO bonds with the perfect heptazine cluster, i.e. O@heptazine (Fig. 3a-2) with 2.34/2.35 Å for D_C1–C2 and 1.35 Å for D_C2–N by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ. More details on the geometry transformation of N-intercalation into heptazine_NV can be clearly supported by the distance evolutions of D_C1–C2, D_C1–N, D_C2–N, and D_N–O extracted from the IRC calculations (Fig. S3a and b†), which present the C1–C2 bond cleavage, C1=N–C2 bond formation, and eventually O (of NO) chemisorbed on heptazine.

The energy barrier (E_b) and the reaction energy for step 1 in S₀ are estimated to be 0.96/0.99 eV and −1.52/−1.57 eV by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ. The small energy barrier and exothermic reaction energy indicate that the N-intercalation of NO into heptazine_NV easily proceeds in S₀. To demonstrate that step 1 occurs preferentially in S₀, we also calculated the potential energy surfaces (PES) in S₁ for comparison, by taking representative points from the IRC curve in S₀ and performing TD-DFT single-point energy calculations in S₁. The almost parallel S₀- and S₁-PES indicate the impossibility of conical intersection (CI) from S₁ decay to S₀ states. The higher energy barrier (2.05/2.07 eV) and endothermic reaction heat (0.02/0.05 eV) in S₁ predicted by TD-ωB97XD/6-31G(d,p) or TD-ωB97XD/aug-cc-pVDZ confirm that step 1 prefers S₀ to S₁ to occur. Therefore, the N_2C vacancy contained in g-CN_NV can effectively trap the N atom of NO at room temperature without illumination.

For step 2, the desorption of the O atom from heptazine must be accomplished with light assistance to overcome the endothermic energy generated by the O–N bond cleavage. In S₀, the D_N–O elongation based on O@heptazine corresponds to an energy profile of a nearly linear lifting until a high plateau; the spontaneous O-detachment from heptazine is thus not going to happen at room temperature. To avoid climbing the uphill slope of PES in S₀, illumination can be used to change the chemical reaction route. The calculated UV-vis spectra (Fig. S3c and d†) of O@heptazine show that the most significant absorption peaks appear at ∼205 nm with a vertical excitation energy of ∼6 eV, belonging to the near UV region of sunlight. As the high excited-state always quickly decays to the S₁ according to Kasha's rule,⁴⁶ the photo-induced hole and electron distributions of O@heptazine in S₁ are presented (Fig. 3b-1). It is found that both the O and N of NO carry positively charged holes upon UV-light irradiation, demonstrating the existence of Coulomb repulsion between them, which is favorable for the O-detachment from heptazine in S₁.

The S₁-PES by a relaxed scanning of TD-DFT shows that the N–O bond breaking of O@heptazine undergoes a very low energy barrier of ∼0.7 eV that is easy to overcome. The TS2 structure in S₁ (Fig. 3b-2) appears at D_N–O = 1.50 Å, which shows the breaking of the N–O bond and the formation of the N–H⋯O hydrogen bond. With the O atom moving away from heptazine, the PES in S₁ and S₀ states (i.e. the curves with filled symbols) approach each other, indicating a high possibility of CI. This conjecture is further supported by the S₀-PES (with hollow symbols) through the rigid scanning using the relaxed S₁-geometries, which is much closer to the S₁-PES. The approximate CI point (Fig. 3b-3) is probably located at D_N–O = 2.00 Å, where the N–O bond is basically broken while the N–H⋯O hydrogen bond still exists. After the decay from S₁ to S₀ states, the O-desorption process corresponds to a slow uphill slope of S₀-PES, which is mainly dominated by the continuous vanishing of the O–N bond. It is noted that the N–H⋯O hydrogen bond is forming, with the length changing from 2.58/2.86 Å in CI at D_N–O = 2.00 Å (Fig. 3b-3) to 2.07/2.11 Å in product O⋯heptazine at D_N–O = 3.00 Å (Fig. 3b-4). This is reasonable because the surface edge is usually active for binding with external species. In step 2, the photochemical process plays an important role in helping the O-desorption from the surface to avoid walking along the long and steep uphill of PES in S₀ and reach the final platform as close as possible.

Fig. 4 The DFT-calculated energy profiles of (a) step 1: chemisorption isomerization of NO₂@heptazine_NV from N-linked to O-linked, with TS1 at D_O1–C1 = 2.14 Å and O-linked-NO₂@heptazine_NV at D_O1–C1 = 1.44 Å in S₀; (b) step 2: N-intercalation of NO₂ into the heptazine_NV by IRC calculations, with the (b-1) TS2-1, (b-2) IM, (b-3) TS2-2, and (b-4) 2O@heptazine in S₀; (c) step 3: singlet ¹O₂ formation on heptazine by IRC calculations, with the TS3 in S₀. The energy barrier E_b (unit: eV) and key interatomic distances (unit: Å) are marked. The data obtained by ωB97XD/aug-cc-pVDZ are labeled in brackets only if the results differ from those by ωB97XD/6-31G(d,p).

In step 3 (Fig. 3c), if the O escapes from binding with the N of heptazine to form a free O atom, it will probably combine with other remaining O@heptazine to form a noncovalent interaction configuration, O⋯O@heptazine (Fig. 3c-1), and finally release oxygen gas under illumination. Step 3 is actually the reaction between the O@heptazine produced in step 1 and the free O atom produced in step 2. Starting from the O⋯O@heptazine configuration (Fig. 3c-1), where O1 forms a hydrogen bond with the H at the edge of heptazine while O2 covalently binds with heptazine, accompanied with the O1 and O2 distance (D_O1–O2) of 3.00 Å, the S₀-PES shows a smooth decrease with D_O1–O2 in the range of 3.00–1.43 Å. The significant energy decrease of 3.24/3.11 eV through a relaxed scanning of ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ is mainly due to the formation of the singlet O₂ (¹O₂) on heptazine, i.e.¹O₂@heptazine (Fig. 3c-2).

However, the triplet O₂ (³O₂) is the final stable state in the atmosphere, thus the multiplicity conversion of oxygen gas from singlet to triplet is supposed to be achieved by photo-assistance.⁴⁷ Starting from ¹O₂@heptazine, we first performed the relaxed PES scanning in both S₀ and T₀ states by manually fixing the D_N–O2 in the range of 1.40–3.00 Å. The turning point of PES trends in S₀ and T₀ appears at D_N–O2 = 1.70 Å, after which the ³O₂ is more stable on heptazine than ¹O₂, consistent with a natural phenomenon. The diverse intersystem crossing (ISC) should occur before D_N–O2 = 1.70 Å. We thus compared the energies in S₁ or T₁ states at D_N–O2 = 1.40, 1.50, and 1.60 Å by relaxed or rigid scanning (Table S2†). Based on ¹O₂@heptazine, the calculated UV-Vis spectra (Fig. S3e and f†) show that ¹O₂@heptazine at D_N–O2 = 1.40 Å can absorb near-UV light sensitively and then quickly decay to the S₁ state. Because the S₁ energy is lower than T₁ at D_N–O2 = 1.40 Å while it is reversed at D_N–O2 = 1.50 Å, the system is supposed to converse the spin state from the S₁ to T₁ states through the ISC during D_N–O2 = 1.40–1.50 Å.⁴⁷ Distinct from the S₁-state photoinduced carrier distribution at D_N–O2 = 1.50 Å (Fig. 3c-3), when the system reaches the T₁ state, a significant coulombic repulsion occurs between O₂ and heptazine in the T₁-state (Fig. 3c-4). This demonstrates that the ISC from S₁ to T₁ states will greatly promote the release of the ³O₂ from heptazine. The energy order reversal between T₁ and T₀ states at D_N–O2 = 1.50 and 1.60 Å shows that the CI point (Fig. 3c-5) is probably located at D_N–O2 = 1.50–1.60 Å, after which the system will decay back to the ground state. Notably, unlike the rising outline of the S₀-PES for O leaving heptazine (Fig. 3b), the T₀-PES (Fig. 3c) shows a descending trend when ³O₂ is getting away from heptazine. We attribute this difference to the formation of the strong chemical bond in ³O₂, which has a more significant effect on the T₀-PES than the N–O bond cleavage. For example, the bond order (BO) in ³O₂ when D_N–O2 = 1.60 Å is calculated to be 1.64 by ωB97XD/6-31G(d,p), while it increased to 1.85 when D_N–O2 = 3.00 Å. Overall, the surface photocatalysis in step 3 plays an important role in driving the system to undergo the electronic-state transitions of S₀ → S₁₇/S₁₂ → S₁ → T₁ → T₀, so that the ³O₂ molecule eventually detaches from heptazine smoothly (Fig. 3c-6).

Fig. 5 Gibbs free energy profiles of (a) NO and (b) NO₂ decompositions on heptazine_NV at T = 300 K and P = 1.00 atm by ωB97XD/6-31G(d,p) calculations. The free energy values relative to the initial reactants of NO/NO₂ and heptazine_NV are labelled to indicate the barrier (G_b) and change (ΔG) for each step.

NO₂ decomposition catalyzed by the N_2C vacancy

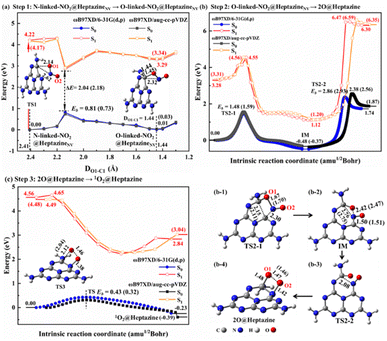
Although NO₂ is a minor NO_X pollutant gas, it is more toxic than NO and can react with water to form harmful HNO₃, HNO₂, and NO, and thus it is also very necessary to study its removal. In this work, we theoretically propose that the NO₂ decomposition process catalyzed by N_2C vacancy would go through four steps, i.e. step 1: thermal isomerization (Fig. 4a), step 2: N-intercalation (Fig. 4b), step 3: ¹O₂ formation (Fig. 4c), and step 4: photo-assisted ³O₂ release.

To facilitate the N-intercalation into heptazine_NV, NO₂@heptazine_NV (Fig. 2h) needs first to form a favorable stereo-structure, which can be achieved by thermal isomerization from N-linked to O-linked-NO₂@heptazine_NV configurations (Fig. 4a). The isomerization process corresponds to a low energy barrier (E_b) of 0.81/0.73 eV for TS1 and a small energy increase of 0.01/0.03 eV for O-linked-NO₂@heptazine_NV, as predicted by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ in S₀. This indicates that the ambient NO₂ gas can be flexibly chemisorbed on heptazine_NVvia N-linkage or O-linkage under slight temperature fluctuations. Besides, the chemisorption isomerization prefers to occur in S₀, as the PES in S₁ is far from that in S₀ with a large energy difference of over 2 eV between their closest points.

For step 2, the N-intercalation of NO₂ into heptazine_NV is accompanied by the N_2C vacancy filled with N of NO₂ and two O of NO₂ chemisorbed on heptazine, i.e. 2O@heptazine. The energy profiles by IRC calculations (Fig. 4b) show that this process will undergo two TSs with the energy barriers of 1.48/1.59 eV for TS2-1 and 2.86/2.93 eV for TS2-2, and two local minima with the energy decrease of −0.48/−0.37 eV for the intermediate (IM) and energy increase of 2.22/2.24 eV for 2O@heptazine, as predicted by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ in S₀. This indicates that the chemical reaction from O-linked-NO₂@heptazine_NV to IM is easier and faster than that from IM to 2O@heptazine. In TS2-1, when the O1 of the NO₂ molecule is bound to the C1 atom of heptazine_NV, the C1–C2 and O1–N bonds are significantly enlarged to 2.15/2.11 and 1.67/1.70 Å, and simultaneously the N–C2 bond is formed. The O1–N distance of 2.42/2.47 Å in IM indicates that the NO₂ molecule is totally decomposed. In TS2-2, after the N is bound with C2, the N is trying to reach the C1 atom to form the conjugated C1=N–C2 bond. However, the steric effect from structural deformation and Coulomb repulsion from negatively charged O1 strongly hinder the N atom from approaching C1, thus resulting in a higher barrier and a larger endothermic reaction energy. Hence, from O-linked-NO₂@heptazine_NV to 2O@heptazine, the N atom binding with the C1 atom is a rate-determining reaction. The other distance evolutions of D_C1–C2, D_C1–N, D_C2–N, and D_O1–N extracted from IRC calculations (Fig. S4a–d†) clearly support the breaking of the C1–C2 bond, formation of the C1=N–C2 bond, and chemical bonding of O1 and O2 with the C1 and C2 atoms of heptazine. In addition, to demonstrate that step 2 prefers to occur in S₀, the IRC curves in S₁ are calculated by extracting representative points from IRC curves in S₀. The almost parallel curves between the S₁ and S₀ states show the absence of CI points; therefore, it is not necessary to use sunlight to force the N-intercalation of NO₂ into heptazine_NV.

For step 3, the reaction from 2O@heptazine to ¹O₂@heptazine is also favorable to proceed in S₀ owing to the non-crossed PES between the S₀ and S₁ states (Fig. 4c). In TS3, the O1 atom leaves the C1 atom for combining with the O2 atom to form a ¹O₂ molecule, which will link with heptazine through the N–O2 bond, named ¹O₂@heptazine. The energy barrier for TS3 is predicted to be 0.43 or 0.32 eV by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ, which is easy to overcome at room temperature. The distance evolutions of D_C1–O1, D_N–O2, and D_O1–O2 extracted from IRC calculations (Fig. S4e and f†) clearly support the breaking of the C1–O1 bond and the stable attachment of the ¹O₂ to heptazine by the N–O2 bond.

For the last step 4, the oxygen gas should also be converted from singlet to triplet through photo-assisted ISC for a final release from heptazine. This step is exactly the same as the second half of step 3 during NO decomposition, referring to the PES as a function of D_N–O2 (Fig. 3c). Thus, the results and discussion about step 4 of NO₂ decomposition are omitted.

NO/NO₂ decomposition catalyzed by the N_2C vacancy at T = 300 K and P = 1.00 atm

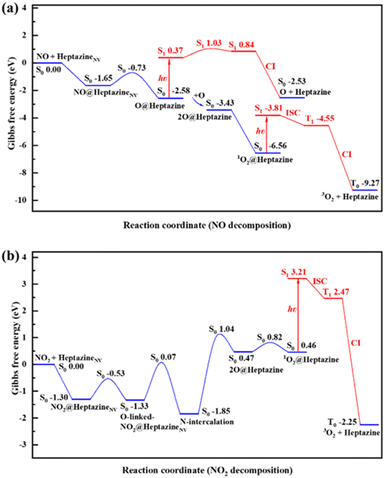
The aforementioned energy profiles merely reflect the change of potential energies in the NO/NO₂ decomposition process.

To consider the effects of temperature and entropy increase on the NO/NO₂ decomposition on heptazine_NV, the Gibbs free energy barrier (G_b) and the change (ΔG) of each step were additionally calculated at room temperature, T = 300 K (Fig. 5), and a higher temperature, T = 500 K, with ambient pressure P = 1.00 atm (Fig. S5†).⁴⁸ Notably, because of the ignorable difference in calculated results of energy profiles between ωB97XD/6-31G(d,p) and ωB97XD/aug-cc-pVDZ, we hereafter only calculated the Gibbs free energies at the level of ωB97XD/6-31G(d,p).

In summary, the NO/NO₂ decomposition mechanism on heptazine_NV is as follows:

and involves surface chemisorptions and reactions in the ground state, and light-driven desorption from the surface in the excited states.

For NO decomposition at 300 K (Fig. 5a), from reactants of NO and heptazine_NV to NO@heptazine_NV, and then to O@heptazine, the exothermic free energies (ΔG = −1.65 and −0.93 eV) and mild barrier (G_b = 0.92 eV) indicate that NO can be easily captured by the N_2C vacancy of heptazine_NV. Compared with the favorable N-intercalation of NO into heptazine_NV, the subsequent O-desorption from heptazine (i.e. O@heptazine → O + heptazine) becomes unfavorable to occur in the S₀ state, which is an endothermic reaction. The free energy difference between O@heptazine and products of O and heptazine in S₀ is calculated to be ΔG = 0.05 eV. But under illumination, the O@heptazine will be first photoexcited (ΔG = 2.95 eV), then go through a free energy barrier (G_b = 0.66 eV) in S₁, and finally decay back to the products of O and heptazine in S₀ through a CI point. And the ΔG decreased to −2.16 eV through photo assistance.

It becomes favorable for the reaction to spontaneously occur in the ambient atmosphere, since light irradiation can alleviate the difficulty of O-desorption. Hence, the room temperature environment exposed to sunlight might promote the release of O from heptazine.

Once O becomes free from heptazine, it will combine with the remaining O@heptazine to form ¹O₂ on heptazine with a free energy decrease (ΔG = −0.85 eV), which is a spontaneous reaction at room temperature. Although the subsequent process from ¹O₂@heptazine to ³O₂ release from heptazine is also spontaneous (ΔG = −2.71 eV), the different electron spin means that it must undergo photoexcitation (ΔG = 2.75 eV), ISC from S₁ to T₁ (ΔG = −0.74 eV), and decay from T₁ to T₀ through CI (ΔG = −4.72 eV) to be successful. The photoexcitation can be continuously provided by sunlight, which can thus ensure the smooth release of ³O₂ from heptazine. Overall, the rate-determining step for NO decomposition on heptazine_NV is the N-intercalation of NO into heptazine_NV with a mild energy barrier.

For NO₂ decomposition (Fig. 5b), the process from reactants of NO₂ and heptazine_NV to the N-intercalation phase is spontaneous with the negative ΔG = −1.30, −0.03, −0.52 eV and mild barriers of G_b = 0.77, 1.40 eV. However, the later process towards 2O@heptazine is relatively difficult to occur due to the large barrier of G_b = 2.89 eV and endothermic free energy of ΔG = 2.32 eV. The following processes from 2O@heptazine to ¹O₂@heptazine (small barrier of G_b = 0.35 eV) and from ¹O₂@heptazine to ³O₂@heptazine (the same as that in NO decomposition) can occur smoothly.

At a higher temperature of T = 500 K (Fig. S5 and Table S3†), the adsorption free energy of NO/NO₂ on heptazine_NV becomes less exothermic, i.e. from −1.65 to −1.30 eV for NO and from −1.30 to −0.88 eV for NO₂, which may be attributed to the higher temperature accelerating molecular vibrations while increasing the detachment possibility of gas species on the solid substrate. In particular, the free energy barriers for NO₂ decomposition on heptazine_NV at T = 500 K are all lifted relative to those at T = 300 K, which indicates that the increase in temperature cannot facilitate the NO₂ decomposition by g-CN_NV film. Meanwhile, the temperature effect on the Gibbs free energy changes and barriers for NO decomposition reactions is much less than that for NO₂ decomposition. The room-temperature environment where the g-CN_NV film is applied may be as favorable as higher temperatures for NO removal.

Notably, once the N vacancy of g-CN_NV is occupied by the N of NO_X, the g-CN_NV film will turn into pristine g-CN and lose the activity for the decomposition of NO_X gas pollutants. Therefore, the g-CN_NV film in practical applications needs to be refreshed regularly through post-annealing treatment to recover the surface reactivity and photocatalytic activity for NOx removal. Note that, by post-annealing the pristine g-CN film at 400 °C with constant N₂ flow, some N atoms can be removed from the tri-s-triazine network to form the C=C bonds.²²

In addition, it is demonstrated that the N_2C vacancy in g-CN_NV film can be well maintained even at higher temperatures. By performing AIMD simulations at T = 500 K and 700 K, the total energies of g-CN_NV (N_2C) keep fluctuating toward stable values (Fig. S6a and b†) and meanwhile there are no significant conformational changes in g-CN_NV (N_2C) during the 10 ps simulations.

Last, it is known that CO or SO₂ in pollutants may poison the catalyst surface and reduce the activity.⁴¹ Therefore, we also tested the adsorptions of common pollutants CO and SO₂ on the surface of g-CN_NV (N_2C). It is found that the CO and SO₂ molecules are just weakly adsorbed on the g-CN_NV (N_2C) surface with much smaller adsorption energies of −0.12 eV (Fig. S6c†) and −0.28 eV (Fig. S6d†) than those of NO (−2.05 eV, Fig. 2c) and NO₂ (−2.28 eV, Fig. 2d). The charge transfer between CO/SO₂ and the surface is almost negligible (less than 0.01e). It is thus demonstrated that the g-CN_NV catalyst is excellent for resisting CO and SO₂ poisoning.

Conclusions

To reduce the emission of NO_X gas pollutants in human production and life, here we propose a green strategy for NO_X removal utilizing the g-CN film containing N vacancies (g-CN_NV). Our computational results show that the g-CN_NV surface can act as a photocatalyst and reactant to synergistically promote the NO/NO₂ decomposition into triplet ³O₂, while the N of NO/NO₂ occupies the N vacancy. The NO/NO₂ decomposition on g-CN_NV film undergoes multiple steps including chemisorption, N intercalation, singlet ¹O₂ formation, and triplet ³O₂ release. Among them, the N-intercalation of NO into g-CN_NV during NO decomposition and chemisorption of two O atoms on g-CN during NO₂ decomposition are their respective rate-determining steps. N vacancies play a key role in trapping NO_X on the surface and subsequently forming favorable configurations for NO_X decomposition. The illumination can help overcome the high barrier in the ground state, achieve intersystem conversion for O₂ molecules from singlet to triplet states, and decay from the excited to ground states through the CI point. The influence of temperature in the process of NO decomposition by g-CN_NV film is smaller than that of NO₂. This work offers a deep understanding of the reaction mechanism of surface photocatalysis for NO_X removal and also a promising strategy for solving practical problems in which coating a well-polymerized g-CN film with adjustable N vacancies (i.e. C-rich g-CN) on the outer walls of buildings or chimneys may be effective for NO_X removal under sunlight irradiation.

Author contributions

Y. W. Yang: methodology, data curation, and writing – original draft. Y. L. Zhao: methodology, writing – review & editing. R. Q. Zhang: funding, computational resources, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the financial support from the Environment and Conservation Fund of Hong Kong (43/2021) and Shenzhen Natural Science Foundation (JCYJ20190813164801693). This work was carried out using the computational facilities, CityU Burgundy, managed and provided by the Computing Services Centre at the City University of Hong Kong (https://www.cityu.edu.hk/).

References

1. Z. Que, X. Ai and S. Wu, Int. J. Miner., Metall. Mater., 2021, 28, 1453–1461.
2. M. V. Twigg, Appl. Catal., B, 2007, 70, 2–15.
3. NIST-JANAF Thermochemical Tables, https://janaf.nist.gov/.
4. J. Zhu, Y. Wei, W. Chen, Z. Zhao and A. Thomas, Chem. Commun., 2010, 46, 6965–6967.
5. B.-s. Tu, W. Sun, Y.-j. Xue, W. Q. Zaman, L.-m. Cao and J. Yang, ACS Sustainable Chem. Eng., 2017, 5, 5200–5207.
6. C. M. Kalamaras, G. G. Olympiou, V. I. Pârvulescu and B. Cojocaru, Appl. Catal., B, 2017, 206, 308–318.
7. F. Guo, M. J. Jensen, L. L. Baxter and W. C. Hecker, Energy Fuels, 2014, 28, 4762–4768.
8. J. Yang, S. Yuan, S. Wang, M. Yang, B. Shen, Q. Zhang, Z. Zhang, F. Wang, L. Xu and Z. Wang, Energy Fuels, 2020, 34, 8726–8731.
9. K. Feng, Y. Hu and T. Cao, Fuel, 2022, 316, 123148.
10. J. Yang, L. Chen, S. Yuan, M. Yang, Y. Huang, J. Su, Z. Zhang, Z. Wang, L. Xu and B. Shen, J. Phys. Chem. C, 2021, 125, 24381–24395.
11. Y.-F. Chen, S. Su, Y.-W. Song, T. Liu, Z.-H. Wang, T. Shu, M.-X. Qing, Y. Wang, S. Hu and Z.-X. Zhang, et al. , Combust. Flame, 2022, 237, 111823.
12. H. Zhang, X. Jiang and J. Liu, Combust. Flame, 2020, 220, 107–118.
13. H. Zhang, J. Liu, J. Shen and X. Jiang, Energy, 2015, 82, 312–321.
14. J. Yang, L. Chen, J. Su, Y. Huang, M. Zhang, M. Gao, M. Yang, S. Yuan, X. Wang and B. Shen, Fuel, 2022, 321, 124065.
15. M. Dong, H. Wang, L. Xu, Y. Zou, B. Shen, X. Wang and J. Yang, J. Phys. Chem. A, 2022, 126, 6148–6159.
16. M. Vennewald, A. Iemhoff, D. Ditz and R. Palkovits, Catal. Sci. Technol., 2022, 12, 1741–1745.
17. Y. Ren, Q. Han, Y. Zhao, H. Wen and Z. Jiang, J. Hazard. Mater., 2021, 404, 124153.
18. G. Jiang, X. Li, M. Lan, T. Shen, X. Lv, F. Dong and S. Zhang, Appl. Catal., B, 2017, 205, 532–540.
19. M. Zhou, G. Dong, J. Ma, F. Dong, C. Wang and J. Sun, Appl. Catal., B, 2020, 273, 119007.
20. J. Cao, J. Zhang, X. Dong, H. Fu, X. Zhang, X. Lv, Y. Li and G. Jiang, Appl. Catal., B, 2019, 249, 266–274.
21. P. Niu, L. C. Yin, Y. Q. Yang, G. Liu and H. M. Chen, Adv. Mater., 2014, 26, 8046–8052.
22. J. Bian, L. Xi, J. Li, Z. Xiong, C. Huang, K. M. Lange, J. Tang, M. Shalom and R. Q. Zhang, Chem. J., 2017, 12, 1005–1012.
23. P. Niu, G. Liu and H.-M. Cheng, J. Phys. Chem. C, 2012, 116, 11013–11018.
24. V. Cantatore and I. Panas, J. Chem. Phys., 2016, 144, 151102.
25. Y. Yang, C. Yin, K. Li, H. Tang, Y. Wang and Z. Wu, J. Electrochem. Soc., 2019, 166, F755–F759.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
30. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
31. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
32. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens.Matter, 2009, 21, 084204.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, 2013.
34. J. Ehrmaier, X. Huang, E. J. Rabe, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2020, 124, 3698–3710.
35. J. Ehrmaier, T. N. V. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754–4764.
36. X. Huang and W. Domcke, J. Phys. Chem. A, 2021, 125, 9917–9931.
37. N. Ullah, S. Chen, Y. Zhao and R. Zhang, J. Phys. Chem. Lett., 2019, 10, 4310–4316.
38. N. Ullah, S. Chen and R. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 23090–23095.
39. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
40. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
41. Y. Yang, K. Li, Y. Meng, Y. Wang and Z. Wu, New J. Chem., 2018, 42, 6873–6879.
42. Y. Meng, X. Qu, K. Li, Y. Yang, Y. Wang and Z. Wu, J. Phys. Chem. C, 2019, 123, 5176–5187.
43. N. Wang, Y. Yang, Y. Wang, K. Li and Z. Wu, Results in Surfaces and Interfaces, 2022, 7, 100055.
44. Y. Meng, K. Li, Y. Yang, Y. Wang and Z. Wu, J. Electrochem. Soc., 2018, 165, F145–F151.
45. T. Lu and Q. Chen, Comput. Theor. Chem., 2021, 1200, 113249.
46. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.
47. M. Kasha, Acta Phys. Pol., A, 1999, 95, 15–36.
48. S. Liu, L. Cheng, K. Li, Y. Wang, Y. Yang and Z. Wu, J. Mol. Graphics Modell., 2018, 80, 293–298.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05872g

---