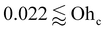Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stood-up drop to determine receding contact angles
Diego
Díaz†
a,
Aman
Bhargava†
 b,
Franziska
Walz
c,
Azadeh
Sharifi
c,
Sajjad
Summaly
c,
Rüdiger
Berger
b,
Franziska
Walz
c,
Azadeh
Sharifi
c,
Sajjad
Summaly
c,
Rüdiger
Berger
 c,
Michael
Kappl
c,
Michael
Kappl
 c,
Hans-Jürgen
Butt
c,
Hans-Jürgen
Butt
 c,
Detlef
Lohse
c,
Detlef
Lohse
 be,
Thomas
Willers
*d,
Vatsal
Sanjay
be,
Thomas
Willers
*d,
Vatsal
Sanjay
 *bf and
Doris
Vollmer
*bf and
Doris
Vollmer
 *c
*c
aDept. of Engineering Mechanics, KTH Royal Institute of Technology, 100 44 Stockholm, Sweden
bPhysics of Fluids Department, Max Planck Center Twente for Complex Fluid Dynamics, Department of Science and Technology, University of Twente, P.O. Box 217, Enschede 7500 AE, Netherlands. E-mail: vatsal.sanjay@comphy-lab.org
cMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: vollmerd@mpip-mainz.mpg.de
dKRÜSS GmBH, Wissenschaftliche Laborgeräte, Borsteler Chaussee 85, 22453 Hamburg, Germany. E-mail: T.Willers@kruss.de
eMax Planck Institute for Dynamics and Self-Organisation, Am Fassberg 17, 37077 Göttingen, Germany
fCoMPhy Lab, Science Laboratories, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
First published on 5th December 2025
Abstract
The wetting behavior of drops on natural and industrial surfaces is determined by the advancing and receding contact angles. They are commonly measured by the sessile drop technique, also called goniometry, which doses liquid through a solid needle. Consequently, this method requires substantial drop volumes, long contact times, tends to be user-dependent, and is difficult to automate. Here, we propose the stood-up drop (SUD) technique as an alternative to measure receding contact angles. The method consists of depositing a liquid drop on a surface by a short liquid jet, at which it spreads radially forming a pancake-shaped film. Then the liquid retracts, forming a spherical cap drop shape (stood-up drop). At this quasi-equilibrium state, the contact angle (θSUD) closely resembles the receding contact angle measured by goniometry. Our method is suitable for a wide variety of surfaces from hydrophilic to hydrophobic, overcoming typical complications of goniometry such as needle-induced distortion of the drop shape, and it reduces user dependence. We delineate when the receding contact angle can be obtained by the stood-up method using volume-of-fluid (VoF) simulations that systematically vary viscosity, contact angle, and deposited drop volume. Finally, we provide simple scaling criteria to predict when the stood-up drop technique works.
1 Introduction
Wetting1 is ubiquitous in nature and technology, shaping phenomena such as drops rolling off plant leaves, animal skin, and insect wings, as well as applications including inkjet printing,2 coatings,3 forensics,4 disease detection,5 and DNA analysis.6 Surface wettability is characterized by measuring contact angles. Primarily, three types of contact angles exist: Young–Dupré's (equilibrium) contact angle, θY, advancing contact angle, θa, and receding contact angle, θr. Despite their relevance, measuring the different contact angles still remains challenging, in particular measuring θr due to distortions of the drop shape by the needle. Therefore, a needle-free methood to measure the receding contact angle would be desired.At thermodynamic equilibrium, a stationary drop on a solid adopts θY owing to the interfacial tension balance at the three phase contact line and follows Young–Dupré's equation:7
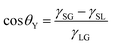 | (1) |
When the three-phase contact line moves, advancing of the liquid front yields θa, whereas retraction over an already wetted region yields θr. Both angles are affected by surface properties such as roughness and chemical heterogeneity,13 surface adaptation,14 and slide electrification.15 In practice, contact angles of resting drops lie within [θr, θa]; these bounds characterize wetting (θa) and de-wetting (θr) behavior on a given surface. The receding angle is indispensable for modeling drop removal. For example, the pull-off force per unit length is γLG(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θr).16,17 Lower θr promotes residual drops during withdrawal (θr < 90°), and θr correlates with practical adhesion in anti-icing18,19 and anti-biofouling20,21 applications. Moreover, θr predicts instabilities of receding lines, the occurrence and duration of rebound,22 and drop–surface friction,23 making it central to drop dynamics on solids.23–26
θr).16,17 Lower θr promotes residual drops during withdrawal (θr < 90°), and θr correlates with practical adhesion in anti-icing18,19 and anti-biofouling20,21 applications. Moreover, θr predicts instabilities of receding lines, the occurrence and duration of rebound,22 and drop–surface friction,23 making it central to drop dynamics on solids.23–26
Standard measurements of θa and θr use sessile-drop goniometry: a needle injects liquid into a sessile drop to increase volume (advancing), then withdraws to decrease volume (receding). Despite algorithmic advances,27–32 this protocol has drawbacks. The needle perturbs the free surface (capillary rise) and especially biases θr at small volumes; needle position can alter the contact-line speed. Typical devices require samples of a few cm2 and volumes of ∼30–50 µL to reach θr, limiting heterogeneous or small specimens. The inflow/outflow cycle and setup time render the method time-consuming and user-dependent.33 An alternative approach has also been proposed, in which a droplet is deposited through a pre-drilled hole in the substrate.34 Although this method can prevent needle induced effects, it represents an idealized configuration,35 which is time consuming and can induce surface damage in fragile samples. This can alter the local topography, compromising the integrity of heterogeneous or patterned surfaces.
Here we introduce the stood-up drop (SUD) method for receding-angle metrology. A short liquid jet (jetting time of a few ms) deposits a thin lamella that spreads radially and then retracts to a spherical-cap drop. After a quasi-equilibrium is reached, the apparent contact angle θSUD closely approximates θr. The measurement completes in ∼10 ms and requires no needle, mitigating deposition artefacts and facilitating automation. We validate SUD by directly comparing θSUD with θr across hydrophilic–hydrophobic substrates, and we delineate when θSUD recovers θr using direct numerical simulations based on a volume-of-fluid (VoF) technique that systematically varies viscosity, static contact angle, and deposited volume. Finally, we summarize simple scaling criteria that predict the SUD regime and practical volume limits, and we highlight conditions under which SUD can fail (e.g., violent oscillations or detachment on highly hydrophobic surfaces). Together, these results position SUD as a fast, needle-free alternative for robust receding-angle characterization.
2 Materials and experimental methods
2.1 Experimental setup: stood-up drop (SUD) device
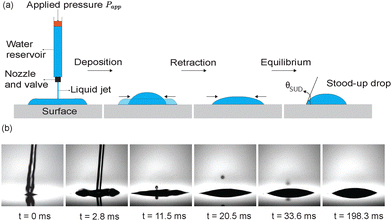
To form drops from a liquid jet, a device designed by KRÜSS company was used. The device generates a liquid jet by applying a constant pressure Papp to a liquid reservoir (Fig. 1a), which is connected to a valve and nozzle. The distance between sample and nozzle was kept at 4 mm. The applied pressure Papp was varied between 100 and 700 mbar. The time at which the valve is open (jetting time τ) can be controlled by software. It should not exceed a few milliseconds to ensure the formation of a thin lamella. If not stated otherwise, τ = 1 ms is used. A liquid jet is generated immediately after the valve opening. After spreading and retraction of the liquid, a stationary drop is formed (Fig. 1b). Here, the contact angle at this stage (θSUD) is measured and compared with θr obtained by Goniometry technique. We determined θSUD values by a polynomial fitting method, which was designed by a python code (SI). This code determines the average of θSUD values from the average of contact angles at the left and right side of drops. Our results consider the θSUD average of the last 50 frames of each video. For a subset of all investigated samples no high-speed recordings were performed. In such cases, the SUD contact angle was determined using the KRÜSS ADVANCE software after drop deposition using the KRÜSS DS3251 SUD dosing unit.The liquid impact process is recorded by a high-speed camera (Photron UX10) at up to 8000 fps. Simultaneous high speed-video experiments were performed from the top of the surface, to study the shape of the drop contact area and pinning of the three-phase contact line. Experiments were repeated at least three times for each surface (in some cases five times), with their wetting nature ranging from hydrophilic to hydrophobic. For each droplet, the contact angle was obtained by averaging the left and right contact angles, and then the mean and standard deviation were calculated across repeated experiments.
2.2 Receding contact angle measurements
Receding contact angles θr were measured by the sessile drop method/Goniometer (KRÜSS, DSA100). First, a 0.5 µL drop of Milli-Q water (18 megaohm) is deposited on the sample. Then, the baseline is positioned at the contact line between drop and surface, while the needle is adjusted to be in the middle of the drop. Afterwards, the volume is increased up to 50 µL at a flow rate of 0.5 µL s−1. Then, the drop is deflated at the same flow rate. A tangent fit method was used to determine receding contact angles by the ADVANCE software of the device. Experiments were repeated at least three times (up to five times in some cases) on different spots of the surface. At each time step, the mean of the left and right contact angles was taken, and the average and standard deviation of these values were then determined over the plateau region of the contact angle vs. drop base diameter plot.2.3 Image processing of contact angle measurements
For automated contact angle measurements using image processing of the high speed recordings, we adapted the open source 4S-SROF toolkit to match our requirements.36 The 4S-SROF toolkit effectively utilizes the OpenCV library37 to manipulate the images, such as separate the drop from its background. We chose morphological transformations for noise reduction, and they proved to be superior to the median filter, guaranteeing the accuracy of our advancing angle measurements.36 We calculated the advancing and receding angle using the tangent fitting method for the final 10 pixels of the drop near the substrate. The Savitzky–Golay filter38 was employed in specific cases to eliminate unwanted noise and enhance the smoothness of the final diagram, facilitating easier interpretation.2.4 Surface preparation
Most investigated surfaces are commercially available or provided by customers from Krüss. These surfaces were cleaned by water and ethanol before usage.3 Simulation methodology
3.1 Governing equations
In this section, we present the governing equations that describe the retraction dynamics of a liquid drop on a solid surface. Following the one-fluid formulation, both the drop and ambient gas are treated as a single continuum, and the interfacial boundary condition is enforced via the localized surface tension force fγ.39 Specifically, the drop's retraction arises from the conversion of interfacial free energy into kinetic energy, countered by viscous dissipation as captured by the Navier–Stokes equation,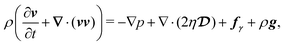 | (2) |
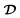 is the symmetric part of the velocity gradient tensor
is the symmetric part of the velocity gradient tensor 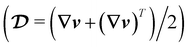 .40 Lastly, g is the acceleration due to gravity.
.40 Lastly, g is the acceleration due to gravity.
3.2 Non-dimensionalization of the governing equations
To non-dimensionalize the governing equations, we use the characteristic scales of the system: the liquid density ρL, the surface tension at the liquid–gas interface γLG, and the maximum post-impact spreading thickness of the drop H. These parameters define the characteristic inertiocapillary timescale τγ and the characteristic inertiocapillary velocity vγ,41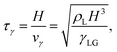 | (3) |
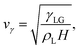 | (4) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) to represent the dimensionless form of the respective variable x, we rewrite the Navier–Stokes equation eqn (2) in its dimensionless form
to represent the dimensionless form of the respective variable x, we rewrite the Navier–Stokes equation eqn (2) in its dimensionless form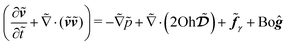 | (5) |
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = pH/γLG is the dimensionless pressure,
= pH/γLG is the dimensionless pressure, 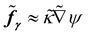 is the dimensionless surface tension force, where κ is the interfacial curvature κ = ∇·
is the dimensionless surface tension force, where κ is the interfacial curvature κ = ∇·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) with
with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) as the normal to the interface marked between the two fluids: liquid with ψ = 1 and gas with ψ = 0. Lastly, the Ohnesorge number and Bond number
as the normal to the interface marked between the two fluids: liquid with ψ = 1 and gas with ψ = 0. Lastly, the Ohnesorge number and Bond number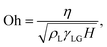 | (6) |
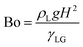 | (7) |
3.3 Numerical setup & domain description
We perform direct numerical simulations using the volume-of-fluid (VoF) method, implemented using the open-source language Basilisk C.42 The simulations solve the governing equations presented in Section 3.1, under the assumption of axial symmetry (see Fig. 2). The bottom boundary of the domain represents the substrate and enforces a no-penetration condition for the normal velocity component. The tangential component is influenced by an implicit slip model, which emerges due to the interpolation of fluid properties in the VoF scheme, despite the no-slip condition being imposed.43 The implicit slip is further constrained to satisfy the prescribed contact angle θ at the first grid cell. The pressure boundary condition at this interface follows a zero-gradient condition (see Fig. 2).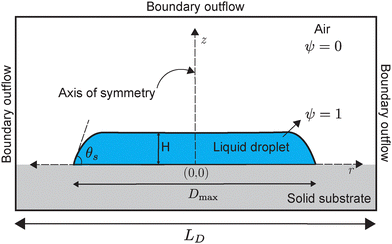 | ||
| Fig. 2 The initial configuration of the drop for the numerical simulations. The configuration resembles a pancake shape, similar to that observed in experiments post-impact. | ||
At the top and right domain boundaries, free-slip conditions are applied to the velocity field, while a Dirichlet zero condition is enforced for pressure. The domain size, denoted as LD, is chosen such that these boundaries remain sufficiently distant to avoid influencing the contact line dynamics. Heuristically LD is chosen to be Dmax/(2H) + 10, where Dmax is the maximum spreading diameter following jet impingement. To enhance computational efficiency and accuracy, adaptive mesh refinement (AMR) is applied in regions exhibiting large velocity gradients. The refinement depth is selected to ensure a minimum of 40 grid cells across the drop thickness, i.e., H > 40Δ, where Δ denotes the smallest grid cell size.
3.4 Initial conditions
The numerical simulations commence with the drop at rest, immediately after reaching the “pancake” configuration following impact (Fig. 2). At this stage, the drop assumes a pancake-like shape, characterized by a thin, radially spread film with an aspect ratio Γ = Dmax/H. Since the drop spreading is directly controlled by the kinetic energy provided by the jet,44 we also assume that there is sufficient kinetic energy to overcome pinning and reach the pancake configuration. This assumption is justified by the drop deposition protocol in experiments where the liquid jet is turned off once a drop is created at the surface. Furthermore, the flow timescales involved in the impact and spreading process are distinct. The transition from an impacting jet to a flattened drop occurs over the kinematic timescale D0/V0 where the subsequent retractions occurs on the inertio-capillary timescale,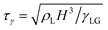 . Here, we focus on the retraction phase only where the influence of left-over kinetic energy from impact is assumed minimal.45
. Here, we focus on the retraction phase only where the influence of left-over kinetic energy from impact is assumed minimal.45
The dimensions of the spread drop are determined by the impact conditions, with the base diameter Dmax and thickness H depending on the volume of the deposited drop which depends on the nozzle flow rate q and jetting time τ, and the balance of inertial and capillary forces during the spreading phase. The volume of the drop Ω is related to the base diameter and thickness, up to the leading order, as
| Ω ∼ qτ ∼ Dmax2H | (8) |
The jetting time is kept constant at τ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ms during the experiments, resulting in drops with a volume of 0.5 µL. However, we do vary the volume of the drop in our simulations, ranging from 0.25–3 µL. The system is modeled under axial symmetry in a three-dimensional framework, ensuring that the retraction dynamics are captured without assuming any two-dimensional simplifications. We note that in the experiments, the drop retraction is not always axisymmetric. The initial state provides a well-defined starting point for investigating the subsequent retraction process, which is governed by surface tension and viscous effects.
ms during the experiments, resulting in drops with a volume of 0.5 µL. However, we do vary the volume of the drop in our simulations, ranging from 0.25–3 µL. The system is modeled under axial symmetry in a three-dimensional framework, ensuring that the retraction dynamics are captured without assuming any two-dimensional simplifications. We note that in the experiments, the drop retraction is not always axisymmetric. The initial state provides a well-defined starting point for investigating the subsequent retraction process, which is governed by surface tension and viscous effects.
4 Results and discussion
4.1 SUD mechanism
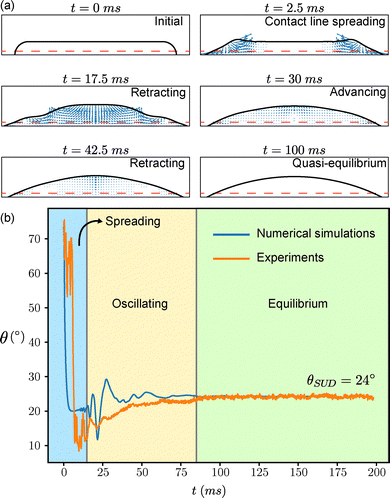
Initially, a liquid jet, ejected from a nozzle at a controlled pressure (see Section 4.2.1), impacts the surface with a speed of approximately 3 m s−1, as measured from the last few frames of the high-speed videos (Fig. 1b and 3a, t = 0+, ms). Subsequently, the liquid spreads radially, converting kinetic energy into surface energy and viscous dissipation, forming a pancake-shaped liquid film until reaching a maximum diameter Dmax. Analogous to impacting drops,46 the impact and spreading duration scales with the inertiocapillary timescale. Consequently, we turn off the jet after roughly 1 ms, (Video S1).The pancake spreading state serves as the initial condition for our simulations, assuming that the internal flow at this moment doesn't influence subsequent retraction dynamics (Fig. 3a) in our simulations. For hydrophilic substrates, the contact line initially spreads to achieve its maximum spreading state. Afterwards, the pancake-shaped drop recoils, converting surface energy back into kinetic energy and viscous dissipation (Fig. 3a), finally forming a static cap-spherical drop characterized by the stood-up contact angle θSUD (Fig. 3, 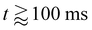 , Video S1).
, Video S1).
In experiments, during spreading, the contact angle significantly decreases until reaching a minimum (Fig. 3b, blue region for both experiments and simulations). The minimum is caused by the large impact pressure, resulting in the formation of a very thin lamellae. As the contact line recedes, first the contact angle oscillates (yellow region). The release of the stored surface energy can cause the oscillations. Oscillations of the contact angle level off after approximately 80 ms at a larger angle.
The temporal development of the contact angle is well reproduced in numerical simulations (Fig. 3b). Oscillations are more pronounced on hydrophobic surfaces (Fig. S1) but they ultimately cease due to viscous dissipation, resulting in a plateau at θSUD (Fig. 3b, blue line). Since no solid needle is required, effects on the drop shape due to the deposition protocol can be ruled out. This facilitates the fitting procedure to calculate contact angles.
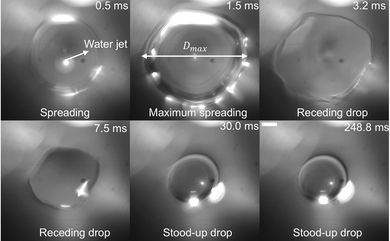
To investigate possible pinning during retraction, we recorded the impacting jet from the top of the substrate using high-speed imaging. No pinning points or residual drops were observed (Fig. 4). The final SUD drop area was clearly circular, Video S2.
4.2 Further experimental results
We stress that increasing Papp increases both the flow rate (volume of liquid ejected per unit time during valve opening) and the maximum attainable SUD drop volume. This volume depends on Papp, the jetting time τ, and the nozzle diameter. At the end of the retraction phase, a SUD behaves like a spherical cap with volume (Fig. 4):
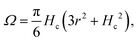 | (9) |
In previous work,47 we showed that the flow rate—defined by the combination of Papp and the jet diameter—is the key factor determining the largest drop volume that still achieves the SUD state. If, for a given flow rate, the final drop volume is below a critical threshold, the contact line recedes after dosing, and the drop's rest angle is the receding contact angle θr. From experiments on six substrates,47 we identified a phenomenological correlation between the flow rate and the maximum drop volume ensuring SUD dosing.
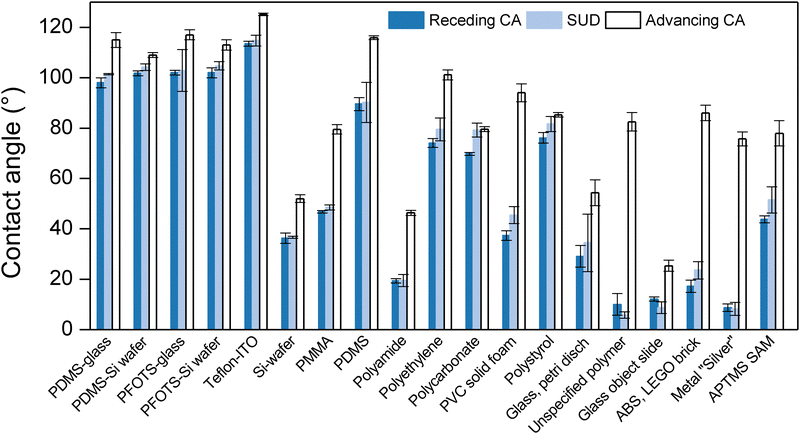
Remarkably, SUD technique is suitable for a hydrophilic surface (bare glass slide), overcoming the difficulties of measuring contact angles for these surfaces by the sessile-drop method, caused by evaporation and drop pinning. As the SUD drop forms in a few miliseconds, evaporation does not affect θSUD values. Moreover, the high-speed of the liquid jet for both spreading and the first period of the retraction phase, avoid efficiently the influence of pinning points on the drop dynamics. These pinning points can prevent the contact line motion during inflation/deflation of drops using goniometry. Determining θr for a very hydrophilic glass slide using goniometry has proven challenging. However, a contact angle of θr = 4.5° has been determined previously by capillary bridges.48 This is in good agreement with our θSUD values of ∼6° (Fig. S3). Therefore, SUD method arises as a reliable alternative to determine θr for surfaces with low wettability.
For the case of hydrophobic surfaces like PFOTS and PDMS surfaces, the equilibrium state at which the SUD is formed takes longer time. This occurs due to the capillary oscillations generated during the retraction phase, when the surface energy is converted back to kinetic energy and viscous dissipation.
Drop oscillations can lead to asymmetric contact line motion and the drops can even slide owing to this asymmetry or that of the surface orientation. The effect is more pronounced when the hydrophobicity increases, as shown for the case of Teflon AF on ITO (Fig. S1). The SUD method fails when: (1) insufficient viscous dissipation allows drops to oscillate violently and settle in an advancing phase or (2) rapid receding motion generates enough upward momentum for the drop to detach from the surface. Both situations are common on highly hydrophobic surfaces, where bubble entrainment during rapid retraction can further complicate the dynamics.49–52 Under these conditions, the SUD state is not the result of a final receding of the contact line, and thus the measured contact angles no longer correspond to θr. Therefore, the SUD technique requires that the final motion of the contact line is a clear, dominant receding event, which is essential for reliably resembling the receding contact angle.
A particular case arises on highly hydrophobic pillared surfaces. At sufficiently high impact pressures, the liquid jet may impale the surface, leading to a localized Wenzel state at the impact spot. If a clean receding phase is achieved at a given pressure without liquid detachment, the SUD state can still be reached. However, at higher pressures the contact line dynamics may be influenced by local liquid penetration, as previously reported for droplets impacting superhydrophobic nanostructured surfaces.53 This scenario would represent an additional limitation of the SUD method, with underlying physics that lies beyond the scope of the present study.
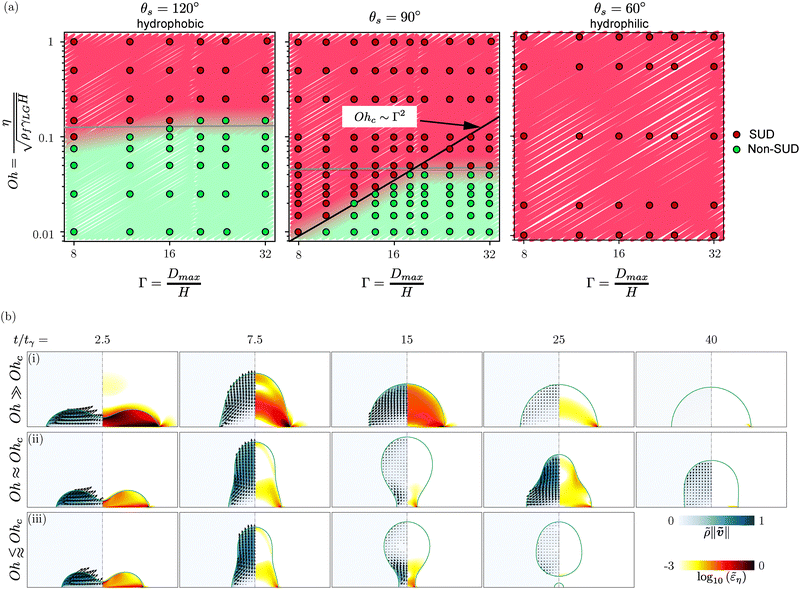
In the following section, we quantitatively analyze when the SUD method works by systematically exploring the parameter space defined by the Ohnesorge number Oh and the aspect ratio Γ at three representative static contact angles of θs = 60° (hydrophilic), θs = 90°, and θs = 120° (hydrophobic).
4.3 Simulation results for the full Oh−Γ parameter space
This section delineates the regions in the Oh−Γ parameter space, for hydrophobic (θs > 90°), θs = 90°, and hydrophilic (θs < 90°) surfaces, where SUD is a viable technique. In the SUD regime, the viscous dissipation is sufficient to ensure an overdamped retracting drop that stays on the surface. Additionally, the total volume of the drop (keeping all other material and flow properties fixed) presents additional constraints on this technique, which is discussed at the end of this section.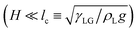 , the amount of viscous dissipation during the retraction phase largely dictates whether a drop remains attached to the surface after contact line recoiling (SUD regime), with or without oscillations or detaches from the surface (non-SUD regime).45
, the amount of viscous dissipation during the retraction phase largely dictates whether a drop remains attached to the surface after contact line recoiling (SUD regime), with or without oscillations or detaches from the surface (non-SUD regime).45
Detached drops often fall back onto the surface. This leads to pronounced oscillations for drops already in a spherical cap shape, which opens the possibility of the final drop at rest to be the result of a wetting process and not of a de-wetting process. Consequently, the contact angle might not resemble the receding angle but rather a contact angle between advancing and receding angle. To systematically characterize the conditions classifying stable SUD formation versus detachment, we explored the parameter space spanned by the Ohnesorge number Oh and aspect ratio Γ across multiple static contact angles θs, as illustrated in Fig. 6.
We observe three distinct mechanisms governing the transition between SUD and non-SUD regimes, dependent on the static contact angle:
1. For highly hydrophobic surfaces (large θs), contact line dissipation is minimal, and the transition is primarily governed by bulk dissipation overcoming the excess surface energy—analogous to the bouncing-to-non-bouncing transition on superhydrophobic surfaces.45 In this regime, the critical Ohnesorge number Ohc remains approximately constant; drops with Oh > Ohc dissipate sufficient energy to remain in the SUD regime, while those with Oh < Ohc detach.
2. For intermediate wettability (θs ≈ 90°), there is a balance between dissipation and released energy as illustrated by the numerical snapshots in Fig. 6(b). For sufficiently large Oh, dissipation in both bulk and contact line produces SUD behavior, with the drop undergoing overdamped oscillations as it dissipates energy (Fig. 6(b-i)). Near the critical threshold Ohc, drops may undergo several oscillation cycles before eventually stabilizing (Fig. 6(b-ii)). The SUD method fails when insufficient viscous dissipation allows drops to oscillate violently and drops settle in an advancing phase. Below Ohc, insufficient viscous dissipation leads to detachment, with the liquid neck pinching off as shown in Fig. 6(b-iii).
3. For hydrophilic surfaces (small θs), contact line dissipation dominates and effectively suppresses detachment across the entire parameter range investigated – encompassing the parameter space relevant for experimental applications. Consequently, as shown in Fig. 6(a) – (θs = 60°), all simulated conditions for hydrophilic surfaces result in stable SUD behavior, making the technique particularly robust for such surfaces.
We develop a theoretical model balancing surface energy and viscous dissipation to quantify these transitions. The initial surface energy of the pancake-shaped drop at t = 0 is Esurf = γLGAsurf. To leading order in Γ, the surface area scales as
| Esurf ∼ γLGH2Γ2. | (10) |
During retraction, viscous dissipation41
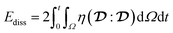 | (11) |
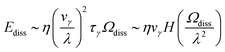 | (12) |
The dominant velocity gradient arises from shear flow with λ ∼ H, giving vγ/H.
The location of viscous dissipation depends critically on the Ohnesorge number. At high Oh, velocity gradients develop throughout the drop immediately-analogous to the high-viscosity limit in Taylor–Culick retraction.54,55 Here, dissipation occurs over the entire bulk volume:
| Ωdiss ∼ H3Γ2 | (13) |
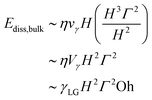 | (14) |
When bulk dissipation dominates and balances the released surface energy, we get
| Ohc ∼ 1, | (15) |
At low Oh, viscous effects remain localized near the retracting contact line, with the central film region remaining nearly stationary initially. Dissipation concentrates in a boundary layer of volume:57,58
| Ωdiss ∼ λ3 | (16) |
The boundary layer thickness λ is bounded by the drop thickness H (Fig. 6). With λ ∼ H, eqn (12) gives
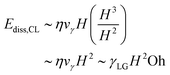 | (17) |
When contact line dissipation dominates and balances the surface energy,
| Ohc ∼ Γ2 | (18) |
These criteria accurately demarcate the SUD and non-SUD regimes in Fig. 6(a) – (θs = 90°). At very large Oh values, the transition becomes controlled primarily by bulk dissipation, resulting in a constant Ohc marked by the gray line for θs = 120° and 90°. Lastly, below a critical static contact angle (exemplified by θs = 60° in Fig. 6a), the system features only SUD behavior.
A drop detaching from the surface obviously poses serious challenges for measurements using the SUD technique. Such detachment can cause the drop to exit the camera frame, entrain bubbles during pinch-off and redeposition,52 or significantly increase the time required to reach equilibrium. Furthermore, detached drops often fall back onto the surface, resulting in uncontrolled secondary deposition unlike the controlled jetting process discussed previously.
Indeed, a key takeaway from the numerical simulations is that SUD technique remains viable for hydrophilic surfaces across the entire parameter space, even at extreme combinations of small Oh and large Γ. For hydrophobic surfaces, however, the technique only works within the restricted range of large Oh and small Γ. Lastly, we stress that apart from the non-SUD cases discussed in this section, the technique can also fail when surfaces are superhydrophobic, causing the jet to bounce instead of depositing a drop, or when drop breakup occurs (Fig. S4). Analysis of lift-off during jet impingement lies beyond our current scope.
5 Conclusions and outlook
In this work, we have introduced and validated the stood-up drop (SUD) technique as an effective method for measuring receding contact angles. Microliter-sized water drops, formed after an impacting liquid jet spreads and recoils on a surface, exhibit a contact angle (θSUD) that remarkably resembles the receding contact angle (θr) measured by traditional goniometry. Our numerical simulations, performed using the volume-of-fluid method, corroborate our experimental findings and provide a theoretical framework for understanding this technique and its limitations.The SUD method offers several key advantages over conventional goniometry. First, it eliminates the need for a solid needle, thereby avoiding distortion of the drop shape during measurement. Second, it dramatically reduces measurement time from minutes to milliseconds, enhancing experimental efficiency. Third, it performs exceptionally well on hydrophilic surfaces, where traditional techniques often struggle due to evaporation and pinning issues. Fourth, it requires smaller sample sizes (≈0.5 µL), making it suitable for testing smaller or heterogeneous surfaces. Fifth: the contact angle after SUD dosing θSUD describes the smallest possible contact angle of a drop at rest on the investigated surface. This in combination with the already established liquid needle dosing33 describing the largest possible contact angle of a drop on the investigated surface allow for the easiest way to determine contact angle hysteresis. By systematically exploring the parameter space defined by the Ohnesorge number (Oh) and aspect ratio (Γ), we have established clear boundaries for the applicability of this technique. For hydrophilic surfaces, the SUD method remains viable across the entire parameter space investigated. For hydrophobic surfaces, its applicability is restricted to combinations of sufficiently large Oh and small Γ, where viscous dissipation prevents detachment. This framework allows researchers to determine a priori whether the SUD technique will provide reliable measurements for their specific systems. While the SUD method exhibits exceptional performance across a wide range of surfaces, it has limitations for highly hydrophobic materials. In these cases, insufficient viscous dissipation can lead to violent oscillations or detachment, preventing the formation of a stable equilibrium state dominated by receding dynamics. Additionally, volume constraints must be considered, as tiny drops present resolution challenges, while large drops deviate from the spherical cap assumption due to gravitational deformation.
Looking forward, the SUD technique opens several promising avenues for research. The temporal dynamics of the surface tension-driven receding process varies significantly between substrates (e.g., 2–3 seconds on PMMA versus approximately 30 ms on other samples). This difference remains poorly understood but might provide valuable insights into a surface's dewetting properties beyond the steady-state contact angle measurements. We have shown that the stood-up drop technique works excellently on smooth surfaces. Future work could explore these dynamic aspects to develop a more comprehensive characterization of surface wettability, especially on more complex substrates such as sticky or textured surfaces. Moreover, the rapid and accurate determination of receding contact angles enabled by the SUD method could enhance our ability to predict contact line instabilities such as drop pinning and splitting. This has practical implications for various applications including spray coatings, self-cleaning surfaces,59,60 anti-icing materials,61 and biofouling-resistant coatings,62 where the receding contact angle offers better correlation with practical adhesion work than the advancing contact angle.1,63 The SUD technique could also be extended to investigate more complex fluids with non-Newtonian properties64,65 or to study the temperature dependence of receding contact angles1 – both relevant for industrial applications. Additionally, combining the SUD method with simultaneous measurements of contact line dynamics might reveal further insights into the fundamental physics of wetting and dewetting processes.66
Author contributions
D. V., T. W. and D. D. planned the experiments. D. D. and F. W. performed the experiments, using a code written by S. S. A. S. supported with the preparation of the samples. V. S., D. L. and A. B. planned the simulations. A. B. ran the simulations. D. D., F. W. and A. B. analyzed the data. D. V., V. S., T. W., D. D. and A. B. designed the structure of the manuscript. D. D., A. B., D. V., T. W., V. S., R. B., M. K., H.-J. B. and D. L. wrote the manuscript. All authors discussed the measurements and approved the manuscript.Conflicts of interest
Thomas Willers is employed by KRÜSS GmBH.Data availability
The codes used for the numerical simulations are available at https://github.com/comphy-lab/Retracting-Droplet. The experimental data is available from the corresponding authors upon reasonable request.The data supporting this article have been included as part of the supplementary information (SI). The supplementary information contains additional images and movies captured from experiments for hydrophilic as well as hydrophobic substrates. See DOI: https://doi.org/10.1039/d5sm00985e.
Acknowledgements
We would like to thank KRÜSS GmBH for their support with measurements. This work was carried out on the national e-infrastructure of SURFsara, a subsidiary of SURF cooperation, the collaborative ICT organization for Dutch education and research. This work was sponsored by NWO – Domain Science for the use of supercomputer facilities. A. B., V. S., A. S., D. D., D. V., H.-J. B., and D. L. acknowledge the Max Planck – University Twente Center for Complex Fluid Dynamics for financial support. We acknowledge the ERC Advanced Grant no. 340391-SUPRO and 740479-DDD. A. B., V. S. and D. L. acknowledge the NWO-ASML connecting industries grant for high-speed immersion lithography. This work is supported by the German Research Foundation (DFG) within the framework Collaborative Research Centre 1194 “Interaction of Transport and Wetting Processes” C07N, T02 (R. B., H.-J. B.). Open Access funding provided by the Max Planck Society. We would like to thank Diego Cortés for assisting in the preparation of samples.Notes and references
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 CrossRef CAS.
- D. Lohse, Annu. Rev. Fluid Mech., 2022, 54, 349–382 CrossRef.
- H. B. Eral, D. t Mannetje and J. M. Oh, Colloid Polym. Sci., 2013, 291, 247–260 Search PubMed.
- D. Attinger, C. Moore, A. Donaldson, A. Jafari and H. A. Stone, Forensic Sci. Int., 2013, 231, 375–396 CrossRef PubMed.
- T. A. Yakhno, O. A. Sedova, A. Sanin and A. Pelyushenko, Tech. Phys., 2003, 48, 399–403 CrossRef CAS.
- D. Brutin, Droplet wetting and evaporation: from pure to complex fluids, Academic Press, 2015 Search PubMed.
- T. Young, Abstracts of the Papers Printed in the Philosophical Transactions of the Royal Society of London, 1832, pp. 171–172 Search PubMed.
- J. W. Drelich, L. Boinovich, E. Chibowski, C. Della Volpe, L. Hołysz, A. Marmur and S. Siboni, Surf. Innovations, 2019, 8, 3–27 CrossRef.
- A. Marmur, Soft Matter, 2006, 2, 12–17 Search PubMed.
- D. Cwikel, Q. Zhao, C. Liu, X. Su and A. Marmur, Langmuir, 2010, 26, 15289–15294 CrossRef CAS PubMed.
- A. Marmur, Eur. Phys. J.: Spec. Top., 2011, 197, 193 CAS.
- A. Marmur, C. Della Volpe, S. Siboni, A. Amirfazli and J. W. Drelich, Surface Innovations, 2017, 5, 3–8 CrossRef.
- C. McPhee, J. Reed and I. Zubizarreta, Developments in Petroleum Science, Elsevier, 2015, vol. 64, pp. 313–345 CAS.
- H.-J. Butt, R. Berger, W. Steffen, D. Vollmer and S. Weber, Langmuir, 2018, 34, 11292–11304 CrossRef CAS.
- A. Stetten, A. Golovko, S. Weber and H.-J. Butt, Soft Matter, 2019, 15, 8667–8679 Search PubMed.
- B. Samuel, H. Zhao and K.-Y. Law, J. Phys. Chem. C, 2011, 115, 14852–14861 Search PubMed.
- A. Dupré and P. Dupré, Théorie Mécanique de la Chaleur, Gauthier-Villars, 1869 Search PubMed.
- A. J. Meuler, J. D. Smith, K. K. Varanasi, J. M. Mabry, G. H. McKinley and R. E. Cohen, ACS Appl. Mater. Interfaces, 2010, 2, 3100–3110 CrossRef PubMed.
- K. Golovin, S. P. Kobaku, D. H. Lee, E. T. DiLoreto, J. M. Mabry and A. Tuteja, Sci. Adv., 2016, 2, e1501496 CrossRef.
- T. H. Duong, J.-F. Briand, A. Margaillan and C. Bressy, ACS Appl. Mater. Interfaces, 2015, 7, 15578–15586 CrossRef CAS.
- Z. Yi, C.-J. Liu, L.-P. Zhu and Y.-Y. Xu, Langmuir, 2015, 31, 7970–7979 CrossRef CAS.
- C. Antonini, F. Villa, I. Bernagozzi, A. Amirfazli and M. Marengo, Langmuir, 2013, 29, 16045–16050 CrossRef CAS.
- N. Gao, D. Geyer, F. Pilat, S. Wooh, D. Vollmer, H.-J. Butt and R. Berger, Nat. Phys., 2018, 14, 191–196 Search PubMed.
- H.-J. Butt, I. V. Roisman, M. Brinkmann, P. Papadopoulos, D. Vollmer and C. Semprebon, Curr. Opin. Colloid Interface Sci., 2014, 19, 343–354 CrossRef CAS.
- V. Liimatainen, M. Vuckovac, V. Jokinen, V. Sariola, M. Hokkanen, Q. Zhou and R. Ras, Nat. Commun., 2017, 8, 1798 CrossRef.
- D. Daniel, J. Timonen, R. Li, S. Velling and J. Aizenberg, Nat. Phys., 2017, 13, 1020–1025 Search PubMed.
- T. Huhtamäki, X. Tian, J. T. Korhonen and R. H. Ras, Nat. Protoc., 2018, 13, 1521–1538 Search PubMed.
- J. T. Korhonen, T. Huhtamäki, O. Ikkala and R. H. Ras, Langmuir, 2013, 29, 3858–3863 CrossRef CAS.
- A. Kalantarian, Development of Axisymmetric Drop Shape Analysis-No Apex (ADSA-NA)., University of Toronto, 2011 Search PubMed.
- M. Hoorfar and A. Neumann, J. Adhes., 2004, 80, 727–743 CrossRef CAS.
- S. Srinivasan, G. H. McKinley and R. E. Cohen, Langmuir, 2011, 27, 13582–13589 CrossRef CAS.
- Z. N. Xu, Rev. Sci. Instrum., 2014, 85, 125107 CrossRef CAS.
- M. Jin, R. Sanedrin, D. Frese, C. Scheithauer and T. Willers, Colloid Polym. Sci., 2016, 294, 657–665 CrossRef CAS.
- D. Y. Kwok, R. Lin, M. Mui and A. W. Neumann, Colloids Surf., A, 1996, 116, 63–77 Search PubMed.
- J. Drelich, Surf. Innovations, 2013, 1, 248–254 Search PubMed.
- S. Shumaly, F. Darvish, X. Li, A. Saal, C. Hinduja, W. Steffen, O. Kukharenko, H.-J. Butt and R. Berger, Langmuir, 2023, 39, 1111–1122 Search PubMed.
- G. Bradski, Dr Dobb's Journal: Software Tools for the Professional Programmer, 2000, 25, 120–123 Search PubMed.
- W. H. Press and S. A. Teukolsky, Comput. Phys, 1990, 4, 669–672 Search PubMed.
- G. Tryggvason, R. Scardovelli and S. Zaleski, Direct Numerical Simulations of Gas-Liquid Multiphase Flows, Cambridge University Press, 2011 Search PubMed.
- G. K. Batchelor, An introduction to fluid dynamics, Cambridge University Press, 2000 Search PubMed.
- V. Sanjay, PhD Thesis – Research UT, graduation UT, University of Twente, Netherlands, 2022.
- S. Popinet and Collaborators, Basilisk, 2013–2025, https://basilisk.fr, Last accessed: July 22, 2025.
- M. Renardy, Y. Renardy and J. Li, J. Comput. Phys., 2001, 171, 243–263 Search PubMed.
- E. J. Watson, J. Fluid Mech., 1964, 20, 481–499 Search PubMed.
- V. Sanjay, P. Chantelot and D. Lohse, J. Fluid Mech., 2023, 958, A26 CrossRef CAS.
- V. Sanjay and D. Lohse, Phys. Rev. Lett., 2025, 134, 104003 CrossRef CAS.
- T. Willers and O. Katrin, European Patent, EP4109072B1, 2022 Search PubMed.
- N. Nagy, Langmuir, 2019, 35, 5202–5212 CrossRef CAS PubMed.
- D. Bartolo, C. Josserand and D. Bonn, Phys. Rev. Lett., 2006, 96, 124501 CrossRef PubMed.
- T. V. Nguyen and M. Ichiki, Microsyst. Nanoeng., 2020, 6, 36 CrossRef PubMed.
- B. Zhang, V. Sanjay, S. Shi, Y. Zhao, C. Lv, X.-Q. Feng and D. Lohse, Phys. Rev. Lett., 2022, 129, 104501 CrossRef CAS.
- V. Sanjay, B. Zhang, C. Lv and D. Lohse, J. Fluid Mech., 2025, 1004, A6 CrossRef CAS.
- X. Deng, F. Schellenberger, P. Papadopoulos, D. Vollmer and H.-J. Butt, Langmuir, 2013, 29, 7847–7856 CrossRef CAS.
- N. Savva and J. W. Bush, J. Fluid Mech., 2009, 626, 211–240 Search PubMed.
- H. Deka and J.-L. Pierson, Phys. Rev. Fluids, 2020, 5, 093603 Search PubMed.
- A. Jha, P. Chantelot, C. Clanet and D. Quéré, Soft Matter, 2020, 16, 7270–7273 RSC.
- P. G. D. Gennes, X. Hua and P. Levinson, J. Fluid Mech., 1990, 212, 55–63 Search PubMed.
- D. Bartolo, C. Josserand and D. Bonn, J. Fluid Mech., 2005, 545, 329–338 CrossRef.
- D. L. Schmidt, R. F. Brady, K. Lam, D. C. Schmidt and M. K. Chaudhury, Langmuir, 2004, 20, 2830–2836 Search PubMed.
- K. M. Wisdom, J. A. Watson, X. Qu, F. Liu, G. S. Watson and C.-H. Chen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 7992–7997 CrossRef CAS.
- F. Wang, Y. Zhuo, Z. He, S. Xiao, J. He and Z. Zhang, Adv. Sci., 2021, 8, 2101163 CrossRef PubMed.
- K. Sun, Y. Gizaw, H. Kusumaatmaja and K. Votchovsky, Soft Matter, 2025, 21, 585–595 RSC.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 Search PubMed.
- M. Jalaal, B. Stoeber and N. J. Balmforth, J. Fluid Mech., 2021, 914, A21 Search PubMed.
- H. L. França, M. Jalaal and C. M. Oishi, Phys. Rev. Res., 2024, 6, 013226 CrossRef.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292 CrossRef.
Footnote |
| † Contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2026 |

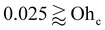
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif)