The effect of the stacking fault on the diffusion of chemisorbed hydrogen atoms inside few-layered graphene

Abstract

We examined the diffusion of hydrogen atoms in mono-, bi- and tetralayer graphene with AB stacking and two bilayer graphene with stacking faults using density functional theory. The bi- and tetralayer graphene provide diffusion pathways with lower energy barriers inside the interlayer space. Inside the bi- and tetralayer graphene with AB stacking, the in-plane diffusion is more favorable than the inter-plane jumping. However, the stacking faults made by sliding layer planes lowers the energy barrier of the inter-plane jumping and the effective frequency of the inter-plane jump is larger than that of the in-plane diffusion inside the graphene layers with the stacking faults. This suggests that hydrogen atoms can diffuse over a long distance inside few-layered graphene with stacking faults jumping consecutively between adjacent layers.

---

1 Introduction

The hydrogenation of carbon-based nano materials has been attractive for various applications including electronic devices and hydrogen storage systems.^1–5 As the hydrogenation patterns strongly affect the physical and/or chemical properties of the hydrogenated graphenes, many researchers have studied the thermodynamic, kinetic and structural characteristics of hydrogen atoms chemisorbed on the graphene surface.^6–13 To finely control the graphene properties, understanding the atomic hydrogen kinetics on the graphene surface is indispensable.

The kinetics of hydrogen atoms adsorbed on the graphene surface has raised particular attention since the spillover mechanism was proposed for hydrogen storage in carbon-based materials.⁵ The diffusion barrier of a hydrogen atom chemically adsorbed on the pristine graphene surface has been estimated to be around 1 eV,^14–16 and a move from the edge of a stable hydrogenated island formed on the graphene surface needs to overcome an energy barrier of around 3 eV.¹⁷ In this regard, it was suggested that in order for the diffusion to take place with ease at room temperature, physisorbed hydrogen atoms^18,19 or defect structures^20,21 should be involved in the spillover process, but those arguments do not seem to be enough for an explanation on the spillover in carbonaceous materials.

Although the present interests are concentrated on monolayer graphene, recent researches revealed that bilayer graphene can show distinct properties such as gate-induced band gap opening²² and chiral quasiparticle.²³ Similar with monolayer graphene, chemically modified bilayer graphene displays different electronic structures from the original bilayer.^24–28 In half hydrogenated bilayer graphene (bilayer graphane) modeled by using the first principle calculations,^25,26 interlayer C–C chemical bonds are formed resulting in a diamond-like structure capped by hydrogen atoms on both outer sides. It was shown by density functional theory calculations that external strain²⁸ or electric bias²⁵ allows the continuous tuning of the band gap of hydrogenated bilayer graphene.

The kinetics of hydrogen atoms adsorbed in multilayer graphene have rarely been investigated. Stable hydrogenation configurations²⁹ and the energy barriers of in-plane diffusion and inter-plane jumping in bulk graphite¹⁶ have been investigated by density functional theory. However, the calculations have been carried out without proper corrections for van der Waals interactions. By tight binding molecular dynamics simulations on graphite, it was found that hydrogen atoms move to adjacent carbon atoms in the same or adjacent sheet with a diffusion barrier of 0.40 eV,³⁰ but more detailed information about the hydrogen atom diffusion through interlayer space is still lacking. In this work, we calculated the diffusion barriers of chemisorbed hydrogen atoms in AB stacking bilayer and tetralayer graphene at the density functional theory level. In addition, we investigated the effect of the stacking fault (e.g. glide defects) on the hydrogen atom diffusion and found that the stacking fault can facilitate the diffusion by lowering the barrier of inter-plane jumping.

2 Computational method

All calculations were performed by a first principles quantum mechanical code, CASTEP program³¹ in the Materials Studio 5.5 package. The electron exchange-correlation functional was represented with the generalized gradient approximation of Perdew, Burke and Ernzerhof (PBE)³² augmented with the Tkatchenko–Scheffler dispersion correction (PBE-TS).^33,34 The convergence tolerance for self-consistent field (SCF) iterations was set to 2.0 × 10⁻⁶ eV per atom and the values of the geometry optimization convergence thresholds for energy change, maximum force, maximum stress, and maximum displacement between optimization cycles are 2 × 10⁻⁵ eV per atom, 0.05 eV Å⁻¹, 0.1 GPa, and 0.002 Å, respectively. Optimizing the unit cell of bulk graphite using PBE, PBE-TS and the local density approximation (LDA)^35,36 the interlayer distance of graphite is 4.271, 3.320 and 3.307 Å, respectively. PBE underestimates the van der Waals interaction between the layer planes and LDA overestimates it, while the PBE-TS result shows better agreement with the experimental value of 3.336 Å.³⁷ Therefore, PBE-TS was chosen as the exchange-correlation functional in all calculations. The core electrons were described by the ultrasoft pseudopotentials.³⁸ To treat the metallic character of graphene, the Gaussian-like smearing scheme³⁹ was adapted with the width of 0.1 eV. In the optimization of the structures, the kinetic energy cutoff of 400 eV was used and the 2 × 2 × 1 k-points were sampled in the first Brillouin zone by Monkhorst and Pack method.⁴⁰ All calculations for hydrogenated states are spin polarized. The transition states were searched by the linear and quadratic synchronous transit method (LST/QST)⁴¹ implemented in CASTEP. The LST/QST method linearly interpolates a reaction pathway connecting reactants and products and finds the maximum energy state. Using that state, another conjugate gradient minimization is performed to locate a stationary point.

When chemisorbed in the multilayer graphene, hydrogen atoms can bind to two types of carbon atoms: (i) carbon A having neighbors directly above and below in the adjacent layers; and (ii) carbon B facing the middle hollow sites of hexagons in adjacent layers (Fig. 1a). Thus, if a hydrogen atom is attached to carbon A (or B) from the upside (or from the downside) of layer 1, it is labeled as 1A_u (or 1B_d). In order to investigate the hydrogen atom diffusion through interlayer space, monolayer (MNL), bilayer (BIL) and tetralayer (TEL) graphene with AB stacking were modeled.

Fig. 1 (a) A schematic description of carbon A and carbon B, (b) the bilayer graphene and (c) the tetralayer graphene with AB stacking. The layer planes are numbered sequentially from bottom to top.

The dimensions of supercells 6 × 6 (MNL), 6 × 6 × 1 (BIL) and 6 × 6 × 2 (TEL) are 14.76 × 14.76 × 15.00, 14.73 × 14.73 × 18.32 and 14.73 × 14.73 × 24.96 Å, respectively. In all models ∼15 Å vacuum region was included in the direction perpendicular to the layer plane. The optimized structures show that the interlayer spacing of bulk graphite is well retained in the BIL and TEL structures (Fig. 1b and c).

3 Results and discussion

3.1 The diffusion of the H atom adsorbed in AB stacking graphenes

Before the kinetics study of the adsorbed hydrogen atom, it should be confirmed that hydrogen atom binding is thermodynamically favorable even in the interlayer space. To this end, we first calculated the binding energy, E_bind of a hydrogen atom using the following equation

E_bind = E(graphene) + E(H(g)) − E(graphene − H), (1)

where E (graphene − H) is the total energy of a hydrogen atom adsorbed on graphene, E (graphene) is the total energy of graphene and E (H(g)) is the total energy of a hydrogen atom in the gas phase. As hydrogen atoms are supplied onto the graphene/graphite surfaces in hydrogenation experiments,^5,42,43 the energy of a hydrogen atom in the gas phase is taken into account in the above equation. For the monolayer, the binding energy is 0.75 eV which agrees well with previous calculation studies (0.71,⁴⁴ 0.74,⁴⁵ 0.84,⁴⁶ 0.87 (ref. 47) eV). The entropy of a hydrogen atom is about 114.71 J mol⁻¹ K in the gas state at T = 298 K and 1 atm pressure.⁴⁸ Assuming that the adsorbed hydrogen atom loses this gas state entropy, the binding energy should be at least TΔS = 0.35 eV for the reaction to take place spontaneously at 298 K. For all possible hydrogenated configurations, the calculated binding energy is larger than 0.50 eV (Table 1), indicating that the hydrogenation reactions are thermodynamically feasible.

Table 1 The hydrogen atom binding energy, E_bind in monolayer (MNL), bilayer (BIL) and tetralayer (TEL) graphene with AB stacking and two glide defect structures, ZIG and ARM made by shifting a plane of BIL in the “zigzag” and the “armchair” directions, respectively

Model	Binding site		Ebind (eV)
a Averaged value.
MNL			0.75
BIL	Outside	2Au	0.73
		2Bu	0.75
	Inside	2Ad	0.63
		2Bd	0.70
TEL	Outside	4Au	0.75
		4Bu	0.76
	Inside	4Ad	0.63
		4Bd	0.70
		3Au	0.63
		3Bu	0.73
		3Ad	0.53
		3Bd	0.66
ZIG	Outside		0.79^a
	Inside		0.71^a
ARM	Outside		0.76^a
	Inside		0.68^a

---

The hydrogen binding occurring in the interlayer space (inside binding) is about 0.02–0.2 eV weaker than that occurring outside of the graphene (outside binding). This instability of the inside binding is caused by a strained structure of the hydrogenated carbon atom. Compared to the outside binding, the inside binding does not allow the hybridization of the hydrogenated carbon to be perfectly transformed into sp³ because the close contact between the adsorbed hydrogen atom and the opposite plane hinders the hydrogenated carbon from protruding (see Fig. S1 of the ESI†).

Next, we calculated the hydrogen diffusion energy barriers. Our calculation shows that the energy barriers are about 1.27–1.29 eV for the in-plane diffusion occurring outside the BIL and TEL (2A_u ↔ 2B_u for BIL and 4A_u ↔ 4B_u for TEL) and these barriers are very similar to that for the diffusion on MNL (Table 2). However, the barriers of the in-plane diffusion paths inside the BIL and TEL are lowered by 0.11–0.38 eV, which is attributed to the destabilized reactants and products as mentioned above and the more stable transition states inside the interlayer space. The stabilization of the transition states can be explained by considering the less deformed (more sp²-like) transition states formed between the layers. For the transition state of the in-plane path outside the BIL, two carbon atoms involved in the diffusion deviate from the plane by 0.189 Å, while inside the BIL they deviate by only 0.079 Å. The less deformed transition states inside the interlayer space are also observed in the TEL model (see Fig. S2 of the ESI†).

Table 2 The hydrogen atom diffusion energy barrier in the graphene models

Model	Diffusion path		Barrier (eV)
			→^a	←^a
a → is for the forward reaction and ← is for the backward reaction.
MNL	In-plane	Ortho	1.27	1.27
BIL	In-plane	2Au → 2Bu	1.27	1.29
		2Ad → 2Bd	1.09	1.16
	Inter-plane	2Ad → 1Au	0.66	0.66
		2Ad → 1Bu	1.32	1.38
		2Bd → 1Bu	1.33	1.32
TEL	In-plane	4Au → 4Bu	1.28	1.29
		4Ad → 4Bd	1.02	1.09
		3Au → 3Bu	1.02	1.11
		3Ad → 3Bd	0.91	1.04
	Inter-plane	4Ad → 3Au	0.58	0.58
		4Ad → 3Bu	1.23	1.32
		4Bd → 3Bu	1.27	1.29
		3Ad → 2Au	0.56	0.56
		3Ad → 2Bu	1.15	1.28
		3Bd → 2Bu	1.19	1.19
ZIG	In-plane	1	1.07	1.08
		2	1.14	1.12
	Inter-plane	3	0.95	0.93
		4	0.85	0.85
		5	0.92	0.93
		6	0.95	0.96
ARM	In-plane	1	1.08	1.08
		2	1.14	1.14
	Inter-plane	3	0.85	0.85
		4	1.18	1.19

---

The energy barrier of the vertical inter-plane jumping is 0.66 eV in the BIL (2A_d ↔ 1A_u), and it reduces in TEL to 0.58 eV (4A_d ↔ 3A_u) or 0.56 eV (3A_d ↔ 2A_u). The barriers of other types of inter-plane jumping also decrease from 1.32–1.38 eV in the BIL to 1.15–1.32 eV in the TEL. In addition, the barriers are lower for the jumpings between layer 2 and 3 than for the corresponding jumpings between layer 3 and 4 of the TEL. The decrease in the energy barriers is closely related to two things: the destabilized reactants and products, and the travel distance of the hydrogen atom during the diffusion reaction. The shorter the travel distance is, the lower the energy barrier becomes. The relationship between the energy barrier and the travel distance will be more discussed later. Except for the vertical transfer, the inter-plane jumpings have larger barriers than the in-plane diffusion paths, and though the energy barrier for the vertical transfer is very low, it is not a useful pathway for the diffusion of the adsorbed hydrogen atom along the basal plane surface. This suggests that the diffusion of the hydrogen atom takes place by the in-plane paths and the inter-plane jumping hardly helps hydrogen atoms to move around inside the graphite layers with ABAB stacking.

3.2 The influence of the glide defects on the diffusion of chemisorbed H atoms

Gliding graphene sheets cause a bulk defect with alternative stacking structures. In the heat-treated vapor-grown carbon fibers the stacking fault with the graphene layers gliding in the “zigzag” direction have been found.⁴⁹ The graphite epitaxially grown on the diamond (111) surface has been reported to have a new crystal structure with AA′ staking in which the layers shift in the “armchair” direction.⁵⁰ We modeled two glide defect structures by modifying the BIL: one by shifting a layer in the “zigzag” direction (ZIG) and the other by shifting in the “armchair” direction (ARM) by a half the hexagon edge width (Fig. 2). The ZIG and ARM structures are less stable than the BIL with AB stacking by 1.17 × 10⁻³ and 2.15 × 10⁻⁴ eV per C_atom, respectively. The interlayer spacing of the ZIG is 3.426 Å and that of the ARM is 3.418 Å which agrees well with the experimental value of 3.43 Å for the AA′ stacking structure.⁵⁰ The hydrogen binding energies in the ZIG and ARM are very similar to those in the BIL structure (Table 1).

Fig. 2 The ZIG and ARM structures and the diffusion paths inside the interlayer space. In the magnified pictures, the dotted arrows indicate the inter-plane jump paths and the solid arrows indicate the in-plane diffusion paths.

In the ARM structure, the energy barrier of the inter-plane path 3 is 0.85 eV, but that of path 4 is 1.18 eV that is larger than those of the in-plane paths. Therefore, hydrogen atoms are expected to diffuse through both the in-plane and inter-plane paths in the ARM structure. In the ZIG structure, two in-plane diffusion paths defined in Fig. 2 have almost the same barriers as those in the BIL structure. Large differences are found in the barriers of the inter-plane jumping. The energy barriers for the inter-plane jumping in the ZIG are less than 1 eV and are lower by about 0.4 eV than those in the BIL. Therefore, because all the possible inter-plane paths in the ZIG have low energy barriers, hydrogen atoms can diffuse along those pathways over a long distance by consecutive jumps between adjacent layers.

The diffusion rate Γ is usually given by the equation⁵¹

Γ = v⁰e^−ΔG/k_BT = v⁰e^ΔS/k_Be^−ΔH/k_BT = v*e^−ΔH/k_BT, (2)

where ΔG, ΔS and ΔH are the activation free energy, the entropy, and the enthalpy of diffusion, respectively, T is the temperature, k_B is Boltzmann's constant, v⁰ is the phonon frequency of a vibrational movement of adsorbed hydrogen atom to the saddle point, and v* is the effective frequency including the entropy effect. To understand the diffusion rate, besides the energy barrier we need to calculate the effective frequencies of the diffusion pathways with different mechanisms. The effective frequency, v* was calculated as the ratio of the product of the phonon frequencies of the initial state to that of the frequencies of the transition state.⁵¹ The finite displacement method was used to calculate the phonon frequencies, which is based on the numerical differentiation of forces on atoms in the cell with atomic displacements by a very small magnitude,⁵² and to reduce the degrees of freedom, the first and second nearest carbon atoms around the reaction center in the upper and lower layers were freely relaxed and the other carbon atoms were fixed during the phonon frequency calculations. The configuration of the fixed carbon atoms is depicted in Fig. S3 of the ESI.† For the phonon frequency calculations, we set the SCF tolerance to 1.0 × 10⁻⁴ eV per atom and only gamma point was considered. In regard to the entropy effect of migration in the ZIG structure, we have calculated the effective frequencies, v* of an inter-plane path 4 and an in-plane diffusion path 1. The effective frequency, v* of the inter-plane jump is 28 048.4 s⁻¹ and that of the in-plane path inside the ZIG is 24 477.9 s⁻¹. The inter-plane jump has a larger effective frequency than the in-plane path. In addition to the lower energy barrier of the inter-plane jump between the layers of ZIG, the larger effective frequency of the inter-plane jump make the inter-plane jumping a more favorable diffusion way.

The lower energy barriers of the inter-plane jumpings in the ZIG structure arise from the short distance through which the hydrogen atom should travel as well as the less tightly bound hydrogen atom inside the interlayer space. In Fig. 3, the linear dependency of the energy barrier on the travel distance is shown. When the sheet-gliding takes place, new inter-plane diffusion paths with short travel distances are generated. This structural change makes the adsorbed hydrogen atoms more easily diffuse in the glide defect structures such as the ZIG than in the AB stacked bilayer graphene. Furthermore, as the glide defect is the bulk defect, it can affect the diffusion kinetics in the greater range compared to the point defects such as vacancies and Stone–Wales defects, and disorder introduced by functionalization, the effect of which is limited within a narrow range around them. Therefore, if chemisorbed hydrogen atoms are to be spread into the bulk, the glide defects would be more suitable for that purpose than the point defects. Especially, hydrogen storage by the spillover onto the graphitic surface could be accomplished more easily by the introduction of the glide defects because one of the main obstacles for understanding and realizing the spillover mechanism is the diffusion of spilled-over hydrogen atoms on graphitic surfaces over a long distance from the metal catalyst on which hydrogen molecules are decomposed to hydrogen atoms.¹⁷

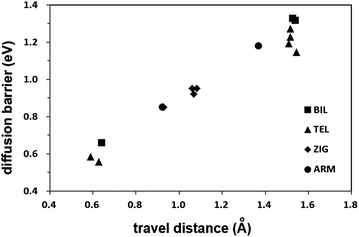Fig. 3 The energy barrier vs. travel distance of the inter-plane jump paths. The travel distance is defined as the distance from the hydrogen atom in the reactant to that in the product.

4 Conclusions

In conclusion, we have calculated the diffusion energy barriers of hydrogen atoms chemisorbed in mono-, bi- and tetralayer graphene with AB stacking and bilayers with glide defect using density functional theory augmented with van der Waals interaction corrections. We found that the stacking fault such as glide defect can lower the diffusion barriers of the inter-plane paths and the inter-plane path has the larger effective frequency, and hence the stacking fault defect can generate new pathways through which hydrogen atoms can proceed jumping back and forth between adjacent layers. In this work, we do not take into account the quantum effects of nuclear motions such as phonon-assisted tunneling. For hydrogen, the quantum effects can reduce the barrier at room temperature by about 10%.¹³ Therefore, the barriers reported here can be renormalized as the 10% smaller value by the quantum effects.

We expect that our results could provide a better understanding of the mechanisms of the hydrogenation processes and hydrogen storage in graphite and multilayer graphene materials. In the inelastic neutron scattering experiments on hydrogen spill-over by the Pt-doped activated carbon (Pt/AC) samples, it was indicated that the spilled-over hydrogen atom on the AC surface could diffuse more than 2.8 nm away from a Pt cluster.⁵³ However, the long distance diffusion of the chemisorbed hydrogen atom has not been fully explained. The present work suggests that the bulk defects possibly existing in the AC carbon could contribute to the long diffusion length. The high mobility of hydrogen atoms inside the ball-milled graphite has been detected by nuclear-magnetic-resonance method.^54–56 Although the latest paper assigned the highly mobile hydrogen motion to the rotation of methyl groups,⁵⁶ given that the mechanical milling could make a lot of defects including the stacking faults in the graphite the fast diffusion inside the ball-milled graphite induced by the stacking faults could be one of the origins of the high mobility of the chemisorbed hydrogen atoms. Lastly, the reduction reaction of azoaromatic compounds separated by graphite foil from the catalytic iron powder⁵⁷ might be explained by the hydrogen atom diffusion inside the graphite layers.

Acknowledgements

This research was supported by the Creative Research Program (2012–2014) of the Korea Atomic Energy Research Institute. We thank Accelrys Korea for the support of modeling software.

References

1. S. Niyogi, E. Bekyarova, J. Hong, S. Khizroev, C. Berger, W. de Heer and R. C. Haddon, J. Phys. Chem. Lett., 2011, 2, 2487.
2. Z. Sun, D. K. James and J. M. Tour, J. Phys. Chem. Lett., 2011, 2, 2425.
3. H. Gao, L. Wang, J. Zhao, F. Ding and J. Lu, J. Phys. Chem. C, 2011, 115, 3236.
4. D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610.
5. J. A. J. Lachawiec, G. Qi and R. T. Yang, Langmuir, 2005, 21, 11418.
6. L. F. Huang, M. Y. Ni, G. R. Zhang, W. H. Zhou, Y. G. Li, X. H. Zheng and Z. J. Zeng, J. Chem. Phys., 2011, 135, 064705.
7. L. F. Huang, M. Y. Ni, Y. G. Li, W. H. Zhou, X. H. Zheng, L. J. Guo and Z. Zeng, Surf. Sci., 2011, 605, 1489.
8. A. A. Dzhurakhalov and F. M. Peeters, Carbon, 2011, 49, 3258.
9. A. R. Muniz and D. Maroudas, J. Appl. Phys., 2010, 108, 113532.
10. V. V. Ivanovskaya, A. Zobelli, D. Teillet-Billy, N. Rougeau, V. Slidis and P. R. Briddon, Eur. Phys. J. B, 2010, 76, 481.
11. R. Balog, B. Jorgensen, J. Wells, E. Laegsgaard, P. Hofmann, F. Besenbacher and L. Hornekaer, J. Am. Chem. Soc., 2009, 131, 8744.
12. D. W. Boukhvalov, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035427.
13. C. P. Herrero and R. Ramirez, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115429.
14. L. F. Huang, M. Y. Ni, X. H. Zheng, W. H. Zhou, Y. G. Li and Z. Zeng, J. Phys. Chem. C, 2010, 114, 22636.
15. D. W. Boukhvalov, Phys. Chem. Chem. Phys., 2010, 12, 15367.
16. Y. Lei, S. A. Shevlin, W. Zhu and Z. X. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 134114.
17. S. S. Han, H. Jung, D. H. Jung, S. H. Choi and N. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155408.
18. G. M. Psofogiannakis and G. E. Froudakis, J. Phys. Chem. C, 2009, 113, 14908.
19. X. Sha, M. T. Knippenberg, A. C. Cooper, G. P. Pez and H. Cheng, J. Phys. Chem. C, 2008, 112, 17465.
20. H. Y. Wu, X. Fan, J. L. Kuo and W. Q. Deng, J. Phys. Chem. C, 2011, 115, 9241.
21. L. F. Huang, M. Y. Ni and Z. Zeng, J. Phys.: Condens. Matter, 2011, 23, 435007.
22. J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo and L. M. K. Vandersypen, Nat. Mater., 2008, 7, 151.
23. E. McCann, D. S. L. Abergel and V. I. Fal'ko, Solid State Commun., 2007, 143, 110.
24. F. M. Koehler, A. Jacobsen, K. Ensslin, C. Stampfer and W. J. Stark, Small, 2010, 6, 1125.
25. D. K. Samarakoon and X. Q. Wang, ACS Nano, 2010, 4, 4126.
26. O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245422.
27. J. M. B. LopesdosSantos, N. M. R. Peres and A. H. CastroNeto, Phys. Rev. Lett., 2007, 99, 256802.
28. Y. Zhang, C. H. Hu, Y. H. Wen, S. Q. Wu and Z. Z. Zhu, New J. Phys., 2011, 13, 063047.
29. W. A. Dino, Y. Miura, H. Nakanishi, H. Kasai and T. Sugimoto, J. Phys. Soc. Jpn., 2003, 72, 1867.
30. C. P. Herrero and R. Ramirez, J. Phys. D: Appl. Phys., 2010, 43, 255402.
31. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
33. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
34. N. Marom, A. Tkatchenko, M. Scheffler and L. Kronik, J. Chem. Theory Comput., 2010, 6, 81.
35. J. P. Perdew and A. Zunger, Phys. Rev. B, 1981, 23, 5048.
36. D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566.
37. V. Baskin and L. Meyer, Phys. Rev., 1955, 100, 544.
38. D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1990, 41, 7892.
39. A. D. Vita, Ph.D. thesis, Keele University, 1992.
40. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
41. N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, Comput. Mater. Sci., 2003, 28, 250.
42. Z. Luo, T. Yu, Z. Ni, S. Lim, H. Hu, J. Shang, L. Liu, Z. Shen and J. Lin, J. Phys. Chem. C, 2011, 115, 1422.
43. A. Nikitin, L. A. Naslund, Z. Zhang and A. Nilsson, Surf. Sci., 2008, 602, 2575.
44. T. Roman, W. A. Dino, H. Nakanishi, H. K. T. Sugimoto and K. Tange, Carbon, 2007, 45, 218.
45. M. Yang, A. Nurbawono, C. Zhang, R. Wu, Y. Feng and Ariando, AIP Adv., 2011, 1, 032109.
46. S. Casolo, O. M. Lovvik, R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2009, 130, 054704.
47. P. O. Lehtinen, A. S. Foster, Y. Ma, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2004, 93, 187202.
48. P. W. Atkins, Physical Chemistry, Oxford University Press, 4th edn, 1990.
49. M. Endo, K. Oshida, K. Kobori, K. Takeuchi, K. Takahashi and M. S. Dresselhaus, J. Mater. Res., 1995, 10, 1461.
50. J. K. Lee, S. C. Lee, J. P. Ahn, S. C. Kim, J. I. B. Wilson and P. John, J. Chem. Phys., 2008, 129, 234709.
51. G. H. Vineyard, J. Phys. Chem. Solids, 1957, 3, 121.
52. B. Montanari and N. M. Harrison, Chem. Phys. Lett., 2002, 364, 528.
53. C.-S. Tsao, Y. Liu, H.-Y. Chuang, H.-H. Tseng, T.-Y. Chen, C.-H. Chen, M.-S. Yu, Q. Li, A. Leuking and S.-H. Chen, J. Phys. Chem. Lett., 2011, 2, 2322.
54. G. Majer, E. Stanik and S. Orimo, J. Alloys Compd., 2003, 356–357, 617.
55. G. Majer, E. Stanik and S. Orimo, J. Alloys Compd., 2004, 377, 316.
56. E. Stanik, G. Majer, S. Orimo, T. Ichikawa and H. Fujii, J. Appl. Phys., 2005, 98, 044302.
57. J. Ye and P. C. Chiu, Environ. Sci. Technol., 2006, 40, 3959.

---

Footnote

† Electronic supplementary information (ESI) available: the structures of hydrogenated graphenes and transition states. See DOI: 10.1039/c3ra46626d

---