DOI:
10.1039/C1MB05262D
(Paper)
Mol. BioSyst., 2012,
8, 378-380
Sedimentation velocity of intrinsically disordered proteins: what information can we actually obtain?†
Received
24th June 2011
, Accepted 13th September 2011
First published on 27th September 2011
Abstract
Intrinsically disordered proteins are a challenge to characterise structurally because of their innate flexibility. Hydrodynamic methods such as sedimentation velocity analytical ultracentrifugation have been proposed as methods for their characterisation. By examining in detail this assumption we show that although velocity measurements do yield information on gross conformation, the information is restricted to only the weight averaged sedimentation and diffusion coefficients of the conformational ensemble.
Introduction
Intrinsically disordered proteins (IDPs) provide a significant challenge to the structural biologist because of their failure to exhibit a unique three dimensional structure.1 Solution techniques have therefore come to the fore in the endeavour to characterise the ensemble of conformations adopted by these proteins.2 In this communication we look critically at one these techniques, sedimentation velocity analytical ultracentrifugation, as a tool for probing the solution conformation of IDPs.
Sedimentation velocity has become a popular technique for characterising protein conformation and heterogeneity because of a largely automated experimental protocol3 that can be combined with the considerable advances in data analysis afforded by a lively and active community of method developers.4–9 The concentration distributions from a typical sedimentation velocity experiment are shown in Fig. 1, which reveals the development of a distinctive S-shaped profile with time. The rate of boundary migration is governed by the sedimentation coefficients of the species present, whereas the broadness of the boundary is dictated by the corresponding diffusion coefficients.10,11 In sufficiently dilute solutions for the effects of thermodynamic and hydrodynamic non-ideality arising from inter-particle interactions to become negligible, these concentration distributions are described by a set of well known mathematical relationships11 that can be solved readily by tried-and-tested numerical methods.3 Such analysis is taken to reflect either a single sedimentation coefficient or, more rigorously, the distribution of sedimentation coefficients for all species present in the solution. Because of this feature, sedimentation velocity is a very attractive method for rapid and rigorous characterisation of solution homogeneity with respect to molecular size as well as for gross conformational analysis. Indeed, there have been several such studies of IDPs (reviewed in ref. 2). Here we examine in detail the consequences of subjecting an ensemble of IDP conformers to sedimentation velocity in order to ascertain the information that can be obtained by this procedure.
 |
| | Fig. 1 A typical sedimentation velocity experiment on a protein. The experiment was carried out at 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm in a Beckman XL-A analytical ultracentrifuge. The time between successive scans was 50 min. The radial point rm denotes the position of the meniscus from which material sediments. The distance between scans is dictated by the rate of sedimentation, while the broadness of the boundaries is given by the diffusion coefficient. Mathematically this is expressed by the Lamm equation (eqn (1)). The boundary shape potentially contains information on the type of interaction because of its sensitivity to interactions between species (eqn (3)). 000 rpm in a Beckman XL-A analytical ultracentrifuge. The time between successive scans was 50 min. The radial point rm denotes the position of the meniscus from which material sediments. The distance between scans is dictated by the rate of sedimentation, while the broadness of the boundaries is given by the diffusion coefficient. Mathematically this is expressed by the Lamm equation (eqn (1)). The boundary shape potentially contains information on the type of interaction because of its sensitivity to interactions between species (eqn (3)). | |
Consideration of sedimentation coefficients for a pool of interconverting isomers
In an analytical ultracentrifuge, the outward radial migration of a single macromolecular species is effected by the gravitational field. Such migration is opposed by a diffusional force arising from the creation of a concentration gradient (Fig. 1). This combination of migration responses is encapsulated mathematically in terms of the sedimentation coefficient (s) and diffusion coefficient (D) by the continuity equation defined by Lamm:10| |  | (1) |
where c is the weight concentration at radial distance r, and t is time of centrifugation at constant angular velocity ω. For a mixture of n independent species this equation requires modification to the form:11,12| |  | (2) |
However, the existence of IDPs in multiple conformations that interconvert freely in solution,1 dictates the inclusion of kinetic terms into the continuity equation for each conformer to accommodate the rates of these interconversions. Consequently, the concentration of a given species, ci, at any point in the centrifuge cell becomes a function of the concentration of any other conformer, cj, as well as of the rates of isomeric interconversion between the i and j conformational states. For illustrative purposes we shall restrict consideration to a mixture of two isomeric states, i and j, a simplification that still affords insight into the effect of isomeric interconversions. The Lamm equations for the two isomers then become:12| |  | (3a) |
and| | 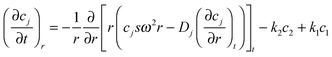 | (3b) |
where k1 is the rate constant for the conversion of i to j, and k2, is the corresponding rate constant for the reverse reaction. Early studies by Longsworth and MacInnes13 revealed the need to consider five possible rate-constant combinations. For two of those combinations, k1 ≫ k2 and k2 ≫ k1, eqn (1) suffices to describe the migration because of the effective elimination of one isomeric state. On the other hand, continuity equations for both species are required in the event that k1 and k2 are sufficiently small for essentially no interconversion of species to occur on the timescale of species separation. A similar requirement pertains to systems for which the rates of species interconversion are of similar magnitude to the rate of species separation (i.e., to systems for which migration is subject to kinetic control). As is evident from Fujita’s treatment of two-state isomerization, we can then derive the continuity equation for the total concentration of n freely interconverting conformers, which takes the form:| |  | (4) |
In that regard the existence of a perceptible population of a given conformational state requires the rate constants for formation of that species to exceed those for its conversion to other states. For slow interconversion between two isomeric states, A ⇆ B, Cann14 has shown that the sedimentation velocity distribution would comprise separate boundaries for A and B, their relative sizes being dependent upon the ratio of the forward and reverse rate constants.
However, IDPs have very shallow free energy profiles—the characteristic that allows them to adopt a multiplicity of conformational states in solution.15 The fact that there is then little difference between rate constants for the formation and depletion of a given isomer leads to the coexistence of multiple iso-energetic conformational states in rapidly established equilibrium. This is the fifth potential situation enunciated by Longsworth and MacInness,13 and also the other limiting case considered by Fujita.11 Because the relative concentrations of isomers coexisting in rapidly established equilibrium are independent of total concentration, the rates of sedimentation and diffusional spreading are invariant across the migrating boundary system. Consequently, the concentration distribution comprises a single symmetrical boundary whose migration is described by eqn (1) with c identified as the total concentration at radial distance r, and s and D as weight-average quantites.11 It therefore follows that the only quantities extractable from a sedimentation velocity experiment on an IDP are average values of the sedimentation and diffusion coefficients: no information on the likely extent of variations in s and D between isomeric states can be extracted. Furthermore, these average values of s and D are obviously dominated by contributions from the more highly populated hydrodynamic states; but it should also be noted that the concentration ci assigned to species i with a sedimentation coefficient si and diffusion coefficient Di in eqn (4) could well include several conformers with very similar migration characteristics.3
Conclusion
This detailed consideration of the continuity equations describing the migration of IDPs in a sedimentation velocity experiment has shown that the only parameters to be derived therefrom are single values of the sedimentation and diffusion coefficients that reflect averages of those for multiplicity of conformational states adopted by these proteins. Although the anomalously low sedimentation coefficients exhibited by intrinsically disordered proteins can be attributed to the presence of highly populated conformational states with extended configurations, the determination of such sedimentation coefficients is not necessarily a diagnostic of intrinsic structure disorder: highly structured but extremely asymmetric proteins also exhibit similar sedimentation velocity behaviour. In this manner, it is similar to studies of proteins in high denaturants. Nevertheless, the ease with which sedimentation and diffusion coefficients can be determined renders their measurement valuable as confirmatory evidence for assessing the reliability of population distributions derived from small angle scattering16,17 and/or NMR studies.18 Their continued measurement thus remains a useful adjunct to the structural modelling of conformer ensembles.
Notes and references
-
P. Tompa, Structure and Function of Intrinsically Disordered Proteins, CRC Press, Boca Raton, 2010 Search PubMed.
-
V. Uversky and S. Longhi, Instrumental Analysis of Intrinsically disordered proteins: Assessing Structure and Conformation, John Wiley and Sons, Inc., Hoboken, NJ, 2010 Search PubMed.
-
D. J. Scott, S. E. Harding and A. J. Rowe, Analytical Ultracentrifugation: Techniques and Methods, Royal Society of Chemistry, Cambridge, United Kingdom, 2005 Search PubMed.
- B. Demeler and H. Saber, Biophys. J., 1998, 74, 444–454 CrossRef CAS.
- B. Demeler, E. Brookes and L. Nagel-Steger, Methods Enzymol., 2009, 454, 87–113 CAS.
- E. Brookes, W. Cao and B. Demeler, Eur. Biophys. J., 2010, 39, 405–414 CrossRef.
- P. Schuck and P. Rossmanith, Biopolymers, 2000, 54, 328–341 CrossRef CAS.
- P. Schuck, M. A. Perugini, N. R. Gonzales, G. J. Howlett and D. Schubert, Biophys. J., 2002, 82, 1096–1111 CrossRef CAS.
- P. Schuck, Eur. Biophys. J., 2009, 39, 1261–1275 CrossRef.
- O. Lamm, Z. Physik. Chem. (Leipzig)., 1929, A143, 177 Search PubMed.
-
H. Fujita, Mathematical Theory of Sedimentation Analysis, Academic Press, New York, 1962 Search PubMed.
-
J. R. Cann, Interacting Macromolecules: The Theory and Practice of Their Electrophoresis, Ultracentrifugation, and Chromatography, Academic Press, New York, 1970 Search PubMed.
- L. G. Longsworth and D. A. MacInnes, J. Gen. Physiol., 1942, 25, 507–516 CrossRef CAS.
- J. R. Cann, Arch. Biochem. Biophys., 1957, 72, 37–41 CrossRef CAS.
- C. K. Fisher and C. M. Stultz, Curr. Opin. Struct. Biol., 2011, 21, 426–431 CrossRef CAS.
- P. Bernado, E. Mylonas, M. V. Petoukhov, M. Blackledge and D. I. Svergun, J. Am. Chem. Soc., 2007, 129, 5656–5664 CrossRef CAS.
- K. Rajasekar, S. T. Muntaha, J. R. Tame, S. Kommareddy, G. Morris, C. W. Wharton, C. M. Thomas, S. A. White, E. I. Hyde and D. J. Scott, J. Biol. Chem., 2010, 285, 15440–15449 CrossRef CAS.
- M. R. Jensen, P. R. Markwick, S. Meier, C. Griesinger, M. Zweckstetter, S. Grzesiek, P. Bernado and M. Blackledge, Structure, 2009, 17, 1169–1185 CrossRef CAS.
Footnote |
| † Published as part of a Molecular BioSystems themed issue on Intrinsically Disordered Proteins: Guest Editor M. Madan Babu. |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm in a Beckman XL-A analytical ultracentrifuge. The time between successive scans was 50 min. The radial point rm denotes the position of the meniscus from which material sediments. The distance between scans is dictated by the rate of sedimentation, while the broadness of the boundaries is given by the diffusion coefficient. Mathematically this is expressed by the Lamm equation (eqn (1)). The boundary shape potentially contains information on the type of interaction because of its sensitivity to interactions between species (eqn (3)).
000 rpm in a Beckman XL-A analytical ultracentrifuge. The time between successive scans was 50 min. The radial point rm denotes the position of the meniscus from which material sediments. The distance between scans is dictated by the rate of sedimentation, while the broadness of the boundaries is given by the diffusion coefficient. Mathematically this is expressed by the Lamm equation (eqn (1)). The boundary shape potentially contains information on the type of interaction because of its sensitivity to interactions between species (eqn (3)).