Spontaneous symmetry breaking in a non-rigid molecule approach to intrinsically disordered proteins†
Rodrick
Wallace
Division of Epidemiology, The New York State Psychiatric Institute, Box 47, 1051 Riverside Dr, NY, NY, 10032 USA. E-mail: rodrick.wallace@gmail.com
First published on 9th September 2011
Abstract
An analog to Longuet-Higgins' non-rigid molecular group theory arguments can be applied to the structure and reaction dynamics of intrinsically disordered proteinsvia a somewhat counterintuitive Morse Function treatment inspired by statistical mechanics, providing possible symmetry classifications of the molecular ‘fuzzy lock-and-key’.
1 Introduction
Many proteins have no unique tertiary structure in isolation, although they have a distinct function, under physiological conditions, in partnership. Called ‘intrinsically disordered proteins’ (IDP), their conformation is determined not only by their amino acid sequence, but also by their interacting partner.1–4 They are, in large measure, without a hydrophobic core. Uversky2 notes that:“An intriguing property of intrinsically unstructured proteins is their capability to undergo disorder-to-order transitions upon functioning. The degree of these structural rearrangements varies over a very wide range, from coil-premolten globule transitions to formation of rigid ordered structures.”
Significantly extending that perspective, Tompa and Fuxreiter4 find:
“There is a consensus that although these proteins are structurally disordered in isolation, they become ordered following binding to their partner(s)—that is, their structures can ultimately be solved in the bound state… To many, this might seem to ‘restore’ the prestige of the classical structure-function paradigm that equated protein function with a well-defined 3D structure.
A closer inspection… reveals that this underlying premise is not generally true: often the part(s) of the complexes that contribute productively to binding and function are structurally ill-defined, and cannot be described by a single conformational state… In static disorder, a region of a protein might adopt multiple stable conformations… By contrast, a protein , or a region of a protein , might constantly fluctuate between a large number of states, and can be best described as a conformational ensemble. The disorder in this case is dynamic.”
It is precisely this accession of static/dynamic order-in-partnership that is of interest here. In general, there will be an initial set of partner-and-IDP conformations Si that is transported to a final set of partnerships Sf in such a manner as to evade the chemical cognition of cellular clean-up machinery. The purpose of this paper is to outline an application of non-rigid molecule theory, as developed by Longuet–Higgins5 and others, to the IDP problem of many locks/many keys. The basic idea might well be described as ‘fuzzy lock theory’, analogous to a generalization of knot theory when defined sets of initial and final conformations are permitted. The essential conceptual difficulty is that one truly wishes to think in classical terms about IDP—which are really complicated quantum systems—using such metaphors as ‘fly casting’6,7 or, as in my own work,8 ‘a snake slithering down a rough hill’. The approach here is via an analog of statistical mechanics applied to non-rigid molecular symmetries.
2 A symmetry argument
Longuet-Higgins,5 in a classic paper, shows that:“The symmetry group of [a non-rigid] molecule is the set of (i) all feasible permutations of the positions and spins of identical nuclei and (ii) all feasible permutation-inversions, which simultaneously invert the coordinates of all particles in the centre of mass.”
The theory arising from this insight has had great success for understanding the spectra of modestly large molecules across much of chemistry and chemical physics.9–12 It can, with some development, be applied to the problem of understanding IDP.
Assume it possible to extend non-rigid molecular group theory to the long, whip-like frond of an IDP anchored at both ends, via a sufficient number of semi-direct and/or wreath products over an appropriate set of finite and/or compact groups.9 These are taken as parameterized by an index of ‘frond length’ L which might simply be the total number of amino acids in the IDP. In general, the number of group elements can be expected to grow exponentially, as ∑Πj|Gj||Hj|L, where |Gk| and |Hk| are the size, in an appropriate sense,9,10 of symmetry groups Gk and Hk. Hence, for large L, we are driven to a spontaneous symmetry breaking statistical mechanics approach on a Morse function, following the arguments of Pettini13 and Matsumoto.14 Typically, many such Morse functions are possible, and we construct one using group representations. See the Mathematical Appendix for a brief summary of standard material on Morse Theory.
Take an appropriate group representation by matrices and construct a ‘pseudo probability’ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) for non-rigid group element ω as
for non-rigid group element ω as
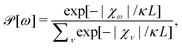 | (1) |
The central idea is that F in the construct
 | (2) |
The essential insight is that, given the powerful generalities of Morse Theory, virtually any good Morse Function will produce spontaneous symmetry breaking under these circumstances, i.e., the behavior of interest is not restricted to a Morse Function based on the system Hamiltonian.
3 Discussion and conclusions
Following Kahraman,16 the observed ‘sloppiness’ of biological lock–key molecular reaction dynamics suggests that binding site symmetry may be greater than binding ligand symmetries: binding ligands may be expected to involve (dual, mirror) subgroups of the non-rigid group symmetries of the IDP frond. Thus the symmetry breaking–making argument becomes↑ L → more flexibility → larger binding site non-rigid symmetry group → more subgroups of possible binding sites for ligand attachment.
‘Fuzzy lock theory’ emerges by supposing the ‘duality’ between a subgroup of the IDP and its binding site can be expressed as
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) α = Cβ α = Cβ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) γ γ | (3) |
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) α is a subgroup (or set of subgroups) of the IDP non-rigid symmetry group,
α is a subgroup (or set of subgroups) of the IDP non-rigid symmetry group, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) γ a similar structure of the target molecule, and Cβ is an appropriate inversion operation or set of them that represents static or dynamic matching of the fuzzy ‘key’ to the fuzzy ‘lock’, in the sense of Tompa and Fuxreiter.4
γ a similar structure of the target molecule, and Cβ is an appropriate inversion operation or set of them that represents static or dynamic matching of the fuzzy ‘key’ to the fuzzy ‘lock’, in the sense of Tompa and Fuxreiter.4
Following the taxonomy of their Table 1, if C is a single element, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,
, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) fixed subgroups, then the matching would be classified as ‘static’. Increasing the number of possible elements in C, or permitting larger sets representing
fixed subgroups, then the matching would be classified as ‘static’. Increasing the number of possible elements in C, or permitting larger sets representing ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) and
and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , leads to progressively more ‘random’ structures in an increasingly dynamic configuration, as the system shifts within an ensemble of possible states, or, perhaps, even a quantum superposition of them.
, leads to progressively more ‘random’ structures in an increasingly dynamic configuration, as the system shifts within an ensemble of possible states, or, perhaps, even a quantum superposition of them.
A complete treatment probably requires a groupoid generalization of non-rigid molecule theory—extension to ‘partial’ symmetries like those of elaborate mosaic tilings, particularly for the target species. This approach has been highly successful in stereochemisty,17 but remains to be done for non-rigid molecule theory.
Perhaps the simplest classical analog is to think of a set of n = L/δ beads of finite mass, each separated by a massless fiber of length δ, under some fixed tension, that are strung together into a vibrating system of total length L. There will be at most n possible ‘normal modes’ to the vibration of that structure. As the ‘temperature’ L increases—increasing n—the number of possible vibration modes increases in direct proportion. For a non-rigid molecular systems the number of group elements would grow with L as the exponent of growth.
Matters are, of course, far more subtle than we have indicated. Fig. 1, adapted from Fig. 6 of Uversky and Dunker,3 shows four increasingly disordered configurations of the same total length (100 polypeptide units), from fully ordered on the left to fully uncoiled. As indicated, they differ markedly, however, in hydrodynamic volume, and this may serve, along with length, to more precisely characterize the necessary temperature analog. For example, taking something of the form ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = f(L,V), for some appropriate function f, where L is the number of polypeptides, V the hydrodynamic volume. An alternative would be to limit L to the number of polypeptides in the unbound whip-like frond.
= f(L,V), for some appropriate function f, where L is the number of polypeptides, V the hydrodynamic volume. An alternative would be to limit L to the number of polypeptides in the unbound whip-like frond.
 | ||
| Fig. 1 Adapted from Fig. 6 of Uversky and Dunker.3 A range of disorder for a 100 polypeptide chain, from fully ordered on the left to fully uncoiled on the right. MG is the molten globule form, PMG the ‘pre’ MG structure. The spheres indicate the relative hydrodynamic volumes which can, along with the native length, be incorporated into a temperature analog. An alternative approach would be to simply take L as the number of polypeptides in the whip-like sector. | ||
The central outcome of the Landau approach, however the temperature-analog is empirically defined, is that the non-rigid molecular group (or groupoid) symmetries, and their associated dynamics, will likely be highly punctuated in that analog. The effect should be observable in the reaction mechanisms of IDP, permitting systematic ‘spectral’ classifications, in the context of the ‘fuzzy lock’ mapping, grossly complex as this will surely prove to be.
4 Mathematical appendix: an introduction to Morse theory
Morse theory examines relations between analytic behavior of a function—the location and character of its critical points—and the underlying topology of the manifold on which the function is defined. We are interested in a number of such functions, for example a ‘free energy’ constructed from group characters, with ‘frond length’ as the ‘temperature’ parameter. These matters can be reformulated from a Morse theory perspective. Here we follow closely the elegant treatments of Pettini13 and Kastner.18The essential idea of Morse theory is to examine an n-dimensional manifold M as decomposed into level sets of some function f: M → R where R is the set of real numbers. The a-level set of f is defined as
| f−1(a) = {x ∈ M: f(x) = a}, |
| Ma = f−1(−∞,a] = {x ∈ M: f(x) ≤ a}. |
These sets describe the whole manifold as a varies between the minimum and maximum of f.
Morse functions are defined as a particular set of smooth functions f: M → R as follows. Suppose a function f has a critical point xc, so that the derivative df(xc) = 0, with critical value f(xc). Then f is a Morse function if its critical points are non-degenerate in the sense that the Hessian matrix of second derivatives at xc, whose elements, in terms of local coordinates are
| Hi,j = ∂2f/∂xi∂xj, |
The index of the critical point is the number of negative eigenvalues of H at xc.
A level set f−1(a) of f is called a critical level if a is a critical value of f, that is, if there is at least one critical point xc ∈ f−1(a).
Again following Pettini,13 the essential results of Morse theory are:
(1) If an interval [a,b] contains no critical values of f, then the topology of f−1[a,v] does not change for any v ∈ (a,b]. Importantly, the result is valid even if f is not a Morse function, but only a smooth function.
(2) If the interval [a,b] contains critical values, the topology of f−1[a,v] changes in a manner determined by the properties of the matrix H at the critical points.
(3) If f: M → R is a Morse function, the set of all the critical points of f is a discrete subset of M, i.e. critical points are isolated. This is Sard's Theorem.
(4) If f: M → R is a Morse function, with M compact, then on a finite interval [a,b] ⊂ R, there is only a finite number of critical points p of f such that f(p) ∈ [a,b]. The set of critical values of f is a discrete set of R.
(5) For any differentiable manifold M, the set of Morse functions on M is an open dense set in the set of real functions of M of differentiability class r for 0 ≤ r ≤ ∞.
(6) Some topological invariants of M, that is, quantities that are the same for all the manifolds that have the same topology as M, can be estimated and sometimes computed exactly once all the critical points of f are known: Let the Morse numbers μi(i = 1,…,m) of a function f on M be the number of critical points of f of index i, (the number of negative eigenvalues of H). The Euler characteristic of the complicated manifold M can be expressed as the alternating sum of the Morse numbers of any Morse function on M,
The Euler characteristic reduces, in the case of a simple polyhedron, to
| χ = V − E + F |
(7) Another important theorem states that, if the interval [a,b] contains a critical value of f with a single critical point xc, then the topology of the set Mb defined above differs from that of Ma in a way which is determined by the index, i, of the critical point. Then Mb is homeomorphic to the manifold obtained from attaching to Ma an i-handle, i.e., the direct product of an i-disk and an (m − i)-disk.
Again, Pettini13 contains both mathematical details and further references. See, for example, Matusmoto.14
Acknowledgements
The author thanks the reviewers for remarks useful in revision.References
- I. Serdyuk, Mol. Bio., 2007, 41, 297–313 Search PubMed.
- V. Uversky, Protein Sci., 2002, 11, 739–756 CrossRef CAS.
- V. Uversky and A. K. Dunker, Biochim. Biophys. Acta, 2010, 1804, 1231–1264 CAS.
- P. Tompa and M. Fuxreiter, Trends Biochem. Sci., 2008, 33(1), 1–8 CrossRef.
- H. Longuet-Higgins, Mol. Phys., 1963, 6, 445–460 CrossRef CAS.
- B. Shoemaker, J. Portman and P. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8868–8873 CrossRef CAS.
- Y. Huang and Z. Liu, J. Mol. Biol., 2009, 393, 1143–1159 CrossRef CAS.
- R. Wallace, BioSystems, 2011, 103, 18–26 CrossRef CAS.
- K. Balasubramanian, J. Chem. Phys., 1980, 72, 665–677 CrossRef CAS.
- K. Balasubramanian, J. Chem. Phys., 2004, 120, 5524–5535 CrossRef CAS.
- M. Schnell, ChemPhysChem, 2010, 11, 758–780 CrossRef CAS.
- A. Iranmanesh and A. Ashrafi, Iran. J. Math. Sci. Informatics, 2008, 3, 21–28 Search PubMed.
- M. Pettini, Geometry and Topology in Hamiltonian Dynamics, Springer, New York, 2007 Search PubMed.
- Y. Matsumoto, An Introduction to Morse Theory, American Mathematical Society, Providence, RI, 2002 Search PubMed.
- L. Landau and E. Lifshitz, Statistical Mechanics, I, Elsevier, New York, 2007 Search PubMed.
- A. Kahraman, The geometry and physicohemistry of protein binding sites and ligands and their detection in electron density maps, PhD dissertation, Cambridge University, UK, 2009 Search PubMed.
- R. Wallace, C. R. Biol., 2011, 334, 263–268 CrossRef CAS.
- M. Kastner, ArXiv 2006, cond-mat/0703401.
Footnote |
| † Published as part of a Molecular BioSystems themed issue on Intrinsically Disordered Proteins: Guest Editor M Madan Babu. |
| This journal is © The Royal Society of Chemistry 2012 |

