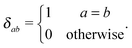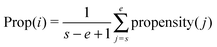Uncertainty analysis in protein disorder prediction

Abstract

A grand challenge in the proteomics and structural genomics era is the prediction of protein structure, including identification of those proteins that are partially or wholly unstructured. A number of predictors for identification of intrinsically disordered proteins (IDPs) have been developed over the last decade, but none can be taken as a fully reliable on its own. Using a single model for prediction is typically inadequate because prediction based on only the most accurate model ignores model uncertainty. In this paper, we present an empirical method to specify and measure uncertainty associated with disorder predictions. In particular, we analyze the uncertainty in the reference model itself and the uncertainty in data. This is achieved by training a set of models and developing several meta predictors on top of them. The best meta predictor achieved comparable or better results than any other single model, suggesting that incorporating different aspects of protein disorder prediction is important for the disorder prediction task. In addition, the best meta-predictor had more balanced sensitivity and specificity than any individual model. We also assessed the effects of changes in disorder prediction as a function of changes in the protein sequence. For collections of homologous sequences, we found that mutations caused many of the predicted disordered residues to be flipped to be predicted as ordered residues, while the reverse was observed much less frequently. These results suggest that disorder tendencies are more sensitive to allowed mutations than structure tendencies and the conservation of disorder is indeed less stable than conservation of structure. Availability: five meta-predictors and four single models developed for this study will be publicly freely accessible for non-commercial use.

---

1 Introduction

Proteins that do not fold into stable 3-D structures, called Intrinsically Disordered Proteins (IDPs), play an important role in a number of biological functions^1–4 and provide relatively unexplored targets for drug discovery.⁵ More specifically, IDPs have vital roles in cell signaling and regulation.^6–9 Bioinformatics approaches suggest that the amount of disorder follows the trend archaea ≈ bacteria < eukaryotes, with about 30%–50% of the proteins in higher eukaryotes containing at least one long region of disorder.¹⁰

Traditionally, the 3-D structures of the proteins are determined by using costly experimental methods such as X-ray crystallography, Overhauser Effect Enhanced Nuclear Magnetic Resonance (NMR) spectroscopy and Circular Dichroism (CD) spectroscopy. The first IDP predictor¹¹ was developed in 1997 in our laboratory, and this event was followed by development of numerous additional disorder predictors by our group and others. The current state of protein disorder predictors with their advantages and drawbacks has been summarized recently.^12–15

Each disorder predictor uses different concepts, different physico-chemical properties, or even different machine learning algorithms. For example, some protein disorder predictors assume that the prediction for each residue is independent of the prediction for other residues while taking into consideration that the predicted disorder tendency of neighboring positions could be beneficial to the disorder prediction task. On the other hand, some other predictors are specific to one type of disorder only, represented by missing residues from X-ray structures. So that, relying on a single disorder predictor is not necessarily the best strategy.

Two sources of uncertainty in disorder prediction are model uncertainty and data uncertainty. Although model uncertainty in disorder prediction depends on the selected model, the relationship between model uncertainty and model selection has not been systematically investigated. Usually, from a space of models, one is selected that is more accurate than several alternatives when tested on a given set of sequences. A limitation of this kind of selection process is that problems arising from model uncertainty are not considered in sufficient depth.

To study the above discussed effects, we developed several protein disorder predictors to analyze uncertainty in disorder prediction. Each of the implemented predictors uses a different machine learning algorithm and/or was trained on a different dataset. Based on the individual predictors, we built five meta-predictors.

In the first part of this study, the aim was to analyze the uncertainty in the disorder prediction. For that purpose, CASP 8 (122 protein sequences)¹⁶ and CASP 9 (117 protein sequences)¹⁷ sequences were used to evaluate the performance of multiple models with respect to accuracy of protein disorder prediction. Our results showed that more than one model deserves consideration in making inferences of disorder prediction and integrating multiple predictors with different flavors is better than using individual components and relying on one predictor.

In the second part of the paper, which to the best of our knowledge has not been done before, the uncertainty in the protein sequence data is analyzed. We analyzed disorder prediction as a function of the effect of change in the data provided to the predictors. We applied our method to 29 489 CASP 8 and 27 450 CASP 9 homologous sequences and studied the effect of change in the sequence similarity on the disorder predictions. Although protein structure is generally more conserved than sequence,^18–20 we found that the regions that are predicted as disorder are sensitive to the changes (mutation) in the sequence unlike the regions that are predicted as structure, suggesting that the disorder predictions are more sensitive to changes in the sequences than structure predictions and the conservation of disorder is indeed less stable than conservation of structure.

2 Related work

The first machine learning method developed for protein disorder prediction, called PONDR VL-XT²¹ and developed in our lab, is based on feed-forward neural networks. It is an enhanced model composed of two separate predictors developed for the N- and C-terminal regions trained on terminal disordered regions characterized by X-ray²² and a specific predictor for middle regions trained on variously characterized long disordered regions. The inputs of these predictors are specific sequence features, including the coordination number, net charge, hydropathy, and the fraction of various amino acid groups, calculated within a given window.

DISOPRED2 ²³ is the first method using support vector machine (SVM) for the protein disorder prediction. DISOPRED2 was trained on a dataset of missing residues of solved structures, separately for N-, C- and middle regions. The input was constructed from PSI-BLAST generated profiles of position specific scoring matrices.²⁴ The main reason for the low false positive rate of DISOPRED2 is one of the advantages of SVM, namely that it can incorporate greater cost of misclassification for one of the classes, therefore it can compensate for unbalanced datasets.

In the case of feed-forward neural networks and SVM the prediction for each residue is independent of the prediction for other residues. On the other hand, DISpro²⁵ uses recurrent networks that can propagate data from later processing stages to earlier stages. DISpro involves the use of evolutionary information in the form of predicted secondary structure and solvent accessibility, and 1D-recursive neural network. In DISpro, the prediction at each position depends on the entire sequence through a recursive network of neighboring positions instead of using a fixed window size. The recently published method OnD-CRF²⁶ uses conditional random fields (CRF) for accurately predicting the transition between structured and disordered regions in proteins. The input was constructed from the amino acid sequence and secondary structure prediction. Both methods, DISpro and OnD-CRF, have the ability to take into account the disorder prediction of neighboring residues.

All aforementioned methods are specific to one type of protein disorder only, represented either by missing residues of X-ray structures or DisProt database.²⁷ Their performance tested on the other dataset resulted in significantly lower efficiencies. This problem was first addressed by the PONDR VSL2 method.^28,29 It is composed of two specialized predictors optimized for short (≤30 residues) and long (>30 residues) disordered regions that are integrated by an independent linear SVM meta-predictor using the inner-product kernel. The inputs of all three methods are composed of various amino acid propensities, sequence complexity, and optionally sequence profiles and secondary-structure predictions, calculated within a sliding fixed local window. At the first level, the two methods predict short and long disordered segments, respectively. The meta-predictor then determines the optimal weight to combine the output of these two composite predictors. This architecture ensured that PONDR VSL2 has a more balanced performance on disordered segments of various lengths.

PONDR-FIT ³⁰ is another meta-predictor based on a consensus artificial neural network (ANN). It was developed by combining the outputs of six individual disorder predictors. For each residue along the sequence, the prediction results of the six individual predictors on a sliding window of 21 residues centered at that residue were fed into a single layer artificial neural network (ANN) with 20 hidden units. The single output at the output layer is the disorder score of the meta-predictor for that centered residue. The meta-predictor (MD)³¹ is developed by combining a set of several orthogonal methods that capture many types of disorder without sacrificing the distinction of the type of disorder that is detected. A simple arithmetic average over different methods slightly improved over the best method. Many other meta-predictors^32–35 have been developed to improve the accuracy of disorder prediction.

To the best of our knowledge, no work has been done before to study uncertainty in protein disorder prediction models and data.

3 Methods

3.1 Datasets

In our experiments two datasets were used for training the predictors. The oneside dataset, derived from PDBSelect³⁶ with pairwise sequence identity ≤ 25%, was used. In this dataset, all residues that lack coordination in the PDB file were considered to be disordered residues. The product that we call oneside dataset contains 389 286 structured residues and 14 908 disordered residues.

The formation of protein complexes often involves segments that undergo disorder-to-order transitions upon formation of the complexes. Then a dataset reduced in such segments, a second dataset, which we will call monomeric dataset, was assembled from single chain PDB structures. This set contains 102 636 ordered and 95 156 disordered residues. Also included in this set were all of the disordered protein segments from the DisProt database.²⁷

3.2 Feature extraction

The quality of the predictor depends on the features to be used. In our predictors, three types of features were used, consisting of amino acid (AA) frequencies, various properties^11,22 and local sequence patterns.

AA frequency-based features are the numbers of the indicated amino acids in a given window of a prespecified length centered at the current residue. For example, FWC means the number of amino acid F plus the number of amino acid W plus the number of amino acid C over a window centered at the current residue. The list of all AA frequency-based features used in our model is shown in Table 1.

Table 1 Amino acid frequency-based features used in our predictors

Features	Features	Features
WFYC	VILM	WCFIYVLHM
WYFEDH	VIYFW	D
E	H	I
M	N	P
R	S	T
V	K	PEVK

---

Property-based features³⁷ are the sum of the residue's property-values. Following previous studies^28,29 a window of length L = 41 centered at each residue in the sequence was used. Since the window has varying sizes at the N-, C-terminal regions,³⁸ we use s and e to adjust the start and the end of the window as follows:

s = max{1,i − (L − 1)/2}

and

e = min{M,i + (L − 1)/2}

where M is the length of the sequence and i is the current position of the residue in the sequence.

Four features were calculated from the properties of the amino acids. The first property, hydrophobicity, which is an important determinant of protein chain folding, was calculated as follows:

There are different scales for hydropathy. We based our calculations on Kyte–Doolittle's scale.³⁹

The second property-based feature that was used is the flexibility.⁴⁰ It was calculated as follows:

Since disordered proteins characterized by different experiments exhibit similar complexity distributions,²¹ which are shifted to lower values compared to, but significantly overlapping with, the distributions for ordered proteins, the complexity of the sequence was used as the third property-based feature in our model. The sequence complexity as measured by Shannon's entropy was calculated as:

where a_n is the amino acid and P_i is the probability of the amino acid residue and was calculated as follows:

Finally, we also used amino acid propensities,⁴¹ which is a scale to measure how likely an amino acid is to be unfolded, which was calculated as:

Sequence pattern-based features were used to capture the local sequence similarity associated with disordered and structured proteins.⁴² For each sequence, we slid a window of length 15 centered at each residue. Then, we measured the similarity between this window and each subsequence of length 15 in the dataset. The score of aligning two subsequences s₁ and s₂ of the same length was measured as:

where Sim(i,j) is the normalized BLOSUM62 score similarity between the corresponding residues in both sequences. The features were constructed by computing the fraction of the disordered subsequences in all k nearest subsequence neighbors to the query subsequence. The subsequence was marked as disordered if it contains a fraction of disordered residues. This disordered residue fraction was determined based on the fraction of the total disordered residues in the training dataset. The fraction of the disordered residues in the oneside dataset was 1% while that in the monomeric dataset was 48%. Five features were constructed out of the sequence pattern features for different values of k = 0.25%, 0.5%, 1%, 2%, and 4% of the training dataset. Therefore, a total of 29 features were constructed for each predictor.

3.3 Disorder prediction models

To model the uncertainty represented by the predictors, the goal was to build a set of models using different datasets such that they capture different information regarding the disorder predictions. Moreover, we chose different machine learning methods of various properties so as to capture various information about the relationship between protein sequence and the disorder prediction. In particular, in our experiments, Conditional Random Field (CRF), Support Vector Machine (SVM), Neural Network (NN) and Logistic Regression (Logit) classifiers were trained for protein disorder prediction. In addition, we used VSL2B developed previously in our lab as an additional predictor that was the most accurate model at CASP 6 and CASP 7 evaluations and overall is still one of the most cited disorder predictors. More recent predictors developed previously were not included in our experiments since we used CASP 8 and CASP 9 proteins for evaluation and we wanted to make sure that these and similar sequences were not considered when training the models that we compared in this study.

Logit is a statistical linear model that makes no assumption about the distribution of the independent variables. NN is a non-linear representational classifier that has the ability to capture the non-linear relationship between the input and the output. SVM is a mathematical model that maps the original finite-dimensional space into a much higher-dimensional space, presumably making the separation easier in that space by finding the hyperplane that maximizes the margin between the two classes. Finally, CRF is a discriminative undirected probabilistic graphical model that captures the correlation between the neighboring residues.

3.4 Testing accuracy

To assess the significance of the results, we performed a 10-fold cross validation on the training dataset. The accuracy of the predictor was measured using a hinge loss error function as follows:
where y is the true prediction value and f(x) is the classifier prediction. To assess the balance between the ordered and disordered amino acids, we calculated sensitivity and specificity. Sensitivity and specificity are statistical measures of the performance of a binary classification test. Sensitivity measures the proportion of actual positives which are correctly identified as such. Specificity measures the proportion of negatives which are correctly identified.

where TP is the number of true positives, TN is the number of true negatives, FP is the number of false positives, and FN is the number of false negatives. In addition, the balanced accuracy was calculated as the average between sensitivity and specificity. To compare multiple classifiers, we used ROC and the area under the curve (AUC) measures. The ROC curve is a graphical plot of true positive rate vs. false positive rate. ROC is used for a binary classifier system as its discrimination threshold is varied.

3.5 Meta-predictors and model uncertainty

Model selection is usually performed to identify the model that achieves the highest performance on any given dataset. This selection is a source of uncertainty in the prediction so that no predictor is fully reliable on its own. To mitigate this problem, a set of different models were trained on different datasets and then a meta-predictor was built on top of the five models described in the previous section. The meta-predictor was built not to compete with the state-of-the-art disorder predictors but the aim is to analyze the uncertainty associated with the disorder prediction.

A common approach for meta-predictors is to use a voting scheme. The prediction for each residue was computed based on the votes from all models on that particular residue. The question is what happens if there is disagreement among the models. One way to handle this issue is based on the weighted average of the votes. In this method, each model is assigned a weight for its vote. The weights are assigned in the training process. Unfortunately, this method requires that all models be trained on the same dataset. Therefore, this strategy cannot be used in our framework. Another simple and commonly used approach is majority voting. Normally, the majority voting is considered to be the best voting scheme in the meta-predictor framework. Here we show that, for disorder prediction using these data and these models, majority voting does not give the best results.

The voting scheme depends on how many votes from the individual models are considered. Five voting schemes for disorder prediction were tested in this paper. For each residue, if at least x = {1,2,…,5} predict disorder (positive), the overall prediction by the given meta-predictor for that residue is that it is in a disordered region and the residue-specific prediction is called Positive Voter x (PVx). The results for the different voting schemes are explained in Section 4.3 and in Table 2.

Table 2 Evaluation of the 10 predictors on CASP 8 and CASP 9. CRF = Conditional Random Field, SVM = Support Vector Machines, NN = Neural Network, Logit = Logistic Regression and PVx = x Positive Voters meta-predictors

	CASP 8				CASP 9
	Sensitivity	Specificity	Accuracy	AUC	Sensitivity	Specificity	Accuracy	AUC
a Best accuracy across all individual models. b Best accuracy across all 10 predictors. c Best balance between sensitivity and specificity.
CRF	0.758 ± 0.060	0.850 ± 0.010	0.804 ± 0.030^a^,^b	0.879 ± 0.031	0.543 ± 0.041	0.847 ± 0.012	0.695 ± 0.021^a	0.773 ± 0.023
SVM	0.572 ± 0.087	0.862 ± 0.010	0.717 ± 0.044	0.760 ± 0.053	0.492 ± 0.035	0.848 ± 0.011	0.670 ± 0.017	0.721 ± 0.021
NN	0.519 ± 0.107	0.877 ± 0.010	0.698 ± 0.054	0.755 ± 0.058	0.468 ± 0.037	0.865 ± 0.011	0.666 ± 0.018	0.729 ± 0.019
Logit	0.599 ± 0.108	0.877 ± 0.013	0.738 ± 0.054	0.798 ± 0.054	0.338 ± 0.032	0.845 ± 0.015	0.591 ± 0.017	0.613 ± 0.026
VSL2B	0.767 ± 0.070	0.828 ± 0.010	0.798 ± 0.035	0.867 ± 0.039	0.557 ± 0.036	0.797 ± 0.012	0.677 ± 0.018	0.709 ± 0.026
PV1	0.860 ± 0.045	0.664 ± 0.015	0.762 ± 0.024	—	0.776 ± 0.028	0.631 ± 0.017	0.704 ± 0.015	—
PV2	0.787 ± 0.064^c	0.803 ± 0.012^c	0.795 ± 0.033^c	—	0.643 ± 0.035^c	0.779 ± 0.014^c	0.711 ± 0.018^b^,^c	—
PV3	0.648 ± 0.091	0.901 ± 0.009	0.774 ± 0.046	—	0.474 ± 0.038	0.882 ± 0.010	0.678 ± 0.019	—
PV4	0.523 ± 0.106	0.949 ± 0.006	0.736 ± 0.053	—	0.315 ± 0.031	0.937 ± 0.008	0.626 ± 0.015	—
PV5	0.397 ± 0.124	0.978 ± 0.003	0.687 ± 0.062	—	0.188 ± 0.026	0.972 ± 0.005	0.580 ± 0.013	—

---

3.6 Data uncertainty

A protein's structure is more evolutionarily conserved than its amino acid sequence.¹⁸ The evolution of disordered proteins is driven by their structure and function just as the evolution of ordered proteins.^19,20 We studied to what extent of sequence similarity the conservation of disorder prediction is persistent. To this end, we applied all 10 predictors (five individual models and five meta-predictors) to CASP 8 and CASP 9 homologous sequences and analyzed the relationship between protein disorder prediction and the sequence similarity.

First, for each CASP 8 and CASP 9 sequence, all-against-all BLAST was performed to search in a non-redundant protein database for all homologous sequences. Default parameters of BLAST were used except that a high E-value was used to avoid bias in local similarity search. We removed all homologous sequences that are either more than 10% longer or shorter than the CASP sequence.

A follow-up step was performed to compute the global similarity between homologous sequences, derived from BLAST, and the CASP sequences. The identity between the CASP sequence and its homologous sequence was computed as the percentage of the perfect match. Hereafter, the sequence similarity and identity are used interchangeably.

We applied all 10 disorder predictors, consisting of five individual predictors described in Section 3.3 and five meta-predictors described in Section 3.5, on both CASP 8 and CASP 9 sequences and their homologous sequences. For each predictor, we computed the percentage of flips from disorder to order and from order to disorder predictions. We then analyzed the conservation of the disordered predictions at multiple levels of similarity for all 10 predictors. The results are summarized in Section 4.4.

4 Results and discussion

4.1 Training disorder predictors

Logit was trained on the monomeric dataset using all three feature sets. NN, consisting of one hidden layer with 10 hidden neurons and a log sigmoid activation function, was trained on the monomeric dataset using the property and sequence pattern features. SVM, with a radial basis kernel function, was trained on the monomeric dataset using the property and sequence pattern features. Finally, CRF was trained on the oneside dataset using property and sequence pattern features. Fig. 1 elucidates the training data for each model. The training dataset, feature set and the parameters for each classifier were optimized using 10 cross validation processes. A widely used disorder predictor VSL2B was added to our set of predictors. Four individual models SVM, NN, Logit and VSL2B use 0.5 as the cut-off value between the disorder and structure predictions. CRF uses 0.03 as the cut-off value.

Fig. 1 Training dataset and feature set for each model.

4.2 Evaluation of models on CASP sequences

In order to compare the performance of the five models described in Section 3.3, CASP 8 and CASP 9 sequences were used. None of the CASP 8 or CASP 9 sequences were used for training any of our five disorder prediction models. The ROC curves of these five models are presented in Fig. 2 and 3, and their accuracies on CASP 8 and CASP 9 are shown in Table 2 and Fig. 4 and 5, respectively.

Fig. 2 ROC for five disorder predictors on CASP 8.

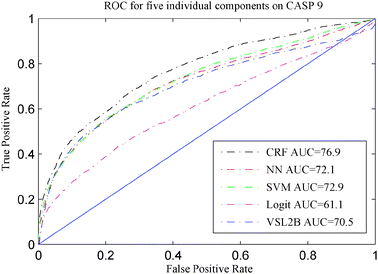Fig. 3 ROC for five disorder predictors on CASP 9.

Fig. 4 Evaluation of 10 predictors on CASP 8.

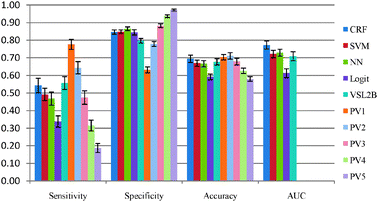Fig. 5 Evaluation of 10 predictors on CASP 9.

Upon comparing our 5 predictors on CASP 8 and CASP 9 data, the CRF was the best model among five individual predictors in terms of accuracy and AUC. This provides evidence that exploiting the correlation between disorder predictions at neighboring residues is beneficial to the disorder prediction task as CRF is the only one of the five models that takes advantage of these correlations. VSL2B and CRF were quite similar on CASP 8. VSL2B had the best sensitivity rate on both CASP 8 and CASP 9 among the five individual models. However, although the VSL2B predictor is applicable to disordered regions of any length and can accurately identify the short disordered regions, it performed worse than CRF on CASP 9. SVM and NN were quite similar on CASP 9. However, SVM had higher sensitivity on CASP 8. All these results suggest that relying on only one predictor is not fully reliable and different datasets have different flavors of disordered proteins.⁴³

It is worth mentioning that, according to the evaluation of the disorder predictions on CASP 8¹⁶ and CASP 9,¹⁷ our CRF predictor also compared well with respect to those disorder predictors that participated in CASP 8 and CASP 9. The CRF predictor was one of the best 6 and 10 predictors with respect to accuracy on CASP 8 and CASP 9, respectively, and was one of the best 11 predictors with respect to AUC on CASP 8. Our CRF model achieved comparable balanced accuracy with OnD-CRF²⁶ on CASP 9 but was superior with respect to AUC.

The power of each of the five single predictors is demonstrated by their application to one of the target proteins from CASP 9. The disorder predictions for all 10 models on the experimentally determined T0631 target sequence are shown in Fig. 6. The C-terminal region (residues 165–168) was predicted correctly by CRF and VSL2B and was predicted incorrectly by the rest of the models. The region in the middle (residues 56–64) was predicted incorrectly by CRF while the rest of the models were in a close agreement on that region. However, VSL2B predicted other regions like residues 102–107 incorrectly. For those cases, no predictor was fully reliable on its own which demonstrated that there is a need to integrate multiple predictors.⁴⁴

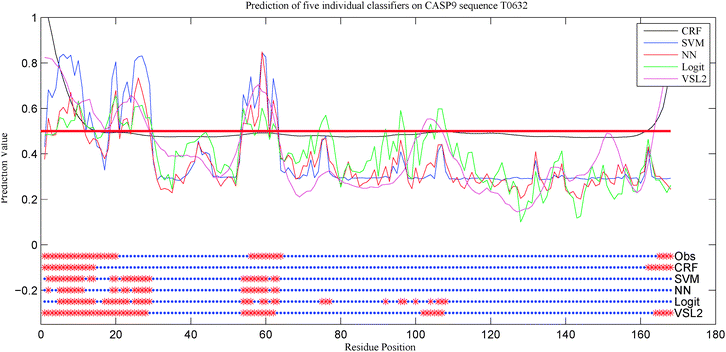Fig. 6 Prediction of the five models on the T0632 target sequence from CASP 9. The top part shows the prediction score of each individual model. The horizontal red line is the threshold used for each classifier. All thresholds are aligned together to simplify the plot. The bottom parts are the final predictions for each model. The top bar, labeled as Obs, represents the true classifications while the other five bars represent the predictions of the five models. The red points represent the disordered residues while the blue points represent the ordered residues.

4.3 Meta-predictors and model uncertainty

As suggested in Section 4.2, the outcome prediction of each protein disorder predictor is not fully reliable on its own. For example, Logit achieved very good results on CASP 8 but performed barely better than random on CASP 9. Therefore choosing the best predictor among a list of predictors and relying on one predictor is typically a source of uncertainty in the disorder prediction. So, integrating several aspects of protein disorder predictors is indeed necessary for this task. A meta-predictor was then built using the five models. Two schemes could be used to integrate the individual components. Since each predictor was trained on different datasets, weights cannot be assigned for each predictor. Therefore, the voting scheme was used to integrate the components of the meta-predictors.

First, we looked at the agreement among the five models described in Section 3.3 in both positive (disordered) and negative (structured) predictions. As illustrated in Fig. 7, the agreement among the models could result either in true or false prediction. The percentage of true agreement is high, especially in regions predicted to be structured. In contrast, the percentage of false prediction is fairly small. These results suggest that the meta-predictor is the most reliable especially for structured regions.

Fig. 7 Fraction of full agreement among five disorder prediction models CRF, SVM, NN, Logit and VSL2B on CASP 8 and CASP 9.

To further analyze the agreement, we tested five integration methods on CASP 8 and CASP 9. For each integration method, a certain number of models were used for the voting on the disorder (positive) prediction. For example, in the case of PV2 meta-predictor, the overall prediction is disorder if any two of the underlying models predict disorder. Otherwise, the prediction is that the residue is in a structured region. Please observe that PV3 is the commonly used majority voting algorithm. The five meta-predictors were applied to CASP 8 and CASP 9 sequences and the results are reported in Table 2. It reveals that the most accurate model of five meta prediction models is PV2. Consistent results were obtained on CASP 8 and CASP 9. In CASP 9, the meta-predictor PV2 outperformed the CRF, while in CASP 8 CRF outperformed the PV2. However, the meta-predictor PV2 is the only predictor that has a good balance between sensitivity and specificity which is a very desirable property for any protein disorder predictor.

In addition, according to the evaluation¹⁷ of the disorder prediction on CASP 9, the meta-predictor PV2 is one of the best 8 disorder predictors with respect to the balanced accuracy.

4.4 Data uncertainty

In this experiment, the objective was to study the effects of changes in the protein sequences on disorder prediction. Collections of protein sequences similar to those of the CASP target sequences were obtained and our 10 disorder predictors were applied to the CASP target sequences and their identified homologous sequences. As pairs of sequences became less identical, regions predicted to be disordered in one sequence flipped to be predicted to be structured in the other and, similarly, regions predicted to be structured in one sequence flipped to be predicted to be disordered in the other. Thus, an analysis was performed on the fraction of flips of prediction from disordered to ordered and flips from ordered to disordered as a function of the sequence identities of the pairs of sequences being compared. By organizing these fractions that flip their order/disorder predictions according to their levels of sequence identities, we end up with a correlation between level of sequence identity and degree of conservation of disorder prediction, providing evidence that protein structure is more evolutionarily conserved than amino acid sequence.¹⁸ Since this analysis was performed for all of the predictors, the various predictors can be evaluated in terms of this measure of their conservation of disorder prediction. Fig. 8 and 9 summarize these data.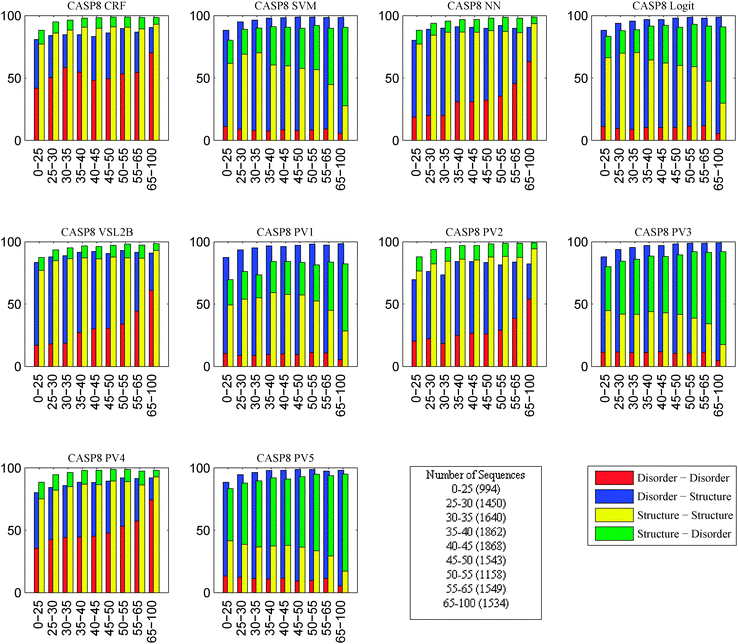

Fig. 8 Breakdown of the fraction of flips between disorder and structure into multiple levels of similarity on CASP 8 sequences. X-axis is the sequence similarity. Y-axis is the percentage of flips. Number in parentheses is the number of homologous sequences that fall in the corresponding sequence similarity category. Red bar represents the fraction of disorder to disorder predictions. Blue bar represents the fraction of disorder to structure predictions. Yellow bar represents the fraction of structure to structure predictions. Green bar represents the fraction of structure to disorder predictions.

Fig. 9 Breakdown of the fraction of flips between disorder and structure into multiple levels of similarity on CASP 9 sequences. X-axis is the sequence similarity. Y-axis is the percentage of flips. Number in parentheses is the number of homologous sequences that fall in the corresponding sequence similarity category. Red bar represents the fraction of disorder to disorder predictions. Blue bar represents the fraction of disorder to structure predictions. Yellow bar represents the fraction of structure to structure predictions. Green bar represents the fraction of structure to disorder predictions.

The most interesting finding is that the fraction of flips from disordered to ordered was larger than that from ordered to disordered. This suggests that a small change in sequence in a disordered region could easily flip prediction to a structured region while regions predicted to be structured were more robust to mutation. As shown in Fig. 8 and 9, the fractions of flips varied a lot among predictors although some of the models, such as SVM and NN, behaved quite similar on both CASP 8 and CASP 9. This supports that the disorder prediction is affected by the changes in the sequence. However, the most accurate predictors PV2, CRF and VSL2B appeared to be also the most stable with respect to changes in sequence.

Two recent studies compared evolutionary models of structured protein regions versus disordered regions. The first study showed that disordered regions have a greater chance of changing and that the sequence changes are structurally nonconservative.¹⁹ In the second study, predictions of secondary structure and predictions of disorder were compared for three evolutionary models, which differed in their choice of amino acid substitution matrices for assignment of the mutations, with the finding that secondary structure predictions are conserved while disorder predictions are not.⁴⁵ Since all three substitution matrices were biased towards the substitutions found in structured proteins, the observed result might result in part from the bias towards structure of the substitution matrices.⁴⁶ Here we did not use evolutionary models but directly compared related sequences for the tendency of order and disorder predictions to be conserved. The greater conservation of predicted order as compared with predicted disorder supports the view that conservation of disorder is indeed less stable than conservation of structure, as suggested,⁴⁵ and that, when conservation of disorder does occur, such an event is highly nontrivial.⁴⁷

Assuming that order and disorder predictions indicate the relative sensitivity of these two types of structures to mutation, how can we understand the bias that mutations flip disorder to order more frequently than the reverse? There is a long history of reports indicating that residues on the surfaces of proteins are much more subject to mutational change as compared to buried residues^48,49 including recent interesting developments showing that there is a quantitative relationship between the degree of conservation and the inverse of the local packing density.⁵⁰ Thus, given that disordered regions are poorly packed if there is any packing at all, it is understandable that the residues in such regions are subject to rapid nonconservative changes just as those recently reported.¹⁹ On the other hand, the packing of structured regions leads to preferences for conserved amino acid changes in order to maintain both the structure and the function of the protein.^48–50 Given the relative lack of constraint regarding mutations in disordered regions and given the strong constraints regarding mutations in structured regions, it is no wonder that mutations are more likely to change structural tendencies from disorder to order compared to the reverse.

Does this tendency for mutations to flip sequences from disorder to order have biological implications? As already suggested, when disorder tendencies are conserved for particular regions, this likely indicates that important functions are being carried out by such regions.⁴⁷ Mutations that increase the tendency for order could also provide a mechanism for disordered regions to evolve into order while gaining structure-dependent functions along the way. In this regard, in two recent studies, the creation of new proteins was studied. In one case, new protein loops were created by mutations leading to intron-to-exon conversion.⁵¹ In the second case, new viral proteins arose by a process called overprinting, in which a coding region of RNA was translated into a new reading frame.⁵² In both cases, the newly created protein was highly polar and disordered. We surmise that if newly created sequences were hydrophobic, then such sequences would be very unlikely to fold into 3D structure and instead would be massively prone to non-specific aggregation and interaction, thus leading to cell death. However, as just mentioned, such newly created disordered sequences could evolve both structure and structure-dependent functions due to the tendency of random mutations to increase structure-forming propensity.

Another interesting related observation is that IDPs are often associated with complex diseases such as cancer, neurodegenerative diseases, cardiovascular diseases, and diabetes,^5,53 likely because errors in signaling and regulation arising from IDPs are important for these disease associations. These associations of IDPs with disease led us to suggest the “disorder in disorders” or the D2 concept.⁵⁴ Analysis of disease-inducing mutations in such IDPs reveals that mutations that cause disorder tendencies to flip to structure tendencies are the most likely mutations in disordered regions to be disease-causing.⁵⁵ Another recent paper provides additional support for this idea.⁵⁶

5 Software

LibSVM⁵⁷ is used for SVM implementation. crChain⁵⁸ is a set of Matlab functions for chain-structured conditional random fields. Matlab R2010b is used for all other implementations.

6 Conclusion

Two sources of uncertainty, model uncertainty and data uncertainty, lead to inaccurate predictions. Model uncertainty follows from the collection of models being compared, the method of selection of the “best model” and, ultimately, the model that is selected. We showed that relying on one predictor is not necessarily the best choice. For example, Logit behaved quite well on CASP 8 but it was nearly random on CASP 9. Therefore, relying on one predictor is a way of inducing uncertainty in disorder prediction. To reduce the model uncertainty, we built a set of meta-predictors using five individual models trained on different datasets. The meta-predictors were tested on CASP 8 and CASP 9 sequences no part of which was used for training our models. The meta-predictor PV2 achieved either higher or comparable accuracy on both CASP 8 and CASP 9 sequences. In addition, the meta-predictor PV2 was the only predictor among models used in our experiments that had a good balance between sensitivity and specificity. The PV2 meta-predictor was also reliable on the structured domains predictions.

Another source of uncertainty is data uncertainty. We analyzed the effects of changes in the protein sequence on the disorder prediction. We showed that protein disorder predictions were affected by the changes in the sequence. Changes in the sequence result in different behavior for the disorder prediction. For example, SVM and NN were quite similar on CASP 8 and CASP 9. However, they behaved very differently on similar sequences as shown in Fig. 8 and 9. This provides an evidence that the disorder predictions are quite sensitive to mutations and that mutations often cause regions with predictions indicating disorder to shift to predictions indicating structure.

Recent studies compared evolutionary models of structured protein regions versus disordered regions.^19,45 The observed result might result in part from the bias towards structure of the substitution matrices used in the evolutionary models. In this study, we directly compared related sequences for the tendency of order and disorder predictions to be conserved. The findings support that conservation of disorder is indeed less stable than conservation of structure.

Still, the most accurate predictors were found to be the most stable with respect to changes in the sequence suggesting that research should be aimed at developing accurate models that also have low uncertainty.

Acknowledgements

This work is funded in part by a grant from the Pennsylvania Department of Health and the US National Foundation of Science grant NSF-CNS-0958854. They specifically disclaim responsibility for any analyses, interpretations, or conclusions.

References

1. A. K. Dunker, C. J. Brown, J. D. Lawson, L. M. Iakoucheva and Z. Obradović, Biochemistry, 2002, 41(21), 6573–6582.
2. U. Midic, C. J. Oldfield, A. K. Dunker, Z. Obradović and V. N. Uversky, BMC Genomics, 2009, 10(suppl 1), S12.
3. U. Midic, C. J. Oldfield, A. K. Dunker, Z. Obradović and V. N. Uversky, Protein Pept. Lett., 2009, 16, 1533–1547.
4. V. N. Uversky, C. J. Oldfield, U. Midic, H. Xie, B. Xue, S. Vucetic, L. M. Iakoucheva, Z. Obradović and A. K. Dunker, BMC Genomics, 2009, 10(suppl 1), S7.
5. L. M. Iakoucheva, C. J. Brown, J. D. Lawson, Z. Obradović and A. Dunker, J. Mol. Biol., 2002, 323, 573–584.
6. H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208.
7. S. Vucetic, H. Xie, L. M. Iakoucheva, C. J. Oldfield, A. K. Dunker, Z. Obradović and V. N. Uversky, J. Proteome Res., 2007, 6(5), 1899–1916.
8. H. Xie, S. Vucetic, L. M. Iakoucheva, C. J. Oldfield, A. K. Dunker, V. N. Uversky and Z. Obradović, J. Proteome Res., 2007, 6(5), 1882–1898.
9. H. Xie, S. Vucetic, L. M. Iakoucheva, C. J. Oldfield, A. K. Dunker, Z. Obradović and V. N. Uversky, J. Proteome Res., 2007, 6(5), 1917–1932.
10. A. K. Dunker, Z. Obradović, P. Romero, E. C. Garner and C. J. Brown, Genome Inform Ser Workshop Genome Inform, 2000, 11, 161–171.
11. P. Romero, Z. Obradović, C. Kissinger, J. E. Villafranca and A. K. Dunker, Proceedings of the International Conference on Neural Networks, 1997, pp. 90–95.
12. F. Ferron, S. Longhi, B. Canard and D. Karlin, Proteins: Struct., Funct., Genet., 2006, 65(1), 1–14.
13. Z. Dosztányi, B. Mészáros and I. Simon, Briefings Bioinf., 2009, 11, 225–243.
14. Z. Dosztányi and P. Tompa, Methods Mol. Biol., 2008, 426, 103–115.
15. M. M. Pentony, J. J. Ward and D. T. Jones, Methods Mol. Biol., 2010, 604, 369–393.
16. O. Noivirt-Brik, J. Prilusky and J. L. Sussman, Proteins: Struct., Funct., Bioinf., 2009, 77, 210–216.
17. B. Monastyrskyy, K. Fidelis, J. Moult, A. Tramontano and A. Kryshtafovych, Proteins: Struct., Funct., Bioinf., 2011 DOI:10.1002/prot.23161.
18. C. Chothia and A. M. Lesk, EMBO J., 1986, 5, 823–826.
19. C. J. Brown, A. K. Johnson and G. W. Daughdrill, Mol. Biol. Evol., 2010, 27(3), 609–621.
20. A. Tóth-Petróczy, B. Mészáros, I. Simon, A. K. Dunker, V. N. Uversky and M. Fuxreiter, Open Proteomics J., 2008, 1, 46–53.
21. P. Romero, Z. Obradović, X. Li, E. C. Garner, C. J. Brown and A. K. Dunker, Proteins: Struct., Funct., Genet., 2001, 42(1), 38–48.
22. X. Li, P. Romero, M. Rani, A. K. Dunker and Z. Obradović, Genome Inform Ser Workshop Genome Inform, 1999, 10, 30–40.
23. J. J. Ward, J. S. Sodhi, L. J. McGuffin, B. Buxton and D. T. Jones, J. Mol. Biol., 2004, 337, 635–645.
24. A. A. Schäffer, L. Aravind, T. L. Madden, S. Shavirin, J. L. Spouge, Y. I. Wolf, E. V. Koonin and S. F. Altschul, Nucleic Acids Res., 2001, 29, 2994–3005.
25. J. Cheng, M. J. Sweredoski and P. Baldi, Data Mining and Knowledge Discovery, 2005, vol. 11, pp. 213–222.
26. L. Wang and U. H. Sauer, Bioinformatics, 2008, 24, 1401–1402.
27. M. Sickmeier, J. A. Hamilton, T. LeGall, V. Vacic, M. S. Cortese, A. Tantos, B. Szabo, P. Tompa, J. Chen, V. N. Uversky, Z. Obradović and A. K. Dunker, Nucleic Acids Res., 2006, 35, D786–D793.
28. K. Peng, P. Radivojac, S. Vucetic, A. K. Dunker and Z. Obradović, BMC Bioinf., 2007, 7, 208.
29. Z. Obradović, K. Peng, S. Vucetic, P. Radivojac and A. K. Dunker, Proteins: Struct., Funct., Genet., 2005, 61(suppl 7), 176–182.
30. B. Xue, R. L. Dunbrack, R. W. Williams, A. K. Dunker and V. N. Uversky, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804(4), 996–1010.
31. A. Schlessinger, M. Punta, G. Yachdav, L. Kajan and B. Rost, PLoS One, 2009, 4(2), e4433.
32. P. Zhang and Z. Obradović, IEEE Int. Conf. Bioinf. Biomed., 2010, pp. 49–52.
33. X. Deng, J. Eickholt and J. Cheng, BMC Bioinf., 2009, 10, 436.
34. T. Ishida and K. Kinoshita, Bioinformatics, 2008, 24(11), 1344–1348.
35. P. Lieutaud, B. Canard and S. Longhi, BMC Genomics, 2008, 9, S25.
36. S. Griep and U. Hobohm, Nucleic Acids Res. Database Issue, 2010, 38, D318–D319.
37. J. Y. Yang and M. Q. Yang, BMC Genomics, 2008, 9(suppl 2), S8.
38. R. Linding, L. J. Jensen, F. Diella, P. Bork, T. J. Gibson and R. B. Russell, Structure (London), 2001, 11, 1453–1459.
39. J. Kyte and R. F. Doolittle, J. Mol. Biol., 1982, 157, 105–132.
40. M. Vihinen, E. Torkkila and P. Riikonen, Proteins: Struct., Funct., Genet., 1994, 19(2), 141–149.
41. R. Linding, R. B. Russell, V. Neduva and T. J. Gibson, Nucleic Acids Res., 2003, 13, 3701–3708.
42. J. Gao, J. J. Thelen, A. K. Dunker and D. Xu, Mol. Cell. Proteomics, 2010, 9(12), 2586–2600.
43. S. Vucetic, C. J. Brown, A. K. Dunker and Z. Obradović, Proteins: Struct., Funct., Genet., 2003, 52(4), 573–584.
44. J. C. Rosenbaum, E. K. Fredrickson, M. L. Oeser, C. M. Garrett-Engele, M. N. Locke, L. A. Richardson, Z. W. Nelson, E. D. Hetrick, T. I. Milac, D. E. Gottschling and R. G. Gardner, Mol. Cell, 2010, 41(1), 93–106.
45. C. Schaefer, A. Schlessinger and B. Rost, Bioinformatics, 2010, 26(5), 625–631.
46. C. J. Brown, A. K. Johnson, A. K. Dunker and G. W. Daughdrill, Curr. Opin. Struct. Biol., 2011, 21(3), 441–446.
47. A. Schlessinger, C. Schaefer, E. Vicedo, M. Schmidberger, M. Punta and B. Rost, Curr. Opin. Struct. Biol., 2011, 21(3), 412–418.
48. S. A. Benner, Adv. Enzyme Regul., 1989, 28, 219–236.
49. D. Bordoa and P. Argos, J. Mol. Biol., 1990, 211(4), 975–988.
50. R. L. Jernigan and A. Kloczkowski, Methods Mol. Biol., 2007, 350, 251–276.
51. S. Fukuchi, K. Homma, Y. Minezaki and K. Nishikawa, J. Mol. Biol., 2006, 355(4), 845–857.
52. C. Rancurel, M. Khosravi, A. K. Dunker, P. R. Romero and D. Karlin, J. Virol., 2009, 83(20), 10719–10736.
53. Y. Cheng, T. LeGall, C. J. Oldfield, A. K. Dunker and V. N. Uversky, Biochemistry, 2006, 45(35), 10448–10460.
54. V. N. Uversky, C. J. Oldfield and A. K. Dunker, Annu. Rev. Biophys., 2008, 37, 215–246.
55. V. Vacic and L. M. Iakoucheva, Mol. BioSyst., 2012 10.1039/c1mb05251a.
56. Y. Hu, Y. Liu, J. Jung, A. K. Dunker and Y. Wang, BMC Genomics , in press.
57. C. C. Chang and C. J. Lin, ACM Transactions on Intelligent Systems and Technology, 2011, 2, 27.
58. M. Schmidt and K. Swersky, crfChain: a library for conditional random field, Software available at http://www.cs.ubc.ca/ schmidtm/Software/crfChain.html, 2010.

---

Footnote

† Published as part of a Molecular BioSystems themed issue on Intrinsically Disordered Proteins: Guest Editor M. Madan Babu.

---