 Open Access Article
Open Access ArticleExploring Li2MgZrO4 as a multifunctional material: structural analysis, polaron conductivity, and wide bandgap for energy and optoelectronic devices
S. Nasri *ab and
A. Oueslatia
*ab and
A. Oueslatia
aLaboratory of Spectroscopic Characterizations and Optics Materials, University of Sfax, Faculty of Sciences of Sfax, B.P. 1171, 3000 Sfax, Tunisia. E-mail: nasri.saber.1@gmail.com
bUniversity of Gafsa, Preparatory Institute for Engineering Studies of Gafsa, El Khayzorane Street – Zaroug, Gafsa – 2112, Tunsia
First published on 12th May 2025
Abstract
The search for advanced materials with tunable electronic and optical properties has driven significant progress in energy storage and optoelectronic technology. Lithium-based mixed-metal oxides stand out among these materials because of their excellent ionic conductivity and structural flexibility. This study focuses on examining the structural, electrical, and optical characteristics of Li2MgZrO4, a ternary oxide featuring a tetragonal layered structure (space group P42/nmc). The material was prepared using a solid-state synthesis method and its single-phase nature was validated by X-ray diffraction analysis combined with Rietveld refinement. Additionally, scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDX) were employed to evaluate the microstructural features and elemental distributions of the compounds. UV-vis-NIR spectroscopy revealed a direct bandgap of 3.41 eV, highlighting the material's potential for optoelectronic applications. Impedance spectroscopy studies demonstrated a non-Debye relaxation behavior and thermally activated conductivity. Examination of AC conductivity using Jonscher's power law and the overlapping large polaron tunneling (OLPT) model revealed that polaronic conduction mechanisms primarily govern charge transport. The activation energy (0.804 eV) further supported thermally activated conduction. These results highlight Li2MgZrO4 as a multifunctional material with considerable potential for applications in solid-state battery design, energy storage systems, and optoelectronic innovations.
1 Introduction
Recent breakthroughs in materials science have been driven by the demand for advanced compounds with tunable electronic and optical properties, particularly for energy storage and optoelectronic applications. In this context, lithium-containing compounds have gained prominence owing to their remarkable ionic conductivities, adaptable structures, and suitability for cutting-edge technologies such as solid-state batteries, sensors, and optical instruments.1,2 Notably, mixed-metal oxides incorporating lithium have garnered considerable attention for their capacity to combine the advantages of various elements, yielding materials with customized electrical, thermal, and optical traits.3,4 A prime example is Li2MgZrO4, a ternary oxide featuring a layered structure akin to perovskites, which serves as an intriguing system for exploring the relationships between crystal chemistry, defect behavior, and practical functionalities.Recent studies have highlighted the potential of lithium-containing ternary oxides for applications in solid-state electrolytes and dielectric materials. For instance, materials like Li3OCl and Li7La3Zr2O12 (LLZO) have demonstrated high ionic conductivity and stability, making them promising candidates for all-solid-state batteries.5,6 Likewise, the optical characteristics of lithium-infused oxides, including LiNbO3 and LiTaO3, have been thoroughly examined for their applications in nonlinear optics and photonic technologies.7,8 Despite these advancements, investigations into Li2MgZrO4 remain scarce, creating an opportunity to further explore its electrical and optical properties.
Li2MgZrO4 crystallizes in a tetragonal structure (space group P42/nmc), where the combination of lithium, magnesium, and zirconium ions creates a complex yet highly tunable material system. The presence of lithium ions facilitates ionic conduction, while magnesium and zirconium contribute to structural stability and covalent bonding, respectively.9,10 This unique composition endows Li2MgZrO4 with a range of desirable properties, including high thermal stability, mechanical robustness, and potential dielectric and optical functionalities. Recent computational studies using density functional theory (DFT) have predicted that Li2MgZrO4 exhibits a wide bandgap and favorable electronic structure, suggesting its suitability for optoelectronic applications11. However, experimental validation of these predictions is still lacking, underscoring the need for systematic investigations.
To address this gap, advanced characterization techniques are essential for elucidating the structural, compositional, and functional characteristics of Li2MgZrO4. Energy-dispersive X-ray spectroscopy (EDX) delivers an effective way to confirm the material's stoichiometry and determine its elemental distribution within the material, ensuring accurate control over its composition during synthesis. Additionally, optical studies such as UV-vis spectroscopy provide valuable information on the material's electronic structure and bandgap, which are crucial for assessing its optoelectronic properties. Together, these techniques complement traditional methods such as X-ray diffraction (XRD) and impedance spectroscopy, providing a comprehensive understanding of the material's fundamental characteristics.
The electrical properties of Li2MgZrO4 are expected to be influenced by factors such as lithium-ion mobility, defect chemistry, and interfacial effects. Comprehending these features proves vital to enhancing the material's effectiveness in applications like solid electrolytes and capacitive energy storage systems. Similarly, the optical properties of Li2MgZrO4, including its bandgap, refractive index, and nonlinear optical response, hold promise for use in photonic technologies such as light-emitting diodes (LEDs) and photodetectors. Recent advances in synthesis techniques, such as solid-state reactions and chemical vapor deposition (CVD), have enabled the production of high-purity Li2MgZrO4 samples, paving the way for detailed characterization.
Within this research, we deliver an in-depth analysis of the electrical and optical characteristics of Li2MgZrO4, integrating theoretical simulations with experimental measurements. By synthesizing high-purity samples and employing advanced characterization techniques, including EDX, impedance spectroscopy, dielectric measurements, and UV-vis-NIR spectroscopy, our goal is to clarify the inherent traits of the material and investigate its possibilities for diverse, multifunctional uses.
This study not only deepens our comprehension of lithium-based ternary oxides but also makes a significant contribution to the ongoing development of materials for sustainable energy and advanced electronics. Our findings provide crucial insights into the dielectric and conduction behaviors of Li2MgZrO4, paving the way for its application in cutting-edge energy storage and optoelectronic technologies.
2 Experimental methodology
Such Li2MgZrO4 material was developed using a solid-state reaction approach. Highly purified raw materials, specifically Li2CO3, MgO, and ZrO2, were meticulously measured in precise stoichiometric proportions, following the reaction equation below:| Li2CO3 + MgO + ZrO2 → Li2MgZrO4 + CO2 |
To achieve a homogeneous blend, the precursor materials were initially pulverized using an agate mortar and pestle to attain fine particle dispersion. Subsequent to this, precise dry-phase homogenization was achieved through spatula-assisted blending to ensure uniform constituent dispersion. To induce the decomposition of Li2CO3 and facilitate the expulsion of CO2 gas, the mixture was subjected to a preheating step in ambient air at 573 K for 8 hours, employing a controlled heating rate of 3 °C min−1. Subsequently, the material underwent a sequence of thermal treatments at progressively elevated temperatures, ranging from 873 K to 1473 K. Each thermal stage was sustained for 6 hours to drive phase formation and enhance crystalline growth. Ultimately, the synthesized material was gradually cooled to ambient temperature at a controlled rate of 2 °C min−1, effectively mitigating thermal stress and fostering the development of a well-ordered crystalline lattice.
The structural phase homogeneity and crystallographic integrity of the synthesized Li2MgZrO4 were meticulously verified via XRD. Diffraction patterns were collected across a Bragg angle range of 10–80° using a Bruker D8 Advance diffractometer, employing a Cu-Kα radiation source (λ = 1.5406 Å, voltage: 40 kV, current: 40 mA) under ambient conditions. Measurements were conducted with a step size of 0.02°, a scan speed of 1° min−1, and a glancing incidence angle of 1°, ensuring high-resolution data. The instrumental resolution was approximately 0.1° in 2θ. The lattice parameters were precisely extracted from the XRD data through Rietveld refinement, executed using Full Proof software, ensuring an accurate structural analysis and confirmation of phase composition.
Energy-dispersive X-ray (EDX) spectra were obtained using a JEOL JSM-7800F field-emission scanning electron microscope (FE-SEM) equipped with an Oxford Instruments X-MaxN 80 EDX detector operating at an accelerating voltage of 15 kV and a probe current of 1 nA. Before analysis, the sample was coated with a thin carbon layer to enhance electrical conductivity and minimize charging effects. Elemental mapping and point analysis were performed across 10–20 randomly selected regions of the Li2MgZrO4 surface to confirm compositional homogeneity, with EDX spectra collected at a detector resolution of 125 eV.
The optical traits of Li2MgZrO4 were examined using UV-vis-NIR spectroscopy to assess its bandgap and absorption features. Diffuse reflectance spectra were recorded using a PerkinElmer Lambda 950 spectrophotometer equipped with a 150 mm integrating sphere.
The instrument operated with a spectral resolution of ±0.2 nm and a wavelength accuracy of ±0.08 nm. Measurements were performed over a range of 200–2500 nm, using a scan speed of 240 nm min−1 and a slit width of 2 nm, ensuring high-precision data acquisition across the full spectral window. For a comprehensive evaluation of light absorption characteristics, the Kubelka–Munk function was applied to convert reflectance into absorption. The optical bandgap was then determined using the Tauc plot method, assuming both direct and indirect electronic transitions, thereby offering insight into the material's electronic structure and its prospects for optoelectronic applications.
The electrical characteristics of Li2MgZrO4 were evaluated using impedance spectroscopy. Measurements were performed with a Solartron 1260 Impedance Analyzer across a frequency range of 10 Hz to 5 MHz, with a measurement resolution of 0.1% in both phase and amplitude. The temperature range was maintained between 373 K and 573 K. An AC voltage of 500 mV was applied during the measurements. For the measurements, a cylindrical pellet with a diameter of 8 mm and a thickness of approximately 1.3 mm was prepared by uniaxial pressing of the synthesized powder at a pressure of 3 t cm−2, followed by sintering at 100 °C for 4 hours to ensure mechanical stability and densification. Silver electrodes were applied to both sides of the pellet using silver paste to ensure good electrical contact. Impedance measurements were conducted under carefully controlled conditions to minimize external interference and enhance data consistency.
3 Results and discussions
3.1 X-ray powder diffraction and morphology examination
The powder X-ray diffraction analysis of Li2MgZrO4 clearly confirms the presence of a single-phase tetragonal structure, with the observed diffraction patterns closely aligning with those reported in previous studies of Li2MgZrO4.12 The well-defined, intense diffraction peaks highlight the material's exceptional crystallinity, an essential attribute for enhancing electrical, dielectric, and ionic conduction properties in solid-state systems.To further corroborate the crystallographic structure, Rietveld refinement was performed on the XRD data, yielding lattice parameters of a = b = 4.202 ± 0.002 Å and c = 9.195 ± 0.005 Å, which closely match the values documented in earlier studies for the P42/nmc space group. This correspondence highlights the accuracy and reliability of our solid-state synthesis approach in achieving phase-pure Li2MgZrO4. Moreover, the lack of secondary phases in the XRD pattern further confirms the material's high phase purity, a crucial aspect for minimizing grain boundary resistance and enhancing both ionic conductivity and dielectric stability.
Fig. 1(a) presents the Rietveld refinement results, showcasing the excellent match between the observed and calculated diffraction patterns, which reinforces the material's structural soundness. Additionally, Fig. 1(b) illustrates the XRD patterns of Li2MgZrO4 synthesized at various temperatures (700 °C, 800 °C, and 900 °C), highlighting the progression of crystallinity and phase stability under different synthesis conditions.
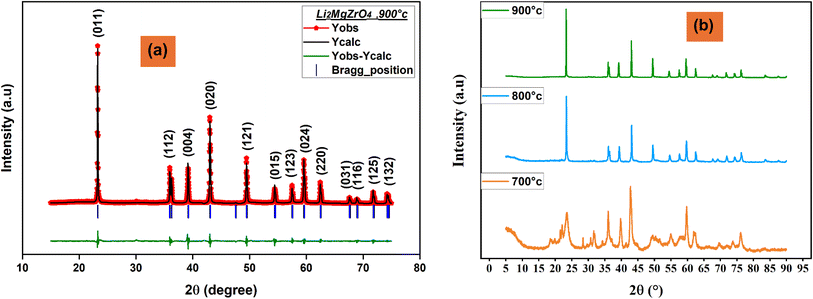 | ||
| Fig. 1 (a) Rietveld refinement pattern of XRD data of Li2MgZrO4 at room temperature, (b): XRD patterns of the sample measured at temperatures of 700 °C, 800 °C, and 900 °C. | ||
The average crystallite size (D) was calculated from the full width at half maximum (FWHM) of the prominent peaks observed in the XRD pattern using Scherrer's equation:13
 | (1) |
 | (2) |
 | (3) |
The evaluated structural parameters are presented in Table 1. As the temperature rises, the D value increases due to enhanced atomic mobility, which promotes grain growth. Simultaneously, the dislocation density δ and lattice strain ε values decreased, confirming the increase in crystallinity with annealing.14 This suggests that larger crystallites form as the temperature rises, leading to a reduction in internal stresses and improved structural integrity.
| Structural parameters | D (nm) | δ × 1015 (m−2) | ε |
|---|---|---|---|
| 900 °C | 36.13 | 0.76 | 0.82 × 10−3 |
| 800 °C | 31.1 | 1.03 | 0.94 × 10−3 |
| 700 °C | 25 | 1.59 | 1.06 × 10−3 |
To enhance the structural evaluation, Fig. 2 provides a grain size distribution histogram, shedding light on the material's morphology and its relationship to electrical and dielectric properties. The inset of Fig. 2 features SEM imaging, displaying a consistent grain distribution with a mean crystallite dimension of 6.39 ± 0.15 μm. The particles show little clustering and a clear, well-formed structure, suggesting a carefully managed microstructural development during synthesis. The lack of cracks or surface flaws underscores the mechanical robustness of Li2MgZrO4, reinforcing its potential for use in energy storage and dielectric technologies.
 | ||
| Fig. 2 Scanning electron microscopy (SEM) images accompanied by a corresponding size distribution histogram. | ||
Fig. 3 presents the EDX spectrum of Li2MgZrO4, revealing the distinct peaks corresponding to each constituent element. The lack of signals associated with impurities underscores the exceptional phase purity and low contamination levels in the synthesized material, reflecting the success of the solid-state reaction approach in producing a chemically uniform product. However, due to the limitations of EDX, lithium could not be directly detected. This is because lithium has a low atomic number, making it difficult to detect using conventional EDX detectors. Furthermore, its atomic number coincides with that of the reference element employed in this analysis, complicating identification.
 | ||
| Fig. 3 Elemental analysis conducted using energy-dispersive X-ray spectroscopy (EDX). Inset: quantitative assessment of the elemental composition. | ||
Precise stoichiometric control is crucial for optimizing the functional performance of Li2MgZrO4. Deviations from the ideal composition may lead to the formation of point defects, secondary phases, or lattice distortions, which could hinder ionic transport and degrade dielectric stability. By ensuring compositional accuracy, this study establishes a strong foundation for understanding the intrinsic electrical and optical properties of Li2MgZrO4.
3.2 Ultraviolet-visible spectroscopy analysis
UV/Vis spectroscopy serves as a common analytical tool for exploring the quantitative optical characterization, such as organic–inorganic hybrid compounds. This process quantifies the light absorbed or transmitted within the ultraviolet (UV) and visible (Vis) portions of the electromagnetic spectrum.15 A crucial value derived from this method is the bandgap, defined as the minimum energy needed to promote an electron from the valence band to the conduction band. Determining the bandgap is vital for evaluating a material's capacity to absorb and emit light, a factor that plays a significant role in its potential use in photovoltaics, light-emitting technologies, and photocatalytic systems.16The interaction between incident light and the semiconductor significantly influences its optical properties. In this study, these characteristics are examined through the absorbance spectrum, as illustrated in Fig. 4(a). By analyzing the absorption spectra, the active absorption bands can be identified, along with the determination of the optical bandgap energy and Urbach energy as functions of incident photon energy.The absorbance spectrum of the Li2MgZrO4 compound, annealed at 900 °C and characterized under ambient conditions within the 200–800 nm wavelength range, reveals two distinct absorption bands at 232 and 310 nm. Notably, the spectrum exhibits strong absorption in the visible region, underscoring its fundamental band characteristics. This absorption arises from electron excitation, in which electrons shift from the valence band to the conduction band. The primary factor governing the energy bandgap is the charge transfer between these bands. Several methods can be employed to determine a material's bandgap energy (Eg).
The inset of Fig. 4(a) illustrates the variation of (dA/dλ) as a function of wavelength (λ). The optical bandgap energy (Eg) of the Li2MgZrO4 compound was derived from the minimum point of the (dA/dλ) curve. It can be estimated using the equation Eg = 1240/λ, where Eg is in electron volts and λ is the wavelength in nanometers. Based on this relationship and the prominent peak observed at 343 nm, the optical bandgap energy is calculated to be approximately 3.615 eV. The observed bandgap places this material in the technologically relevant category of wide-gap semiconductors (0.5 to 5 eV), suitable for UV photonics and high-power electronics.17
Nevertheless, this approach cannot differentiate between direct and indirect bandgaps. Addressing this limitation, Tauc's method well-suited for powdered materials was employed, utilizing the following relationship:18
| (αhν)n = A(hν − Eg) | (4) |
In this context, α is the absorption coefficient, n defines the nature of the optical transition (with n = 1/2 for direct and n = 2 for indirect allowed transitions), and A is a constant related to the transition probability, indicating the degree of structural disorder in the material.19
As shown in Fig. 4(b), the plots of (αhν)1/2 and (αhν)2 versus photon energy hν exhibit linear regions, the extrapolation of which yields the bandgap energies, Eg, with Egd and Egi representing the direct and indirect bandgaps, respectively. The calculated values are 3.41 (±0.32) eV for n = 1/2 and 2.45 (±0.24) eV for n = 2. Assuming a direct transition, the parameter A was determined from the slope of the linear fit in the Tauc plot and found to be approximately 469 nm−1 eV−1.
The close agreement between the bandgap value obtained via the dA/dλ method and the Tauc plot supports the presence of a dominant direct transition. To ascertain whether the material possesses a direct or indirect bandgap, a mathematical validation is required.20
Ln(αhν) = ln(A) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(hν − Eg) ln(hν − Eg)
| (5) |
Fig. 4(c) illustrates the variation of ln(αhν) as a function of ln(hν − Eg). The transition mode can be determined by analyzing the slope of the linear region. By fitting this portion of the curve, a value of n = 0.54211 was established, affirming that the studied compound exhibits a direct bandgap with an energy gap of approximately 3.41 eV. Compared to indirect bandgaps, direct bandgaps are well known for their superior luminous efficiency, as they enable nearly all the energy to be emitted as light without the involvement of phonons.21,22 Consequently, the studied sample holds potential for use in light-emitting diode (LED) manufacturing.
To assess the extent of disorder near the optical band edge, the Urbach energy, an empirical parameter, must be determined.23 The exponential absorption tail observed in the absorbance spectrum arises from localized states within the defect region. By analyzing the dependence of ln(α) on incident photon energy, as shown in Fig. 4(d), the Urbach tail can be estimated using the following expression:24
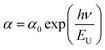 | (6) |
In this equation, (α0) is a constant, and (EU) represents the energy associated with the width of the exponential tail of localized states within the forbidden bandgap.25 The Urbach energy provides valuable insight into the degree of structural and thermal disorder in a material.26 It is obtained by taking the reciprocal of the slope of the linear region in the plot of ln(α) versus photon energy. In this study, the Urbach energy was found to be 0.2 eV, indicating that Li2MgZrO4 exhibits a slightly higher degree of disorder.
Urbach energy can be further evaluated using the following expression:
 | (7) |
The value of σ was determined to be approximately 0.13. This parameter, which reflects the strength of the electron–phonon interaction Ee–ph, can be expressed as:28
 | (8) |
The estimated electron–phonon interaction energy, Ee–ph, is approximately 5.12 eV. This interaction describes the coupling between electrons and lattice vibrations (phonons) and plays a critical role in determining the electrical resistivity, superconductivity, and thermal properties of the material.
3.3 Investigation of impedance characteristics
Impedance spectroscopy is a crucial analytical tool in materials science, offering deep insights into the electrical properties of various substances. This technique enables researchers to identify and analyze the effects of microstructural features such as particles, grain boundaries, and electrode interfaces on overall conductivity. By disentangling these contributions, it clarifies the mechanisms governing charge transport. Additionally, impedance analysis serves as a powerful method for assessing how temperature variations, frequency changes, and structural modifications influence a material's electrical behavior. Its precision and versatility make it indispensable for understanding advanced materials.29Fig. 5 illustrates the frequency-dependent real portion of the complex impedance, Z′(ω), plotted alongside its imaginary counterpart, Z′′(ω), across various temperatures. This graphical method, recognized as Cole–Cole plot or Nyquist diagram, is a standard tool in material characterization. Typically, Nyquist plots for dielectric materials feature three semicircular arcs, each representing contributions from the bulk grain, grain boundaries, and electrode–material interfaces, which together define the material's total impedance.
 | ||
| Fig. 5 Nyquist plots (Z′′ vs. Z′) for Li2MgZrO4 compound in the temperature range from 373 K to 573 K with the inset showing the equivalent circuit model used for the fitting procedure. | ||
At high frequencies, the curves predominantly reflect the bulk grain's impedance, while the low-frequency region emphasizes the role of grain boundaries. Ultralow frequencies, on the other hand, reveal processes at the electrode–material interface.
In Fig. 5, the impedance spectra exhibit a single, flattened semicircular arc that persists across all measured temperatures, indicating that the electrical response of the material is predominantly governed by grain (bulk) effects, with negligible contributions electrode interactions. The decreasing radius of the arc with increasing temperature indicates improved conductivity within the material. Furthermore, the positioning of the arc centers below the real axis implies non-Debye relaxation behavior, suggesting complex charge transport mechanisms within the ceramic.30 To analyze the electrical characteristics, an equivalent circuit representing grain effects was simulated using Z-View software, with the optimal circuit configuration shown in the insets of Fig. 5. The resulting variable derived from this model are compiled in Table 2.
| T (K) | R (106 Ω) | C (10−11 F) | CPE1 (10−9 F) | α1 | CPE2 (10−6 F) | α2 |
|---|---|---|---|---|---|---|
| 373 | 378.45 | 27.22 | 0.36 | 0.742 | 0.069 | 0.871 |
| 393 | 204.63 | 27.65 | 0.39 | 0.755 | 0.077 | 0.963 |
| 413 | 104.72 | 27.72 | 0.48 | 0.754 | 0.125 | 0.941 |
| 433 | 77.25 | 28.55 | 0.54 | 0.754 | 0.133 | 0.933 |
| 453 | 42.62 | 29.45 | 0.63 | 0.753 | 0.209 | 0.924 |
| 473 | 33.45 | 29.93 | 0.71 | 0.754 | 0.321 | 0.915 |
| 493 | 22.11 | 31.18 | 0.77 | 0.756 | 0.728 | 0.910 |
| 513 | 15.45 | 30.72 | 0.85 | 0.756 | 1.341 | 0.898 |
| 533 | 8.68 | 31.82 | 0.97 | 0.758 | 2.672 | 0.891 |
| 553 | 6.68 | 31.18 | 0.98 | 0.759 | 3.758 | 0.885 |
| 573 | 5.28 | 31.89 | 1.07 | 0.761 | 4.112 | 0.894 |
The temperature-dependent variation of the grain resistance Rg is presented in Fig. 6. As the temperature rises, Rg decreases significantly, which aligns with the negative temperature coefficient of resistance (NTCR) behavior discussed earlier. This trend is characteristic of thermally activated conduction mechanisms, where increased thermal energy promotes the mobility of charge carriers, thereby reducing resistance. The decrease in Rg with temperature further supports the expectation of enhanced ionic or electronic conductivity at elevated temperatures, a phenomenon widely observed in ceramic materials.31
The frequency-dependent behavior of the real part of impedance, Z′(ω), across temperatures ranging from 373 K to 573 K is illustrated in Fig. 7. The data reveals a sigmoidal trend, where Z′(ω) attains higher values in the low-frequency regime. With increasing frequency and temperature, Z′(ω) gradually decreases, consistent with the negative temperature coefficient of resistance. This trend correlates with a rise in AC conductivity at elevated temperatures. In the high-frequency range, Z′(ω) shows minimal temperature dependence, causing the curves to merge, as seen in the Fig. 7. This behavior is attributed to the release of space charges and a reduction in barrier properties, which contribute to enhanced AC conductivity.32
 | ||
| Fig. 7 Frequency dependence of the real part (Z′) over a range for temperatures spanning from 373 K to 573 K. | ||
The frequency dependence of the imaginary part of impedance, Z′′(ω), represents a loss spectrum, as depicted in Fig. 8. The variation of Z′′(ω) with frequency exhibits distinct relaxation peaks that shift with temperature. These peaks arise when the frequency of the applied electric field matches the hopping frequency of localized charge carriers. The relaxation peaks are notably broader than those predicted by an ideal Debye model, confirming non-Debye relaxation behavior.33 This broadening indicates the presence of multiple relaxation time constants, reflecting complex relaxation mechanisms rather than a single exponential decay typical of Debye-type relaxation.34
At higher frequencies, the (Z′′) values for all measured temperatures converge into a single curve. This merging aligns with the trends observed in the real part of impedance (Z′) and suggests the potential role of space charge effects in influencing the material's overall impedance characteristics.35 As a whole, these insights emphasize the intricate relationship between grain contributions and space charge dynamics dictating the electrical characteristics of the material. This interplay highlights the importance of both microstructural features and charge carrier interactions in determining the material's response across different experimental conditions.
3.4 Analysis of electrical modulus properties
To delve deeper into the relaxation dynamics of Li2MgZrO4, an in-depth examination of the complex modulus spectra was performed. The complex electric modulus acts as a potent instrument for investigating electrical relaxation phenomena, particularly in elucidating space charge distribution and its impact on minimizing electrode-induced distortions. Defined as the reciprocal of the complex permittivity, the electric modulus offers an alternative framework for analyzing dielectric relaxation processes. In materials where dielectric displacement stays consistent, the electric modulus primarily reflects the relaxation characteristics of the electric field within the system. The complex modulus can be mathematically represented by the following formula:36,37
 | (9) |
Within this framework M*(ω) represents the complex electric modulus, ε*(ω) denotes the complex permittivity while M′(ω) indicates the real component of the electric modulus, M′′(ω) is the imaginary part, ω signifies the angular frequency, and j is the imaginary unit. This formalism is particularly advantageous in systems where electrode polarization and high permittivity obscure bulk relaxation processes, as it emphasizes the material's intrinsic properties by minimizing electrode effects. Analyzing the intricate properties of the complex modulus provides researchers with a deeper understanding of the dielectric relaxation behavior and charge transport mechanisms of a material, which are fundamental aspects in the advancement of state-of-the-art electronics and highly efficient energy storage systems.
Fig. 9 depicts the real component of the electric modulus (M′) as a function of frequency at various temperatures, providing insights into the charge carrier dynamics within the material. At low frequencies, M′ approaches near-zero values, showing little dependence on temperature. This phenomenon indicates that charge transport is primarily governed by extensive charge carrier migration, with minimal influence from electrode-induced polarization or interfacial capacitance effects. The presence of a characteristic S-shaped profile in the modulus spectrum reinforces the significance of mobile charge carriers in facilitating conduction. With increasing frequency, exhibits a gradual rise, though this increase becomes less significant at elevated temperatures, suggesting a shift toward short range carrier mobility. This is particularly evident at higher frequencies, where a subtle dispersion emerges. Eventually, M′ stabilizes, reaching a near-constant value, which may correspond to conductivity relaxation within the material. This saturation at intermediate to high frequencies suggests a weakening of the forces governing charge mobility under the applied electric field. At lower frequencies, ions oscillate within their potential energy wells, while at higher frequencies, their response to the electric field diminishes. Collectively, these observations highlight a conduction mechanism driven by both long-range carrier movement and temperature-dependent relaxation processes, with minimal impact from polarization effects.
 | ||
| Fig. 9 The frequency-dependent behavior of the real component of the electric modulus (M′) at different temperatures. | ||
Fig. 10 depicts the frequency-dependent variation of the imaginary component of the electric modulus (M′′) for the synthesized compound across a range of temperatures. At each measured temperature, M′′ manifests a distinct peak at a characteristic frequency (ωmax), signifying conductivity relaxation phenomena within the material. In the ceramic lattice, this peak initially emerges in the low-frequency region and progressively migrates toward higher frequencies as the temperature increases. Such distinctive curve morphology underscores an acceleration in the relaxation process, attributed to thermally stimulated charge transport.38
 | ||
| Fig. 10 The frequency-dependent variation of the imaginary component of the electric modulus (M′′) measured at various temperatures. | ||
The temperature-driven evolution of the M′′ peak offers profound understanding into the relaxation dynamics and conductivity characteristics of the material. The presence of these peaks indicates a shift in charge carrier mobility, transitioning from extended-range conduction to localized hopping mechanisms. In an ideal Debye-type relaxation system, all dipoles would exhibit an identical relaxation time. However, the asymmetric broadening of the M′′ peaks suggests a pronounced deviation from Debye behavior, implying a dispersion of relaxation times within the material. This deviation underscores the intricate nature of the relaxation mechanisms and the pivotal role of temperature in modulating charge transport phenomena. The relaxation time (τ), representing the characteristic timescale over which the system undergoes relaxation, is determined using the equation:39
 | (10) |
In this context, fmax denotes the frequency corresponding to the peak response on the curve. The mean activation energy of the charge carriers is determined by applying the Arrhenius equation:40
 | (11) |
Within this equation, τ0 stands for the pre-exponential factor, kB denotes the Boltzmann constant, and T represents the absolute temperature.
The activation energy (Ea) is extracted by analyzing the linear correlation in a plot of ln(τ) versus 1000/T, as illustrated in Fig. 11. From the experimental data, we derive an activation energy value of 0.804 ± 0.023. Additionally, the inset of Fig. 11 shows a plot of log(ωmax) versus absolute temperature, which provides a consistent estimate of the activation energy. These findings affirm that Li2MgZrO4 exhibits thermally-driven relaxation characteristics. As the temperature rises, charge carriers or dipoles gain enhanced mobility, allowing them to react more swiftly to external electric fields, especially at elevated frequencies. This behavior is pivotal in both electronic and optoelectronic devices, where materials must adjust seamlessly to fluctuating signals over a broad temperature range. Such attributes underscore the material's promise in cutting-edge technologies, where flexibility and efficiency in diverse conditions are paramount. The heightened responsiveness of the charge carriers emphasizes the material's potential to excel in environments that demand dynamic thermal and electrical performance.
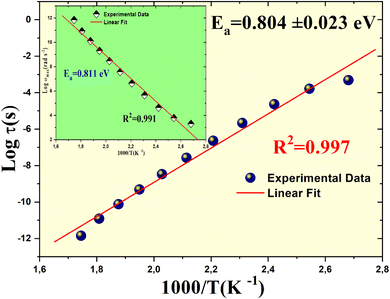 | ||
| Fig. 11 Variation of ln(τ × T) as a function of 1000/T with the inset showing the plot of log(ωmax) versus absolute temperature. | ||
The representation of the combined spectra of the imaginary electric modulus (M′′) and impedance (Z′′) for the Li2MgZrO4 compound, as depicted in Fig. 12, has been deliberately chosen to elucidate the distinction between short-range and long-range charge carrier dynamics. This method provides a more profound understanding of the material's conduction mechanisms. A significant disparity between the peak frequencies of M′′ (fmax(M′′)) and Z′′ (fmax(Z′′)) unmistakably points to a localized conduction process, aligning with observations reported in previous studies.41
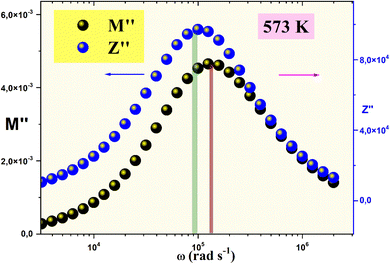 | ||
| Fig. 12 Combined spectra of the imaginary electric modulus (M′′) and impedance (Z′′) for the Li2MgZrO4 compound at a selected temperature. | ||
A wealth of literature highlights that the convergence of M′′ and Z′′ peaks at a single frequency is a hallmark of long-range charge transport dominating the relaxation dynamics. By contrast, a pronounced divergence between fmax(M′′) and fmax(Z′′) unveils a regime of short-range charge mobility, where carriers are confined to localized hopping within discrete potential wells.42 In the present study, this material exhibits a consistent offset between these peak frequencies across a range of temperatures, signaling a prevalence of short-range charge dynamics. This behavior not only underscores the localized nature of conduction but also suggests a temperature-modulated interplay between carrier confinement and mobility, offering a nuanced perspective on the material's dielectric response that that could guide its optimization for cutting-edge applications.
3.5 AC electrical conductivity
Fig. 13(a) illustrates the intricate interplay between temperature and frequency in shaping the AC conductivity of Li2MgZrO4. At higher frequencies, the AC component emerges as the dominant factor influencing conductivity, whereas at lower frequencies, the temperature-dependent DC conductivity takes precedence. In this DC-dominated regime, the material shows little response to changes in frequency, producing the characteristic plateau observed within this range. As the frequency increases, the impact of AC conductivity becomes more pronounced, driving a notable increase in conductivity values and establishing a clear dependence on frequency. This transition from DC-dominated to AC-dominated behavior occurs at a critical frequency known as the “hopping frequency”. Notably, this hopping frequency shifts toward higher values with increasing temperature, highlighting the thermally activated nature of the ion transport process.This behavior closely mirrors Funke's jump relaxation model (JRM), offering critical insights into ion dynamics within the material. At low frequencies, ions have ample time to hop between neighboring sites, facilitating long-range movement and ensuring stable DC conductivity. In contrast, at higher frequencies, the swift oscillations impede the ions' ability to complete successful hops, restricting their motion and leading to the emergence of AC-conductivity features. The interplay between successful and unsuccessful hopping events at these elevated frequencies explains the observed frequency-dependent variations in AC conductivity.43
Furthermore, this phenomenon can be attributed to the activation energy required for ion hopping, which decreases with increasing temperature. This reduction in activation energy facilitates more frequent hopping events, thereby enhancing both the magnitude and frequency dependence of AC conductivity.44 The nuanced relationship between temperature, frequency, and ion mobility underscores the complex mechanisms governing electrical transport in Li2MgZrO4 making it a compelling subject for further investigation in solid-state ionics.
The electrical conductivity observed in the material can be effectively interpreted using Jonscher's power law, a well-established framework for analyzing the universal dielectric response (UDR).45 This approach not only elucidates the underlying mechanisms governing electrical characteristics but also emphasizes the relationship between microscopic ion dynamics and macroscopic transport phenomena.
Additionally, the hopping mechanism outlined in this model aligns with experimental observations, showing that conductivity is influenced by thermal activation at lower frequencies and by frequency-dependent processes at higher frequencies. This twofold reliance underscores the intricate nature of ion transport in solid electrolytes, offering useful insights for enhancing material performance in energy storage and conversion technologies. The relationship is expressed as:46
| σac(ω, T) = σdc(T) + AωS | (12) |
Fig. 13(b) displays a graph of ln(σdc × T) versus 1000/T, adhering to the Arrhenius relationship, a widely recognized model for characterizing the temperature dependence of DC conductivity in ceramic materials. The Arrhenius equation is given by:
σdc = Tσ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(kBT − Ea) exp(kBT − Ea)
| (13) |
In this context, σ0 is the pre-exponential factor associated with electrical conductivity, kB is Boltzmann's constant, and Ea represents the activation energy. The determined activation energy is Ea = 0.674 ± 0.005 eV.
Exploring the charge transport mechanisms in Li2MgZrO4 materials is crucial for understanding their electrical properties. The temperature-dependent behavior of the exponent s provides valuable insights into the dominant conduction mechanisms. Several theoretical models have been proposed to explain the variation of s, frequently combining quantum mechanical tunneling with charge carrier hopping. In these models, entities like electrons, polarons, or ions traverse energy barriers, shedding light on the underlying conduction processes.
One such framework is overlapping large polaron tunneling (OLPT), which describes the motion of large polarons. In this model, neighboring potential wells overlap considerably, enabling efficient charge transport. Conversely, non-overlapping small-polaron tunneling (NSPT) involves charge transfer through small polarons that hop between isolated states with minimal overlap. Another model, correlated barrier hopping (CBH), explains conduction as charge carriers hopping between localized sites while being affected by Coulomb interactions and energy barriers. Additionally, pure quantum mechanical tunneling (QMT) accounts for charge carriers traversing barriers without the need for thermal activation.47
By examining the temperature dependence of s, researchers can identify the most suitable model to describe charge transport in Li2MgZrO4 materials. This investigation not only enhances our understanding of conduction mechanisms but also aids in tailoring material properties for specific technological applications, such as energy storage, solid-state batteries, and advanced electronics.
Fig. 13(c) illustrates the variation of the exponent s with temperature, revealing a trend where s initially decreases before experiencing a slight increase at higher temperatures. This behavior is consistent with the overlapping large polaron tunneling (OLPT) model, which describes charge transport dominated by large polarons moving through overlapping potential wells.
In the framework of the overlapping large polaron tunneling (OLPT) model, AC conductivity is attributed to the tunneling behavior of polarons, driven by the interaction between the distortion fields surrounding these charge carriers.48 For larger polarons, the extensive Coulomb interactions cause the potential wells at adjacent sites to overlap or merge, significantly reducing the energy barrier for polaron transfer between sites. This facilitates their efficient movement across the lattice, enhancing AC conductivity. The reduction in the energy barrier lowers the energetic cost of hopping, which directly influences the energy dissipation associated with charge carrier motion. The merging of potential wells, a result of the expansive Coulomb interactions, plays a critical role in enabling polarons to tunnel between neighboring sites with minimal resistance.
In the case of Li2MgZrO4, the presence of lithium (Li) ions, which are highly mobile, likely contributes to the formation of polarons. The interaction between these polarons and the surrounding lattice, including the Mg and Zr cations, creates distortion fields that influence the tunneling process. The merging of potential wells due to the expansive Coulomb interactions plays a critical role in enabling polarons to tunnel between neighboring sites with minimal resistance. The reduction in the energy barrier for polaron hopping in Li2MgZrO4 can be attributed to the specific structural and electronic properties of the material. The presence of Zr, with its relatively high polarizability, may further enhance the overlapping of potential wells, promoting polaron tunneling. Additionally, the Mg ions, which are less mobile compared to Li, provide a stable framework that supports the formation and movement of polarons. The interplay between these ions creates a conducive environment for the OLPT mechanism, where the polarons can move efficiently through the lattice.
This behavior underscores the significance of polaron dynamics in governing the electrical properties of materials, particularly those that rely on polaronic conduction. In systems such as lithium-ion conductors and other solid electrolytes, where charge transport is influenced by similar hopping mechanisms, understanding and controlling polaron behavior through compositional or structural modifications can enhance both electronic and ionic conductivity. This, in turn, plays a crucial role in optimizing material performance for energy storage applications. In Li2MgZrO4, the OLPT mechanism is particularly relevant due to the material's unique ionic environment. The combination of highly mobile Li ions and the stabilizing influence of Mg and Zr ions creates an ideal system for studying polaron dynamics. The temperature and frequency dependence of AC conductivity in Li2MgZrO4 further underscores the importance of polaron tunneling in this material. At higher temperatures, the thermal energy can further reduce the energy barrier for polaron hopping, increasing the conductivity. Similarly, at higher frequencies, the polarons may respond more readily to the alternating electric field, leading to an increase in AC conductivity. These properties make Li2MgZrO4 a promising candidate for applications in solid-state electrolytes and other energy storage technologies.
As per the OLPT model, the AC conductivity is characterized by:
 | (14) |
The jump distance Rω is determined by solving the equation below:
 | (15) |
In this expression,  and α denotes the reciprocal of the localization length.
and α denotes the reciprocal of the localization length.
Per the overlapping large polaron tunneling (OLPT) model, the potential wells of large polarons at two distinct sites intersect, leading to a reduction in the energy required for polaron hopping, as outlined in the following description.49
 | (16) |
In this context, WHO stands for the energy needed for polarons to jump, R indicates the spacing between polaron locations, and rp refers to the size of the polaron. It is once more assumed that WHO stays the same for all locations, while the separation R is viewed as a varying factor. The parameters WHO and Rω can be figured out using the formulas given below:50
 | (17) |
 | (18) |
The frequency factor “s” in this setup is described as:
 | (19) |
The theoretical predictions of the OLPT model, as shown in Fig. 13(d), show a remarkable correlation with the experimental data. The various parameters used in the fitting process are detailed in Table 3.
| Frequency (kHz) | WH0 (eV) | N (eV−1 cm−1) | α (Å−1) | rp (Å) | Rω (Å) | |
|---|---|---|---|---|---|---|
| OLPT model | 103 | 0.14 | 2.15 × 1031 | 0.62 | 1.11 | 2.67 |
| 3.98 × 102 | 0.19 | 7.11 × 1029 | 0.57 | 1.02 | 2.89 | |
| 10 | 0.23 | 3.77 × 1028 | 0.53 | 0.87 | 3.01 |
These electrical properties are governed by polaronic conduction, space charge effects, lattice dynamics, and defect-driven relaxation mechanisms. Impedance and modulus analyses further corroborate this interpretation, revealing a temperature-dependent decrease in bulk resistance owing to thermally activated ionic mobility and defect-enhanced polaron hopping processes that enable efficient charge transport with minimal energy loss. The frequency-dependent transition from long-range ionic migration (low frequencies) to localized hopping (high frequencies) underscores the versatility of the material across the operational regimes. Insights from impedance, modulus, and (OLPT) studies suggest that controlled doping or compositional tuning could further optimize polaron mobility and ionic conductivity, enhancing the performance of the material in these advanced applications. Together, these findings highlight the multifunctional potential of Li2MgZrO4 for applications such as solid-state electrolytes, UV-transparent optoelectronics, and energy storage systems, where minimal power dissipation is paramount,51 as well as in high-power circuit applications requiring robust charge transport.
4 Conclusion
This investigation provides an extensive exploration of the structural, optical, and electrical facets of Li2MgZrO4, accentuating its versatility as a multifunctional material for energy storage and optoelectronic applications. XRD analysis validated the high phase purity and crystallinity of the compound, while SEM and EDX yielded profound insights into its microstructural framework and elemental distribution. Optical characterization confirmed a direct bandgap of 3.41 eV, reinforcing its feasibility for optoelectronic devices.Impedance spectroscopy was used to elucidate temperature-responsive electrical attributes, revealing a distinct non-Debye relaxation mechanism as the principal transport phenomenon. AC conductivity evaluation, interpreted using Jonscher's power law and the OLPT framework, indicated polaronic conduction as the primary mechanism, exhibiting an activation energy of 0.804 eV. These empirical findings accentuate the promise of Li2MgZrO4 for deployment in solid-state electrolytes, capacitive energy matrices, and optoelectronic configurations. Prospective research should prioritize refining synthesis methodologies to augment their electrical efficacy and investigate their seamless integration into pragmatic device architectures. This study establishes a robust groundwork for future exploration of lithium-based mixed-metal oxides as next-generation functional materials.
Ethical statement
The authors declare that this study complies with ethical standards for scientific research. No human or animal subjects were involved in this work. All data and findings presented in this manuscript are original and have not been fabricated, manipulated, or misrepresented. The authors have no conflicts of interest to disclose. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sector.Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request. Any additional materials, including raw data and analysis files, can be provided in compliance with institutional and journal guidelines.Author contributions
Pr Nasri Saber: conceptualization, methodology, investigation, formal analysis, writing original draft preparation, and visualization. Pr Oueslati Abderezek: validation, resources, data curation, writing review, supervision. Ensuring the accuracy and depth of the findings. Both authors collaborated on the overall design of the study, discussed the results, and approved the final manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.References
- M. York, K. Larson, K. C. Harris, E. Carmona, P. Albertus, R. Sharma, M. Noked, E. Strauss, H. Ragones and D. Golodnitsky, Recent advances in solid-state beyond lithium batteries, J. Solid State Electrochem., 2022, 26, 1851–1869 Search PubMed.
- J. Zhang, N. Zhao, M. Zhang, Y. Li, P. K. Chu, X. Guo, Z. Di, X. Wang and H. Li, Flexible and Ion-Conducting Membrane Electrolytes for Solid-State Lithium Batteries, Nano Energy, 2016, 28, 447–454 Search PubMed.
- J. B. Goodenough and K. S. Park, The Li-Ion Rechargeable Battery: A Perspective, J. Am. Chem. Soc., 2013, 135, 1167–1176 Search PubMed.
- M. Armand and J.-M. Tarascon, Building Better Batteries, Nature, 2008, 451, 652–657 Search PubMed.
- Q. H. Nguyen, Van T. Luu, H. L. Nguyen, Y.-W. Lee, Y. Cho, Se Y. Kim, Y.-S. Jun and W. Ahn, Garnet Solid Electrolytes for Lithium Metal Batteries, Nano Energy, 2021, 61, 535–554 Search PubMed.
- J. Xu, P. Gu, J. Zhang, H. Xue and H. Pang, Copper-Based Nanomaterials for High-Performance Lithium-Ion Batteries, Part. Part. Syst. Charact., 2016, 33, 784–810 Search PubMed.
- Di Zhu, L. Shao, M. Yu, R. Cheng, B. Desiatov, C. J. Xin, Y. Hu, J. Holzgrafe, S. Ghosh, A. Shams-Ansari, E. Puma, N. Sinclair, C. Reimer, M. Zhang and M. Lončar, Integrated photonics on thin-film lithium niobate, Adv. Opt. Photonics, 2021, 13, 242–352 Search PubMed.
- Y. X. Zhou, S. Yi, Z. X. Fang, J. Lu, Z. Hu, W. Zhao and Y. Wang, Research on a new type of near-infrared phosphor Li2MgZrO4:Cr3+- synthesis, crystal structure, photoluminescence and thermal stability, Opt. Mater., 2021, 117, 111209 Search PubMed.
- L. M. Mohan, S. Som, R. K. Singh and C.-H. Lu, Synthesis, spectroscopic characterization and estimation of Judd–Ofelt parameters for Dy3+ activated Li2MgZrO4 double perovskite materials, Polyhedron, 2020, 177, 114322 Search PubMed.
- Zheng, S. Ma, S. He, Q. Guan, L. Chao, J. Qiao and M. Yonghong, Luminescence properties and energy transfer of broadband NIR phosphor Li2MgZrO4: 1.0%Cr3+, y%Yb3, Spectrochim. Acta, Part A, 2024, 314, 124200 Search PubMed.
- K. Hoang, M. Oh and Y. Choi, Electronic structure and properties of lithium-rich complex oxides, ACS Appl. Electron. Mater., 2019, 22, 75–81 Search PubMed.
- Y. Wen, S. Xiao and X. Yang, Novel red-emitting phosphor Li2MgZrO4:Mn4+, Ga3+ for warm white LEDs based on blue-emitting chip, RSC Adv., 2019, 9, 5354 Search PubMed.
- P. Abinash, D. Alagarasan, R. Ganesan, S. Bisoyid and R. Naik, Influence of time dependent laser-irradiation for tuning the linear–nonlinear optical response of quaternary Ag10In15S15Se60 films for optoelectronic applications, RSC Adv., 2023, 13, 4236 Search PubMed.
- S. Giri, P. Priyadarshini, D. Alagarasan, R. Ganesanc and R. Naik, Annealing-induced phase transformation in In10Se70Te20 thin films and its structural, optical and morphological changes for optoelectronic applications, RSC Adv., 2023, 13, 24955 Search PubMed.
- M. Picollo, M. Aceto and T. Vitorino, UV-Vis spectroscopy, Phys. Sci. Rev., 2019, 4, 20180008 Search PubMed.
- A. M. Smith and S. Nie, Semiconductor nanocrystals: structure, properties, and band gap engineering, Accounts Chem. Res., 2010, 43, 190–200 Search PubMed.
- Zhou, S. Yi, Z. X. Fang, J. Lu, Z. Hu, W. Zhao and Y. Wang, Research on a new type of near-infrared phosphor Li2MgZrO4:Cr3+ synthesis, crystal structure, photoluminescence and thermal stability, Opt. Mater., 2021, 117, 111209 Search PubMed.
- H. Nagabhushana, B. M. Nagabhushana, M. Kumar, H. B. Premkumar, C. Shivakumara and R. P. S. Chakradhar, Synthesis, characterization and photoluminescence properties of CaSiO3: Dy3+ nanophosphors, Philos. Mag., 2010, 90, 3567–3579 Search PubMed.
- R. Naik, C. Kumar, R. Ganesan and K. S. Sangunni, Effect of Te addition on the optical properties of As2S3 thin film, Mater. Chem. Phys., 2011, 130, 750–754 Search PubMed.
- M. Mnakri, H. Souissi, M. Tliha, M. Ben gzaiel, S. Znaidia and A. Oueslati, Exploring the structural electrical, optical and theoretical study of KCrP2O7: a look through Racah theory, J. Mol. Struct., 2025, 1328, 141359 Search PubMed.
- C. Wang, X. Fan, Y. Tan, W. Wei and Y. Tang, High-Temperature Reversible Phase Transition and Switchable Dielectric and Semiconductor Properties in a 2D Hybrid [(C3H12N2O)CdCl4]n, Eur. J. Inorg. Chem., 2019, 24, 2907–2911 Search PubMed.
- A. B. A. Hajji, M. Wali, R. Dhahri, E. Dhahri, J. F. M. L. Mariano and M. Jemmali, A comprehensive study of the structural, magnetic and optoelectronic behavior of Ni0.6Mn0.4Cr2O4 chromite for magneto optical devices, Ceram. Int., 2025, 2, 5051 Search PubMed.
- S. A. Moyez and S. Roy, Thermal engineering of lead-free nanostructured CH3NH3SnCl3 perovskite material for thin-film solar cell, J. Nanopart. Res., 2018, 20, 2–13 Search PubMed.
- M. ben gzaiel, I. Garoui, F. N. Almutairi, I. Mbarek and O. A, Lead-Free halide perovskites for optoelectronic application: Investigation of structural, optical, electric and dielectric behaviors, Opt. Mater., 2024, 154, 115664 Search PubMed.
- M. Behera, S. Behera and R. Naik, Optical band gap tuning by laser induced Bi diffusion into As2Se3 film probed by spectroscopic techniques, RSC Adv., 2017, 7, 18428–18437 Search PubMed.
- Naik, S. Jena, R. Ganesan and N. K. Sahoo, Photo-induced optical bleaching in Ge12Sb25S63 amorphous chalcogenide thin films: effect of 532 nm laser illumination, Laser Phys., 2015, 25, 036001 Search PubMed.
- T. A. Hameed, S. H. Moustafa, H. Shaban and B. A. Mansour, The effect of selenium on the structural, morphology, optical, electrical properties of Cu2Te thin films for thermoelectric and photovoltaic applications, Opt. Mater., 2020, 109, 110308 Search PubMed.
- M. Krimi, F. Hajlaoui, M. S. M. Abdelbaky, S. Garcia-Granda and A. Ben Rhaiem, Investigation of optical, dielectric, and conduction mechanism in lead-free perovskite CsMnBr3, RSC Adv., 2024, 14, 10219–10228 Search PubMed.
- S. Nasri, A. Jraba, I. Garoui, A. Oueslatia and E. Elaloui, Potassium tin chloride (K2SnCl6) as a lead-free perovskite: anti-solvent synthesis, structural characterization, and charge transport properties, RSC Adv., 2025, 15, 5369 Search PubMed.
- S. Mathlouthi, A. Oueslati and B. Louati, Vibrational analysis and conduction models in cesium gadolinium pyrophosphate compound, J. Alloys Compd., 2019, 794, 417–424 Search PubMed.
- S. Nasri, M. Megdiche and M. Gargouri, Electrical conduction and dielectric properties of a newly synthesized single phase: Ag0.4Na0.6FeP2O7, Phys. B, 2014, 451, 120–127 Search PubMed.
- M. Boukthir, N. Chakchouk, S. Dammak, S. M. Altarif, K. Karoui, A. Mahmoud, F. Boschini and A. Ben Rhaiem, Optical and electrical conduction mechanisms of the ceramic LiMnO2 as cathode active materials for lithium-ion batteries, Ionics, 2025, 31, 1299–1313 Search PubMed.
- P. Sengupta, P. Sadhukhan, A. Ray, R. Ray, S. Bhattacharyya and S. Das, Temperature and frequency dependent dielectric response of C3H7NH3PbI3: a new hybrid perovskite, J. Appl. Phys., 2020, 127, 204103 Search PubMed.
- S. Nasri, M. Megdiche and M. Gargouri, DC conductivity and study of AC electrical conduction mechanisms by non-overlapping small polaron tunneling model in LiFeP2O7 ceramic, Ceram. Int., 2016, 42, 943–951 Search PubMed.
- S. Das, S. Senapati, G. K. Pradhan, S. Varadharajanperumal and R. Naik, A Facile Microwave-Assisted Nanoflower-to-Nanosphere Morphology Tuning of CuSe1−xTe1+x for Optoelectronic and Dielectric Applications, ACS Appl. Nano Mater., 2023, 6, 5298–5312 Search PubMed.
- M. B. Bechir and M. H. Dhaou, Study of charge transfer mechanism and dielectric relaxation of all-inorganic perovskite CsSnCl3, RSC Adv., 2021, 11, 21767–21780 Search PubMed.
- A. Parida, S. Senapati, S. Samal, S. Bisoyi and R. Naik, One-Pot Hydrothermal Synthesis of SnMnS Nanosheets for Dielectric Energy Storage Applications, ACS Appl. Nano Mater., 2023, 6, 11230–11241 Search PubMed.
- S. Singh, A. Yadav, M. Kumari and P. M. Sarun, Analysis of giant dielectric permittivity and electrical properties for energy storage devices through impedance spectroscopy in CaCu3Ti4O12, J. Mater. Sci.: Mater. Electron., 2022, 33, 9395 Search PubMed.
- M. Ben Bechir and M. Akermi, Structural, morphological, electrical, and dielectric properties of Na2Cu5(Si2O7)2 for ASSIBs, RSC Adv., 2024, 14, 9228 Search PubMed.
- K. Moualhi, Y. Moualhi and M. Zouaoui, Investigation of conduction mechanisms and permittivity–conductivity correlation in a Gd based perovskite structure, RSC Adv., 2024, 14, 4142 Search PubMed.
- J. Boonlakhorn, J. Prachamon, J. Manyam, S. Krongsuk, P. Thongbai and P. Srepusharawoot, Colossal dielectric permittivity, reduced loss tangent and the microstructure of Ca1−xCdxCu3Ti4O12−2yF2y ceramics, RSC Adv., 2021, 27, 16396 Search PubMed.
- M. Coşkun, Ö. Polat, F. M. Coşkun, Z. Durmuş, M. Çağlar and A. Türüt, The electrical modulus and other dielectric properties by the impedance spectroscopy of LaCrO3 and LaCr0.90Ir0.10O3 perovskites, RSC Adv., 2018, 8, 4634 Search PubMed.
- M. Bouzidi, M. B. Bechir, D. R. Almalawi, I. H. Smaili and F. Aljuaid, From Molecular Salt to Layered Network: Cation-Driven Tuning of Band Gap, Structure, and Charge Transport in A3Bi2I9 (A = Cs, Rb) Perovskites, RSC Adv., 2024, 14, 23058–23072 Search PubMed.
- S. Nasri, M. Megdiche and M. Gargouri, The investigation of dielectric properties and ac conductivity of new ceramic diphosphate Ag0.6Na0.4FeP2O7 using impedance spectroscopy method, Phys. E, 2016, 84, 182–190 Search PubMed.
- M. B. Bechir and F. Alresheedi, Interpretation of Dielectric Behavior and Polaron Hopping in Lead-Free Antimony-Based Double Perovskite, RSC Adv., 2023, 13, 34703–34714 Search PubMed.
- S. Ahmed, S. Nasri, R. BenSghaier, L. Latrous and A. Megriche, Doping effects of transition metals and rare earth ions in KMPO4:Ln ceramics: implications for electrical and microstructural characteristics, Mater. Chem. Phys., 2024, 317, 129167 Search PubMed.
- S. Nasri, A. Oueslati, I. Chaabane and M. Gargouri, AC conductivity, electric modulus analysis and electrical conduction mechanism of RbFeP2O7 ceramic compound, Ceram. Int., 2016, 42, 14041–14048 Search PubMed.
- M. Megdiche, C. Perrin-pellegrino and M. Gargouri, Conduction mechanism study by overlapping large-polaron tunnelling model in SrNiP2O7 ceramic compound, J. Alloys Compd., 2014, 584, 209–215 Search PubMed.
- M. B. Bechir and A. B. Rhaiem, Structural Phase Transition, Vibrational Analysis, Ionic Conductivity and Conduction Mechanism Studies in an Organic-Inorganic Hybrid Crystal: [N(CH3)3H]2CdCl4, J. Solid State Chem., 2021, 296, 122021 Search PubMed.
- F. Abdel-Wahab, M. Abdel-Baki and H. Abdel Maksoud, Insight into OLPT model conduction mechanism and dielectric relaxation of lead borate glass containing Cr and Ge ions, Indian J. Phys., 2023, 97, 1759–1768 Search PubMed.
- D. Sahoo, S. Senapati, S. Samal, S. Bisoyi and R. Naik, Facile hydrothermally synthesized nanosheets-based Cu0.06−x Ni0.03Sn0.03+xS0.12 flower for optoelectronic and dielectric applications, Materials Today Electronics, 2023, 3, 100030 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |




