Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ti3BN monolayer: the MXene-like material predicted by first-principles calculations†
Dandan Wanga,
ZhongHui Sunab,
DongXue Han *a,
Lei Liu
*a,
Lei Liu c and
Li Niua
c and
Li Niua
aState Key Laboratory of Electroanalytical Chemistry, c/o Engineering Laboratory for Modern Analytical Techniques, Changchun Institute of Applied Chemistry, Chinese Academy of Science, Changchun, 130022, Jilin, P. R. China. E-mail: dxhan@ciac.ac.cn; Fax: +86 4318526 2800; Tel: +86 4318526 2425
bUniversity of Chinese Academy of Sciences, Beijing, 100049, P. R. China
cState Key Laboratory of Luminescence and Applications, CIOMP, Chinese Academy of Sciences, No. 3888 Dongnanhu Road, Changchun, 130033, Jilin, P. R. China
First published on 17th February 2017
Abstract
The discovery of graphene and other two-dimensional (2D) materials has set the foundation for exploring and designing novel single layered sheets. The family of 2D materials encompasses a wide selection of compositions including almost all the elements of the periodic table and they have the potential to play a fundamental role in the future of electronics, composite materials and energy technology. Therefore, searching for new 2D materials is a big challenge in materials science. In this work, we theoretically designed a monolayer of Ti3BN following the strategy of “atomic transmutation”. The Ti3BN monolayer can be considered as three Ti-atomic layers being interleaved with one N-atomic layer and one B-atomic layer, in the sequence of Ti1–N–Ti2–B–Ti3. The moderate cohesive energy, positive phonon frequencies and high melting point are the best guarantees for good stability of Ti3BN. Based on a global minimum structures search using the particle-swarm optimization (PSO) method, Ti3BN is the lowest energy structure in 2D space, which holds great promise for the realization of layered Ti3BN in experiment. Based on density functional theory (DFT) calculations, Ti3BN is intrinsically metallic and its electronic properties can be modulated by varying the surface groups, such as OH or F-termination. If realized in experiment, it may find applications in many aspects.
1. Introduction
Since graphene was realized experimentally in 2004,1 2D materials have attracted significant interest and a large variety of freestanding monolayer solids have been successfully fabricated, such as hexagonal boron nitride (h-BN),2 metal chalcogenides (MoS2, WS2),3,4 silicene5 and so on. Due to their unique electronic, chemical, and mechanical properties, those 2D materials have found wide applications in supercapacitors,6 solar cells,7 lithium ion batteries8 and water splitting application9 and other areas of energy and environment.Recently, a new family of graphene-like 2D materials termed as MXenes were successfully synthesized by selectively extracting the “A” element from the layered MAX phases (A is an A-group element, mostly Al or Si) in the aqueous HF.10 MAX phases are a large (>60 members) family of layered ternary early transition-metal carbides, nitrides, and carbonitrides with P63/mmc symmetry.11 To date, several MXenes have been synthesized successfully, including Ti3C2,12 Ti2C,13 Ta4C3,14 V2C,15 TiNbC,16 Nb2C17 and Mo2C.18
With the increasing interest in MXenes, a mass of experimental and theoretical efforts related to their synthesis, structures, properties and potential applications have been made experimentally and theoretically.19,20 Among the as-synthesized MXene phases, the most studied MXene is Ti3C2, prepared by immersing Ti3AlC2 in HF solutions at room temperature.12 Ti3C2 was predicted theoretically to be good electrical conductors and its electrical conductivities can be tuned by different surface terminations.21 What's more, Ti3C2 have been proved to be very promising as anode materials for Li-ion batteries and as hydrogen storage media.22,23
Motivated by the Ti3C2 monolayer, which is composed of three Ti-atomic layers being interleaved with two C-atomic layers, herein we designed a new 2D material of Ti3BN by performing density functional theory (DFT) calculations following the strategy of “atomic transmutation”, which means substituting certain types of elements with their neighboring elements in the periodic table but the total number of valence electrons is kept unchanged.24,25 A major breakthrough has been made in finding and designing novel materials. For example, if one were to substitute the oxide ions in ZnO with N and F, one would ultimately obtain Zn2NF whose conduction and valence band edges are more favorable for water splitting.26 When two C atoms in graphene were transmutated with one B atom and one N atom, h-BN with wide band gap and new functionalities will be obtained.27 Therefore Ti3BN monolayer can be thought of as obtained by substituting the two C-atomic layers of Ti3C2 monolayer with one nitrogen-atomic layer and one boron-atomic layer, respectively, in consideration of that nitrogen and boron are two nearest-neighbors of carbon in the periodic table and Ti3BN is isoelectronic to Ti3C2.
2. Computational method
DFT calculations were performed within the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation28 and the projected augmented wave (PAW) method29,30 as implemented in the Vienna ab initio simulation package (VASP). To reach convergence criteria for both energy and forces, a special k-point sampling with a k-point separation of 0.04 Å−1 is applied for the Brillouin-zone integration and the cutoff energy for the plane wave basis set is 408 eV. The ground state geometries of the 2D Ti3BN are obtained with all the atomic positions relaxed until their residual forces are less than 0.01 eV Å−1. In building the monolayer models, a vacuum thickness of 15 Å is adopted to avoid the interactions between adjacent layers. The phonon dispersion curves of Ti3BN monolayer was calculated using the density functional perturbation theory (DFPT)31,32 as implemented in the PHONOPY program interfaced with VASP. To obtain the accurate electronic properties of Ti3BN monolayer, hybrid functional calculations using Hetd–Scuseria–Ernzerhof (HSE06) functional33 have been employed.The thermal stability of Ti3BN monolayer was assessed by first-principles molecular dynamics (MD) calculations using the PAW pseudo-potential and PBE functional as implemented in VASP.34 For each temperature, a preheating for 1 ps was applied for the initial geometry structure. And the MD calculations were in NVT ensemble, lasting for 10 ps with a time step of 1.0 fs. To control the temperature, Nosé–Hoover method was applied.35
The global minimum structure for Ti3BN monolayer was searched by particle-swarm optimization (PSO) method within the evolution algorithm which was implemented in CALYPSO code.36–38 The population size was set as 30, and the number of generation was maintained at 25. Unit cells containing 5, 10, and 15 atoms were considered. The structure relaxations during the PSO searching were carried by using PBE functional as implemented in VASP.
3. Results and discussion
3.1 Structural properties and stability of Ti3BN monolayer
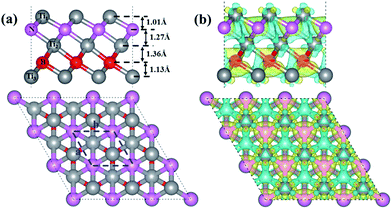
The optimized structure of our designed Ti3BN monolayer is shown in Fig. 1(a). Similar with Ti3C2 monolayer, Ti3BN monolayer is crystallized in the space group P3m1 (no. 156) and each unit cell contains five atoms, all in different atomic planes with the sequence of Ti1–N–Ti2–B–Ti3. To avoid the interactions between the Ti3BN monolayer and its periodic images among the normal direction, a vacuum layer of 15 Å is used and the calculated lattice constants for the unit cell are a = b = 3.095 Å. In Ti3BN monolayer, the length of Ti1–N and N–Ti2 bonds (2.054 and 2.195 Å) are shorter than those of corresponding Ti–C bonds (2.064 and 2.212 Å)19,20 in Ti3C2 monolayer, while the Ti2–B and B–Ti3 bond lengths are 2.249 and 2.117 Å, respectively, longer than those of corresponding Ti–C bonds in Ti3C2 monolayer. The thickness of Ti3BN monolayer is 4.78 Å with the atomic layer distances of 1.01, 1.27, 1.36 and 1.13 Å, respectively.To elucidate the chemical bonding and stabilization mechanism of Ti3BN monolayer, the deformation electronic density39 has been calculated. As shown in Fig. 1(b), there is remarkable electron transfer from Ti atoms to N atoms and from Ti atoms to B atoms, indicating the electronically stabilization in the Ti3BN monolayer. Bader charge analysis shows that the net charges on N and B atom are −1.65 e and −1.57 e and those on Ti1, Ti2, and Ti3 atom are 0.97 e, 1.34 e and 0.91 e, respectively. The electron localization function39 of Ti3BN monolayer is also calculated to highlight the electron distribution. As seen from the isosurfaces of electron localization functions presented in Fig. S1,† the electrons are complete delocalized around the Ti atoms, and widely distributed in the N and B frameworks, which also suggests the electron transfer from Ti atoms to N and B atoms.
Although Ti3BN monolayer possesses similar structure properties with Ti3C2 monolayer, the question whether Ti3BN monolayer is as stable as Ti3C2 or not need to be answered. The cohesive energy of Ti3BN monolayer is a useful argument for evaluating its stability, defined as Ecoh = (xETi + yEN + zEB − ETi3BN)/(x + y + z), where ETi, EN, EB and ETi3BN are the total energies of a single Ti atom, a single N atom, a single B atom and Ti3BN monolayer, x, y and z are the number of Ti, N, and B atoms in the supercell, respectively. Based on our DFT calculations, the cohesive energy of Ti3BN monolayer is 7.46 eV per atom, which is a little smaller than that of graphene (7.95 eV per atom)40 and higher than that of Ti3C2 (about 7.00 eV).13 The relatively large cohesive energy of Ti3BN monolayer indicates that Ti3BN monolayer is a stable phase with strong chemical bonds. What's more, the small cohesive energy difference between Ti3BN monolayer and Ti3BN bulk (7.46 eV per atom vs. 7.82 eV per atom) means that it’s favorable to obtain Ti3BN monolayer from its bulk phase. The elastic constants of Ti3BN monolayer were then calculated to be C11 = C22 = 202.11 N m−1, C12 = C21 = 59.24 N m−1, which satisfy the mechanical stability criteria, indicating that the Ti3BN monolayer is also mechanically stable.
The kinetic stability of Ti3BN monolayer has been further confirmed by its phonon dispersion along the high-symmetry directions in the first Brillouin zone. As shown in Fig. 2(a), there is no appreciable imaginary frequency in the phonon dispersion curves, implying the good kinetic stability of Ti3BN monolayer. The highest frequency of Ti3BN monolayer is 653.60 cm−1, higher than that of the widely studied MoS2 monolayer (473 cm−1)40 and silicene (580 cm−1).40 The high frequency suggests that the related bonds in Ti3BN monolayer are strong.
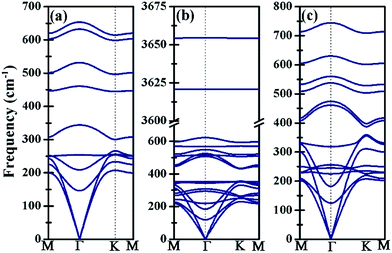 | ||
| Fig. 2 Phonon dispersion curves of (a) bare Ti3BN monolayer; (b) Ti3BN(OH)2-IV monolayer; (c) Ti3BNF2-I monolayer. | ||
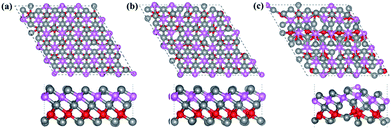
Finally, the thermal stability of Ti3BN monolayer was investigated by first-principles molecular dynamics (MD) calculations. A 5 × 5 supercell containing 125 atoms was used here and three individual MD calculations for Ti3BN monolayer at temperatures of 500 K, 800 K, and 1000 K were performed. Fig. 3 presents the snapshots of Ti3BN monolayer at the end of 10 ps MD calculations. These snapshots show that Ti3BN monolayer can maintain its structural integrity throughout a 10 ps dynamical calculation up to 800 K, however will be disrupted at the temperature of 1000 K. Those results reveal that the Ti3BN monolayer has good thermal stability and the melting point of Ti3BN monolayer is between 800 K and 1000 K.
3.2 Global minimum search for Ti3BN monolayer in 2D space
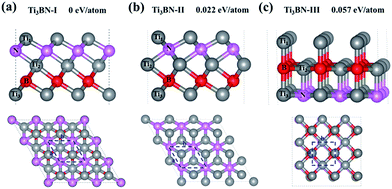
Although Ti3BN monolayer has good stability based on the above results, the doubt about that the Ti3BN monolayer is a local minimum or a global minimum needs to be solved. It's well known that the global minimum structure is more likely to be realized experimentally. Therefore, we carried out a global search for the lowest energy structure of Ti3BN monolayer in the 2D space by adopting the first-principles based particle-swarm optimization method. After 25 generations, three low-energy structures for 2D Ti3BN were obtained, labelled as Ti3BN-I, Ti3BN-II, and Ti3BN-III in the order of increasing energy.As shown in Fig. 4, in which the relative energy per atom is presented, the global minimum structure is Ti3BN-I, which is just the above discussed Ti3BN monolayer. Interestingly, Ti3BN-II is also crystallized in the space group P3m1 (no. 156). The geometric construction, thickness, atomic layer distances of Ti3BN-II is similar with that of Ti3BN-I, while the biggest difference between them is the N-atomic layer just located above the B-atomic layer and the Ti1-atomic layer above the Ti3-atomic layer in Ti3BN-II monolayer. The length of Ti1–N, N–Ti2, Ti2–B, and B–Ti3 bond in Ti3BN-II monolayer is 2.043 Å, 2.202 Å, 2.254 Å, and 2.116 Å, respectively. Considering structure Ti3BN-III, it is 0.057 eV per atom higher in energy than Ti3BN-I. This high energy might be due to the more nonbonding electrons of Ti1 atoms.
3.3 Electronic properties of Ti3BN monolayer
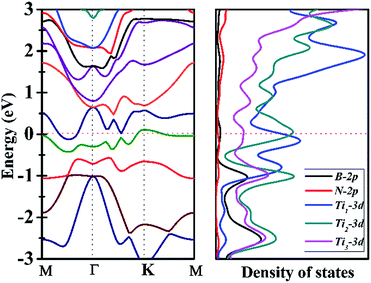
Since Ti3BN-I monolayer holds great potential to be realized in experiment, does it have intriguing properties and promising applications? To figure out this issue, we have studied the electrical properties of the Ti3BN-I monolayer using the hybrid density functional calculations. Fig. 5 illustrates the band structure and partial density of state (PDOS) of Ti3BN-I monolayer. Obviously, a conduction band and a valence band across through the Fermi level, indicating that Ti3BN monolayer has metallic properties. The PDOS analysis shows that mainly the Ti-3d states, especially the 3d states of Ti atoms from surface atomic layer, contribute to the high density of electron states around the Fermi level. Note that the high density of states near the Fermi level means available carriers which are beneficial to the high electric conductivity of the Ti3BN monolayer.3.4 Surface modification of Ti3BN monolayer by OH and F termination
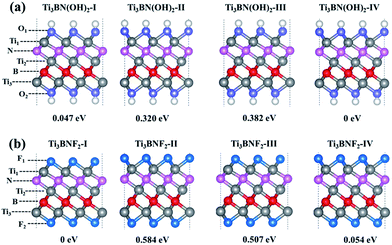
Moreover, the high DOS at the Fermi level mainly originated from Ti1 and Ti3 atoms indicates the high activity of surface Ti atoms, suggesting the feasibility in the surface modification and even in composite materials for Ti3BN monolayer. For example, our theoretical studies have shown that the electronic properties of Ti3BN can be tuned by surface functional groups (–OH, –F). Herein, four possible geometry structures of Ti3BN monolayer with hydroxylated, and fluorinated surfaces are considered, as presented in Fig. 6. The top views of Ti3BNF2-I and Ti3BNF2-II configurations are depicted in Fig. S2.† In configuration I, all the –OH or –F groups are located above the hollow sites between the three neighboring C/B atoms or point directly toward the Ti2 atoms on both sides of Ti3BN monolayer. In configuration II, all the –OH or –F groups are oriented above the topmost sites of C and B atoms on the two sides of Ti3BN monolayer, respectively. Afterwards, we can view the asymmetric arrangement of configuration III and IV as the combination of configuration I and II.The structural stability of different Ti3BN(OH)2 and Ti3BNF2 configurations can be estimated by comparing their relative total energies. For Ti3BN(OH)2, configuration IV is energetically most favorable. Ti3BN(OH)2-IV is energetically lower than Ti3BN(OH)2-I, Ti3BN(OH)2-II and Ti 3BN(OH)2-III by 0.047, 0.320, and 0.382 eV per unit cell, respectively. While for Ti3BNF2, configuration I is energetically most favorable, with its energy lower than that of Ti3BNF2-II, Ti3BNF2-III and Ti3BNF2-IV by 0.584, 0.507, and 0.054 eV per unit cell, respectively. Phonon dispersions of Ti3BN(OH)2-IV and Ti3BNF2-I has been further calculated to investigate their kinetic stability, as shown in Fig. 2(b) and (c). As expected, there are no imaginary frequencies in the phonon dispersion curves. The phonons at about 3654.56 cm−1 and 3620.86 cm−1 for Ti3BN(OH)2-IV should be dominated by the OH groups, and the phonons at about 744.73 cm−1 for Ti3BNF2-I should be due to the F groups. These high-frequency phonons indicate the strong bond nature of the related bonds (Ti–O and Ti–F).
In comparison with bare Ti3BN, the OH or F-terminated Ti3BN monolayer have smaller lattice constants. With terminal groups, the bond lengths of N–Ti2 and Ti2–B shrink, while the bonds between the Ti1–N and B–Ti3 are elongated except the Ti1–N bonds of Ti3BNF2-I and Ti3BNF2-III. Those results imply that the surface groups strongly interact with the original Ti3BN block, in accordance with the corresponding phonon dispersions. For clearance, the calculated lattice constants and bond lengths are presented in Table S1.†
Though the Ti3BN monolayer is metallic, its hydroxylated or fluorinated derivatives may be narrow-gap semiconductors or metals, depending on the geometrical arrangements of surface F and OH groups. Seen from Fig. 7(a), for Ti3BN with surface OH groups, the most favorable Ti3BN(OH)2-IV has a semiconducting character, with a direct band gap of 0.09 eV. Ti3BN(OH)2-II also shows the electronic properties of direct semiconductor, and the band gap is 0.16 eV. However, Ti3BN(OH)2-I and Ti3BN(OH)2-III is metallic. For Ti3BN with F-termination (Fig. 7(b)), the most stable configuration of Ti3BNF2-I and the metastable configuration of Ti3BNF2-III are metals. On the contrary, the band structures of Ti3BNF2-II and Ti3BNF2-IV demonstrate their indirect semiconducting characters, with the band gap of 0.07 eV and 0.37 eV, respectively. Those theoretical results prove that the electronic structure of Ti3BN monolayer can be modulated by varying the surface functional groups.
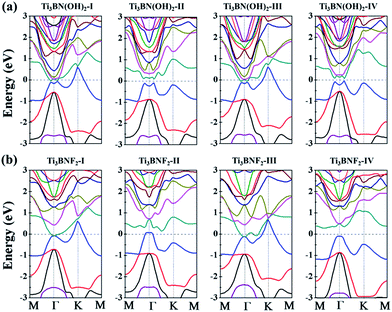 | ||
| Fig. 7 Band structures of the hydroxylated and fluorinated Ti3BN monolayer obtained from hybrid functional calculations: (a) Ti3BN(OH)2; (b) Ti3BNF2. | ||
4. Conclusions
In summary, we designed a new inorganic 2D material of Ti3BN monolayer following the strategy of “atomic transmutation” by performing DFT calculations. In Ti3BN monolayer, the Ti–B and Ti–N bonds are strong and the geometry structure is similar with the reported MXenes. The high cohesive energy, elastic constants, and absence of imaginary phonon frequencies prove that the Ti3BN monolayer possess dynamic and mechanical stability. Particularly, MD simulation results verify that Ti3BN monolayer can maintain its structural stability up to at least 800 K. The PSO method revealed that Ti3BN monolayer is the global minimum structure in 2D space, suggesting the possibility to realize Ti3BN monolayer in experiment. What's more, the electronic properties of Ti3BN monolayer can be modified by varying the surface functional groups and their geometrical configurations. Therefore, if Ti3BN is realized, it may find wide applications, such as in electrics, composite materials, Li-ion batteries and so on.Acknowledgements
This work was supported by NSFC, China (21225524, 21527806, 21622509 and 21475122), Department of Science and Techniques of Jilin Province (20150201001GX and 20150203002YY), Jilin Province Development and Reform Commission (2016C014), Science and Technology Bureau of Changchun (15SS05).References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- L. H. Li and Y. Chen, Adv. Funct. Mater., 2016, 26, 2594–2608 CrossRef CAS.
- L. Dominik and K. Andras, ACS Nano, 2012, 6, 10070–10075 CrossRef PubMed.
- B. Liu, W. J. Zhao, Z. J. Ding, I. Verzhbitskiy, L. J. Li, J. P. Lu, J. Y. Chen, G. Eda and K. P. Loh, Adv. Mater., 2016, 28, 6457–6464 CrossRef CAS PubMed.
- T. Li, C. Eugenio, C. Daniele, G. Carlo, F. Marco, D. Madan, M. Alessandro and A. Deji, Nat. Nanotechnol., 2015, 10, 227–231 CrossRef PubMed.
- X. Y. Zhang, S. H. Sun, X. J. Sun, Y. R. Zhao, L. Chen, Y. Yang, W. Lu and D. B. Li, Light: Sci. Appl., 2016, 5, e16130 CrossRef CAS.
- W. Wei, K. Sun and Y. H. Hu, J. Mater. Chem. A, 2016, 4, 12398–12401 CAS.
- C. X. Peng, B. D. Chen, Y. Qin, S. H. Yang, C. Z. Li, Y. H. Zuo, S. Y. Liu and J. H. Yang, ACS Nano, 2012, 6, 1074–1081 CrossRef CAS PubMed.
- H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232–3238 CrossRef CAS.
- S. Kajiyama, L. Szabova, K. Sodeyama, H. Iinuma, R. Morita, K. Gotoh, Y. Tateyama, M. Okubo and A. Yamada, ACS Nano, 2016, 10, 3334–3341 CrossRef CAS PubMed.
- M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281 CrossRef CAS.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- T. S. Zhao, S. H. Zhang, Y. Guo and Q. Wang, Nanoscale, 2016, 8, 233–242 RSC.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- M. Naguib, J. Halim, J. Lu, K. M. Cook, L. Hultman, Y. Gogotsi and M. W. Barsoum, J. Am. Chem. Soc., 2013, 135, 15966–15969 CrossRef CAS PubMed.
- O. Mashtalir, M. Naguib, V. N. Mochalin, Y. Dall'Agnese, M. Heon, M. W. Barsoum and Y. Gogotsi, Nat. Commun., 2013, 4, 1716–1723 CrossRef PubMed.
- J. P. Hu, B. Xu, C. Y. Ouyang, Y. Zhang and S. Y. A. Yang, RSC Adv., 2016, 6, 27467–27474 RSC.
- C. Xu, L. Wang, Z. Liu, L. Chen, J. K. Guo, N. Kang, X.-L. Ma, H.-M. Cheng and W. Ren, Nat. Mater., 2015, 14, 1135–1141 CrossRef CAS PubMed.
- S. K. Kim, Y.-J. Zhang, H. Bergstrom, R. Michalsky and A. Peterson, ACS Catal., 2016, 6, 2003–2013 CrossRef CAS.
- Q. Tang, Z. Zhou and P. Shen, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS PubMed.
- S. Lai, J. Jeon, S. K. Jang, J. Xu, Y. J. Choi, J.-H. Park, E. Hwang and S. Lee, Nanoscale, 2015, 7, 19390–19396 RSC.
- D. Er, J. Li, M. Naguib, Y. Gogotsi and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 11173–11179 CAS.
- Q. K. Hu, D. D. Sun, Q. H. Wu, H. Y. Wang, L. B. Wang, B. Z. Liu, A. G. Zhou and J. L. He, J. Phys. Chem. A, 2013, 117, 14253–14260 CrossRef CAS PubMed.
- J.-H. Yang, Y. Zhang, W. J. Yin, X. G. Gong, B. I. Yakobson and S.-H. Wei, Nano Lett., 2016, 16, 1110–1117 CrossRef CAS PubMed.
- C. Zhang and Q. Sun, J. Phys. Chem. Lett., 2016, 7, 2664–2670 CrossRef CAS PubMed.
- Y. Kubota, K. Watanabe, O. Tsuda and T. Taniguchi, Science, 2007, 317, 932–934 CrossRef CAS PubMed.
- S. R. Lingampalli, K. Manjunath, S. Shenoy, U. V. Waghmare and C. N. R. Rao, J. Am. Chem. Soc., 2016, 138, 8228–8234 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Furthmüller, J. Hafner and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 15606 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- B. Stefano, S. De Gironcoli and A. Dal Corso, Rev. Mod. Phys., 2001, 73, 515 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. E. Tuckerman, J. Chem. Phys., 1992, 97, 2635 CrossRef.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- X. Y. Luo, J. H. Yang, H. Y. Liu, X. J. Wu, Y. C. Wang, Y. M. Ma, S.-H. Wei, X. G. Gong and H. J. Xiang, J. Am. Chem. Soc., 2011, 133, 16285–16290 CrossRef CAS PubMed.
- Y. C. Wang, M. S. Miao, J. Lv, L. Zhu, K. T. Yin, H. Y. Liu and Y. M. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef PubMed.
- H. J. Zhang, Y. F. Li, J. H. Hou, K. X. Tu and Z. F. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651 CrossRef CAS PubMed.
- Y. F. Li, Y. L. Liao and Z. F. Chen, Angew. Chem., Int. Ed., 2014, 53, 7248–7252 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00483d |
| This journal is © The Royal Society of Chemistry 2017 |