Theoretical understanding of single-stranded DNA assisted dispersion of graphene†
Arun K.
Manna
a and
Swapan K.
Pati
*ab
aTheoretical Sciences Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, 560064, India. E-mail: pati@jncasr.ac.in; Fax: +91-80-22082766/2767; Tel: +91-80-22082839/2575
bNew Chemistry Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, 560064, India. E-mail: pati@jncasr.ac.in; Fax: +91-80-22082766/2767; Tel: +91-80-22082839/2575
First published on 18th October 2012
Abstract
Using atomistic molecular dynamics (MD) simulation, we investigate the structure and energetic of single-stranded DNA (ssDNA) assisted solubilisation of single-layer graphene in aqueous medium at room temperature. We choose four different ssDNA oligonucleotides of homologous base sequences; namely, ssdA12, ssdG12, ssdC12, ssdT12 (A = Adenine, G = Guanine, C = Cytosine and T = Thymine), and one mixed base-sequence ssd(AGTC)3, as the representative ssDNA for studying graphene dispersion in aqueous solution. We consider analysing different nucleobase binding modes and the role of several competing forces acting on ssDNA in contact with graphene in aqueous solution over the course of 30 ns MD simulation. Our simulation results show that there exist simultaneously two major competing forces: nucleobase–nucleobase intra-molecular π–π stacking interactions and nucleobase–graphene inter-molecular π–π stacking interactions. The former interactions help to maintain ssDNA helical geometry, whereas the latter interactions assist the ssDNA with becoming surface adsorbed on graphene. Note that both types of interactions strongly depend on the chemical nature of nucleobase and the sequence type present in various ssDNA. The calculated binding free energy strength between various ssDNA and graphene follows the order of: ssd(AGTC)3 > ssdA12 > ssdG12 > ssdC12 > ssdT12. The trend in binding free energy has been rationalized in terms of the adsorption strength of individual nucleoside over graphene, number of base–graphene π-stacks, together with the nature of nucleobase (purine: A, G and pyrimidine: C, T) present in different ssDNA sequences. We find two types of ssDNA assembly on graphene; namely, coiling and elongated networks, as was also observed in recent experiment. Interestingly, the larger extent of base–graphene π-stacking interactions found for ssd(AGTC)3 helps in forming an elongated network on graphene, and consequently, results in higher binding free energy strength. Thus, our results suggest that a mixed nucleobase sequence ssDNA, such as ssd(AGTC)3, would be potential candidate in dispersing graphene in aqueous solution than any other homologous base sequences containing ssDNA. Additionally, we also perform the electronic structure calculations for these ssDNA–graphene composites to explore the electronic properties in details using density functional theory. We believe that our simulation results together with first-principles calculations provide great microscopic detail in understanding the ssDNA assisted dispersion of graphene in aqueous environments.
1. Introduction
Applications of carbon based nanomaterials, such as two-dimensional (2D) graphene, one-dimensional (1D) carbon nanotubes and zero-dimensional (0D) fullerenes, as molecular diagnostics, biosensors, DNA sequencing and biochip and in bio-medical treatments are of increasing interest among researchers since past few years.1,2 Carbon nanostructures can be broadly functionalized and their low-dimensional electronic properties are sensitive to molecular adsorption. Graphene, an sp2 hybridized 2D hexagonal nanocarbon crystal, is considered as promising a nanoscale building block for new generation applications, for example, a substrate material for dispersion of polymer, nanoparticles, and delivering essential drug molecules to the cells, etc.3–5 Recent reports also highlight its potential device application in nanoelectronics because of its remarkable mechanical, electrical and thermal properties.6–9Dispersion of carbon nanostructures using DNA/or any biopolymer has significant impact in isolating these structures from their mixtures. Furthermore, rapid, selective, and cost-effective analysis of biomolecules is important in clinical diagnostics, DNA sequencing and various treatment processes. Significant advancement has been made in this direction employing carbon based nanostructures, such as, carbon nanotubes,10–12 carbon nanodots,13,14 and carbon nanofibers.15 Recently, Tan et al. have proposed to use ssDNA and carbon nanotubes for the homogenous detection of biomolecules16,17 Both experimental and simulation work predicts that the single walled carbon nanotubes could be completely wrapped by ssDNA molecules through noncovalent interactions, and thus, providing a route to separate out nanotubes with different chirality.18–47 Moreover, carbon nanotubes can act as a protector of DNA strands during cellular delivery.48 Much attention has been given to the dispersion and solubilisation of carbon nanotubes using various ssDNA oligonucleotides. However, there are hardly any reports on interactions of ssDNA with 2D graphene. A recent experiment49 by Saliha et al. has demonstrated that two competing π-stacking interactions exist: base–base π-stacking and base–graphene π-stacking, when ssDNA is added in graphene solution. A crossover between these two competing interactions results in two distinct ssDNA pattern formations, small spherical particles and elongated networks, on the graphene surface. A molecular simulation study50 by Zhao explores various self-assembly structures of duplex DNA onto the graphene and carbon nanotube surfaces, highlighting the importance of π-stacking interactions between the nucleotides and nanostructure surfaces in aqueous environments. This study considers double stranded DNA, which is comparatively more rigid than ssDNA. A more flexible oligomer, such as ssDNA, would be better candidate for the dispersion of 2D graphene in solution. As mentioned above, the experiment by Saliha et al. involves the use of the ssDNA oligonucleotide in contact with graphene and found two distinct pattern formations. Although the work qualitatively explains the underlying reason behind the two distinct self-assembly patterns, it does not unravel the microscopic origin of the observation. Moreover, it does not consider what would be the role of base sequences on the formation of self-assembly nanostructures on graphene. Indeed, it is a really challenging task to probe them by experiment due to the experimental complexity. In this regard, molecular simulations can provide useful insight to rationalize the experimental findings by analysing the microscopic details. To our knowledge, there is no such study, which considers the effects of various base sequences and explicit usage of environmental conditions on the patterning of ssDNA self-assembled nanostructures on graphene.
In the present study, we use classical molecular dynamics simulations to explore the structural topology and energetic of ssDNA hybridized with graphene in aqueous environments. For a detailed analysis, we first consider the single nucleoside (A, G, C and T) interacting with graphene, and then, focus on the formation of various oligonucleotide assembled on graphene surface. We consider four different homologous dodecamer ssDNA oligonucleotides of varying base sequences; namely ssdA12, ssdT12, ssdG12 and ssdC12, on graphene surface. We also consider a 12 base pairs ssDNA which consist of a consecutive repeats of A–G–T–C, i.e. ssd(AGTC)3. We find that all the ssDNA oligonucleotides loose its helical shape and strongly hybridize with graphene through π–π stacking interactions between nucleobase and graphene surface. The interaction order among different ssDNA with graphene follows the extent of base–graphene π–π stacking interactions. Additionally, we also calculate and analyse the electronic structure of ssDNA adsorbed graphene hybrids using density functional theory.
2. Computational details
Classical MD simulations are performed considering two-dimensional neutral single-layer graphene sheet within a periodic box of dimensions 10.22 × 10.23 × 50 nm3 at 300 K temperature and 1 atmospheric (atm) pressure in aqueous solution. To obtain the microscopic picture of the ssDNA specificity towards the graphene sheet, simulations are performed by considering ssdA12, ssdG12, ssdC12, ssdT12, and a mixture of nucleobase sequences, ssd(AGTC)3 of discrete strands, which are modelled from duplex B-DNA using NAB51 (Nucleic Acid Builder) module of Amber 11 Tools Package.52 The AMBER99 force fields53 are used to model ssDNA. The graphene carbon atoms are modeled as uncharged Lennard-Jones particles (using C sp2 parameters from the AMBER99 force field) as reported in the literature for the study of graphene and single-walled carbon nanotubes.50,54–57 The negatively charged backbones of ssDNA are neutralized using Na+ counter ions. The total number of Na+ ions needed to neutralize each of the ssDNA systems is 11. The transferable intermolecular potential three point (TIP3P) model58 is considered for the water solvent. All the MD simulations are performed using GROMACS simulations package59 with an initial water box of dimensions as mentioned above. The initial configuration for the hybrid systems is considered by keeping the ssDNA at ∼5.0 Å distance away from the graphene plane. The high energy contacts between the atoms in the initial conformations of graphene, ssDNA and the hybrid systems are removed by minimizing the energy of each system using steepest decent integration method. Following that, MD simulations are performed using leap-frog algorithm for integrating Newton's equation of motion for 30 ns at constant temperature (300 K) and pressure (1 bar). Long-range electrostatic interactions are calculated with the Particle Mesh Ewald (PME) method.60 In order to get a clear picture about the dynamical assembly formation of ssDNA, the position of all graphene atoms is allowed to relax throughout the MD simulations. The time step for the MD simulation is 1.5 fs (femtosecond) and the atomic coordinates are recorded at every 7.5 ps (picoseconds) for trajectory analysis. Analysis and visualization of MD trajectories are performed with VMD software.61The Thermodynamics Integration (TI)62 method, as implemented in GROMACS code, is employed to compute the binding free energies between the ssDNA and graphene by introducing various coupling parameters (λ) in the Hamiltonian (H). Following previous studies63,64 the binding free energies, ΔFbind, are calculated by considering a thermodynamics cycle as shown in Fig. 1. ΔFbind is defined as the free energy difference between the bound and unbound states.
| ΔFbind = ΔFbound1 − ΔFunbound2 |
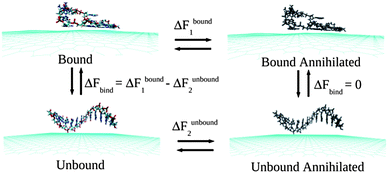 | ||
| Fig. 1 A schematic of the thermodynamic cycle used for the free energy calculation. All systems contain explicit water molecules and counter ions, which are not shown for the better clarity of the figure. | ||
To understand the electronic behaviours of various ssDNA adsorbed graphene composites, we have calculated the electronic structure using density functional theory (DFT) calculations as implemented in SIESTA,65 which uses numerical atomic orbital basis sets. We consider norm-conserving pseudopotentials in the fully nonlocal Kleinman–Bylander form,66 and a real space mesh size of 300 Ry energy cut-off employing Γ-point calculations for all the modelled systems within the DFT calculations. We have performed non spin-polarized calculations within generalized gradient approximation (GGA) considering Perdew–Burke–Ernzerhof (PBE)67 exchange and correlation functional using double ς polarized (DZP) basis sets for all the atomic valence electrons. We consider each hybrid system within a box of dimensions 90 × 90 × 60 Å3 to ensure the negligible interactions between the periodic images.
3. Results and discussions
To understand the assembly phenomena of various ssDNA on graphene surface in aqueous media, we need to understand the two distinctive processes: the process of ssDNA solvation and subsequently, the adsorption of different ssDNA on graphene. Consequently, we study and analyse the results of these two different processes stepwise.First, we look at the solvation processes of all ssDNA considered in the present study at physiological conditions, i.e., 300 K temperature and 1 atm pressure using a NPT ensemble. For this, we consider all five individual ssDNA (ssdA12, ssdG12, ssdC12, ssdT12 and ssd(AGTC)3) in presence of explicit TIP3P water molecules and Na+ counter ions in a simulation box of dimensions 70 × 70 × 70 Å3. We find that all the ssDNA interact with the solvent water molecules through strong hydrogen bonding interactions, which is characterised by H-bonds involving a H-bond donor and acceptor distance of 0.25–0.30 nm and 165–175° angle of ∠donor⋯H⋯acceptor. The strength of H-bonding interactions varies with the number of H bonds formed in the solution, which in turn depend on the nature of various ssDNA. Note that, all the ssDNA in gaseous phase maintains their helical S shape as the counter part of duplex DNA, because of the stabilization gains through inter-base π–π stacking interactions. However, in aqueous medium, there is a competition between this inter-base π–π stacking interactions and H-bonding interactions between the ssDNA and solvent water molecules. In fact, we find that the H-bonding interactions try to destroy ssDNA's helical structure and consequently, solubilise them in aqueous medium. Note that, unlike duplex B-DNA, the ssDNA is very flexible in bond torsional angles at least within the dinucleotide levels as well as within the sugar-phosphate backbone levels.
In fact, the solvation energy should be lower in comparison to the energy require to destroy π–π stacking interactions and bond torsional rotations along the DNA sugar-phosphate backbone. In the process of various ssDNA solvation, the number of inter-base π–π stacking interactions decreases, while the intra-molecular (within ssDNA) and inter-molecular (between ssDNA and water) H-bonding interactions increases. Therefore, we consider looking at the average number of each type of H-bonds over the 30 ns simulation times. We also focus on the interaction energy between the ssDNA and water molecules in order to quantify the solvation strength of various ssDNA in aqueous solution. We find that ssdG12forms larger number of H-bonds (little above 150 as given in Table 1) with the water molecules, and consequently, results in greater solvation energy (140.03 kcal mol−1) among all the ssDNA. The average number of H-bonds for both ssdA12 and ssd(AGTC)3 is about 134, while the H-bonds number is about 131 and 123 for ssdC12 and ssdT12, respectively (see Table 1). We note that the number of H-bonding sites available to solvent water molecules present in each nucleobase is 7, 6, 5 and 4 for G, A, C and T, respectively. As a result of that, the ssdG12, ssdA12 and ssd(AGTC)3 show large number of H-bonds formation with solvent water in comparison to other ssDNA, and thereby, resulting in higher interaction strength with water (higher negative interaction energy). Moreover, as given in Table 1, the average number of H-bonds between various ssDNA, with water follows the same order as the average number of H-bonding sites present in each polynucleotide. The greater extent of solvation energy found for ssdG12 and ssd(AGTC)3 compared to other ssDNA may also be accounted for by the presence of large average surface area exposed to the solvent water molecules. However, we find almost similar interaction energies for the ssdA12, ssdC12 and ssdT12, and relatively moderate interaction energy for mixed sequence, ssd(AGTC)3. Also note that the average number of H-bonds within the various ssDNA is less than 1 with the exception found for ssdC12, for which the number is found to be 2, indicating its greater extent of intra-molecular folding compared to others. Overall, our analysis shows that both the nucleobase π–π stacking interactions within each ssDNA and H-bonding interactions between the ssDNA and solvent water molecules have to be overcome for the stable composite formation with graphene.
| Systems | Average number of H-bonds within ssDNA | Average number of H-bonds between ssDNA and water | E int (in kcal mol−1) between ssDNA and water |
|---|---|---|---|
| ssdA12 | 0.24 | 134.40 | −122.73 |
| sssG12 | 0.14 | 150.47 | −140.03 |
| ssdC12 | 2.26 | 131.91 | −124.09 |
| ssdT12 | 0.67 | 123.87 | −123.25 |
| ssd(AGTC)3 | 0.88 | 134.10 | −126.45 |
| Graphene@ssdA12 | 1.80 | 123.94 | −105.82 |
| Graphene@ssdG12 | 2.57 | 141.60 | −124.25 |
| Graphene@ssdC12 | 2.80 | 120.44 | −110.06 |
| Graphene@ssdT12 | 2.35 | 107.03 | −101.53 |
| Graphene@ssd(AGTC)3 | 1.46 | 125.53 | −114.60 |
Now, before we begin analysing the assembly processes of various ssDNA onto graphene surface, we first look at the stability of monolayer and AB stacked bi-layer graphene in presence of explicit water solvent at T = 300 K and P = 1 atm, in order to validate the reliability of empirical force field used in the present study. Moreover, although, pristine graphene is hydrophobic in nature, it is important to study the interaction between the solvent water molecules and graphene surface to understand the detailed atomic picture of graphene dispersion by various ssDNA. Note that, each single-layer of the graphene model contains 4032 C atoms, and for the initial configuration of bi-layer graphene, we choose the inter-layer separation of 3.4 Å, and no water molecules in between the graphene layers. In the MD simulation, we have not considered any geometric constraint and allowed all the graphene carbon atoms to relax during the simulations. Our simulation results show that the graphene layer remains stable at the simulation conditions, and there is no penetration of solvent water molecules within the two layers for the bi-layer graphene, as also expected from the periodic boundary conditions of the two-dimensional sheet. We find that the average interlayer separation for the bi-layer graphene varies from 3.3 to 3.6 Å over the simulation time. The average interaction energy between two layers is found to be −1.21 kcal mol−1 per layer C atoms. Additionally, the binding free energy is found to be 0.04 kcal mol−1 per layer C atoms. However, we find a significant corrugation of graphitic layer during the simulation. This is because of the long-range fluctuation at finite temperature, which is fully consistent with the Mermin–Wagner theorem68 and with the intrinsic rippling observed in graphene.69 Our simulations results on mono and bi-layer graphene clearly demonstrate the reliability of the empirical force field employed in the present study.
In order to understand the interaction strength of various ssDNA polynucleotides with graphene, it is important to quantify the binding affinity of different nucleosides with graphene in aqueous environments at room temperature. Previous DFT studies have shown that G binds strongly with graphene, while A, C, and T have similar binding strength.70 However, other studies show that the nucleobase binding affinity goes as: G > A > T > C,71,72 which is expected from their chemical nature. Note that, the reported values of binding affinities for different nucleobases are calculated based on mainly gas-phase DFT calculations, where only the work by Varghese et al. consider the solvation effects, by implicitly taking into account the dielectric continuum of water. However, in the presence of explicit water molecules, two competing forces are simultaneously present: base–graphene π-stacking interaction and nucleobase solvation by water. To the best of our knowledge, there are no such studies examining the effect of explicit water molecules in estimating the binding free energy of individual nucleobases with graphene. Here, we consider calculating the binding free energy of various nucleosides interacting with graphene in aqueous medium using the TI methods as described above. To model the nucleoside–graphene system, we choose each of individual nucleoside initially placed at 4.0 Å distance apart from a rectangular periodic graphene containing 416 C atoms, where the plane of the nucleoside is aligned parallel to the graphene surface. From a 15 ns MD simulation, we find that C and T pyrimidine nucleosides bind strongly to the graphene, whereas the purine nucleosides, A and G, show relatively lesser binding affinity. The calculated binding free energy of different nucleosides are −4.17 kcal mol−1 for A, −5.77 kcal mol−1 for G, −9.00 kcal mol−1 for C and −6.65 kcal mol−1 for T, and the binding sequence follows as: C > T > G > A. Note that, the binding free energy order does not agree with the previously reported results. However, the lesser extent of binding free energy found for T than C is due to the presence of an additional bulky methyl group in T nucleoside, which causes structural destabilization, while adsorbing on graphene surface. This is well consistent with the experimental results73 reporting higher binding energy for polythymidine than polycytosine oligonucleotide. It is interesting to note that, the larger the number of polar sites available in nucleoside, the greater the extent of solvation free energy, which consequently results in lower binding affinity of the nucleoside for the graphene. Thus, the observed discrepancy in predicting the order of binding strength is mainly because of the nucleoside solvation effects by explicit water molecules, and partly may also be due to the presence of thermal and dynamical fluctuation during the simulation, which were not taken into account in previous studies.71,72 It is worth mentioning that the binding free energy order found from our simulation may vary depending on the environmental conditions and length as well as base-sequences of various ssDNA.
Next, we investigate the detailed atomistic picture of assembly phenomena of various ssDNA onto graphene surface with the progress of simulation time up to a total time of 30 ns. Note that the hybrid simulation is a complex process and needs systematic study in order to understand the details of the interaction mechanism. In the initial model structure, we consider the ssDNA and graphene hybrid, where the helical axis of ssDNA is placed parallel to the graphene surface, and maintaining an initial distance of about 5.0 Å from the plane of the graphene surface. The initial geometrical orientation of ssDNA with respect to the graphene would provide the details understanding of adsorption mechanism of various ssDNA during the course of MD simulations. The schematic of a simulation set up is depicted in Fig. 2. As has already been mentioned, we have considered five sets of individual simulation with varying the base sequences of ssDNA. To this end, we choose two pure purine polynucleotides, namely, ssdA12 and ssdG12, and two pyrimidine polynucleotides, namely, ssdC12 and ssdT12. Additionally, we also consider a DNA polynucleotide of AGTC consecutive base-sequences, i.e. ssd(AGTC)3, where the two terminal nucleobases (A and C) are of different type. Note that, all the polynucleotides are modelled from their corresponding duplex B-DNA structure of dodecamer size (i.e., polymer of 12 nucleotides). Consequently, each of the model ssDNA contains 12 nucleobase of varying sequences. Here, we discuss the assembly processes of various ssDNA on graphene surface over 30 ns simulation time step-wise. We would also analyse the results at 10, 20, 30 ns simulation time in detail.
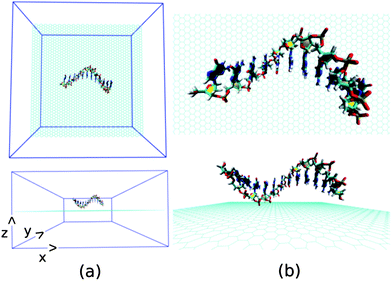 | ||
| Fig. 2 The schematic of initial simulation system for a representative system: graphene@ssdG12 (explicit water molecules and counter ions are not shown for better figure quality). | ||
First, we analyse the results obtained for the ssdA12 adsorption onto graphene surface in aqueous solution. The configurations of graphene@ssdA12 hybrid at different simulation time are shown in Fig. 3. Our simulation results show that within a time period of 10 ns, most of the A nucleobases formed stable π-stacks with the flat graphene surface. After 10 ns MD simulation, we find 9 number of A nucleobase formed stable π-stacked onto graphene surface, while 3 A nucleobases still maintain their intra-base π-stacks within the ssdA12. Further progress in simulation time neither change the ssdA12 conformations adsorbed onto graphene nor altered the number of base–graphene and base–base π-stacks, as given in Table 2. This clearly indicates that the hybrid system has attained its stable conformation. Moreover, the calculated interaction energy between the ssdA12 and graphene does not show significant changes after the 5 ns simulation time, as shown in Fig. S1,† suggesting that the stable assembly has been formed within this period of MD simulation. Also, the root mean square deviation (RMSD) of ssdA12 with respect to the final energy minimized structure also suggests the formation of stable graphene@ssdA12 hybrid (see Fig. S1†). The average interaction energy and binding free energy per nucleotide between ssdA12 and graphene is calculated to be −19.34 kcal mol−1and −4.56 kcal mol−1, respectively.
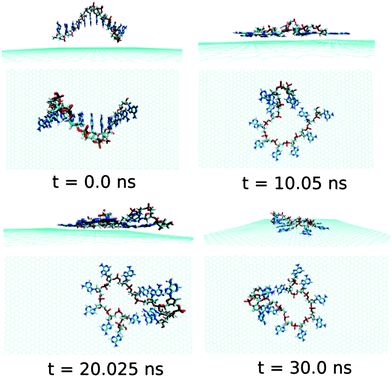 | ||
| Fig. 3 The simulated structures at various time interval for graphene@ssdA12. The water and ions are not shown for better clarity of the figure. | ||
| Systems | E int (kcal mol−1) | ΔFbind (kcal mol−1) | No. of base–graphene π stacks | No. of base–base π stacks | ||||
|---|---|---|---|---|---|---|---|---|
| 10 ns | 20 ns | 30 ns | 10 ns | 20 ns | 30 ns | |||
| Graphene@ssdA12 | −19.34 | −4.56 | 9 | 9 | 9 | 3 | 3 | 3 |
| Graphene@ssdG12 | −13.02 | −4.14 | 4 | 6 | 6 | 7 | 6 | 5 |
| Graphene@ssdC12 | −10.86 | −3.57 | 4 | 7 | 7 | 4 | 3 | 2 |
| Graphene@ssdT12 | −15.48 | −2.18 | 7 | 8 | 8 | 3 | 3 | 3 |
| Graphene@ssd(AGTC)3 | −20.84 | −5.92 | 11 | 10 | 11 | 1 | 1 | 1 |
We also find that the average number of H-bonds between the ssdA12 and solvent water molecules has been reduced to 123 from 134, and thereby, an increase in the H-bonding interaction energy (increase in the negative interaction strength) in comparison to the free ssdA12 in aqueous environment occurs (see Table 1). However, there is a small increment in the number of intra-molecular H-bonds, which indicate the structural coiling behaviour as also found over the progress of simulation time. A detailed structural analysis reveal that the 2nd A nucleobase from 5′end forms stable H-bonds with the 1st A nucleobase from 3′end of the adsorbed ssdA12, resulting in a coiled structure. Also note that, this H-bonded A–A nucleobase pair forms a stable π-stack on the graphene surface.
Now, we discuss and analyse the dynamical adsorption process of ssdG12 polynucleotide onto graphene surface in aqueous solution at T = 300 K and P = 1 atm. The details of the structural changes during the progress of simulation are shown in Fig. 4.We find that the ssdG12 forms a stable composite with graphene after 20 ns of MD simulation, as indicative from the RMSD and average interaction energy diagrams calculated over the simulation time. Our results show that at 10 ns simulation time, the number of nucleobase–graphene π-stacks is 4, whereas the number of base–base π-stacks is 7. With the progress in simulation time, the number of base–graphene π-stacks is increased to 6, and the number of base–base π-stacks is decreased to 5 after 30 ns simulation. This clearly indicates the greater binding affinity of ssdG12 with respect to the prolonged simulation time. However, we find a stable trajectory over 30 ns simulation time. The calculated interaction energy between ssdG12 and graphene, and binding free energy per nucleotide are found to be −13.02 kcal mol−1 and −4.14 kcal mol−1, respectively. Note that both the interaction and binding free energy are comparatively higher than the values obtained for ssdA12 adsorption on graphene. This demonstrates the greater extent of adsorption propensity of ssdA12 on graphene surface than ssdG12. The higher interaction and binding free energy obtained for ssdG12 adsorption on graphene than ssdA12 can be accounted for the less number of base–graphene π-stacking interactions for the former composite compared to the latter one. The adsorption process significantly reduces the average number of H-bonds between the ssdG12 and water molecules, which results in higher solvent–ssDNA interaction energy than in graphene free ssdG12 in aqueous solution. We also find a small average number (2.5) of intra-molecular H-bonds within ssdG12 when adsorbed onto graphene surface. A closer look at the simulated structure after 20 ns shows that the two G nucleobases, between 4th adenine from 5′end and 2nd adenine from 3′end, form stable intra-molecular H-bonds on graphene surface. Note that, both the purine base sequence containing ssDNA (ssdA12 and ssdG12) form stable and planar intra-molecular H-bonds, and consequently, increases the average number of H-bonds within ssDNA, as given in Table 1. These analyses prove that the helical shape of ssdG12 is completely destroyed upon adsorption on graphene, forming a folded conformation onto the graphene flat surface.
 | ||
| Fig. 4 The simulated structures at various time intervals for graphene@ssdG12. The water and ions are not shown for better clarity. | ||
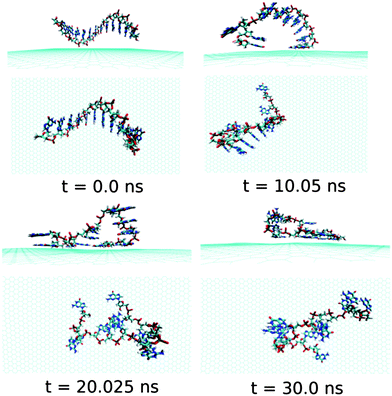
Next, we examine the adsorption processes of the pyrimidine base sequence containing two ssDNA polynucleotides, namely ssdC12 and ssdT12, on the 2D flat surface of graphene in aqueous medium. As shown in Fig. S1,† the small fluctuation in interaction energy between the ssDNA and graphene, and the measured RMSD over the simulation time indicate that both the ssDNAs form stable hybrids with graphene within the 30 ns simulation time. The structures for the interactions of ssdC12 and ssdT12 with graphene at different simulation times are shown in Fig. 5 and Fig. 6, respectively. The graphene–ssDNA interaction energy (binding free energy) estimated for ssdC12 and ssdT12 are found to be −10.86 kcal mol−1 (−3.57 kcal mol−1) and −15.48 kcal mol−1 (−2.18 kcal mol−1), respectively. The higher interaction strength found for ssdT12 is due the presence of larger number of nucleobase–graphene π-stacking interactions compared to ssdC12 adsorption.
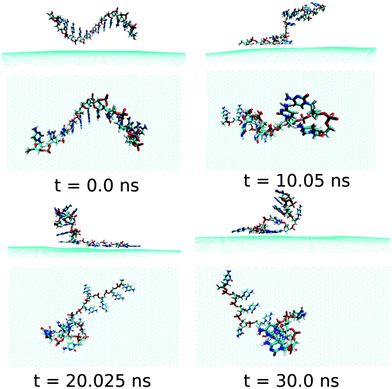 | ||
| Fig. 5 The simulated structures at various time intervals for graphene@ssdC12. The water and ions are not shown for better clarity. | ||
Additionally, the presence of 5 H-bonding modes for C nucleobase than only 4 H-bonding modes in T encompasses a larger number of H-bonding interactions with solvent water molecules for the former nucleobase, hence, reducing the extent of graphene–ssDNA interactions. In fact, as expected, we find a larger extent of both interaction energy and binding free energy for these two pyrimidine nucleobase ssDNA polynucleotide (ssdC12 and ssdT12) as compared to the purine base sequence containing ssdA12 and ssdG12 polynucleotide. This is because of the presence of larger π-surface (two-rings) in purine nucleobase, which results in greater π-stacking interactions with graphene π-surface than what is expected in single-ring containing pyrimidine nucleobases. Moreover, it is known that the strength of nucleobase interaction with graphene goes as: G > A > T > C,71,72 which in turn follows their hydrophobicity order.74 The order of the binding strength found in our study is well consistent with the individual base–graphene binding strength, at least with respect to the purine and pyrimidine base-sequences. Moreover, our simulation results are consistent with the previous results obtained for nucleobase interactions with single-walled carbon nanotubes.63 Also, as can be seen from Table 1, both the ssDNA form a small number of intra-molecular H-bonds, suggesting their intra-molecular folding behaviours.
At this point, it is important to investigate the effect of a mixed base sequence to compare and contrast the binding strength, and explore their dynamical conformational changes during the simulation process. To achieve this, we choose a ssDNA consisting of a consecutive repeat of AGTC base sequence forming ssd(AGTC)3 polynucleotide. Note that this particular ssDNA contains two different terminal nucleobases, i.e., A and C at the 5′and 3′end of ssDNA, respectively. The calculated graphene–ssDNA interaction energy as well as RMSD (see in Fig. S1†) show a large conformational fluctuations of ssd(AGTC)3 with the progress in simulation time. This is due to the presence of hetero base sequences in the ssDNA considered here. It is also to be noted that after 25 ns of simulation, both the fluctuations become almost constant, reaching equilibrated values with minimum deviations.
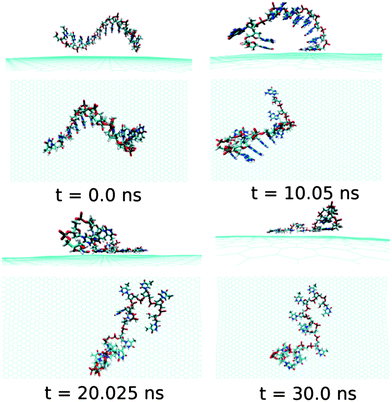 | ||
| Fig. 6 The simulated structures at various time intervals for graphene@ssdT12. The water and ions are not shown for better clarity. | ||
As can be seen from Fig. 7 and Table 2, almost all the nucleobase form stable π-stacks with the graphene surface. During the 30 ns simulation time, the number of nucleobase–graphene π-stacks changes from 11 (10 ns) to 10 (20 ns), which is further changed to 11 at 30 ns, whereas the number of base–base π-stacks remains at the constant number of 1. We find that at 10 ns simulation, the ssd(AGTC)3 form a stable adsorbed π-stacked structure, where 11 nucleobases are strongly adsorbed onto graphene surface, forming a circular flat structure. Further increase in simulation time causes an elongated structure on the graphene surface which does not alter with the progress of simulation time. The detailed structural changes during the progress of simulation are shown in Fig. 7. The calculated interaction energy and binding free energy are found to be −20.84 kcal mol−1 and −5.92 kcal mol−1, respectively. We find the greater extent of binding strength for ssd(AGTC)3 adsorption on graphene surface in comparison to the other hybrids. This can be accounted for the larger number of nucleobase–graphene π-stacking interactions. Moreover, due to the adsorption onto graphene, the average number of H-bonds with the solvent water molecules is significantly reduced compared to the free ssDNA solvation, which gives rise to a lesser extent of solvation strength by the water molecules. However, we find a small average number of intra-molecular H-bonds (1.5) than in any other graphene–ssDNA hybrid, supporting its solely π-stacking stabilized elongated network formation on graphene surface.
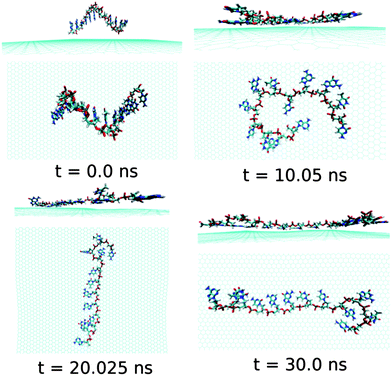 | ||
| Fig. 7 The simulated structures at various time interval for graphene@ssd(AGTC)3. The water and ions are not shown for better clarity. | ||
To further investigate the electronic structure of ssDNA adsorbed graphene composites, we consider studying these composites within DFT calculations. To this end, we model these systems from the final equilibrated structures obtained from MD simulation of individual composites followed by energy minimization using the steepest descent method. We consider the ssDNA with a rectangular graphene fragment, whose edges are terminated with the hydrogen atoms for the dangling bonds. We model these molecular hybrid systems in a vacuum, that is, we do not take into account any environmental effects. Moreover, we choose to add hydrogen atoms to the negatively charged phosphate groups to neutralize the system following previous reports.75,76 The total number of atoms present in these model systems is as follows: 1456 for graphene@ssdA12, 1210 for graphene@ssdG12, 1264 for graphene@ssdC12, 1208 for graphene@ssdT12, and 1543 for graphene@ssd(AGTC)3. We only consider optimizing the position of the added hydrogen atoms present in each composite using DFT. All the partially optimized structures of model systems are shown in Fig. 8.
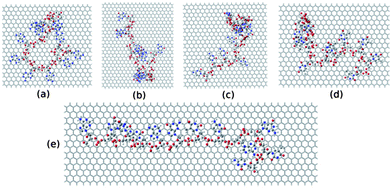 | ||
| Fig. 8 The model structures considered for the DFT study. (a), (b), (c), (d) and (e) represent structure of ssdG12, ssdA12, ssdC12, ssdT12, and ssd(AGTC)3 adsorbed onto the hydrogen terminated graphene fragment, respectively. | ||
First, we consider the DFT computed interaction energy between graphene and various ssDNA in their folded conformations. To accomplish this, we calculate interaction energy by subtracting the energy of graphene and ssDNA components from the total energy of the respective hybrid composite. The calculated values per nucleobase are −9.21, −15.66, −16.45, −18.73 and −13.02 kcal mol−1 for ssdA12, ssdG12, ssdC12, ssdT12, and ssd(AGTC)3, respectively. The predicted interaction strength follows the order: ssdT12 > ssdC12 > ssdG12 > ssd(AGTC)3 > ssdA12. Note that the DFT computed trend in interaction energy does not follow either the interaction energy or binding free energy trend estimated from 30 ns MD simulation. This may be due to the lack of any environmental effects considered in DFT calculations and, also, because of the absence of quantum effects studied in classical MD simulation. Moreover, we do not find any interfacial charge-transfer between graphene and various ssDNA, suggesting the importance of non-covalent van der Waals and π–π stacking interaction for stabilization of these nano-biocomposites. Furthermore, we also consider calculating the electronic density of states (DOS) together with the projected density of states (pDOS) of individual components, and the distribution of highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) for analysing the electronic structure of these model composites in detail. We present the electronic DOS and pDOS in Fig. S2(a).† We find the significant electronic states at the Fermi energy for all ssDNA–graphene hybrids. The pDOS analysis reveals that the major contribution to the DOS at the Fermi energy mainly comes from the graphene component of these composites. However, a small contribution to the total DOS also comes from the ssDNA component, in particular, from π-stacked nucleobases, for the ssdC12 and ssdT12 adsorbed graphene complexes. This is also clear from their small HOMO–LUMO gap values: 44 and 38 meV for ssdC12 and ssdT12, respectively, in their free wrapped conformations. The orbital contributions from ssDNA to the DOS for other systems occur at relatively lower in energy. We also find that all the bio-composites show very small HOMO–LUMO electronic gap values, indicating their near-conducting behaviours. The calculated gap values for ssdA12, ssdG12, ssdC12, ssdT12, and ssd(AGTC)3 adsorbed graphene hybrids are 3, 10, 1, 2, 5 meV, respectively, which are very small in comparison to the thermal energy at room temperature (26 meV). In fact, we find that these calculated gap values resemble the HOMO–LUMO gap values of their rectangular graphene fragments. Our analysis also shows that these small gap values arise mainly because of the presence of graphene zigzag edge states, which is consistent with the HOMO and LUMO frontier molecular orbital diagrams as shown in Fig. S2.† We find that these two molecular orbitals are mainly localized on the zigzag carbon edges of all the graphene fragments considered. However, in an infinite graphene sheet, there are no edge states. Here, edge passivation by hydrogen atoms causes partially occupied edge states at the Fermi level, resulting in metallic behaviour, which needs to be excluded for mimicking infinite graphene sheet. Furthermore, the 2D graphene surface becomes corrugated by the ssDNA adsorption. Thus, it is anticipated that the ssDNA adsorbed infinite graphene hybrid would act as small gap semiconductor.
4. Conclusions
In conclusion, we have shown that the biologically important various ssDNA oligonucleotides can serve as efficient dispersing agents for graphene in aqueous medium using all atom MD simulation at room temperature and 1 atm pressure. Our simulation results show that when ssDNA is added to the aqueous solution of graphene, there exist three simultaneous competing forces: first, the base–base π–π stacking interactions within ssDNA, favouring the native ssDNA helical shape, second, H-bonding interactions with solvent water molecules, helping ssDNA solubilisation process, and third, the base–graphene π–π-stacking interactions, which assist ssDNA adsorption on graphene. Results obtained for various ssDNA oligonucleotides interaction with graphene show that the binding free energy order is: ssd(AGTC)3 < ssdA12 < ssdG12 < ssdC12 < ssdT12, indicating the importance of both π–π stacking as well as H-bonding interactions. Interestingly, we find that the interactions follow the same trend as obtained for single nucleoside interaction with graphene in aqueous solution. This clearly demonstrates that the nature of nucleobase, not the sugar phosphate backbone, together with the number of base–graphene π-stacks, are the key determining factors while solubilising graphene with different ssDNA in aqueous solution. We also find two distinctive ssDNA assemblies, namely coiling and elongated network structures, on graphene surface resulting from two competing forces acting on ssDNA in graphene solution. Moreover, our results suggest that the hetero-base sequences containing ssDNA, such as ssd(AGTC)3, are the most suitable candidates within the ssDNA structures considered here, compared to any other ssDNA while dispersing graphene like materials in aqueous solution. Additionally, we have also studied detailed electronic structures of these ssDNA–graphene composites, highlighting their conduction properties. We believe that our results certainly would help in understanding the detailed underlined mechanisms for the ssDNA assisted graphene dispersion in aqueous solution.Acknowledgements
AKM acknowledges CSIR, Govt. of India for senior research fellowship and SKP acknowledges DST, Govt. of India and AOARD for research funding.Notes and references
- A. Cerf, T. Alava, R. A. Barton and H. G. Craighead, Nano Lett., 2011, 11, 4232–4238 CrossRef CAS.
- J. Shendure and H. Ji, Nat. Biotechnol., 2008, 26, 1135–1145 CrossRef CAS.
- C. H. Lu, H. H. Yang, C. L. Zhu, X. Chen and G. N. Chen, Angew. Chem., Int. Ed., 2009, 48, 4785–4787 CrossRef CAS.
- B. Das, B. Choudhury, A. Gomathi, A. K. Manna, S. K. Pati and C. N. R. Rao, ChemPhysChem, 2011, 12, 937–943 CrossRef CAS.
- K. S. Subrahmanyam, A. K. Manna, S. K. Pati and C. N. R. Rao, Chem. Phys. Lett., 2010, 497, 70–75 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS.
- X. D. Wen, L. Hand, V. Labet, T. Yang, R. Hoffmann, N. Ashcroft, A. R. Oganov and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6833 CrossRef CAS.
- J. H. Seol, I. Jo, A. L. Moore, L. Lindsay, Z. H. Aitken, M. T. Pettes, X. Li, Z. Yao, R. Huang, D. Broido, N. Mingo, R. S. Ruoff and L. Shi, Science, 2010, 328, 213–216 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS.
- Z. Liu, X. Li, S. M. Tabakman, K. Jiang, S. Fan and H. Dai, J. Am. Chem. Soc., 2008, 130, 13540–13541 CrossRef CAS.
- Y. Chen, H. Liu, T. Ye, J. Kim and C. Mao, J. Am. Chem. Soc., 2007, 129, 8696–8697 CrossRef CAS.
- D. A. Heller, H. Jin, B. M. Martinez, D. Patel, B. M. Miller, T.-K. Yeung, P. V. Jena, C. Hobartner, T. Ha, S. K. Silverman and M. S. Strano, Nat. Nanotechnol., 2009, 4, 114–120 CrossRef CAS.
- L. Cao, X. Wang, M. J. Meziani, F. Lu, H. Wang, P. G. Luo, Y. Lin, B. A. Harruff, L. M. Veca, D. Murray, S.-Y. Xie and Y.-P. Sun, J. Am. Chem. Soc., 2007, 129, 11318–11319 CrossRef CAS.
- C. C. Fu, H. Y. Lee, K. Chen, T. S. Lim, H. Y. Wu, P. K. Lin, P. K. Wei, P. H. Tsao, H. C. Chang and W. Fann, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 727 CrossRef CAS.
- C. Hao, L. Ding, X. Zhang and H. Ju, Anal. Chem., 2007, 79, 4442–4447 CrossRef CAS.
- R. Yang, J. Jin, Y. Chen, N. Shao, H. Kang, Z. Xiao, Z. Tang, Y. Wu, Z. Zhu and W. Tan, J. Am. Chem. Soc., 2008, 130, 8351–8358 CrossRef CAS.
- Z. Zhu, Z. Tang, J. A. Phillips, R. Yang, H. Wang and W. Tan, J. Am. Chem. Soc., 2008, 130, 10856–10857 CrossRef CAS.
- M. Zheng, A. Jagota, E. D. Semke, B. A. Diner, R. S. McLean, S. R. Lustig, R. E. Richardson and N. G. Tassi, Nat. Mater., 2003, 2, 338–342 CrossRef CAS.
- K. A. Williams, P. T. M. Veenhuizen, B. G. de la Torre, R. Eritja and C. Dekker, Nature, 2002, 420, 761 CrossRef CAS.
- D. Pantarotto, R. Singh, D. McCarthy, M. Erhardt, J. P. Briand, M. Prato, K. Kostarelos and A. Bianco, Angew. Chem., 2004, 116, 5354–5358 CrossRef.
- R. Singh, D. Pantarotto, D. McCarthy, O. Chaloin, J. Hoebeke, D. Charalambos, J. P. Briand, M. Prato, A. Bianco and K. Kostarelos, J. Am. Chem. Soc., 2005, 127, 4388–4396 CrossRef CAS.
- N. Nakashima, S. Okuzono, H. Murakami, T. Nakai and K. Yoshikawa, Chem. Lett., 2003, 32, 456–457 CrossRef CAS.
- C. Staii, A. T. Johnson Jr, M. Chen and A. Gelperin, Nano Lett., 2005, 5, 1774–1778 CrossRef CAS.
- C. Dwyer, M. Guthold, M. Falvo, S. Washburn, R. Superfine and D. Erie, Nanotechnology, 2002, 13, 601 CrossRef CAS.
- H. Gao, Y. Kong, D. Cui and C. S. Ozkan, Nano Lett., 2003, 3, 471–473 CrossRef CAS.
- D. A. Heller, E. S. Jeng, T. K. Yeung, B. M. Martinez, A. E. Moll, J. B. Gastala and M. S. Strano, Science, 2006, 311, 508–511 CrossRef CAS.
- S. E. Baker, W. Cai, T. L. Lasseter, K. P. Weidkamp and R. J. Hamers, Nano Lett., 2002, 2, 1413–1417 CrossRef CAS.
- X. Tu, S. Manohar, A. Jagota and M. Zheng, Nature, 2009, 460, 250–253 CrossRef CAS.
- M. S. Strano, M. Zheng, A. Jagota, G. B. Onoa, D. A. Heller, P. W. Barone and M. L. Usrey, Nano Lett., 2004, 4, 543–550 CrossRef CAS.
- M. Zheng, A. Jagota, M. S. Strano, A. P. Santos, P. Barone, S. G. Chou, B. A. Diner, M. S. Dresselhaus, R. S. Mclean and G. B. Onoa, Science, 2003, 302, 1545–1548 CrossRef CAS.
- S. Daniel, T. P. Rao, K. S. Rao, S. U. Rani, G. Naidu, H. Y. Lee and T. Kawai, Sens. Actuators, B, 2007, 122, 672–682 CrossRef.
- S. Li, P. He, J. Dong, Z. Guo and L. Dai, J. Am. Chem. Soc., 2005, 127, 14–15 CrossRef CAS.
- A. Bianco, K. Kostarelos and M. Prato, Curr. Opin. Chem. Biol., 2005, 9, 674–679 CrossRef CAS.
- S. Wang, R. Wang, P. Sellin and Q. Zhang, Biochem. Biophys. Res. Commun., 2004, 325, 1433–1437 CrossRef CAS.
- X. Zhao and J. K. Johnson, J. Am. Chem. Soc., 2007, 129, 10438–10445 CrossRef CAS.
- H. Gao and Y. Kong, Annu. Rev. Mater. Res., 2004, 34, 123–150 CrossRef CAS.
- W. Martin, W. Zhu and G. Krilov, J. Phys. Chem. B, 2008, 112, 16076–16089 CrossRef CAS.
- R. R. Johnson, A. T. C. Johnson and M. L. Klein, Nano Lett., 2008, 8, 69–75 CrossRef CAS.
- R. R. Johnson, A. Kohlmeyer, A. T. C. Johnson and M. L. Klein, Nano Lett., 2009, 9, 537–541 CrossRef CAS.
- B. Gigliotti, B. Sakizzie, D. S. Bethune, R. M. Shelby and J. N. Cha, Nano Lett., 2006, 6, 159–164 CrossRef CAS.
- S. Manohar, T. Tang and A. Jagota, J. Phys. Chem. C, 2007, 111, 17835–17845 CAS.
- G. Lu, P. Maragakis and E. Kaxiras, Nano Lett., 2005, 5, 897–900 CrossRef CAS.
- Z. Xiao, X. Wang, X. Xu, H. Zhang, Y. Li and Y. Wang, J. Phys. Chem. C, 2011, 115, 21546–21558 CAS.
- M. V. Karachevtsev and V. A. Karachevtsev, J. Phys. Chem. B, 2011, 115, 9271–9279 CrossRef CAS.
- D. Roxbury, J. Mittal and A. Jagota, Nano Lett., 2012, 12, 1464–1469 CrossRef CAS.
- D. Roxbury, X. Tu, M. Zheng and A. Jagota, Langmuir, 2011, 27, 8282–8293 CrossRef CAS.
- H. Cathcart, V. Nicolosi, J. M. Hughes, W. J. Blau, J. M. Kelly, S. J. Quinn and J. N. Coleman, J. Am. Chem. Soc., 2008, 130, 12734–12744 CrossRef CAS.
- Y. Wu, J. A. Phillips, H. Liu, R. Yang and W. Tan, ACS Nano, 2008, 2, 2023–2028 CrossRef CAS.
- S. Akca, A. Foroughi, D. Frochtzwajg and H. W. C. Postma, PLoS One, 2011, 6, e18442 CAS.
- X. Zhao, J. Phys. Chem. C, 2011, 115, 6181–6189 CAS.
- J. Macke Thomas and A. Case David, in Molecular Modeling of Nucleic Acids, American Chemical Society, 1997, pp. 379–393 Search PubMed.
- T. A. D. D. A. David Case, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossvai, K. F. Wong, F. Paesani, J. Vanicek, J. Liu, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M. J. CHsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollmann, AMBER 11, University of California, San Francisco, 2010 Search PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- J. Zou, B. Ji, X.-Q. Feng and H. Gao, Nano Lett., 2006, 6, 430–434 CrossRef CAS.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190 CrossRef CAS.
- Zhao and J. K. Johnson, J. Am. Chem. Soc., 2007, 129, 10438–10445 CrossRef CAS.
- C.-L. Cheng and G.-J. Zhao, Nanoscale, 2012, 4, 2301–2305 RSC.
- W. L. Jorgensen, J. Am. Chem. Soc., 1981, 103, 335–340 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- C. Chipot, Theory and Applications in Chemistry and Biology, Springer Verlag, Berlin, 2007, vol. 10, pp. 978–973 Search PubMed.
- R. R. Johnson, A. Johnson and M. L. Klein, Small, 2010, 6, 31–34 CrossRef CAS.
- P. K. Samanta, G. Periyasamy, A. K. Manna and S. K. Pati, J. Mater. Chem., 2012, 22, 6774–6781 RSC.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- K. Burke, J. P. Perdew and M. Ernzerhof, Int. J. Quantum Chem., 1997, 61, 287–293 CrossRef CAS.
- N. D. Mermin, Phys. Rev., 1968, 176, 250–254 CrossRef.
- A. Fasolino, J. H. Los and M. I. Katsnelson, Nat. Mater., 2007, 6, 858–861 CrossRef CAS.
- S. Gowtham, R. H. Scheicher, R. Ahuja, R. Pandey and S. P. Karna, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 033401 CrossRef.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2008, 10, 2722–2729 RSC.
- N. Varghese, U. Mogera, A. Govindaraj, A. Das, P. K. Maiti, A. K. Sood and C. Rao, ChemPhysChem, 2009, 10, 206–210 CrossRef CAS.
- S. Manohar, A. R. Mantz, K. E. Bancroft, C. Y. Hui, A. Jagota and D. V. Vezenov, Nano Lett., 2008, 8, 4365–4372 CrossRef CAS.
- W. Saenger, Principles of Nucleic Acid Structure, New York, 1984 Search PubMed.
- C. D. M. Churchill and S. D. Wetmore, Phys. Chem. Chem. Phys., 2011, 13, 16373–16383 RSC.
- P. Maragakis, R. L. Barnett, E. Kaxiras, M. Elstner and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 241104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2tb00184e |
| This journal is © The Royal Society of Chemistry 2013 |
