Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct evidence for ligand-enhanced activity of Cu(I) sites†
Elvira Gouatieu
Dongmo‡
 ab,
Shabnam
Haque‡
ab,
Shabnam
Haque‡
 a,
Florian
Kreuter
a,
Florian
Kreuter
 a,
Toshiki
Wulf
a,
Toshiki
Wulf
 ac,
Jiaye
Jin
ac,
Jiaye
Jin
 *a,
Ralf
Tonner-Zech
*a,
Ralf
Tonner-Zech
 *a,
Thomas
Heine
*a,
Thomas
Heine
 *bcd and
Knut R.
Asmis
*bcd and
Knut R.
Asmis
 *a
*a
aWilhelm-Ostwald-Institut für Physikalische und Theoretische Chemie, Universität Leipzig, Linnéstr. 2, 04103 Leipzig, Germany. E-mail: jiaye.jin@uni-leipzig.de; ralf.tonner@uni-leipzig.de; knut.asmis@uni-leipzig.de
bInstitute of Resource Ecology, Research Site Leipzig, Helmholtz-Zentrum Dresden-Rossendorf, Permoserstr. 15, 04318 Leipzig, Germany
cFaculty of Chemistry and Food Chemistry, School of Science, TU Dresden, 01062 Dresden, Germany. E-mail: thomas.heine@tu-dresden.de
dDepartment of Chemistry and ibs for Nanomedicine, Yonsei University, Seodaemun-gu, Seoul 120-749, Republic of Korea
First published on 16th August 2024
Abstract
Little is known about the strong mediating effect of the ligand sphere and the coordination geometry on the strength and isotopologue selectivity of hydrogen adsorption on the undercoordinated copper(I) site. Here, we explore this effect using gas-phase complexes Cu+(H2O)(H2)n (with n ≤ 3) as model systems. Cu+(H2O) attracts dihydrogen (82 kJ mol−1) more strongly than bare Cu+ (64 kJ mol−1) does. Combining experimental and computational methods, we demonstrate a high isotopologue selectivity in dihydrogen binding to Cu+(H2O), which results from a large difference in the adsorption zero-point energies (2.8 kJ mol−1 between D2 and H2, including an anharmonic contribution of 0.4 kJ mol−1). We investigate its origins and the bond strengthening between Cu+ and H2 upon addition of a single H2O ligand. We discuss the role of the environment and the coordination geometry of the adsorption site in achieving a high selectivity and the ramifications for identifying and designing future materials for adsorptive dihydrogen isotopologue separation.
Introduction
Porous materials containing under-coordinated Cu(I) centres with a strong tendency to adsorb dihydrogen are promising candidates for efficient H2/D2 separation.1–5 A benchmark material with such centres is the metal–organic framework (MOF) Cu(I)-MFU-4l, containing trigonal pyramidal Cu+ sites linked by BTDD (bis-(1H-1,2,3-triazolo-[4,5-b],[4′,5′-i])dibenzo-[1,4]-dioxin).2,4,5 Its high D2/H2 adsorption selectivity of 11 at the relatively high temperature of 100 K is due to the combination of high enthalpies of adsorption for H2 (31 kJ mol−1) and D2 (34 kJ mol−1) and the relatively high difference of these values between the two isotopologues. The latter is governed by the zero-point energy (ZPE) difference, and leads to a strong preference towards adsorption of the higher mass isotopologue.6–8The rational design of high-performance separation materials requires a detailed understanding of the binding of dihydrogen isotopologues to metal centres, particularly Cu(I), which has shown a strong dihydrogen affinity in many cases.2–4 However, spectroscopic studies of dihydrogen coordinated to Cu(I) centres in bulk materials typically suffer from structural heterogeneity, complicating an in-depth understanding. This can be avoided by performing experiments on well-defined and isolated gas-phase complexes using vibrational action spectroscopy in combination with electronic structure calculations.9 This approach allows characterization of the geometric structure of relevant M–H2 motifs,10 and also provides a deeper understanding of their binding nature as well as the isotopologue selectivity.
The adsorption thermodynamics of H2 isotopologues at binding sites in porous materials are governed by the ZPE effects associated with the conversion of the three translational and two rotational degrees of freedom of free H2 into five molecule-adsorption-site vibrations.11 These low-frequency vibrational modes usually display strongly anharmonic behaviour and pronounced nuclear quantum effects,12 raising a research interest in model complexes that show the influence of these vibrational modes on dihydrogen isotopologue separation.
A recent spectroscopic and theoretical study of the Cu+(H2)4 complex and its isotopologues revealed a substantial red-shift of the dihydrogen stretching frequency (νHH = 3729 cm−1 and νDD = 2678 cm−1) upon complexation (νHH = 4162 cm−1 and νDD = 2994 cm−1).13 The exceptionally high sequential bond dissociation energy (BDE) for Cu+(H2)n → Cu+(H2)n−1 + H2 with n = 1 of 64 kJ mol−1 reduces to only 21 kJ mol−1 with n = 4.13,14 This study motivated the investigation of H2-affine Cu(I) complexes with oxygen-donor ligands that can significantly increase the Cu+–H2 BDE.8,14,15 The aqua complex Cu+(H2O), arguably the simplest such system, represents a useful model for an undercoordinated adsorption site in a zeolite or a MOF. The experimental BDE of the Cu+–H2 bond in Cu+(H2O)(H2) is 82 kJ mol−1,14 which is 18 kJ mol−1 larger than that in Cu+(H2). Such high BDEs are desirable for adsorptive separation of dihydrogen isotopologues, both because they allow higher operating temperatures and also because they typically result in larger ZPE differences, which lead to a higher selectivity.
In this paper, we disentangle why a single H2O ligand already markedly strengthens the Cu(I)–H2 interaction. We first investigate the interaction of dihydrogen and its isotopologues with Cu+(H2O) by ion-trap mass spectrometry at variable temperature. We then combine cryogenic ion-trap vibrational action spectroscopy16,17 of Cu+(H2O)(H2)2 isotopologues with quantum-chemical calculations to characterize their structures and vibrational properties. Finally, we make use of bond analysis methods to rationalize the strong chemical bonding of H2 to the Cu(I) centre as well as the large ZPE difference of the dihydrogen isotopologues in order to identify the relevant factors that govern the isotopologue selectivity of dihydrogen adsorption.
Results and analysis
Ion-trap mass spectrometry
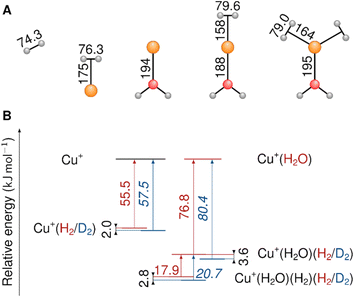
We begin our investigation by characterizing the adsorption yield of H2 and D2 on mass-selected Cu+(H2O) cations confined (on average) for 50 ms in an ion-trap reactor under multiple-collision conditions at ion-trap temperatures ranging from 295 K to 15 K. Under these conditions, Cu+(H2O)(H2/D2)n complexes with n ≤ 4 can be formed via three-body collisions. Their relative abundances are detected using time-of-flight (TOF) mass spectrometry. Integration over the corresponding normalized TOF-MS peaks yields the relative ion yields (see Fig. S1† for all TOF mass spectra and relative ion yields).Summation over all ion yields with n > 0 represents the total relative yields of (H2/D2)-containing complexes, which is plotted as a function of ion-trap temperature between 15 K and 200 K in Fig. 1. The formation of dihydrogen complexes is already observed at room temperature, confirming the relatively strong interaction between the Cu(I) cation and dihydrogen.14 Ion yields larger than ∼4% are observed for temperatures of 200 K and below. Dihydrogen adsorption increases with decreasing temperature. Moreover, at sufficiently low temperatures (<80 K) the adsorption of additional dihydrogen molecules is possible leading to the formation of n > 2 complexes (see Fig. S1†). The ion yields in Fig. 1 show that D2-containing complexes are more likely formed than the H2-containing complexes over the complete temperature range, revealing a substantial isotope effect in dihydrogen adsorption at Cu+(H2O). This isotopologue selectivity increases with decreasing temperature, reaching a maximum at 120 K. At lower temperatures the contribution of n > 2 complexes and eventually saturation of the dihydrogen binding sites needs to be considered.
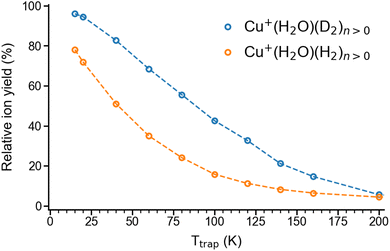 | ||
| Fig. 1 Total relative ion yield of Cu+(H2O)(H2)n>0 and Cu+(H2O)(D2)n>0 for ion trap temperatures ranging from 15 K to 200 K, obtained from the TOF mass spectra shown in Fig. S1.† The TOF mass spectra were recorded after storing Cu+(H2O) cations on average 50 ms in a temperature-controlled ion trap filled with roughly 1 mbar of H2 or D2. | ||
Infrared photodissociation spectra
In order to characterize the nature of H2/D2 adsorption on Cu+(H2O) in a more detailed way, we measured vibrational action spectra of the complexes using infrared photodissociation (IRPD) spectroscopy. For a comparison of the experimental IRPD spectra to computed IR spectra it proves helpful to measure the IRPD spectra in the linear absorption regime in the range of interest (2500–4500 cm−1), which covers the excitations of the O–H/O–D and H–H/D–D fundamental transitions. To avoid spectral overlap of the ligand-specific excitations, e.g., O–H/O–D stretching transitions, we focus on the Cu+(D2O)(H2) and Cu+(H2O)(D2) complexes here.The BDE for Cu+(D2O)(H2) → Cu+(D2O) + H2 is too high to allow for efficient single-photon dissociation. Therefore the IRPD spectra of the n = 2 complexes, Cu+(D2O)(H2)2 and Cu+(H2O)(D2)2, were measured and these are compared to the corresponding calculated IR spectra in Fig. 2 (see Fig. S2† for the IPRD spectra of Cu+(H2O)(H2)2 and Cu+(D2O)(D2)2). The most prominent IRPD bands (see Table 1 for band positions) are assigned to the partly-resolved rovibrational transitions of the symmetric (νsOH/D) and the antisymmetric O–H/O–D stretching fundamentals (νasOH/D). The corresponding bands in the IRPD spectrum of Cu+(H2O)(D2)2 are observed at 3628 cm−1 (νsOH) and 3700 cm−1 (νasOH), which is 4 cm−1 higher than the previously reported values for Cu+(H2O)Ar2.18 Likewise, νsOD and νsOD for Cu+(D2O)(H2)2 are at 2651 cm−1 and 2751 cm−1, only 2 cm−1 different from the bands for Cu+(D2O)Ar2. This minor effect of dihydrogen adsorption on the O–H/O–D stretching frequencies in Cu+(H2O/D2O) is in line with H2/D2 binding directly to the Cu+ cation.
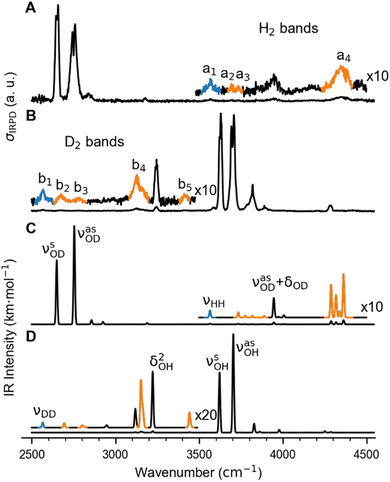 | ||
| Fig. 2 Vibrational spectra of Cu+(D2O)(H2)2 and Cu+(H2O)(D2)2. (A) and (B): Experimental IRPD spectra. (C) and (D): Predicted infrared spectra considering anharmonic contributions (VPT2/MP2/def2-TZVPP) as well as a 10 cm−1 wide Gaussian lineshape function. Bands related to the excitation of the dihydrogen stretching fundamentals νHH (a1) and νDD (b1), are color-coded in blue and the corresponding combination bands in orange (see Table 1 for the band assignments). | ||
| Label | IRPD | Calculated frequency (intensity) | Assignmenta |
|---|---|---|---|
| a Labeling of vibrational modes: ν (stretching), νs (symmetric stretching), νas (antisymmetric stretching), δ (bending), δIP (in-plane bending), δOOP (out-of-plane bending), τOOP (out-of-plane hindered rotation, or libration). Only modes with IR intensities larger than 0.1 km mol−1 are listed. b Values are obtained from the fitting of the rovibrational profiles (see Fig. S2). | |||
| Cu + (D 2 O)(H 2 ) 2 | |||
| 2651b | 2650 (112) | ν sOD | |
| 2751b | 2754 (165) | ν aOD | |
| 2840 | 2857 (7) | ν asOD + δOOPOD | |
| 3177 | 3190 (2) | ν asOD+ δIPOD | |
| a1 | 3568 | 3564 (0.7), 3563 (0.2) | ν HH |
| a2 | 3693 | 3698 (0.1) | ν HH+ τOOPOD |
| a3 | 3733 | 3733 (17), 3777 (18) |
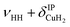
|
| 3944 | 3945 (2), 4005 (0.3) | ν asOD + δDOD | |
| a4 | 4350 | 4287 (4), 4362 (5), 4316 (2), 4338 (0.7) | ν HH + νCuH2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Cu + (H 2 O)(D 2 ) 2 | |||
| b1 | 2567 | 2566 (0.4), 2568 (0.1) | ν DD |
| b2 | 2675 | 2692 (0.2), 2695 (0.1) |
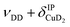
|
| b3 | 2783 | 2800 (0.2), 2810 (0.1) |
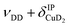 , νDD + δD2CuD2 , νDD + δD2CuD2 |
| b4 | 3125 | 3151 (0.3), 3151 (2), 3158 (1), 3165 (1) | ν DD+ νCuD2 |
| 3244 | 3222 (3) | 2 × δDOD | |
| b5 | 3414 | 3441 (0.5), 3442 (0.3), 3450 (0.1) | ν DD + νDCuD |
| 3628b | 3622 (198) | ν sOH | |
| 3700b | 3703 (120) | ν aOH | |
| 3819 | 3826 (18) | ν aOH + τOOPOH | |
| 3889, 3900 | 3860 (4) |
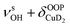
|
|
| 4207 | 4170 (0.1) |
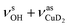
|
|
| 4283 | 4250 (3), 4286 (1) | ||
The bands related to the excitation of H–H stretching mode (νHH) are best observed in the IRPD spectrum of Cu+(D2O)(H2)2, shown in Fig. 2A, and labelled a1–4. The νHH fundamental (a1) appears at 3568 cm−1, substantially lower than the νHH fundamentals at 3729 cm−1 in the previously reported IRPD spectrum of Cu+(H2)4, indicating a stronger Cu+–H2 interaction in Cu+(D2O)(H2)2 than in Cu+(H2)4.13 Features with excitation energies above a1 are observed at 3693 cm−1 (a2), 3733 cm−1 (a3) and 4350 cm−1 (a4). These are tentatively assigned to combination bands (orange-coloured bands in Fig. 2B). Corresponding features are also observed in the IRPD spectrum of Cu+(H2O)(D2)2 (Fig. 2B). They are assigned to the νDD fundamental (b1, 2567 cm−1) as well as the combination bands at 2675 cm−1 (b2), 2783 cm−1 (b3), 3125 cm−1 (b4) and 3414 cm−1 (b5).
Computational results
When compared to the bond length in the free hydrogen molecule, the H–H distance in the Cu+(H2O)(H2) and Cu+(H2O)(H2)2 complexes is elongated by 5.3 pm and 4.7 pm, respectively (see Table S6†). This activation of the H–H (D–D) bond is substantially larger than the 2.3–3.1 pm reported for Cu(H2)4+ and is in line with the much stronger redshift of the H–H (D–D) stretching fundamental observed for the present system.
Only the VPT2 IR bands involving excitation of H2 or D2 stretching modes, either as a fundamental (blue bands) or as part of a combination transition (orange bands), are color-coded. Based on the agreement between the experimental and computed vibrational spectra shown in Fig. 2, we can unambiguously assign all the observed bands (see Table 2). The excitation of the H–H (D–D) stretching fundamental a1 (b1) is observed at νHH = 3568 cm−1 (νDD = 2567 cm−1), resulting in a frequency ratio νHH/νDD of 1.390. This ratio is close to the value of 1.388 obtained from the VPT2 IR spectra, confirming the high quality of the MP2/def2-TZVPP potential along the vibrational mode. The combination bands a2 to a4, observed at 3693 cm−1, 3733 cm−1, and 4350 cm−1, respectively, are assigned to combined excitations of the H–H stretching modes (νHH) with either of the following low-frequency vibrational modes: out-of-plane OD hindered rotation (τOOPOD), in-plane Cu+–H2 bending (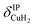 ), and Cu+–H2 stretching modes (νCuH2). For the latter two modes, the present assignment is similar to the one made previously for the IRPD spectrum of Cu+(H2)4.13 Analogously, the combination bands b2 to b5, observed at 2675 cm−1, 2783 cm−1, 3125 cm−1 and 3414 cm−1, respectively, are assigned to combination excitations of one of the two D–D stretching modes (νDD) with Cu+–D2 bending (
), and Cu+–H2 stretching modes (νCuH2). For the latter two modes, the present assignment is similar to the one made previously for the IRPD spectrum of Cu+(H2)4.13 Analogously, the combination bands b2 to b5, observed at 2675 cm−1, 2783 cm−1, 3125 cm−1 and 3414 cm−1, respectively, are assigned to combination excitations of one of the two D–D stretching modes (νDD) with Cu+–D2 bending (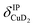 and
and 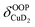 ) or the Cu+–D2 stretching excitations (
) or the Cu+–D2 stretching excitations (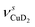 and νDCuD).
and νDCuD).
| Cu+(H2O)(H2)-(H2) | Cu+(H2O)-(H2) | Cu+-(H2) | |
|---|---|---|---|
| a All energies in kJ mol−1, bond distances in Å computed with B3LYP-D4/TZ2P. Fragments are closed-shell species Cu+L0–3 and H2 (L = H2O, H2). b Percentage values give the relative contributions of dispersion and electronic effects to ΔEint. c Percentage values give the relative contributions to the attractive pEDA terms ΔEelstat and ΔEorb. d Percentage values give the relative contributions of the NOCV to ΔEorb. e Distance between Cu and the centre of the H2 fragment. | |||
| ΔEint | −71 | −112 | −95 |
| ΔEint(disp)b | −3(4%) | −2(2%) | −2(2%) |
| ΔEint(elec)b | −68(96%) | −110(98%) | −93(98%) |
| ΔEPauli | 193 | 188 | 189 |
| ΔEelstatc | −151(58%) | −172(58%) | −155(55%) |
| ΔEorbc | −110(42%) | −126(42%) | −127(45%) |
| ΔE1(σ(H2)→ Cu(d))d | −58(53%) | −79(63%) | −69(54%) |
| ΔE2(Cu(d)→ σ*(H2)) d | −24(22%) | −19(15%) | −38(30%) |
| ΔE3(Cu(d)→ σ*(H2)) d | −26(24%) | −25(20%) | −18(14%) |
| ΔEprep | 44 | 5 | 4 |
| ΔEprep(H2) | 4 | 5 | 4 |
| ΔEprep(Cu+L0–3) | 40 | 0 | 0 |
| ΔEbond | −27 | −107 | −91 |
| r(Cu–H2)e | 1.72 | 1.64 | 1.70 |
The remarkably good agreement between the IRPD and VPT2 spectra in Fig. 2, which is discussed in detail in the ESI,† confirms that the chosen computational method provides an adequate description of also the low-frequency M+–H2/D2 vibrational modes, which play an important role in modelling the isotopologue selectivity. However, this appears to be in part due to a favourable error compensation between, i.e., the neglect of substantial relativistic effects, basis set insufficiencies, and the overestimation of London dispersion interaction inherent in the MP2 method (see ESI†).
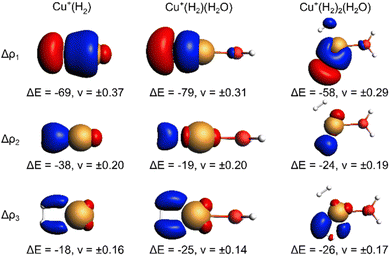
The EDA-NOCV results for the complexes investigated in this work are shown in Table 2. They confirm a donor–acceptor-type interaction in the Cu+–H2 bond in all investigated complexes (Cu+(H2O)(H2)2, Cu+(H2O)(H2), and Cu+(H2)). At first glance, the stronger bonding in Cu+(H2O)(H2) compared to Cu+(H2) is due to an increase in the electrostatic attraction (difference ΔΔEelstat = −17 kJ mol−1) while the orbital interaction (ΔEorb) and Pauli repulsion (ΔEPauli) do not change significantly. However, a closer look reveals a more intriguing trend. The bond in Cu+(H2) is significantly longer compared to Cu+(H2O)(H2). If we analyse the main deformation densities (Fig. 4), we find that upon coordination of H2O, the σ-donation from σ(H2) into the d-orbitals at Cu (ΔE1) increases by 10 kJ mol−1. But the in-plane back-bonding (ΔE2) decreases by a larger amount (−19 kJ mol−1), while the out-of-plane back-bonding (ΔE3) is slightly increased (+7 kJ mol−1). This reduced in-plane back-bonding is due to the involvement of the Cu(d)-orbitals in the bonding to the H2O ligand, which can be seen in the deformation densities Δρ1 and Δρ2 in Fig. 4. This leads to a lower Pauli repulsion and allows the H2 molecule to bind closer to the Cu centre. While orbital attraction and Pauli repulsion thus balance at the same values compared to Cu+(H2), the electrostatic attraction is increased. The main reason is thus lowering of Pauli repulsion leading to a shorter Cu–H2 distance in Cu+(H2O)(H2).
The weakening of the Cu+–H2 bond in Cu+(H2O)(H2)2 compared to Cu+(H2O)(H2) is attributed mainly to the large preparation energy resulting from the transition from a linear to a trigonal structure. Additionally, the larger bond lengths are due to the stronger Pauli repulsion between the higher number of ligands and contribute to this phenomenon because they weaken the attractive interactions compared to Cu+(H2O)(H2).
Note that the Cu+–H2O bond is stronger in Cu+(H2O)(H2) compared to Cu+(H2O), which is mainly due to reduced Pauli repulsion as an effect of the back-bonding contributions from Cu+ to H2 (see NOCV in Fig. S9 in ESI†). Adding another H2 molecule, i.e. the formation of Cu+(H2O)(H2)2, leads to a weaker Cu+–H2O bond due to competition of the three ligands for the electrons at the central atom.
Anharmonic contribution to the BDEs for different isotopologues
As shown in Table 3, going from Cu+(H2O)(H2)2 to Cu+(H2O)(T2)2, the BDE of the H2 isotopologue increases due to the increasing mass of the isotopologues and the consequently lower ZPE. The difference in the adsorption ZPE between the D2 and the H2 complexes is 2.8 kJ mol−1 (1.0 kJ mol−1 between T2 and D2), which is slightly larger than the one observed in Cu(I)-MFU-4l (2.5 kJ mol−1) by I. Weinrauch et al.4 and about one-third greater than the ZPE change for the exchange reaction Cu+(D2)3(H2) + D2 → Cu+(D2)4 + H2 (2.1 kJ mol−1) observed in the previous study conducted by some of us.13| Species | D 0 | Δ desZPE | Anharmonic contribution |
|---|---|---|---|
| Cu+(H2O)(H2)2 | 16.9 | −10.8 | 0.8 |
| Cu+(H2O)(D2)2 | 19.7 | −8.0 | 0.4 |
| Cu+(H2O)(T2)2 | 21.0 | −6.7 | 0.3 |
| Cu+(H2O)(HD)2 | 18.4 | −9.3 | 0.6 |
| Cu+(H2O)(HT)2 | 19.2 | −8.5 | 0.5 |
| Cu+(H2O)(DT)2 | 20.4 | −7.3 | 0.3 |
Our calculations also show that the anharmonic contribution to the H2 desorption ZPE for the Cu+(H2O)(H2)2 → Cu+(H2O)(H2) + H2 reaction is more than three times as big as the value obtained for free H2 (0.2 kJ mol−1). Similar factors are observed for D2 (3.1) and T2 (3.1). This demonstrates the substantial influence of anharmonic contributions on the thermodynamic equilibrium of the isotopologue exchange reaction, reducing, e.g., the energy difference between H2 and D2 adsorption by 12%. As expected, the anharmonic contributions to the vibrational frequencies and ZPEs are inversely proportional to the reduced mass of the dihydrogen isotopologue.
H2 isotopologue selectivity
As shown in Fig. 5, the predicted isotopologue selectivity of H2 adsorption is much higher at Cu+(H2O) (B) than at Cu+ (A) and decreases again for a second H2 adsorbing at Cu+(H2O)(H2). We study two scenarios for the resulting Cu+(H2O)(H2)2 complex: in the first one, we assume that the second H2 molecule adsorbs at the free space of a hypothetical Cu+(H2O)(H2) complex where H2O and the first H2 are already positioned as in Cu+(H2O)(H2)2, thus mimicking a scenario as it could occur on an undercoordinated adsorption site in a porous solid (C). Here, only the six degrees of freedom of the considered H2 molecule are taken into account to calculate the isotopologue selectivity of dihydrogen adsorption, an approach that has been used in previous studies of MOFs.4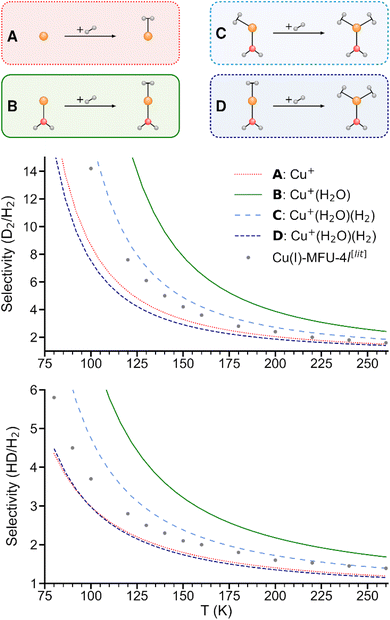 | ||
| Fig. 5 Predicted selectivities for dihydrogen isotopologue adsorption at Cu+, Cu+(H2O), and Cu+(H2O)(H2) as a function of temperature. For the latter, two models are compared (see text). Literature data of Cu(I)-MFU-4l are shown for comparison.4 | ||
In the second one (D), all complexes are fully optimized and the degrees of freedom of all involved H2 moieties are considered, which can be compared directly with the IRPD experiments. As a consequence of the weaker binding energy per H2 molecule, the ZPE per H2 and finally the overall selectivity is reduced significantly.
We conclude that a model with a rigid ligand structure is insufficient when dealing with structurally flexible adsorption sites such as undercoordinated metal ions, as it will lead to spurious results due to ligand reorientation. Conversely, as evidenced by prior studies,4,8 rigid adsorption sites with structurally constraining ligands like in the hypothetical starting structure in Fig. 5C may be essential for achieving a high adsorption energy and isotopologue selectivity.
Summary and conclusions
We elucidated the strong hydrogen isotopologue selectivity of undercoordinated Cu(I) sites by examining the model complexes Cu+(H2O)(H2)n (with n = 0, 1, 2) using experiment and theory. Both Cu+(H2O) and Cu+(H2O)(H2/D2) show an obvious isotope effect in the adsorption of H2 and D2. The observed vibrational spectra of Cu+(H2O)(H2)2 and its isotopologues in the range from 2500–4500 cm−1 match the calculated frequencies of the fundamentals and related combination bands of H2/D2 when taking anharmonicity into account. This suggests that these systems are ideal model complexes for gas-phase studies of the chemistry at individual active sites as they occur in framework materials. The stronger H2 affinity of Cu(I) coordinated by a single oxygen-donor ligand, in comparison to the bare cation, is explained by EDA and traced back to lowering of Pauli repulsion which allows the H2 molecule to bind closer to the Cu centre. Finally, we used the computational data to predict the dihydrogen isotopologue selectivity of the formation of Cu+(H2O)(H2)n complexes, observing a significant selectivity decrease for n = 2 vs. n = 1. The present study underlines that the structural environment of undercoordinated metal centres in framework materials play a crucial role in the local chemistry and demonstrate particular promise for rigid frameworks with highly exposed metal sites.Methods
Experimental methods
The experiments were performed on the Leipzig 5 K ring-electrode ion-trap triple mass spectrometer described previously.16 Cu+(H2O) cations are transferred to the gas phase from a 5 mmol CuSO4 (Sigma Aldrich: CuSO4·5H2O 99% in CH3OH 99.9% and distilled water) solution using a nanospray ion source under open atmospheric conditions, while the Cu+(D2O) cations are produced via H/D exchange in moist air conditions saturated with heavy water vapour (99.9% D2O). The beam of cations is skimmed, thermalized to room temperature in a Helium-filled radio-frequency ion guide, and then mass-selected in a quadrupole mass filter. Mass-selected Cu+(H2O/D2O) ions are continuously trapped in a radio-frequency ring-electrode ion trap, held at a temperature in-between 15 K and 295 K using a closed-cycle helium cryostat and filled with ≈ 1 mbar H2(D2). Cu+(H2O/D2O)(H2/D2)n adducts are formed by three-body collisions and thermalized to the ambient temperature by many collisions with other gas molecules.All cations are extracted from the ion trap every 100 ms and weakly focused both temporally and spatially into the centre of the extraction region of an orthogonally mounted double-focusing reflectron time-of-flight (TOF) mass spectrometer. For the determination of the ion yields, the ions are extracted and accelerated without using the reflectron. Furthermore, TOF mass spectra are recorded for TOF extraction delay times ranging from 100 μs to 135 μs and summed to account for incomplete temporal focusing of the extracted ions. The absolute ion yield Ij of the j'th ion is obtained by integration of the corresponding TOF peak, which is assumed proportional to the number of detected cations of a particular mass-to-charge ratio. Multiple TOF mass spectra are measured and averaged to determine the relative ion yield 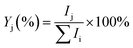 .
.
IRPD spectra are measured using the IR1MS2 scheme.25 To this end, the cation packet extracted from the ion trap is accelerated into the reflectron stage and refocused in the initial extraction region. Prior to reacceleration towards the MCP detector, ions with a particular mass-to-charge ratio are selectively irradiated with a properly timed, widely wavelength tunable (750–7000 cm−1) IR laser pulse (bandwidth: ∼3.5 cm−1), supplied by an optical parametric oscillator/amplifier (LaserVision) laser system.26 IRPD spectra are recorded by continuously scanning the laser wavelength that is monitored online using a HighFinesse WS6-600 wavelength meter. The scan speed is set to obtain an averaged TOF mass spectrum over 40–80 laser shots every 2 cm−1. Typically, four scans are measured and averaged to obtain each IRPD spectrum. The photodissociation cross section σIRPD determined as described previously.16,27
Computational methods
Structure optimizations and single point energy calculations were performed using coupled cluster theory with single, double, and perturbative triple excitations, i.e. CCSD(T), utilizing CFOUR 2.1.28 The heavily augmented correlation-consistent aug-cc-pVTZ basis set was used for all atoms except for copper, where the version with an effective core potential (ECP), i.e. aug-cc-pVTZ-PP, was used to take into consideration relativistic effects. The combination will be referred to as “aug-cc-pVTZ(-PP)” henceforth. Very tight SCF convergence criteria for the Hartree–Fock equations and the coupled cluster amplitudes equations were used (10−10 hartree, i.e. SCF_CONV = 10 and CC_CONV = 10). The geometry optimizations were performed using analytically evaluated gradients with good starting geometry in Z-matrix files and tighter thresholds. During the geometry optimizations, the RMS gradients were converged to 10−9 hartree.Vibrational analysis (calculation of vibrational frequencies and intensities as well as ZPEs) was performed using standard second-order vibrational perturbation theory (VPT2) without any resonance treatment on a potential energy surface obtained with second-order Møller–Plesset perturbation theory (MP2) in conjunction with the def2-TZVPP basis set using the Gaussian29 program package. For the preceding geometry optimization, internal coordinates and very tight geometry convergence criteria were used. The frozen-core approximation was applied throughout by specifying five orbitals (DROPMO = 1 > 5), i.e. freezing the 1s, 2s, and the three 2p orbitals of the Cu atom. The full details of the computed structures for Cu+(H2O)(H2)0,1,2 complexes are given in the ESI.†
For calculation of dihydrogen isotopologue selectivities, harmonic vibrational frequencies obtained with the Gaussian program package were used and two approaches are contrasted. One, which was used for all systems considered, follows a previous methodology,4,7 which relies on the calculation of the partition functions for the individual contributions of each of the six normal modes of H2 in the field of the frozen adsorption site structure. Here, we used the fragment structure of the fully optimized complex. The harmonic approximation was applied to analyse five of the six modes (νHH, νCuH2, 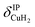 ,
, 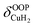 ,
, 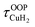 ) of the adsorbed hydrogen isotopologues, which are visualized in Fig. S6† (see ESI†). The sixth mode, i.e. the quasi-free rotation of H2 about the Cu–H2 axis, was treated using the model of the rigid rotor rotating in the plane. For Cu+(H2O)(H2)2, this was contrasted with a second approach, which uses fully relaxed structures and considers the change of the vibrational properties of both H2 upon binding of the second, i.e. considering twelve vibrational modes in Cu+(H2O)(H2)2, six in Cu+(H2O)(H2) and the six in free H2.
) of the adsorbed hydrogen isotopologues, which are visualized in Fig. S6† (see ESI†). The sixth mode, i.e. the quasi-free rotation of H2 about the Cu–H2 axis, was treated using the model of the rigid rotor rotating in the plane. For Cu+(H2O)(H2)2, this was contrasted with a second approach, which uses fully relaxed structures and considers the change of the vibrational properties of both H2 upon binding of the second, i.e. considering twelve vibrational modes in Cu+(H2O)(H2)2, six in Cu+(H2O)(H2) and the six in free H2.
The bonding analysis with the EDA-NOCV analysis, was performed using the Amsterdam Modeling Suite (AMS, version 2021.105),30 where complexes and their fragments are optimized beforehand. All DFT calculations, were carried out using the B3LYP functional31 with D4 dispersion correction of Grimme32 and TZ2P basis set.33 The selection of the xc-functional is based on the benchmark study presented in ESI.† Relativistic effects were considered using the zeroth-order regular approximation (ZORA).34 Symmetry was not considered. The SCF convergence criterion was set to 10−6 Eh, indicated by the keyword ‘Very Good’ as a numerical quality indicator. Geometry optimization accounted for the energy criterion at 3 × 10−3 Eh and the gradient criterion at 10−3 Eh Å−1.
Data availability
The data that support the findings of this study are openly available in zenodo at https://doi.org/10.5281/zenodo.12554684.Author contributions
EGD and SH contributed equally. SH and JJ performed the experiments. EGD performed the CCSD(T) and MP2 calculations, vibrational analysis and the selectivity calculations. FK carried out the bonding analysis. TH, KA and RTZ conceived the original idea of the project. All authors provided feedback and contributed to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG) Project ID 443871192 – GRK 2721: “Hydrogen Isotopes, 1,2,3H”. EGD and TH thank the Center for Information Services and High Performance Computing (ZIH) at TU Dresden for computational resources as well as Johannes Hoja and A. Daniel Boese at University of Graz for fruitful scientific discussions and computational resources. JJ and KA thank André Fielicke (Fritz-Haber-Institut der Max-Planck-Gesellschaft) for helpful disucssions of low-frequency M+–H2 modes. SH, JJ and KA thank Alexandra Giermann for the preparation of sample solutions.References
- (a) D. Sengupta, P. Melix, S. Bose, J. Duncan, X. Wang, M. R. Mian, K. O. Kirlikovali, F. Joodaki, T. Islamoglu, T. Yildirim, R. Q. Snurr and O. K. Farha, J. Am. Chem. Soc., 2023, 145, 20492 CrossRef CAS; (b) B. R. Barnett, H. A. Evans, G. M. Su, H. Z. H. Jiang, R. Chakraborty, D. Banyeretse, T. J. Hartman, M. B. Martinez, B. A. Trump and J. D. Tarver, others, J. Am. Chem. Soc., 2021, 143, 14884 CrossRef CAS PubMed.
- R. Xiong, L. Zhang, P. Li, W. Luo, T. Tang, B. Ao, G. Sang, C. Chen, X. Yan, J. Chen and M. Hirscher, Chem. Eng. J., 2020, 391, 123485 CrossRef CAS.
- B. Ipek, R. A. Pollock, C. M. Brown, D. Uner and R. F. Lobo, J. Phys. Chem. C, 2018, 122, 540 CrossRef CAS.
- I. Weinrauch, I. Savchenko, D. Denysenko, S. M. Souliou, H.-H. Kim, M. Le Tacon, L. L. Daemen, Y. Cheng, A. Mavrandonakis, A. J. Ramirez-Cuesta, D. Volkmer, G. Schütz, M. Hirscher and T. Heine, Nat. Commun., 2017, 8, 14496 CrossRef CAS PubMed.
- J. Teufel, H. Oh, M. Hirscher, M. Wahiduzzaman, L. Zhechkov, A. Kuc, T. Heine, D. Denysenko and D. Volkmer, Adv. Mater., 2013, 25, 635 CrossRef CAS PubMed.
- H. Oh and M. Hirscher, Eur. J. Inorg. Chem., 2016, 2016, 4278 CrossRef CAS.
- T. Wulf and T. Heine, Int. J. Quantum Chem., 2018, 118, e25545 CrossRef.
- T. Wulf and T. Heine, J. Phys. Chem. C, 2020, 124, 9409 CrossRef CAS.
- (a) K. R. Asmis, A. Fielicke, G. von Helden and G. Meijer, in Atomic clusters, ed. D. Woodruff, Elsevier, Amsterdam and Boston, 2007, pp. 327–375 Search PubMed; (b) E. J. Bieske and O. Dopfer, Chem. Rev., 2000, 100, 3963 CrossRef CAS PubMed; (c) J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16, 267 Search PubMed; (d) M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22, 407 Search PubMed; (e) A. Fielicke, Chem. Soc. Rev., 2023, 52, 3778 RSC.
- (a) V. Dryza and E. J. Bieske, Int. Rev. Phys. Chem., 2013, 32, 559 Search PubMed; (b) V. Dryza, B. L. J. Poad and E. J. Bieske, Phys. Chem. Chem. Phys., 2012, 14, 14954 RSC.
- (a) G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479 CrossRef CAS PubMed; (b) K. Sillar, A. Hofmann and J. Sauer, J. Am. Chem. Soc., 2009, 131, 4143 CrossRef CAS PubMed.
- (a) F. Dahlmann, C. Lochmann, A. N. Marimuthu, M. Lara-Moreno, T. Stoecklin, P. Halvick, M. Raoult, O. Dulieu, R. Wild, S. Schlemmer and others, J. Chem. Phys., 2021, 155 Search PubMed; (b) F. Dahlmann, P. Jusko, M. Lara-Moreno, P. Halvick, A. N. Marimuthu, T. Michaelsen, R. Wild, K. Geistlinger, S. Schlemmer, T. Stoecklin, R. Wester and S. Brünken, Mol. Phys., 2022, 120 Search PubMed; (c) M. Jia, J. Vanbuel, P. Ferrari, E. M. Fernández, S. Gewinner, W. Schöllkopf, M. T. Nguyen, A. Fielicke and E. Janssens, J. Phys. Chem. C, 2018, 122, 18247 CrossRef CAS; (d) I. Swart, F. M. F. de Groot, B. M. Weckhuysen, P. Gruene, G. Meijer and A. Fielicke, J. Phys. Chem. A, 2008, 112, 1139 CrossRef CAS PubMed.
- J. Jin, T. Wulf, M. Jorewitz, T. Heine and K. R. Asmis, Phys. Chem. Chem. Phys., 2023, 25, 5262 RSC.
- P. R. Kemper, P. Weis, M. T. Bowers and P. Maître, J. Am. Chem. Soc., 1998, 120, 13494 CrossRef CAS.
- (a) P. Maitre and C. W. Bauschlicher, J. Phys. Chem., 1993, 97, 11912 CrossRef CAS; (b) R. H. Crabtree, Chem. Rev., 2016, 116, 8750 CrossRef CAS PubMed; (c) G. J. Kubas, Metal Dihydrogen and S-Bond Complexes: Structure, Theory, and Reactivity, Springer Science & Business Media, 2001 CrossRef.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34, 1 Search PubMed.
- K. R. Asmis, M. Brümmer, C. Kaposta, G. Santambrogio, G. von Helden, G. Meijer, K. Rademann and L. Wöste, Phys. Chem. Chem. Phys., 2002, 4, 1101 RSC.
- P. D. Carnegie, A. B. McCoy and M. A. Duncan, J. Phys. Chem. A, 2009, 113, 4849 CrossRef CAS PubMed.
- T. Ziegler and A. Rauk, Theoret. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley, 2000, vol. 15, pp. 1–86 Search PubMed.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS.
- T. Ziegler and A. Rauk, Theoret. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- M. Mayer and K. R. Asmis, J. Phys. Chem. A, 2021, 125, 2801 CrossRef CAS.
- W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. B, 1993, 10, 1716 CrossRef CAS.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35, 507 Search PubMed.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum chemical program package, 2024 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. W. Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision C.01), Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04582c |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |