Photoelectron spectroscopy of cryogenically cooled NiO₂⁻via slow photoelectron velocity-map imaging

Abstract

High-resolution anion photoelectron spectra of cryogenically cooled NiO₂⁻ anions, obtained using slow photoelectron velocity-map imaging (cryo-SEVI), are presented in tandem with coupled cluster electronic structure calculations including relativistic effects. The experimental spectra encompass the X̃¹Σ_g⁺ ← X̃²Π_g, ã³Π_g ← X̃²Π_g, and ùΠ_g ← X̃²Π_g photodetachment transitions of linear ONiO^0/−, revealing previously unobserved vibrational structure in all three electronic bands. The high-resolution afforded by cryo-SEVI allows for the extraction of vibrational frequencies for each state, consistent with those previously measured in the ground state and in good agreement with scalar-relativistic coupled-cluster calculations. Previously unobserved vibrational structure is observed in the ã³Π_g and ùΠ_g states and is tentatively assigned. Further, a refined electron affinity of 3.0464(7) eV for NiO₂ is obtained as well as precise term energies for the ã and à states of NiO₂ of 0.3982(7) and 0.7422(10) eV, respectively. Numerous Franck–Condon forbidden transitions involving the doubly degenerate ν₂ bending mode are observed and ascribed to Herzberg-Teller coupling to an excited electronic state.

---

I. Introduction

Nickel oxides are an important class of catalytic materials with a wide range of industrial applications including the formation of syngas,^1,2 oxidative dehydrogenation of alkanes,^3,4 and carbon monoxide oxidation.⁵ Therefore, understanding their properties is of both technological and fundamental importance. While much of the emphasis of nickel oxide catalysis involves condensed phase experiments, the gas phase study of isolated mass-selected metal oxide clusters provides a complementary molecular-level understanding of the structure and reactivity of these species.^6,7 Here, we report high-resolution anion photoelectron spectra of cryogenically cooled NiO₂⁻, revealing a wealth of vibronic structure throughout the three lowest-lying electronic states of NiO₂.

There are relatively few experimental studies concerning the structure^8–12 and reactivity of NiO₂^0/−.^13–16 Neutral NiO₂ was first studied in gas matrices, where three isomers were identified in an Ar matrix:⁹ cyclic Ni(O₂), bent NiOO, and linear ONiO (referred to as NiO₂ hereafter). Subsequent work in Ne matrices found preferential formation of NiO₂ with trace Ni(O₂), allowing for the extraction of two and three vibrational frequencies for these species, respectively.¹² In the gas phase, anion photoelectron spectroscopy (PES) has been used to probe the geometric and electronic structure of these species. The first PES study of NiO₂⁻ was performed by Wu and coworkers,¹⁰ who observed photodetachment from both the bent Ni(O₂) and linear NiO₂ anions, finding the electron affinity (EA) of Ni(O₂) to be 0.82(3) eV, considerably lower than that of NiO₂ at 3.05(1) eV. The NiO₂ band showed partially resolved vibrational structure with a frequency of 750 cm⁻¹. This work also found transitions to two low-lying electronic states of NiO₂ with term energies of 0.40(2) and 0.77(3) eV. Subsequent anion PES work performed by Ramond et al.¹¹ reexamined the ground state spectrum of NiO₂ with improved resolution, yielding a refined EA of 3.043(5) eV as well as the v₁ symmetric stretch frequency of 745(30) cm⁻¹ from a progression in this mode.

The electronic and vibrational structure of NiO₂ pose a considerable challenge to theory owing to its multireference nature.^17,18 Treatments using density functional theory,^9,12,19–21 coupled cluster methods,²¹ and multireference methods²² have found a Σ_g⁺ ground electronic term for linear NiO₂ that lies 0.7–1.5 eV below the Ni(O₂) structure. In both structures, there are numerous low-lying singlet and triplet species calculated to reside within ∼2 eV of the ground state. The most definitive of these works is a joint multiconfiguration self-consistent field (MCSCF) and multireference configuration interaction (MRCI) study by Hübner,²² which finds a ¹Σ_g⁺ ground state with ³Π_g and ¹Π_g states lying 0.537 and 0.943 eV higher in energy, in good agreement with the observed term energies from anion PES. Less work has been done on the NiO₂⁻ anion, with an early DFT study by Gustev et al.²⁰ finding a ²A₂ bent ground state and more recent DFT work by Deng and coworkers¹⁹ finding a linear ²Π_g ground state.

Here, we utilize slow electron velocity-map imaging spectroscopy of cryogenically-cooled anions (cryo-SEVI), a high-resolution variant of anion photoelectron spectroscopy, to study the photodetachment of NiO₂⁻. In this method, cold ions are detached with a tunable laser and the resultant electron kinetic energy distribution is analyzed by a velocity-map imaging (VMI) spectrometer that is optimized for the detection of slow electrons, yielding photoelectron spectra with sub-meV resolution.^23,24 Revisiting the photoelectron spectra of NiO₂⁻ with cryo-SEVI provides substantial improvements in resolution over previous work. Beyond well-resolved vibrational structure in the ground and excited states, we observe a number of Franck–Condon (FC)-forbidden transitions in the ground state that display behavior distinct from that of the FC-allowed transitions near the photodetachment threshold. These features are ascribed to vibronic coupling to an excited electronic state. Our findings are supported by scalar-relativistic coupled-cluster calculations, with computed term energies and vibrational frequencies in good agreement with our observed spectra.

II. Experimental methods

The cryo-SEVI method has been described in detail previously.^23,25,26 Here, NiO₂⁻ anions are formed via laser ablation using a rotating and translating nickel disk onto which a frequency-doubled Nd:YAG is focused. The resulting plasma is entrained within a pulse of He carrier gas from an Even-Lavie solenoid valve,²⁷ with residual O₂ in this carrier gas serving to form NiO₂⁻ as it passes through a narrow channel to foster collisional cooling and cluster formation. The ions then pass through a skimmer before entering a radiofrequency (RF) hexapole ion guide and RF quadrupole mass filter that direct them into a linear RF octupole ion trap held at 5 K and filled with a buffer gas mixture of 20 : 80 H₂ : He. Collisions with this cold buffer gas mixture result in effective vibrational, rotational, and electronic cooling of the ions, leading to internal temperatures of around 10 K.^26,28–30

The ions are held approximately 40 ms in the trap before being extracted into an orthogonal Wiley-McLaren time-of-flight mass spectrometer³¹ and focused into the interaction region of a standard three-plate Eppink-Parker VMI electrostatic lens assembly.³² In the VMI spectrometer, the ions are photodetached using the frequency-doubled output of a dye laser pumped by the second harmonic of a Nd:YAG laser operating at 20 Hz.

The resulting photoelectrons are projected onto a 2D detector comprising two chevron-stacked microchannel plates coupled to a phosphor screen, which is photographed by a CCD camera after each laser shot.³³ Each image is analyzed for individual electron events for which the centroids are calculated and binned into a 1024 × 1024 grid.³⁴ The three-dimensional electron velocity distribution is reconstructed from the accumulated images using an inverse-Abel method.³⁵ The radial position of features in the reconstructed image is related to electron kinetic energy (eKE) by acquiring VMI images for detachment from atomic F⁻ at several photon energies.³⁶

The VMI spectrometer has an approximately constant resolving power, ΔeKE/eKE,³² yielding the highest eKE resolution for slow photoelectrons. As such, a SEVI spectrum is acquired by first taking an overview spectrum at a sufficiently high photon energy to access all (or most) of the photodetachment transitions before tuning the detachment laser to energies slightly above features of interest. This procedure results in the collection of high-resolution spectra over narrow energy windows that are then concatenated and scaled to match intensities in the overview spectrum, which is less sensitive to variation of the photodetachment cross section with photon energy. Spectra are plotted as a function of electron binding energy (eBE), given by eBE = hv − eKE.

III. Computational methods

Electronic structure calculations for the X̃²Π_g state of NiO₂⁻ and the X̃¹Σ_g⁺ state of NiO₂ have been carried out at the coupled-cluster singles doubles augmented with a noniterative triples [CCSD(T)]³⁷ level of theory to determine the equilibrium structures and the harmonic vibrational frequencies of these states as well as to enable Franck–Condon simulation for the electron detachment transitions from the electronic ground state of NiO₂⁻ to that of NiO₂. Scalar-relativistic effects have been taken into account using spin-free exact two-component theory in its one-electron variant (SFX2C-1e)^38,39 together with the aug-cc-pVTZ basis set^40–42 recontracted for SFX2C-1e calculations. Calculations using a hierarchy of CC methods including CCSD,⁴³ CC singles doubles triples (CCSDT),^44,45 and CC singles doubles triples quadruples (CCSDTQ)^46,47 have also been performed for the X̃¹Σ_g⁺ state of NiO₂ to examine the reliability of the CCSD(T) results, as this state exhibits strong electron-correlation effects.^17,18 The results of this analysis are outlined in Table S1 of the ESI.† Harmonic frequency calculations have been performed by means of numerical differentiation of analytically evaluated gradients using the analytic-gradient techniques for the CC methods and the SFX2C-1e scheme as implemented in the CFOUR program package.^48–55 FC simulations presented here employ the double-harmonic approximation using the fcsquared module⁵⁶ of the CFOUR program.

We have also performed SFX2C-1e equation-of-motion coupled-cluster singles doubles (EOM-CCSD)⁵⁷ and EOM-CC singles doubles triples (EOM-CCSDT)^58,59 calculations to determine the excitation energies of NiO₂ in the anionic equilibrium structure. These are combined with the computed vertical detachment energy for the ground X̃¹Σ_g⁺ state of NiO₂ to describe the vertical detachment energies from the ground state of NiO₂⁻ to these excited states of NiO₂. Here, aug-cc-pVQZ basis sets were used for EOM-CCSD calculations. The triples corrections have been obtained as the differences between EOM-CCSDT and EOM-CCSD results using cc-pVDZ basis sets. All calculations have been performed using the CFOUR program package,^53,55 except that the EOM-CCSDT calculations of triplet excited states have been carried out using the MRCC program package.^60–62

IV. Results and discussion

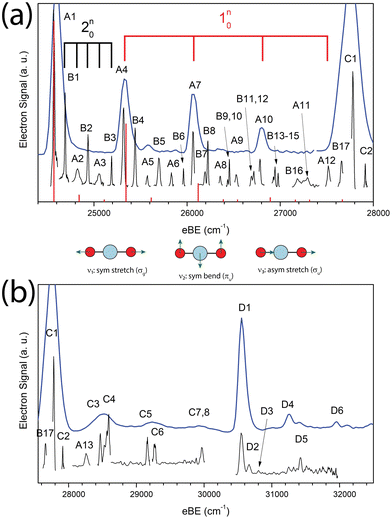
The cryo-SEVI spectrum of NiO₂⁻ is presented in Fig. 1. Fig. 1a shows the lower-eBE region of structure, spanning 24 400–28 000 cm⁻¹ and covering the ground state band of the NiO₂ ← NiO₂⁻ photodetachment transition previously observed.^10,11 The higher-energy region of the spectra shown in Fig. 1b spans 27 550–32 500 cm⁻¹ and encompasses detachment transitions to excited electronic states of NiO₂ as will be discussed in Sections IV.A and IV.D. In both figures, a low-resolution overview spectrum (blue) is displayed above high-resolution composite spectra (black) taken at several photon energies.

Fig. 1 Cryo-SEVI spectra of NiO₂⁻ showing detachment to the (a) X̃¹Σ_g⁺ ground state and (b) ã³Π_g and ùΠ_g excited states. Blue traces are low-resolution overview scans taken with photon energies of 30 394 and 35 025 cm⁻¹ for panels (a) and (b), respectively. Black traces are high-resolution scans taken at variable photon energies, while red stick spectra in (a) represent FC simulations for the X̃¹Σ_g⁺ ← X̃²Π_g photodetachment transition from NiO₂⁻. Vibrational modes for the ground state are depicted below the ground-state spectrum.

These spectra represent a significant improvement over previous anion photoelectron spectroscopy studies.^10,11 The improved resolution afforded by the cryo-SEVI method reveals not only the electronic transitions to the three lowest-lying states of NiO₂ (features A1, C1, D1, respectively) previously observed, but also a manifold of transitions to vibrationally excited states of the neutral species. Peak assignments, electron binding energies (eBEs), as well as shifts from peak A1 are presented in Tables 1–3, while extracted experimental parameters are presented in Table 4.

Table 1 Peak positions, shifts from peak A1, and assignments, in units of cm⁻¹, for the X̃¹Σ_g⁺ ← X̃²Π_g detachment transitions of NiO₂⁻. Uncertainty in the peak positions correspond to one standard deviation from a Gaussian fit to the highest-resolution experimental trace for each feature

Peak	eBE	Shift	Assignment
A1	24 571(6)	—	0^00
B1	24 691(7)	120	2^10
A2	24 815(13)	244	2^20
B2	24 936(8)	365	2^30
A3	25 061(12)	490	2^40
B3	25 190(7)	619	2^50
A4	25 316(6)	745	1^10
B4	25 442(9)	871	1^102^10
A5	25 572(9)	1001	1^102^20
B5	25 700(8)	1129	1^102^30
A6	25 832(9)	1261	1^102^40
B6	25 961(7)	1390	1^102^50
A7	26 065(8)	1494	1^20
B7	26 192(9)	1621	1^102^70
B8	26 223(7)	1652	1^202^10
A8	26 356(9)	1786	1^202^20
B9	26 436(6)	1865	1^102^90
B10	26 454(7)	1883	1^202^30
A9	26 529(11)	1957	3^20
B11	26 692(9)	2121	2^103^20
B12	26 716(9)	2145	1^202^50
A10	26 783(9)	2212	1^30
B13	26 928(10)	2357	1^102^10
B14	26 945(7)	2374	1^202^70
B15	26 978(7)	2406	1^302^30
B16	27 187(28)	2616	1^202^90
A11	27 283(35)	2712	1^103^20
A12	27 519(11)	2948	1^40
B17	27 660(11)	3089	1^402^10
A13	28 260(11)	3689	1^50

---

Table 2 Peak positions, shifts from peak C1, and assignments, in units of cm⁻¹, for the ã³Π_g ← X̃²Π_g detachment transitions of NiO₂⁻. Uncertainty in the peak positions correspond to one standard deviation from a Gaussian fit to the highest-resolution experimental trace for each feature

Peak	eBE	Shift	Assignment
C1	27 783(3)	—	ã^3Πg0^00
C2	27 913(5)	131	2^10
C3	28 468(11)	685	1^10
C4	28 589(13)	807	1^102^10
C5	29 162(12)	1380	1^20
C6	29 271(17)	1488	1^202^10
C7	29 883(9)	2100	1^30
C8	29 968(15)	2186	1^302^10

---

Table 3 Peak positions, shifts from peak D1, and assignments, in units of cm⁻¹, for the ùΠ_g ← X̃²Π_g detachment transitions of NiO₂⁻. Uncertainty in the peak positions correspond to one standard deviation from a Gaussian fit to the highest-resolution experimental trace for each feature

Peak	eBE	Shift	Assignment
D1	30 557(7)	—	Ã^1Πg0^00
D2	30 669(12)	112	2^10
D3	30 814(10)	257	2^20
D4	31 263(19)	706	1^10
D5	31 422(16)	865	1^102^10
D6	31 944(9)	1275	1^20

---

Table 4 Experimental parameters for the various states of NiO₂ probed in this work, extracted from the cryo-SEVI spectra of photodetachment of NiO₂⁻, along with comparison to our SFX2C-1e-CCSD(T)/aug-cc-pVTZ theoretical calculations for the ground state and EOM-CCSDT/cc-pVDZ calculations for the excited state term energies. Available literature values are presented

	Parameter	Calculated	SEVI	Literature
a Ref. 11. b Ref. 12. c Ref. 10.
X̃^1Σg^+
	EA (eV)		3.0464(7)	3.043(5)^a
	ω 1 (cm^−1)	774	745(6)	749^b
	ω 2 (cm^−1)	135	120(7)
	ω 3 (cm^−1)	985	978(16)	977.5^b
ã^3Πg
	T e (eV)	0.56	0.3982(7)	0.40(2)^c
	ω 1 (cm^−1)		685(11)
	ω 2 (cm^−1)		131(5)
Ã^1Πg
	T e (eV)	0.88	0.7422(10)	0.77(3)^c
	ω 1 (cm^−1)		706(19)
	ω 2 (cm^−1)		112(12)

---

In the case of the NiO₂ ground state band, assignments of features are facilitated by our SFX2C-1e-CCSD(T)/aug-cc-pVTZ calculations, which allow for FC simulations to be performed for detachment transitions terminating in the X̃¹Σ_g⁺ state of NiO₂. This simulated spectrum facilitates the definitive vibrational assignments in this state and suggests vibrational assignments for the ã and à states of NiO₂. Notably, there are several strong transitions (B1–17) observed in this spectrum that are not reproduced by our simulations. Moreover, these features (B1–B5, for example) are clearly not present in the overview spectrum and retain considerable intensity near detachment threshold. This trend is depicted in Fig. 2, in which spectra collected at three photon energies highlight the differing behavior of these features as the photodetachment threshold is approached. As discussed in Section IV.C, our assignments for the B peaks all involve odd changes of vibrational quanta in the non-totally symmetric ν₂ bending mode and are hence Franck–Condon forbidden.

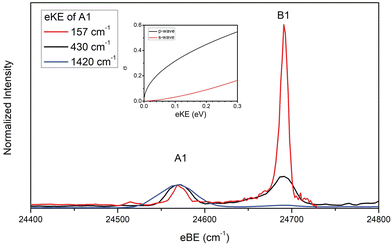Fig. 2 Cryo-SEVI spectra of NiO₂⁻ at three photon energies illustrating the differing signal attenuation for features A1 and B1 as eKE decreases. The intensity of each scan has been normalized to feature A1. Photon energies employed are 25 991 (blue), 25 001 (black), and 24 728 cm⁻¹ (red). Insert: photodetachment cross-section as a function of kinetic energy for s- and p-wave detachment as outlined by the Wigner threshold law.⁶⁷

Vibrational frequencies were not calculated for the two observed excited states of NiO₂, though the even spacing of levels and intensity patterns in the cryo-SEVI spectra lend themselves to tentative assignments to different vibrational levels of these two states of NiO₂ (Section IV.D).

IV.A Computational results

Our coupled-cluster calculations confirm that the electronic ground state of NiO₂ is the X¹Σ_g⁺ state, while the ground state of NiO₂⁻ is determined as the X̃²Π_g state. The valence orbitals of NiO₂ are composed of the Ni 4s and 3d orbitals and the O 2s and 2p orbitals, as shown in Fig. 3. The corresponding orbital compositions are summarized in Table 5. The Ni 3d_xz and 3d_yz orbitals together with the O 2p_x and 2p_y orbitals form the 1π_g bonding orbitals and the 2π_g anti-bonding orbitals. The Ni 3d_x²−y² and 3d_xy orbitals do not mix with oxygen valence orbitals and form the non-bonding 1δ_g orbitals. The 2σ_g⁺ orbitals consist of contributions from the Ni orbitals and the O 2s and 2p_z orbitals. The 1σ_g⁺ orbitals are mainly composed of the O 2s and 2p_z orbitals with a small contribution from the Ni 4s orbitals. The ground state of NiO₂ takes a closed-shell configuration (1σ_g⁺)²(1σ_u⁺)²(2σ_g⁺)²(1δ_g)⁴(3σ_g⁺)²(2σ_u⁺)²(1π_u)⁴(1π_g)⁴(2π_g)⁰, with the anti-bonding 2π_g orbitals left unoccupied. Since the 1σ_g⁺, 2σ_g⁺, 1δ_g, 3σ_g⁺, 1π_g orbitals are fully occupied for all electronic states discussed here, we will use the occupation numbers for the 3σ_g⁺, 2σ_u⁺, 1π_u, and 2π_g orbitals to denote electronic states. In this notation the ground state of NiO₂ is represented as (3σ_g⁺)²(2σ_u⁺)²(1π_u)⁴(2π_g)⁰. The ground X̃²Π_g state of NiO₂⁻ places the excess electron in the 2π_g orbital, which is expected to weaken the Ni–O bond.

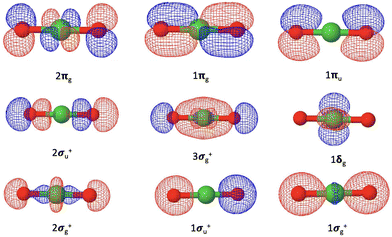Fig. 3 Valence molecular orbitals of NiO₂ originating from the Ni 4s and 3d orbitals and the O 2s and 2p orbitals.

Table 5 The principal compositions of valence molecular orbitals of NiO₂. Significant secondary contributions are enclosed in the brackets

Molecular orbitals	Compositions
1σg^+	O 2s
1σu^+	O 2s
2σg^+	Ni 3dz^2 [O 2s and 2pz]
1δg	Ni 3dx^2−y^2 and 3dxy
3σg^+	O 2s, 2pz [Ni 4s, 3d0]
2σu^+	O 2s, 2pz
1πu	O 2px and 2py
1πg	O 2px and 2py [Ni 3dxz and 3dyz]
2πg	Ni 3dxz and 3dyz [O 2px and 2py]

---

Although the ground state wave function of NiO₂ is dominated by a closed shell (3σ_g⁺)²(2σ_u⁺)²(1π_u)⁴(2π_g)⁰ configuration, this electronic state exhibits strong electron correlation because of the low-lying anti-bonding 2π_g orbitals. An analysis in the ESI† shows that CCSD(T) calculations provide reasonably accurate structure and frequencies, in spite of the slow convergence of the CC series. The CCSD(T) results perhaps slightly overestimate the vibrational frequency of the bending mode ω₂ and underestimate those of the antisymmetric stretching and symmetric stretching modes (ω₃ and ω₁). The ground state of NiO₂⁻ is dominated by the (3σ_g⁺)² (2σ_u⁺)² (1π_u)⁴ (2π_g)¹ configuration. As discussed in the ESI,† the CCSD(T) results are also reasonably accurate for this electronic state.

We have summarized the adiabatic electron affinity, equilibrium structures, and harmonic frequencies computed at the SFX2C-1e-CCSD(T)/aug-cc-pVTZ level of theory in Table 6 and have utilized these parameters in the FC simulations presented in Fig. 1. As expected, the occupation of an anti-bonding 2π_g orbital in NiO₂⁻ significantly increases the Ni–O bond length, e.g., the difference between the Ni–O bond lengths in NiO₂ and NiO₂⁻ computed at the CCSD(T) level amounts to 0.034 Å. The population of this orbital also reduces the asymmetric stretching frequency of NiO₂⁻ by around 70 cm⁻¹. The large change in the Ni–O bond length leads to a significant FC progression for the photodetachment transitions from the X̃²Π_g state of NiO₂⁻ to the X̃¹Σ_g⁺ of NiO₂ due to the FC activity of the symmetric stretch ω₁ (σ_g) mode, which is responsible for much of the vibrational structure observed in the photoelectron spectrum of NiO₂⁻.

Table 6 Computed adiabatic electron affinity (EA_a), bond lengths, and harmonic vibrational frequencies for the X¹Σ_g⁺ state of NiO₂ and the X̃²Π_g state of NiO₂⁻. Scalar-relativistic effects have been taken into account using the SFX2C-1e scheme. The aug-cc-pVTZ basis sets recontracted for the SFX2C-1e scheme have been used. Reported values are in cm⁻¹ except for bond length, which is reported in Å

	R(Ni–O)	ω 1 (σg)	ω 2 (πu)	ω 3 (σu)	EAa
NiO2	1.609	774	135	985	24 523
NiO2^−	1.643	772	96	915	—

---

Excitation of a 3σ_g⁺, 1π_u or 2σ_u electron into an anti-bonding 2π_g orbital gives rise to several low-lying excited states of NiO₂. The lowest excited state of NiO₂ is a ³Π_g state with the leading configuration (3σ_g⁺)¹(2σ_u⁺)²(1π_u)⁴(2π_g)¹, which resides 0.56 eV above the ground X̃¹Σ_g⁺ state. The corresponding singlet ¹Π_g state lies 0.88 eV above the ground state. Both states can be accessed from the ground X̃²Π_g state of NiO₂⁻ by detaching a 3σ_g⁺ electron. Meanwhile, the detachment of a 1π_u electron or a 2σ_u electron leads to a manifold of (3σ_g⁺)²(2σ_u⁺)²(1π_u)³(2π_g)¹ states and a manifold of (3σ_g⁺)²(2σ_u⁺)¹(1π_u)⁴(2π_g)¹ states lying around 1.1 eV and 2 eV above the ground state, respectively. These findings are in good agreement with the MRCI calculations of Hübner,²² and are outlined in Table S2 (ESI†). Details about the EOM-CC computations for excitation energies are documented in the ESI.†

IV.B Ground state Franck–Condon allowed transitions

Table 1 lists the vibrational assignments of features arising from the X̃¹Σ_g⁺ ← X̃²Π_g transition. These assignments are informed by the results of our FC simulations as well as the previously reported photoelectron spectrum of Ramond et al.¹¹ As features A1–13 are largely reproduced in the simulated spectra, they are assigned to Franck–Condon allowed transitions within the X̃¹Σ_g⁺ ← X̃²Π_g photodetachment band of NiO₂. FC-allowed transitions include all Δv transitions in totally symmetric vibrational modes (σ_g for linear species) and even Δv transitions along non-totally symmetric modes.⁶³

Most prominent among these features is A1, here assigned as the 0⁰₀ vibrational origin, allowing for the extraction of a refined electron affinity for NiO₂ and providing an order of magnitude improvement in the precision of this measurement of 3.0464(7) eV, compared to 3.043(5) eV in ref. 11. The measured EA here is in good agreement with our calculated value of 3.0405 eV.

Beyond the vibrational origin is a wealth of vibrational structure, owing to an extended progression in the v₁ symmetric stretch of NiO₂, where there 1¹₀, 1²₀, 1³₀, 1⁴₀, and 1⁵₀ transitions are observed (A4, A7, A10, A12, A13, respectively). Weak but allowed transitions involving the non-totally symmetric v₂ bending and v₃ anti-symmetric stretching modes contribute to the remainder of the A-features in this band, with a short progression in the v₂ bending coordinate (2²₀ and 2⁴₀, corresponding to A2 and A3, respectively), the appearance of the FC-allowed 3²₀ transition (A9), and several combination bands including A5, A6, and A8 (see Table 1).

From the harmonic progressions along v₁ and v₂ and the appearance of the 3²₀ transition, we obtain the frequencies of all three vibrational modes of the X̃¹Σ_g⁺ state of NiO₂. These values, v₁ = 745(6), v₂ = 122(18), and v₃ = 978(16) cm⁻¹, are in good agreement with those previously reported from photoelectron spectroscopy (v₁ = 745(30) cm⁻¹)¹¹ and FTIR studies of NiO₂ in a Ne matrix (v₁ = 749 and v₃ = 977.5 cm⁻¹),¹² as well as our calculated values (Table 6) of v₁ = 774, v₂ = 135, and v₃ = 985 cm⁻¹. Further, the observed frequency for the v₂ bending mode matches well with an observed but unassigned feature in the Ne matrix data at 129.9 cm⁻¹,⁹ suggesting that this peak was from IR excitation of the v₂ mode.

IV.C Ground state Franck–Condon forbidden transitions

We now consider the assignments to the features in the X̃¹Σ_g⁺ ← X̃²Π_g band that are not reproduced by our FC simulations, peaks B1–B17 (Table 1). The spacing of these features is consistently ∼120 cm⁻¹ above that of an allowed transition (as is the case for B1–B9, B13, B17) or ∼240 cm⁻¹ above another “B” feature (as is the case for B9 → B11, B10 → B12, B12 → B14, B13 → B15, B14 → B16). The similarity of these spacings with that of our measured value for the v₂ bending frequency (122(18) cm⁻¹) suggests these features arise from transitions terminating in odd quanta of the non-totally symmetric v₂ mode. We thus assign peaks B1–B17 to transitions of this type to neutral levels with π_u vibrational symmetry.

These transitions are Franck–Condon forbidden but can arise through Herzberg-Teller (HT) coupling to an excited electronic state with the appropriate symmetry.^29,64–66 Briefly, two vibronic states, a and b, can mix through HT-coupling provided their electronic and vibrational symmetries Γ_elec and Γ_vib, respectively, satisfy⁶³

Γ^a_elec ⊗ Γ^a_vib ⊗ Γ^b_elec ⊗ Γ^b_vib ⊃ Γ_TS (1)

Here Γ_TS is the totally symmetric representation within the molecular point group. This mixing then creates two new states |a₀〉 = c_1a|a〉 + c_2a|b〉 and |b₀〉 = c_1b|a〉 + c_2b|b〉, each an admixture of the two zero-order vibronic levels. Thus, if detachment to state b is FC-allowed, then detachment to state a₀ becomes allowed, but will display the electronic character of state b.

In the present case, the electronic and vibrational symmetries of the final states in features B1–B17, Γ^a_elec and Γ^a_vib, are Σ_g⁺ and π_u, respectively. These states can only be observed if they mix with a state b that is FC-allowed for detachment from the anion, i.e. Γ^b_vib = σ_g, thereby requiring that the excited electronic state HT-coupled to this state be of Π_u symmetry. Our calculations (Table S2, ESI†) find that such an excited state resides 2.24 eV above the neutral ground state.

The presence of vibronic coupling here is affirmed by the differing behavior of the FC-forbidden and FC-allowed features as the photon energy is changed, as shown in Fig. 2. Here, cryo-SEVI spectra are plotted at three photon energies, showing that as the photon energy is lowered and approaches the detachment threshold, the intensity of features A1 and A2 drops precipitously relative to that of B1 and B3. This effect is ascribed to a reduced photodetachment cross section for feature A1 and A3 at low eKE. Such a difference can be related to the relative scaling of the detachment cross sections at low eKE's, given by the Wigner threshold law:⁶⁷

σ ∝ (eKE)^l+1/2, (2)

where σ is the detachment cross section and l is the angular momentum of the detached electron. Thus, photodetachment is suppressed more strongly at low eKE for detachment of higher l electrons (see inset of Fig. 2), due to the centrifugal barrier experienced by the departing electron.

For detachment to the X̃¹Σ_g⁺ state of NiO₂, selection rules for molecular photodetachment prohibit detachment of l = 0 electrons, and p-wave detachment dominates.⁶⁸ Conversely, transitions terminating in odd quanta along the v₂ normal coordinate do so in a neutral level with a contribution from an excited state of Π_u symmetry, for which detachment can proceed via l = 0 (s-wave) transitions.

The disparity in near-threshold cross-section between the “A” and “B” features is a tell-tale sign of HT coupling in cryo-SEVI spectra,^29,64–66 as this indicates that “B” features correspond to detachment with lower values of l than the “A” features, reflecting the electronic character of the Π_u electronic state that lends intensity to these transitions. Consequently, spectra for the “B” peaks can be obtained closer to photodetachment threshold, where cryo-SEVI resolution is improved, leading to narrower features as was observed in the cryo-SEVI spectra of the indenyl and nitrate anions.^66,69 As such, we are able to refine our determined value for the v₂ bending mode of NiO₂ from the position of B1 as 120(7) cm⁻¹.

IV.D Excited state transitions

Beyond the strongest vibrational transitions in the X̃¹Σ_g⁺ manifold reside the strong features C1 and D1. The positions of these features (3.4447(4) and 3.7886(9) eV, respectively) coincide with the previously observed onset of transitions assigned to the ã¹Δ_g and b̃¹Σ_g⁺ states (3.45(2) and 3.82(3) eV, respectively) of NiO₂ based on a molecular orbital picture.¹⁰ Subsequent theoretical work, however, has determined the low-lying states of NiO₂ as the ã³Π_g and ùΠ_g states.²² These assignments agree with our EOM-CC calculations, which find the same state ordering. We thus assign C1 and D1 as the vibrational origins of the ã³Π_g ← X̃²Π_g and ùΠ_g ← X̃²Π_g transitions, with term energies of 0.3982(7) and 0.7422(10) eV, respectively, determined by the shift in peak location from A1. These reported term energies are more precise than those previously reported (0.40(2) and 0.77(3) eV, respectively),¹⁰ and are in good agreement with our computed term energies of 0.56 and 0.88 eV, validating this reassignment.

Numerous weaker features reside beyond peaks C1 and D1 (C2–C8, D2–D6) that report on the vibrational structure of the ã³Π_g and ùΠ_g excited states (Tables 2 and 3). In the ã³Π_g state, there appears to be a progression of a vibrational feature with a frequency of 685(11) cm⁻¹ as well as the appearance of the vibrational fundamental and combination bands involving a mode with frequency of 130(5) cm⁻¹. Similarly, in the ùΠ_g state, there appear to be two progressions in features with average spacings of 112(12) and 705(19) cm⁻¹. While we do not have theoretical calculations to make definitive assignments to these features, their relative spacing are close to those of the v₁ and v₂ vibrational modes that dominate the structure in the ground state of spectrum NiO₂. We thus tentatively assign the observed structure to activity along the v₁ and v₂ vibrational modes of NiO₂ in the ã³Π_g and ùΠ_g excited states with vibrational frequencies of 685(11) and 130(5) cm⁻¹ (ã³Π_g) as well as 705(19) and 112(12) cm⁻¹ (ùΠ_g), respectively (outlined in Table 4).

Conclusion

Here, we report high-resolution cryo-SEVI spectra of NiO₂⁻ showing photodetachment to the X̃¹Σ_g⁺, ã³Π_g, and ùΠ_g states of NiO₂. In the ground state, we observe FC-allowed transitions involving the v₁ symmetric stretch, v₂ bending, and v₃ anti-symmetric stretch from which we extract vibrational frequencies of v₁ = 745(6), v₂ = 122(18), and v₃ = 978(16) cm⁻¹, in good agreement with previously reported values. These assignments are facilitated by FC simulations using the SFX2C-1e-CCSD(T)/aug-cc-pVTZ geometries and vibrational frequencies for NiO₂^0/−. Notably, we observe extended FC-forbidden progressions to final states with odd quanta in the v₂ bending coordinate that we ascribe to vibronic coupling to the Π_u excited state of NiO₂, calculated to reside 2.24 eV above the ground state. From the onset of structure in the ground and excited states, we are able to refine the electron affinity and term energies of NiO₂ and its first two excited states (EA = 3.0464(7) eV, T_e(ã³Π_g) = 0.3982(7) eV, T_e(ùΠ_g) = 0.7422(10) eV), in good agreement with our calculated values.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research conducted at UC Berkeley is funded by the Air Force Office of Scientific Research under Grant No. FA9550-19-1-0051 and the work done at Johns Hopkins University is supported by Department of Energy Early Career Research Program under Award Number DE-SC0020317. M. C. B. thanks the Army Research Office for a National Defense Science and Engineering Graduate fellowship. J. A. L. thanks the Alexander von Humboldt Foundation for a Feodor Lynen Research Fellowship.

References

1. N. A. K. Aramouni, J. G. Touma, B. Abu Tarboush, J. Zeaiter and M. N. Ahmad, Renewable Sustainable Energy Rev., 2018, 82, 2570–2585.
2. C. Alvarez-Galvan, M. Melian, L. Ruiz-Matas, J. L. Eslava, R. M. Navarro, M. Ahmadi, B. Roldan Cuenya and J. L. G. Fierro, Front. Chem., 2019, 7, 104.
3. E. Heracleous, A. F. Lee, K. Wilson and A. A. Lemonidou, J. Catal., 2005, 231, 159–171.
4. Y. L. Zhou, F. F. Wei, J. Lin, L. Li, X. Y. Li, H. F. Qi, X. L. Pan, X. Y. Liu, C. D. Huang, S. Lin and X. D. Wang, ACS Catal., 2020, 10, 7619–7629.
5. S. Dey, G. C. Dhal, D. Mohan and R. Prasad, Adv. Compos. Hybrid Mater., 2019, 2, 626–656.
6. A. W. Castleman, Catal. Lett., 2011, 141, 1243–1253.
7. J. L. Mason, C. N. Folluo and C. C. Jarrold, J. Chem. Phys., 2021, 154, 200901.
8. H. Huber and G. A. Ozin, Can J. Chem., 1972, 50, 3746–3747.
9. A. Citra, G. V. Chertihin, L. Andrews and M. Neurock, J. Phys. Chem. A, 1997, 101, 3109–3118.
10. H. B. Wu and L. S. Wang, J. Chem. Phys., 1997, 107, 16–21.
11. T. M. Ramond, G. E. Davico, F. Hellberg, F. Svedberg, P. Salen, P. Soderqvist and W. C. Lineberger, J. Mol. Spectrosc., 2002, 216, 1–14.
12. F. Allouti, L. Manceron and M. E. Alikhani, Phys. Chem. Chem. Phys., 2006, 8, 448–455.
13. W. D. Vann, R. L. Wagner and A. W. Castleman, J. Phys. Chem. A, 1998, 102, 1708–1718.
14. M. C. Oliveira, J. Marcalo, M. C. Vieira and M. A. A. Ferreira, Int. J. Mass Spectrom., 1999, 185, 825–835.
15. J. U. Reveles, G. E. Johnson, S. N. Khanna and A. W. Castleman, J. Phys. Chem. C, 2010, 114, 5438–5446.
16. C. Salvitti, M. Rosi, F. Pepi, A. Troiani and G. de Petris, Chem. Phys. Lett., 2021, 776, 138555.
17. M. R. A. Blomberg, E. M. Siegbahn and A. Strich, Chem. Phys., 1985, 97, 287–301.
18. C. W. Bauschlicher, J. Phys. Chem. A, 2004, 108, 2871–2873.
19. K. Deng, J. L. Yang and Q. S. Zhu, J. Chem. Phys., 2003, 118, 6868–6873.
20. G. L. Gutsev, B. K. Rao and P. Jena, J. Phys. Chem. A, 2000, 104, 11961–11971.
21. E. L. Uzunova, H. Mikosch and G. S. Nikolov, J. Chem. Phys., 2008, 128, 094307.
22. O. Hubner and H. J. Himmel, J. Phys. Chem. A, 2012, 116, 9181–9188.
23. D. M. Neumark, J. Phys. Chem. A, 2008, 112, 13287–13301.
24. M. L. Weichman and D. M. Neumark, Annu. Rev. Phys. Chem., 2018, 69, 101–124.
25. A. Osterwalder, M. J. Nee, J. Zhou and D. M. Neumark, J. Chem. Phys., 2004, 121, 6317–6322.
26. C. Hock, J. B. Kim, M. L. Weichman, T. I. Yacovitch and D. M. Neumark, J. Chem. Phys., 2012, 137, 244201.
27. U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, J. Chem. Phys., 2000, 112, 8068–8071.
28. J. B. Kim, C. Hock, T. I. Yacovitch and D. M. Neumark, J. Phys. Chem. A, 2013, 117, 8126–8131.
29. J. A. DeVine, M. L. Weichman, B. Laws, J. Chang, M. C. Babin, G. Balerdi, C. J. Xie, C. L. Malbon, W. C. Lineberger, D. R. Yarkony, R. W. Field, S. T. Gibson, J. Y. Ma, H. Guo and D. M. Neumark, Science, 2017, 358, 336–339.
30. M. C. Babin, J. A. DeVine, M. L. Weichman and D. M. Neumark, J. Chem. Phys., 2018, 149, 174306.
31. W. C. Wiley and I. H. Mclaren, Rev. Sci. Instrum., 1955, 26, 1150–1157.
32. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
33. D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447.
34. M. B. Doyle, C. Abeyasera and A. G. Suits, NuACQ, http://faculty.missouri.edu/suitsa/NuAqc.html.
35. E. W. Hansen and P. L. Law, J. Opt. Soc. Am. A, 1985, 2, 510–520.
36. C. Blondel, C. Delsart and F. Goldfarb, J. Phys. B: At. Mol. Phys., 2001, 34, L281–L288.
37. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
38. K. G. Dyall, J. Chem. Phys., 2001, 115, 9136–9143.
39. W. J. Liu and D. L. Peng, J. Chem. Phys., 2009, 131, 031104.
40. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
41. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
42. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
43. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
44. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041–7050.
45. G. E. Scuseria and H. F. Schaefer, Chem. Phys. Lett., 1988, 152, 382–386.
46. S. A. Kucharski and R. J. Bartlett, Theor. Chim. Acta, 1991, 80, 387–405.
47. N. Oliphant and L. Adamowicz, J. Chem. Phys., 1991, 95, 6645–6651.
48. J. Gauss, J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1991, 95, 2623–2638.
49. J. F. Stanton, J. Gauss, J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1991, 94, 4334–4345.
50. J. D. Watts, J. Gauss and R. J. Bartlett, Chem. Phys. Lett., 1992, 200, 1–7.
51. L. Cheng and J. Gauss, J. Chem. Phys., 2011, 135, 084114.
52. D. A. Matthews and J. F. Stanton, J. Chem. Phys., 2015, 142, 064108.
53. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T. C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108.
54. D. A. Matthews, J. Chem. Theory Comput., 2020, 16, 6195–6206.
55. J. G. J. F. Stanton, L. Cheng, M. E. Harding, D. A. Matthews, P. G. Szalay, CFOUR, coupled-cluster techniques for computational chemistry, a quantum-chemical program package, with contributions from, A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, S. Blaschke, Y. J. Bomble, S. Burger, O. Christiansen, D. Datta, F. Engel, R. Faber, J. Greiner, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, G. M. Kopper, W. J. Lauderdale, F. Lipparini, T. Metzroth, L. A. Mück, T. Nottoli, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen) and ECP routines by, A. V. Mitin and C. van Wüllen, For the current version, see (http://www.cfour.de).
56. S. M. Rabidoux, V. Eijkhout and J. F. Stanton, J. Chem. Theory Comput., 2016, 12, 728–739.
57. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
58. K. Kowalski and P. Piecuch, J. Chem. Phys., 2001, 115, 643–651.
59. S. A. Kucharski, M. Wloch, M. Musial and R. J. Bartlett, J. Chem. Phys., 2001, 115, 8263–8266.
60. M. Kallay and P. R. Surjan, J. Chem. Phys., 2001, 115, 2945–2954.
61. M. Kallay and J. Gauss, J. Chem. Phys., 2004, 121, 9257–9269.
62. M. Kallay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csoka, P. B. Szabo, L. Gyevi-Nagy, B. Hegely, I. Ladjanszki, L. Szegedy, B. Ladoczki, K. Petrov, M. Farkas, P. D. Mezei and A. Ganyecz, J. Chem. Phys., 2020, 152, 074107.
63. G. Herzberg, Electronic spectra and electronic structure of polyatomic molecules, Van Nostrand Reinhold Company, Princeton, NJ, 1966.
64. J. A. DeVine, A. Abou Taka, M. C. Babin, M. L. Weichman, H. P. Hratchian and D. M. Neumark, J. Chem. Phys., 2018, 148, 222810.
65. M. L. Weichman, L. Cheng, J. B. Kim, J. F. Stanton and D. M. Neumark, J. Chem. Phys., 2017, 146, 224309.
66. M. C. Babin, J. A. DeVine, M. DeWitt, J. F. Stanton and D. M. Neumark, J. Phys. Chem. Lett., 2020, 11, 395–400.
67. E. P. Wigner, Phys. Rev., 1948, 73, 1002–1009.
68. K. J. Reed, A. H. Zimmerman, H. C. Andersen and J. I. Brauman, J. Chem. Phys., 1976, 64, 1368–1375.
69. J. B. Kim, M. L. Weichman, T. I. Yacovitch, C. Shih and D. M. Neumark, J. Chem. Phys., 2013, 139, 104301.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02396b

‡ Current address: Department of Chemistry and Chemical Biology, Harvard University, 12 Oxford St, Cambridge, MA 02138, USA.

§ Current address: Department of Chemistry, Princeton University, Princeton, New Jersey 08544, USA.

¶ Current address: KLA Corporation, 1 Technology Dr, Milpitas, CA 95035.

---