Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of crystallite size on the structure and magnetism of ferrihydrite†
Xiaoming
Wang
ab,
Mengqiang
Zhu
b,
Luuk K.
Koopal
c,
Wei
Li
d,
Wenqian
Xu
e,
Fan
Liu
a,
Jing
Zhang
f,
Qingsong
Liu
gh,
Xionghan
Feng
*a and
Donald L.
Sparks
i
aKey Laboratory of Arable Land Conservation (Middle and Lower Reaches of Yangtse River), Ministry of Agriculture, College of Resources and Environment, Huazhong Agricultural University, Wuhan 430070, China. E-mail: fxh73@mail.hzau.edu.cn; Fax: +86 27 87288618; Tel: +86 27 87280271
bDepartment of Ecosystem Science and Management, University of Wyoming, Laramie, WY 82071, USA
cPhysical Chemistry and Soft Matter, Wageningen University, Dreijenplein 6, 6703 HB Wageningen, Netherlands
dKey Laboratory of Surficial Geochemistry, Ministry of Education, School of Earth Sciences and Engineering, Nanjing University, Nanjing 210093, China
eDepartment of Chemistry, Brookhaven National Lab, Upton, New York 11973, USA
fBeijing Synchrotron Radiation Facility, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100039, China
gState Key Laboratory of Lithospheric Evolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
hFunction Laboratory for Marine Geology, National Oceanography Laboratory, Qingdao 266061, China
iEnvironmental Soil Chemistry Group, Delaware Environmental Institute and Department of Plant and Soil Sciences, University of Delaware, Newark, Delaware 19716, USA
First published on 15th December 2015
Abstract
The structure and magnetic properties of nano-sized (1.6 to 4.4 nm) ferrihydrite samples are systematically investigated through a combination of X-ray diffraction (XRD), X-ray pair distribution function (PDF), X-ray absorption spectroscopy (XAS) and magnetic analyses. The XRD, PDF and Fe K-edge XAS data of the ferrihydrite samples are all fitted well with the Michel ferrihydrite model, indicating similar local-, medium- and long-range ordered structures. PDF and XAS fitting results indicate that, with increasing crystallite size, the average coordination numbers of Fe–Fe and the unit cell parameter c increase, while Fe2 and Fe3 vacancies and the unit cell parameter a decrease. Mössbauer results indicate that the surface layer is relatively disordered, which might have been caused by the random distribution of Fe vacancies. These results support Hiemstra's surface-depletion model in terms of the location of disorder and the variations of Fe2 and Fe3 occupancies with size. Magnetic data indicate that the ferrihydrite samples show antiferromagnetism superimposed with a ferromagnetic-like moment at lower temperatures (100 K and 10 K), but ferrihydrite is paramagnetic at room temperature. In addition, both the magnetization and coercivity decrease with increasing ferrihydrite crystallite size due to strong surface effects in fine-grained ferrihydrites. Smaller ferrihydrite samples show less magnetic hyperfine splitting and a lower unblocking temperature (TB) than larger samples. The dependence of magnetic properties on grain size for nano-sized ferrihydrite provides a practical way to determine the crystallite size of ferrihydrite quantitatively in natural environments or artificial systems.
Nano impactDespite numerous studies, the surface structure and magnetism of ferrihydrite are still not clearly understood. In this study, ferrihydrite samples with different crystallite sizes were found to share similar short-, medium- and long-range structures, but with decreasing size, the Fe–Fe coordination numbers decreased and the surface layer disorder increased. An investigation of the magnetization indicated that magnetization decreases with increasing size. Smaller samples exhibit lower magnetic-order temperature and unblocking temperatures. In contrast, for ordered, relatively large ferrihydrites, magnetic enhancement with size was found. It is therefore predicted that the change in magnetization with size likely has a minimum. The present structure and magnetization results significantly contribute to the understanding of the ferrihydrite structure, its surface reactivity and its magnetic behavior in the environment. |
Introduction
Metastable nano-crystalline ferrihydrites are ubiquitous in environmental systems including surface water, soils, sediments, living organisms and even extraterrestrial substances.1 Ferrihydrite serves as the most important precursor for other crystalline iron (oxyhydr)oxides (i.e., hematite and goethite) produced in the natural environment during weathering or pedogenic processes.2–5 Among natural iron oxides, ferrihydrite has the smallest particle size, generally ranging from 1 to 7 nm,6–8 which leads to ferrihydrite having a strong cementing capacity, large surface area and high reactivity.6 Therefore, it plays an important role in the formation of soil aggregates and the mobility and bioavailability of contaminants and nutrients1,9–11 and has been widely applied in the degradation of organic contaminants12 and removal of inorganic pollutants, such as phosphate,13 arsenic(III),14 and heavy metals.15Based on the number of peaks resolved from powder X-ray diffraction (XRD) patterns, two types of ferrihydrite are commonly distinguished, namely two-line ferrihydrite (2LFh) and six-line ferrihydrite (6LFh).2 They differ mainly in their crystallite size and degree of structural disorder.16 Most 2LFh particles have a crystallite size of ∼2 nm and a highly defected and water-rich structure.17,18 The largest synthesized ferrihydrite particles (10–12 nm) are ordered ferrimagnetic ferrihydrite (ferrifh) particles formed by the hydrothermal aging of 2LFh at 175 °C in the presence of citrate.18 Ferrifh has an ordered, largely defect-free structure with fewer cation vacancies and less lattice strain than 2LFh.18 For particles larger than 8 nm, the ferrihydrite thermodynamic stability sharply drops with increasing particle size, leading to the formation of nano-goethite and nano-hematite.19,20
Due to the poorly crystalline nature of ferrihydrite, its structure has still not been fully resolved, especially its surface structure and the origin of the disorder. An early structural model by Drits et al.16 suggested that ferrihydrite is a multiphase material. More recently, based on X-ray pair distribution function (PDF) analysis, Michel et al.18,21 proposed a single-phase model for ferrihydrite with a basic structure related to the Baker–Figgis δ-Keggin cluster22 consisting of 13 iron atoms and 40 oxygen atoms,21 which was most recently evidenced by Sadeghi et al.23 According to Michel et al.,21 the ideal structure of ferrihydrite consists of three types of Fe sites (Fe1, Fe2 and Fe3). Fe1 and Fe2 (60% and 20% of the total Fe sites, respectively) are octahedrally coordinated, while Fe3 (20%) is tetrahedrally coordinated. However, the Michel model is controversial in relation to the valence bond theory, and the calculated composition disagrees with some experimental data.24 Furthermore, the model data cannot correctly reproduce all the XRD peaks of 6LFh,25,26 while the XRD data of ferrifh can be fitted well with the Michel model.18 Most recently, Hiemstra17 proposed a modified Michel model in which the ferrihydrite consists of a defect-free mineral core and a defect- and water-rich surface layer that is depleted in the Fe2 and Fe3 polyhedra. Hence, all disorder is projected in the surface layer. According to this model, dehydration alters only the ferrihydrite surface layers without changing the structure of the mineral core, which is in good agreement with the experimental observation by Xu et al.27 that 2LFh was largely dehydrated to ordered ferrihydrite without significant changes in the mineral structure.
For iron oxide nanoparticles, several size-dependent physicochemical properties have been reported for ferrihydrite,13,17,18 as well as for hematite and goethite.6,19,28,29 In general, the complex nature of the magnetism of iron oxide nanoparticles is well studied.30 However, the effects of the crystallite size of ferrihydrite on its magnetic properties are not fully explored. It has been reported that both 2LFh31 and 6LFh32 display antiferromagnetism as well as weak ferromagnetic-like behavior at low temperature and superparamagnetic behavior, with a low-temperature transition between blocked and unblocked magnetic states. Upon aging of phosphated ferrihydrite (2LFh),3 a maghemite-like phase (ferrimagnetic) named “hydromaghemite” is obtained as an intermediate product, while no ferrimagnetic phases appear upon aging of 6LFh with adsorbed phosphate.33 As mentioned above, aging 2LFh in the presence of citrate leads to the formation of large crystallites of ordered ferrimagnetic ferrihydrites (ferrifh) as a metastable intermediate product.18 Furthermore, the incorporation of foreign elements into ferrihydrite may change its magnetic properties; for instance, upon incorporating Si, the magnetic-ordering temperature decreases with increasing Si content in ferrihydrite.34,35
To extend our knowledge of the dependence of the magnetic properties of ferrihydrites on their crystallite sizes and structure, the magnetic properties of four extremely fine-grained (∼1–5 nm) ferrihydrite samples have been investigated in the present study. The key factor for such small particles is the large contribution of the surface layer to the particle behavior. Therefore, the surface layer effects will be most clearly revealed with such particles, and the results should be well suited for elucidating whether and how surface layer defects affect the magnetic properties. Alternatively, magnetization results may provide information on the surface layer structure and assist in resolving the structure dispute. To achieve our goal, the structure of the four ferrihydrite samples was characterized in detail first by using XRD, the PDF derived from high-energy X-ray total scattering data, and Fe K-edge X-ray absorption spectroscopy (XAS). In principle, the structure of the particles has been analyzed on the basis of the structural model of Michel et al.21 Subsequently, the magnetic properties of ultra-fine nanoparticles were examined through magnetic susceptibility measurements and Mössbauer spectroscopy. Special attention has been paid to signals that point to surface layer defects and a structure that may correspond to Hiemstra's model.17 The magnetization results are discussed in relation to the structural information.
Materials and methods
Ferrihydrite synthesis
Four ferrihydrite samples with different crystallite sizes were synthesized by changing the hydrolysis rate of Fe3+ by using different temperatures and procedures.2,36 The detailed synthesis procedures have been described by Wang et al.13 and the samples were labeled as 2LFh_1, 5LFh_2, 5LFh_3 and 6LFh_4, in which the first number indicates the number of diffraction lines in the XRD pattern, while the last number indicates the increasing order of crystallite size.13Structural characterization of ferrihydrite samples
The program PDFgui was used to fit the data of G(r) functions to obtain the structural parameters.40 The starting model was based on the published structure for ferrihydrite (ICSD #158475).21 For all fits, the following parameters were varied during each refinement process: scale factor, vibrational correlation terms (δ2), unit cell parameters (a and c), most atomic positions except for few special locations, isotropic displacement parameters (U11, U22 and U33), the occupancies of Fe sites (the occupancies of Fe2 and Fe3 were set the same because of their correlation) and the two resolution parameters, i.e., damping (Qdamp) and broadening (Qbroad) factors. In addition, the coherent scattering domain (CSD) sizes of the ferrihydrite samples were fixed at the values obtained from the XRD fitting by assuming spherical particles.21Rw values, calculated between rmin = 1 Å and rmax = 20 Å, represent the goodness-of-fit of the ferrihydrite samples.
Magnetic characterization of ferrihydrite samples
Results
Structure of ferrihydrite
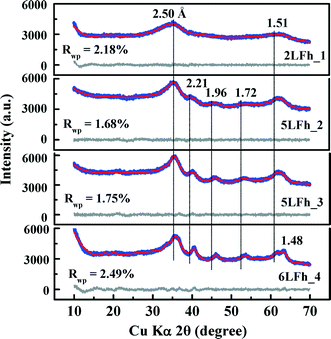
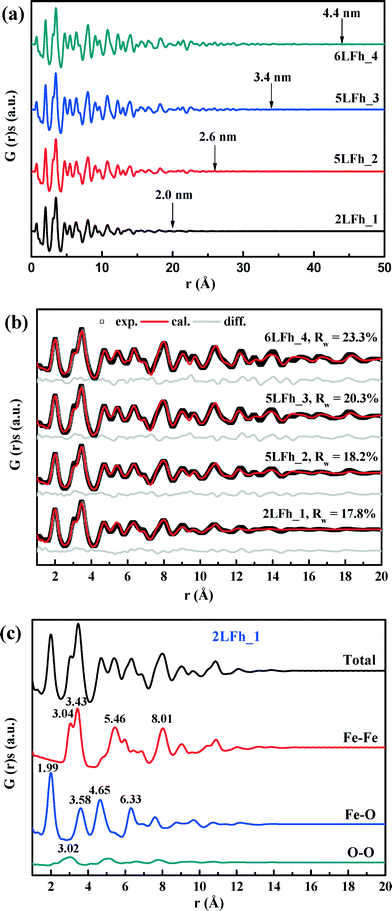
The results of fitting of the XRD data for the studied ferrihydrites (red lines) using the Rietveld method are shown in Fig. 1 and Table SI-1.† Small differences between the observed and fitted patterns (grey lines) indicate that the XRD data can be fitted well with the Michel model,21 implying that the long-range bulk structures of 2LFh_1 to 6LFh_4 are very similar. The excellent fitting indicates that the obtained crystallite sizes are reasonable; they amount to 1.6, 2.6, 3.4 and 4.4 nm respectively for 2LFh_1, 5LFh_2, 5LFh_3 and 6LFh_4, i.e., the crystallite size increases from 2LFh_1 to 6LFh_4. However, the obtained unit cell parameters (Table SI-1†) are likely not entirely realistic, because there was no strict restriction for the atomic positions and other structural factors during fitting with the present method. More reliable values have been obtained by PDF analysis.
A comparison of the G(r) functions between 1 and 20 Å (Fig. 2b) reveals that all ferrihydrite samples share nearly the same atomic arrangement, i.e., they have a similar medium-range structure. To quantify structural variations caused by crystallite size changes, the G(r) functions were modeled against the Michel model.21 The Rw values indicate that the simulated G(r) is in good agreement with the experimental data (Fig. 2b). The results show that (Table 1), with increasing crystallite size, the unit cell parameter a decreases, while the unit cell parameter c and Fe2 and Fe3 site occupancies all increase, broadly consistent with existing reports.18,21 In addition, the deconvolution of the total G(r) in the calculated G(r) of the Fe–O, Fe–Fe and O–O atomic pairs for 2LFh_1 is shown in Fig. 2c. The first three peaks in the G(r) functions correspond to (i) the Fe–O atomic pairs in the FeO6 octahedra with an Fe–O bond length of 1.99 Å, (ii) Fe–Fe pairs between two edge-sharing FeO6 octahedra with an Fe–Fe distance of 3.04 Å and (iii) Fe–Fe pairs between two corner-sharing octahedra and/or tetrahedra with an Fe–Fe distance of 3.43 Å.
| Parameters | Samples | |||
|---|---|---|---|---|
| 2LFh_1 | 5LFh_2 | 5LFh_3 | 6LFh_4 | |
| a and c: unit cell parameters; Fe2 and Fe3 occ.: the occupancy of Fe2 and Fe3 were set equal; Qdamp: damping factor; δ2: vibrational correlation terms; crystallite diameters: the sp-diameters of the ferrihydrite samples were fixed at the values obtained from XRD fitting; Rw values were calculated between rmin = 1 Å and rmax = 20 Å. | ||||
| a (Å) | 6.017(12) | 6.010(11) | 5.991(9) | 5.995(9) |
| c (Å) | 9.074(33) | 9.122(27) | 9.142(23) | 9.227(24) |
| Fe2 and Fe3 (occ.) | 0.825(39) | 0.845(38) | 0.859(34) | 0.882(34) |
| Q damp | 0.077(13) | 0.090(6) | 0.085(5) | 0.083(4) |
| δ 2 | 2.70(36) | 3.06(41) | 2.98(42) | 3.09(45) |
| Scale factor | 1.235 | 1.014 | 1.044 | 0.944 |
| Diameter (Å) | 16 | 26 | 34 | 44 |
| R w (%) | 17.8 | 18.2 | 20.3 | 23.3 |
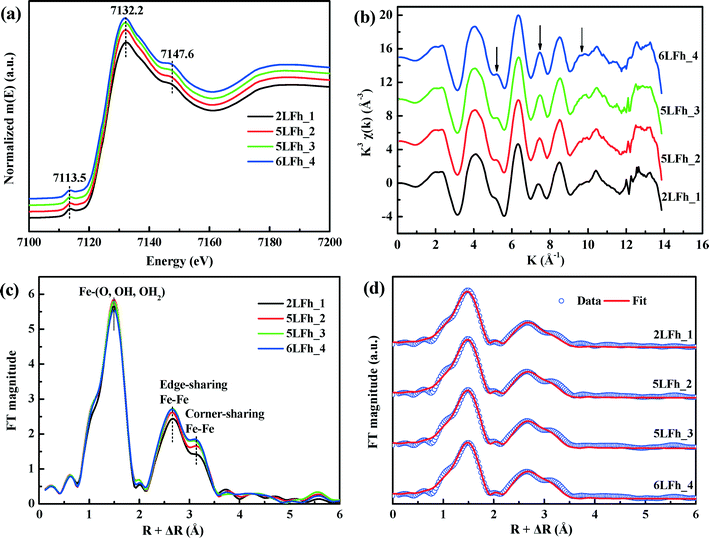
The k space EXAFS spectra of the samples (Fig. 3b) are also similar and consistent with previous reports.42,52 The peak intensities at ∼5, ∼7.5 and ∼9.5 Å (see the arrows) are representative of high-shell backscattering signals;52 they slightly decrease with decreasing crystallite size, suggesting a slightly reduced number of nearest Fe neighbors.
The radial structural functions (RSFs) (i.e., Fourier transform) of the K-edge EXAFS are shown in Fig. 3c. The first large peak corresponds to the first nearest neighbors (O, OH or OH2) of the absorbing Fe atoms, the second shell results from Fe–Fe edge-sharing of FeO6 octahedra, and the third shell can be ascribed to Fe–Fe corner-sharing configurations.52 The similar RSFs of the ferrihydrite samples suggest that they have similar Fe local coordination environments, consistent with the PDF results (Fig. 2). However, the amplitude of the two Fe–Fe coordination peaks gradually decreases with decreasing size, which implies decreasing average coordination numbers (CNs) of neighboring Fe atoms and/or a gradually increasing degree of disorder of Fe–Fe arrangements with decreasing crystallite size.
The EXAFS spectra were fitted by including the Fe–O and Fe–Fe single-scattering paths obtained from the Michel model and the Fe–O–O multiple-scattering (MS) path. The MS path parameters were correlated as described by Mikutta.50 The spectra and the fits are compared in Fig. 3d, and the obtained structural parameters are listed in Table 2. The results indicate that the first-shell Fe–O coordination has an average Fe–O bond length of 1.97 ± 0.01 Å for all samples with the corresponding coordination number (CNFe–O) ranging from 5.20 ± 0.18 to 5.46 ± 0.23, in good agreement with the PDF results (Fig. 2c) and the reported XAS fitting results.50,52,53 The average Fe–Fe1 distance of 3.04 ± 0.01 Å and the Fe–Fe2 distance of 3.43 ± 0.02 Å correspond to, respectively, two edge-sharing FeO6 octahedra and two bent corner-sharing FeO6 octahedra or to corner sharing between an FeO6 octahedron and an FeO4 tetrahedron.27,52 Further, these values are in good agreement with the PDF results (Fig. 2c). With the crystallite size increasing from 2LFh_1 to 6LFh_4, the CNs of Fe–Fe1 and Fe–Fe2 increase from 2.50 ± 0.40 to 2.84 ± 0.50 and from 3.71 ± 0.55 to 4.65 ± 0.68, respectively.
| Samples | Path | R (Å) | CNsb | σ 2 (Å2) | ΔE0d (eV) | R-factore (%) |
|---|---|---|---|---|---|---|
| a Inter-atomic distances. b Coordination numbers. c Debye–Waller factors of Fe–O and Fe–Fe. The Debye–Waller factors of all samples were around 0.011 for Fe–O and 0.015 for Fe–Fe determined from the R-space fit. Then, the Debye–Waller factors of Fe–O and Fe–Fe of all samples were fixed to these values to allow an equal comparison of the other parameters. d ΔE0 is the threshold energy correction. e R-factor indicates the goodness of the fits. | ||||||
| 2LFh_1 | Fe–O | 1.97(1) | 5.20(18) | 0.011 | −3.4(9) | 0.8 |
| Fe–Fe1 | 3.04(1) | 2.50(40) | 0.015 | |||
| Fe–Fe2 | 3.44(1) | 3.71(55) | 0.015 | |||
| 5LFh_2 | Fe–O | 1.97(1) | 5.46(23) | 0.011 | −3.5(10) | 1.1 |
| Fe–Fe1 | 3.04(1) | 2.72(51) | 0.015 | |||
| Fe–Fe2 | 3.43(1) | 4.31(69) | 0.015 | |||
| 5LFh_3 | Fe–O | 1.97(1) | 5.44(23) | 0.011 | −3.6(10) | 1.1 |
| Fe–Fe1 | 3.04(1) | 2.81(49) | 0.015 | |||
| Fe–Fe2 | 3.42(1) | 4.46(66) | 0.015 | |||
| 6LFh_4 | Fe–O | 1.97(1) | 5.29(23) | 0.011 | −3.4(11) | 1.1 |
| Fe–Fe1 | 3.04(1) | 2.84(50) | 0.015 | |||
| Fe–Fe2 | 3.43(1) | 4.65(68) | 0.015 | |||
The general conclusion based on the analysis results of the XRD, PDF and X-ray absorption spectra is that the studied samples possess a common long-, medium- and local-range structure. The ferrihydrite crystallite size has little influence on the average Fe–O, Fe–Fe1 and Fe–Fe2 coordination distances, but the average Fe–Fe CNs increase with increasing size of the ferrihydrite crystallites. The variation of CNs is consistent with classic particle size effects, i.e., smaller particles have less neighboring Fe atoms around each Fe center because the percentages of the surface Fe sites increase with decreasing size, leading to less neighboring Fe. In addition, this also implies a weaker order of Fe–Fe arrangements for smaller ferrihydrites, whereas the location of the disorder could not be revealed. In the next section, it will be shown that the analysis of the Mössbauer spectra at 295 K provides further information.
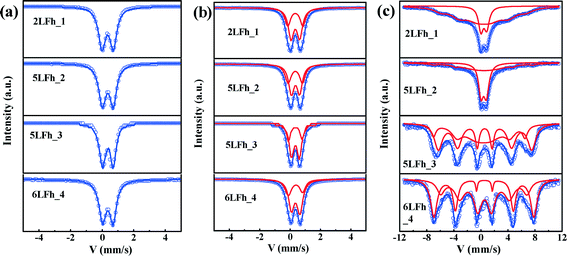
Mössbauer spectra at room temperature
At 295 K, the Mössbauer spectra of all ferrihydrite samples present a paramagnetic doublet (Fig. 4a and b). The first set of average parameters was obtained by fitting the spectra with one doublet (Fig. 4a). The results show (Table 3) that the central shifts (Cs) for samples of different sizes are close to each other and range from 0.343 to 0.360 mm s−1; the quadrupole splittings (Qs) range from 0.717 to 0.625 mm s−1 and show a decreasing trend with increasing crystallite size. These values are consistent with the one-doublet fitting results previously reported.31,54 However, due to the broad doublets and high line widths observed in the present samples, the use of only one doublet is insufficient for good fits; this is also indicated by the high χ2 values (Table 3).| Samples | Fitting modes | Fitting parameters | ||||
|---|---|---|---|---|---|---|
| Reduced χ2 | C s (mm s−1) | Q s (mm s−1) | Site population (%) | |||
| 2LFh_1 | Single doublet | 15.97 | 0.347(1) | 0.717(1) | 100 | |
| Two doublets | Site 1 | 2.67 | 0.343(9) | 0.994(14) | 38.4(32) | |
| Site 2 | 0.347(6) | 0.566(9) | 61.6(32) | |||
| 5LFh_2 | Single doublet | 12.97 | 0.355(1) | 0.684(1) | 100 | |
| Two doublets | Site 1 | 1.95 | 0.342(10) | 0.937(16) | 41.9(37) | |
| Site 2 | 0.357(6) | 0.541(9) | 58.1(36) | |||
| 5LFh_3 | Single doublet | 3.71 | 0.343(1) | 0.625(1) | 100 | |
| Two doublets | Site 1 | 1.11 | 0.334(18) | 0.894(29) | 31.7(73) | |
| Site 2 | 0.346(11) | 0.509(18) | 68.3(73) | |||
| 6LFh_4 | Single doublet | 10.18 | 0.360(1) | 0.664(1) | 100 | |
| Two doublets | Site 1 | 3.66 | 0.350(2) | 0.938(7) | 33.9(78) | |
| Site 2 | 0.367(1) | 0.556(2) | 66.1(78) | |||
Using two doublets provides better fits of the spectra (Table 3) and may allow for a distinction between the core and surface regions of the particles.55–57 The range of Cs values is similar to that for one-doublet fitting and the variation in the Cs values is not correlated with the crystallite size of the ferrihydrites. The Qs values of the ferrihydrite samples obtained with two-doublet fitting slightly decrease (for both sites) with increasing crystallite size. According to Cornell and Schwertmann,2 relatively high Qs values correspond to a high degree of distortion of FeO6 octahedra. Therefore, the present results indicate that the degree of distortion of the FeO6 octahedra increases with decreasing crystallite size, similar to the results of one-doublet fitting. Additionally, the Qs values for doublet 1 are larger than those for doublet 2, implying that doublet 1 belongs to FeO6 octahedra in the surface layer.2
The site populations of doublet 2 (core) are larger than those of doublet 1 (layer), and the difference between them increases with increasing crystallite size, which results from an increasing surface layer contribution with decreasing crystallite size. The site population of doublet 1 is plotted against the crystallite size, wherein a gradually decreasing trend is observed for the site population with crystallite size. The magnitude of the site population of doublet 1 is approximately 40% for 2LFh_1 and 5LFh_2 and approximately 33% for 5LFh_3 and 6LFh_4. These results indicate that the contribution of the surface layer increases with decreasing crystallite size. As the surface layer becomes more disordered (higher Qs) than the core, the disorder will progressively increase with decreasing crystallite size. The combination of this information with the PDF fitting results (a certain amount of Fe vacancies exists in the structure) indicates that the disordered surface structure is derived from the random arrangement of Fe vacancies at or near the surface as well as minor stacking faults. The observation that the disorder of the surface layer increases with decreasing crystallite size is consistent with the variation of Fe vacancies as a function of size, as obtained from the PDF fitting (Table 1). In other words, crystallites with a smaller size have a higher amount of Fe2 and Fe3 vacancies, which leads to a higher degree of disorder in the surface layer. These results support Hiemstra's surface-depletion model,17i.e., the surface layer of ferrihydrite is depleted by Fe2 and Fe3 and smaller ferrihydrites have a higher percentage of poorly coordinated Fe sites in the surface layer.
Magnetic hyperfine splitting at low temperature
At 20 K, the Mössbauer spectra of the ferrihydrite samples show magnetic hyperfine splitting due to the weakness or even disappearance of the relaxation effect caused by their superparamagnetic behavior.51,58,59 The degree of splitting is related to the crystallite size (Fig. 4c and Table SI-2†). The spectra of samples 2LFh_1 and 5LFh_2, which have a relatively small size, split doublet 2 at 295 K into one sextet at 20 K, while samples 5LFh_3 and 6LFh_4, which have a relatively large size, split the two doublets at 295 K into two sextets at 20 K (Fig. 4). Therefore, the ferrihydrite samples have no definite magnetic-ordering temperature, but they order magnetically at varying temperatures, as determined by their crystallite size. This is consistent with the report of Schwertmann et al.,35 who suggested that a ferrihydrite with a smaller crystallite size (formed at a higher Fe3+ hydrolysis rate) had a lower magnetic ordering temperature. In addition, the Mössbauer spectra at room temperature of different-sized BiFeO3 nanoparticles also show a similar trend with size.58 Comparing the Mössbauer spectra of the ferrihydrite samples at 20 K, the intensities of the sextet peaks increase and the spectral line widths significantly decrease with increasing crystallite size; this can be ascribed to the decrease of the superparamagnetic behavior with increasing size. The hyperfine splitting and hyperfine magnetic-field intensity decrease with decreasing crystallite size (Table SI-2†). Below a certain crystallite size, the hyperfine splitting is suppressed. The suppression of the material's intrinsic spin may be caused by uncompensated spins at the surface, strain anisotropies and noncollinear magnetic ordering.58 In the present situation, the quadrupole splitting results indicate that, especially for particles with relatively small crystallite sizes, a large part of the disorder is located in the surface layer; therefore, uncompensated spins in the surface layer will be the main reason for the reduced hyperfine splitting and reduced magnetic-field intensity.Magnetization hysteresis loops and ZFC-FC curves
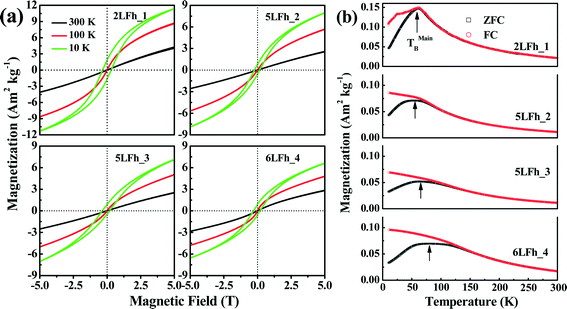
The magnetization curves measured at 10, 100 and 300 K are shown in Fig. 5a. The shape of the magnetization curves depends on both the measurement temperature and crystallite size. Overall, the magnetization curves are nearly linear at 300 K and have a sigmoidal shape at 100 K and 10 K. A clear hysteresis loop is observed only at 10 K and none of the samples are saturated in magnetization at 5 T. The non-saturated linear pattern indicates a paramagnetic component, which is consistent with the Mössbauer results at room temperature, while the sigmoidal pattern suggests the presence of a saturated superparamagnetic component.60At 10 K, the remanent magnetizations for the studied samples range from 0.79 to 1.84 A m2 kg−1, and the coercivities (Bc) are in the range of 0.16 to 0.30 T (Table 4). This indicates that ferrihydrite is paramagnetic at room temperature but is magnetically ordered at very low temperatures, e.g., ferromagnetic-like moment. A similar magnetic behavior has been reported by Guyodo et al.32 for 6LFh samples of different sizes, by Michel et al.18 for ferrifh and by Berquó et al.34 for Si-incorporated ferrihydrites of sizes ranging from 1 to 25 nm.
| Temperatures | 10 K | 100 K | 300 K | |||
|---|---|---|---|---|---|---|
| Parameters | Coercivity (T) | Remanent magnetization (A m2 kg−1) | Magnetization at 5 T (A m2 kg−1) | Magnetization at 5 T (A m2 kg−1) | Magnetization at 5 T (A m2 kg−1) | Unblocking temperature (K) |
| 2LFh_1 | 0.30 | 1.84 | 11.37 | 8.60 | 4.26 | 60 |
| 5LFh_2 | 0.16 | 0.79 | 7.97 | 5.66 | 2.59 | 60 |
| 5LFh_3 | 0.18 | 0.89 | 7.15 | 5.01 | 2.54 | 65 |
| 6LFh_4 | 0.18 | 0.93 | 6.63 | 4.79 | 2.86 | 80 |
The dependence of magnetization at an applied field of 5 T on crystallite size is shown in Fig. 6a. With increasing crystallite size, the magnetization of the ferrihydrite samples decreases. With increasing temperature, the magnetization also decreases (Fig. 6a and Table 4).
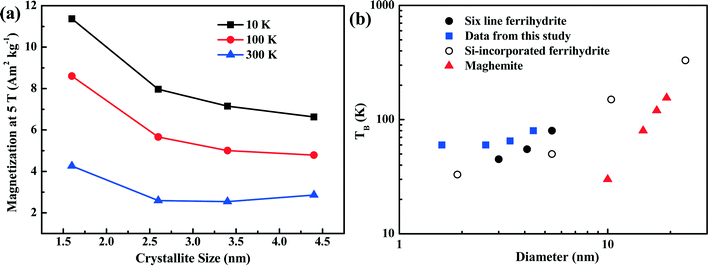 | ||
| Fig. 6 Magnetization characteristics as a function of crystallite size. Panel (a) shows the magnetization of the four ferrihydrites for an applied field of 5 T and at three temperatures. Panel (b) shows the unblocking temperature (TB) of various ferrihydrites and maghemite as a function of grain size. The data from the present study (blue squares) are compared with theoretical maghemite data taken from Liu et al.,3 6LFh data from Guyodo et al.,32 and data for Si-incorporated ferrihydrites from Berquó et al.34 | ||
The ZFC (black) and FC (red) curves are shown in Fig. 5b. For antiferromagnetic minerals with high coercivity, the ZFC curve is analogous to the curve of temperature-dependent magnetic susceptibility, and the peak in the ZFC curve signifies the unblocking temperature (TB) (Fig. 5b).34 The broadening of peaks in the ZFC curves with increasing crystallite size likely reflects the widening of the crystallite size distribution with increasing average crystallite size. It also emphasizes that the peak presents the average TB indicated by the arrows in Fig. 5b. The FC curve is enhanced at low temperature compared to the ZFC curve because an additional thermal remanent magnetization is acquired. The point where the FC and ZFC curves converge is also an indication of TB. The TB obtained from the convergence point corresponds to the maximum estimate of TB. With increasing crystallite size, the average TB and maximum estimate of TB slightly increase from approximately 60 to 80–100 K, and the largest increase is observed between 5LFh_3 and 6LFh_4 (Table 4).
In summary, the present magnetization results confirm that ferrihydrite is antiferromagnetic with a small ferromagnetic-like moment at low temperatures. In general, a ferromagnetic-like moment can originate from either the uncompensated spins present inside the particles and/or at the surface of the particles32,60 or, for large particles, the arrangement of magnetic moments at tetrahedral and octahedral Fe sites.18 For our extremely fine-grained particles, the latter mechanism is not applicable; therefore, uncompensated spins present inside the particles and/or in the surface layer should be responsible for the ferromagnetic-like moment. The Mössbauer data at room temperature have shown that the disorder is largely located in the surface layer. Therefore, the uncompensated spins in the surface layer will lead to the small ferromagnetic-like moments.
Discussion
Presence of tetrahedral coordination of Fe in ferrihydrite
It has been reported that the shape, position and intensity of the pre-edge peak of the Fe K-edge XAS are related to the oxidation state and coordination of Fe in minerals.61 However, the interpretation of this peak for ferrihydrite is debated. Zhao et al.51 found that the pre-edge peak area of ferrihydrite was significantly larger (20–80%) than those of goethite and hematite, which have only the octahedral coordination of Fe, and slightly smaller than that of magnetite (∼36%) with tetrahedral coordination. Therefore, they inferred that ferrihydrite samples may contain 20–30% tetrahedral coordination. In contrast, some years later, Manceau and Gates49 found that the peak area of ferrihydrite is only 0–20% larger than that of hematite and suggested that the increase in peak area is related not only to the CNs of Fe but also to the geometry of the Fe sites; they claimed that almost all Fe existed in octahedral coordination and that the pre-edge peak cannot be used to determine the percentage of tetrahedral coordination.When the peak areas of the present ferrihydrite samples are compared with those of goethite, hematite and magnetite (Fig. 7), the results are similar to those of Zhao et al. The peak areas of the ferrihydrite samples are considerably greater than those of goethite and hematite, but somewhat smaller than that of magnetite. According to the PDF analysis, the relative Fe3 (tetrahedral Fe) site occupancy of the present samples ranges from 0.82 to 0.88 (Table 1).
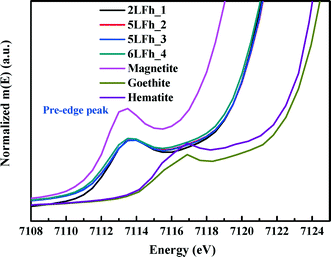 | ||
| Fig. 7 Comparison of the Fe K-edge XAS pre-edge peaks among magnetite, hematite, goethite and the four ferrihydrite samples. | ||
Additionally, the results of PDF and XAS fitting show that the second Fe–Fe coordination distance is approximately 3.44 Å (Fig. 2 and Table 2), which is consistent with the reports of Michel et al.47 and Xu et al.27 According to Xu et al.,27 an Fe–Fe coordination distance of 3.44 Å can serve as indirect evidence of the presence of tetrahedral Fe. Consideration of the additional information about tetrahedral Fe in combination with the present agreement with Zhao's results suggests that Zhao's conclusion is sound. However, we have no further arguments to oppose the view of Manceau and Gates.
Effects of crystallite size on the structure of ferrihydrite
In spite of great advancements towards revealing the basic structure of ferrihydrite in previous studies,18,21,23 there remain disputes over the bulk and surface structures of ferrihydrite with a wide range of grain sizes. This has hindered an accurate understanding of the grain size-dependent properties of ferrihydrite. Our results indicate that ferrihydrites with different crystallite sizes share a common short-, medium- and long-range structure (Fig. 1–3). Given that the “ordered” ferrihydrite with a large size (i.e., ferrifh, 10–12 nm, Michel et al.18) shares a PDF similar to 2LFh, it is suggested that ferrihydrites with different sizes possess a relatively stable bulk or core structure. This is confirmed by the present XRD, PDF and XAS data of the ferrihydrite samples with different crystallite sizes (1.6–4.4 nm), similar to those of the commonly found fine-grained natural ferrihydrites.Nevertheless, the results also indicate a certain degree of distortion: the average Fe–Fe CNs increase with increasing size of the ferrihydrite crystallites (Table 2). A similar increase has been observed in Al–Fe oxyhydroxide co-precipitates42,52 and hydroxybenzoic acid–Fe co-precipitates.50 In addition, anisotropic variations in lattice dimensions indicate size-dependent structural relaxation in ferrihydrite (Table 1), consistent with a reduction in strain with increasing crystallite size.18 A certain number of Fe vacancies exist in the ferrihydrite structure, and Fe vacancies/defects increase with decreasing ferrihydrite crystallite size (Table 1). The combination of these results with a detailed analysis of the Mössbauer spectra at 295 K leads to the conclusion that the surface layer is the region with higher disorder (Table 3) and that the smaller ferrihydrites have a higher percentage of poorly coordinated Fe sites in the surface layer. In summary, the present results support the view that the particle cores have the same structure, that the surface layer is relatively disordered, and that the latter disorder increases with decreasing crystallite size; they therefore support the ferrihydrite structure model suggested by Hiemstra.17
Based on electron diffraction analysis, Janney et al.62,63 concluded that 6LFh was distinctly different from 2LFh. They found that 2LFh contained highly disordered material and crystallites with structures based on the hexagonal and cubic stacking of close-packed layers of O2− and OH− ions, while 6LFh contained structures based on the double-hexagonal stacking of close-packed layers of O2−. Clearly, these results indicate greater differences between 2LFh and 6LFh than those indicated by the present results. Although the basic core structure remains the same with varying crystallite size, the PDF and XAS fitting results indicate that the unit cell parameters, Fe occupancies and Fe–Fe coordination numbers all change somewhat with crystallite size (Tables 1 and 2). Therefore, the structure of the 2LFh particles is different from that of the 6LFh particles. The present results are in good agreement with several other reports, which suggested that the primary difference among ferrihydrites of different sizes is the size of the coherent scattering domain.16,32,47
Magnetization of ferrihydrite and its environmental application
With accurate constraints on the structure of the studied ferrihydrite samples, the origin and grain size dependence of their magnetism can be well resolved. The present results confirm that ferrihydrite shows antiferromagnetism superimposed with a small ferromagnetic-like moment at low temperatures and that the ferromagnetic-like moment is largely due to the uncompensated spins in the surface layer. For nano-sized strongly magnetic particles, such as magnetite64 or ferrifh (ordered ferrihydrite),18 the presence of uncompensated surface spins weakens the bulk magnetic properties, resulting in a positive correlation between grain size and magnetization. In contrast, the magnetization of nano-sized antiferromagnetic minerals such as hematite originates from uncompensated surface spins, and a negative correlation between magnetization and grain size was observed.65 Similar to hematite, the magnetization at 5 T of the studied ferrihydrites gradually increases with decreasing size (Table 4 and Fig. 6a). It should be noted that the smallest sample, 2LFh_1, has much higher values of Bc and magnetization than the other samples. We tentatively interpret that the elevated coercivity Bc is due to either the enhanced surface anisotropy or the enhanced stress between the core and surface shell. Such a stress has also been used to explain the higher Bc values of the low-temperature oxidized magnetite with a stoichiometric magnetite core surrounded by a maghemite shell.66 The much higher magnetization of 2LFh_1 further indicates that the uncompensated spins in the surface layer could also significantly contribute to its bulk magnetization because of its poor crystallinity.For the studied ferrihydrites, the surface layer structure most likely dominates the changes in magnetism with size, and the decrease in magnetization with increasing size could be attributed to the lowering of uncompensated surface spins. This is in contrast with the behavior of ordered and larger ferrihydrites (ferrifh),18 in which the bulk structure dominates and the ordering of electron spin moments of the bulk Fe accounts for the enhancement in magnetism with increasing size. Considering the opposite magnetization trends observed for the present particles (1.6–4.4 nm, Fig. 6a) and ferrifh (10–12 nm), we predict that with a continuously increasing size of ferrihydrites from small disordered particles to relatively large ordered crystallites, there is likely a transient point at which the magnetization is minimum. If this is true, a gradual transformation of relatively smaller 2LFh with crystallite sizes of several nm into relatively larger ferrihydrites with crystallite sizes of 10–12 nm might first result in a decrease in magnetism followed by a significant increase in magnetism.
As ferrihydrite is the most important precursor for other secondary magnetic minerals formed through pedogenesis (e.g., ferrifh, magnetite and maghemite),3,18 the magnetic properties of ferrihydrite with different sizes are important for determining the evolution of the related minerals and explaining the magnetic enhancement in aerobic soils. Therefore, to understand the environmental significance of ferrihydrite in natural samples, it is essential to have information on the ferrihydrite grain size. In Fig. 6b, we summarize the correlation between the TB and grain size of synthetic ferrihydrites. Compared to the theoretical curve for maghemite,3 ferrihydrites have much higher unblocking temperatures due to their higher anisotropy constants. For the extremely fine-grained ferrihydrites (1–5 nm), variation in the values of TB exists among samples with similar sizes synthesized under different conditions (Fig. 6b). For ferrihydrite samples in the grain-size range (∼1–10 nm), the decrease in crystallite size and the presence of Si both lead to the decrease in TB (Fig. 6b). This strongly indicates that the distribution of the uncompensated surface spins of ferrihydrites as well as their grain sizes affect TB. Such complexity should be considered when constructing the relationship between ferrihydrites and other iron oxides in natural samples. Nevertheless, an overall positive correlation exists between TB and the grain size of ferrihydrites; thus, TB is anyhow a useful and practical proxy to quantify the changes in the grain size of ferrihydrites in natural samples provided that the natural conditions are relatively similar.
Conclusions
The structural characterization of the present samples based on the Michel model parameters reveals that ferrihydrite samples with small grains share a common short-, medium- and long-range structure with a large size of ferrihydrite (i.e., ferrifh). Meanwhile, both the average CNs of Fe–Fe and Fe2 and Fe3 occupancies increase with crystallite size, suggesting that smaller ferrihydrites exhibit higher structural disorder. Further, the Mössbauer results at 295 K indicate that the surface layer is relatively disordered, which might be caused by the randomly distributed Fe vacancies at or near the surface and minor stacking faults. This observation supports Hiemstra's surface-depletion model in terms of the location of disorder and the variations of Fe2 and Fe3 occupancies with size. This clarification of the relationship between the ferrihydrite size and structure, and especially the surface structure, is useful for understanding and exploring the adsorption on ferrihydrites and its interaction with other nanoparticles in natural environments.Magnetic data verify that ferrihydrite samples show antiferromagnetism with a ferromagnetic-like moment at lower temperatures (100 K and 10 K), but they are paramagnetic at room temperature (300 K). Smaller ferrihydrites show less magnetic hyperfine splitting and a lower unblocking temperature (TB). In addition, magnetization decreases with increasing crystallite size for disordered ferrihydrite, while an enhancement in magnetism with increasing size is shown for ordered ferrihydrite. It is therefore predicted that with increasing size of ferrihydrites, a transient point occurs at which the magnetization is minimum. Considering that the transformation of ferrihydrite to different iron oxides plays an important role in the mineralogical evolution of iron oxides and magnetic enhancement during pedogenesis, the size-dependent structure and magnetic properties of disordered ferrihydrite provide important basic information for better understanding of these evolution processes.
Acknowledgements
The authors gratefully acknowledge the National Natural Science Foundation of China (NSFC Grant No. 41471194 and 41571448) and the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB15020402) for financial support to this research. The U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences supported the use of the National Synchrotron Light Source, Brookhaven National Laboratory under contract no. DE-AC02-98CH10886. We greatly thank Prof. Dejun Fu and Dr. Renzheng Xiao at Wuhan University for their support with Mössbauer spectra collection and analyses. We are grateful to the associate editor and two anonymous reviewers who helped improve the manuscript considerably.References
- J. L. Jambor and J. E. Dutrizac, Chem. Rev., 1998, 98, 2549–2585 CrossRef CAS PubMed.
- R. M. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, Wiley-VCH, Weinheim, Germany, 2003 Search PubMed.
- Q. S. Liu, V. Barron, J. Torrent, S. G. Eeckhout and C. L. Deng, J. Geophys. Res.: Solid Earth, 2008, 113, B01103 Search PubMed.
- Q. S. Liu, A. P. Roberts, J. C. Larrasoana, S. K. Banerjee, Y. Guyodo, L. Tauxe and F. Oldfield, Rev. Geophys., 2012, 50, RG4002 CrossRef.
- X. M. Wang, M. Q. Zhu, S. Lan, M. Ginder-Vogel, F. Liu and X. H. Feng, Chem. Geol., 2015, 415, 37–46 CrossRef CAS.
- M. F. Hochella, S. K. Lower, P. A. Maurice, R. L. Penn, N. Sahai, D. L. Sparks and B. S. Twining, Science, 2008, 319, 1631–1635 CrossRef CAS PubMed.
- A. C. Cismasu, C. Levard, F. M. Michel and G. E. Brown, Geochim. Cosmochim. Acta, 2013, 119, 46–60 CrossRef CAS.
- N. Pinney and D. Morgan, Geochim. Cosmochim. Acta, 2013, 120, 514–530 CrossRef CAS.
- M. F. Hochella, T. Kasama, A. Putnis, C. V. Putnis and J. N. Moore, Am. Mineral., 2005, 90, 718–724 CrossRef CAS.
- K. Kaiser, R. Mikutta and G. Guggenberger, Soil Sci. Soc. Am. J., 2007, 71, 711–719 CrossRef CAS.
- F. E. Rhoton, M. J. M. Romkens, J. M. Bigham, T. M. Zobeck and D. R. Upchurch, Soil Sci. Soc. Am. J., 2003, 67, 1220–1226 CrossRef CAS.
- J. Filip, R. Zboril, O. Schneeweiss, J. Zeman, M. Cernik, P. Kvapil and M. Otyepka, Environ. Sci. Technol., 2007, 41, 4367–4374 CrossRef CAS PubMed.
- X. M. Wang, W. Li, R. Harrington, F. Liu, J. B. Parise, X. H. Feng and D. L. Sparks, Environ. Sci. Technol., 2013, 47, 10322–10331 CAS.
- A. Voegelin and S. J. Hug, Environ. Sci. Technol., 2003, 37, 972–978 CrossRef CAS PubMed.
- A. C. Scheinost, S. Abend, K. I. Pandya and D. L. Sparks, Environ. Sci. Technol., 2001, 35, 1090–1096 CrossRef CAS PubMed.
- V. A. Drits, B. A. Sakharov, A. L. Salyn and A. Manceau, Clay Miner., 1993, 28, 185–207 CAS.
- T. Hiemstra, Geochim. Cosmochim. Acta, 2013, 105, 316–325 CrossRef CAS.
- F. M. Michel, V. Barron, J. Torrent, M. P. Morales, C. J. Serna, J. F. Boily, Q. S. Liu, A. Ambrosini, A. C. Cismasu and G. E. Brown, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2787–2792 CrossRef CAS PubMed.
- A. Navrotsky, L. Mazeina and J. Majzlan, Geochim. Cosmochim. Acta, 2008, 72, A673–A673 Search PubMed.
- T. Hiemstra, Geochim. Cosmochim. Acta, 2015, 158, 179–198 CrossRef CAS.
- F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, Science, 2007, 316, 1726–1729 CrossRef CAS PubMed.
- W. H. Casey, Chem. Rev., 2006, 106, 1–16 CrossRef CAS PubMed.
- O. Sadeghi, L. N. Zakharov and M. Nyman, Science, 2015, 347, 1359–1362 CrossRef CAS PubMed.
- A. Manceau, Am. Mineral., 2011, 96, 521–533 CrossRef CAS.
- A. Manceau, Clay Miner., 2009, 44, 19–34 CrossRef CAS.
- D. G. Rancourt and J. F. Meunier, Am. Mineral., 2008, 93, 1412–1417 CrossRef CAS.
- W. Q. Xu, D. B. Hausner, R. Harrington, P. L. Lee, D. R. Strongin and J. B. Parise, Am. Mineral., 2011, 96, 513–520 CrossRef CAS.
- Z. X. Jiang, Q. S. Liu, C. Colombo, V. Barron, J. Torrent and P. X. Hu, Geophys. J. Int., 2014, 196, 131–144 CrossRef CAS.
- G. Rubasinghege, R. W. Lentz, M. M. Scherer and V. H. Grassian, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6628–6633 CrossRef CAS PubMed.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. V. Elst and R. N. Muller, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS PubMed.
- H. Tuysuz, E. L. Salabas, C. Weidenthaler and F. Schuth, J. Am. Chem. Soc., 2008, 130, 280–287 CrossRef PubMed.
- Y. Guyodo, S. K. Banerjee, R. L. Penn, D. Burleson, T. S. Berquó, T. Seda and P. Solheid, Phys. Earth Planet. Inter., 2006, 154, 222–233 CrossRef CAS.
- V. Barron, J. Torrent and E. de Grave, Am. Mineral., 2003, 88, 1679–1688 CrossRef CAS.
- T. S. Berquó, S. K. Banerjee, R. G. Ford, R. L. Penn and T. Pichler, J. Geophys. Res.: Solid Earth, 2007, 112, B02102 Search PubMed.
- U. Schwertmann, J. I. Friedl and A. Kyek, Clays Clay Miner., 2004, 52, 221–226 CrossRef CAS.
- J. J. Erbs, B. Gilbert and R. L. Penn, J. Phys. Chem. C, 2008, 112, 12127–12133 CAS.
- P. J. Chupas, X. Y. Qiu, J. C. Hanson, P. L. Lee, C. P. Grey and S. J. L. Billinge, J. Appl. Crystallogr., 2003, 36, 1342–1347 CrossRef CAS.
- A. P. Hammersley, ESRF Internal Report, ESRF98HA01T, FIT2D V9.129 Reference Manual V3.1., 1998 Search PubMed.
- X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37, 678 CrossRef CAS.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Bozin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- A. Hofmann, D. Vantelon, E. Montarges-Pelletier, F. Villain, O. Gardoll, A. Razafitianamaharavo and J. Ghanbaja, J. Colloid Interface Sci., 2013, 407, 76–88 CrossRef CAS PubMed.
- A. L. Ankudinov and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R1712–R1715 CrossRef CAS.
- E. Murad and J. Cashion, Mössbauer Spectroscopy of Environmental Materials and Their Industrial Utilization, Klüwer Academic Publication, Dordrecht, the Netherlands, 2004 Search PubMed.
- A. Neumann, T. L. Olson and M. M. Scherer, Environ. Sci. Technol., 2013, 47, 6969–6977 CrossRef CAS PubMed.
- K. Lagarec and D. G. Rancourt, Recoil-Mössbauer Spectral Analysis Software for Windows, Department of Physics, University of Ottawa, Ontario, 1998 Search PubMed.
- F. M. Michel, L. Ehm, G. Liu, W. Q. Han, S. M. Antao, P. J. Chupas, P. L. Lee, K. Knorr, H. Eulert, J. Kim, C. P. Grey, A. J. Celestian, J. Gillow, M. A. A. Schoonen, D. R. Strongin and J. B. Parise, Chem. Mater., 2007, 19, 1489–1496 CrossRef CAS.
- M. Q. Zhu, C. L. Farrow, J. E. Post, K. J. T. Livi, S. J. L. Billinge, M. Ginder-Vogel and D. L. Sparks, Geochim. Cosmochim. Acta, 2012, 81, 39–55 CrossRef CAS.
- A. Manceau and W. P. Gates, Clays Clay Miner., 1997, 45, 448–460 CAS.
- C. Mikutta, Geochim. Cosmochim. Acta, 2011, 75, 5122–5139 CrossRef CAS.
- J. M. Zhao, F. E. Huggins, Z. Feng and G. P. Huffman, Clays Clay Miner., 1994, 42, 737–746 CAS.
- Y. T. Liu and D. Hesterberg, Environ. Sci. Technol., 2011, 45, 6283–6289 CrossRef CAS PubMed.
- F. Maillot, G. Morin, Y. H. Wang, D. Bonnin, P. Ildefonse, C. Chaneac and G. Calas, Geochim. Cosmochim. Acta, 2011, 75, 2708–2720 CrossRef CAS.
- J. G. Stevens, A. M. Khasanov and D. R. Mabe, Hyperfine Interact., 2005, 161, 83–92 CrossRef CAS.
- E. Murad, Phys. Chem. Miner., 1996, 23, 248–262 CrossRef CAS.
- E. Murad and U. Schwertmann, Am. Mineral., 1980, 65, 1044–1049 Search PubMed.
- A. M. van der Kraan, Phys. Status Solidi A, 1973, 18, 215–226 CrossRef CAS.
- T. J. Park, G. C. Papaefthymiou, A. J. Viescas, A. R. Moodenbaugh and S. S. Wong, Nano Lett., 2007, 7, 766–772 CrossRef CAS PubMed.
- A. Hartnett, L. H. Bottger, B. F. Matzanke and C. J. Carrano, J. Inorg. Biochem., 2012, 116, 188–194 CrossRef CAS PubMed.
- R. S. Zergenyi, A. M. Hirt, S. Zimmermann, J. P. Dobson and W. Lowrie, J. Geophys. Res.: Solid Earth, 2000, 105, 8297–8303 CrossRef CAS.
- M. Wilke, F. Farges, P. E. Petit, G. E. Brown and F. Martin, Am. Mineral., 2001, 86, 714–730 CrossRef CAS.
- D. E. Janney, J. M. Cowley and P. R. Buseck, Am. Mineral., 2000, 85, 1180–1187 CrossRef CAS.
- D. E. Janney, J. M. Cowley and P. R. Buseck, Am. Mineral., 2001, 86, 327–335 CrossRef.
- M. P. Morales, S. Veintemillas-Verdaguer, M. I. Montero, C. J. Serna, A. Roig, L. Casas, B. Martinez and F. Sandiumenge, Chem. Mater., 1999, 11, 3058–3064 CrossRef CAS.
- Z. X. Jiang, Q. S. Liu, V. Barron, J. Torrent and Y. J. Yu, J. Geophys. Res.: Solid Earth, 2012, 117, B02102 Search PubMed.
- Q. S. Liu, S. K. Banerjee, M. J. Jackson, C. L. Deng, Y. X. Pan and R. X. Zhu, Geophys. J. Int., 2004, 158, 506–514 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5en00191a |
| This journal is © The Royal Society of Chemistry 2016 |