Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fuelling electrocatalysis at a single nanoparticle by ion flow in a nanoconfined electrolyte layer†
Louis
Godeffroy
,
Viacheslav
Shkirskiy
 ,
Jean-Marc
Noël
,
Jean-Marc
Noël
 ,
Jean-François
Lemineur
,
Jean-François
Lemineur
 and
Frédéric
Kanoufi
and
Frédéric
Kanoufi
 *
*
Université Paris Cité, CNRS, ITODYS, F-75013 Paris, France. E-mail: frederic.kanoufi@u-paris.fr
First published on 13th March 2023
Abstract
We explore the possibility of coupling the transport of ions and water in a nanochannel with the chemical transformation of a reactant at an individual catalytic nanoparticle (NP). Such configuration could be interesting for constructing artificial photosynthesis devices coupling the asymmetric production of ions at the catalytic NP, with the ion selectivity of the nanochannels acting as ion pumps. Herein we propose to observe how such ion pumping can be coupled to an electrochemical reaction operated at the level of an individual electrocatalytic Pt NP. This is achieved by confining a (reservoir) droplet of electrolyte to within a few micrometres away from an electrocatalytic Pt NP on an electrode. While the region of the electrode confined by the reservoir and the NP are cathodically polarised, operando optical microscopy reveals the growth of an electrolyte nanodroplet on top of the NP. This suggests that the electrocatalysis of the oxygen reduction reaction operates at the NP and that an electrolyte nanochannel is formed – acting as an ion pump – between the reservoir and the NP. We have described here the optically imaged phenomena and their relevance to the characterization of the electrolyte nanochannel linking the NPs to the electrolyte microreservoir. Additionally, we have addressed the capacity of the nanochannel to transport ions and solvent flow to the NP.
1. Introduction
Within the last decade, nanofluidics has evidenced the complexity and richness of the transport of ions and fluids in nanoconfined regions.1,2 This has been made possible by advances in the preparation of devices made of a channel or a pore presenting a characteristic aperture in the nanometer range. Various types of nanodevices, made of different materials and morphologies, have been engineered, such as nanopores, nanochannels and nanopipettes, which have been used to study the fundamentals of molecular and ionic transport at the nanoscale.The interest in such nanoconfinement of fluids and electrolytes lies in the way they challenge continuum electrostatics and hydrodynamics. On the one hand, within charged walls separated by a distance comparable to the thickness of the electrical double layer, EDL, the ionic conductivity is no longer governed by the electrolyte bulk conductivity, but rather by the wall’s surface charge, suggesting the electrolyte electroneutrality is not respected anymore. This allows establishing much higher ionic fluxes than in the bulk. On the other hand, enhanced mass transport of fluids has been observed in sub-2 nm channels based on the breakdown of continuum hydrodynamics (no-slip condition at walls).3,4 These enhanced transport regimes open promising paths for various applications related to energy harvesting (e.g. desalination, water purification or energy conversion and storage processes).2,5
Several of these systems are powered by applying of an electrical voltage between electrolyte reservoirs or compartments separated by the nanofluidic device. They are then inherently coupled to electrochemical processes,5 even though the contribution of electrochemistry in nanofluidic systems, and particularly of the electrochemical conversion of reactants, has been much less explored.6–9 The overlapping fields of nanochannel confinement and electrochemistry, or of ion transport and electron transfer, rely on another nanoscale component: an electrode with nanometre dimension, or nanoelectrode. This has been investigated using either nanopipettes, easily manufactured and used to confine a nanoscale region of an electrode by an electrolyte droplet,10–13 or devices known as nanogap electrochemical cells,9 where two working electrodes are separated by tens of nanometres of electrolyte. The latter have been obtained by approaching nanoelectrodes to an electrode,14,15 or using modern nanofabrication techniques for nanopore electrode arrays8,16–18 and nanochannels.19–23
The advantage of nanoelectrodes is their ability to produce electrochemical reactions at enhanced mass transfer rates. It then allows exploring novel phenomena, and the combination of geometric nanoconfinement and nanoelectrochemistry has facilitated single molecule electrochemical studies while highlighting the effect of the EDL, particularly through the accumulation, transport and nanoconfinement of ions, on the electrochemical response at the nanoscale.
Chemical conversion at enhanced mass transfer rates is another key element for the development of sustainable energy conversion/storage devices exploiting electrochemical or photochemical processes such as photoelectrochemical cells, electrolysers, redox-flow batteries, fuel cells, etc. These devices all exploit nanoparticles (NPs), for example used as catalysts, which brings the possibility to generate products with turnovers reaching the ultimate limit of the reactant (or product) mass transfer rate.
In this work, we explore the possibility of coupling all these nanoscale components, meaning the transport of ions and water within a nanochannel, and the chemical transformation of a reactant at an individual catalytic NP. Such coupling is pertinent to trigger the production of ions at the NP inducing an asymmetric gradient of chemical composition on both sides of the nanochannel which may then act as an ion pump. The strategy was for example employed to construct photosynthesis-inspired photoelectrochemical cells to harvest energy from light.24 Herein we propose to observe how ion transport-based pumping can be coupled to an electrochemical reaction operated at a catalytic NP. This is investigated by a local electrochemical probe technique known as scanning electrochemical cell microscopy, SECCM,10,25 which uses pipettes to confine droplets of electrolyte onto electroactive surfaces to evaluate their local electrochemical activity. This technique, coupled to optical monitoring,26–28 enables confinement of a droplet of electrolyte at a desired and controlled location on an electrode, and particularly in this work, in the vicinity of optically-spotted individual NPs.27,29 Moreover, this experimental situation is insightful in the context of SECCM methodology as it would correspond to a mean to probe indirectly or unwillingly electroactive regions (supposedly non-immersed) outside the droplet meniscus. We apprehend this situation in the context of the electrocatalysis of O2 and water reduction, eqn (1) and (2) respectively, engaged at an ITO electrode decorated with Pt NPs.
| O2 + 2H2O + 4e− → 4HO− | (1) |
| 2H2O + 2e− → H2 + 2HO− | (2) |
The process is followed operando by a label-free optical microscopy technique which allows direct visualisation of the meniscus formed by the electrolyte droplet and individual NPs. The results demonstrate that while the electrochemical reactions occur within the meniscus, the NPs immobilised outside the meniscus also show electrochemical activity, which was revealed by optical microscopy. This work details the phenomena observed optically during the electrochemical experiment and how they can be explained on the basis of the formation of an electrolytic nanochannel between the meniscus acting as a reservoir and the external NPs. It is suggested that O2 reduction, ORR, is taking place at these external NPs, which, based on eqn (1), would produce high concentrations of OH− ions in the vicinity of the NPs, driving a flow of ions and water across the electrolytic nanochannel.
The aim of this work is to investigate these hypotheses on the basis of information gathered by optical microscopy and complemented with surface analyses. This approach enables the characterization of the electrolyte nanochannel connecting the NPs and the electrolyte reservoir, as well as the flow of ions and solvent it carries to maintain the electrocatalytic reaction at the NP. Finally, an analytical model of the electrokinetic transport mode within the nanochannel is provided.
In the framework of iontronics, this work provides discussion on how to couple ion transport within a nanochannel and an electrocatalytic reaction at a nanodomain. It may be used in different ways either using controlled flow in nanochannels to control and therefore study electrocatalytic reactions at the nanoscale, or using electrochemistry at nanocatalysts to trigger and therefore investigate or promote mass transfer into nanochannels.
2. Results and discussions
2.1. Phenomenological description
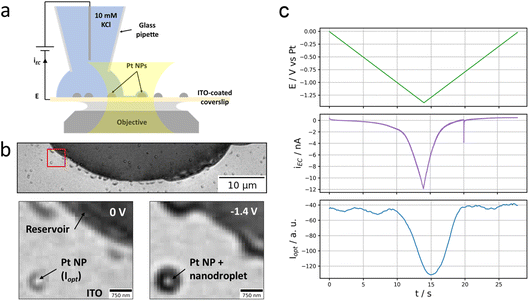
As depicted in Fig. 1a and b, the experiment consists of optically monitoring the electrochemical behaviour of individual Pt NPs sparingly dispersed onto an electrode such that some individual NPs could be located close to (but not within) a microscopic electrolyte reservoir (aqueous 10 mM KCl solution). The electrode was obtained by the electrodeposition of Pt NPs, of size ranging from 100 to 300 nm, onto an ITO-coated glass coverslip which – owing to both its electrical conductivity and optical transparency – can be used as an electrode material for electrochemical solicitation and as an optical sensor enabling optical microscopy monitoring.The ITO-coated face of the coverslip is observed optically: the coverslip is mounted atop an inverted optical microscope contacted by an index-matching oil to a 63× 1.4 numerical aperture (NA) oil immersion microscope objective. Illuminated through the objective by an incoherent white light source, the reflected image of the electroactive ITO surface covered with Pt NPs is collected onto a colour camera at 20 frames per second (fps).
The Pt NP-coated ITO surface is also connected to a potentiostat and operated as the working electrode, WE, of an electrochemical cell. The electrochemical cell is closed by approaching a micropipette with an opening diameter of ca. 20 μm filled with an aqueous 10 mM KCl solution (and loaded with a Pt wire acting as both counter and quasi-reference electrode) to the ITO surface until a meniscus has formed. The micrometric droplet formed by the meniscus is used to confine an electrochemical cell onto a micrometric region of the ITO electrode.
Optical microscopy, in reflection mode, has been used to probe different electrochemical phase formation,26,28,30 in such confined electrochemical cells, with sub-droplet imaging resolution. The optical readout in this reflection mode imaging is sensitive to local changes in refractive index and particularly to the local formation of gas bubbles in a liquid environment.31,32 It should also enable visualizing reciprocally liquid droplets in a gaseous environment. As an illustration, Fig. 1b shows the optical image (full and zoomed view) of the ITO surface with a portion of the micrometric droplet formed upon approaching the pipette. From its higher refractive index, the footprint of the meniscus appears as the dark region in the image. Some dark islands surrounding the edge of the meniscus are residues of electrolyte. Some brighter disk patterns surrounded by a darker corona are also detected sporadically on the image, both inside and outside the electrolyte droplet; they correspond to electrodeposited Pt NPs.
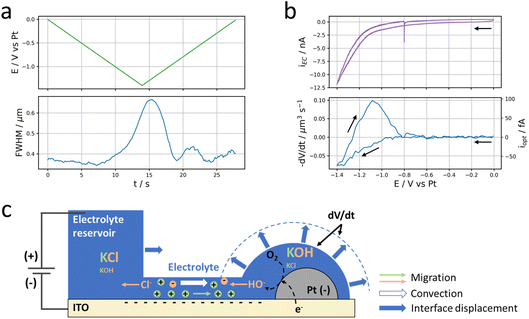
A reductive potential ramp (Fig. 1c, green line) is then applied at the ITO with respect to the Pt wire inserted into the micropipette, acting as both counter and quasi-reference electrode. For potential E ≤ −0.5 V vs. Pt, a cathodic electrochemical current, iEC (Fig. 1c, purple line), is flowing through the ITO working electrode. For E ≤ −1.1 V vs. Pt, a sharper decrease in current is observed resulting in an ohmic-type (reversible) response corresponding to charge transfer limitation (with resistance Rct = dE/diEC ≈ 3 × 107 Ω in the region of −1.4 V < E < −1.1 V). We did not seek to detail particularly the phenomena occurring at the meniscus-coated ITO surface during these electrochemical measurements, but the first reduction process is most likely associated to the reduction of O2 present in the electrolyte, eqn (1), while the second one most likely corresponds to the electrolyte discharge i.e., water reduction, eqn (2). These processes may occur both at the ITO surface and at the Pt NPs immersed in the electrolyte.
We rather focused on the phenomena occurring outside the electrolyte reservoir. An example is shown in the bottom part images of Fig. 1b showing a zoomed region where an individual Pt NP is located ca. 2.5 μm away from the electrolyte meniscus. These images taken at the start of the potential ramp (E = 0 V, left image) or at the most extreme cathodic potential (E = −1.4 V, right image) show that the NP experiences a change in optical contrast (darkening) during the polarisation of the ITO at negative potentials. The phenomenon is quite general as tens of Pt NPs sitting nearby but outside the electrolyte droplet – even though they do not seem to be connected to the electrolyte reservoir and should therefore not be active – experience similar optical intensity changes. The variation of the optical intensity of the NP, iopt evaluated as mentioned in the Material and methods section, along the ITO electrode polarisation waveform is presented in Fig. 1c (blue line) and compared to the electrochemical current response of the electrode portion connected to the electrolyte reservoir (purple line). Following the same trend as the electrochemical current, the NP’s optical intensity gradually decreases from ca. −1 V vs. Pt during the negative potential scan, levels off and then increases symmetrically during the positive potential scan.
To explain this observation, we suggest that the peripheral Pt NPs actually are – to some extent – electrically connected to the electrolyte reservoir via a thin electrolyte film. This would allow electrochemical reactions such as oxygen, eqn (1), and water, eqn (2), reduction to occur at the surface of the peripheral Pt NPs. According to eqn (1) and (2), this would locally consume water and then drive a flow of water across the thin electrolyte film. On the other hand, they would also generate very high concentrations of OH− ions which would drive a flow of ions and water across the thin electrolyte film to compensate for the strong ion concentration gradient created between the electrolyte reservoir on one side and the peripheral Pt NPs on the other side.
2.2. The thin wetting layer around an electrolyte meniscus
The contact of the electrolyte with the ITO surface produces a ca. 30 μm diameter electrolyte droplet with apparent contact angle θ ≈ 60°, i.e. a situation of partial wetting of the ITO surface. First, we discuss the possible presence of a thin liquid film close to the contact line of the electrolyte droplet. The spreading of liquid on a solid surface and its dynamics have received considerable attention.33–36 Depending on the wetting of the solid surface by the liquid, the spreading of the liquid may imply the formation of a thin precursor film of liquid. In the complete wetting regime, the dynamics of the liquid’s spreading is achieved by a thin precursor film extending to mm lengths and with a thickness typically in the nm range. Its presence has been evidenced by interferometric or ellipsometric37 (with μm spatial resolution), or AFM measurements (for higher resolution imaging),38 most often during the slow spreading of model non-volatile (and often viscous) liquid droplets.In the partial wetting regime, the liquid is forming a droplet of static contact angle (θ > 0°) on the surface and the existence of the precursor film is not generic:35,39,40 its presence was not detected for model non-volatile liquids,39 and then was not considered in the case of water evaporation–condensation on solid surfaces.35,41 However, a water precursor thin film of smaller extent (μm-long) could be imaged on partially wetted surfaces by cryo-transmission electron microscopy.42 While water can form non-zero contact angle droplets on various oxygen or oxide (hydrophilic) surfaces, such as ITO, different attractive intermolecular forces at the metal oxide–electrolyte interface, such as the electrostatic forces involved in the formation of the electric double layer or interfacial O–H bonds, could be invoked to explain the possible formation of water precursor films in the partial wetting regime.
Here, the ITO surface is far from being a model system for water-droplet wetting. Indeed, as observed experimentally, the ITO is usually partially wetted by water, with an advancing contact angle θa ≈ 60°, and with considerable contact angle hysteresis >30°.43 The latter may be explained by the ITO surface roughness in the nm range and most likely from the contrast in wetting behaviour between the two components of ITO: the hydrophilic nature of SnO2 and hydrophobic one of In2O3 (respectively θ ≈ 16° and 106°).44 These conditions may then be favourable for the formation of thin electrolyte precursor film.
We took advantage of the reflection-based colour imaging configuration and used the local variation in optical intensity as a proxy of the local thickness of a thin precursor film, as described in the ESI.† Reflectivity images recorded, under monochromatic observation with ultra-sensitive sCMOS camera, at 532 ± 4 nm (green) and at 450 ± 10 nm (blue) of the same droplet are shown in Fig. 2a and b respectively. The green image shows that compared to bare ITO a more reflective region (see the red ROI with reflectivity 1.04 in Fig. 2a) surrounds by about 4 μm the electrolyte droplet. This region reveals the presence of water on the ITO surface. Its contrast enhancement in the green channel also allowed quantification of the apparent thickness of this thin electrolyte film using a simple optical model based on the Fresnel formalism (details in the ESI†) summarized in Fig. 2c. In brief, assuming for simplicity the reflectivity is that of a sandwiched layer of water between an ITO layer and a semi-infinite air medium, from the reflectivity measured in the green and blue images the equivalent thickness of the water layer is evaluated as h = 7 ± 1 nm. Noteworthy, ITO coatings are rough at the several nm scale, the optical estimate, from such mean-field approximation, represents the apparent optical mass of electrolyte in contact with the ITO coating. It is possible that the wetting film extent is actually supported by the porous structure of the ITO layer.
Another way to prove the existence of the thin electrolyte film is to image its footprint by post-mortem SEM after the potential cycling experiment. Using secondary electron at low accelerating voltage, SEM images were obtained with a contrast that enhances surface effects (relative to bulk). On the SEM image presented in Fig. 3a, which was acquired in the same location as Fig. 1b, one can clearly determine the original position of the droplet reservoir as the electrolyte ‘crust’ (circular dark region). This reservoir is surrounded by a <1 μm annular region of clean bare ITO and by a halo region dotted with a multitude of white nanocrystals. As can be seen in another SEM image, Fig. 3c, this halo can extend up to tens of μm, approximately the same extent as that of the thin water precursor film measured optically in Fig. 2a. In higher magnification SEM images (Fig. 3b), elongated needle-shaped or truncated cube-shaped nanocrystals as small as 50 nm could be detected within the precursor film region. It indicates that the precursor film is made of electrolyte rather than water, and that the precursor film is not just due to the evaporation–condensation of water from the droplet, but rather results from the electrolyte spreading and solute diffusing from the droplet reservoir.
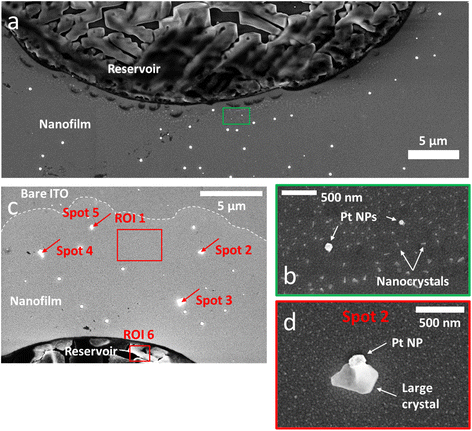 | ||
| Fig. 3 SEM. (a) SEM image acquired post-mortem in the same location as Fig. 1b. (b) High-magnification SEM of the ROI highlighted in green in (a) showing two Pt NPs surrounded by a multitude of nanocrystals forming all around the electrolyte reservoir. (c) SEM image of another part of the sample showing the expansion of the nanofilm (brighter region delimited by the dotted line). This region, not monitored optically, shows larger crystals formed around some Pt NPs. The red rectangles and arrows highlight the regions and spots analysed by EDX (see Table 1). (d) High-magnification SEM image of the Pt NP and crystal called “spot 2” in (c). | ||
A similar behaviour of salt crystallization near an electrolyte reservoir was reported in the case of vertical surfaces dipped into electrolytes. Days-long evaporation experiments led to crystal creeping along the vertical surface.45 The role of the precursor electrolyte film to confine the precipitation dynamics was also emphasized. An empty region between the reservoir and the halo of nanocrystals was also reported and was attributed to the overlapping of different regions of electrolyte consumption for the crystallization process during the drying step.45 Hence, the empty region between the reservoir and the nanocrystals halo detected here suggests that both regions have overlapping electrolyte diffusion fields during the drying step (where the electrolyte supersaturation is vanishing). In turn, this supports that both the reservoir and the precursor film precipitate electrolyte salts, meaning that the precursor film likely contains electrolyte.
Interestingly, after the potential cycling experiment was performed, it was possible to find on SEM images products of the electrochemical reactions left within the region of this thin precursor electrolyte film. Fig. 3c and d show that larger cubic crystals were formed around some Pt NPs. An EDX analysis of these crystals (Table 1) revealed a K/Cl ratio (on average K/Cl = 4.9 ± 2.3) larger than that measured in the crystallized region of the droplet reservoir (K/Cl = 1). Based on this finding, these larger crystals precipitating on Pt NPs were assumed to be KOH crystals. Noteworthy, the EDX analysis of the nanocrystals within the halo could not reveal the exact composition of the footprint (Table 1, first column) due to the low amount of material.
To summarize, from the surface analysis of the region surrounding the electrolyte droplet/reservoir, we showed that a thin film, of 7 nm equivalent thickness, of electrolyte spreads a few μm from the contact line of the droplet reservoir. This nanofilm is then connecting electrolytically Pt NPs present in this region. When the ITO is polarized, and electrochemical current is measured, electrochemical reactions can be driven at these external NPs as well. The formation of KOH crystals around some external Pt NPs indeed suggests that they are engaged in reactions producing HO− ions such as O2 or water reduction, eqn (1) and (2). It also suggests that a flow of K+ ions across the thin electrolyte film towards the Pt NPs is privileged.
2.3. Observing the fluid dynamics during Pt NP electrochemistry
Now that we have demonstrated that peripheral Pt NPs located outside (up to several μm from) the electrolyte droplet may be electrolytically connected to the reservoir, we investigate more closely what happens around these Pt NPs upon potential cycling.In Fig. 1, we showed that the potential cycling is associated with a darkening of the optical pattern of Pt NPs. As will be discussed in more detail below, this darkening is depicted as the local accumulation of electrolyte (i.e., the growth of a nanodroplet) around the NP during the electrochemical process. The growth dynamics of this electrolyte nanodroplet can be probed by a careful frame-by-frame inspection of the point spread function (PSF) of the optical pattern associated with individual Pt NPs. In addition to the optical intensity (defined as the amplitude of the PSF), this data treatment also gives access to two other meaningful parameters: the full width at half maximum of the PSF (FWHM) and the (x, y) position of the optical centre of mass characterizing the NP or the NP + nanodroplet assembly. The FWHM is discussed in Fig. 4. It is a proxy for the growth of the electrolyte nanodroplet surrounding the NP. The motion of the centre of mass is discussed in Fig. 5, and reveals the dynamics of the spreading of the nanodroplet on the surface during its growth.
 | ||
| Fig. 4 Local current. (a) Evolution of the applied potential at the ITO electrode (top, green) and the FWHM of the Pt NP discussed in Fig. 1 (bottom, blue) over time. (b) Electrochemical (top, purple) and optical CV (bottom, blue) in terms of current and volumetric flow rate. (c) Schematic description of the electrokinetic transport through the thin electrolyte film and nanodroplet volume variation (dV/dt) induced by electrolysis at the Pt NP. Migration of ions corresponds to electrophoretic, EP, contribution and convection to electro-osmotic, EO, contribution. The volume variation of the nanodroplet corresponds to the difference between the volume of the plain hemisphere and that delimited by the dashed line. | ||
Fig. 4b presents the evolution of the time derivative of V with the electrode potential, compared to the electrochemical cyclic voltammetry (CV). Actually, dV/dt corresponds to the volumetric flow rate of electrolyte that is feeding the nanodroplet to sustain its growth.
The flow of electrolyte takes place through the thin electrolyte film impregnating the ITO electrode and the NP around the reservoir droplet. This flow of electrolyte is likely due to electrolytic (faradaic) current passing through the ITO surface and likely through the NP. A tentative description of this electrochemically-induced motion of fluid towards the NP is detailed below and schematized in Fig. 4c. It has similarities with the electrochemically-induced motion of particles in the vicinity of an electrode during electrolysis,46–49 and is actually commonly employed for the electrophoretic deposition of particles on electrode surfaces.
The deformation of liquid droplets upon potential actuation is usually known as electrowetting. Under such conditions it was also possible to produce metastable liquid structures formed by a larger droplet connected via a liquid film to many smaller droplets.50,51 However, strictly speaking, electrowetting corresponds to the change in electrode surface charge, meaning in the absence of faradaic current,52 or such structures become unstable when the liquid becomes too conductive.50 The electrowetting contribution is ruled out and an electrolytic contribution is most likely here.
The electrolytic current (cathodic) at the ITO electrode is expected to initiate a reduction at the (more active) Pt NP. Regardless of the exact nature of the electrochemical reaction (oxygen or water reduction, eqn (1) or (2) respectively), one HO− ion per electron is produced in the thin layer of electrolyte surrounding the Pt NP. To compensate this negative charge imbalance, the flux of electrogenerated HO− at the NP surface is accompanied by a flux of ions between the reservoir and the NP region, specifically by a flux of incoming K+ ions from the reservoir and an opposite flux of HO− and Cl− towards the reservoir. In a first approximation, these fluxes are operated at a constant K+ concentration within the thin film and nanodroplet regions.‡ The transport of these ions is sustained by the potential difference between the negatively polarized NP (and ITO) and the positively polarized counter electrode located in the reservoir (Fig. 4c). The electrochemical double layer formed at the negatively charged ITO surface is of a size comparable with the electrolyte nanofilm thickness. Owing to such nanoconfinement, the electrolyte composition is then controlled by the ITO surface charge, ensuring an excess of K+ concentration in the nanofilm (see details below). Moreover the potential bias applied between the NP and the counter-electrode implies the thin electrolyte nanofilm is subjected to a horizontal electric field inducing an electro-osmotic displacement of the electrolyte across the nanofilm. The negatively charged surfaces of the ITO and NP suggest the electro-osmotic flow is directed towards the NP. Both migration of K+ and electroosmotic flow of electrolyte across the thin electrolyte layer could explain – as in capillary electrophoresis – the incoming of electrolyte and the growth of an electrolyte nanodroplet around the Pt NP while cathodic current is flowing.
In a first approximation, the nanodroplet growth is then related to the equilibration of the electroneutrality through electrophoretic incoming of K+ ions, and one could use the nanodroplet volume variations as a proxy for the electrogeneration of HO− ions i.e., for the electrochemical current, iNP, flowing at the Pt NP. Assuming a constant concentration, Cb, of K+ ions in the nanodroplet, the flow of a volume ΔV of electrolyte in the nanodroplet of initial volume V0 should read as follows:
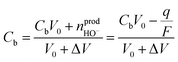 | (3) |
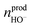 represents the amount of HO− ions produced by the electrochemical reaction (which is equal to the amount of injected electrons i.e., the charge q divided by the Faraday constant F). Now by time derivation, eqn (4) provides the following expression for the optically inferred current, iopt, associated to the nanodroplet volume variation:
represents the amount of HO− ions produced by the electrochemical reaction (which is equal to the amount of injected electrons i.e., the charge q divided by the Faraday constant F). Now by time derivation, eqn (4) provides the following expression for the optically inferred current, iopt, associated to the nanodroplet volume variation: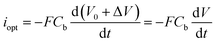 | (4) |
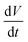 the volumetric flow rate. This relationship allows to transpose the volumetric flow rate in Fig. 4b into an electrochemical current. The currents obtained in this way are of the order of tens of fA, which is far below what state-of-the-art potentiostats are capable of measuring directly. Hence, this demonstrates the strong potential of optical microscopies for studying electrochemical systems. Until now, most electrocatalysts investigated by optical microscopy were so via the formation of gas nanobubbles and in a semi-quantitative manner.31,53 Noteworthy, the electrolytic generation of a gas nanobubble at a 100 nm nanoelectrode requires much higher currents, of the order of tens of pA.54,55
the volumetric flow rate. This relationship allows to transpose the volumetric flow rate in Fig. 4b into an electrochemical current. The currents obtained in this way are of the order of tens of fA, which is far below what state-of-the-art potentiostats are capable of measuring directly. Hence, this demonstrates the strong potential of optical microscopies for studying electrochemical systems. Until now, most electrocatalysts investigated by optical microscopy were so via the formation of gas nanobubbles and in a semi-quantitative manner.31,53 Noteworthy, the electrolytic generation of a gas nanobubble at a 100 nm nanoelectrode requires much higher currents, of the order of tens of pA.54,55
Interestingly, whereas the shape of the optically inferred CV is similar to the electrochemical CV during the negative potential scan, they are very different during the positive potential scan. This suggests that the emptying of the nanodroplet is not potential dependent. Once the potential becomes less negative to maintain a flow of water towards the Pt NP, the latter empties itself at a constant rate and not progressively as the potential increases. This leads to the positive current peak in the optical CV. This may originate from two reasons. On the one hand, based on the difference in Laplace pressure between the nanodroplet (higher pressure) and the reservoir, one would expect the nanodroplet to drain into the reservoir. However this pressure difference is also experienced (and balanced from the electrophoretic flux and electrolysis) during the growth of the nanodroplet. Based on the reversibility of the electrochemical trace one would expect a reversibility of the electrophoretic and Laplace pressure contribution. Laplace pressure difference may then not explain alone the flow in the direction of the reservoir at −1.2 V on the backward potential scan while a considerable flow in the direction of the NP is measured during the forward scan. On the other hand, the electrokinetic transport of ions within the thin electrolyte layer ensures the nanodroplet is a region of high KOH concentration while the micrometric reservoir is a region of low KOH concentration. The condition promotes the diffusion–osmotic transport of electrolyte through the thin electrolyte layer.56 This type of transport was observed in various nanochannels that divide compartments of different concentrations. It is similar to osmosis between compartments separated by a semi-permeable membrane. In the case of a permeable nanochannel separating compartments like here, the diffusion–osmosis results in the flow of electrolytes from the more concentrated to the less concentrated region.56 The electrolyte in the nanodroplet region would contain higher KOH concentration than the electrolyte reservoir which would induce a diffusion–osmotic flow of the nanodroplet content from the NP towards the reservoir, leading to the nanodroplet deflating. Finally, both Laplace pressure difference and diffusion–osmotic flow may explain the nanodroplet’s deflating.
 | ||
| Fig. 5 Pinning of the nanodroplet. (a) Evolution of the applied potential (top, green) and of the displacement (with respect to its initial position) along the normal and tangential direction of the Pt NP discussed in Fig. 1 (bottom) over time. The directions are defined in (b) compared to the reservoir’s contact line passing through the NP’s initial centre of mass. (c) Trajectory of the Pt NP with a colour scale conveying its optical intensity. | ||
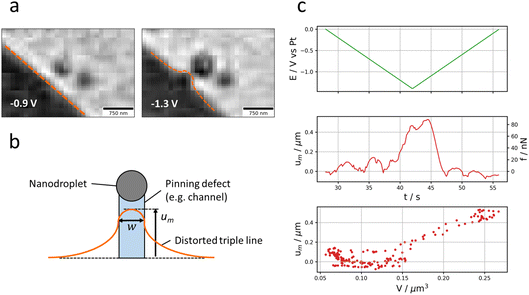
2.3.2.1. Asymmetric growth of the nanodroplet. Fig. 5a presents the displacement of the nanodroplet’s centre of mass (strictly speaking of the ensemble NP + nanodroplet) during the potential cycle. To better visualise these effects, the (x, y) coordinate system is transformed into a coordinate system relative to the contact triple line of the microdroplet (reservoir) pointing along the normal and the tangential direction of the contact triple line (Fig. 5b). The normal axis is actually the shortest distance separating the NP from the contact triple line. As shown in Fig. 5a, the nanodroplet’s centre of mass shifts in correspondence to the potential program: the displacement (with respect to the initial position of the Pt NP) is maximum around the inversion potential when the optical intensity is maximum (in absolute value, Fig. 1c). It is also directed mostly along the normal direction (the NP–reservoir axis). For better visualisation, the trajectory of the optical centre of mass was plotted in 2D on the corresponding optical image with a colour scale conveying the optical intensity (Fig. 5c). On this plot, it becomes evident that the larger the nanodroplet (i.e., the higher the optical intensity), the closer the optical centre of mass sits to the electrolyte reservoir. This is evident during both the forward potential scan where the nanodroplet’s growth is associated with its displacement towards the reservoir and the backward potential scan where the nanodroplet’s deflating is associated with its displacement away from the reservoir. This apparent motion of the NP + nanodroplet could express movement of the Pt NP alone towards/away from the electrolyte reservoir, but since the displacement comes back to original position at the end of the potential cycle, this observation is more likely to demonstrate that the asymmetric growth/deflating of the nanodroplet results from the direction of the flow of electrolyte: from the reservoir to the nanodroplet during its growth and vice versa during its deflation.
The preferred growth towards and deflation away from the reservoir confirms our hypothesis of electrokinetic flow from the reservoir. It further suggests that the NP is a high surface energy defect site pinching the nanodroplet and that the liquid is entering (or exiting) the nanodroplet from the reservoir’s side.
2.3.2.2. Deformation of the reservoir meniscus. Further evidence of such directed liquid flow can also be detected from the reservoir’s side, particularly when the NP is closer to the reservoir’s contact triple line as reported in Fig. 6a. In this figure, it is indeed possible to see that at negative potentials (when current is flowing), the reservoir’s contact triple line is bent outwards as the nanodroplet swells. The dynamics of this contact triple line deformation is detailed in the time series of Fig. 6a. It is characterized by a pinched region of ≈300 nm in the normal direction and extends over 700 nm in the tangential direction. The shape of the contact line deformation is consistent with theoretical works showing how the shape of droplets can be distorted by various types of physical or chemical defects (of local high energy) present on surfaces.36,57,58 As described in Fig. 6b, the triple line’s elastic deformation is predicted to be convex within the region of the defect, yet concave outside that region with a tail decaying logarithmically. The pulling force of the defect, f, is evaluated from the elongation of the triple line, um. This elongation at the centre of the defect (Fig. 6b) is proportional to the pulling force from the defect, according to (from the predicted profiles in ref. 57):
| f ≈ 2πγθ2um/3 | (5) |
The dynamics of the triple line deformation reveals the velocity, v, of the electrolyte flow within the electrolyte nanofilm: the higher the velocity, the higher the pulling of electrolyte from the reservoir. This is illustrated by Fig. 6c showing that during the whole process, the estimated pulling force varies linearly with the volume of the nanodroplet growing at the NP.
The triple line deformation further allows estimating the apparent width, w, of the defect from the distance between the inflexion points of the distorted triple line (here w ≈ 300 nm). Noteworthy, the convex part of the distorted triple line should be pinned at high energy sites of the surface. Hence, the motion of the triple line towards the NP suggests that it is due to a force pulling the reservoir along the entire reservoir–NP distance. The trajectory of the triple line during the electrolysis at the NP, then shows, as detailed in Fig. 6b, the trace of the channel supporting the flow of electrolyte within the thin electrolyte film.
2.4. Discussion
In this section, we summarize and propose an analytical model of the observed processes schematized in Fig. 4c.Electrocatalytic Pt NPs dispersed on a polarized electrode and held a few μm away from an electrolyte droplet acting as a reservoir can be electrochemically activated by ion transport through a ca. h ≈ 7 nm thin film of electrolyte surrounding the electrolyte droplet reservoir. Here, HO− ions are electrogenerated either by oxygen or water reduction. To satisfy electroneutrality, the flux of HO− electrogeneration is sustained by transport of ions across the thin film, a priori of K+ from the reservoir to the NP site and of HO− and Cl− from the NP site to the reservoir.
In addition, the negative polarization of both the ITO electrode and NP’s surface and the flow of an electrochemical current induce an electro-osmotic flow of electrolyte from the electrolyte reservoir to the NP explaining the swelling of a ∼μm diameter electrolyte nanodroplet at the NP site. The electroosmotic flow is also associated with the local deformation of the reservoir’s meniscus triple line suggesting the flow of electrolyte is operated within a nanochannel of width w ≈ 300 nm.
The observed phenomena driven by the electrochemical transformation at the catalytic Pt NP are then associated to the transport of ions and water within a nanochannel of dimensions height: h = 7 nm, width: w = 300 nm and length: L ≈ 1–3 μm (given by the distance separating the NP and the reservoir). Because the electrochemical signal is correlated to the growth of the electrolyte nanodroplet and to the advance of the reservoir’s front towards the NP, the order of magnitude of the electrochemical current flowing at the NP during the electrocatalytic reaction can be evaluated. This can be achieved by recalling that the electrocatalytic current at the NP, iNP, corresponds to the ionic current flowing through the electrolyte nanochannel connecting the reservoir and the NP. From the nanodroplet volume change, we were able to evaluate the contribution of electro-osmosis, EO, to this nanofluidic transport, which is of the order of a few tens (<50) of fA. For sure, it is associated to an electrokinetic contribution during NP polarization.
Ion transport in nanofluidic channels such as nanotubes,1,56 nanopores59,60 or between nanogap-separated planar walls20,61 is well documented, both experimentally and theoretically, including in the context of electrochemical processes.6,13,21,22,62,63 Unlike in the above-mentioned systems, the nanochannel formed here by a thin layer of electrolyte atop the ITO electrode is by essence asymmetrical, as only the ITO surface may be polarized and only the upper electrolyte/air interface may be set in motion.
We elaborate here an analytical evaluation of both electrophoretic, EP, and electro-osmotic, EO, contributions of the ionic current in the given configuration. It is following on the analytical developments proposed for describing the steady-state distribution of the electrolyte ions, potential and fluid velocity between symmetrically charged planes56,61,64,65 or charged nanotubes,66 according to Poisson–Nernst–Planck (PNP) and Poisson–Boltzmann (PB) equations. Briefly, nanogaps of dimension comparable to the Debye length of the electrolyte enable the nanoconfinement of the ion of the electrolyte with opposite charge to that of the walls. For a negatively charged wall, such as the negatively polarized ITO electrode considered in our work, the 7 nm thin electrolyte layer is then mostly composed of K+ ions. The electrolyte nanolayer then behaves as a selective membrane enabling the transport of the majority ionic carrier, K+, in a first approximation excluding the transport of minority carriers i.e., the negatively charged Cl− ions and electrogenerated HO− ions. It can be shown, from PB, that the distribution of the K+ concentration C+(z) and Cl− concentration C−(z) along the z-direction (vertical axis) in the layer follows the potential distribution, φ(z), such that
| C+(z) = Cbe−φ(z) | (6+) |
| C−(z) = Cbeφ(z) | (6−) |
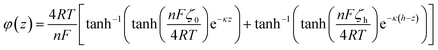 | (7) |
Here, for a 10 mM KCl electrolyte the Debye length is κ−1 = 3 nm, and using ζh = 0 for the air/electrolyte interface, the potential distribution reduces to
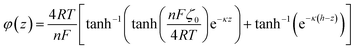 | (8) |
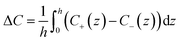 | (9) |
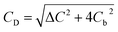 .
.
For the negatively charged ITO surface, ζ0 < 0 so the solution potential is also negative and C+(z) > Cb > C−(z), confirming that the counterion K+ is the majority carrier in the channel while Cl− are partly expelled from it.
When an electrochemical current is flowing through the system, an ionic current of the same value is flowing through the channel. The latter is characterized by the potential drop, ΔU, along the channel length i.e., a longitudinal electric field Ex = ΔU/L. The nanochannel is then submitted to both the formerly described local vertical electric field, Ez = −dφ/dz, and the longitudinal electric field, Ex. If the vertical field freezes the ion population in the channel, the longitudinal field is responsible for the transport of ions from the reservoir to the NP. The composition of the electrolyte transported is then fixed by the frozen concentrations of all ions present in the nanochannel, meaning the electrolyte is transported at concentration CD rather than Cb (the concentration inside the reservoir). The electrophoretic current, IEP, flowing through the channel is then given from the flux of electrical charges or current density of diffusion/migration of each ion, respectively J+ and J−, with:
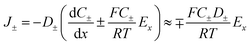 | (10) |
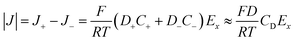 | (11) |
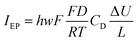 | (12) |
This electrophoretic current, IEP, can be compared to the electro-osmotic current, IEO. As proposed by Vlassiouk et al.,66 the electro-osmotic contribution can be evaluated by integration along the vertical axis of the vEO(z)C±(z) contributions, where the electro-osmotic velocity, vEO, is evaluated from the potential distribution in solution, φ(z). In brief, the electro-osmotic flow within the nanochannel carries the frozen charge imbalance, ΔC, of the electrolyte nanolayer along the longitudinal electric field, Ex, in this case from the reservoir to the nanodroplet. In the end, IEO is given by:66
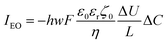 | (13) |
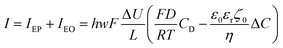 | (14) |
Going back to the data extracted in this work from the nanodroplet’s growth, the EO current could be evaluated from the EO flow rate, Q, approximated from the change in nanodroplet volume, dV/dt, from |IEO| = FQ = dV/dt. For metal oxide film electrodes, such as ITO, surface charge measurements are scarce. The zeta potential of atomic layer deposited indium or tin oxide films have been recently reported.44 At open circuit potential, in 10 mM KCl (pH = 7) solution, the zeta potential is <10 mV, in agreement with a negative value of ζ0 under the cathodic polarization imposed by the electrochemical experiment and by the direction of the EO flow towards the NP. From the knowledge of the EO flow and the predicted IEO/IEP values, one can evaluate the total ionic current I for different (negative) ITO surface charges |σ0|. This is illustrated in Fig. 7d showing that for surface charges higher than a few mC m−2, the total current for the electrocatalytic reaction at the NP is below 1 pA, and between 300 and 100 fA for realistic charges densities higher than 10 mC m−2 (equivalent to 0.06 e nm−2 or values of |ζ0| > 40 mV).
The total current that can be probed in this configuration is actually one order of magnitude lower than the mass transfer limited reduction current (for ORR): for the dNP ≈ 100 nm NP used herein and a 0.5 mM [O2] concentration with diffusion coefficient DO2 ≈ 10−5 cm2 s−1, one expects a mass transfer limited ORR current at a hemispherical nanoelectrode of Ilim = π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2FDO2[O2]dNP ≈ 10 pA. An application of such experimental system, for example with better-defined channels, could be to evaluate the electrocatalytic activity of single nanodomains. Here it would require either smaller NPs (to decrease the mass transfer limit) or more concentrated bulk electrolyte (to increase the ion current). We actually attempted to increase this concentration. However, using a higher concentration (100 mM) we ran into other experimental issues. First, as the triple line motion velocity is also proportional to the bulk concentration, it resulted in the motion of the whole droplet, rapidly submerging the particles. Then in this configuration one cannot prevent the evaporation of the liquid and to some extent salt crystals may be formed at the interface.
2FDO2[O2]dNP ≈ 10 pA. An application of such experimental system, for example with better-defined channels, could be to evaluate the electrocatalytic activity of single nanodomains. Here it would require either smaller NPs (to decrease the mass transfer limit) or more concentrated bulk electrolyte (to increase the ion current). We actually attempted to increase this concentration. However, using a higher concentration (100 mM) we ran into other experimental issues. First, as the triple line motion velocity is also proportional to the bulk concentration, it resulted in the motion of the whole droplet, rapidly submerging the particles. Then in this configuration one cannot prevent the evaporation of the liquid and to some extent salt crystals may be formed at the interface.
Next, we address the reversibility of the process and the anodic-like (oxidation) apparent current associated with the nanodroplet’s deflation. First, the reversibility of the negative (cathodic) EO current variation with electrode bias is consistent with the proposed model. Indeed, as was mentioned in the descriptive part, the electrode response in the most cathodic region is resistive: the electrochemical current varies linearly with the potential bias, ΔU. Hence, one expects from eqn (14) that dV/dt varies linearly with the electrochemical current or the electrode bias, as observed experimentally, and in agreement with the charge transfer resistive behaviour.
However, the proposed theoretical framework cannot explain the large (anodic) positive current and peak detected when negligible currents are flowing through the circuit (see Fig. 4). In this region of electrode bias and current, the electrokinetic regime is likely negligible. However, at this stage, the electrokinetic regime has already transported mostly K+ ions (and to a lesser extent Cl− ions) into the nanodroplet from the reservoir. The electrokinetic regime would have also drawn Cl− ions, partly expelled from the nanochannel, towards the anode (counter-electrode, Pt wire inside the micropipette). This suggests that at the end of the electrokinetic regime, the side of the nanochannel in contact with the reservoir is overall depleted in KCl compared to the bulk, Cb. Similarly, the nanodroplet is more concentrated than the bulk electrolyte in both KCl and KOH. When no more electrochemical current is flowing through the system, the electrolyte concentration difference between the left (reservoir, Cres) and right (nanodroplet, CND) extremities of the nanochannel then meets conditions favourable for diffusion–osmotic transport through the nanochannel.56 In brief, the two compartments with Cres < CND (for both KCl and KOH) connected by a nanochannel will equilibrate their respective concentrations by flow of electrolytic solution from the more concentrated compartment to the less concentrated one. In nanofluidic channels, the expression of the flow reads:
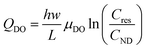 | (15) |
3. Conclusion
Nano/micropipettes are commonly used, in the SECCM configuration, to confine electrolyte droplets onto an electrode surface, enabling probing of its local electrochemical activity at the nano/microscale. We monitored by optical microscopy the electrochemical activity of an ITO electrode decorated with Pt NPs using micropipettes confining 10 mM KCl electrolyte microdroplets (the reservoir). When the ITO surface is polarised in the ORR or water reduction potential region, and a reduction current is flowing through the system, we observed that NPs located a few micrometres away from the electrolyte reservoir also became active. This is visualized optically as the growth of an electrolyte nanodroplet (typically of 1 μm3 volume) around the Pt NP.Such experiment suggests that these electroactive Pt NPs are electrolytically connected through an apparently invisible nanofilm of electrolyte to the nearby reservoir. This work describes this nanofilm and how it allows transporting the electrolyte back and forth between both compartments.
We first demonstrate, from reflectivity imaging of the ITO surface and post-mortem SEM imaging that the reservoir of electrolyte is indeed surrounded by a thin layer of liquid. This nanofilm is composed of electrolyte as the SEM images of the region reveal a multitude of salt nanocrystals after evaporation of the liquid. From reflectivity microscopy images, it is shown that a nanofilm of electrolyte of thickness 7 nm may extend up to tens of micrometres away from the reservoir. In addition, large crystals of about 0.5 μm, most probably composed of KOH, could be detected by SEM-EDX on some of the Pt NPs present in this nanofilm, which confirms that an electrochemical reaction has taken place on the active Pt NPs and that it is accompanied by an active transport of electrolyte from the reservoir to the NP.
The dynamics of ion and water transport across the nanofilm is further probed optically through the deformation of the contact triple line of the electrolyte meniscus simultaneously with the growth of the nanodroplet around the active NP. The triple line deformation suggested that the nanochannel width is about 300 nm, while the nanodroplet growth allowed evaluating the electro-osmotic flow of electrolyte through the nanochannel (or a flow of 50 fL s−1).
We then proposed a steady-state model to rationalize the ion transport across this nanochannel. If the surface properties of the ITO electrode are difficult to evaluate, it is shown that for such nanofilm of size comparable to the Debye length, K+ cations are the majority carriers transported both electrophoretically and electro-osmotically in the direction of the negatively polarized NP. It allows estimating an order of magnitude of the electrokinetic current flowing through the nanochannel to maintain the electrolysis at the NP. The inferred current was in the range of a few hundreds of fA, indicating that the ORR occurring at the NP is limited by transport across the nanofilm.
This work suggests that research using nano/microdroplet confined electrochemistry (SECCM) may be measuring or at least driving electrochemical reactions outside the droplet and one should be cautious to the presence of highly reactive domains outside the presumed inspected region. This points to the role of ion transport within electrolyte nanolayers in electrochemistry, for example impacting corrosion in buried interfaces.
On the other hand, this study demonstrates the potential to combine electrochemical reactions at nanocatalysts with iontronics (ionic transport in nanochannels). Further improvement in reaction kinetics may be achieved by enhancing the nanofilm transport properties, the electrolyte concentration and electrode wall surface charge or zeta-potential, or through the size of the electrocatalytic NP. The experimental setup used here is more a curiosity and using more conventional and reproducible lithographically fabricated systems could provide new avenues for investigating (electro)catalytic reactions driven by nanoconfined ion flows at the nanoscale and at the individual nanocatalyst level. Iontronics could then provide an interesting way of apprehending single nanocatalyst’s electrochemistry. Adding a nanocatalyst at one exit of an ionic nanochannel could also allow triggering of electrochemically out-of-equilibrium conditions enabling analysis of ion transport modes in nanochannels. For example, electroosmotic flow was inspected here during cathodic polarisation, while the reverse polarisation may allow describing the dynamics of other osmotic processes with currently high interest.68
4. Materials and methods
4.1. Chemicals
Chemicals were used as received. KCl (ACS reagent) was purchased from Acros Organics and K2PtCl6 from Sigma-Aldrich. Solutions were prepared with ultrapure water with a resistivity higher than 18.2 MΩ cm. Micropipettes were fabricated inhouse by pulling borosilicate glass capillaries (outer diameter: 1.0 mm, inner diameter: 0.5 mm, Sutter Instrument) with a P-2000 laser puller (Sutter Instrument). ITO-coated coverslips with a resistivity of 15–30 Ω cm were purchased from SPI. They were sonicated in ethanol for 500 s and dried with an argon flux before use.4.2. Preparation of the Pt NPs
The Pt NPs were electrodeposited on ITO by chronoamperometry at −0.7 V vs. Pt for 100 s in 1 mM K2PtCl6 + 0.1 M KCl (reference electrode: Pt wire, counter electrode: stainless steel grid). After electrodeposition, the ITO substrate was rinsed with copious amounts of ultrapure water.4.3. Opto-electrochemical setup
The full description of the opto-electrochemical setup was already published elsewhere.28 Briefly, the ITO-coated coverslip is placed on an inverted microscope (Axio Observer 7, Zeiss) and is illuminated from the backside through a 63× oil immersion objective (Plan Apochromat, Zeiss, NA = 1.4) with a nonpolarized white light. A CMOS camera (UI-3080CP Rev. 2, IDS) operating at 20 frames per second collects the reflected light through the same objective during electrochemistry. The monochromatic estimate of the thin electrolyte layer thickness was obtained from imaging with a back illuminated sCMOS Photometrics camera (Teledyne). The working principle of interference reflection microscopy (IRM) is detailed elsewhere.31 The opto-electrochemical experiments are performed using a CHI760e potentiostat (CH Instruments), which is triggered together with the camera by a waveform generator. The ITO is used as the working electrode and a Pt wire (Goodfellow, diameter: 100 μm) as quasi-reference counter electrode (QRCE) in a two-electrode configuration. To form the microelectrochemical cell/micrometric electrolyte reservoir, a micropipette (opening diameter: ca. 20 μm) – containing the electrolyte and the Pt wire – is approached close to the ITO owing to a 3-axis microcontroller.4.4. SEM-EDX
The SEM images were acquired on a Gemini SEM 360 from Zeiss, with an acceleration voltage of 5 kV. The microscope was equipped with an energy dispersive X-ray (EDX) detector from Oxford Instruments. For EDX analysis, the microscope aperture was expanded to 60 μm and the acceleration voltage increased to 8 kV. The spectra were processed using the AZtec software.4.5. Optical image processing
The optical images were processed using homemade Python routines. After separating the colour channels to select only the blue channel (≈450 nm) which is the most sensitive to the presence of water on top of the Pt NPs, the frames are cropped around the NP of interest. A 2D Gaussian fit is then applied to all crops to extract the amplitude, the FWHM and the centroid position of the particle’s PSF over time. The FWHM is further smoothed using a Savitzky–Golay filter and differentiated with respect to time to determine the volumetric flow rate and finally the electrochemical current associated with the NP according to eqn (4).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially financially supported by the ANR PRC program (DIADEM project, ANR-21-CE29-0021) and through the CNRS and Université Paris Cité. The authors acknowledge the ITODYS SEM facility, the Ile-de-France region and IDEX for financial support of the AFM-Beam-Rex platform, and ENS Paris-Saclay for PhD scholarship.References
- N. Kavokine, R. R. Netz and L. Bocquet, Annu. Rev. Fluid Mech., 2021, 53, 377–410 CrossRef.
- K. Xiao, L. Jiang and M. Antonietti, Joule, 2019, 3, 2364–2380 CrossRef CAS.
- E. Secchi, S. Marbach, A. Niguès, D. Stein, A. Siria and L. Bocquet, Nature, 2016, 537, 210–213 CrossRef CAS PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- M. A. Alkhadra, X. Su, M. E. Suss, H. Tian, E. N. Guyes, A. N. Shocron, K. M. Conforti, J. P. de Souza, N. Kim, M. Tedesco, K. Khoiruddin, I. G. Wenten, J. G. Santiago, T. A. Hatton and M. Z. Bazant, Chem. Rev., 2022, 122, 13547–13635 CrossRef CAS PubMed.
- K. Mathwig, T. J. Aartsma, G. W. Canters and S. G. Lemay, Annu. Rev. Anal. Chem., 2014, 7, 383–404 CrossRef CAS PubMed.
- K. Fu and P. W. Bohn, ACS Cent. Sci., 2018, 4, 20–29 CrossRef CAS PubMed.
- K. Fu, S.-R. Kwon, D. Han and P. W. Bohn, Acc. Chem. Res., 2020, 53, 719–728 CrossRef CAS PubMed.
- H. S. White and K. McKelvey, Curr. Opin. Electrochem., 2018, 7, 48–53 CrossRef CAS.
- C. L. Bentley, J. Edmondson, G. N. Meloni, D. Perry, V. Shkirskiy and P. R. Unwin, Anal. Chem., 2019, 91, 84–108 CrossRef CAS PubMed.
- X. Xu, D. Valavanis, P. Ciocci, S. Confederat, F. Marcuccio, J.-F. Lemineur, P. Actis, F. Kanoufi and P. R. Unwin, Anal. Chem., 2023, 95, 319–356 CrossRef CAS PubMed.
- J. C. Byers, B. Paulose Nadappuram, D. Perry, K. McKelvey, A. W. Colburn and P. R. Unwin, Anal. Chem., 2015, 87, 10450–10456 CrossRef CAS PubMed.
- I. J. McPherson, P. Brown, G. N. Meloni and P. R. Unwin, Anal. Chem., 2021, 93, 16302–16307 CrossRef CAS PubMed.
- P. Sun and M. V. Mirkin, J. Am. Chem. Soc., 2008, 130, 8241–8250 CrossRef CAS PubMed.
- J. H. Bae, Y. Yu and M. V Mirkin, J. Phys. Chem. Lett., 2017, 8, 1338–1342 CrossRef CAS PubMed.
- D. Han, G. M. Crouch, K. Fu, L. P. Zaino III and P. W. Bohn, Chem. Sci., 2017, 8, 5345–5355 RSC.
- V. Sundaresan and P. W. Bohn, Chem. Sci., 2020, 11, 10951–10958 RSC.
- C. Ma, W. Xu, W. R. A. Wichert and P. W. Bohn, ACS Nano, 2016, 10, 3658–3664 CrossRef CAS PubMed.
- P. S. Singh, H.-S. M. Chan, S. Kang and S. G. Lemay, J. Am. Chem. Soc., 2011, 133, 18289–18295 CrossRef CAS PubMed.
- S. Kang, K. Mathwig and S. G. Lemay, Lab Chip, 2012, 12, 1262–1267 RSC.
- Z. A. Kostiuchenko and S. G. Lemay, Anal. Chem., 2020, 92, 2847–2852 CrossRef CAS PubMed.
- Z. A. Kostiuchenko, J. Z. Cui and S. G. Lemay, J. Phys. Chem. C, 2020, 124, 2656–2663 CrossRef CAS PubMed.
- J. Xiong, Q. Chen, M. A. Edwards and H. S. White, ACS Nano, 2015, 9, 8520–8529 CrossRef CAS PubMed.
- Q. Zhang, T. Xiao, N. Yan, Z. Liu, J. Zhai and X. Diao, Nano Energy, 2016, 28, 188–194 CrossRef CAS.
- S. X. Guo, C. L. Bentley, M. Kang, A. M. Bond, P. R. Unwin and J. Zhang, Acc. Chem. Res., 2022, 55, 241–251 CrossRef CAS PubMed.
- D. Valavanis, P. Ciocci, G. N. Meloni, P. Morris, J.-F. Lemineur, I. J. McPherson, F. Kanoufi and P. R. Unwin, Faraday Discuss., 2022, 233, 122–148 RSC.
- E. B. Tetteh, D. Valavanis, E. Daviddi, X. Xu, C. Santana Santos, E. Ventosa, D. Martín-Yerga, W. Schuhmann and P. R. Unwin, Angew. Chem., Int. Ed., 2023, 62, e202214493 CrossRef CAS PubMed.
- L. Godeffroy, J.-F. Lemineur, V. Shkirskiy, M. Miranda Vieira, J.-M. Noël and F. Kanoufi, Small Methods, 2022, 6, 2200659 CrossRef CAS PubMed.
- P. Saha, J. W. Hill, J. D. Walmsley and C. M. Hill, Anal. Chem., 2018, 90, 12832–12839 CrossRef CAS PubMed.
- L. Godeffroy, P. Ciocci, A. Nsabimana, M. Miranda Vieira, J.-M. Noël, C. Combellas, J.-F. Lemineur and F. Kanoufi, Angew. Chem., Int. Ed., 2021, 60, 16980–16983 CrossRef CAS PubMed.
- J.-F. Lemineur, P. Ciocci, J.-M. Noël, H. Ge, C. Combellas and F. Kanoufi, ACS Nano, 2021, 15, 2643–2653 CrossRef CAS PubMed.
- P. Ciocci, J.-F. Lemineur, J.-M. Noël, C. Combellas and F. Kanoufi, Electrochim. Acta, 2021, 386, 138498 CrossRef CAS.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- M. N. Popescu, G. Oshanin, S. Dietrich and A.-M. Cazabat, J. Phys.: Condens. Matter, 2012, 24, 243102 CrossRef CAS PubMed.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid. Mech., 2013, 45, 269–292 CrossRef.
- P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena, Springer New York, New York, NY, 2004 Search PubMed.
- L. Leger, M. Erman, A. M. Guinet-Picard, D. Ausserre and C. Strazielle, Phys. Rev. Lett., 1988, 60, 2390–2393 CrossRef CAS PubMed.
- S. Villette, M. P. Valignat, A. M. Cazabat, F. A. Schabert and A. Kalachev, Phys. A, 1997, 236, 123–129 CrossRef CAS.
- M. Voué, M. P. Valignat, G. Oshanin, A. M. Cazabat and J. De Coninck, Langmuir, 1998, 14, 5951–5958 CrossRef.
- M. J. de Ruijter, J. De Coninck and G. Oshanin, Langmuir, 1999, 15, 2209–2216 CrossRef CAS.
- R. Narhe, D. Beysens and V. S. Nikolayev, Langmuir, 2004, 20, 1213–1221 CrossRef CAS PubMed.
- H. S. Grewal, H. Nam Kim, I.-J. Cho and E.-S. Yoon, Sci. Rep., 2015, 5, 14159 CrossRef CAS PubMed.
- J. S. Kim, R. H. Friend and F. Cacialli, J. Appl. Phys., 1999, 86, 2774–2778 CrossRef CAS.
- Z. Xia, V. Rozyyev, A. U. Mane, J. W. Elam and S. B. Darling, Langmuir, 2021, 37, 11618–11624 CrossRef CAS PubMed.
- M. J. Qazi, H. Salim, C. A. W. Doorman, E. Jambon-Puillet and N. Shahidzadeh, Sci. Adv., 2019, 5, eaax1853 CrossRef CAS PubMed.
- Y. Solomentsev, M. Böhmer and J. L. Anderson, Langmuir, 1997, 13, 6058–6068 CrossRef CAS.
- Y. Solomentsev, M. Bevan and J. L. Anderson, Langmuir, 2000, 16, 9208–9216 CrossRef CAS.
- P. J. Sides, Langmuir, 2001, 17, 5791–5800 CrossRef CAS.
- J. Kim, J. L. Anderson, S. Garoff and P. J. Sides, Langmuir, 2002, 18, 5387–5391 CrossRef CAS.
- F. Mugele and S. Herminghaus, Appl. Phys. Lett., 2002, 81, 2303–2305 CrossRef CAS.
- A. Klingner and F. Mugele, J. Appl. Phys., 2004, 95, 2918–2920 CrossRef CAS.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705 CrossRef CAS.
- R. Hao, Y. Fan, T. J. Anderson and B. Zhang, Anal. Chem., 2020, 92, 3682–3688 CrossRef CAS PubMed.
- M. A. Edwards, H. S. White and H. Ren, ACS Nano, 2019, 13, 6330–6340 CrossRef CAS PubMed.
- Q. Chen, L. Luo, H. Faraji, S. W. Feldberg and H. S. White, J. Phys. Chem. Lett., 2014, 5, 3539–3544 CrossRef CAS PubMed.
- C. Lee, C. Cottin-Bizonne, A.-L. Biance, P. Joseph, L. Bocquet and C. Ybert, Phys. Rev. Lett., 2014, 112, 244501 CrossRef CAS PubMed.
- F. Kanoufi, C. Combellas and M. E. R. Shanahan, Langmuir, 2003, 19, 6711–6716 CrossRef CAS.
- M. E. R. Shanahan, Colloids Surf., A, 1999, 156, 71–77 CrossRef CAS.
- H. S. White and A. Bund, Langmuir, 2008, 24, 2212–2218 CrossRef CAS PubMed.
- Y.-L. Ying, Z.-L. Hu, S. Zhang, Y. Qing, A. Fragasso, G. Maglia, A. Meller, H. Bayley, C. Dekker and Y.-T. Long, Nat. Nanotechnol., 2022, 17, 1136–1146 CrossRef CAS PubMed.
- D. Stein, M. Kruithof and C. Dekker, Phys. Rev. Lett., 2004, 93, 35901 CrossRef PubMed.
- R.-J. Yu, S.-W. Xu, S. Paul, Y.-L. Ying, L.-F. Cui, H. Daiguji, W.-L. Hsu and Y.-T. Long, ACS Sens., 2021, 6, 335–339 CrossRef CAS PubMed.
- E. Kätelhön, K. J. Krause, K. Mathwig, S. G. Lemay and B. Wolfrum, ACS Nano, 2014, 8, 4924–4930 CrossRef PubMed.
- N. Calander, Anal. Chem., 2009, 81, 8347–8353 CrossRef CAS PubMed.
- A. L. Garcia, L. K. Ista, D. N. Petsev, M. J. O’Brien, P. Bisong, A. A. Mammoli, S. R. J. Brueck and G. P. López, Lab Chip, 2005, 5, 1271–1276 RSC.
- I. Vlassiouk, S. Smirnov and Z. Siwy, Nano Lett., 2008, 8, 1978–1985 CrossRef CAS PubMed.
- D. G. Haywood, Z. D. Harms and S. C. Jacobson, Anal. Chem., 2014, 86, 11174–11180 CrossRef CAS PubMed.
- S. Marbach and L. Bocquet, Chem. Soc. Rev., 2019, 48, 3102–3144 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the evaluation of the electrolyte thin layer from optical image. See DOI: https://doi.org/10.1039/d3fd00032j |
| ‡ Noteworthy, this condition may not be satisfied in the region of the counter electrode where H+ ions are electrogenerated. However, this region inside the micropipette is several mm away from the ITO surface. |
| This journal is © The Royal Society of Chemistry 2023 |