Photosensitization mechanisms at the air–water interface of aqueous aerosols

Abstract

Photosensitization reactions are believed to provide a key contribution to the overall oxidation chemistry of the Earth's atmosphere. Generally, these processes take place on the surface of aqueous aerosols, where organic surfactants accumulate and react, either directly or indirectly, with the activated photosensitizer. However, the mechanisms involved in these important interfacial phenomena are still poorly known. This work sheds light on the reaction mechanisms of the photosensitizer imidazole-2-carboxaldehyde through ab initio (QM/MM) molecular dynamics simulations and high-level ab initio calculations. The nature of the lowest excited states of the system (singlets and triplets) is described in detail for the first time in the gas phase, in bulk water, and at the air–water interface, and possible intersystem crossing mechanisms leading to the reactive triplet state are analyzed. Moreover, the reactive triplet state is shown to be unstable at the air–water surface in a pure water aerosol. The combination of this finding with the results obtained for simple surfactant-photosensitizer models, together with experimental data from the literature, suggests that photosensitization reactions assisted by imidazole-2-carboxaldehyde at the surface of aqueous droplets can only occur in the presence of surfactant species, such as fatty acids, that stabilize the photoactivated triplet at the interface. These findings should help the interpretation of field measurements and the design of new laboratory experiments to better understand atmospheric photosensitization processes.

---

Introduction

Most organic compounds emitted into the atmosphere are not photochemically active. Indeed, their degradation chemistry usually proceeds through indirect oxidation processes involving reactions with HO, HO₂, or other oxidizing species that can be generated photochemically.^1,2 Nevertheless, in recent years, there has been growing interest in the potential role of photooxidation mechanisms triggered by brown carbon photosensitizers.³ As a rule, atmospheric photosensitizers absorb light in the tropospheric actinic region (>290 nm) and are excited to a singlet state that evolves into a long-lived triplet state via intersystem crossing (ISC) with a large quantum yield. The triplet state is a highly reactive species that combines with a substrate, typically another organic species in the medium (type I reactions), or with triplet molecular oxygen (type II reactions), initiating the oxidation reactions, as schematized in Fig. 1. Photosensitization typically occurs through electron, hydrogen or energy transfer mechanisms.⁴ Very often the photosensitizer is not consumed in the process and the photosensitization in that case becomes a catalytic reaction. There is increasing evidence that photosensitization facilitates the oxidation of a large variety of organic compounds in the troposphere (e.g. saturated hydrocarbons, monoterpenes, and alcohols), and that it can represent a significant source of secondary organic aerosols (SOAs). Photosensitizers can be emitted into the atmosphere directly through combustion processes (e.g., in the case of polycyclic aromatic hydrocarbons and aromatic ketones) or be formed through the oxidation of primary organic compounds (e.g. in the case of pyruvic acid and imidazole derivatives).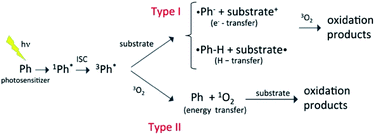

Fig. 1 Schematic representation of different types of photosensitization process,^3,4 where the photosensitizer excited to a triplet state reacts with a substrate by electron or hydrogen transfer, or transfers energy to triplet molecular oxygen. In the latter case, the oxygen molecule is excited to the singlet state that then reacts with the substrate.

Photosensitization appears to be particularly meaningful at surfaces and interfaces.^5–9 The study of photochemical processes at aqueous interfaces has deserved numerous recent theoretical and experimental studies because the solvation effects at the interface appear to enhance the reactivity, compared to the gas phase or bulk water solution (for recent reviews and perspectives, see for instance ref. 8 and 10–13). This heterogeneous chemistry has great atmospheric and environmental significance,^3,14–16 but also presents strong implications for the development of efficient technologies in photocatalysis.¹⁷ The composition of atmospheric organic aerosols may be highly complex.¹⁸ Aqueous aerosols often display a liquid water core coated with an organic surfactant layer. Humic acids, fatty acids, amino acids, proteins, lipids, and other biogenic materials, for instance, are known to accumulate in oceanic surface microlayers.^19–23 Photosensitizers typically exhibit a propensity for partitioning to the organic/water interface, and this tendency might be a key factor explaining the importance of the aerosol surface in photosensitization chemistry.²⁴ However, this hypothesis has not yet been fully assessed and further work is needed to clarify the role solvation plays in determining photosensitization mechanisms in water droplets and aerosols.

A common photosensitizer found in the troposphere is imidazole-2-carboxaldehyde (IC, Fig. 2). Imidazole derivatives such as IC are produced from glyoxal reactions in aqueous aerosol particles (see ref. 8 and 25 and references cited therein). IC has been the focus of many experimental studies^9,24,26–32 but apart from some simple computations,⁹ its photochemistry has not been investigated theoretically. Some measurements have revealed that IC can lead to significant SOA production,^29,30 although some others³¹ suggest that more abundant photosensitizer species, such as humic-like substances, may contribute more significantly to SOA growth. As for other aldehydes, photodissociation and reaction with OH represent potential degradation pathways that could limit the importance of IC's role as a photosensitizer. Very recently, experimental work has been devoted to studying the photophysical properties of IC,²⁷ as well as the pH-dependent equilibrium between its aldehyde and geminal diol forms,³³ which are key aspects for understanding the photochemistry. However, a thorough description of the electronic states of the IC photosensitizer, the photoactivation mechanisms, or the solvation effects in bulk water and at the air–water interface on the reactivity have not been addressed. In this respect, the contribution of theoretical chemistry can be an invaluable asset because molecular modeling provides microscopic information that is often difficult to obtain experimentally, for example to separate interfacial and bulk contributions, or to identify elementary reaction steps.

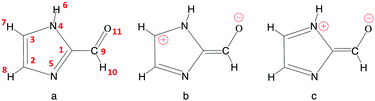Fig. 2 Imidazole-2-carboxaldehyde (IC). Atom numbering used in this work (a), and possible formal mesomeric electronic structures for the π system (b and c).

Here, we report an in-depth theoretical investigation on the photophysical properties of this atmospheric photosensitizer in a water droplet, and analyze the plausible photoactivation and photosensitization mechanisms, paying special attention to how these properties and mechanisms change between the bulk aqueous solution and the droplet surface. We use an elaborated computational approach based on the combination of quantum/classical (or QM/MM) molecular dynamics (MD) simulations,³⁴ and multi-reference configuration interaction (MRCI) ab initio calculations, which has been applied in recent years to analyze interfacial effects on a variety of primary photochemical processes.^35–46

Methodology

The excited states and photophysical properties of IC in bulk water solution and at the air–water interface have been computed by combining QM/MM MD simulations and high-level MRCI calculations. The MD simulations have been carried out for the electronic singlet ground state (S₀), and for the reactive lowest triplet state (T₁) of IC. The methods used are briefly described here; further details can be found in the ESI.†

In the QM/MM MD simulations, IC (singlet or triplet state) is described quantum mechanically at the B3LYP⁴⁷ level using the 6-31G(d) basis set (see ESI Table S1† for the accuracy of this basis set). Water molecules are described classically with the flexible TIP3P force-field.^48,49 The simulation box contains 499 water molecules and one IC molecule. We use a cubic box for bulk simulations and a rectangular box for interface simulations with periodic boundary conditions, as described in the ESI.† We assume the NVT ensemble at 298 K. After equilibration, the simulations have been carried out for 125 ps (singlet) or 50 ps (triplet), saving snapshots regularly to be used afterwards for calculating the photophysical properties at the MRCI/cc-pVTZ level. One of such snapshots at the air–water interface is displayed in Fig. 3. The snapshot illustrates the fact that the CO bond in IC is mainly pointing towards the water layer, as could intuitively be expected (see the probability distribution in Fig. S1†).

Fig. 3 Snapshot from the QM/MM MD simulation of IC(S₀) at the air–water interface.

The simulation for the triplet state at the interface deserves some comments. We have found that after the thermalization process of IC(T₁) at the interface (see the ESI† for details), the system quickly diffuses to the internal water layers within the timescale of the simulation of ∼50 ps (Fig. S2†). This result indicates the absence of a meaningful free energy barrier for the transfer of IC(T₁) to the bulk phase, and the lack of a significant affinity of the triplet state for the air–water interface, in contrast to the singlet. This fact has important implications for the photosensitization mechanisms in aerosols that will be discussed in the last section of this paper.

For comparison, a series of gas phase computations have been done too. In this case, the calculations simply assume the optimized geometry of IC. For consistency with the QM/MM MD simulations, the geometry optimization has been done at the B3LYP/6-31G(d) level and the photophysical properties are computed at the MRCI/cc-pVTZ level.

Note that, of the two possible arrangements of the aldehyde group, s-cis and the s-trans, the latter (i.e., the one appearing in Fig. 2) is the most stable and results for this conformation only are considered. Besides, we will only consider the aldehyde form of IC, which is the most abundant species for pH > 5.³³ At lower pH, the equilibrium with the diol form should be considered.

Results and discussion

Structural properties of IC in S₀ and T₁ electronic states

Table 1 summarizes the main structural properties obtained in the gas phase, in bulk water and at the air–water interface for IC(S₀) and IC(T₁). The first remarkable result is the large differences found for all IC bond lengths between the ground singlet (S₀) and the lowest triplet (T₁) states (except for the C₃N₄ bond, for which differences are small). As shown, in going from the singlet to the triplet state, the C₉O₁₁, C₁N₅ and C₂C₃ bond lengths significantly increase, while those of C₁C₉ and C₂N₅ decrease by a comparable amount. These bond length changes lead to the conclusion that in the triplet state T₁ (compared to S₀) the weight of the zwitterionic mesomeric form in Fig. 2b is significant. This qualitative analysis is consistent with the very large dipole moment obtained for T₁ (7.39 D in the gas phase).

Table 1 Calculated bond distances (Å) and dipole moments (D) of the IC photosensitizer in the singlet ground state (S₀) and lowest triplet state (T₁) in the gas phase, at the air–water interface and in bulk water. Gas phase values correspond to B3LYP/6-31G(d) optimized geometries, while values at the air–water interface and bulk water correspond to averages over the QM/MM MD simulations. Dipole moments have been obtained by single-point MRCI/cc-pVTZ calculations. For atom numbering, see Fig. 2a

	C9O11	C1C9	C1N5	C2N5	C2C3	C3N4	μ
S 0
Gas	1.222	1.458	1.329	1.363	1.386	1.364	2.95
Interf.	1.228 (0.020)	1.456 (0.029)	1.340 (0.023)	1.363 (0.025)	1.390 (0.024)	1.362 (0.024)	4.90 (0.57)
Bulk	1.229 (0.018)	1.453 (0.028)	1.341 (0.023)	1.362 (0.023)	1.390 (0.024)	1.360 (0.024)	5.29 (0.67)
T 1
Gas	1.286	1.394	1.412	1.314	1.437	1.367	7.39
Interf.	1.285 (0.021)	1.409 (0.025)	1.412 (0.032)	1.322 (0.023)	1.436 (0.025)	1.374 (0.028)	8.99 (0.75)
Bulk	1.286 (0.022)	1.410 (0.024)	1.410 (0.031)	1.323 (0.023)	1.436 (0.028)	1.372 (0.028)	9.47 (0.81)

---

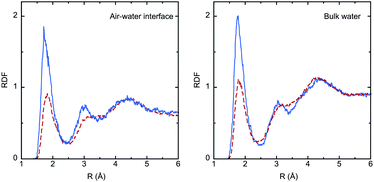
The solvation effect on bond lengths is noticeable in some cases (up to 0.01 Å), but there are no major differences between the interface and the bulk, despite the larger electronic polarization in the last case, as reflected by the values of the dipole moment (μ_bulk > μ_interface). Analysis of solute–solvent radial distribution functions (RDFs) reveals the formation of strong hydrogen bonds involving the IC oxygen atom and water hydrogen atoms, as shown in Fig. 4. The larger dipole moment of the triplet compared to the singlet implies much stronger interactions with water, and this is reflected by the significantly higher intensity of the first peak in the RDFs (roughly by a factor of 2). Integration of this peak leads to the average number of water molecules in the first shell of the oxygen atom: 0.8 (S₀) and 1.2 (T₁) in the bulk, and 0.7 (S₀) and 1.1 (T₁) at the interface.

Fig. 4 Radial distribution functions (RDFs) for O(IC)⋯H(water) hydrogen-bond interactions from the QM/MM MD simulations of IC(S₀) (dashed red lines) and IC(T₁) (plain blue lines) at the air–water interface and in bulk water. The RDFs consider the two H atoms in all water molecules.

Electronic states of IC in the gas phase

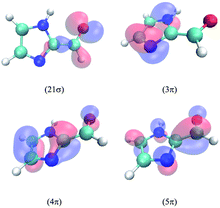
The lowest three singlet and triplet electronic states of IC calculated at the MRCI/cc-pVTZ//B3LYP/6-31G(d) level are described in Table 2. The relevant molecular orbitals are drawn in Fig. 5. In all excited states, the excited electron lies on the lowest unoccupied molecular orbital, the 5π anti-bonding orbital, which is highly delocalized over the molecule. The first excited singlet state corresponds to the electronic transition from the highest occupied molecular orbital 21σ, dominated by the oxygen non-bonding orbital n, and the second to a transition from the 4π orbital, which is highly delocalized in the molecule. In the case of the triplets, T₁ and T₃ involve an electron transition from the 4π and 3π orbitals, respectively. The latter lies mainly on the imidazole ring, and this will be relevant for the discussion of the spin–orbit coupling (SOC) terms below. T₂ involves a transition from the 21σ orbital. As seen, the calculations predict a much larger singlet–triplet splitting for the 4π5π configuration (about 1.7 eV) compared to the 21σ5π configuration (about 0.6 eV). Interestingly, the energy of T₃ lies between the energies of S₁ and S₂, while those of T₁ and T₂ are significantly lower than those of both singlets.

Table 2 Ground and lowest excited singlet and triplet states of IC in the gas phase at the MRCI/cc-pVTZ//B3LYP/6-31G(d) level. Relative energies with respect to the ground singlet state (ΔE in eV), oscillator strength for electronic excitation from the ground state (f), and dipole moment (μ in D). The main electronic configurations are indicated in each case. The coefficient of these configurations is always within 0.9 ± 0.006

State	Configuration	Type	ΔE	f	μ
S0 (X^1A)	…20σ^221σ^23π^24π^2		0.00		2.95
S1 (A^1A)	…20σ^23π^24π^221σ5π	n → π*	4.09	0.0000	3.36
S2 (B^1A)	…20σ^221σ^23π^24π5π	π → π*	4.73	0.4885	7.91
T1 (a^3A)	…20σ^221σ^23π^24π5π	π → π*	3.01		7.39
T2 (b^3A)	…20σ^23π^24π^221σ5π	n → π*	3.47		3.40
T3 (c^3A)	…20σ^221σ^23π4π^25π	π → π*	4.36		7.33

---

Fig. 5 Contour plots of the most significant orbitals of IC calculated in the gas phase.

The oscillator strength for the S₀ → S₁ excitation is zero, as it corresponds to a “symmetry forbidden” electronic transition, while that for the S₀ → S₂ excitation is quite large and should correspond to the main transition involved in the broad, experimentally observed band in different solvents around 280 nm.^26,33,50 According to experimental measurements, the band exhibits a pronounced redshift from non-polar to polar solvents, and this was interpreted as an indication that the main transition in the band is π → π* in origin,²⁶ as predicted by our calculations.

Table 2 also contains the values of the dipole moment of IC in different excited states. The reported values clearly indicate that the excited states (singlet or triplet) involving π → π* transitions have a large dipole moment (around 7–8 D), which is much larger than the dipole moment for the ground state (2.95 D) or the excited states involving n → π* transitions (about 3.4 D). This finding explains the observed solvatochromism in the absorption band in the 280 nm region,²⁶ and anticipates the important role of hydration effects in determining the photophysical properties and photosensitization mechanisms of IC in aqueous media.

Photophysical properties in pure water droplets

Fig. 6 displays the Franck–Condon energy histograms (fitted by Gaussian distributions) for the electronic excitations in the course of the IC(S₀) simulation at the air–water interface and in bulk water. The corresponding average energies are given in the figure caption. All distribution curves have a width of around 1 eV, which reflects the large fluctuations of the excitation energies in the aqueous phase. For instance, the absorption energy for the S₀ → S₁ transition in bulk water varies between roughly 3.5 eV and 4.5 eV. If we compare the average excitation energies with the results in the gas phase (Table 2), it appears that the excited states exhibiting a high dipole moment, namely S₂, T₁, and to a lesser extent T₃, are stabilized with respect to the ground state S₀ by the solvation effect. The histograms in Fig. 6 show that the energy distribution for the lowest triplet T₁ is significantly lower in energy than the curves for the singlet states, and does not overlap them, while the excited singlets, S₁ and S₂, exhibit a strong overlap with T₃, and to a lesser extent with T₂.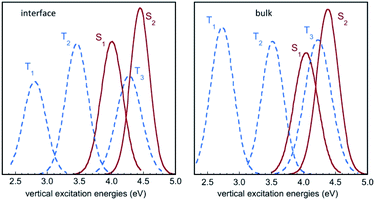

Fig. 6 Histograms of vertical excitation energies to the singlet and triplet excited states S₁, S₂, T₁, T₂ and T₃ from S₀, in the course of the QM/MM MD simulation for IC(S₀) at the air–water interface and in bulk water. The curves represent Gaussian functions fitting the calculated histograms (see also Fig. S3†). Average values for S₁, S₂, T₁, T₂ and T₃ are (in eV) 4.06, 4.50, 2.86, 3.52 and 4.31 at the air–water interface, and 4.09, 4.42, 2.81, 3.58 and 4.30 in bulk water, respectively.

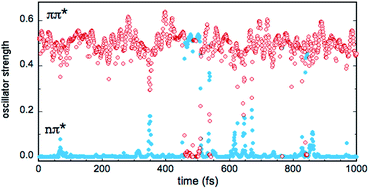
In the gas phase, the excited states S₁ and S₂ correspond to n → π* and π → π* transitions, respectively, while T₁, T₂ and T₃ correspond to π → π*, n → π* and π → π* transitions, respectively (see Table 2). This scheme is largely preserved in the MD simulations, although sporadically, there are crossings between the S₁ and S₂ singlets and between the T₂ and T₃ triplets. In other words, the (nπ*) and (ππ*) character of the states is reversed in a few points. In the case of the singlets, this symmetry change is reflected by the values of the S₀ → S₁ and S₀ → S₂ oscillator strengths f, as shown in Fig. 7 (simulation in bulk water). Occasionally, the relative stability of the (nπ*) (small f value) and (ππ*) (large f value) states is reversed, but the inversion occurs rarely and lasts only a few fs (the equivalent inversion at the air–water interface is even more rare). In the case of the triplets T₂ and T₃, only one single event of this type has been found in the course of the simulations in bulk water and at the interface. Obviously, during the simulations, the planar symmetry of the system is broken due to vibrational motions of the solute and continuous rearrangements of the surrounding water molecules in the solvation shells. Hence, formally, a pure (ππ*) or (nπ*) character never exists and the excited states always contain a certain mixing. In this respect, the out-of-plane bending of the aldehyde group is expected to play a particularly interesting role since it destroys the planar symmetry of the molecule and prevents π delocalization between the ring and the carbonyl group. In fact, in all simulations, though the system remains globally in the s-trans conformation, there are large oscillations of the N₅=C₁–C₉=O₁₁ dihedral angle, which fluctuate within 180° ± 45°.

Fig. 7 Fluctuations of the oscillator strengths for S₀ → S₁ (blue plain circles) and S₀ → S₂ (red open circles) electronic transitions over one picosecond of the QM/MM MD simulation of IC in bulk water. The values for transitions with mainly (nπ*) or (ππ*) character are indicated.

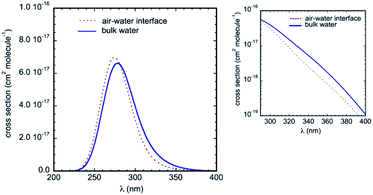
The calculated UV-Vis absorption spectra in bulk water and at the air–water interface are displayed in Fig. 8. They include electronic transitions to the lowest two singlets S₁ and S₂ and present a strong and broad absorption band centered at about 280 nm. Compared to the gas phase, the simulations predict a substantial red-shift of the band due to the solvatochromic effect (we take as reference the symmetry allowed transition in the gas phase at 4.73 eV, i.e. 262 nm, see Table 2). These results are in very good agreement with available experimental data, which reported an absorption maximum in aqueous solution at 287 nm,^33,50 and a net bathochromic shift of the band from hexane to acetonitrile and water.²⁶ Note that in our calculations, the red-shift in bulk water (maximum at 279 nm) is slightly more pronounced than the red-shift at the air–water interface (maximum at 275 nm). Qualitatively, this difference is consistent with the lower effective polarity of the air–water interface,⁵¹ which is associated sometimes with that of a low polarity solvent.^11,52 Though the polarity of the air–water interface remains a debatable issue,^11,53 the simulations at the interface predict somewhat weaker IC–water interactions than in bulk solution (as revealed by the RDFs) and hence a smaller solvatochromic effect is indeed expected. Owing to this bulk–interface band shift, and despite a marginally higher intensity of the absorption band at the interface, the cross-sections over the whole tropospheric actinic region are larger in bulk solution (see the inset in Fig. 8).

Fig. 8 Absorption spectrum of IC in bulk water and at the air–water interface obtained from combined QM/MM MD simulations and MRCI/cc-pVTZ calculations. The inset shows the detail in the tropospheric actinic region on a logarithmic scale.

The emission spectrum of the excited triplet state of IC corresponding to radiative deactivation via phosphorescence has been studied experimentally. The spectrum extends over the wavelength range 400–600 nm with a maximum at 470 nm.²⁷ Computations in the gas phase for the triplet optimized geometry at the B3LYP/6-31G(d) level (ΔE calculations at the CCSD(T)/aug-cc-pVTZ level in this case) lead to an S₀–T₁ energy difference of 2.8 eV (443 nm). Considering that solvation effects should decrease the energy difference a little, the agreement with the experiment seems satisfactory.

Photosensitization mechanism on aqueous aerosols

The photoactivation of IC starts by light absorption in the solar wavelength region, which, as shown above, involves mainly a transition to S₂. ISC to the triplet states can then occur either directly from this state, or after internal conversion to S₁. According to El-Sayed rules,^54,55 ISC is more likely to occur between (ππ*) and (nπ*) states, rather than between states of the same molecular orbital type, and in the present case, this corresponds to S₁T₁, S₂T₂ or S₁T₃ couplings. Calculations of SOC matrix elements for different solute–solvent configurations confirm that S₁T₁ and S₂T₂ couplings display significantly larger SOC values than the other couplings (Table 3). However, a small SOC is found for S₁T₃, which can be explained by the small overlap between the 21σ and 3π orbitals (Fig. 5). Looking at the S₁T₁ and S₂T₂ energy gaps provides further insight into the possible ISC mechanisms. Here, the singlet–triplet energy differences have been estimated at the equilibrium geometries of the excited S₁ and S₂ singlets, and using the results obtained for the ground state (Fig. 6), we will assume that the energy gaps fluctuate within a range of ca. ±0.5 eV. The calculations have been carried out within the TD-DFT approach (B3LYP/cc-pVTZ//B3LYP/6-31G(d) level). The solvation effect has been accounted for using a simple continuum model with a variable dielectric constant (PCM solvation model⁵⁶). For bulk water, we take ε = 78. As said above, for the air–water interface, polarization effects can be compared to those of a low polarity medium. Though this assumption has obvious limitations,¹¹ we have used different values of the dielectric constant (from 2 to 50) to check the influence of this property on singlet–triplet energy gaps. Energy gaps, optimized cartesian coordinates and selected interatomic distances are displayed in Tables S2–S4,† respectively. The computations clearly show that the S₁T₁ gap remains significantly smaller than the S₂T₂ gap in all surroundings, though the difference tends to decrease a little with increasing dielectric constant. The gap amounts to ∼0.4 eV for S₁T₁ and ∼0.9 eV for S₂T₂. Considering that the expected range of fluctuations for these properties is ±0.5 eV, the results indicate that S₁T₁ interactions are more likely to be involved in ISC mechanisms than S₂T₂ interactions. Thus, after light absorption to S₂, the main mechanism leading to T₁ would involve fast internal conversion to S₁ followed by S₁T₁ ISC. It is interesting to note that the excited state geometries display some large modifications compared to the ground state geometry, especially for the S₁ state and the C₁C₉ and C₉O₁₁ bond lengths, which stem from the mesomeric effects.

Table 3 Average values of the spin–orbit coupling (SOC) matrix elements (cm⁻¹) for different singlet–triplet couplings at the air–water interface and in bulk water. The values are given for the M_s = 0 term of the triplet and have been obtained at the MRCI/cc-pVTZ level using a set of selected snapshots from the IC(S₀) simulation (see the ESI for further details). Standard deviations are given in parentheses. Large values of the standard deviations in some singlet–triplet couplings are explained by the inversion of (ππ*) and (nπ*) states in some of the configurations considered for the computations

	Interface	Bulk
S1T1	9.8 (2.6)	16.7 (4.5)
S1T2	1.2 (1.1)	2.4 (3.7)
S1T3	1.0 (0.7)	2.0 (1.3)
S2T1	1.5 (1.3)	3.1 (4.6)
S2T2	8.1 (2.1)	13.3 (3.6)
S2T3	0.6 (0.5)	1.1 (0.9)

---

As discussed in the introduction, the surface of aerosols is expected to be the main scenario where photosensitization reactions occur, because photosensitizers and VOC reagents tend to accumulate at the air–water interface. Tinel et al.⁵⁷ studied IC photosensitization in the presence of nonanoic acid as a surfactant and emphasized the role the coated interface plays to (1) increase the propensity of IC to partition to the interface, and (2) promote the radical–radical reactions there. In another study, Woods et al.⁹ measured the decay of the excited IC triplet on the surface of NaCl aerosol particles having IC concentrations beyond the aqueous solubility. A biexponential decay with lifetimes of about 20 ns and 132 ns has been observed and attributed to, respectively, self-quenching in a pure IC layer covering the aerosol (H-abstraction) and quenching by Cl⁻ anions in the IC aqueous phase near the aerosol surface. Both studies highlight the role of the coated interface to promote the photosensitization process, and this role is further stressed by our QM/MM MD simulations.

As mentioned in the Methodology section, IC(T₁) has a short lifetime at the interface, in contrast to IC(S₀). Once formed, IC(T₁) penetrates the internal water layers in a very short timescale of ∼50 ps. The large charge separation in IC(T₁) can explain this result because it leads to stronger hydrogen bonds with water molecules, as clearly shown by the RDFs in Fig. 4. Calculated solvation free energies in water using the PCM model confirm the higher hydrophilicity of the triplet compared to the singlet (−6.3 and −8.0 kcal mol⁻¹ for the singlet and triplet, respectively, B3LYP/6-31G(d) calculations). This fact has major implications for the photosensitization mechanism in microdroplets and aerosols. It indicates that IC adsorbed on the surface of water droplets and excited to T₁ has a small probability to react with other species there. Experimental rate constants for the reaction of IC(T₁) with many substrates such as ³O₂ (k = 2.7 × 10⁹ M⁻¹ s⁻¹),²⁷ halide anions (k_q(I⁻) = 5.33 × 10⁹ M⁻¹ s⁻¹, k_q(Br⁻) = 6.27 × 10⁶ M⁻¹ s⁻¹, k_q(Cl⁻) = 1.31 × 10⁵ M⁻¹ s⁻¹),^9,58 or several H-donors^28,59 are available in the literature. If, as an example, we consider the reaction with triplet oxygen (type II reactions in Fig. 1), assuming a saturated oxygen concentration of 2.6 × 10⁻⁴ M,⁶⁰ the pseudo first order constant amounts to k = 7.0 × 10⁵ s⁻¹, corresponding to a half-life time close to a microsecond. Therefore, interfacial photosensitization reactions of IC are not likely to be meaningful in water droplets unless the surface is coated by compounds capable of providing a suitable driving force to stabilize the excited triplet, as experimentally observed in the studies by Tinel et al.⁵⁷ and Woods et al.⁹

The partition of IC(T₁) to the interface in that case can be favored by interactions with the surfactant. Ab initio calculations carried out in this work at the B3LYP/cc-pVTZ level for the complex formed between IC(T₁) and a simple surfactant model (CH₃CH₂COOH) lead to an interaction energy as large as ΔE = −10.2 kcal mol⁻¹. Though the stabilization of chemical species at aqueous interfaces is a complex issue that needs consideration of enthalpic and entropic contributions,¹¹ a large IC–surfactant interaction appears as a necessary condition for photosensitization reactions to occur at the interface of aqueous organic aerosols.

Conclusions

The molecular dynamics simulations carried out in this study provide the hitherto missing theoretical framework allowing a better understanding of the photosensitization mechanisms of IC at the surface of aqueous aerosols, whose atmospheric relevance is now widely recognized. The results reveal that the photosensitization mechanisms are more complex than previously thought.

In the present study, we have described the nature of the lowest excited singlet and triplet states likely to be involved in IC photosensitization mechanisms. Though different pathways can contribute to populating the reactive state T₁, according to our computations the most plausible mechanism would be (1) light absorption to the (symmetry allowed) bright state S₂ (4π5π* configuration), (2) internal conversion to S₁ (21σ5π), and (3) favorable ISC (El-Sayed rules) to T₁ (4π5π* configuration).

However, the analysis of solvation effects has led to the conclusion that the reactive triplet state T₁ is not stable at the air–water interface of a pure water droplet. This finding has broad implications for the assessment of the atmospheric significance of IC photosensitization reactions. IC is preferably produced in organic rich media, such as organic aerosols, and our results suggest that the photochemistry observed in laboratory experiments occurs in some interfacial sublayer where the triplet state can be stabilized. IC(T₁) is characterized by a large dipole moment (μ = 7.39 D in the gas phase) due to the lengthening of the C–O bond length and the appearance of a large negative charge on the oxygen atom. Good H-donor surfactants such as fatty acids may compete with water to stabilize this charge and stabilize the triplet. Reactions with these surfactants, with other organic compounds coating the surface, or with oxygen from air, can then take place initiating the photosensitization process. In the absence of stabilizing surfactants, IC(T₁) should rapidly migrate to the bulk phase and eventually react with other species there. Since the available reactants at the interface and in bulk differ by their hydrophobicity/hydrophilicity balance, the short interfacial lifetime of T₁ constitutes an important selectivity factor for photosensitization in aqueous aerosols.

The short interfacial lifetime of T₁ is due to its great dipole moment and the presence of a large charge separation, leading to strong hydrogen bonds with water molecules. Large dipole moments have also been predicted for other electronic states involving π → π* excitations, in particular for the bright S₂ excited state, and therefore a short interfacial lifetime comparable to that of T1 is expected for those states. Nevertheless, the involved timescale (a few tens of ps) is presumably large enough to allow relaxation through ultrafast internal conversion processes at the interface.

The theoretical results reported in this work should help design future experiments on IC and, more broadly, on photosensitization reactions at the surface of aqueous aerosols, thus allowing progress in the evaluation of the atmospheric relevance of this heterogeneous chemistry.

Author contributions

M. F. R.-L. and J. M. A. designed the research; M. F. R.-L., M. T. C. M.-C., J. S. F., and J. M. A. performed the research; M. F. R.-L., M. T. C. M.-C., J. S. F., and J. M. A. analyzed the data; and M. F. R.-L. wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. M. A. thanks the Catalan CSUC for providing computational resources and the Spanish Ministerio de Ciencia e Innovación for a grant (project PID2019-109518GB-I00). M. T. C. M.-C. and M. F. R.-L. are grateful to the French CINES (project lct2550) and TGCC (project gen5132) for providing computational resources.

References

1. B. J. Finlayson-Pitts and J. N. Pitts, Chemistry of the upper and lower atmosphere: theory, experiments, and applications, Academic Press, San Diego, CA, 2000.
2. S. Gligorovski, R. Strekowski, S. Barbati and D. Vione, Chem. Rev., 2015, 115, 13051–13092.
3. E. Gomez Alvarez, H. Wortham, R. Strekowski, C. Zetzsch and S. Gligorovski, Environ. Sci. Technol., 2012, 46, 1955–1963.
4. M. S. Baptista, J. Cadet, P. Di Mascio, A. A. Ghogare, A. Greer, M. R. Hamblin, C. Lorente, S. C. Nunez, M. S. Ribeiro and A. H. Thomas, Photochem. Photobiol., 2017, 93, 912–919.
5. S. Rossignol, L. Tinel, A. Bianco, M. Passananti, M. Brigante, D. J. Donaldson and C. George, Science, 2016, 353, 699–702.
6. H. Fu, R. Ciuraru, Y. Dupart, M. Passananti, L. Tinel, S. Rossignol, S. Perrier, D. J. Donaldson, J. Chen and C. George, J. Am. Chem. Soc., 2015, 137, 8348–8351.
7. M. Bruggemann, N. Hayeck and C. George, Nat. Comm., 2018, 9, 1–8.
8. C. George, M. Ammann, B. D'Anna, D. Donaldson and S. A. Nizkorodov, Chem. Rev., 2015, 115, 4218–4258.
9. E. Woods III, O. T. Harris, W. E. Leiter, N. E. Burner, P. Ofosuhene, A. Krez, M. A. Hilton and K. A. Burke, ACS Earth Space Chem., 2020, 4, 1424–1434.
10. J. Zhong, M. Kumar, J. M. Anglada, M. T. C. Martins-Costa, M. F. Ruiz-Lopez, X. C. Zeng and J. S. Francisco, Annu. Rev. Phys. Chem., 2019, 70, 45–69.
11. M. F. Ruiz-Lopez, J. S. Francisco, M. T. C. Martins-Costa and J. M. Anglada, Nat. Rev. Chem., 2020, 4, 459–475.
12. J. M. Anglada, M. T. C. Martins-Costa, J. S. Francisco and M. F. Ruiz-López, J. Am. Chem. Soc., 2020, 142, 16140–16155.
13. M. F. Ruiz-Lopez, Science, 2021, 374, 686–687.
14. A. E. Reed Harris, A. Pajunoja, M. Cazaunau, A. Gratien, E. Pangui, A. Monod, E. C. Griffith, A. Virtanen, J. F. Doussin and V. Vaida, J. Phys. Chem. A, 2017, 121, 3327–3339.
15. D. J. Donaldson and K. T. Valsaraj, Environ. Sci. Technol., 2010, 44, 865–873.
16. A. R. Ravishankara, Science, 1997, 276, 1058–1065.
17. M. Kozlowski and T. Yoon, J. Org. Chem., 2016, 81, 6895–6897.
18. Y. S. Djikaev and E. Ruckenstein, Adv. Colloid Interface Sci., 2019, 265, 45–67.
19. R. Ciuraru, L. Fine, M. van Pinxteren, B. D'Anna, H. Herrmann and C. George, Sci. Rep., 2015, 5, 12741.
20. R. Ciuraru, L. Fine, M. van Pinxteren, B. D'Anna, H. Herrmann and C. George, Environ. SCi. Technol., 2015, 49, 13199–13205.
21. M. Brüggemann, N. Hayeck, C. Bonnineau, S. Pesce, P. A. Alpert, S. Perrier, C. Zuth, T. Hoffmann, J. Chen and C. George, Faraday Discuss., 2017, 200, 59–74.
22. M. Shrestha, M. Luo, Y. Li, B. Xiang, W. Xiong and V. H. Grassian, Chem. Sci., 2018, 9, 5716–5723.
23. R. J. Rapf and V. Vaida, Phys. Chem. Chem. Phys., 2016, 18, 20067–20084.
24. L. Tinel, S. Rossignol, A. Bianco, M. Passananti, S. Perrier, X. Wang, M. Brigante, D. J. Donaldson and C. George, Environ. SCi. Technol., 2016, 50, 11041–11048.
25. B. Ervens and R. Volkamer, Atmos. Chem. Phys., 2010, 10, 8219–8244.
26. W.-Y. Li, X. Li, S. Jockusch, H. Wang, B. Xu, Y. Wu, W. G. Tsui, H.-L. Dai, V. F. McNeill and Y. Rao, J. Phys. Chem. A, 2016, 120, 9042–9048.
27. T. Felber, T. Schaefer and H. Herrmann, J. Phys. Chem. A, 2020, 124, 10029–10039.
28. L. González Palacios, P. Corral Arroyo, K. Z. Aregahegn, S. S. Steimer, T. Bartels-Rausch, B. Nozière, C. George, M. Ammann and R. Volkamer, Atmos. Chem. Phys., 2016, 16, 11823–11836.
29. K. Z. Aregahegn, B. Nozière and C. George, Faraday Discuss., 2013, 165, 123–134.
30. S. p. Rossignol, K. Z. Aregahegn, L. Tinel, L. Fine, B. Nozière and C. George, Environ. Sci. Technol., 2014, 48, 3218–3227.
31. W. G. Tsui, Y. Rao, H.-L. Dai and V. F. McNeill, Environ. Sci. Technol., 2017, 51, 7496–7501.
32. S. Li, X. Jiang, M. Roveretto, C. George, L. Liu, W. Jiang, Q. Zhang, W. Wang, M. Ge and L. Du, Atmos. Chem. Phys., 2019, 19, 9887–9902.
33. J. M. Ackendorf, M. G. Ippolito and M. M. Galloway, Environ. Sci. Technol. Lett., 2017, 4, 551–555.
34. M. T. C. Martins-Costa and M. F. Ruiz-López, Chem. Phys., 2007, 332, 341–347.
35. M. T. C. Martins-Costa and M. F. Ruiz-Lopez, Phys. Chem. Chem. Phys., 2011, 13, 11579–11582.
36. M. T. C. Martins-Costa, J. M. Anglada, J. S. Francisco and M. Ruiz-Lopez, Angew. Chem., Int. Ed., 2012, 51, 5413–5417.
37. M. T. C. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-Lopez, J. Am. Chem. Soc., 2012, 134, 11821–11827.
38. M. T. C. Martins-Costa and M. F. Ruiz-Lopez, J. Phys. Chem. B, 2013, 117, 12469–12474.
39. J. M. Anglada, M. T. C. Martins-Costa, M. F. Ruiz-Lopez and J. S. Francisco, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11618–11623.
40. M. T. C. Martins-Costa, F. F. Garcia-Prieto and M. F. Ruiz-Lopez, Org. & Biomol. Chem., 2015, 13, 1673–1679.
41. M. T. C. Martins-Costa and M. F. Ruiz-López, in Quantum Modeling of Complex Molecular Systems, ed. J.-L. Rivail, M. F. Ruiz-Lopez and X. Assfeld, Springer International Publishing, Cham, 2015, pp. 303–324,  DOI:10.1007/978-3-319-21626-3_11.
42. M. T. C. Martins-Costa, J. M. Anglada and M. F. Ruiz-Lopez, ChemPhysChem, 2017, 18, 2747–2755.
43. M. T. C. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-López, J. Am. Chem. Soc., 2018, 140, 12341–12344.
44. M. T. C. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-Lopez, Chem. -Eur. J., 2019, 25, 13899–13904.
45. M. F. Ruiz-Lopez, M. T. Martins-Costa, J. M. Anglada and J. S. Francisco, J. Am. Chem. Soc., 2019, 141, 16564–16568.
46. M. T. C. Martins-Costa and M. F. Ruiz-López, ChemPhysChem, 2020, 21, 2263–2271.
47. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
48. W. L. Jorgensen, J. Chandrashekar, J. D. Madura, W. R. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
49. L. X. Dang and B. M. Pettitt, J. Phys. Chem., 1987, 91, 3349–3354.
50. T. Felber, T. Schaefer and H. Herrmann, J. Phys. Chem. A, 2019, 123, 1505–1513.
51. M. C. Martins-Costa and M. Ruiz-Lopez, Theoret. Chem. Acc., 2015, 134, 17.
52. H. F. Wang, E. Borguet and K. B. Eisenthal, J. Phys. Chem. B, 1998, 102, 4927–4932.
53. S. Sen, S. Yamaguchi and T. Tahara, Angew. Chem., Int. Ed., 2009, 48, 6439–6442.
54. M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838.
55. C. M. Marian, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 187–203.
56. J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226.
57. L. Tinel, S. Rossignol, A. Bianco, M. Passananti, S. Perrier, X. M. Wang, M. Brigante, D. J. Donaldson and C. George, Environ. Sci. Technol., 2016, 50, 11041–11048.
58. L. Tinel, S. Dumas and C. George, C. R. Chim., 2014, 17, 801–807.
59. P. Corral Arroyo, T. Bartels-Rausch, P. A. Alpert, S. Dumas, S. Perrier, C. George and M. Ammann, Environ. Sci. Technol., 2018, 52, 7680–7688.
60. H. Herrmann, T. Schaefer, A. Tilgner, S. A. Styler, C. Weller, M. Teich and T. Otto, Chem. Rev., 2015, 115, 4259–4334.

---

Footnote

† Electronic supplementary information (ESI) available: Details on methods, Tables S1–S4 and Fig. S1–S3. See DOI: 10.1039/d1sc06866k

---