Large variability and complexity of isothermal solubility for a series of redox-active phenothiazines

Abstract

The development of redox-active organic molecules (ROM) with large solubilities in all states of charge in organic electrolytes is imperative to the continued development of non-aqueous redox flow batteries. The capability to a priori predict ROM solubility would be a game changer, allowing for a move away from time and resource consuming trial-and-error approaches to materials design and deployment. However, it is not presently clear that such predictions are generally possible, even for chemically related ROM, given the large number of physicochemical factors in play. Here we use quantitative structure–property relationships (QSPR) to examine solubility trends for a set of thirty phenothiazine derivatives. The solubility in all states of charge (neutral and charged forms) of these molecules were obtained experimentally, and multiple linear regression models were used to correlate these properties with a large set (>100) of molecular descriptors. Minimal QSPR models rationalizing these data include four-to-six molecular descriptors, and cannot be further reduced. However, even such relatively complex models show limited ability to predict solubility of an unknown homologous compound. Thus, even in the controlled experimental environment, “predicting” the solubility may not be easy, suggesting the need for high-throughput measurements to develop the large data sets required for machine-informed materials design. The NMR method presented in this study is promising in this regard as it lends itself to automation.

---

Introduction

Redox-active organic molecules (ROM) are of interest for many applications, including (opto)electronics, energy generation, energy storage, sensing, and catalysis.^1–7 For energy storage, advanced technologies are required for effective utilization and greater adoption of intermittent renewable energy resources such as solar and wind. With their wide electrochemical stability windows, non-aqueous redox flow batteries (NAqRFB) can operate at higher voltages, which potentially increases their energy density, than their aqueous counterparts, making this technology promising for mid to large-scale energy storage.^8–12

Current techno-economic models suggest that NAqRFB, to be competitive with other energy storage technologies, need to operate with large ROM molarities (3–5 M).^13,14 As ROM are composed of earth-abundant elements and offer almost unlimited synthetic tunability, their large-scale production is not likely to be resource limited. However, their limited solubilities in organic electrolytes is a major concern, as it prevents the attainment of the large energy densities that remain a key potential advantage of NAqRFB over aqueous redox flow batteries.^13,15 Efforts to improve solubility are hampered by limited understanding of the factors that govern ROM solubility in different states of charge, e.g., the neutral and singly or multiply charged states.^15–19

Though several methods have been reported, there exist practical issues of measuring molecular solubilities in concentrated solutions containing reactive radical species. The spectrophotometric method, where a calibration curve is constructed using known concentrations to determine the optical density and the concentration of a suitably diluted saturated solution, often fails to determine the solubility of charged molecules as the ongoing decomposition of radical ions leads to variations in the absorption properties over time; moreover, this method is both time and material consuming compared to other techniques.²⁰ Solubility determination using weight measurements is limited by the supporting electrolyte's interference with the mass of the ROM and the requirement of additional analyses (e.g., ¹H NMR) to ensure the complete evaporation of the solvent.²¹ The Shake flask method is restricted by the inability to account for volume expansion, and does not allow one to observe complete dissolution accurately due to the intense colors of radical ions; further, errors arise from solvent evaporation if the experiment requires long times to attain complete dissolution.^22,23 A means to overcome errors from volume expansion during dissolution is by densimetry or pycnometry: the volume of the solution is calculated from the density. Here we used an NMR spectroscopic method,²⁴ where the solubility is determined by comparing the resonance signals from the solute and standard to directly obtain mole fractions of the solution components. In charged solutions, radical ions were neutralized prior to this NMR analysis, as otherwise nuclear resonances become shifted, broadened, or completely unobserved through their interaction with paramagnetic species present in solution.

While it is beneficial to measure ROM solubility a posteriori, moving beyond such heuristic approaches requires the capability to predict the properties of interest a priori. Quantitative structure–activity/property relationships (QSAR/QSPR) correlate chemical structures with physicochemical properties across a range of compounds. With this approach, regression models are used to statistically correlate predictor variables (molecular descriptors) and the response variables (chemical and physical properties). Over the last decade, this approach has made inroads into the development of materials for flow batteries, though the field is still dominated by trial and error. For example, Sigman and co-workers constructed QSPR models to characterize chemical properties over small sets of homologous ROM, including their stability and solubility.^21,25–31 Aspuru-Guzik and co-workers made advances in using machine learning for ROM design.^32–38 Lengeling and co-workers predicted solubility for organic semiconductors and drug compounds.³⁷ In this study, we describe a QSPR model to rationalize solubility trends for neutral and charged phenothiazine (PT) molecules in a set of 30 homologous ROM (Fig. 1).

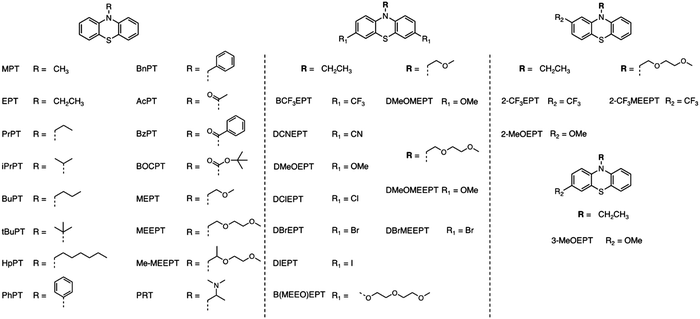Fig. 1 Chemical structures and abbreviations of the phenothiazine (PT) derivatives examined in this study.

Among the active materials (posolytes) that are used to store positive charge in NAqRFBs, the PT derivatives have been studied extensively.^{12,23,39–43} Several approaches to increase PT solubility in their neutral and charged states have been demonstrated,^{12,23,24,39,41} but a complete physicochemical understanding of the solubility trends is lacking. In the experiments reported here, the PT radical cation is paired with tetrafluoroborate anion (BF₄⁻). The solubility in acetonitrile (ACN), with or without electrolyte (0.5 M tetraethylammonium tetrafluoroborate, TEABF₄) was determined experimentally, and these data were used to develop the QSPR models. While the QSPR methods described here “work”, the models are complex, and provide limited insight into the multiplicity of factors that control solubility, suggesting that this statistical approach cannot replace high-throughput solubility studies. So many factors acting in so many ways affect ROM solubility that “predicting” this parameter over a sufficiently large and diverse set of neutral and charged ROM may be practically impossible.

Methods

Solubility determination using ¹H NMR spectroscopy²⁴

A saturated solution was prepared by adding an excess amount of a PT to electrolyte (ACN or 0.5 M TEABF₄ in ACN) and then dissolving this material by vortexing and/or heating. The solution was stored overnight to equilibrate, after which the precipitate was removed by filtering the solution through a microporous syringe filter (25 mm, PTFE). With liquid PT derivatives, where two phases were observed (e.g. BuPT and HpPT) upon equilibration, the saturated solution was carefully removed using a syringe. An NMR sample was then prepared by mixing a known aliquot (100 μL) of the saturated solution with an aliquot (100 μL) of an NMR standard (1,4-bis(trifluoromethyl)benzene) at a known concentration (1.0 M) in deuterated dimethyl sulfoxide, DMSO-d₆ (Fig. S1, ESI†). To this mixture, 300 μL DMSO-d₆ was added. The NMR standard conveniently yields singlet resonances both in the ¹H and ¹⁹F NMR spectra. By referencing the ¹H and ¹⁹F resonances to this standard, it is possible to determine the mole fractions not only of organic components (such as ACN, TEA cation, and PTs) but also of fluorinated inorganic anions, so it can also be used for alkali electrolytes, in which the electrolyte cation cannot be quantified by ¹H NMR. The NMR spectra were recorded using a 25 s delay between the excitation pulses to ensure the complete relaxation of the magnetic nuclei between the pulses. The solubility was calculated by integrating the solute and the standard peaks in the ¹H NMR spectrum and obtaining their ratios (Fig. S2, ESI,† see example with 2-CF₃EPT shown in Fig. 1).⁴⁴ When analyzing radical cations, excess sodium thiosulfate (Na₂S₂O₃) was added to the DMSO solution to reduce the species. The quenching of radical cations can be recognized through the color change of the solution. All measurements were carried out at 298 K.

Solubility determination using the weighing method

A weighing method was also employed to determine the solubilities and compare the results with the NMR method. Three PT derivatives with low, moderate, and high solubilities determined by the NMR method were analyzed (Table 1). For solubility determination, a saturated solution of the compound was prepared (as described in the NMR solubility method). Then, a known volume of the saturated solution was measured into tared vial. The solvent was evaporated using a Schlenk line. The mass of the compound in that known volume was obtained. The concentration of the compound was calculated using the volume of the solution and the mass of the compound obtained. This method cannot be used to determine the solubility in the presence of a supporting electrolyte and, hence, the solubility comparison was limited to sample solutions in ACN.

Table 1 Comparison of two solubility methods – NMR and weighing method

Neutral	Solubility (M)		Radical cation salts	Solubility (M)
	Weighing method	NMR method		Weighing method	NMR method
2-CF3EPT	0.925 ± 0.001	0.96 ± 0.01	MEEPT-BF4	0.512 ± 0.001	0.526 ± 0.004
3-MeOEPT	0.2119 ± 0.0002	0.225 ± 0.005	2-CF3MEEPT-BF4	0.195 ± 0.001	0.185 ± 0.001
DBrEPT	0.0546 ± 0.0003	0.0576 ± 0.0005	DBrEPT-BF4	0.0847 ± 0.0005	0.0751 ± 0.0006

---

QSPR models for PT solubility

As we were interested in using molecular shape-dependent descriptors (computational workflow used for descriptor generation is presented in Fig. 2), it was important to obtain representative conformations of the PT molecules. Conformational searches, based on an internal coordinate Monte Carlo (MC) method, were performed using the BOSS 4.9 script, with 500 starting structures used to sample the molecular conformational space.⁴⁵ The energy scoring was based on the OPLS-AA forcefield.^46,47 The conformers generated were then subject to geometry optimization with the PM6 semi-empirical method.⁴⁸ Select conformers, excluding duplicate minima, were subsequently used for optimization using density functional theory (DFT) with the B3LYP functional and 6-311G(d,p) basis set^49,50 using the CPCM implicit solvation model^51,52 with ACN as the solvent in the Gaussian 16 software suite.⁵³ This approach was used to provide a consistent set of results from previous modeling studies of PT.^39,54–57 Normal mode calculations were used to verify that all DFT-optimized structures are minima on the potential energy surface.

Fig. 2 Computational workflow used in modeling, where Schr – the Mulliken partial charge on the sulfur atom, RP – the redox potential from DFT computations, SsssN – the sum of electro-topological state indices for N atom, ZMIC3 – the order-3 Z-modified information content, AATS7i, ATSC2Z, ATSC4v, ATSC3p are Moreau–Broto autocorrelation of topological structure (ATS) descriptors associated with the Gasteiger's ionization potential, atomic number, VdW volume, and polarizability.

Molecular descriptors derived from the DFT calculations (Fig. 3) include dipole moment, polarizability, thermal energy, heat capacity, configurational entropy, Mulliken charges on the sulfur and nitrogen atoms in the aromatic core, adiabatic ionization potentials, and solvation energies. Additional descriptors, such as the solvent accessible surface area (SASA),⁵⁸ the butterfly angle between the planes of the phenyl rings in PT, and conformationally weighted Sterimol values⁵⁹ were also included; the latter were used to account for the conformational degrees of freedom.⁵⁹ The PT conformers for these analyses were generated using the MOPAC 2016⁶⁰ software with semi-empirical PM6-D3H4 method,⁶¹ which has been shown to perform well in other systems.⁶² The temperature for the Boltzmann distribution was 298 K, and the energy cutoff for conformers was 20.9 kJ mol⁻¹. These calculations used the publicly available wSterimol package written in Python.⁵⁹

Fig. 3 Representations of select molecular descriptors used in the QSPR models: (a) the butterfly angle (depicted in red) of PT; (b) the solvent accessible surface as determined by assuming the PT (yellow) and solvent (blue) molecules as spheres; (c) sterimol values L and B5 of 2-CF₃EPT; (d) Mulliken partial atomic charges, here shown for the radical cation of 3,7-B(MEEO)EPT, with positive and negative partial charges are depicted in red and green, respectively.

The Python library ‘Mordred’ was used to generate 1800+ descriptors for each neutral ROM from 48 basic categories. A complete table of these descriptors can be found in the original publication by Moriwaki et al.⁶³ A large fraction of these descriptors can be rejected as they are linearly dependent over the data set. Highly correlated (with the Pearson's correlation coefficient >0.9) descriptors and descriptors with almost constant (variance threshold >0.9) values for all molecules were removed to reduce the dimensionality of descriptor space. A description of this filtering is available in ESI.†

QSPR modeling was carried out using the multiple linear regression (MLR) approach⁶⁴via built-in functions from the statistics and machine learning and bioinformatics toolboxes in MATLAB.⁶⁵ The procedure and the algorithms involved are presented in detail by Guo et al.³¹ To obtain MLR models, forward stepwise linear regression was performed with cross-validation and selection of training and validation sets were automated with pre-set rules as explained in the ESI.† To ensure the models avoided overfitting, several validation techniques – such as k-fold cross validation (CV) and leave-one-out (LOO) CV method – were used. k-fold validation R², Q² from the LOO CV method, along with Pearson R² values for the training and whole set are available in the ESI.†

Results and discussion

PT solubility determination

The PT set includes N–R derivatives (Fig. 1), where R are small alkyl groups, (Me, Et, Pr, i-Pr) larger aliphatic chains (Hp, Ph, Bz), or glycol chains (ME, MEE, Me-MEE), linear or branched. Other PT derivatives include symmetric and asymmetric substitution with electron donating and electron withdrawing groups on the phenyl rings. The charged PT (radical cations) were isolated as tetrafluoroborate salts using chemical oxidation of the corresponding PT with nitrosonium tetrafluoroborate (NOBF₄); note that ^tBuPT, AcPT, BOCPT, BzPT, PRT, DIEPT, DCNEPT, 2-MeOEPT, and 3-MeOEPT formed unstable radical cations.

The solubilities of both neutral and charged PT were determined at 298 K using the NMR method. To not limit solubility determination to one method and compare the accuracy of the NMR method, selected PT had solubilities determined using the weighing method (Table 1); these PTs were chosen as their NMR solubilities spanned small, moderate, and large solubility. The solubilities obtained using the two methods were comparable within the limits of experimental uncertainty.

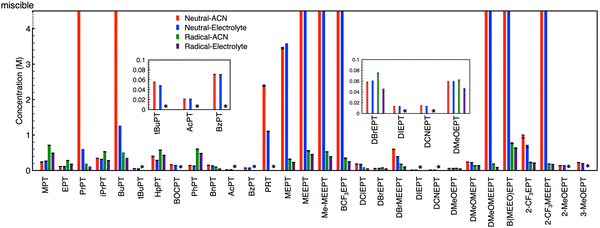
Fig. 4 provides the complete set of NMR-determined solubilities for both neutral PT and the radical-cation salts in the solvent (ACN) and electrolyte (0.5 M TEABF₄ in ACN). Some radical-cation salts (denoted by an asterisk * in the figure) decomposed before isolation; no estimates are provided for these salts. Neutral PT with glycol chains are viscous liquids that are miscible with the solvent and electrolyte, so their solubilities are also not reported. PrPT (in ACN) and BCF₃EPT formed viscous solutions, in these cases solubility could not be determined as no precipitate was observed. Among the N-alkylated PTs, the n-butyl derivative is the most soluble. In general, for neutral PT, introduction of long glycol chains, charged (e.g., onium) and trifluoromethyl groups, and asymmetry improve the solubility. For the BF₄⁻ derived radical-cation salts, the solubilities are <1 M, regardless of the functional groups on the PT. Smaller solubilities are observed in the presence of electrolyte as can be expected due to increased ionic association in such solutions.

Fig. 4 Solubility of various phenothiazines in their neutral and charged forms in acetonitrile and 0.5 M TEABF₄/ACN labeled “electrolyte” (*: unstable radical cations failed to be isolated as solids).

Interestingly, some of the N-alkyl substituted PT compounds show larger solubility in the charged state compared to the neutral state, while for other derivatives, the radical-cation salts have smaller solubilities compared to the corresponding neutral precursors. Most of the miscible (neutral) PT show significantly smaller solubilities in their charged state when coupled with BF₄⁻ as the counter-anion. Overall, the data set shows great variability, but no obvious trends. This high variability suggests multiple factors are in play across the varied chemical landscape.

QSPR modeling

To derive the QSPR models, the data were divided into training and validation sets. The selection of the training and the validation set was automated in an iterative way to choose the best performing validation/training sets with few constraints to let certain data points remain exclusively only in the training set so that the structure variability could be captured effectively. The PT core is rigid for all derivatives, though there is a change in the “butterfly angle” when the molecule is oxidized.^54,66,67 Importantly, a large degree of structural variability is possible given the chemical groups appended to the PT cores. To account for these conformers and find low-energy structures, a molecular dynamics (MD)-based conformation search was implemented, with select low energy conformations followed by geometry optimizations with both semi-empirical and DFT-based approaches, as described in the Methods.

To reduce the computational cost associated with MLR, the number of descriptors was reduced to 125 by using the descriptor reduction method explained in the ESI.† The select molecular descriptors and their values are provided in the ESI† (note that the descriptor sets differ for the neutral and charged PT). Even after using pre-set rules to identify the best performing models, the stepwise MLR computations yielded 50 and 72 different, yet comparably performing, four-to-six-descriptor models for neutral and radical-cation systems, respectively, requiring human arbitration among these models. The down-selection ultimately resulted in seven models for neutral PT and ten models for charged PT. Data on the QSPR models after the initial benchmark are provided in the ESI.† A close examination of the MLR models reveals that the molecular descriptors in the best-performing models recurred frequently, though in different combinations (as the descriptors are linearly correlated over the data set). Notably, the molecular descriptors of primary importance in the neutral models differ from those for the charged PT. We further note that the availability of data points in this study, though we have a large number of systems, is limited, as many phenothiazine derivatives are either miscible (which cannot be used in modeling since a numerical value for solubility cannot be obtained) or have solubilities less than 0.5 M in the solvent/electrolyte of choice. To examine the impact of the clustering, we systematically removed data points for the model input below 0.5 M to observe how the fit would change, as detailed further in the ESI.† Importantly, it was observed that neither the model fit nor the prediction were significantly affected by this alteration (Fig. S8 and S9, ESI†).

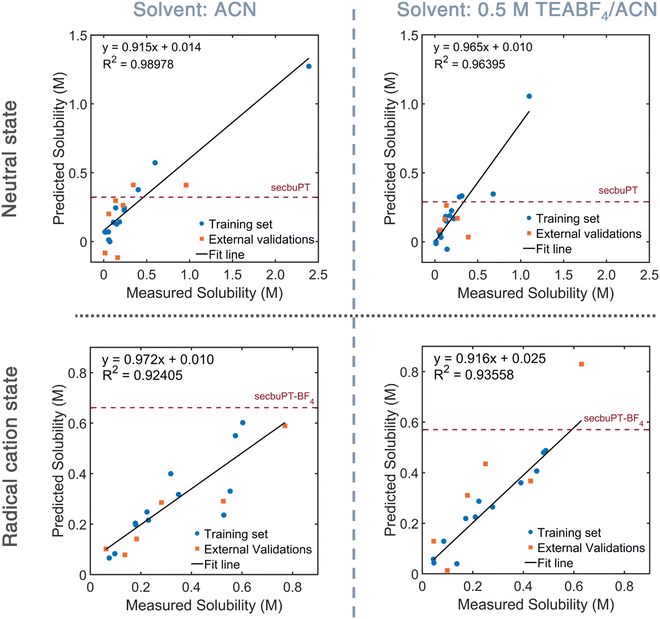
To explore the predictive capability of the QSPR models, the down-selected models were used to estimate the solubility of neutral and charged sec-butyl-PT in ACN and 0.5 M TEABF₄ solution. Representative plots are shown in Fig. 5, and numerical data are given in Table 2. For the neutral compound, the model and experimental estimates are within 28% of each other. The QSPR model for the neutral PT used the following molecular descriptors: Schr – the Mulliken partial charge on the sulfur atom, RP – the redox potential derived from DFT, SsssN – the sum of electro-topological state indices for a nitrogen atom with three σ bonds (as in the N in the PT core),^68,69 and ZMIC3 – the order-3 Z-modified information content.^70,71 For the PT radical-cation six-descriptor QSPR model, the model estimate is within 15% of the experimental estimate. This QSPR model uses four Moreau–Broto autocorrelation of topological structure (ATS) associated with the atomic number and Gasteiger's ionization potential and polarizability, and a molecular descriptor that describes partition coefficient/surface area. A Moreau–Broto autocorrelator describes how an atomic property correlates over the atomic connectivity graph, with the lag representing the number of chemical bonds between the correlated atoms; each such correlation is taken over the entire molecule.^72–76 ATSC7p, which is the centered Moreau–Broto autocorrelation of lag 7 weighted by atomic polarizability, characterizes the distribution of polarizability, including the correlations between the polarizable atoms in the chains and the S atom in the PT ring.

Fig. 5 Predictive models for neutral and charged of sec-butylPT in ACN and 0.5 M TEABF₄ in ACN.

Table 2 Experimental and predicted solubilities of neutral and radical cation forms of sec-butylPT in ACN and electrolyte (0.5 M TEABF₄ in ACN)

sec-ButylPT or sec-butylPT^+˙BF4^−	Experimental solubility (M)	Predicted solubility (M)
Neutral in ACN	0.44	0.32
Neutral in electrolyte	0.40	0.29
Radical cation salt in ACN	0.60	0.66
Radical cation salt in electrolyte	0.50	0.57

---

Perhaps it is not surprising that at least four-to-six descriptors are necessary to obtain even limited quality QSPR models over a set of 30 compounds. When the solubility is small, it is determined by interactions of PT molecules (or their radical ions) with the solvent and electrolyte. When the solubility is large, it is additionally limited by aggregation. For PT, stacking of the aromatic rings is observed both in the neutral and charged states in reported X-ray crystal structures, so solubility is a complex property. QSPR is a statistical tool, offering no explanation as to why certain descriptors are selected while other descriptors are rejected, yet the prominence of certain types of molecular descriptors begs explanation.

For the radical cation, we believe that the QSPR selections hint that (i) charge delocalization and (ii) the surface area of solvophilic groups are important factors in determining solubility. This delocalization is implicit in the QSPR model, as the most important descriptors are ATS correlators for atoms in the PT “heads” and “tails,” as the molecule strives to achieve the optimum balance of polarity and polarizability between the head group and the appendages. A greater delocalization of the positive charge over the PT core and lowering of charge in this core helps to reduce localization of this charge in the heteroatoms, which increases the association of the radical cations with anions, thereby decreasing their solubility. The importance of the ring nitrogen is also suggested by the SsssN descriptor that is prominent in the QSPR models for neutral PT molecules.

The second important factor is the increase in the solvophilic area. Without substitution, the solvophobic PT molecule (in either state of charge) has very small solubility. That is, the increased solubility originates entirely through the substitution, hence the importance of solvent interactions in the appendages. This is seen from the best QSPR models, which always include molecular descriptors associated with such interactions, e.g., molecular descriptors such as PEOE_VSA (which describes the surface area contributions to binned partial charges in the molecule) and PNSA (which describes the partial negative surface area) that characterize these interactions.

Finally, the shape matters. Generally, molecular asymmetry increases the solubility (discussed further in ESI†). This asymmetry can be characterized by the moment of inertia about the principal axis. This trend can be explained through the increased polarity (at low solubility) and frustration of packing of oddly shaped molecules that inhibits crystallization (at high solubility).

Conclusions

Solubilities for neutral and charged ROM in organic electrolytes are important quantities that determine the energy density of battery fluids. This property is difficult to predict computationally as it reflects the complexity of molecular interactions in multicomponent systems. Still, how difficult is this “difficult?” This is the question that our colleague and friend Susan Odom, a brilliant and inquisitive scientist, posed before us at the onset of this study. If the general trends are difficult to elucidate, could these trends be recognized in a smaller set of related ROM? As Susan amassed a large collection of phenothiazine derivatives, we decided to find out.

To answer Susan's question, we obtained isothermal solubilities for 30 phenothiazine derivatives in their neutral and charged states. We were able to isolate the charged forms (of 21 derivatives) that were stable under ambient conditions for the duration of experimental analysis. We then used QSPR to correlate these measurements with molecular descriptors, starting with a set of 1800+ descriptors. The simplest QSPR models that we found involved four-to-six molecular descriptors, as required for a fairly complex chemical space, and even with so many descriptors, the model quality was middling. The QSPR models were only moderately successful in predicting the solubility of an unknown PT compound within 10–15% deviation from the experimental value when charged state was considered. In conclusion, predicting ROM solubility proved to be as challenging to a statistics program as it is to a human chemist. Modeling the solubility of a molecule class such as PT with only a few descriptors is difficult as solubility is affected by multiple attributes of such a molecule in varying degrees. Nevertheless, by using a higher number of descriptors (with statistical and analytical validation to reject overfitting) we were able to obtain a general understanding of how to increase PT solubility.

The analysis of molecular descriptors that were selected by successful models hints the contributions of factors such as a surface area with delocalized positive charges, effects due to asymmetry and entropy, the susceptibility of the N atom on the PT core, the contribution of substituents at 3,7 positions, and the effectiveness of these contributions with respect to strain/steric and charge hindrance that positively affect the solubility of PT derivatives. The high variability in the data and “irreducible complexity” of QSPR models are sobering. In flow batteries, the temperature and composition change continuously during electrochemical cycling. If the machine-based “prediction” of ROM solubility is so problematic even in the tightly controlled environment, how much more difficult would it be in a realistic setting? Predictive modeling/machine learning can be an effective tool, when utilized within an applicable context. However, a task such as the determination of solubility of a complex organic molecule in a non-aqueous solution environment is rather limited due to the unavailability high-throughput synthesis and solubility measurement methods. Hence, the success of efficient and robust prediction is hindered in non-trivial systems as this case.

Thus, our results suggest that in the foreseeable future ROM solubility trends will be discerned through experimental measurements, and developing high-throughput methodologies should be prioritized. In this connection, the NMR method presented in this study is of considerable interest, as it easily lends itself to the automation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported as part of the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a U.S. Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government. C. R. acknowledges support from the National Science Foundation through the Established Program to Stimulate Competitive Research (EPSCoR) Track 2 program under cooperative agreement number 2019574. We acknowledge the University of Kentucky Center for Computational Sciences and Information Technology Services Research Computing for their fantastic support and collaboration and use of the Lipscomb Compute Cluster and associated research computing resources.

References

1. O. Ostroverkhova, Organic Optoelectronic Materials: Mechanisms and Applications, Chem. Rev., 2016, 116(22), 13279–13412.
2. G. Kwon, Y. Ko, Y. Kim, K. Kim and K. Kang, Versatile Redox-Active Organic Materials for Rechargeable Energy Storage, Acc. Chem. Res., 2021, 54(23), 4423–4433.
3. J. Hopkins, K. Fidanovski, A. Lauto and D. Mawad, All-Organic Semiconductors for Electrochemical Biosensors: An Overview of Recent Progress in Material Design, Front. Bioeng. Biotechnol., 2019, 7, 237.
4. M. Stolar and T. Baumgartner, Organic n-type materials for charge transport and charge storage applications, Phys. Chem. Chem. Phys., 2013, 15(23), 9007–9024.
5. T. B. Schon, B. T. McAllister, P.-F. Li and D. S. Seferos, The rise of organic electrode materials for energy storage, Chem. Soc. Rev., 2016, 45, 6345–6404.
6. E. Steckhan, Indirect Electroorganic Syntheses—A Modern Chapter of Organic Electrochemistry [New Synthetic Methods (59)], Angew. Chem., Int. Ed. Engl., 1986, 25(8), 683–701.
7. X. Jia, Radical Cation Salts: From Single-Electron Oxidation to C–H Activation, Synthesis, 2016, 48, 18–30.
8. K. Gong, Q. Fang, S. Gu, S. F. Y. Li and Y. Yan, Nonaqueous redox-flow batteries: organic solvents, supporting electrolytes, and redox pairs, Energy Environ. Sci., 2015, 8, 3515–3530.
9. Y. Yan, S. G. Robinson, M. S. Sigman and M. S. Sanford, Mechanism-Based Design of a High-Potential Catholyte Enables a 3.2 V All-Organic Nonaqueous Redox Flow Battery, J. Am. Chem. Soc., 2019, 141, 15301–15306.
10. J. Chai, A. Lashgari, X. Wang and J. J. Jiang, Extending the Redox Potentials of Metal-Free Anolytes: Towards High Energy Density Redox Flow Batteries, J. Electrochem. Soc., 2020, 167(10), 100556.
11. Y. Yan, T. P. Vaid and M. S. Sanford, Bis(diisopropylamino)cyclopropenium-arene Cations as High Oxidation Potential and High Stability Catholytes for Non-aqueous Redox Flow Batteries, J. Am. Chem. Soc., 2020, 142, 17564–17571.
12. N. H. Attanayake, Z. Liang, Y. Wang, A. P. Kaur, S. R. Parkin, J. K. Mobley, R. H. Ewoldt, J. Landon and S. A. Odom, Dual function organic active materials for nonaqueous redox flow batteries, Mater. Adv., 2021, 2(4), 1390–1401.
13. R. M. Darling, K. G. Gallagher, J. A. Kowalski, S. Ha and F. R. Brushett, Pathways to Low-Cost Electrochemical Energy Storage: A Comparison of Aqueous and Nonaqueous Flow Batteries, Energy Environ. Sci., 2014, 7, 3459–3477.
14. R. Dmello, J. D. Milshtein, F. R. Brushett and K. C. Smith, Cost-driven Materials Selection Criteria for Redox Flow Battery Electrolytes, J. Power Sources, 2016, 330, 261–272.
15. Y. Ding, C. Zhang, L. Zhang, Y. Zhou and G. Yu, Molecular engineering of organic electroactive materials for redox flow batteries, Chem. Soc. Rev., 2018, 47(1), 69–103.
16. S. G. Robinson, Y. Yan, K. H. Hendriks, M. S. Sanford and M. S. Sigman, Developing a predictive solubility model for monomeric and oligomeric cyclopropenium-based flow battery catholytes, J. Am. Chem. Soc., 2019, 141, 10171–10176.
17. L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput, K. Persson and L. A. Curtiss, Accelerating Electrolyte Discovery for Energy Storage with High-Throughput Screening, J. Phys. Chem. Lett., 2015, 6(2), 283–291.
18. Y. Zhao, E. S. Sarnello, L. A. Robertson, J. Zhang, Z. Shi, Z. Yu, S. R. Bheemireddy, Y. Z, T. Li, R. S. Assary, L. Cheng, Z. Zhang, L. Zhang and I. A. Shkrob, Competitive Pi-Stacking and H-Bond Piling Increase Solubility of Heterocyclic Redoxmers, J. Phys. Chem. B, 2020, 142, 10409–10418.
19. C. W. Coley, R. Barzilay, W. H. Green, T. S. Jaakkola and K. F. Jensen, Convolutional Embedding of Attributed Molecular Graphs for Physical Property Prediction, J. Chem. Inf. Model., 2017, 57(8), 1757–1772.
20. C. G. Armstrong, R. W. Hogue and K. E. Toghill, Application of the dianion croconate violet for symmetric organic non-aqueous redox flow battery electrolytes, J. Power Sources, 2019, 440, 227037.
21. S. G. Robinson, Y. Yan, K. H. Hendriks, M. S. Sanford and M. S. Sigman, Developing a Predictive Solubility Model for Monomeric and Oligomeric Cyclopropenium-Based Flow Battery Catholytes, J. Am. Chem. Soc., 2019, 141(26), 10171–10176.
22. J. D. Milshtein, A. P. Kaur, M. D. Casselman, J. A. Kowalski, S. Modekrutti, P. L. Zhang, N. Harsha Attanayake, C. F. Elliott, S. R. Parkin, C. Risko, F. R. Brushett and S. A. Odom, High current density, long duration cycling of soluble organic active species for non-aqueous redox flow batteries, Energy Environ. Sci., 2016, 9(11), 3531–3543.
23. A. P. Kaur, N. E. Holubowitch, S. Ergun, C. F. Elliott and S. A. Odom, A Highly Soluble Organic Catholyte for Non-Aqueous Redox Flow Batteries, Energy Technol., 2015, 3(5), 476–480.
24. Y. Wang, A. P. Kaur, N. H. Attanayake, Z. Yu, T. M. Suduwella, L. Cheng, S. A. Odom and R. H. Ewoldt, Viscous flow properties and hydrodynamic diameter of phenothiazine-based redox-active molecules in different supporting salt environments, Phys. Fluids, 2020, 32(8), 083108.
25. Y. Yan, S. G. Robinson, M. S. Sigman and M. S. Sanford, Mechanism-Based Design of a High-Potential Catholyte Enables a 3.2 V All-Organic Nonaqueous Redox Flow Battery, J. Am. Chem. Soc., 2019, 141(38), 15301–15306.
26. J. Werth and M. S. Sigman, Connecting and Analyzing Enantioselective Bifunctional Hydrogen Bond Donor Catalysis Using Data Science Tools, J. Am. Chem. Soc., 2020, 142(38), 16382–16391.
27. C. S. Sevov, D. P. Hickey, M. E. Cook, S. G. Robinson, S. Barnett, S. D. Minteer, M. S. Sigman and M. S. Sanford, Physical Organic Approach to Persistent, Cyclable, Low-Potential Electrolytes for Flow Battery Applications, J. Am. Chem. Soc., 2017, 139(8), 2924–2927.
28. S. G. Robinson and M. S. Sigman, Integrating Electrochemical and Statistical Analysis Tools for Molecular Design and Mechanistic Understanding, Acc. Chem. Res., 2020, 53(2), 289–299.
29. J. P. Reid and M. S. Sigman, Comparing quantitative prediction methods for the discovery of small-molecule chiral catalysts, Nat. Rev. Chem., 2018, 2(10), 290–305.
30. J. P. Reid and M. S. Sigman, Holistic prediction of enantioselectivity in asymmetric catalysis, Nature, 2019, 571(7765), 343–348.
31. J.-Y. Guo, Y. Minko, C. B. Santiago and M. S. Sigman, Developing Comprehensive Computational Parameter Sets To Describe the Performance of Pyridine-Oxazoline and Related Ligands, ACS Catal., 2017, 7(6), 4144–4151.
32. B. Sanchez-Lengeling and A. Aspuru-Guzik, Learning More, with Less, ACS Cent. Sci., 2017, 3(4), 275–277.
33. B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361(6400), 360–365.
34. E. Putin, A. Asadulaev, Y. Ivanenkov, V. Aladinskiy, B. Sanchez-Lengeling, A. Aspuru-Guzik and A. Zhavoronkov, Reinforced Adversarial Neural Computer for de Novo Molecular Design, J. Chem. Inf. Model., 2018, 58(6), 1194–1204.
35. R. Gomez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernandez-Lobato, B. Sanchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules, ACS Cent. Sci., 2018, 4(2), 268–276.
36. J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, Neural Networks for the Prediction of Organic Chemistry Reactions, ACS Cent. Sci., 2016, 2(10), 725–732.
37. B. Sanchez-Lengeling, L. M. Roch, J. D. Perea, S. Langner, C. J. Brabec and A. Aspuru-Guzik, A Bayesian Approach to Predict Solubility Parameters, Adv. Theory Simul., 2019, 2(1), 1800069.
38. S. Kim, A. Jinich and A. Aspuru-Guzik, MultiDK: A Multiple Descriptor Multiple Kernel Approach for Molecular Discovery and Its Application to Organic Flow Battery Electrolytes, J. Chem. Inf. Model., 2017, 57(4), 657–668.
39. J. D. Milshtein, A. P. Kaur, M. D. Casselman, J. A. Kowalski, S. Modekrutti, P. L. Zhang, N. H. Attanayake, C. F. Elliott, S. R. Parkin, C. Risko, F. R. Brushett and S. A. Odom, High Current Density, Long Duration Cycling of Soluble Organic Active Species for Non-Aqueous Redox Flow Batteries, Energy Environ. Sci., 2016, 9, 3531–3543.
40. J. A. Kowalski, M. D. Casselman, A. P. Kaur, J. D. Milshtein, C. F. Elliott, S. Modekrutti, N. H. Attanayake, N. Zhang, S. R. Parkin, C. Risko, F. R. Brushett and S. A. Odom, A Stable Two-Electron-Donating Phenothiazine for Application in Nonaqueous Redox Flow Batteries, J. Mater. Chem. A, 2017, 5, 24371–24379.
41. N. H. Attanayake, J. A. Kowalski, K. Greco, M. D. Casselman, J. D. Milshtein, S. J. Chapman, S. R. Parkin, F. R. Brushett and S. A. Odom, Tailoring Two-Electron Donating Phenothiazines to Enable High Concentration Redox Electrolytes for Use in Nonaqueous Redox Flow Batteries, Chem. Mater., 2019, 31, 4353–4363.
42. A. P. Kaur, O. C. Harris, N. H. Attanayake, Z. Liang, S. R. Parkin, M. H. Tang and S. A. Odom, Quantifying Environmental Effects on the Solution and Solid-State Stability of Phenothiazine Radical Cations, Chem. Mater., 2020, 32(7), 3007–3017.
43. N. H. Attanayake, A. P. Kaur, T. M. Suduwella, C. F. Elliott, S. R. Parkin and S. A. Odom, A Stable, Highly Oxidizing Radical Cation, New J. Chem., 2020, 44, 18138–18148.
44. M. Li, S. A. Odom, A. R. Pancoast, L. A. Robertson, T. P. Vaid, G. Agarwal, H. A. Doan, Y. Wang, T. M. Suduwella, S. R. Bheemireddy, R. H. Ewoldt, R. S. Assary, L. Zhang, M. S. Sigman and S. D. Minteer, Experimental Protocols for Studying Organic Non-aqueous Redox Flow Batteries, ACS Energy Lett., 2021, 6(11), 3932–3943.
45. W. L. Jorgensen and J. Tirado-Rives, Molecular modeling of organic and biomolecular systems using BOSS and MCPRO, J. Comput. Chem., 2005, 26(16), 1689–1700.
46. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236.
47. M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, Improved Peptide and Protein Torsional Energetics with the OPLSAA Force Field, J. Chem. Theory Comput., 2015, 11(7), 3499–3509.
48. J. J. P. Stewart, Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements, J. Mol. Model., 2007, 13(12), 1173–1213.
49. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789.
50. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: Gen. Phys., 1988, 38(6), 3098–3100.
51. V. Barone and M. Cossi, Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model, J. Phys. Chem. A, 1998, 102(11), 1995–2001.
52. A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993,(5), 799–805.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Wallingford, CT, 2016.
54. S. A. Odom, C. Risko, M. D. Casselman, C. F. Elliott, N. H. Attanayake and S. Modekrutti, 1,9,10-Substituted Phenothiazine Derivatives with Strained Radical Cations and use thereof, US Pat., 10854911, 2020.
55. K. A. Narayana, M. D. Casselman, C. F. Elliott, S. Ergun, S. R. Parkin, C. Risko and S. A. Odom, N-Substituted Phenothiazine Derivatives: How the Stability of the Neutral and Radical Cation Forms Affects Overcharge Performance in Lithium-ion Batteries, ChemPhysChem, 2015, 16, 1179–1189.
56. A. P. Kaur, M. D. Casselman, C. F. Elliott, S. R. Parkin, C. Risko and S. A. Odom, Overcharge protection of lithium-ion batteries above 4 V with a perfluorinated phenothiazine derivative, J. Mater. Chem. A, 2016, 4(15), 5410–5414.
57. M. D. Casselman, A. P. Kaur, K. A. Narayana, C. F. Elliott, C. Risko and S. A. Odom, The Fate of Phenothiazine-based Redox Shuttles in Lithium-ion Batteries, Phys. Chem. Chem. Phys., 2015, 17, 6905–6912.
58. B. Lee and F. M. Richards, The interpretation of protein structures: Estimation of static accessibility, J. Mol. Biol., 1971, 55(3), 379-IN4.
59. A. V. Brethomé, S. P. Fletcher and R. S. Paton, Conformational Effects on Physical-Organic Descriptors: The Case of Sterimol Steric Parameters, ACS Catal., 2019, 9(3), 2313–2323.
60. J. J. P. Stewart, MOPAC: A semiempirical molecular orbital program, J. Comput.-Aided Mol. Des., 1990, 4(1), 1–103.
61. J. Rezac and P. Hobza, Advanced Corrections of Hydrogen Bonding and Dispersion for Semiempirical Quantum Mechanical Methods, J. Chem. Theory Comput., 2012, 8(1), 141–151.
62. K. Kriz and J. Rezac, Benchmarking of Semiempirical Quantum-Mechanical Methods on Systems Relevant to Computer-Aided Drug Design, J. Chem. Inf. Model., 2020, 60(3), 1453–1460.
63. H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, Mordred: a molecular descriptor calculator, J. Cheminf., 2018, 10(1), 4.
64. P. Liu and W. Long, Current mathematical methods used in QSAR/QSPR studies, Int. J. Mol. Sci., 2009, 10(5), 1978–1998.
65. MATLAB, 9.7.0.1190202 (R2019b), The MathWorks Inc., Natick, Massachusetts, 2019.
66. C. F. Elliott, K. E. Fraser, S. A. Odom and C. Risko, Steric Manipulation as a Mechanism for Tuning the Reduction and Oxidation Potentials of Phenothiazines, J. Phys. Chem. A, 2021, 125(1), 272–278.
67. M. D. Casselman, C. F. Elliott, S. Modekrutti, P. L. Zhang, S. R. Parkin, C. Risko and S. A. Odom, Beyond the Hammett Effect: Using Strain to Alter the Landscape of Electrochemical Potentials, ChemPhysChem, 2017, 18(16), 2142–2146.
68. L. B. Kier and L. H. Hall, Pharm. Res., 1990, 07(8), 801–807.
69. L. H. Hall, B. Mohney and L. B. Kier, The Electrotopological State: An Atom Index for QSAR, Quant. Struct.-Act. Relat., 1991, 10(1), 43–51.
70. S. C. Basak, V. R. Magnuson, G. J. Niemi, R. R. Regal and G. D. Veith, Topological indices: their nature, mutual relatedness, and applications, Math. Modell., 1987, 8, 300–305.
71. S. C. Basak, V. R. Magnuson, G. J. Niemi and R. R. Regal, Determining structural similarity of chemicals using graph-theoretic indices, Discrete Appl. Math., 1988, 19(1–3), 17–44.
72. B. Hollas, An Analysis of the Autocorrelation Descriptor for Molecules, J. Math. Chem., 2003, 33(2), 91–101.
73. G. Moreau and P. Broto, The autocorrelation of a topological structure: A new molecular descriptor, Nouv. J. Chim., 1980, 4, 359–360.
74. P. Broto, G. Moreau and C. Vandycke, Molecular structures perception auto correlation descriptor and structure activity relationship studies auto correlation descriptor, Eur. J. Med. Chem., 1984, 19(1), 66–70.
75. P. Broto, G. Moreau and C. Vandycke, Molecular structures perception auto correlation descriptor and structure activity relationship studies perception of molecules topological structure and 3 dimensional structure, Eur. J. Med. Chem., 1984, 19(1), 61–65.
76. J. Devillers and A. T. Balaban, Topological Indices and Related Descriptors in QSAR and QSPAR, Taylor & Francis, 2000.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00598k

‡ The authors contributed equally to the manuscript.

---