Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A low-cost tabletop tensile tester with optical extensometer†‡
Mogens
Hinge
 *a,
Jeremiah A.
Johnson
*a,
Jeremiah A.
Johnson
 *b and
Martin L.
Henriksen
*b and
Martin L.
Henriksen
 *ab
*ab
aPlastic and Polymer Engineering, Department of Biological and Chemical Engineering, Aarhus University, Aabogade 40, Aarhus N, DK-8200, Denmark. E-mail: hinge@bce.au.dk; lahn@bce.au.dk
bDepartment of Chemistry, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA. E-mail: jaj2109@mit.edu
First published on 17th August 2021
Abstract
High quality mechanical testing normally demands costly test equipment. This work presents a low cost (∼$500) fully customizable tensile tester that is designed from locally sourced and readily available components and, together with custom made operation software, delivers data of similar quality to commercial equipment. The instrument is small, light, and movable (e.g., it is suitable for a standard fume hood) and should be of interest to laboratories with limited access to advanced characterization facilities. All details are provided for future adaptation and customization.
Introduction
The need for basic mechanical property testing of new polymers and soft matter has increased over the past decade as researchers seek functional1,2 and sustainable3–5 materials, polymers, and elastomers that can potentially replace existing materials. One key parameter for material evaluation is the Young's modulus (E), which can be determined from tensile testing.6–9 The tensile testing experiment is normally performed on commercial equipment of very high quality that gives useful data on materials with a wide range of E values. Nevertheless, the price and availability of such equipment may limit its broad access to researchers, especially in academic laboratories.10,11 Several factors (e.g., equipment rigidity, data acquisition type, sampling rate) determine the optimal choice of equipment, but for certain materials/fields (e.g., gels, tissue engineering, thin films, soft elastomers, etc.) equipment demand may not justify investment in existing commercial instrumentation. Moreover, in chemical research laboratories, solvent evaporation from experimental materials (e.g., gels) may limit where samples can be safely tested (e.g., in a fume hood). Finally, in the COVID-19 era, limited laboratory occupancy can create bottlenecks when multiple researchers seek to use a single instrument; the ability to rapidly produce low-cost alternative instrumentation could be transformative.For laboratories and scientists who seek to add tensile testing to their repertoire, or scale their tensile testing throughput, a small, low cost, locally sourced tensile testing instrument would be advantageous. Few alternatives are available,12–14 but the price, complexity or lack of rigidity, documentation, or calibration can be reasons for not pursuing the design. Herein, a Custom-Made low-cost Tensile Tester (CMTT) with a video extensometer that can be built for ∼$500 is described (Fig. 1). This instrument was developed using the following design principles: (1) it should be cheap to source and build, (2) it should use low-cost components made locally and with simple tooling, and (3) it must allow full access and control of raw data. We believe that this low-cost CMTT instrument should be readily available to researchers and significantly lower the barrier-to-entry for those interested in developing or augmenting their mechanical testing capabilities.
Experimental
The core of the CMTT is based on a Screw-Driven Linear Actuator System (2000-Bundle, OpenBuilds, US) with a moving sledge. Custom-made grips are attached on the moving sledge and on a base mount, both of which are carefully aligned to each other and fastened on an aluminum base plate (Fig. S1–S5, ESI†). The CMTT described here is designed with a 100 N load cell (Parallel beam, TAL220, HT Sensor Technology). The sled is driven with a NEMA 17 stepper motor (1704HS168A) and controlled by a stepper motor driver (Big Easy Driver or Pololu driver) connected to custom designed electronics. Two inter-changeable electronic solutions are proposed employing a microcontroller (Uno or Nano, Arduino, IT). An industrial amplifier (HX711, Avia Semiconductor, CN) with internal 24 bit A/D conversion is used to read the load cell and is connected to the micro controller. An electronic schematic is provided for both microcontroller solutions (Fig. S6 and S7, ESI†). A printed circuit board solution for the Arduino NANO (Fig. S8 and S9, ESI†) and the microcontroller source code (SI: Arduino Code) are made in EAGLE (v 7.7.0 standard edition, CadSoft Computer, GmbH) and Arduino IDE (Arduino v 1.8.5, IT), respectively. The Arduino is connected via RS232 to a computer (ThinkPad T650, Lenovo) running a standalone program (Open Object Pascal, Lazarus IDE15) handling data acquisition from the microcontroller, and a USB web camera (YoLuKe, CN) is applied as a video extensometer. The same program enables manual control of the equipment as well as setup and execution of experiments. A bill of materials (BOM) for all mechanical and electronic parts is provided in the ESI† together with a step-by-step guide for assembly, calibration, and experimental execution.Each image acquired by the web camera is timestamped and saved for post-processing if necessary (SI: Post-processing by ImageJ). Subsequently, the user-defined area of interest (AOI) is cropped out. To increase the signal-to-noise ratio, the cropped image is converted into an 8 bit grey scale (BGray),16 and the pixel values (0–255) in the horizontal direction (x = 0 to x = n) are summed for each line of pixels (y = 0 to y = m) as given by eqn (1).
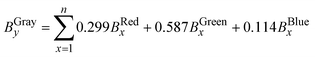 | (1) |
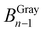 ) and the given pixel (
) and the given pixel (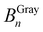 ) are calculated during the summation.
) are calculated during the summation.
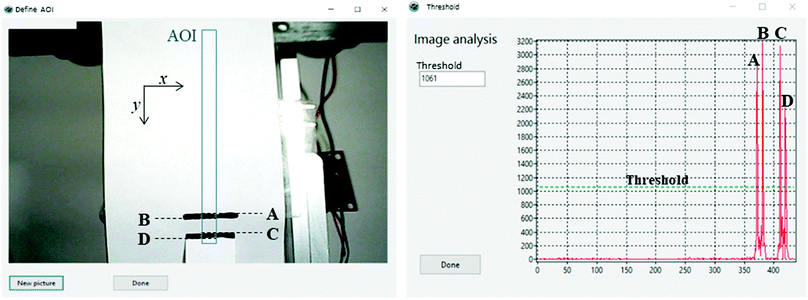
A calibration example can be seen in Fig. 2 (left), where a piece of white paper marked with a black line is moved relative to another paper with a black line. An AOI is defined (blue rectangle) for the calibration. The AOI contrast changes calculated by eqn (1) are illustrated in Fig. 2 (right). The peak annotated A in Fig. 2 (right) corresponds to the top of the upper line in Fig. 2 (left), indicating the contrast change from white to black. Moreover, B indicates the contrast change from black to white, C from white to black, and D from black to white. When the contrast change exceeds the user-defined threshold (dashed line, Fig. 2, right) the pixel position is noted (yA1); the next time the contrast change surpasses the threshold the pixel position is denoted (yA2). The peak apex for peak A is calculated as the average pixel value of yA1 and yA2. Peaks B, C, and D apexes are calculated following the same procedure. The center of the upper line is subsequently calculated as the average of peak apexes A and B, and the center of the lower line is calculated from apexes C and D. Thus, the distance in pixels between the centers of the two lines can be used to calculate the strain. Be aware, optics that produce distorted images with convex or non-linear appearances (e.g., fisheye lenses) will demand careful calibration.
The control system is designed so that the sampling rate is limited by the computer performing the image analysis and data handling. The HX711 samples at 80 Hz in a running average (n = 16) (excluding outliers) on the microcontroller and transmits to the main program on request. All raw data are saved at one Hz (maximum sample rate without failure was 3.33 Hz) in a semicolon separated ASCII file together with: date and time, time difference (ms), distance moved (steps), measured force (N), first line (pixel), last line (pixel), line difference (pixel).
The distance is calibrated by measuring the grip-to-grip distance with a Vernier caliper (±0.02 mm, General Tools & Instruments, US). The sledge is moved 6400 steps between distance measurements repeated 10 times (Fig. 3, left, cross). The load cell is calibrated by mounting a spring scale (50 N/5000 g, Ajax Scientific, US) on the grips, moving the sledge until the scale shows 1000 g, and adjusting the CalFactor to give a load cell response of 1000 g (repeated for 2500 g and 5000 g). Subsequently, the load cell response is measured from 0.25 N to 49.7 N at 10 mm min−1 to validate calibration and linearity (Fig. 3, left, circles). Optical extensometer calibration is performed by clamping a piece of paper with a marking on the bottom grip; another paper with a similar marking is clamped to the sled grip as shown in Fig. 2. Three color combinations are tested (Fig. 3, right); white lines on black paper (WoB), green lines on blue paper (GoB), and black lines on white paper (BoW). An image is acquired after the paper is mounted and the pixels between the marks are determined in ImageJ (1.51r). The initial distances between the marks are determined with a Vernier caliper to 25.61, 11.46, and 14.10 mm for the WoB, GoB, and BoW, respectively.
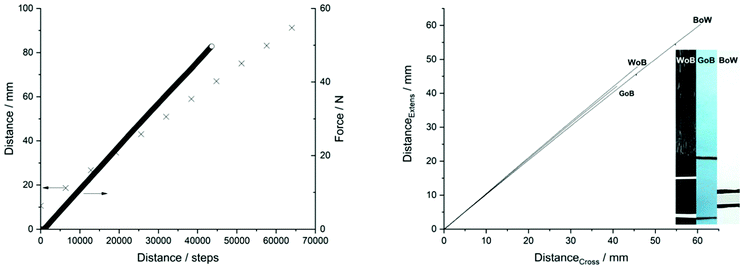 | ||
| Fig. 3 Left: Steps vs. distance and steps vs. force show a strong linear correlation. Right: Crosshead vs. image analyzed distances between two marks show a strong linear correlation. | ||
Calibrations of the load, cross-head displacement, and extensometer are given in Fig. 3. It is seen from Fig. 3 (left, cross) that a linear correlation between steps and distance moved by the sled is evident with 794 steps mm−1 in linear motion. The lead screw has a pitch of 8 mm and the motor has 6400 steps per revolution giving a theoretical value of 800 step mm−1, which compared to the experimental value gives an error of 0.75%. Moreover, Fig. 3 (left) shows a linear response from the load cell as a function of steps (circles). The video extensometer calibration, Fig. 3 (right), shows an initial distance between the marks of 143, 68, and 83 pixels for WoB, GoB, and BoW, respectively, and translates into 5.6, 5.9 and 5.9 pixels mm−1. A linear correlation between distance moved and distance determined is found with a slope of 1.03 ± 0.03. The minor variation from a slope of 1.00 arises from quantification errors during image calibration (error <0.4 pixel). These results further verify that the web camera and algorithm are sufficiently robust and that distance can be measured independently of color on either paper or marking ink.
The CMTT is benchmarked against an Instron 8848 Microtester with a Fast Track 8800 module. The Instron is operated with Instron Console (v. 8.4), Wavemaker Editor (v. 9.2.00), and Wavemaker Runtime (v. 9.2.00). Obtained data are post-processed by deleting duplicates and reducing the data by 90% as described elsewhere.17 Three test materials were marked and applied (Fig. S10, ESI†); (1) Manila paper (45 × 10 × 0.25 mm, file folder, staples, US) cut across (CD) and along (MD) the machining direction, crosshead speed 2 mm min−1, 50 N load cell. (2) Polypropylene (PP) (40 × 2 × 0.20 mm, 16 oz. cup Nexclear, FabriKal, US), cross head speed 2 mm min−1, 2 kN load cell; (3) rubber band (42 × 3.30 × 1.10 mm, Economy rubber band, Staples, US), cross head speed 40 mm min−1, 2 kN load cell. Data are shifted to start from 0.2 MPa to compensate for different toe regions arising due to sample mounting differences.
Results and discussion
The stress as a function of strain (crosshead strain) for each of the three materials are shown in Fig. 4. Manila paper CD (Fig. 4A) has similar ductility and ultimate tensile strength (UTS), but significant differences from 0.5 to 3.0% strain are observed between the two instruments. The video extensor data for the CMTT rather than grip-to-grip distance (Fig. S11, ESI†) supports the higher E and shape measured by Instron. E differences could arise due to the manufacturing direction of the Manila sample; however, the same E yet different UTS values between CD and MD were observed (Fig. S13, ESI†), which is discussed further below. For PP (Fig. 4B), the two pieces of equipment give similar curvature, but the CMTT ends at slightly higher stresses. For the rubber band (Fig. 4C), a clear difference is seen in signal-to-noise levels between CMTT and Instron. The low noise on the CMTT is due to the sampling algorithm on the microcontroller. For the Instron, slippage before rupture of the rubber band could not be prevented, because further tightening would damage the samples.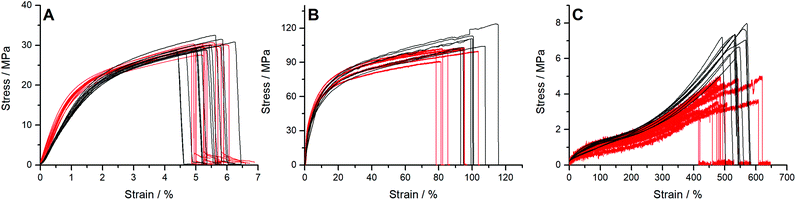 | ||
| Fig. 4 Strain as a function of stress responses from the CMTT and Instron for (A) Manila paper (CD) (B) polypropylene (C) Rubber band. Black line: CMTT. Red line: Instron. | ||
Calculated E, UTS, ductility, and toughness values can be found in Table 1 for each material as measured on the two machines. E for the Manila paper and the rubber's ductility and toughness (for reasons described below) are statistically different in this comparison. It is further seen that the coefficients of variation (standard deviation divided by mean value) is similar for both instruments. Variations are ascribed to sample preparation, sample homogeneity, and mounting/handling, and ranges from 3% to 23% in most cases below ≈12%. The calibration results (Fig. 3) have a coefficient of variation of less than 1% documenting linear responses with respect to displacement, force, and extensometer. From the material comparison (Table 1), the coefficient of variance is a decade higher than the inaccuracies found in the CMTT calibration.
| Material | CMTT | Instron | |||||
|---|---|---|---|---|---|---|---|
| Papere | PP | Rubber | Paper | PP | Rubber | ||
| a Strain: 0.0–1.0%. b Strain: 0.0–5.0%. c Strain: 0–50%. d Strain: 100–200%. e Paper cut in machine direction showed E: 1500(130) MPa; UTS: 49(4.5) MPa; εb: 3.9(0.3)%; U: 1.1(0.3) MJ m−3 (Fig. S13, ESI). | |||||||
| E (MPa) | 1300(72)a | 920(88)b | 1.3(0.3)c | 1700(44)a | 860(70)b | 1.3(0.3)c | |
| 0.6(0.1)d | 0.4(0.1)d | ||||||
| UTS (MPa) | 31(1.3) | 110(7.6) | 7.1(0.6) | 30(1.2) | 100(4.0) | 4.3(0.6) | |
| ε b (%) | 5.2(0.6) | 100(7.6) | 540(20) | 5.1(0.6) | 88(9.8) | 500(60) | |
| U (MJ m−3) | 1.1(0.2) | 86(6.3) | 17(2.0) | 1.1(0.2) | 74(8.7) | 11(2.6) | |
| Repetitions | 14 | 7 | 11 | 13 | 7 | 13 | |
The video extensometer is an important feature, enabling measurement of materials that undergo large elongations or have high strengths.10,18 Moreover, it does not damage small/weak samples as a clip-on extensometer can. Fig. S11 and S12 (ESI†) show the advantages of using an extensometer rather than assuming deformation changes equal to the grip-to-grip distance. Further, the extensometer enables post processing and rupture position analysis as images are saved during the experimental runs. The advantage is exemplified by the PP sample in Fig. 5 where the real time extensometer data (Fig. 5, blue) went out of the AOI at 90% strain. The recorded images of the experiment were post-processed resulting in the green trace in Fig. 5. Gratifyingly, the grip-to-grip (Fig. 5, black), video extensometer, and post-processed data are in good agreement, demonstrating the robustness of the CMTT. The video extensometer and post-processed strains show similar values; the artefact at a stress of ≈30 MPa is removed in the post-processing. Finally, the post-processing includes the data until sample rupture.
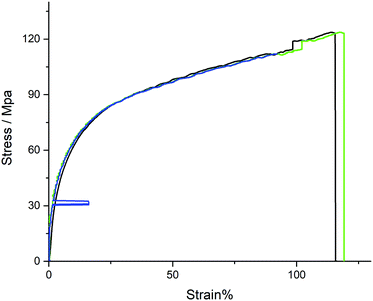 | ||
| Fig. 5 Results from a PP experiment measured on the CMTT, where strain is calculated from grip-to-grip (black), extensometer (blue), and post-processed via ImageJ (green). | ||
We note that the algorithm developed herein is not limited to specific test specimen geometries, and the user has the ability to reprocess the data should something go wrong (i.e. varying light intensities or contrast changes) during the experiment. The most common challenges are poor contrast or high strain rates, which cause the line pigment to spread over a larger area, thus reducing the contrast. Thus, the possibility of post-processing the data with a lower threshold will recover the measurement.
In general, the stress versus strain curves have similar steep slopes at the begin for PP and the expected double plateau for rubbers (Fig. 4). The difference in E for Manila paper measured on the CMTT and Instron could arise from the production direction of the paper. However, as noted above, the result from the different paper orientations in Fig. S13 (ESI†) gives the same E but different UTS for CD and MD, respectively (Table 1). This difference in E (Fig. 4A) is ascribed to bending of the aluminium CMTT frame. For low strength materials (PP and rubber) the data from the CMTT and the commercial Instron are similar or better quality.
The CMTT presented here should enable further customization for various needs. For example, clamps or supporting pads can be 3D printed to expand the availability and usefulness, or the electronics and GUI can be combined with a more powerful load cell together with a more rigid frame (angle brackets, dual motor actuator, etc.) to support testing of high-strength materials such as metals and composites. In addition to tensile testing on the CMTT, the grips can be modified to enable compression and three or four point bending tests. The algorithm for video analysis can be modified to accommodate the different test tool settings. Testing samples under various environmental conditions can be achieved by addition of, e.g., a heat chamber, water bath, or placing the CMTT in a glove box under inert atmosphere. Finally, the scalable design and the algorithms can hopefully assist other researchers in exploring, customizing and developing specialized equipment as found for in situ SEM19 and TEM20 characterization.
Conclusions
A low cost (∼$500) tabletop tensile tester has been demonstrated. All design, electronic, and data handling algorithms are accessible, customizable, and sourced locally. The performance is benchmarked against commercial equipment using Manila paper, polypropylene, and rubber; the results are not statistically different, i.e., high quality data are obtained on the simple and customizable tensile tester with extensometer add-on. We believe that these results should spur the continued development of low cost laboratory equipment for materials characterization, which may reduce bottlenecks in materials research.Author contributions
The manuscript was written through equally contributions of all authors off which all have approved the final version of the manuscript.Funding sources
Danish Innovation Foundation (FI No. 5152-00003A), Fulbright, Knud Højgaards Fond, Thomas B. Thriges Fond, Augustinus Fonden, Fabrikant P. A. Fiskers Fond, Christian og Ottilia Brorsons Rejselegat, Reinholdt W. Jorck og Hustrus Fond, Dir. Einar Hansen og hustru fru Vera Hansens Fond, Carl og Ellen Hertz’ Videnskabslegat.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors greatly acknowledge Dr Alan F. Schwartzman for access to the Instron at the NanoLab at MIT.References
- P. Shieh, W. Zhang, K. E. L. Husted, S. L. Kristufek, B. Xiong, D. J. Lundberg, J. Lem, D. Veysset, Y. Sun, K. A. Nelson, D. L. Plata and J. A. Johnson, Nature, 2020, 583, 542–547 CrossRef CAS PubMed.
- Z. Wang, L. Guo, H. Xiao, H. Cong and S. Wang, Mater. Horiz., 2020, 7, 282–288 RSC.
- M. E. Lamm, L. Song, Z. Wang, M. A. Rahman, B. Lamm, L. Fu and C. Tang, Macromolecules, 2019, 52, 8967–8975 CrossRef CAS.
- P. Suvannasara, S. Tateyama, A. Miyasato, K. Matsumura, T. Shimoda, T. Ito, Y. Yamagata, T. Fujita, N. Takaya and T. Kaneko, Macromolecules, 2014, 47, 1586–1593 CrossRef CAS.
- M. A. Hillmyer, Science, 2017, 358, 868–870 CrossRef CAS PubMed.
- J. R. Davis, Tensile Testing, ASM International, 2nd edn, 2004 Search PubMed.
- ISO 527-(1-5):2012, Int. Organ. Stand.
- P. Hollman, M. Larsson, P. Hedenqvist and S. Hogmark, Surf. Coat. Technol., 1997, 90, 234–238 CrossRef CAS.
- R. J. Schaefer, in Harris’ Shock and Vibration Handbook, ed. C. M. Harris and A. G. Piersol, McGraw-Hill, 5th edn, 2002 Search PubMed.
- H. B. Motra, J. Hildebrand and A. Dimmig-Osburg, Int. J. Eng. Sci. Res. Technol., 2014, 17, 260–269 Search PubMed.
- K. Miller, J. Biomech., 2001, 34, 651–657 CrossRef CAS PubMed.
- J. R. Amend and H. Lipson, Proceedings of the ASME Design Engineering Technical Conference, American Society of Mechanical Engineers Digital Collection, 2011, vol. 6, pp. 685–693 Search PubMed.
- J. H. Arrizabalaga, A. D. Simmons and M. U. Nollert, J. Chem. Educ., 2017, 94, 530–533 CrossRef CAS.
- R. Wang, N. Leber, C. Buhl, N. Verdonschot, P. J. Dijkstra and M. Karperien, Polym. Adv. Technol., 2014, 25, 568–574 CrossRef CAS.
- Free Pascal IDE, 2018.
- ITU-R Recommendation BT.601-7, BT Ser.
- M. Hinge and M. L. Henriksen, Open Sci. Framework, 2018 DOI:10.17605/OSF.IO/XW9VG.
- D. L. Butler, E. S. Grood, F. R. Noyes, R. F. Zernicke and K. Brackett, J. Biomech., 1984, 17, 579–596 CrossRef CAS PubMed.
- L. Bodelot, L. Pavić, S. Hallais, J. Charliac and B. Lebental, Sci. Rep., 2019, 9, 1–11 CAS.
- K. Nandy, D. W. Collinson, C. M. Scheftic and L. C. Brinson, PLoS One, 2018, 13, e0197999 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00598g |
| ‡ The data associated with this work is available through the Open Science Framework DOI: 10.17605/OSF.IO/CWP28 (link: https://osf.io/cwp28/). |
| This journal is © The Royal Society of Chemistry 2021 |