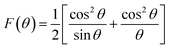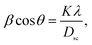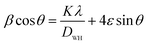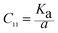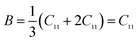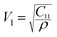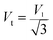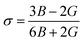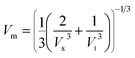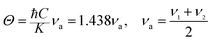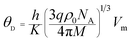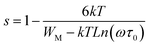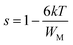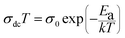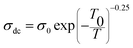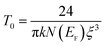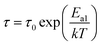Open Access Article
Open Access ArticleInvestigation of the structural, optical, elastic and electrical properties of spinel LiZn2Fe3O8 nanoparticles annealed at two distinct temperatures†
D. Bouokkezea,
J. Massoudi *b,
W. Hzeza,
M. Smari
*b,
W. Hzeza,
M. Smari b,
A. Bougoffab,
K. Khirouni
b,
A. Bougoffab,
K. Khirouni a,
E. Dhahri
a,
E. Dhahri b and
L. Bessaisc
b and
L. Bessaisc
aLaboratoire de Physique des Matériaux et des Nanomatériaux appliquée à l’Environnement, Faculté des Sciences de Gabès cité Erriadh, Université de Gabès, 6079 Gabès, Tunisia
bLaboratoire de Physique Appliquée, Faculté des Sciences de Sfax, Université de Sfax, B.P. 1171, Sfax 3000, Tunisia. E-mail: jalel.massoudi@gmail.com
cICMPE (UMR 7182), CNRS, UPEC, Université Paris Est, 94320 Thiais, France
First published on 11th December 2019
Abstract
Nanoparticles of Li0.5ZnFe1.5O4 (LiZn2Fe3O8) with the spinel structure were prepared by a sol–gel auto-combustion method at two different annealing temperatures. X-ray diffractograms and Rietveld refinement confirmed the formation of the spinel structure. The morphology was analyzed by electron microscopy, which showed that the grains were composed of different crystallites. Elastic properties were determined from infrared spectroscopy. It was found that the elastic parameters increased with the increase in annealing temperatures. The band gap depends on the annealing temperature and it decreased on increasing the particle size. The conductivity of the specimen annealed at 500 °C followed either the Jonscher's model or Drude's model depending on the temperature range. This conductivity decreased when the annealing temperature was raised by 600 °C. AC conductivity was found to be controlled by the hopping model. A single relaxation phenomenon was evidenced for each sample from impedance analysis. The Nyquist diagram proved that the samples were simultaneously capacitive and resistive and also supported the presence of multiple relaxation times.
1. Introduction
Ceramics like metals and polymers are receiving significant attention from scientists and even companies on account of their interesting features that lead to various potential applications.1 Among them, spinel, with formula AB2O4, where A represents a tetrahedral site and B refers to an octahedral site,2 has received special interest. On account of having multiple properties, scientists have never stopped considering spinel as an exciting matter for potential applications. Iron ions with magnetic properties due to their unpaired d electrons and electrical properties due to the relatively easy release of d electrons make most ferrite spinels multiferroic. These features elucidate why more scientific curiosity is targeted towards ferrite as compared to other spinels, as evidenced by the tremendous number of characterizations conducted on it.3–6 It has been found that ferrite possesses many applicable distinguishable properties,7,8 which are sensitive to composition.6 In this context, ferrite has been treated with a wide range of chemical elements, such as Zr, Zn,9 Ni,10 and Co,11 for better satisfying the requirements of today. Relatively strong qualities were obtained by inserting Zn into the matrix, e.g., the high electrical resistivity of ZnFe2O4.12 This high resistivity makes ferrite with Zn a suitable candidate for certain applications, such as circulators, isolators, and phase shifters.6 Doping with Zn seems to expand the range of applications of spinel. For further widening this range, one of the practical hints is to fill the A-site with lithium13 because ferrite with lithium has been found to serve as an excellent solid-state electrolyte.4 In this paper, we elaborate and report the spinel oxide of Li0.5ZnFe1.5O4. Since it contains zinc with a relatively low volatilization temperature, it involves a low sintering temperature, which makes the preparation process less expensive as compared with that of other spinels.14According to Reddy et al., one may predict some physical properties of ferrite by looking at the magnitude and type of its conductivity.8 However, which carriers are responsible for conductivity in lithium ferrite with a spinel structure is a matter of debate. This poor understanding of the origin of conductivity is due to the simultaneous presence of Li+ with mixed-valence transition metal ions, Fe2+ and Fe3+ in our case. This paper addresses the electrical properties of the considered lithium zinc ferrite. Since conductivity depends on the preparation conditions including annealing temperature,15,16 we annealed the specimens in question at 500 °C and 1100 °C. After discussing the structure of the liquid phase, we explain in detail the transport properties by combining conductivity and impedance formalism. The optical properties, under UV-visible irradiation, are reported. The main aim of this study is to determine some key optical and elastic parameters pertaining to the size of the particle; in spite of being equivalent, they provide distinct information. Further characterizations will be conducted.
2. Experimental section
Analytical reagents of Fe(NO3)3·9H2O, Zn(NO3)2·6H2O, LiNO3 and C6H8O7 were obtained from Sigma-Aldrich and used as received without purification. Li0.5ZnFe1.5O4 was synthesized by a facile sol–gel auto combustion method followed by annealing at 500 and 1100 °C. In a typical experiment, stoichiometric amounts of Fe(NO3)3·9H2O, Zn(NO3)2·6H2O and LiNO3 were dissolved in 100 ml of distilled water with vigorous stirring to form a solution, followed by the addition of citric acid (C6H8O7) with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of metal cation (Fe + Zn + Li) to citric acid. The resulting mixed solution was magnetically stirred at 80 °C until a viscous gel was formed. The viscous gel was heated on a hot plate at 300 °C until it self-ignited, yielding dark brown ash. The auto combustion was completed within a minute. The as-burnt powder ferrites were then pelletized and finally annealed separately at 500 °C and 1100 °C for 8 h in an electrical muffle furnace and cooled slowly to room temperature to obtain single-phase samples of LiZn2Fe3O8 with two different particle sizes.
2 molar ratio of metal cation (Fe + Zn + Li) to citric acid. The resulting mixed solution was magnetically stirred at 80 °C until a viscous gel was formed. The viscous gel was heated on a hot plate at 300 °C until it self-ignited, yielding dark brown ash. The auto combustion was completed within a minute. The as-burnt powder ferrites were then pelletized and finally annealed separately at 500 °C and 1100 °C for 8 h in an electrical muffle furnace and cooled slowly to room temperature to obtain single-phase samples of LiZn2Fe3O8 with two different particle sizes.
The phase-purity and crystal structure of these ferrites were examined by X-ray diffraction spectroscopy at room temperature. A BRUKER diffractometer with CuKα radiation (λ = 1.5406 Å) in the 2θ range of 20 to 70° was used, with a step of 0.02° and an acquisition time of 1 s for each step. Surface morphological characterization and the chemical compositions of the synthesized samples were investigated using a Merlin scanning electron microscope (SEM) equipped with an energy dispersive X-ray (EDX) microanalyzer. Transmission electron microscopy (TEM) images were obtained with an FEI Tecnai F20 microscope. The thermal analysis of the prepared samples was carried out using thermogravimetric analysis (TGA) and thermal difference analysis (DTA) system – Q600 SDT at a step rate of 10 °C min−1 in an air atmosphere from 30 °C to 1000 °C. Fourier transform infrared (FTIR) spectra were recorded using a Shimadzu-8700 FTIR spectrometer over the range of 4000–400 cm−1. The Raman spectra were recorded using a SENTERRA spectrometer (Bruker, Germany) with laser excitation of 532 nm at room temperature. The electrical characterization was conducted by impedance spectroscopy using an Agilent 4294A impedance analyzer. Before starting this characterization, the samples had to be in the form of dipoles so a silver thin film of nanometers thickness was coated on the face of each pellet using a vacuum thermal evaporator. A silver wire was then attached by silver lacquer on each side. The explored range of frequency was between 40 Hz and 110 MHz. The temperature ranged from 300 K to 600 K. The samples were characterized under an excitation alternative signal of 50 mV. Absorption spectra were obtained at room temperature using a Shimadzu UV-3101PC scanning spectrophotometer.
3. Results and discussion
3.1 Thermal analysis
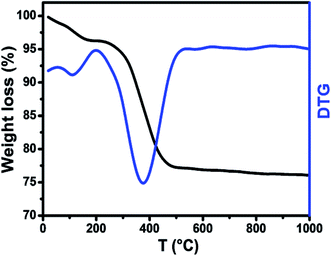
In order to investigate the formation process of the Li0.5ZnFe1.5O4 powders, thermogravimetric measurements were used to analyze the thermal behavior of the reagents. Fig. 1 shows the typical TGA and DTG curves obtained for the as-burnt powder. It can be seen from Fig. 1 that the TGA curve can be divided into three regions with various processes taking place in each region, i.e., 10–175 °C, 175–425 and 425–1000 °C. In the first region (10–175 °C) the initial weight loss in the TGA curves is due to the loss of water molecules with a mass loss of 4%. A major weight loss can be seen in the second region (175–425 °C) in the TGA curve and the DTG curve could be attributed to the decomposition of unreacted reactants present in the as-prepared samples. The third region (425–1000 °C) of the TGA curve could be attributed to the crystallization of the self-combusted final product. It was concluded from the TGA results that an optimal temperature of 450 °C is suitable for annealing the as-prepared sample, and thus the samples that were used for further characterization were annealed at 500 °C (Zn500) and 1100 °C (Zn1100) for 8 h.3.2 Structure and morphology
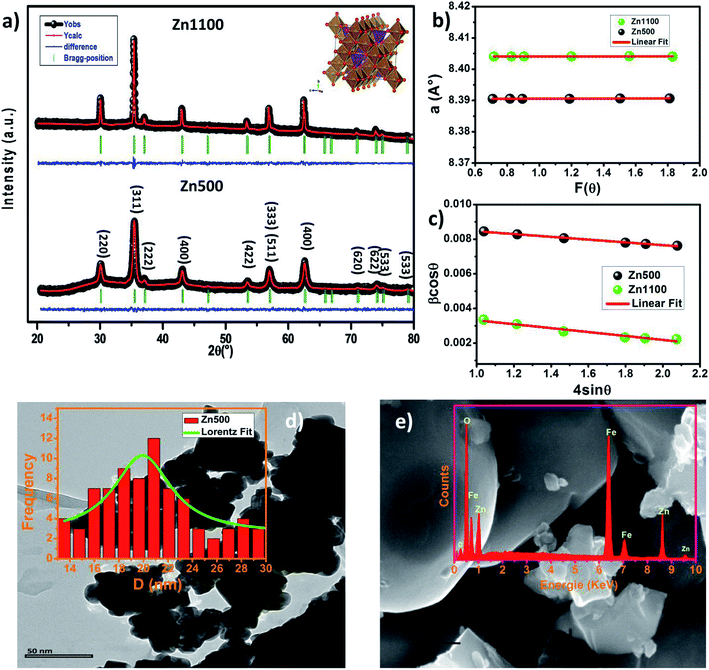
The Rietveld refinement of the X-ray diffraction patterns of LiZn2Fe3O8 ferrites obtained for Zn500 and Zn1100 are shown in Fig. 2(a). The Rietveld FULLPROF program was used for the structural refinements.17 The XRD spectra confirmed the formation of a single-phase cubic spinel structure with a space group (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) without any extra peaks of a secondary phase (ZnO or Fe2O3) and there is a good agreement between the calculated and observed profiles. As the sintering temperature increases, the peak width decreases due to an increase in crystallite size. The obtained Rietveld refinement parameters for the two samples were computed and are given in Table 1. More details in the Rietveld analyses have been reported in our previous work.18 Fitting parameters were found to be comparable to those of similar spinel ferrite samples.18,19 The unit cell parameters and atomic positions along with the AO6 octahedral and BO4 tetrahedral sites of the Li–Zn ferrite are shown in the inset of Fig. 2(a). For minimizing both systematic and random errors, an accurate estimation of the exact lattice constant a0 was made using the extrapolation function F(θ), i.e., the Nelson–Riley (N–R) function, for each reflection of the studied ferrite samples.20
m) without any extra peaks of a secondary phase (ZnO or Fe2O3) and there is a good agreement between the calculated and observed profiles. As the sintering temperature increases, the peak width decreases due to an increase in crystallite size. The obtained Rietveld refinement parameters for the two samples were computed and are given in Table 1. More details in the Rietveld analyses have been reported in our previous work.18 Fitting parameters were found to be comparable to those of similar spinel ferrite samples.18,19 The unit cell parameters and atomic positions along with the AO6 octahedral and BO4 tetrahedral sites of the Li–Zn ferrite are shown in the inset of Fig. 2(a). For minimizing both systematic and random errors, an accurate estimation of the exact lattice constant a0 was made using the extrapolation function F(θ), i.e., the Nelson–Riley (N–R) function, for each reflection of the studied ferrite samples.20| Parameter | Zn500 | Zn1100 |
|---|---|---|
| a0 (Å) | 8.390 | 8.404 |
| ar (Å) | 8.391 | 8.405 |
| V (Å3) | 590.674 | 593.763 |
| Rp (%) | 25.7 | 50.7 |
| Rwp (%) | 12.8 | 17.7 |
| Re (%) | 11.6 | 14.5 |
| χ2 | 1.211 | 1.477 |
| DSC (nm) | 17 | 45 |
| DW–H (nm) | 15 | 32 |
| ε | −8.10−4 | −10−3 |
The values of the lattice parameters obtained from each reflected plane were plotted against the N–R function and are shown in Fig. 2(c). It can be observed from Table 1 that there is a small deviation between the exact (a0) and Rietveld (aR) values of the lattice parameter. The exact values of the lattice parameter were observed to be slightly small as compared to the Rietveld values. It is also evident that both the exact and Rietveld lattice parameters decrease with the decrease in the particle size. G. Datt et al.21 have reported that the decrease in the lattice constant with the increase of the annealing temperature of the Ni–Co ferrite nanoparticles is attributed to the presence of OH− groups in the crystalline structure due to the synthesis process. However, the low values of the goodness of fit χ2 are quite satisfactory for the refinement, indicating that the quality of fit for these XRD patterns was quite good and that the samples obtained were of high quality. The average crystallite size of the ferrite samples was calculated by using the Scherrer equation for the line broadening of the most intense (311) peak:22
This gives a linear relationship between β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and 4
θ and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and the intercept of the line gives the crystallite size DW–H while the slope gives the induced strain (ε). Representative Williamson–Hall (W–H) plots of Li0.5ZnFe1.5O4 synthesized at different annealing temperatures are shown in Fig. 2(b). It is possible to observe that the straight line intercepts all points, indicating the presence of a homogeneous microstrain and a homogeneous crystallite size distribution.23 Average crystallite sizes calculated by using Scherrer's formula and the Williamson–Hall plot are listed in Table 1 for the two samples. The lattice microstrain of each sample obtained using the Williamson–Hall method displays a positive value, indicating lattice expansion.23 As can be seen in Table 1 the average particle size estimated from the Scherrer equation is quite different from that obtained by the W–H plot. This difference can be explained by the fact that the micro-stress can induce a larger widening of the diffraction peak, whereas, in the Scherrer equation, the total width of the diffraction peak is taken into account in the calculation.23
θ and the intercept of the line gives the crystallite size DW–H while the slope gives the induced strain (ε). Representative Williamson–Hall (W–H) plots of Li0.5ZnFe1.5O4 synthesized at different annealing temperatures are shown in Fig. 2(b). It is possible to observe that the straight line intercepts all points, indicating the presence of a homogeneous microstrain and a homogeneous crystallite size distribution.23 Average crystallite sizes calculated by using Scherrer's formula and the Williamson–Hall plot are listed in Table 1 for the two samples. The lattice microstrain of each sample obtained using the Williamson–Hall method displays a positive value, indicating lattice expansion.23 As can be seen in Table 1 the average particle size estimated from the Scherrer equation is quite different from that obtained by the W–H plot. This difference can be explained by the fact that the micro-stress can induce a larger widening of the diffraction peak, whereas, in the Scherrer equation, the total width of the diffraction peak is taken into account in the calculation.23
The X-ray density (ρX-ray), apparent density (ρm), porosity (P), specific surface area (S) and X-ray parameters, viz. the A-site radii (rA), B-site radii (rB), tetrahedral bond length (dAL), octahedral bond length (dBL), the jump length of the A-site (LA) and jump length of the B-site (LB) are shown in (Table 2), and were calculated using the standard relations shown in eqn (S1)–(S15), respectively (ESI).† Table 2 shows that the length of the tetrahedral link, the length of the octahedral link, the tetrahedral edge, the shared and non-shared octahedral edge increase with the increase in the annealing temperature. This may be due to the large distance between magnetic ions. The increase in crystallite size resulted in a decrease in the porosity, which has the effect of increasing the apparent density, as we have seen experimentally. The specific surface area decreased from 72.6 to 27.6 m2 g−1 with the increase in the particle size. However, the high surface area value of LiZn2Fe3O8 nanoparticles suggests that Zn500 nanoparticles could be used as sensors for detecting gases.24
| Parameter | Zn500 | Zn1100 |
|---|---|---|
| LA (Å) | 3.633 | 3.639 |
| LB (Å) | 2.966 | 2.971 |
| RA (Å) | 1.904 | 1.907 |
| RB (Å) | 2.047 | 2.050 |
| rA (Å) | 0.584 | 0.587 |
| rB (Å) | 0.727 | 0.730 |
| dAL (Å) | 1.904 | 1.907 |
| dBL (Å) | 2.048 | 2.052 |
| dBE (Å) | 2.824 | 2.829 |
| dAE (Å) | 3.109 | 3.114 |
| dBEu (Å) | 2.968 | 2.973 |
| ρX-ray (g cm−3) | 4.86 | 4.84 |
| ρth (g cm−3) | 3.71 | 3.97 |
| P (%) | 24 | 18 |
| S (m2 g−1) | 72.6 | 27.6 |
The high-resolution TEM image of a single grain (single-crystalline nature) is shown in Fig. 2(d). The TEM image depicts that the particles are non-uniform in size and spherical in nature with some agglomerations. The average particle size estimated from the TEM image was 22 nm (inset of Fig. 2(d)). We also carried out SEM studies. Fig. 2(e) shows the typical SEM image of sample Zn1100. The average grain size increased to the micrometer range for this sample. It is worth mentioning that the average particle size is in agreement with the crystallite size deduced from the XRD data for the sample Zn500, which indicates the single domain nature of the sample. However, the increase in the annealing temperature up to 1100 °C led to the formation of particles with size corresponding to the multi-domain state for the sample Zn1100. Evidently, the particle sizes observed by SEM are several times larger than the crystallite size calculated from XRD, which indicates that each particle consists of several crystallized grains. In order to check the existence of all elements in these compounds, energy dispersive X-ray analysis (EDAX) in field emission SEM was carried out, which indicated no inhomogeneity of the chemical composition. The EDAX spectrum represented in the inset of Fig. 2(d) reveals the presence of Zn, Fe and O elements. It was not possible to detect Li for the obvious reason that the X-ray fluorescence is extremely low for elements such as Li or Be. The presence of peaks due to other elements, as either dopants or impurities, was not detected, which confirmed the purity of synthesized material.
3.3 Infra-red and elastic properties
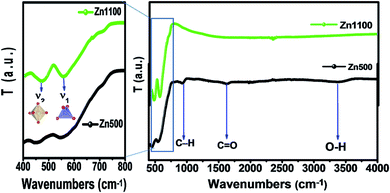
The bands in the infrared range in solids are generally attributed to ion vibrations in the crystal lattice. The FTIR spectra of the Li–Zn ferrite nanoparticles were also obtained and exhibit absorption bands in good agreement with the FTIR characteristic bands of the ferrite spinel (Fig. 3). However, for spinel ferrites, the vibrational band around 600 cm−1 corresponds to the intrinsic stretching vibration of the tetrahedral site and the vibrational band around 400 cm−1 is attributed to the stretching vibration of metal cations in the octahedral site.25,26 For the Zn500 sample, absorption bands at 3200 to 3600 cm−1 may be related to water symmetric stretching and anti-symmetric stretching (O–H) vibrations.27 The peak observed at around 1627 cm−1 is attributed to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations.28 The peak at about 930 cm−1 can be assigned to C–H bending vibrations.28 The presence of such hydroxyl species causes the nanocrystals to be easily dispersed in polar solvents and the dispersions are also stable such that they can be used in many optoelectronic applications. These bands vanish completely in the Zn1100 sample. The appearance of bands around 2300–2400 cm−1 is due to the atmospheric CO2 absorbed on the surface of NPs during the FTIR measurements.28 However, the presence of the two modes ν1 and ν2 for both samples is due to the stretching vibration of metal cations in the tetrahedral and octahedral sites, respectively. The positions of IR absorption peaks of Li–Zn ferrite are illustrated in Table 3. These absorption bands further confirm the formation of the spinel-structured Li–Zn ferrite. Waldron found evidence that the FTIR spectra are useful for calculating the threshold energy Eth associated with the electronic transition from the threshold wavenumber νth, which is determined from the maximum point of the absorption spectra, where it reaches a limiting value.29,30 The threshold energy can be calculated using the following relation:
O stretching vibrations.28 The peak at about 930 cm−1 can be assigned to C–H bending vibrations.28 The presence of such hydroxyl species causes the nanocrystals to be easily dispersed in polar solvents and the dispersions are also stable such that they can be used in many optoelectronic applications. These bands vanish completely in the Zn1100 sample. The appearance of bands around 2300–2400 cm−1 is due to the atmospheric CO2 absorbed on the surface of NPs during the FTIR measurements.28 However, the presence of the two modes ν1 and ν2 for both samples is due to the stretching vibration of metal cations in the tetrahedral and octahedral sites, respectively. The positions of IR absorption peaks of Li–Zn ferrite are illustrated in Table 3. These absorption bands further confirm the formation of the spinel-structured Li–Zn ferrite. Waldron found evidence that the FTIR spectra are useful for calculating the threshold energy Eth associated with the electronic transition from the threshold wavenumber νth, which is determined from the maximum point of the absorption spectra, where it reaches a limiting value.29,30 The threshold energy can be calculated using the following relation:| Eth = hCνth |
| Parameter | Zn500 | Zn1100 |
|---|---|---|
| υ1 (cm−1) | 546 | 561 |
| υ2 (cm−1) | 453 | 470 |
| υa (cm−1) | 499.5 | 515.5 |
| υth (cm−1) | 849 | 767 |
| Eth (eV) | 0.105 | 0.095 |
| K1 (N m−1) | 275 | 291 |
| K2 (N m−1) | 189 | 203.4 |
| Ka (N m−1) | 232 | 247 |
| C11 (GPa) | 277 | 294 |
| B (GPa) | 277 | 294 |
| Vl (m s−1) | 7547 | 7798 |
| Vt (m s−1) | 4357 | 4502 |
| G (GPa) | 92.3 | 98.1 |
| σ | 0.35 | 0.35 |
| E (GPa) | 249 | 265 |
| Vm (m s−1) | 4837.3 | 4998.2 |
| ΘD (K) | 718 | 741 |
| θD (K) | 656 | 678 |
It is well known that the wavenumbers (ν1,2) of the infrared active phonon modes are connected to the force constant (F) and reduced mass (μ) of the metal–oxygen bond; the values of the force constants for the A-site (Kt) and B-site (Ko) were calculated using the following formula:27,31,32
| Kt,o = 4π2C2ν1,22u |
Elastic constants can be used to measure the resistance of a crystal to an externally applied stress. Therefore, the elastic properties of ferrites are important in industry because their elastic data determine the strength of the materials under various strained conditions. In basic research, the study of the elastic properties of ferrites is useful for obtaining insight into the nature of the inter-atomic and inter-ionic forces and their thermal behavior. For the spinel ferrite and garnet systems, Modi et al.34–37 developed a technique based on the infrared spectroscopy and structural data to calculate the elastic parameters. The stiffness constants (according to Waldron,30 for the material systems with cubic symmetry possessing isotropic nature, C11 = C12), bulk modulus B, Young's modulus E, rigidity modulus G, Poisson's ratio σ, longitudinal wave velocity Vl, transverse wave velocity Vt and mean velocity Vm were calculated using the following relations:29,35
Stiffness constant:
Bulk modulus:
Transverse wave velocity:
Longitudinal wave velocity:
Rigidity modulus:
| G = ρVt2 |
Poisson's ratio:
Young's modulus:
| E = (1 + σ)2G |
Mean wave velocity:
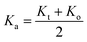 is the average force constant, a is lattice parameter and ρ is the X-ray density.
is the average force constant, a is lattice parameter and ρ is the X-ray density.
The variation of the elastic modulus of Li–Zn ferrite samples can be noticed from Table 3. The value of the Poisson's ratio (σ = 0.35) remains constant as a function of the annealing temperature and lies in the range of −1 to 0.5, which is in accordance with the theory of isotropic elasticity38 (hence good elastic behavior). This value of the Poisson ratio is in good agreement with other spinel ferrites.29,36,37 The calculated values of G, σ, E, Vt, Vl and Vm for the two samples are consistent with those obtained from the ultrasonic pulse transmission (UPT) technique39–41 and for various ferrite spinels using FTIR data.42,43 In addition, unless corrected to a void-free state, the measured elastic moduli are not significant. Therefore, the values of elastic moduli have been corrected to zero porosity using the Hosselman and Fulrath model, Ledbetter and Datta model and elastics theories (see ESI†). The values of elastic moduli are given in Table S1 (ESI†). These values are higher than the uncorrected data of the elastic moduli. Moreover, the values of elastic moduli and Poisson's ratio decreased with an increase in the annealing temperature, while the uncorrected data of the elastic moduli increase, which suggests the strong effect of the porosity on the elastic properties. Generally, the variations in elastic moduli are sensitive to inter-atomic bonding lengths. However, A. Bhaskar et al.44 reported that the increase in the values of the elastic moduli suggests that the strength of the interatomic bonding between the ions of Mn added Mg–Cu–Zn ferrites increases with an increase in the sintering temperature. Therefore, the decrease in the elastic moduli for pore-free Li–Zn ferrites may be due to a decrease in the inter-atomic bonding between various atoms in the lattice.
To distinguish whether the material under investigation is ductile or brittle in nature, according to the Pugh criteria,45,46 a useful value of bulk modulus to rigidity modulus, B0/G0, was inspected. B0/G0 must be greater than 1.75 for the ductile nature and less than 1.75 for the brittle nature. The calculated values of B0/G0 in our case (according to Ledbetter and Datta model) were 4.55 and 4.02 for Zn500 and Zn1100, respectively, qualifying for a ductile nature.
Finally, the Debye temperature is the temperature at which the maximum vibration of the network takes place and simplifies the integration of thermal capacity. It was calculated using the equation given by Waldron:47
From the mean velocity Vm, the Debye temperature can also be estimated by using Anderson's formula:48
3.4 Raman spectroscopy analysis
Raman spectroscopy provides an important tool for probing the structural properties of synthesized Li0.5ZnFe1.5O4 ferrites. Raman spectra of the Li–Zn ferrite (Zn500 and Zn1100) were collected at room temperature in the spectral range of 100–800 cm−1 and are shown in Fig. 4. According to literature, only 5 Raman active phonons (A1g + Eg + 3F2g) are known for the cubic spinel structure belonging to the Oh (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) space group.49 The A1g and F2g(1) phonons are associated with the symmetric stretching of metal–oxygen bonds and the translation movement of the whole at the tetrahedral site, respectively. The Eg, F2g(3) and F2g(2) modes represent the symmetric, asymmetric bending and asymmetric stretching vibrations of the metal–oxygen bonds at the octahedral site, respectively.50 In order to determine the natural frequency of the Raman results, we have carried out a deconvolution of the experimental data with the Lorentzian peak shape function and the best-fit values for the peak positions are given in Table 4. No signal associated with secondary phases or impurities has been identified, especially for hematite (α-Fe2O3) impurities, which is consistent with the XRD data. The Raman bands observed at 164, 316, 445, and 523 cm−1 could be attributed to the F2g(1), Eg, F2g(2), and F2g(3) Raman modes, respectively. The last peak, at about 637 cm−1, corresponds to a phonon with A1g symmetry and can be deconvoluted into two Lorentzian-shaped peaks at 637 cm−1 and 675 cm−1; these peaks are typically characteristic of the mixed-as well inverse-spinel. Therefore, a detailed analysis of the asymmetry of some modes could be employed to estimate the cation disorder in the spinel structure. The Raman spectra confirmed the formation of the phase pure Fd
m) space group.49 The A1g and F2g(1) phonons are associated with the symmetric stretching of metal–oxygen bonds and the translation movement of the whole at the tetrahedral site, respectively. The Eg, F2g(3) and F2g(2) modes represent the symmetric, asymmetric bending and asymmetric stretching vibrations of the metal–oxygen bonds at the octahedral site, respectively.50 In order to determine the natural frequency of the Raman results, we have carried out a deconvolution of the experimental data with the Lorentzian peak shape function and the best-fit values for the peak positions are given in Table 4. No signal associated with secondary phases or impurities has been identified, especially for hematite (α-Fe2O3) impurities, which is consistent with the XRD data. The Raman bands observed at 164, 316, 445, and 523 cm−1 could be attributed to the F2g(1), Eg, F2g(2), and F2g(3) Raman modes, respectively. The last peak, at about 637 cm−1, corresponds to a phonon with A1g symmetry and can be deconvoluted into two Lorentzian-shaped peaks at 637 cm−1 and 675 cm−1; these peaks are typically characteristic of the mixed-as well inverse-spinel. Therefore, a detailed analysis of the asymmetry of some modes could be employed to estimate the cation disorder in the spinel structure. The Raman spectra confirmed the formation of the phase pure Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m spinel ferrite LiZn2Fe3O8 nanoparticles.
m spinel ferrite LiZn2Fe3O8 nanoparticles.
| Raman mode | Zn1100 | Zn500 | Assigned mode | ||
|---|---|---|---|---|---|
| Position (cm−1) | FWHM | Position (cm−1) | FWHM | Assigned polyhedra | |
| A1g | 637 | 74 | 624 | 81 | FeO4 tetrahedra |
| F2g(3) | 523 | 57 | 505 | 62 | FeO6 octahedra |
| F2g(2) | 445 | 59 | 433 | 79 | FeO6 octahedra |
| Eg | 316 | 44 | 294 | 67 | FeO6 octahedra |
| F2g(1) | 164 | 15 | 137 | 70 | FeO4 tetrahedra |
It can be seen that the Raman modes of the Zn500 sample are enlarged and their frequencies are shifted to the lowest values compared to those of the Zn1100 sample. However, a breakdown of the momentum conservation rule occurs when the particle size (around 20 nm in our case) is sufficiently smaller than the wavelength of the exciting radiation (532 nm); this leads to the selection rule for the momentum vector (q′ ≈ 0), and is replaced by the q′-vector relaxation model.50 Therefore, this broadening and shifting of Raman modes in nanoparticles may be due to phonon confinement and variations in phonon relaxation with particle size. These results are comparable to those previously obtained in spinel ferrite nanoparticles by Datt et al.21 as well as Wang et al.51
Moreover, Zn vacancies were formed in the crystal lattice at such a high temperature. This led to the reduction of some of the Fe3+ ions from the B-site to Fe2+ ions to compensate for the loss of Zn, which eventually hopped to the Zn site. The local system is no longer in equilibrium with its neighbors after the hopping of the central Fe ions towards the A-sites from their initial stable configurations. To stabilize the new ion positions, other surrounding ions must move accordingly. Therefore, this hopping process will have a substantial impact on the vibrational frequencies of the associated modes of the BO6 octahedral site. The proposed hopping process is also supported through conductivity studies, which will be discussed in the next section. Note that this ion jumping leads to the presence of Fe2+ and Fe3+ in the system, which increases the conductivity with increasing temperature.
3.5 Electrical characterization
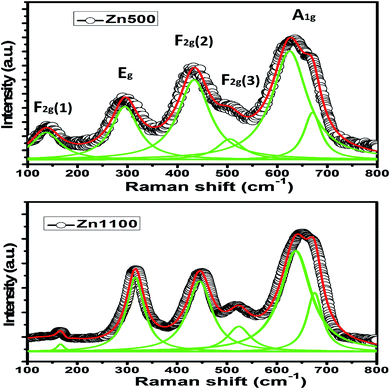
Regarding Zn500, the conductivity responds to the frequency in two different ways depending on the temperature. It reacts to frequency in conformity with Jonscher's law (σAC = Aωs where A is a constant and ω is the angular frequency)52 up to 590 K; beyond that, it varies with frequency in agreement with Drude's model. Further, the frequency-independent region extends thermally to 590 K, above which it begins shrinking.
Concerning Zn1100, the conductivity is correlated with frequency according to Jonscher's model over the entire explored temperature scale. The low-frequency plateau continuously becomes larger as temperature increases. The low-temperature peak in Fig. 5(c) shifts to the right side of the plot with temperature. It seems to be out of the tested frequency scale for relatively high temperatures. The representative conductivity curve fitted to Jonscher's model is shown in Fig. S1 (ESI†).
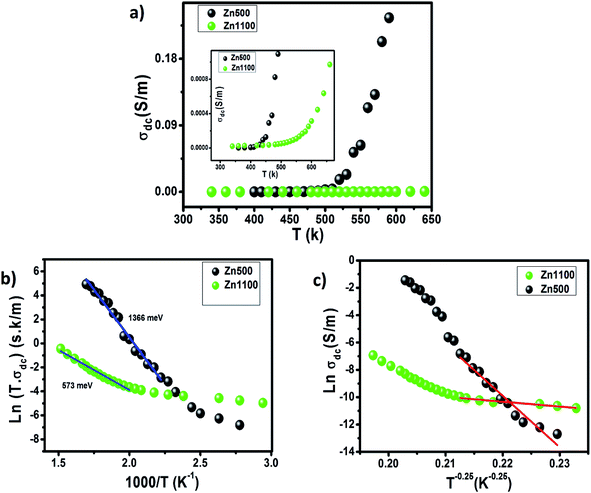
According to S. F. Mansour et al.3 along with M. Abdullah Dar and coworkers,53 frequency contributes to an increase in the number of mobile carriers by virtue of its pumping force. On this basis, we inferred that the mobile carriers at low frequencies are the ones unleashed due only to temperature, whereas the mobile carriers at high frequencies are those released due to temperature as well as frequency; i.e., the free carriers are boosted in number as frequency increases. It makes sense that the conductivity of a semiconductor increases with frequency. This information is not in opposition to M. Abdullah Dar's insight.53 Thus, we conclude from Fig. 5 that Zn500, down to 590 K, and Zn1100 behave as though they were semiconductors; this is corroborated by the continuous increase in their σdc upon heating.
The conductivity of Zn500 above 600 K will be discussed separately. On the one hand, the direct decrease in σAC without increasing frequency over the dispersive region is a typical feature of metals. On the other hand, the increase in σdc with temperature is typical behavior for semiconductors. We concluded that above 600 K, Zn500 functions as a metal or semiconductor, according to the frequency.
The number of mobile carriers in Zn1100 is supposed to increase with frequency as mentioned above; however, the σAC does not. This implies that the concentration of mobile carriers no longer controls the conductivity at 600 K and so, in addition to carriers and their charges, mobility plays a role in conductivity.54 Therefore, the decrease in σAC refers to a restriction in mobility; this is ascribed with confidence to the presence of gas carriers at such frequencies. The scattering due to the vibration of ions may contribute to the decrease in mobility.
We will only consider the low-temperature peak seen in Fig. 5(c); we surmised that the absence of peaks in Fig. 5(a and b) is somehow related to the annealing temperature. The alternating voltage of 50 meV causes free carriers to move through matter along its direction, resulting in a net electrical conductivity. Certain mobile carriers are unable to keep up with the excitation above a specific frequency,55 which reduces the conductivity. This elucidates the appearance of a peak in Fig. 5(c). According to R. W. Christy, mobility is boosted exponentially as temperature increases; a slight increase in temperature makes carriers move even faster, implying that the frequency, beyond which they no longer follow the excitation, is also thermally activated.54 This explains why the peak, before disappearing, shifts toward higher frequencies once there is continuous heating.
The microstructure of ferrite with zinc is so sensitive to annealing temperature in the opinion of A. M. Kumar,16 whose results proved that the grain boundary concentration peaks at 1100 °C. It is boosted with annealing temperature up to 1100 °C, which means that the grain boundaries within the current samples are strongly expected to increase in concentration on going from 500 °C to 1100 °C. Since they serve as barriers capable of impeding carriers from going around, it is harder for carriers to move through Zn1100 due to their possession of further inter-grains. It can be concluded that the mobility of carriers in Zn1100 is relatively low. Since the mobility somehow mirrors relaxation frequency, (this point will be made in detail on treating impedance formalism), it becomes evident that the relaxation frequency of Zn1100 at a given temperature is lower as compared to Zn500; this is an argument for elucidating why peaks appear in Fig. 5(c) but not in Fig. 1(a). We assume the peaks in Fig. 5(a) are out of the explored frequency scale and may emerge beyond 10 MHz.
The curves in Fig. 5(c) are closer to each other as compared to the others, which is a strong sign that the conductivity of Zn1100 is less dependent on temperature. Annealing at 1100 °C stems the creation of further barriers to restrict carriers from moving, reinforcing A. M. Kumar's insight.16 This idea is supported by Fig. 7(a); the extra barriers are assumed to be intergrains.
The dominant conduction mechanism according to which σAC occurs will be discussed in this section. On the one hand, certain researchers think that the increase of this parameter is proof of the hopping process;56,57 on the other hand, others have proved that a rise in σAC is sometimes due to other mechanisms like tunneling.58 It becomes clear that by itself, the conductivity spectrum is not a powerful tool for approaching alternating conductivity in terms of mode of transport. The popular alternative is to consider the thermal variation of the frequency exponent “s” appearing in Jonscher's law, shown in Fig. 6 as estimated from the dispersive regime in Fig. 5.
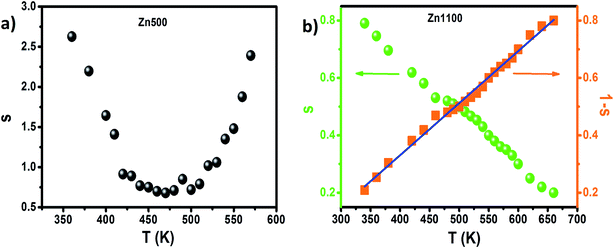 | ||
| Fig. 6 (a) Thermal variation of exponent “s” for Zn500. (b) Thermal variation of exponent “s” and “1 − s” for Zn1100. | ||
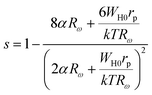
In the case of the Zn500 sample, according to the overlapping large polaron tunneling (OLPT) model,59 the values of “s” decrease with increasing temperatures to a minimum value and then rise when the temperature increases. This is in good agreement with the obtained results in the studied temperatures (Fig. 6(a)). Therefore, the OLPT model is usually described as the predominant conduction mechanism in the semiconducting Zn500 sample. In this conduction type, the large-polaron wells at two sites are assumed to overlap, thus reducing the polaron hopping energy, which is given by:
| WH = WH0(1 − rp/R) |
where α is the spatial extent of the polaron, Rω is the hopping length at the angular frequency ω, k is the Boltzmann constant and T is the temperature. The higher values of activation energy in our case also support this argument. Likewise, conductivity can be approached by polarons with tunneling between Fe2+ and Fe3+ sites. This factor indicates that the sample displays the commonly observed electrical characteristic after the endothermic transition and that a charge-ordering transition takes place in the prepared material. The polaron formation in the nano ferrite system can be due to the defect levels introduced by the size reduction. The same behavior is presented for other spinel ferrite nanoparticles.61,62 However, a detailed theoretical study is essential for exploring the different aspects of this type of conduction mechanism in nanostructured Li–Zn ferrite.
For the Zn1100 sample, “s” decreases gradually upon heating, which proves that transport from one site towards an equivalent site takes place predominantly, but not exclusively, in conformity with the correlated barrier hopping (CBH) model.63 According to this model, the transport process arises by a single or bipolaron hopping mechanism through the Coulomb barrier between two trap centers. The frequency exponent “s” in this model can be expressed as follows:63
The values of WM were determined from the slope of the curve of 1 s versus the temperature for the Zn1100 sample (Fig. 6(b)). A value of WM = 286 meV was obtained. However, if the maximum barrier height WM = Ea/2, bipolaron hopping dominates, while if WM is a quarter of the activation energy Ea, the single polaron dominates the conduction mechanism (the values of Ea were extracted from the σdc fits with small polaron hopping (SPH) model (Fig. 7(b)). From the above-mentioned considerations, the maximum barrier height WM is approximately half of the activation energy, which indicates that the bipolaron hopping is the dominant conduction mechanism for this sample. This behavior indicates that the conduction process is dominated by the jumping mechanism and confirms the thermal activation of materials. It can be said that the annealing temperature of the Li–Zn ferrite sample largely influences the conduction mechanism. The change in the s value with respect to temperature is an indication of the thermally active polarization mechanism.
Fig. 7(a) illustrates the thermal variation of σdc, the magnitude of which for every single specimen goes up intensively and then slightly as temperature increases. The space between the curves becomes continuously larger up to 580 K, beyond which it becomes almost constant. This indicates that thermal activation in σdc is a typical trend for semiconductors.
The σdc of Zn500 is higher as compared with that of Zn1100, which is in agreement with many works. Some reports have stated that the σdc of ferrite compounds like the spinel structure runs inversely to the sintering temperature.8,15 Varying the latter from 500 °C to 1100 °C caused the σdc to be greatly restricted. At 490 K, it was decreased by one hundred S m−1, while it was reduced by one thousand S m−1 at 590 K. Such a strange large drop in magnitude refers to more grain boundaries with ultrafine grains within Zn1100.8,16 This implies that grains along with grain boundaries are very sensitive to the value of the annealing temperature. It does not oppose the common information that says the microstructure depends on the annealing temperature.65,66 In order to acquire information about the type of conduction mechanism present in this spinel ferrite, two hopping models were used to fit the experimental data of Fig. 7(a) at different temperatures. At high temperature, the small polaron hopping (SPH) model can be mathematically described by the following relation:67
where T0 is the characteristic temperature coefficient, being a measure of the degree of disorder, given by67
where ξ represents the decay length of the localized wave function (the value of ξ is equal to the cation–cation distance for the octahedral sites in Li0.5ZnFe1.5O4) and N(EF) is the density of the localized states at the Fermi level EF. The obtained T0 values from the best fit to the data (Fig. 7(c)) are 2 × 1010 K and 1.62 × 106 K, for Zn500 and Zn1100, respectively. In ferrite materials, these values can be used to calculate the density of the localized states at the Fermi level. The obtained T0 values suggest that the density of states at the Fermi level is lower in Zn500 samples (N(EF) = 1.6 × 1017 eV cm−3 for Zn500 and 2 × 1021 eV cm−3 for Zn1100 sample). This result can be explained by the presence of only one type of ferrite particle in the Zn500 sample, while the annealed sample at 1100 °C contained a mixture of substances.70 Using the value of T0, at a particular temperature T, the activation energy W is given by67
| W = 0.25kT3/4T01/4 |
Assuming the value of ξ to be equal to the cation–cation distance for the octahedral sites in Li–Zn ferrite, which is about 3 Å, and using the values of N(EF), the hopping range of polarons R is given by67
| R = ξ1/4/(8πkN(EF)T1/4 |
The calculated values of W at 350 K are 0.65 eV and 0.062 eV for the Zn500 and Zn1100 samples, respectively. The values of the hopping range of polarons R at 350 K for both the studied compounds were found to be 71 Å for sample Zn500 and 6.7 Å for sample Zn1100. Therefore, our results suggest that the conduction mechanism in our ferrite spinel is governed by the SPH model in the high-temperature region and by the VRH model in the low-temperature region (polaronic in nature).
In spite of being volatile, Zn ions were remarkably found to never escape from the spinel structure because annealing goes up to 1100 °C.3,15 Therefore, we conclude that on firing Li0.5ZnFe1.5O4 at 500 °C and even 1100 °C, the zinc content remains almost stoichiometric. Thus, the valence of Zn with Fe is governed by how many oxygen and lithium vacancies were created in the tested samples.
Annealing at 1100 °C certainly forces a finite fraction of lithium and oxygen to distill out of the surface of the pellet.5 The loss of oxygen enhances the release of electrons while the volatilization of zinc promotes the formation of holes. Since these two mechanisms function against each other, we ought to determine which one dominates under our annealing conditions. According to M. Amemiya et al.,7 the concentrations of created electrons and holes, due to firing lithium ferrite at 1100 °C and under an oxygen atmosphere, were almost equal. From this information, we believe that on annealing the tested specimens under similar conditions, the effects due to the volatilization of zinc and oxygen cancel each other. Due to the presence of nitrogen under atmospheric conditions, more electrons are present in the considered system and there is more evaporation of oxygen as compared to an environment containing oxygen only.
Assuming that the free carriers in this specimen are only electrons, σdc of Zn1100 is larger as compared to σdc of Zn500 because electrons are lighter than ions. Since this is not the case, our assumption is wrong and the dominant free carriers in Zn1100 are also ions. To recap, the electrical conductivities of both samples are absolutely ionic. Although Zn and O ions may participate in conduction, lithium with a relatively smaller weight is certainly the mobile ion. Nevertheless, we are incapable of judging whether it is a lithium vacancy and/or lithium interstitial.
The frequency-dependent and independent regions together are a signature of a relaxation phenomenon.
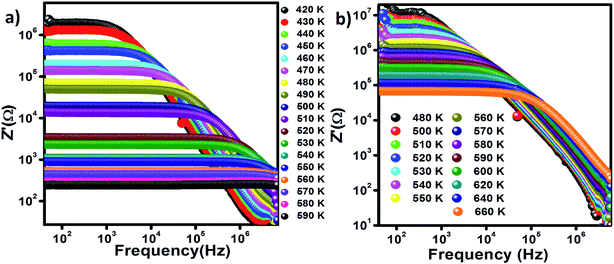
Grain boundaries and grains are essentially active through low and high-frequency ranges, respectively.72 The mismatch between the low-frequency Z′ of Zn500 and Zn1100 is great, whereas the difference between their high-frequency Z′ is small. We deduce that annealing temperature impacts more on grain boundaries than grains. We corroborate this idea from A. M. Kumar et al., who postulated that grain boundaries in spinels increase in concentration with annealing temperature.16
The magnitude of the low-frequency Z′ is great, which indicates that something is impeding carriers from moving easily at low frequencies where grain boundaries are active. When the free carriers reach those boundaries, they accumulate. However, the magnitude of the high-frequency Z′ is low, so we assumed that there were no such resistive obstacles that are capable of restricting carriers from moving over the high-frequency range where grain boundaries are supposed to be active. This implies that carriers no longer reach them by virtue of the short period.68,73 We, therefore, concluded that the space charge phenomenon occurs at low frequencies but not at high frequencies where carriers are unleashed from grain boundaries.74
The spectroscopic display of normalized Z′′, the imaginary component of impedance, for Zn500 and Zn1100 at variable temperatures is indicated in Fig. 9(a and b). It does not conflict with the common behavior of lithium matter with spinel structure.75 Both plots appear similar to each other in terms of shape. Z′′ at a given temperature has frequency up to a specific value termed relaxation frequency, beyond which it begins falling, forming a peak. That cut-off frequency shifts towards higher values as temperature increases. It increases relatively rapidly with temperature in Fig. 9(a).
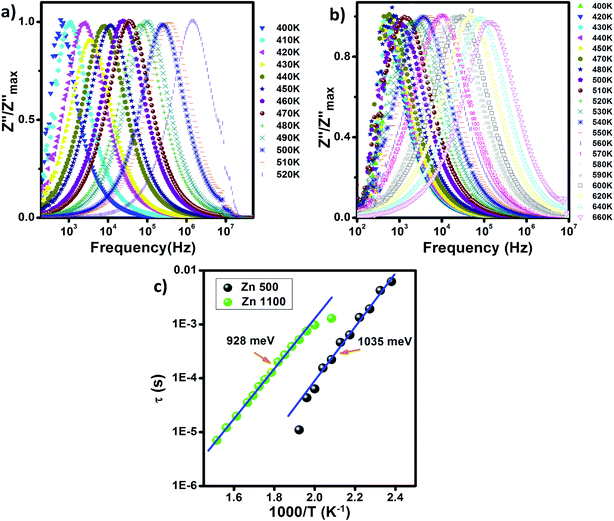 | ||
| Fig. 9 Frequency-dependence of normalized Z′′ (a) Zn500 and (b) Zn1100. (c) Arrhenius plots of relaxation time (τ) in the Zn500 and Zn1000 samples. | ||
The presence of only one peak indicates that only the single relaxation phenomenon is covered through the explored frequency scale. We associate this with grain boundaries being more active at low frequencies than grains.76 The lack of grain response may be explained either by the grains being conductive relative to grain boundaries, or that the measured frequency range is too limited to cover them.
The relaxation frequency reflects the degree of ease with which carriers move over matter, across which an alternating electric field is applied.77 We wanted to determine whether the cut off frequency is somehow proportional to mobility. The continuous rise in its value, as illustrated in Fig. 9(a and b), is an asymptote of mobility within Zn1100 and Zn500 (T < 520 K), which is thermally activated. Once carriers travel a path, they may collide with ions. When the temperature is sufficiently high, the ions will vibrate more and more around their equilibrium positions, resulting in more collisions, which could reduce the mobility. Since this is not the case, we concluded that the scattering phenomenon within Zn1100 and Zn500 (T < 520 K) is not significant.
An increase in the annealing temperature by 600 °C sharply restricts the relaxation frequency. For instance, at 520 K, it was approximately 1 MHz for Zn500, while being just 2 kHz for Zn1100, which means that it is harder for carriers within Zn1100 to move. This insight is one of the arguments explaining why the conductivity of Zn500 is relatively great as shown in Fig. 5.
Each peak in Fig. 9 is wide, which is an indication of the distribution of relaxation time.73 The period required for accomplishing hopping from one site to an equivalent site is not the same. The existence of no single relaxation time is due to multiple causes, for instance, dipole–dipole interactions78 and defects.
Since there are multiple relaxation times, the concept of just “relaxation time” does not make sense for the entire specimen. The most accurate concept is “mean relaxation time” denoted as τ. This value at a given temperature is deduced from the relaxation frequency.79 We plotted τ versus one thousand over temperature in Fig. 9(c), which increased linearly for both samples, implying that τ varies with temperature according to Arrhenius law:69
Temperature ranges, where τ of Zn500 and Zn1100 fit the Arrhenius model, do not overlap. Thus, it is not possible to compare the activation energies from Fig. 9(c). Also, the temperature scales, over which activation energies for conduction and relaxation phenomena in Zn500 were estimated, do not extend, and in turn, it is impossible to compare them with each other. In contrast, these distinct activation energies of Zn1100 were estimated over nearly the same temperature ranges. On the one hand, the conduction activation energy of 1366 meV for Zn500 is higher than its relaxation energy of 1035 meV, which agrees with M. Idrees's point.68 According to Idrees, the relaxation phenomena involve only hopping energy, whereas the conduction process requires disorder and binding energies in addition to hopping energy. On the other hand, the mismatch of approximately 331 meV is not negligible, implying that conduction and relaxation processes within Zn500 are due to the different types of carriers.
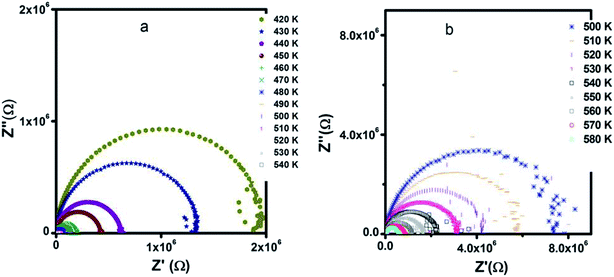
The Nyquist diagrams of Zn500 along with Zn1100 at selected temperatures are indicated in Fig. 10. They are typical for spinel.79 The patterns of curves at a fixed temperature are close. The data at a given temperature falls into a semicircle. That curve becomes smaller with increasing temperature.
Since reporters normally simulate the loop using a capacitor and resistor connected to each other in parallel, we suggest that the current specimens are simultaneously capacitive and resistive.
The presence of only one semicircle indicates that the single relaxation phenomenon occurs over the measured frequency range as deduced from Fig. 9.
The restriction in diameter refers to an increase in conductivity with temperature.73 Here, we reconsider the movement of carriers. An ion of tiny size is subject to the quantum mechanical rules; therefore, they can tunnel through, in addition to hopping over, barriers. The former mechanism depends predominantly on the width of barriers, but slightly on temperature. However, the hopping process is strongly temperature sensitive, as is resistance, as shown in Fig. 10. Therefore, carriers with high energy contribute to conductivity according to the hopping mechanism, rather than the tunneling process; this corroborates the above conductivity analysis.
Since the pattern remains unperturbed in spite of annealing at different temperatures (500 °C and 1100 °C), we inferred that increasing the annealing temperature by 600 °C does not influence the type of active regions. It is worth noting that annealing from 500 °C to 1100 °C neither creates further microstructure-like surface layers nor cancels out already existing regions such as grain boundaries. The loop with the center below the real axis is a little smooth, unlike a perfect semicircle; this reinforces the distribution of relaxation time.73
Finally, these results suggest that both LiZn2Fe3O8 samples (Zn500 and Zn1110) can be promising in the use of fuel cells (higher conductivity), microwave application and low temperature co-fired ceramics (LTCC) technology applications.
3.6 Optical characterization
It is known from past reports that the sizes and morphologies greatly affect the optical properties of semiconductor nanomaterials.80,81 Fig. 11(a) shows the room temperature UV-visible absorption spectra of the two annealed samples of LiZn2Fe3O8 in the range 450–1100 nm, in which the absorption edges were found to be in the visible region, illustrating its suitability for visible light photocatalysis and photovoltaic application. The strong absorption can generally be related to the electronic transition from the valence band to the conduction band (O2p Fe3d). In other words, a considerable amount of visible light was absorbed due to electron excitation from the O2p level (valence band) to the Fe3d level (conduction band).82 However, the band gap energies calculated by plotting the Tauc relation83 with photon energy hν (Fig. 11(b)) were found to be 1.41 and 1.36 eV for Zn500 and Zn1100, respectively. This indicates that the band gap decreases with the increase in particle size. The decrease in the band gap could be attributed to the basis of weak quantum confinement effects.84 A red shift for our samples was observed when compared to the pure bulk ZnFe2O4 (1.9 eV).85 This decrease in band gap may be attributed to the additional sub-band-gap energy levels that were induced by interface defects and the abundant surfaces in the agglomerated nanoparticles and to interfacial chemical conditions.84,85 Since these values of the bandgap energies are greater than the theoretical value of the energy needed for water splitting (λ > 1.23 eV),86 the lithium zinc ferrite samples are therefore suitable for the role of solar light photocatalysts.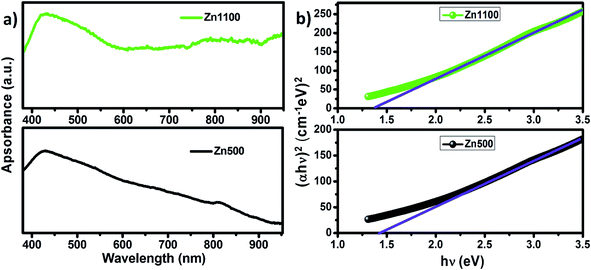 | ||
| Fig. 11 (a) UV-visible absorption spectra of Zn500 and Zn1100. (b) Band-gap determination for Zn500 and Zn1100. | ||
4. Conclusion
We prepared LiZn2Fe3O8 with the spinel structure using a sol–gel auto-combustion route with an annealing temperature of 500 °C and 1100 °C. From X-ray diffraction investigation, it was found that both samples crystallized in the cubic spinel structure with the space group (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The crystallite size increased and a micro-stress was induced when the annealing temperature was increased. Morphological observations confirmed the crystalline structure and showed that the grains were composed of several crystallites. FTIR and Raman spectroscopies affirmed the purity and the existing chemical bonds. They also allowed the extraction of the elastic parameters, which were found to increase with annealing temperature. In contrast, it was found that the band gap was reduced when the annealing temperature was increased. This behavior was attributed to the increase in the grain size.
m). The crystallite size increased and a micro-stress was induced when the annealing temperature was increased. Morphological observations confirmed the crystalline structure and showed that the grains were composed of several crystallites. FTIR and Raman spectroscopies affirmed the purity and the existing chemical bonds. They also allowed the extraction of the elastic parameters, which were found to increase with annealing temperature. In contrast, it was found that the band gap was reduced when the annealing temperature was increased. This behavior was attributed to the increase in the grain size.
The dc conductivity was found to be controlled by small polarons hopping at high temperatures and there was variable range hopping at lower temperatures; this was reduced when the annealing temperature was increased. Finally, ac conductivity followed the Jonscher or Drude model for the sample annealed at 500 °C and only varied according to the Jonscher model for the sample annealed at 1100 °C. This change is correlated to the effects of grains and grain boundaries.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Tunisian Ministry of Higher Education and Scientific Research.References
- F. A. Chyad, A. R. Jabur and S. A. Abed, Energy Procedia, 2017, 119, 52–60 CrossRef.
- D. Narsimulu, M. Venkateswarlu and N. Satyanarayana, AIP Conf. Proc., 2015, 1665, 1–3 Search PubMed.
- S. F. Mansour, F. Al-Hazmi and M. A. Abdo, J. Alloys Compd., 2019, 792, 626–637 CrossRef CAS.
- D. Venkatesh and K. V. Ramesh, Int. J. Mod. Phys. B, 2017, 31, 1–14 CrossRef.
- L. G. Van Uitert, J. Chem. Phys., 1955, 23, 1883–1887 CrossRef CAS.
- R. Manjula, V. R. K. Murthy and J. Sobhanadri, J. Appl. Phys., 1986, 59, 2929–2932 CrossRef CAS.
- M. Amemiya, J. Inorg. Nucl. Chem., 1972, 34, 3405–3417 CrossRef CAS.
- P. V. B. Reddy, B. Ramesh and C. G. Reddy, Phys. B, 2010, 405, 18520–21856 CrossRef.
- S. K. Gurav, S. E. Shirsath, R. H. Kadam, S. M. Patange, K. S. Lohar and D. R. Mane, Mater. Res. Bull., 2013, 48, 3530–3536 CrossRef CAS.
- M. I. Rosales, E. Amano, M. P. Cuautle and R. Valenzuela, Materials Science and Engineering: B, 1997, 49, 221–226 CrossRef.
- P. Sharma, P. Thakur, J. L. Mattei, P. Queffelec and A. Thakur, J. Magn. Magn. Mater., 2016, 407, 17–23 CrossRef CAS.
- M. Shoba and S. Kaleemulla, J. Phys. Chem. Solids, 2017, 111, 447–457 CrossRef CAS.
- S. F. Mansour, M. A. Abdo and F. L. Kzar, J. Magn. Magn. Mater., 2018, 465, 176–185 CrossRef CAS.
- M. Srivastava, R. K. Mishra, J. Singh, N. Srivastava, N. H. Kim and J. H. Lee, J. Alloys Compd., 2015, 645, 171–177 CrossRef CAS.
- D. R. Secrist and H. L. Turk, J. Am. Ceram. Soc., 1970, 53, 683–686 CrossRef CAS.
- A. M. Kumar, M. C. Varma, C. L. Dube, K. H. Rao and S. C. Kashyap, J. Magn. Magn. Mater., 2008, 320, 1995–2000 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- R. Lahouli, J. Massoudi, M. Smari, H. Rahmouni, K. Khirouni, E. Dhahri and L. Bessais, RSC Adv., 2019, 9, 19949–19964 RSC.
- S. M. Masoudpanah, S. A. Seyyed Ebrahimi, M. Derakhshani and S. M. Mirkazemi, J. Magn. Magn. Mater., 2014, 370, 122–126 CrossRef CAS.
- S. G. Gawas, S. S. Meena, P. Bhatt and V. M. S. Verenkar, Mater. Chem. Front., 2018, 2, 300 RSC.
- G. Datt, M. S. Bishwas, M. M. Raja and A. C. Abhyankar, Nanoscale, 2016, 8, 5200–5213 RSC.
- G. Kumar, R. K. Kotnala, J. Shah, V. Kumar, A. Kumar, P. Dhimana and M. Singhd, Phys. Chem. Chem. Phys., 2017, 19, 16669 RSC.
- N. Gonçalves, J. Carvalho, Z. Lima and J. Sasaki, Mater. Lett., 2012, 72, 36–38 CrossRef.
- E. R. Kumara, C. Srinivasb, M. S. Seehrac, M. Deeptyb, I. Pradeepe, A. S. Kamzin, M. V. K. Meharg and N. K. Mohanh, Sens. Actuators, A, 2018, 279, 10–16 CrossRef.
- B. K. Chatterjee, K. Bhattacharjee, A. Dey, C. K. Ghosh and K. K. Chattopadhyay, Dalton Trans., 2014, 43, 7930 RSC.
- S. K. Gore, R. S. Mane, M. Naushad, S. S. Jadhav, M. K. Zate, Z. A. Alothmanc and B. K. N. Hui, Dalton Trans., 2015, 44, 6384 RSC.
- K. K. Bamzai, G. Kour, B. Kaur, M. Arora and R. P. Pant, J. Magn. Magn. Mater., 2013, 345, 255–260 CrossRef CAS.
- A. Nairan, M. Khan, U. Khan, M. Iqbal, S. Riaz and S. Naseem, Nanomaterials, 2016, 6, 73 CrossRef PubMed.
- K. B. Modi, S. J. Shah, N. B. Pujara, T. K. Pathak, N. H. Vasoya and I. G. Jhala, J. Mol. Struct., 2013, 1049, 250–262 CrossRef CAS.
- R. D. Waldron, Phys. Rev., 1955, 99, 1727–1735 CrossRef CAS.
- R. S. Yadav, J. Havlica, J. Masilko, L. Kalina, J. Wasserbauer, M. Hajdúchová, V. Enev, I. Kuřitka and Z. Kožáková, J. Magn. Magn. Mater., 2015, 394, 439–447 CrossRef.
- N. Bouhadouza, A. Rais, S. Kaoua, M. Moreau, K. Taibi and A. Addou, Ceram. Int., 2015, 41, 11687–11692 CrossRef CAS.
- K. A. Mohammed, A. D. Al-Rawas, A. M. Gismelseed, A. Sellai, H. M. Widatallah, A. Yousif, M. E. Elzain and M. Shongwe, Phys. B, 2012, 407, 795–804 CrossRef CAS.
- S. S. Bhatu, V. K. Lakhani, A. R. Tanna, N. H. Vasoya, J. U. Buch, P. U. Sharma, U. N. Trivedi, H. H. Joshi and K. B. Modi, Indian J. Pure Appl. Phys., 2007, 45, 596–608 CAS.
- K. B. Modi, P. Y. Raval, S. J. Shah, C. R. Kathad, S. l. V. Dulera, M. V. Popat, K. B. Zankat, K. G. Saija, T. K. Pathak, N. H. Vasoya, V. K. Lakhani, U. Chandra and P. K. Jha, Inorg. Chem., 2015, 54, 1543–1555 CrossRef CAS PubMed.
- K. B. Modi, M. K. Rangolia, M. C. Chhantbar and H. H. Joshi, J. Mater. Sci., 2006, 41, 7308–7318 CrossRef CAS.
- K. B. Modi, M. C. Chhantbar and H. H. Joshi, Ceram. Int., 2006, 32, 111–114 CrossRef CAS.
- M. B. Mohamed and A. M. Wahba, Ceram. Int., 2014, 40, 11773–11780 CrossRef CAS.
- D. Ravinder and P. K. Raju, Phys. Status Solidi A, 1993, 136, 351 CrossRef CAS.
- S. S. Desaia, S. M. Patangeb, A. D. Patilc, S. K. Gored and S. S. Jadhav, J. Alloys Compd., 2019, 133, 171–177 Search PubMed.
- R. A. Pawar, S. S. Desai, S. M. Patange, S. S. Jadhav and K. M. Jadhav, Phys. B, 2017, 510, 74–79 CrossRef CAS.
- T. R. Tatarchuk, N. D. Paliychuk, M. Bououdina, B. Al-Najar, M. Pacia, W. Macyk and A. Shyichuk, J. Alloys Compd., 2018, 731, 1256–1266 CrossRef CAS.
- A. V. Anupama, V. Rathod, V. M. Jali and B. Sahoo, J. Alloys Compd., 2017, 728, 1091–1100 CrossRef CAS.
- A. Bhaskar and S. R. Murthy, J. Magn. Magn. Mater., 2014, 355, 100–103 CrossRef CAS.
- K. B. Modi, S. J. Shah, T. K. Pathak, N. H. Vasoya, V. K. Lakhani and A. K. Yahya, AIP Conf. Proc., 2014, 1591, 1115–1117 CrossRef CAS.
- K. B. Modi, S. V. Dulera, N. H. Vasoya, P. Y. Raval, P. R. Pansara, K. G. Saija and K. M. Jadhav, AIP Conf. Proc., 2016, 1728, 20655 CrossRef.
- S. A. Mazen, S. F. Mansour, E. Dhahri, H. M. Zaki and T. A. Elmosalami, J. Alloys Compd., 2009, 470, 294 CrossRef CAS.
- Physics Acoustics, ed. O. L. Anderson and W. P. Mason, Academic Press, New York, 1965, vol. 3B, pp. 43–95 Search PubMed.
- V. D'Ippolito, G. B. Andreozzi, D. Bersani and P. P. Lottici, J. Raman Spectrosc., 2015, 46, 1255–1264 CrossRef.
- M. Virumbrales-del Olmo, A. Delgado-Cabello, A. Andrada-Chacón, J. Sánchez-Benítez, E. Urones-Garrote, V. Blanco-Gutiérrez, M. J. Torralvo and R. Sáez-Puchea, Phys. Chem. Chem. Phys., 2017, 19, 8363–8372 RSC.
- Y. Wang, L. Li, Y. Zhang, X. Chen, S. Fang and G. Li, J. Phys. Chem. C, 2017, 12135, 19467–19477 CrossRef.
- H. Rahmouni, B. Cherif, M. Smari, E. Dhahri, N. Moutia and K. Khirouni, Phys. B, 2015, 473, 1–6 CrossRef CAS.
- M. A. Dar, K. M. Batoo, V. Verma, W. A. Siddiqui and R. K. Kotnala, J. Alloys Compd., 2010, 493, 553–560 CrossRef CAS.
- R. W. Christy, Am. J. Phys., 1960, 28, 457–461 CrossRef CAS.
- E. V. Gopalan, K. A. Malini, S. Saravanan, D. S. Kumar, Y. Yoshida and M. R. Anantharaman, J. Phys. D: Appl. Phys., 2008, 41, 1–9 Search PubMed.
- A. Dutta, C. Bharti and T. P. Sinha, Indian J. Eng. Mater. Sci., 2008, 181–186 CAS.
- A. A. Dakhel, Solid-State Electron., 2005, 49, 1996–2001 CrossRef CAS.
- B. Keskin, A. Altindal, U. Avciata and A. Gul, Bull. Mater. Sci., 2014, 37, 461–468 CrossRef CAS.
- H. Trabelsi, M. Bejar, E. Dhahri, M. P. F. Graça, M. A. Valente and K. Khirouni, Phys. E, 2018, 99, 75–81 CrossRef CAS.
- B. Swiatek-Tran, H. A. Kołodziej, A. Vogt and V. H. Tran, RSC Adv., 2015, 5, 9539 RSC.
- R. K. Panda, R. Muduli, S. K. Kar and D. Behera, J. Alloys Compd., 2014, 615, 899–905 CrossRef CAS.
- E. V. Gopalan, K. A. Malini, S. Sagar, D. S. Kumar, Y. Yoshida, I. A. Al-Omari and M. R. Anantharaman, J. Phys. D: Appl. Phys., 2009, 42, 165005 CrossRef.
- Y. Ben Taher, A. Oueslati, N. K. Maaloul, K. Khirouni and M. Gargouri, Appl. Phys. A, 2015, 120, 1537–1543 CrossRef CAS.
- K. H. Mahmoud, F. M. Abdel-Rahim, K. Atef and Y. B. Saddeek, Curr. Appl. Phys., 2011, 11, 55–60 CrossRef.
- G. Zang, J. Zhang, P. Zheng, J. Wang and C. Wang, J. Phys. D: Appl. Phys., 2005, 38, 1824–1827 CrossRef CAS.
- D. Ravinder, Mater. Lett., 1999, 40, 205–208 CrossRef CAS.
- N. F. Mott and E. A. Davis, Electronic Process in Non-crystalline Materials, Clarendon Press, Oxford, 1979 Search PubMed.
- M. Idrees, M. Nadeem, M. Atif, M. Siddique, M. Mehmood and M. M. Hassan, Acta Mater., 2011, 59, 1338–1345 CrossRef CAS.
- S. B. Amor, A. Benali, M. Bejar, E. Dhahri, K. Khirouni, M. A. Valente, M. P. F. Graça, F. Al-Turjman, J. Rodriguez and A. Radwan, J. Mol. Struct., 2019, 1184, 298–304 CrossRef CAS.
- H. Rahmouni, A. Benali, B. Cherif, E. Dhahri, M. Boukhobza, K. Khirouni and M. Sajieddine, Phys. B, 2015, 466–467, 31–37 CrossRef CAS.
- M. B. Hossen and A. K. M. A. Hossain, J. Adv. Ceram., 2015, 4, 217–225 CrossRef CAS.
- R. P. Pawar and V. Puri, Ceram. Int., 2014, 40, 10423–10430 CrossRef CAS.
- R. Ranjan, R. Kumar, N. Kumar, B. Behera and R. N. P. Choudhary, J. Alloys Compd., 2011, 509, 6388–6394 CrossRef CAS.
- G. R. Gajula, L. R. Buddiga and N. Vattikunta, Mater. Chem. Phys., 2019, 230, 331–336 CrossRef CAS.
- M. Shah, M. Nadeem and M. Atif, J. Appl. Phys., 2012, 112, 1–8 CrossRef.
- A. Shukla and R. N. P. Choudhary, Curr. Appl. Phys., 2011, 11, 414–422 CrossRef.
- A. Dutta, C. Bharti and T. P. Sinha, Phys. B, 2008, 403, 3389–3393 CrossRef CAS.
- C. E. Ciomaga, M. T. Buscaglia, V. Buscaglia and L. Mitoseriu, J. Appl. Phys., 2011, 110, 1–7 CrossRef.
- G. R. Gajula, L. R. Buddiga, K. N. Chidambara Kumar, C. Arun Kumar and M. Dasari, Journal of Science: Advanced Materials and Devices, 2018, 3, 230–235 Search PubMed.
- X. Bai, J. Wei, B. Tian, Y. Liu, T. Reiss, N. Guiblin, P. Gemeiner, B. Dkhil and I. C. Infante, J. Phys. Chem. C, 2016, 120, 3595–3601 CrossRef CAS.
- A. Lassoued, B. Dkhil, A. Gadria and S. Ammara, Results Phys., 2017, 7, 3007–3015 CrossRef.
- R. Sharma, S. Bansal and S. Singhal, RSC Adv., 2015, 5, 6006 RSC.
- X. Li, Y. Hou, Q. Zhao and L. Wang, J. Colloid Interface Sci., 2011, 358, 102–108 CrossRef CAS PubMed.
- N. Kislov, S. S. Srinivasan, Y. Emirov and E. K. Stefanakos, Materials Science and Engineering: B, 2008, 153, 70–773 CrossRef CAS.
- A. Manikandan, J. J. Vijaya, M. Sundararajan, C. Meganathan, L. J. Kennedy and M. Bououdina, Superlattices Microstruct., 2013, 118–131 CrossRef CAS.
- K. N. Harish, H. S. B. Naik, P. N. P. Kumar and R. Viswanath, Catal. Sci. Technol., 2012, 2, 1033–1039 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Relations and formulae used to calculate various structural and elastic parameters, representative fitted conductivity curve to Jonscher's model. See DOI: 10.1039/c9ra07569k |
| This journal is © The Royal Society of Chemistry 2019 |