Open Access Article
Open Access ArticleNoncentrosymmetric tellurite halides created by a depolymerization strategy: toward strong SHG intensity and wide bandgap†
Dan-Dan
Zhou
abc,
Chun-Li
Hu
ab,
Xin-Wei
Zhang
ac,
Jiang-Gao
Mao
 abc and
Fang
Kong
abc and
Fang
Kong
 *abc
*abc
aState Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, 350002, P. R. China. E-mail: kongfang@fjirsm.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing, 100049, P. R. China
cFujian College, University of Chinese Academy of Sciences, Fuzhou, 350002, P. R. China
First published on 5th November 2024
Abstract
The design and synthesis of nonlinear optical (NLO) materials with a strong second harmonic generation (SHG) effect and wide band gap is a long-standing challenge because of their inverse relationship, especially for metal tellurites. We found that a lower degree of polymerization of tellurite groups corresponds to a higher proportion of non-centrosymmetric (NCS) structures formed. Based on Pauling's rule #4, introduction of cations (Al3+/Ga3+) with higher coordination numbers and lower valence states than Te4+ into the reaction system decreases the connectivity among tellurite groups. By regulating the reaction conditions, CS Ga(Te3O7)Br and NCS M2(OH)(TeO3)(Te2O5)X (M = Al, Ga; X = Br, Cl) were successfully synthesized, which represent the first examples of Ga/Al-tellurite-Cl/Br. The NCS compounds have presented strong SHG intensities (4.0–9.8 × KDP) and wide bandgaps (3.89–4.35 eV). And M2(OH)(TeO3)(Te2O5)X (M = Ga, Al; X = Br, Cl) are the only examples of metal tellurites with band gap exceeding 4.0 eV and SHG intensity exceeding 4 × KDP. This work provides an effective strategy for the design and synthesis of tellurite-based NLO materials with a strong SHG effect and wide bandgap.
Introduction
Metal oxides, which contain stereo-chemically active lone pair (SCALP) electrons, such as iodates, selenites, and tellurites, have garnered significant attention in the field of optoelectronics.1–5 This interest is primarily due to their strong second harmonic generation (SHG) intensity, broad transparency range, tunable coordination modes, and favorable crystal growth habit.6–9 The SHG materials with potential applications need to satisfy the conditions of a large SHG coefficient, wide band gap, moderate birefringence, and high laser induced damage threshold (LIDT).10–16 However, it is challenging to meet these conditions simultaneously because of the inverse relationship among some of the parameters, represented by band gap and SHG effect.17,18 Therefore, it is still an urgent need in the academic community to obtain new nonlinear optical (NLO) crystals with strong SHG intensity and wide bandgap.19Compared with selenite and iodate groups, tellurites are more prone to form polymerized anions,20,21 such as zero-dimensional (0D) clusters,22 1D chains,23 2D layers24 and 3D structures,25 which are beneficial to enrich the structural system of metal oxides. However, these abundant polymeric forms are not beneficial to the generation of excellent NLO effects in tellurite systems and may even play an inhibitory role. Taking tellurite structures reported in the past decade as an example, among the 375 compounds, 110 had a degree of polymerization of tellurite groups greater than or equal to 3 (Fig. 1). Among the 110 trimeric or higher degree of polymerization tellurite compounds, 15% exhibit the non-centrosymmetric (NCS) structure. In contrast, among the 265 dimeric or isolated tellurite compounds, the proportion of NCS structures reaches as high as 28%, which is approximately twice the rate observed in the former. Therefore, the feasible design strategy to reduce the degree of polymerization of tellurite is a key step to promote the formation of the NCS structure.
 | ||
| Fig. 1 The polymerization status and percentage of centrosymmetric (CS) and NCS of tellurite compounds reported in the past decade. | ||
According to Pauling's rule #4, the central cations with high valency and small coordination numbers tend not to share polyhedron elements with one another.26,27 So, Ga3+/Al3+ with low valency and high coordination number (compared with Te4+) can be introduced to separate the tellurite groups. More importantly, the introduction of Ga3+/Al3+ without d–d transition is beneficial to enhance the band gap of compounds (compared with a d0-transition metal). For instance, our group has successfully synthesized α- and β-Ba2[GaF4(IO3)2](IO3)28 (4.61 and 4.35 eV) through aliovalent substitution of α- and β-Ba2[VO2F2(IO3)2](IO3)29 (2.59 and 2.55 eV), the band gap of which is greatly improved. In addition, halogen ions with completely different coordination modes from oxygen ions can also be introduced to block the extension of the lone pair containing groups.30–32
Based on the above considerations, we focused our attention on the Ga/Al-tellurite-Cl/Br system which is an unknown frontier to be developed. By adjusting the reaction conditions and regulating the ratio of reactants Ga2O3/Al2O3 and TeO2, six new tellurite halides, namely, Ga(Te3O7)Br (1), Ga2(OH)(TeO3)(Te2O5)Br (2), Ga2(OH)(TeO3)(Te2O5)Br0.5Cl0.5 (3), Ga2(OH)(TeO3)(Te2O5)Cl (4), Al2(OH)(TeO3)(Te2O5)Br (5) and Al2(OH)(TeO3)(Te2O5)Cl (6) were successfully synthesized. It is worth noting that compounds 2–6 can exhibit strong SHG intensities (4.0–9.8 × KDP) and wide bandgaps (3.89–4.35 eV), which represent the first examples of tellurite chlorides/bromides with SHG intensity larger than 4.0 × KDP and bandgap higher than 3.70 eV (Tables S1 and S2†). Herein, we report their syntheses, structures and optical properties.
Results and discussion
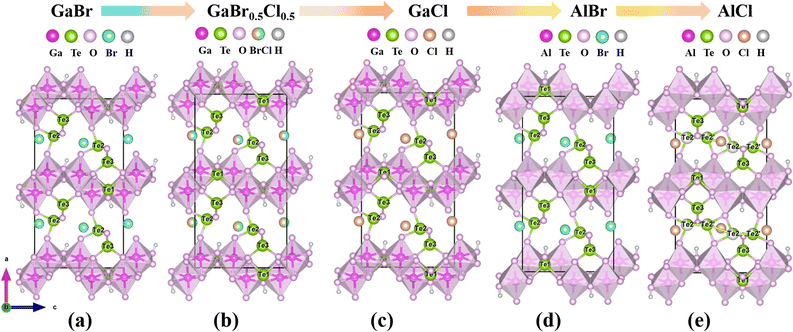
These compounds feature the first examples of gallium/aluminum tellurite chlorides/bromides. All the compounds were synthesized by using a mild hydrothermal method (S1, Fig. S1†). Their pure phases were also obtained successfully except compound 5 (Fig. S2†). Their scanning electron microscopy (SEM) images and elemental distribution maps are shown in Fig. S3.† The crystal structures were determined by single-crystal X-ray diffraction (Table 1). Compound 1 crystallizes in the CS space group P21/c (No. 14), isostructural with Fe(Te3O7)Br.33 Its layered structure is composed of 1D [Te3O8]4− chains bridged by [Ga2O8]10− dimers with Br− anions isolated between the interlayers (Fig. 2a–c). The [Te3O8]4− polyanion was formed by the interconnection of Te(1)O3, Te(2)O4 and Te(3)O3 groups (Fig. S4†). To decrease the polymerization degree of tellurite groups in Ga(Te3O7)Br (1), the nGa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nTe was increased from 1
nTe was increased from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 2
3 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. A new structure, M2(OH)(TeO3)(Te2O5)X (M = Ga, Al; X = Br, Cl), was obtained successfully. The largest polymerization degree of tellurite groups is 2 in this structure. As we expected, these compounds crystallize in an NCS space group (Pca21, No. 29).
3. A new structure, M2(OH)(TeO3)(Te2O5)X (M = Ga, Al; X = Br, Cl), was obtained successfully. The largest polymerization degree of tellurite groups is 2 in this structure. As we expected, these compounds crystallize in an NCS space group (Pca21, No. 29).
| Molecular formula | Ga(Te3O7)Br (1) | Ga2(OH)(TeO3) (Te2O5)Br (2) | Ga2(OH)(TeO3)(Te2O5)Br0.5Cl0.5 (3) | Ga2(OH)(TeO3) (Te2O5)Cl (4) | Al2(OH)(TeO3) (Te2O5)Br (5) | Al2(OH)(TeO3) (Te2O5)Cl (6) |
|---|---|---|---|---|---|---|
| a R 1 = ∑‖Fo| − |Fc‖/∑|Fo|, wR2 = {∑w[(Fo)2 − (Fc)2]2/∑w[(Fo)2]2}1/2. | ||||||
| Formula weight | 644.43 | 746.15 | 723.92 | 701.69 | 660.67 | 616.22 |
| Space group | P21/c | Pca21 | Pca21 | Pca21 | Pca21 | Pca21 |
| F(000) | 1112.0 | 1300.0 | 1264.0 | 1228.0 | 1151.5 | 1080.9 |
| a (Å) | 10.8789(15) | 16.0138(4) | 15.8664(14) | 15.7196(12) | 15.7796(5) | 15.5617(14) |
| b (Å) | 7.2613(8) | 7.0036(2) | 6.9672(6) | 6.9503(7) | 6.8824(2) | 6.8243(7) |
| c (Å) | 10.8143(13) | 8.4023(2) | 8.3796(7) | 8.3540(8) | 8.2042(2) | 8.1594(8) |
| α (deg) | 90 | 90 | 90 | 90 | 90 | 90 |
| β (deg) | 108.529(13) | 90 | 90 | 90 | 90 | 90 |
| γ (deg) | 90 | 90 | 90 | 90 | 90 | 90 |
| V (Å−3) | 809.99(18) | 942.35(4) | 926.32(14) | 912.72(14) | 890.99(4) | 866.51(15) |
| Z | 4 | 4 | 4 | 4 | 4 | 4 |
| D c (g cm−3) | 5.285 | 5.259 | 5.191 | 5.106 | 4.925 | 4.724 |
| Flack | — | 0.033(14) | 0.01(5) | 0.02(2) | 0.017(12) | 0.02(5) |
| GOF on F2 | 1.030 | 1.111 | 1.065 | 1.198 | 1.064 | 0.972 |
| R 1, wR2[I > 2σ(I)]a | 0.0267, 0.0448 | 0.0247, 0.0583 | 0.0273, 0.0612 | 0.0273, 0.0654 | 0.0214, 0.0517 | 0.0293, 0.0920 |
| R 1, wR2 (all data)a | 0.0378, 0.0497 | 0.0254, 0.0586 | 0.0283, 0.0622 | 0.0281, 0.0658 | 0.0217, 0.0519 | 0.0326, 0.0957 |
Owing to the isostructural nature of compounds 2–6, the structure of 2 is chosen as a representative example. Its asymmetric unit is composed of 2 Ga, 3 Te, 1 Br and 9 O atoms, all of which are located in the general site. The Ga(1) and Ga(2) atoms are six-coordinated with oxygen atoms to form an octahedral geometry, which is different from the GaO5 polyhedron in compound 1 (Fig. S5†). The Ga–O bond lengths are in the range of 1.865(9)–2.096(9) and 1.905(9)–2.027(8) Å for Ga(1)O6 and Ga(2)O6 octahedra respectively. The Ga(1)O6 and Ga(2)O6 octahedra were interconnected into a Ga2O10 dimer by edge-sharing, which were condensed together via O⋯O edges to a 1D gallium oxide wavy chain along the c direction (Fig. 2d). The three Te atoms are in the TeO3 triangular pyramids with Te–O bond lengths in the range of 1.828(8)–1.977(8) Å. Te(1)O3 is isolated while Te(2)O3 and Te(3)O3 are corner-shared into a [Te2O5]2− dimer. The gallium wavy chains are bridged by Te(1)O3 groups into 2D layers parallel to the bc plane, which are further linked via Te2O5 dimers into a 3D cationic framework with Ga3Te3 six-member polyhedral ring (MPR) tunnels along the b-axis (Fig. 2e and f). The isolated halide anions are located in the 6-MPR tunnels to balance the charge. The bond valences for Te and Ga were calculated to be 3.685–3.896 and 3.129–3.141, suggesting their oxidation states of +4 and +3 respectively (Table S3†).
The relationship between compounds 2–6 is shown in Fig. 3. The differences among the five isostructural compounds primarily stem from M(III) cations and halide anions. From compounds 2 to 6, the cations are transferred from Ga3+ to Al3+ with a smaller radius. In the structure of the same metal, halide anions transition from Br to Cl with a smaller radius. Additionally, the Te(2) atoms in compound 6 are disordered. Combined with Table 1 we can find that the unit cell parameters are decreased gradually as the atomic number decreases from Ga to Al and from Br to Cl. From compound 2 to 6, the axial lengths of a, b, and c decreased by 2.8%, 2.6% and 2.9% respectively, and the volume decreased by 8.0%. The changes for the distortion degree (Δd) of the octahedral groups in compounds 2–6 were also studied.34 From Fig. 4 we can find that the distortion degrees of M(1)O6 (M = Ga, Al) are decreasing gradually from 0.357 to 0.279, while those of M(2)O6 octahedra are almost increasing from 0.241 to 0.288 (Table S4†). Interestingly, there has been little change in the average distortion degrees of M(1)O6 and M(2)O6 for compounds 2–6. These results show that the distortion degree of GaO6 and AlO6 groups are comparable to those of the tetravalent d0 transition metal, such as Ti4+ and Zr4+, but the III A main group metals avoid the d–d transition, which can effectively widen the band gap of the target compounds.35
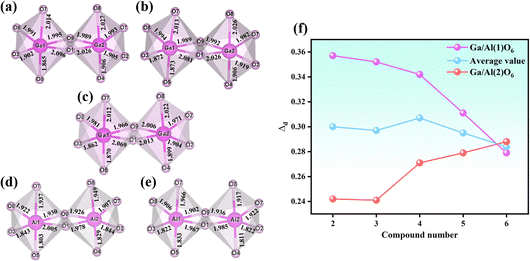 | ||
| Fig. 4 Diagram of the coordination environment of 2 (a), 3 (b), 4 (c), 5 (d), and 6 (e). The comparative diagram of the GaO6/AlO6 octahedral distortion degree in the five compounds (f). | ||
Since compounds 2–6 crystallize in polar space groups, it is necessary to find out which anionic groups contribute the most. From Table S5,† we can find that the local dipole moments of TeO3 in compounds 2–6 are in the range of 9.986–13.072 D (D = Debye), which is considerable to the reported values in the literature.36,37 Compared with the TeO3 group, the dipole moments for MO6 (M = Ga, Al) octahedra are much weaker. Similar to the situation for the distortion degree, the dipole moments of Ga(1)O6 are larger than those of Ga(2)O6. Differently, the dipole moments of AlO6 are obviously larger than those of GaO6 octahedra. Due to the symmetry of the structures, the X and Y components of the net dipole moments for compounds 2–6 are cancelled out. The Z components of Te(1)O3 and Te(3)O3, M(1)O6 and M(2)O6 (M = Ga, Al) have been cancelled out mostly. So, the net dipole moments of the unit cell are mainly derived from Te(2)O3 groups. These results can also be obtained from the structures of the compounds. Fig. S6† shows the arrangements of Te(1)O3, Te(2)O3 and Te(3)O3 groups in compound 2. The green arrows represent the polarization direction of the triangular pyramids. It can be seen that the polarization directions for pairs of Te(1)O3 are almost completely opposite, and the same applies to Te(3)O3 pairs. Only Te(2)O3 groups exhibit net polarization along the c direction (represented by yellow arrows).
Thermogravimetric analysis was conducted to assess the thermal stability of the compounds under a nitrogen atmosphere, with temperatures ranging from 20 to 1200 °C. As can be seen from Fig. S7,† compound 1 is stable before 460 °C. Loss of weight ends around 1100 °C, corresponding to the release of bromine and TeO2. Although compounds 2, 3, 4 and 6 contain hydroxyl groups, they still have good stability and are stable before 420 °C. The weight loss curves of these samples demonstrated analogous characteristics, commencing at 420 °C and culminating around 1100 °C. This range corresponds to the loss of hydroxyl, halogens, and TeO2. The infrared spectra were measured within 4000–400 cm−1 (Fig. S8†). In particular, the bands in the region of 605–781 cm−1 can be ascribed to the stretching and bending vibrations of Te–O bonds. The peaks at 410–556 cm−1 and 404–535 cm−1 can be ascribed to the stretching vibration peak of Ga–O and Al–O, respectively. These assignments align with the findings previously documented in the literature.38–40 Meanwhile, the bands ranging from 3448 to 3470 cm−1 were attributed to the stretching vibration of O–H bonds in compounds 2, 3, 4, and 6. Overall, the infrared transmission range of these samples is approximately 3.0–5.1 μm, considering the difference in the infrared cut-off measurement between powder samples and large crystals.
The UV-vis-NIR diffuse reflectance spectra for the five compounds were tested within the wavelength range of 200–2000 nm. The UV cut-off wavelengths for the compounds were 291 nm (1), 289 nm (2), 280 nm (3), 271 nm (4), and 261 nm (6), respectively (Fig. S9†). And these materials are almost completely transparent within the range of 0.5–2.0 μm. The optical diffuse reflectance spectral data were fitted with careful consideration of the Urbach tail effect.41 Utilizing the energy band data above the Urbach tail, the data were fitted to both indirect and direct band gap functions. As illustrated in Fig. S10a,†1 exhibits an Urbach energy of 0.10 eV, and its linearity in the direct band gap fitting within the range of 3.88–4.02 eV is superior to its linearity in the indirect band gap fitting. Consequently, we conclude that 1 is a direct band gap compound with a band gap value of 3.80 eV. For 2, it has an Urbach energy of 0.10 eV, and its linearity in the direct band gap fitting within the range of 3.92–4.11 eV is also better than its linearity in the indirect band gap fitting. Therefore, 2 is similarly identified as a direct band gap compound with a band gap value of 3.89 eV. Following the same methodology, we fitted 3, 4, and 6. The fitting results indicate that all three compounds are more consistent with direct band gap characteristics, with band gap values of 4.03 eV, 4.25 eV, and 4.35 eV, respectively. Accordingly, their band gaps show a gradually increasing trend, reaching 4.35 eV. It is worth noting that although metal tellurites have been well studied, metal tellurites with SHG intensity stronger than 3 × KDP and band gap larger than 3.70 eV are still very rare (Table S1†).42–44
Large band gaps are advantageous for enhancing the laser-induced damage threshold (LIDT). We calculated the LIDT of compounds 2, 3, 4, and 6 using the reported powder method. The measured powder LIDT values of these compounds were 37.8, 48.2, 28.3 and 44.3 MW cm−2, respectively, which are 9.5, 12.1, 7.1 and 11.1 times higher than those of AGS (4 MW cm−2) under the same irradiation conditions.
The SHG signals of compounds 2–6 and KDP samples, with particle sizes ranging from 150 to 210 μm, were measured under 1064 nm laser radiation, based on the NCS space group of compounds 2–6. The results showed that the polar compounds can exhibit strong NLO response, with SHG intensities of 9.8 × KDP (2), 7.9 × KDP (3), 5.9 × KDP (4), and 4.0 × KDP (6) respectively (Fig. 5). The SHG intensities of all four compounds exhibited the same trend, increasing with the increase of particle size, indicating that compounds 2, 3, 4 and 6 can realize phase matching. It is interesting that the SHG intensities of compounds 2 to 6 exhibit an arithmetic progression with a tolerance of 2 × KDP. The SHG intensity difference between Ga2(OH)(TeO3)(Te2O5)Br (2) and Ga2(OH)(TeO3)(Te2O5)Cl (4) is twice that of Ga2(OH)(TeO3)(Te2O5)Cl (4) and Al2(OH)(TeO3)(Te2O5)Cl (6). It is thus clear that the influence of halogens on the SHG intensity is much larger than that of III A metals. In addition, the experimental SHG coefficient deff(exp) value of compounds 2, 3, 4, and 6 can be estimated through eqn (1).45
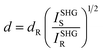 | (1) |
 | ||
| Fig. 5 SHG intensity (a) and phase-matching curves (b) for 2, 3, 4, and 6; the comparison diagram of SHG intensity and band gap of compounds 2, 3, 4, and 6 (c). | ||
I SHGS and ISHGR are SHG counts from the sample and reference, respectively. Using dR = 0.39 pm V−1 for KDP, the deff(exp) of compounds 2, 3, 4, and 6 were determined to be 1.22 pm V−1, 1.10 pm V−1, 0.95 pm V−1, and 0.78 pm V−1 respectively.
To investigate the electronic structure and optical properties of 1, 2, 4, and 6, theoretical calculations were conducted utilizing density functional theory (DFT).46 Fig. S11† presents the band structures of 1, 2, 4, and 6 at high symmetry points within the first Brillouin zone. From Table S6† we can find that the highest valence band (H-VB) and lowest conduction band (L-CB) for 2, 4, and 6 are located at different K-points (X and G for H-VB and L-CB). These compounds are classified as indirect bandgap compounds, with calculated band gaps of 2.80 eV, 2.94 eV and 3.12 eV respectively, which contradicts the results of optical diffuse reflectance spectral data. A similar phenomenon was also observed in the literature, such as Li4CdSn2S7.16 For compound 1, both H-VB and L-CB are located at point B, so Ga(Te3O7)Br (1) is a direct bandgap structure with a calculated band gap of 2.73 eV. It is important to note that the band gap values derived from the GGA-PBE function generally fall below the experimental results due to its inherent limitations.47–49
The birefringence (Δn) of compounds 2, 4, and 6 was measured using a ZEISS Axio Scope A1 polarizing microscope at λ = 546 nm. The optical path differences (R) for compounds 2, 4, and 6 with thicknesses (T) of 25.82 μm, 33.54 μm, and 36.37 μm were 1.937 μm, 1.851 μm, and 2.192 μm, respectively. According to the formula R = Δn × T, the experimental birefringence of compounds 2, 4, and 6 at 546 nm was determined to be 0.075, 0.055, and 0.060, respectively.
Fig. 6 illustrates the total and partial density of states (DOS) for 1, 2, 4 and 6, all of which exhibit similar characteristics. Te-5s5p exhibited a distinct overlap with the O-2s2p electronic state, indicative of a strong Te–O bonding interaction. The CB bottom of 1, 2, 4, and 6 was dominated by empty Te-5p orbitals, while the VB top of 1 and 2 was dominated by O-2p and Br-4p nonbonding orbitals, and the VB top of 4 and 6 was dominated by O-2p and Cl-3p nonbonding orbitals. Therefore, the band gaps of 1 and 2 were mainly determined by Te, O and Br atoms, while the band gaps of 4 and 6 were mainly determined by Te, O and Cl atoms.
Isostructural compounds serve as an ideal model for examining the SHG effect and its origins. According to the space group and Kleinman symmetry, 2, 4, and 6 have three independent SHG-tensors, namely d31 (=d15), d32 (=d24), and d33, respectively, among which d32 is the largest. The computed absolute values of d32 in the static limit were 3.74 pm V−1, 2.45 pm V−1, and 1.87 pm V−1 for 2, 4 and 6. Based on the SHG tensors, the theoretical effective SHG coefficient deff is found to be 2.45 pm V−1, 1.45 pm V−1, and 1.11 pm V−1 for 2, 4 and 6, which are larger than the estimated deff(exp) value (1.22 pm V−1, 0.95 pm V−1, and 0.78 pm V−1). The discrepancy can be attributed to the inferior crystal quality of the tested powder compared to the ideal crystal assumed in theoretical calculations. In addition, their distributions of SHG effects were calculated by the SHG-weighed electron density. As illustrated in Fig. 7, the SHG effects of VB in 2 were predominantly derived from O-2p and Br-4p nonbonding orbitals, whereas those in the VB of 4 and 6 stemmed from O-2p and Cl-3p nonbonding orbitals primarily. In CB, the SHG effects for all three compounds were chiefly derived from Te-5p orbitals, supplemented by a minor contribution from O-2p orbitals.
 | ||
| Fig. 7 SHG density of d32 in the valence band (a), (c), (e) and conduction band (b), (d), (f) of 2, 4, and 6, respectively. | ||
Based on the overall SHG density of VB and CB, the contribution of each building block in 2, 4 and 6 was calculated. For compound 2, the contribution percentage of the [Ga2O9(OH)]13− dimer, [TeO3]2− group, and Br− anion to SHG effects are 16.3%, 51.1%, and 32.2% respectively. For compound 4, the contribution percentages are 18.9%, 56.2%, and 24.5% respectively for [Ga2O9(OH)]13−, [TeO3]2− and Cl−. For compound 6, the contributions of [Al2O9(OH)]13−, [TeO3]2− and isolated Cl− were calculated to be 16.8%, 57.9%, and 25.0% respectively. So, the strong SHG responses of the polar compounds can be attributed to the synergistic effect of GaO6/AlO6 octahedra, [TeO3] groups and halogens ions. It can also be found that TeO3 groups have played a major role (51.1–57.9%), while the contribution of the octahedral group remains relatively stable (16.3–18.9%) in each compound, and the contribution of Br− (32.2%) is significantly greater than that of Cl− (24.5–25.0%). Therefore, introducing polarizable halogen ions into lone pair systems is an effective method to create new compounds with a strong NLO effect.
Conclusions
In summary, the first examples of gallium/aluminum tellurite chlorides/bromides have been successfully synthesized by a mild hydrothermal method. Ga(Te3O7)Br (1) crystalized in the CS space group. When the Ga/Te ratio was increased to 2/3, polar compounds Ga2(OH)(TeO3)(Te2O5)Br (2), Ga2(OH)(TeO3)(Te2O5)Br0.5Cl0.5 (3), Ga2(OH)(TeO3)(Te2O5)Cl (4), Al2(OH)(TeO3)(Te2O5)Br (5), and Al2(OH)(TeO3)(Te2O5)Cl (6) were obtained. Their SHG intensities and bandgaps were measured to be 4.0–9.8 × KDP and 3.89–4.35 eV respectively, which represent the first examples of tellurite chlorides/bromides with strong SHG intensity and wide bandgap. Although they are isostructural compounds, their SHG intensities decreased gradually from compounds 2, 3, 4 to 6, and the optical bandgaps show the exact opposite trend. Theoretical calculations further confirmed this result. And the TeO3 groups account for over 50% of the SHG contribution, with halogen ions being the next largest contributors, and the contribution from the Ga/Al dimers being the least significant. This work demonstrates the effectiveness of the depolymerization strategy in the design and synthesis of tellurite-based NLO materials with a strong SHG effect and a wide bandgap.Data availability
The data that support the findings of this study are available in the ESI† of this article.Author contributions
Dan-Dan Zhou: investigation, formal analysis, writing – original draft. Chun-Li Hu: theoretical calculations. Xin-Wei Zhang: investigation, formal analysis. Jiang-Gao Mao: supervision, resources, funding acquisition. Fang Kong: conceptualization, project administration, writing – review & editing. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 22475215, 22031009, 22375201 and 21921001), the NSF of Fujian Province (Grant No. 2024J010039, 2023J01216) and the Self-deployment Project Research Program of Haixi Institutes, Chinese Academy of Sciences (CXZX-2022-GH06). We would like to express our gratitude to Prof. Jian-Han Zhang from Sanming College for his invaluable assistance with the band gap fitting of UV-vis-NIR spectra. We also extend our thanks to Dr Bing-Xuan Li and Mr Ming-Zhi Zhang from the Fujian Institute of Research on the Structure of Matter, for their significant contributions to the laser-induced damage threshold test and birefringence test.Notes and references
- Y. J. Jia, Y. G. Chen, Y. Guo, X. F. Guan, C. B. Li, B. X. Li, M. M. Liu and X. M. Zhang, Angew. Chem., Int. Ed., 2019, 58, 17194–17198 CrossRef PubMed
.
- L. Xiong, L. M. Wu and L. Chen, Angew. Chem., Int. Ed., 2021, 60, 25063–25067 CrossRef
.
- S. X. Yang, H. P. Wu, Z. G. Hu, J. Y. Wang, Y. C. Wu and H. W. Yu, Small, 2023, 20, 2306459 CrossRef PubMed
.
- F. G. You, F. Liang, Q. Huang, Z. G. Hu, Y. C. Wu and Z. S. Lin, J. Am. Chem. Soc., 2018, 141, 748–752 CrossRef
.
- J. J. Zhou, H. P. Wu, H. W. Yu, S. T. Jiang, Z. G. Hu, J. Y. Wang, Y. C. Wu and P. S. Halasyamani, J. Am. Chem. Soc., 2020, 142, 4616–4620 CrossRef
.
- J. Chen, C. L. Hu, F. Kong and J. G. Mao, Acc. Chem. Res., 2021, 54, 2775–2783 CrossRef CAS
.
- X. H. Dong, H. B. Huang, L. Huang, Y. Q. Zhou, B. B. Zhang, H. M. Zeng, Z. E. Lin and G. H. Zou, Angew. Chem., Int. Ed., 2024, 63, e202318976 CrossRef CAS PubMed
.
- G. Peng, C. S. Lin, H. X. Fan, K. C. Chen, B. X. Li, G. Zhang and N. Ye, Angew. Chem., Int. Ed., 2021, 60, 17415–17418 CrossRef CAS PubMed
.
- P. F. Li, C. L. Hu, J. G. Mao and F. Kong, Chem. Sci., 2024, 15, 7104–7110 RSC
.
- L. Kang, M. L. Zhou, J. Y. Yao, Z. S. Lin, Y. C. Wu and C. T. Chen, J. Am. Chem. Soc., 2015, 137, 13049–13059 CrossRef CAS PubMed
.
- Y. W. Kang and Q. Wu, Coord. Chem. Rev., 2024, 498, 215458 CrossRef CAS
.
- M. Mutailipu, J. Han, Z. Li, F. M. Li, J. J. Li, F. F. Zhang, X. F. Long, Z. H. Yang and S. L. Pan, Nat. Photonics, 2023, 17, 694–701 CrossRef CAS
.
- Y. Y. Yang, Y. Xiao, B. X. Li, Y. G. Chen, P. H. Guo, B. B. Zhang and X. M. Zhang, J. Am. Chem. Soc., 2023, 145, 22577–22583 CrossRef CAS PubMed
.
- W. B. Zhang, X. L. Hou, S. J. Han and S. L. Pan, Coord. Chem. Rev., 2024, 505, 215664 CrossRef CAS
.
- J. H. Zhang, D. J. Clark, J. A. Brant, K. A. Rosmus, P. Grima, J. W. Lekse, J. I. Jang and J. A. Aitken, Chem. Mater., 2020, 32, 8947–8955 CrossRef CAS
.
- J. H. Zhang, S. S. Stoyko, A. J. Craig, P. Grima, J. W. Kotchey, J. I. Jang and J. A. Aitken, Chem. Mater., 2020, 32, 10045–10054 CrossRef CAS
.
- Y. L. Hu, C. Wu, X. X. Jiang, Z. J. Wang, Z. P. Huang, Z. S. Lin, X. F. Long, M. G. Humphrey and C. Zhang, J. Am. Chem. Soc., 2021, 143, 12455–12459 CrossRef CAS PubMed
.
- P. F. Li, C. L. Hu, B. X. Li, J. G. Mao and F. Kong, Inorg. Chem., 2024, 63, 4011–4016 CrossRef CAS PubMed
.
- Y. P. Song, H. W. Yu, B. X. Li, X. Q. Li, Y. Zhou, Y. Q. Li, C. He, G. Zhang, J. H. Luo and S. G. Zhao, Adv. Funct. Mater., 2024, 34, 2310407 CrossRef CAS
.
- L. Lin, X. Jiang, C. Wu, Z. Lin, Z. Huang, M. G. Humphrey and C. Zhang, Chem. Mater., 2021, 33, 5555–5562 CrossRef CAS
.
- P. F. Li, C. L. Hu, J. G. Mao and F. Kong, Coord. Chem. Rev., 2024, 517, 216000 CrossRef CAS
.
- T. Sivakumar, H. Y. Chang, J. Baek and P. S. Halasyamani, Chem. Mater., 2007, 19, 4710–4715 CrossRef CAS
.
- T. Wang, Y. G. Chen, Y. Guo, F. Wang, Q. Song, Y. J. Jia and X. M. Zhang, Dalton Trans., 2020, 49, 4914–4919 RSC
.
- H. Y. Li and K. H. Lii, Dalton Trans., 2021, 50, 8189–8195 RSC
.
- B. Zhang, J. H. Wu, C. L. Hu, Y. F. Li, F. Kong and J. G. Mao, Inorg. Chem. Front., 2023, 10, 1328–1337 RSC
.
- J. George, D. Waroquiers, D. Di Stefano, G. Petretto, G. M. Rignanese and G. Hautier, Angew. Chem., Int. Ed., 2020, 59, 7569–7575 CrossRef CAS
.
- P. F. Li, C. L. Hu, Y. F. Li, J. G. Mao and F. Kong, J. Am. Chem. Soc., 2024, 146, 7868–7874 CrossRef CAS
.
- J. Chen, C. L. Hu, F. F. Mao, J. H. Feng and J. G. Mao, Angew. Chem., Int. Ed., 2019, 58, 2098–2102 CrossRef CAS
.
- H. W. Yu, M. L. Nisbet and K. R. Poeppelmeier, J. Am. Chem. Soc., 2018, 140, 8868–8876 CrossRef CAS PubMed
.
- M. Yan, C. L. Hu, R. L. Tang, W. D. Yao, W. L. Liu and S. P. Guo, Chem. Sci., 2024, 15, 8500–8505 RSC
.
- G. H. Zou, C. S. Lin, H. Jo, G. Nam, T. S. You and K. M. Ok, Angew. Chem., Int. Ed., 2016, 55, 12078–12082 CrossRef CAS
.
- H. T. Qiu, F. M. Li, Z. Li, Z. H. Yang, S. L. Pan and M. Mutailipu, J. Am. Chem. Soc., 2023, 145, 24401–24407 CrossRef CAS
.
- D. Zhang, R. K. Kremer, P. Lemmens, K. Y. Choi, J. Liu, M. H. Whangbo, H. Berger, Y. Skourski and M. Johnsson, Inorg. Chem., 2011, 50, 12877–12885 CrossRef CAS PubMed
.
- P. S. Halasyamani, Chem. Mater., 2004, 16, 3586–3592 CrossRef CAS
.
- Z. Y. Bai and K. M. Ok, Coord. Chem. Rev., 2023, 490, 215212 CrossRef CAS
.
- J. J. Zhang, Z. H. Zhang, W. G. Zhang, Q. X. Zheng, Y. X. Sun, C. Q. Zhang and X. T. Tao, Chem. Mater., 2011, 23, 3752–3761 CrossRef CAS
.
- D. W. Lee, D. B. Bak, S. B. Kim, J. Kim and K. M. Ok, Inorg. Chem., 2012, 51, 7844–7850 CrossRef CAS PubMed
.
- P. F. Li, F. Kong and J. G. Mao, J. Solid State Chem., 2020, 286, 121288 CrossRef CAS
.
- S.
W. Bae, J. Yoo, S. Lee, K. Y. Choi and K. M. Ok, Inorg. Chem., 2016, 55, 1347–1353 CrossRef CAS
.
- Y. H. She, J. M. Jiao, Z. Wang, J. Chai, S. Jie, N. Ye, Z. G. Hu, Y. C. Wu and C. G. Li, Inorg. Chem. Front., 2023, 10, 6557–6565 RSC
.
- J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi, 1966, 15, 627 CrossRef CAS
.
- K. C. Chen, C. S. Lin, G. Peng, Y. Chen, H. Z. Huang, E. Z. Chen, Y. X. Min, T. Yan, M. Luo and N. Ye, Chem. Mater., 2022, 34, 399–404 CrossRef CAS
.
- Q. Wang, X. H. Dong, L. Huang, K. M. Ok, Z. E. Lin and G. H. Zou, Small, 2023, 19, 2302797 CrossRef CAS PubMed
.
- Q. Wu, J. F. Zhou, X. M. Liu, X. X. Jiang, Q. X. Zhang, Z. S. Lin and M. J. Xia, Inorg. Chem., 2021, 60, 18512–18520 CrossRef CAS PubMed
.
- S. K. KURTZ and T. T. PERRY, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS
.
- H. P. Wu, Z. J. Wei, Z. G. Hu, J. Y. Wang, Y. C. Wu and H. W. Yu, Angew. Chem., Int. Ed., 2024, 63, e202406318 CrossRef CAS PubMed
.
- Z. Y. Bai, J. Lee, H. Kim, Y. Kuk, M. H. Choi, C. L. Hu and K. M. Ok, Small, 2023, 19, 2207709 CrossRef CAS
.
- F. Xu, X. Xu, B. X. Li, G. Zhang, C. Zheng, J. D. Chen and N. Ye, Inorg. Chem. Front., 2024, 11, 2105–2115 RSC
.
- P. F. Li, C. L. Hu, J. G. Mao and F. Kong, Laser Photonics Rev., 2024, 2401488, DOI:10.1002/lpor.202401488
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section, computational method, important bond distances and bond valences, calculated distortion degree, PXRD patterns, elemental analysis, TGA curves, IR spectrum, UV-visible-NIR diffuse reflectance spectrum, and band structures. CCDC 2380471–2380476. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc06403h |
| This journal is © The Royal Society of Chemistry 2024 |